Optimal Solution to the Two-Stage Hybrid Flow Shop Scheduling Problem with Removal and Transportation Times

Abstract

The two-stage hybrid flow shop scheduling problem with removal and transportation times is addressed in this paper. The maximum completion time is the objective function to be minimized. This scheduling problem is modeling real-life situations encountered in manufacturing and industrial areas. On the other hand, the studied problem is a challenging one from a theoretical point of view since it is NP-Hard in a strong sense. In addition, the problem is symmetric in the following sense. Scheduling from the second stage to the first provides the same optimal solution as the studied problem. This propriety allows extending all the proposed procedures to the symmetric problem in order to improve the quality of the obtained solution. Based on the existing literature and to the best of our knowledge, this study is the first one addressing the removal time and the transportation time in the hybrid flow shop environment simultaneously. In order to solve the studied problem optimally, a heuristic composed of two phases is proposed, and a new family of lower bounds is developed. In addition, an exact Branch and Bound algorithm is presented to solve the hard test problems. These hard instances are unsolved by the proposed heuristic. In order to evaluate the performance of the proposed procedures, an extensive experimental study is carried out over benchmark test problems with a size of up to 200 jobs. The obtained computational results provide strong evidence that the presented procedures are very effective since 90% of test problems are solved optimally within a moderate time of 47.44 s. Furthermore, the unsolved test problems present a relative gap of only 2.4%.

1. Introduction

The Hybrid Flow Shop (HFS) is composed of serial production stages, where each stage contains a set of identical and parallel machines. At least one of the stages contains more than one machine to be considered an HFS. The machines are intended to process a set of jobs consecutively from the first stage to the last one in that order. This is the flow side of the HFS. Each machine in each stage is able to process at most one job at the same time, and a given job is processed by only one machine in each stage. The HFS is a generalization of other interesting shops, including the single machine, the parallel machine and the flow shop. The scheduling problem in an HFS environment is a very interesting scheduling problem encountered in several real-life situations, especially in manufacturing processes such as the electronic ships industry [1], the cable industry [2], and the textile industry [3]. On the other hand, the HFS scheduling problem and several of its variants are shown to be NP-Hard in the strong sense, which constitutes a theoretical challenge. The HFS scheduling problem is extensively studied, and abundant literature is provided [4,5,6,7]. Solving the HFS scheduling problems optimally or approximately is the topic of extensive studies where several algorithms are proposed. These algorithms are the heuristics, metaheuristics and exact procedures. In this context, the reader is referred to [4,5] for more details on the HFS scheduling problems.

Modeling real-life situations accurately over the HFS scheduling problem requires taking into consideration the parameters (restrictions) with high impact as much as possible, including the job release times, setup times, machine unavailability, etc. Taking into consideration these restrictions (release date, setup times, etc.) according to the real situation allows for narrowing the gap between the theory and the practical aspects. In this context, authors in [8] studied an HFS scheduling problem with setup times and proposed a genetic algorithm to solve it efficiently and approximately. The setup time parameter is encountered in an industrial area, where machines require a time duration for their preparation to process jobs. In this case, the setup time is not neglected compared to the processing times. An HFS scheduling problem with lag times and sequence-dependent setup times was addressed in [9]. In order to solve the latter problem approximately, an immune algorithm was proposed and evaluated over an intensive experimental study. In [10], an HFS scheduling problem with multiprocessor tasks was addressed. In this kind of real-life scheduling problem, a job requires more than a machine to be processed. For the latter problem, an efficient genetic algorithm was proposed. An HFS scheduling problem with transportation times was examined in [11]. The transportation time parameter is required in several real-life applications. Indeed, this situation is encountered where the transportation time between the stages is comparable to the processing times and, therefore, cannot be neglected. The latter problem was solved using a Simulated Annealing metaheuristic.

The removal time for a job is the required time to remove a finished processed job from a machine. Removal time is among the encountered real-life parameters (restrictions) in the manufacturing and industrial areas. In these cases, the removal time is comparable to the processing time and cannot be neglected. Thus the removal time is taken into consideration separately from the processing time. This situation occurs, for example, in the steel industry where a produced part is extracted from a mold during a removal time that is more important than the processing time itself. In addition, the removal time restriction is encountered in the bio-process industry, where fermentation techniques are utilized [12]. In some HFS scheduling problems, the transportation time between stages is neglected compared to the processing time. This occurs when the stages are close to each other [13]. In other real-world situations, the transportation time of a job is an important factor and cannot be neglected.

In this study, the two-stage HFS scheduling problem with removal and transportation times between the stages is examined. In this problem, two serial stages with identical parallel machines for each one are used to process a set of jobs. Each job is processed in a machine from the first stage, removed, and transported to the second stage. A machine in the latter stage processes the job, and the processed job is then removed. The makespan (maximum completion time) is the objective function to be minimized.

After exploring much of the presented literature for the HFS problem, to the best of our knowledge, there is no study taking into consideration the removal times and the transportation time simultaneously for an HFS scheduling problem to date. Consequently, the related work literature review will be restricted to HFS scheduling problems with transportation times or removal times.

In this context, the authors of [14] studied the HFS problem with transportation time, sequence setup time and rework. An efficient Enhanced Harmony Search Algorithm was proposed to solve the studied problem. The HFS problem with dynamic transportation waiting time is examined in [15], where a memetic algorithm is proposed to provide a near-optimal solution. An HFS problem with transportation time and setup time is addressed in [16]. In order to solve the latter problem, an effective electromagnetism metaheuristic is presented. In [11], an HFS problem with transportation and setup times is examined with respective objective functions of the total tardiness and total completion time. A simulated annealing metaheuristic is proposed to tackle this problem. The HFS problem with robotic transportation time and release dates is studied in [17]. The makespan is minimized, and an ant colony optimization algorithm, as well as a genetic algorithms, are proposed. The two-stage HFS problem with transportation restrictions is treated in [18]. In the latter problem, the second stage is composed of two identical and parallel machines, while the first stage contains only one machine. The transportation between stages is ensured by a transporter with a capacity of one, and an efficient heuristic algorithm is proposed to determine a near-optimal solution. In [19], an HFS problem with transportation time and batching restrictions is considered, and a polynomial time heuristic is proposed for a particular case. For the general case, a pseudo-polynomial algorithm is presented. In [20], an HFS problem with robots’ transportation and blocking restrictions is considered. An efficient simulated annealing metaheuristic is proposed for the makespan minimization. An extensive experimental study provides strong evidence of the effectiveness and efficiency of the proposed procedure. The two-stage HFS problem with robots’ transportation between stages is addressed in [21]. Two dedicated machines are contained in the first stage, while the second stage has only one machine. A complexity study of the considered problem, as well as some of its particular cases, is performed. For the NP-hard ones, two efficient heuristics are developed.

In [22], an HFS problem with setup and removal times is addressed. Four heuristic algorithms are proposed and assessed over an intensive experimental study, which shows their efficiency. An HFS problem with removal time and precedence constraints is addressed in [23]. In the latter research work, the authors proposed six heuristic algorithms, which are shown to be efficient in a computational study. The authors of [24] examined an HFS problem with setup and removal times. The parallel machines in each stage are unrelated. In order to approximately solve the latter studied problem, a heuristic algorithm is proposed to provide an initial solution. This initial solution is then improved over the application of a simulated annealing metaheuristic. An intensive experimental study shows the efficiency of the proposed algorithm. A real-world HFS scheduling problem with removal time and other restrictions is considered in [12]. An exact algorithm based on a mixed-integer formulation is proposed. This formulation is enriched by new inequalities, and the computational results provide strong evidence that the proposed algorithm is efficient for industrial instances (small size test problems).

According to the existing literature, the HFS scheduling problem with transportation and removal times has not been addressed; thus, the open gap lies in studying this kind of problem and trying to provide efficient procedures to solve it.

In this work, firstly, the studied problem is formally defined, and a set of its interesting properties is established. These properties concern the complexity and the symmetry of the studied problem. Secondly, a new family of lower bounds is proposed. These lower bounds are of two categories. The first category is based on the optimal solution to the parallel machine scheduling problem with release dates and delivery times. The second category is based on the idle machine times. Thirdly, a new two-phase heuristic is proposed. The first phase builds an initial solution and the second phase improves it. The optimal solution to the parallel machine scheduling problem with release dates and delivery times is used in the latter heuristic. Finally, an exact Branch and Bound algorithm is developed. This procedure includes efficient lower bounds and dominance rules, allowing to reduce the size of the search tree. An extensive experimental study is carried out to evaluate the performance and the efficiency of the proposed procedures.

The parallel machine scheduling problem with release dates and delivery times plays a key role in the development of the proposed procedures. For further insight into the latter problem, the readers are referred to [25,26,27,28,29].

The contributions of this study are scientific and practical. These contributions are:

• To the best of our knowledge, this is the first time the hybrid flowshop scheduling problem with transportation and removal times is addressed.
• Proposal of new interesting and useful proprieties for the studied problem, allowing the improvement of the solution.
• Development of a new set of efficient lower bounds.
• Proposal of a heuristic algorithm that is able to provide the optimal solution or near-optimal solution within an acceptable computational time.
• Presentation of Branch and Bound exact procedure able to optimally solve hard test problems within an acceptable computational time.
• Allowing to model real-world manufacturing systems, where the removal and transportation times are not neglected as in the steel industry.

The rest of this paper is organized as follows. The studied scheduling problem is formally defined in Section 2, in addition to the presentation of some of its interesting properties. A family of tight and new lower bounds is the topic of Section 3. In Section 4, a heuristic algorithm, which is composed of two phases, is proposed. The details of an exact Branch and Bound algorithm are presented in Section 5. In order to evaluate the performance of the proposed algorithms, an intensive experimental study is carried out in Section 6. Finally, a conclusion summarizing the main findings and presenting the possible extensions of this work is presented.

2. Problem Statement and Proprieties

This section is intended to define the studied problem and the presentation of some of its relevant proprieties.

2.1. Problem Statement

The two-stage hybrid flow shop scheduling problem with removal and transportation times is stated as follows. A set $J=\left\{1,...,n\right\}$ of n jobs has to be processed in a production shop composed of two serial stages $S_1$ and $S_2$. Each stage $S_i$$\left(i=1,2\right)$ contains a set $M_{i,1},\dots ,M_{i,m_i}$ of $m_i$ identical parallel machines such that $n>max\left(m_1,m_2\right)$. Each job $j\in J$ is first processed in an available machine from $S_1$ during $p_{1,j}$. After that, the job is removed from this machine during $r{m}_{1,j}$. Once removed, the job $j\in J$ is transported to a buffer belonging to the second stage $S_2$ during $t_j$. In stage $S_2$, an available machine treats the job j during $p_{2,j}$. The removal of job j from this machine takes $r{m}_{2,j}$ units of time. The completed processed job remains in the machine until it is removed and released. The buffer’s capacity is too large to store all the jobs. All the machines and jobs are available for processing from time zero. The processing times $p_{i,j}$, the removal times $r{m}_{i,j}$, and the transportation times $t_j$ are assumed to be positive integers and deterministic $\left(i=1,2\mathrm{and}j\in J\right)$. Each machine processes at most one job at the same time, and the preemption is not allowed. Each job $j\in J$ is processed by only one machine in each stage. The main purpose is to determine a feasible schedule ${\sigma }^{*}$ that minimizes the maximum completion time (makespan). More precisely, for a feasible schedule $\sigma$ if $s_{i,j}\left(\sigma \right)$ is the starting time of job j in stage $S_i$ then $c_{i,j}\left(\sigma \right)=s_{i,j}\left(\sigma \right)+p_{i,j}+r{m}_{i,j}$ is its completion time. It is worth mentioning that $s_{i,j}\left(\sigma \right)+p_{i,j}$ is the completion processing time of job j in stage $S_i$, and at the same time, it is the earliest date to start the removal operation. Since, the machine will not be available until the job j is removed, the removal operation should start as soon as possible (at $s_{i,j}\left(\sigma \right)+p_{i,j}$). Therefore, the makespan, which is denoted $C_{max}$, is given by the expression: $C_{max}\left(\sigma \right)={\displaystyle \underset{j\in J}{max}}{c}_{2,j}\left(\sigma \right)$. In this case, the optimal makespan $C_{max}^{*}$ and the requested optimal schedule ${\sigma }^{*}$ satisfy: $C_{max}^{*}=C_{max}\left({\sigma }^{*}\right)={\displaystyle \underset{\sigma \in \Delta }{min}}{C}_{max}\left(\sigma \right)$ with $\Delta$ as the set of feasible schedules.

Using the three-field notation $\alpha \left|\beta \right|\gamma$ [30], the studied scheduling problem is denoted $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$. In the latter notation, $F2$ refers to a flow shop with two stages and $P_{m_1},P_{m_2}$ are indicating that each stage contains parallel machines. The jobs characteristics’ $r{m}_{i,j}$ and $t_j$ are the removal and the transportation times. The last and third field is reserved for the objective function to be minimized, which is the maximum completion time (makespan) in this study. In the following is a summary of the latter notations.

• $n:$ number of jobs.
• $m_1:$ number of machines in the first stage $S_1$.
• $m_2:$ number of machines in the second stage $S_2$.
• $p_{i,j}:$ processing time of job j in stage $S_i$ $(1\le j\le n$, $1\le i\le 2)$.
• $r{m}_{i,j}:$ removal time of job j in stage $S_i$ $(1\le j\le n$, $1\le i\le 2)$.
• $t_j:$ transportation time of job j $(1\le j\le n)$.
• $s_{i,j}\left(\sigma \right):$ starting time of job j in stage $S_i$ $(1\le j\le n$, $1\le i\le 2)$ relatively to schedule $\sigma$.
• $c_{i,j}\left(\sigma \right):$ completion time of job j in stage $S_i$ $(1\le j\le n$, $1\le i\le 2)$ relatively to schedule $\sigma$.
• $C_{max}\left(\sigma \right):$ makespan of schedule $\sigma$.
• $C_{max}^{*}:$ optimal makespan.

To illustrate the studied problem, the following example is presented.

Example 1.

Consider the instance with $n=5$, and $m_1=m_2=2$. The processing times $p_{i,j}$ and the transportation times $t_j$ ($i=1,2$ and $j\in J$) are presented in

Table 1. Data of Example 1.

j	1	2	3	4	5
$p_{1,j}$	1	2	1	2	2
$r{m}_{1,j}$	1	1	2	1	2
$t_j$	2	1	1	1	2
$p_{2,j}$	2	1	1	2	1
$r{m}_{2,j}$	1	1	1	1	1

.

Figure 1 presents a feasible schedule for the addressed scheduling problem, relative to the data provided in Table 1.

In Figure 1, job 4 is not removed from machine $M_{1,2}$ immediately after finishing processing (at time 5). Instead of that, the beginning of the removal operation is postponed until time 7. Therefore, the release of job 4 from machine $M_{1,2}$ is performed at time 8. Then the removal time is not a part of the processing time for job 4. In addition, within time interval $[5,7]$, job 4 remains in machine $M_{1,2}$ and blocks it, i.e., no other job is processed within this time interval. The period $[5,7]$ is a waiting period for removing job 4.

2.2. Proprieties

In this section, two relevant results are presented, where the first one is about the complexity of the current problem. The second result concerns the introduction of another problem called the “symmetric” or “reverse” or “backward” problem relative to the studied problem. These two problems have the same optimal solution, which suggests the systematic investigation of both of them in order to improve the obtained results.

2.2.1. Complexity

In addition to its practical interest, the two-stage hybrid flow shop scheduling problem is a challenging one from a theoretical point of view. This is due to the following lemma (Lemma 1).

Lemma 1.

The problem $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ is strongly NP-Hard.

Proof. 

The two-stage hybrid flow shop problem $\left(F_2\left(P_{m_1},P_{m_2}\right)\left|\right|C_{max}\right)$ is strongly NP-Hard [31]. Since, $F_2\left(P_{m_1},P_{m_2}\right)\left|\right|C_{max}$ is a particular case of $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$$\left(r{m}_{i,j}=t_j=0\right)$, then $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ is strongly NP-Hard. □

2.2.2. Symmetry

Definition 1.

Naturally, $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ has a reverse problem, which is obtained by inverting the flow of the jobs from stage $S_2$ toward stage $S_1$. Formally, the reverse problem is obtained by setting up: First stage $S_1^R=S_2$, second stage $S_2^R=S_1$, the processing, removal, and transportation times $p_{1,j}^R=r{m}_{2,j}$, $r{m}_{1,j}^R=p_{2,j}$, $p_{2,j}^R=r{m}_{1,j}$, $r{m}_{2,j}^R=p_{1,j}$, $t_j^R$ $=t_j$, $M_{1,k}^R=M_{2,k}$ $\left(1\le k\le m_2\right)$, and $M_{2,k}^R=M_{1,k}$ $\left(1\le k\le m_1\right)$. The studied problem ($S_1$ to $S_2$) is the forward problem and the reverse problem ($S_2$ to $S_1$) is the backward problem. The reverse problem is denoted $F_2\left(P_{m_2},P_{m_1}\right)\left|r{m}_{1,j}^R,t_j\right|C_{max}$ and defined as the symmetric of $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$.

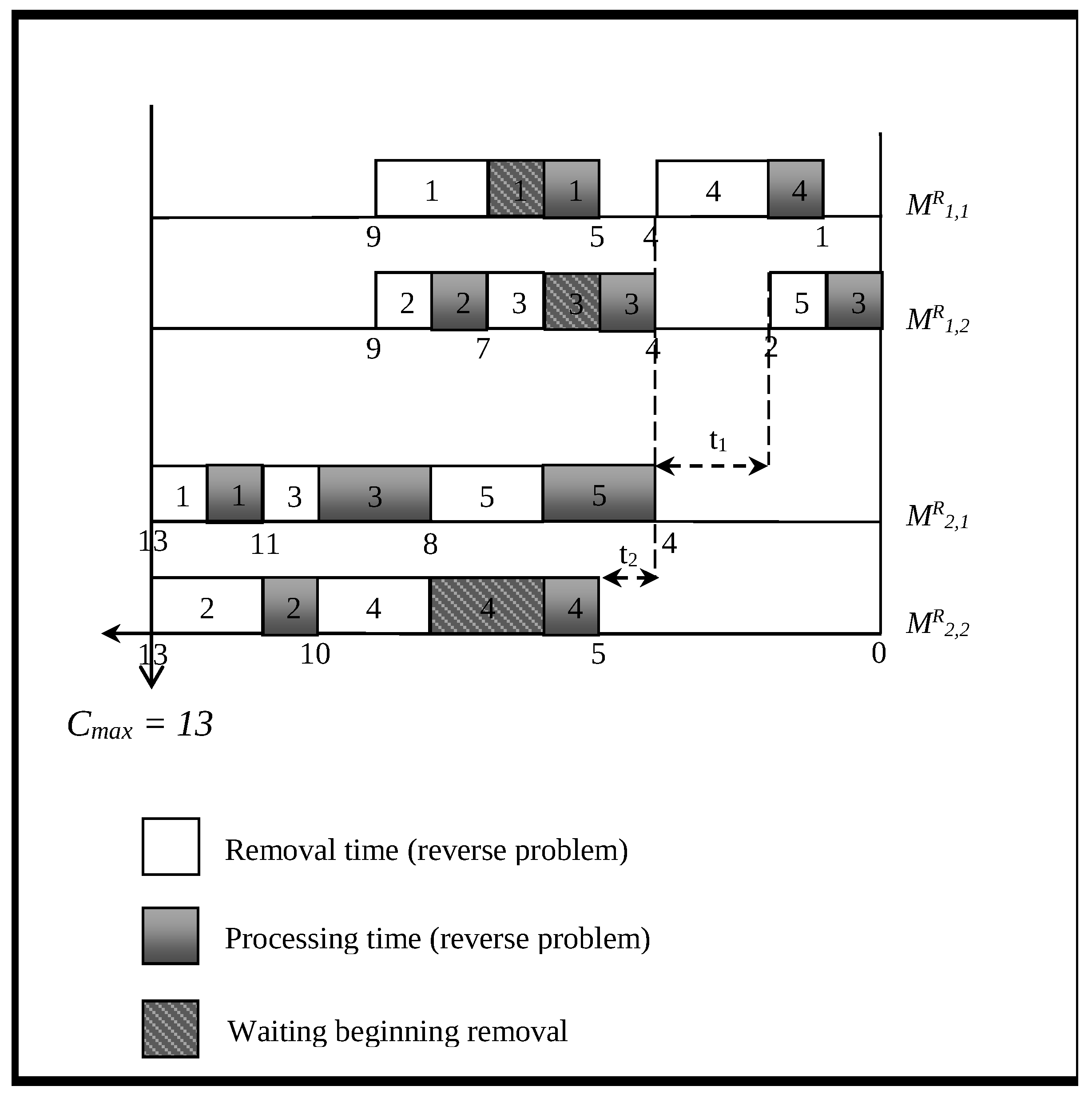
In Figure 2, the reverse feasible schedule for the reverse (backward) problem is presented for Example 1.

The studied scheduling problem and its corresponding problem present the following interesting propriety.

Proposition 1.

$F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ and $F_2\left(P_{m_2},P_{m_1}\right)\left|r{m}_{1,j}^R,t_j\right|C_{max}$ are equivalent, i.e., any feasible schedule for one of these two problems is also a feasible schedule for the other problem with equal makespan.

Proof. 

Consider $\sigma$ as a feasible schedule for $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ with a maximum completion time $C_{max}$. All the allocations of jobs to the machines and their sequences are kept as in $\sigma$. The jobs are right-shifted until the last scheduled ones in the machines of $S_2$ reach $C_{max}$. Therefore, a feasible schedule ${\sigma }^{{}^R}$ for the backward problem is obtained. The timeline scale t is transformed to a new one: $t^R=C_{max}-t$. According to the construction of ${\sigma }^{{}^R}$, the critical paths for ${\sigma }^{{}^R}$ and $\sigma$ are the same. Thus, ${\sigma }^{{}^R}$ and $\sigma$ have the same makespan. The same reasoning holds for the backward problem, and the equivalency of the two problems is proven. □

The latter proposition yields the following result.

Corollary 1.

Optimal solutions for $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ and $F_2\left(P_{m_2},P_{m_1}\right)\left|r{m}_{1,j}^R,t_j\right|C_{max}$ are the same.

Proof. 

Let ${\sigma }^{*}$ be an optimal schedule for $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ with optimal makespan $C_{max}^{*}$. According to the latter proposition (Proposition 1), the reverse schedule for the backward problem ${\sigma }_R^{*}$ has the same makespan $C_{max}^{*}$. Assume that there is another schedule ${\sigma }^R$ (${\sigma }^R\ne {\sigma }_R^{*}$) for the backward problem with better solution C ($C<C_{max}^{*}$). Based on the latter proposition (Proposition 1), the corresponding schedule of the forward problem has the same makespan C. This means that there is a schedule $\sigma$ for $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ with makespan $C<C_{max}^{*}$. This contradicts the fact that $C_{max}^{*}$ is the optimal makespan for the forward problem. Conversely, following the same reasoning for the backward problem, an optimal schedule for the backward problem induces an optimal schedule for the forward problem. □

Remark 1.

Consequently, the reverse scheduling problem $F_2\left(P_{m_2},P_{m_1}\right)\left|r{m}_{1,j}^R,t_j\right|C_{max}$ is automatically explored in order to provide a better solution.

3. Lower Bounds

In this section, two types of lower bounds are proposed for the studied scheduling problem. The first type consists in relaxing the capacity of a stage and keeping the other one as it is. This means that the number of machines in a selected stage is assumed to be infinite while the capacity of the other one is kept as it is. The second type of lower bound considers an estimation of the minimum idle machine times based on the Shortest Processing Time rule (SPT). Prior to the presentation of the lower bounds, the following notations are adopted.

For each stage $S_i$ ($i=1,2)$ and each job $j\in J,$ a release date $r_{i,j}$ and a delivery time $q_{i,j}$ are defined as follows.

$$\left\{\begin{array}{c}{r}_{2,j}=p_{1,j}+r{m}_{1,j}+t_j\hfill \\ r_{1,j}=0\hfill \end{array}\right.,\mathrm{and}\left\{\begin{array}{c}{q}_{1,j}=t_j+p_{2,j}+r{m}_{2,j}\\ q_{2,j}=0,\end{array}\right.$$

3.1. A Stage Capacity Relaxation Based Lower Bound

A relaxation of $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ consists in assuming that the number of machines in the second stage $S_2$ is infinite. This is the capacity relaxation of $S_2$. Therefore, an arriving job to stage $S_2$ is processed and removed immediately without waiting for an available machine. This means that after arrival, a job j leaves $S_2$ exactly after $p_{2,j}+r{m}_{2,j}$ unites of time. Consequently, the obtained capacity relaxed problem in stage $S_1$ is a parallel machine scheduling problem with release dates and delivery times $P_{m_1}\left|r_j,q_j\right|C_{max}$, where the release date $r_j=0$, the processing time $p_j=p_{1,j}+r{m}_{1,j}$, and the delivery time $q_j=t_j+p_{2,j}+r{m}_{2,j}$$\left(j\in J\right)$.

Thus, a lower bound for the already defined problem $P_{m_1}\left|r_j,q_j\right|C_{max}$, is also a lower bound for the $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$. Trivially, an optimal value $C_{max}^{*,1}$ for the problem $P_{m_1}\left|r_j,q_j\right|C_{max}$ is a lower bound for the studied problem. Then a lower bound for the problem $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ is expressed as follows.

$$L{B}_1=C_{max}^{*,1}$$

The same reasoning is applied and the stage $S_1$ capacity relaxation yields a parallel machine problem $P_{m_2}\left|r_j,q_j\right|C_{max}$ on the second stage $S_2$. This problem is characterized by a release date $r_j=p_{1,j}+r{m}_{1,j}+t_j$, the processing time $p_j=p_{2,j}+r{m}_{2,j}$, and a delivery time $q_j=0$$\left(j\in J\right)$.

Therefore, if $C_{max}^{*,2}$ is the optimal makespan of $P_{m_2}\left|r_j,q_j\right|C_{max}$, then a lower bound for the studied problem is given by:

$$L{B}_2=C_{max}^{*,2}$$

Remark 2.

The presented exact Branch and Bound algorithm in [25] is used to solve the parallel machine scheduling problem $P_m\left|r_j,q_j\right|C_{max}.$ Since the $P_m\left|r_j,q_j\right|C_{max}$ problem is NP-Hard, it might happen that within a time limit, the latter problem is not solved optimally. In this case, the best obtained lower bound while solving the problem is picked instead of $C_{max}^1$ or(and) $C_{max}^2$ in the expressions of $L{B}_1$ or(and) $L{B}_2.$

3.2. An Idle Time-Based Lower Bound

Due to the flow shop constraint, idle machine times are observed in the second stage $S_2$. The current lower bound is based on an estimation of the minimum idle machine time. This lower bound is presented in the following proposition.

Proposition 2.

If

• $\overline{t_j}$ is the $jth$ element in the increasing sorted list of $t_j$ for $j\in J$,
• $Id\left(m_2\right)$ is the sum of completion times of the $m_2$ jobs with smallest $p_{1,j}+r{m}_{1,j}$ scheduled on stage $S_1$ according to the SPT rule,
  then the problem $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ has a lower bound expressed as follows.

  $$L{B}_{Id}^2=⌈{\displaystyle \frac{Id\left(m_2\right)+{\displaystyle \sum _{j=1}^{m_2}}{\overline{t}}_j+{\displaystyle \sum _{j\in J}}\left(p_{2,j}+r{m}_{2,j}\right)}{m_2}}⌉$$

Proof. 

Consider an optimal schedule ${\sigma }^{*}$ with optimal makespan $C_{max}^{*}$. For this optimal schedule, let $s_k$ be the starting processing time of the first processed job $j_k$ in machine $M_{2,k}$$\left(1\le k\le m_2\right)$. Thus,

$$s_k+P{R}_k\le C_{max}^{*}$$

(1)

where $P{R}_k$ is the total processing and removal times in machine $M_{2,k}$. In addition,

$$s_k\ge c_{1,j_k}+t_{j_k}$$

(2)

where $c_{1,j_k}$ is the completion time of job $j_k$ in stage $S_1$. According to (2), ${\displaystyle \sum _{k=1}^{m_2}}{s}_k\ge {\displaystyle \sum _{k=1}^{m_2}}{c}_{1,j_k}+{\displaystyle \sum _{k=1}^{m_2}}\overline{t_k}$. Furthermore, ${\displaystyle \sum _{k=1}^{m_2}}{c}_{1,j_k}\ge I\left(m_2\right)$ [32]. Then,

$${\displaystyle \sum _{k=1}^{m_2}}{s}_k\ge I\left(m_2\right)+{\displaystyle \sum _{k=1}^{m_2}}\overline{t_k}$$

(3)

Based on (2) and (3), we have $I\left(m_2\right)+{\displaystyle \sum _{k=1}^{m_2}}\overline{t_k}+{\displaystyle \sum _{j\in J}}\left(p_{2,j}+r{m}_{2,j}\right)\le$${\displaystyle \sum _{k=1}^{m_2}}\left(s_k+P{R}_k\right)\le m_2{C}_{max}^{*}$. Thus, $⌈{\displaystyle \frac{Id\left(m_2\right)+{\displaystyle \sum _{k=1}^{m_2}}{\overline{t}}_j+{\displaystyle \sum _{j\in J}}\left(p_{2,j}+r{m}_{2,j}\right)}{m_2}}⌉\le C_{max}^{*}$, which ends the proof. □

Corollary 2.

Based on the symmetry of the studied problem, the following expression is a valid lower bound for the problem $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$.

$$L{B}_{Id}^1=⌈{\displaystyle \frac{Id\left(m_1\right)+{\displaystyle \sum _{k=1}^{m_1}}{\overline{t}}_j+{\displaystyle \sum _{j\in J}}\left(r{m}_{1,j}+p_{1,j}\right)}{m_1}}⌉$$

where $Id\left(m_1\right)$ is the sum of completion times of the $m_1$ jobs with smallest $p_{2,j}+r{m}_{2,j}$ scheduled on stage $S_2$ according to the SPT rule for the backward problem.

An immediate trivial result is given in the following corollary.

Corollary 3.

A valid lower bound for $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ is expressed as follows.

$$LB=\left(L{B}_1,L{B}_2,L{B}_{Id}^1,L{B}_{Id}^2\right)$$

(4)

4. Heuristic Algorithm

A heuristic algorithm is proposed in this section. This heuristic is mainly based on the optimal solution to the parallel machine scheduling problem with release dates and delivery times ($P_{m_{}}\left|r_j,q_j\right|C_{max}$). Two consecutive phases comprise this heuristic. The first phase is a constructive one allowing to obtain an initial solution. The second phase is an improvement phase that might enhance the initial solution. This section starts by presenting a useful result relating two parallel machines scheduling problems, where the respective objective functions are the maximum completion time ($C_{max}$) and the maximum lateness ($L_{max}$).

Proposition 3.

The two scheduling problems $P_m\left|r_j,q_j\right|C_{max}$, $P_m\left|r_j,d_j\right|L_{max}$ are equivalents. In other words, these two problems have the same optimal solution.

Proof. 

The $P_m\left|r_j,q_j\right|C_{max}$ problem is transformed into the $P_m\left|r_j,d_j\right|L_{max}$ problem by setting for each job j $\in J$ a due date $d_j=C-q_j$, where C is an upper bound for $C_{max}^{*}$ (optimal solution). Conversely, starting from the $P_m\left|r_j,d_j\right|L_{max}$ problem and setting $D={\displaystyle \underset{j\in J}{max}}\left(d_j\right)$, then, naturally, a delivery time for each job $j\in J$ is given by $q_j=D-d_j$. If $s_j$ denotes the starting time of the job j in a feasible schedule, then the maximum lateness satisfies $L_{max}={\displaystyle \underset{j\in J}{max}}\left(s_j+p_j-d_j\right)={\displaystyle \underset{j\in J}{max}}\left(s_j+p_j-D+q_j\right)={\displaystyle \underset{j\in J}{max}}\left(s_j+p_j+q_j\right)-D=C_{max}-D$. Therefore,

$$L_{max}=C_{max}-D.$$

□

In the sequel, the first phase of the proposed heuristic is presented over the following pseudo-code.

PHASE I: Initial solution

I.1

Initialization: $m=m_1$, $r_j=0,$ $p_j=p_{1,j}+r{m}_{1,j}$, and $q_j=t_j+$$p_{2,j}+r{m}_{2,j}$$\left(j\in J\right)$.

I.2

Solve the obtained problem $P_m\left|r_j,q_j\right|C_{max}$.

I.3

Collect the completion time $c_{\mathbf{1},\mathbf{j}}$ for each $j\in J$, of the solution to (I.2).

I.4

Set $m=m_2$, $r_j=c_{1,j}+t_j$, $p_j=p_{2,j}+r{m}_{2,j}$, and $q_j=$ 0 $\left(j\in J\right).$

I.5

Solve the obtained problem $P_m\left|r_j,q_j\right|C_{max}$.

I.6

For each $j\in J$ , Set $s_{2,j}$ as the starting processing time of the solution in (I.5).

I.7

Set $U{B}^F=$${\displaystyle \underset{j\in J}{max}}\left(s_{2,j}+p_{2,j}+r{m}_{2,j}\right)$.

The inputs of phase one are $p_{1,j}$, $p_{2,j}$, $r{m}_{1,j}$, $r{m}_{2,j}$, $t_j$, $m_1$, and $m_1$$(1\le j\le n)$. The output is an initial feasible solution. The first phase consists in consecutively solving two parallel machine scheduling problems $P_m\left|r_j,q_j\right|C_{max}$ such that the flow constraint is satisfied. In other terms, a job cannot start processing in the second stage $S_2$ before completing processing and removing in the first stage $S_1$ and before being transported to stage $S_2$. The inputs for the first problem $P_{m_1}\left|r_j,q_j\right|C_{max}$ are presented in (I.1). These inputs state that the delivery time $q_j$ takes into account the transportation time as well as the processing and the removal times in stage $S_2$ ($q_j=t_j+$ $p_{2,j}+r{m}_{2,j}$). This is the minimum elapsed time after leaving stage $S_1$. The solution to $P_{m_1}\left|r_j,q_j\right|C_{max}$ (I.2, I.3) provides a feasible schedule in which the completion times are denoted $c_{\mathbf{1},\mathbf{j}}$. The inputs for the second parallel machine problem are displayed in (I.4). The flow constraint is satisfied by setting the release dates for $P_{m_2}\left|r_j,q_j\right|C_{max}$ as $r_j=c_{\mathbf{1},\mathbf{j}}+t_j$. This is the minimum duration to reach $S_2$ after exiting $S_1$. The resolution of the second parallel machine problem is performed in (I.5). These two feasible schedules allow obtaining a feasible one for the problem $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ by concatenating them. There are no contradictions since $r_j=c_{\mathbf{1},\mathbf{j}}+t_j$. The value of the upper bound $U{B}^F$ (upper bound for the forward problem) is trivially obtained in steps (I.6, I.7).

Once an initial feasible solution is obtained, the improvement phase starts. A pseudo-code of this phase is presented as follows.

PHASE II: Improvement phase

II.1

Set $m=m_1$, $r_j=0,$ $p_j=p_{1,j}+r{m}_{1,j}$, and $d_j=$$s_{2,j}-t_j$$\left(j\in J\right)$.

II.2

Solve the problem $P_m\left|r_j,d_j\right|L_{max}$.

II.3

Set $c_{\mathbf{1},\mathbf{j}}$($j\in J$) as the completion time of the solution in (II.2).

II.4

If$L_{max}^{*}=0$ then go to (II.10), Else $U{B}^F:=U{B}^F+L_{max}^{*}$.

II.5

Set $m=m_2$, $r_j=c_{1,j}+t_j,$ $p_j=p_{2,j}+r{m}_{2,j}$, and $q_j=$ 0 $\left(j\in J\right).$

II.6

Solve the problem $P_m\left|r_j,q_j\right|C_{max}$.

II.7

For each $j\in J$ set $s_{2,j}$ as the starting time for the solution in (II.6).

II.8

If$C_{max}^{*}<U{B}^F$ then Set $U{B}^F:=C_{max}^{*}.$

II.9

Go to (II.1).

II.10

STOP.

It is worth mentioning that the input of phase two is the already obtained initial solution in phase one, and the output is an improved solution. The current phase is intended to enhance the initial solution. This is performed by iteratively visiting each time stage and keeping the other one as it is. The schedule in the visited stage is modified without contradiction with the fixed schedule in the other stage. This guarantees a feasible schedule for the studied problem at the end of each iteration. At the beginning of this phase, the schedule in the second stage $S_2$ is maintained, and in the first stage $S_1$ the due date $d_j$ of each job is set to $d_j=$$s_{2,j}-t_j$ where $s_{2,j}$ are the starting time in the schedule of $S_2$. Thus, any new schedule in $S_1$ does not contradict the one in $S_2$ (II.1). A parallel machine scheduling problem with lateness as the objective function $P_m\left|r_j,d_j\right|L_{max}$ is then solved (II.2). Consequently, the optimal lateness satisfies $L_{max}^{*}\le 0$, and two cases have to be considered. The first case is obtained when $L_{max}^{*}=0$, where no enhancement is detected and the improvement phase is halted. The second encountered case is for $L_{max}^{*}<0$, where an improvement is obtained and the new upper bound’s value is readjusted as: $UB:=UB+L_{max}^{*}$ (II.3). In the latter case, the procedure is to be continued, and the second stage is visited by fixing the already obtained schedule in $S_1$. A new parallel machine problem is obtained in $S_1$ (II.6), with inputs as cited in (II.5). The release dates in $S_2$ are set $r_j=c_{1,j}+t_j$ where $c_{1,j}$ are the completion times in $S_1$. This allows to avoid any contradiction with the new obtained schedule in $S_2$ after solving the problem $P_m\left|r_j,q_j\right|C_{max}$ (II.6). If the obtained optimal makespan $C_{max}^{*}$ satisfies $C_{max}^{*}<U{B}^F$, then an improvement is detected and the upper bound is readjusted as $U{B}^F:=C_{max}^{*}$ (II.8). The procedure is then restarted from the first stage $S_1$ (II.9). The whole procedure is halted when $L_{max}^{*}=0$.

Because of the symmetry of the studied problem, the current heuristic is applied to the reverse (backward) problem, and the obtained upper bound is denoted $U{B}^R$. Therefore, the resulting final upper bound after exploring the studied problem and its reverse is:

$$UB=min\left(U{B}^F,U{B}^R\right)$$

(5)

Remark 3.

The main component of the latter heuristic is the resolution of the two NP-Hard problems $P_m\left|r_j,q_j\right|C_{max}$ and $P_m\left|r_j,d_j\right|L_{max}$. This is obtained by running the proposed exact algorithm in [25]. In the case where an optimal solution is not reached within a prefixed limit time, the best upper bound (best lateness) and the corresponding feasible schedule are considered.

5. Exact Procedure

In the previous sections, a set of lower bounds and a heuristic algorithm are proposed. Obviously, if the values of the heuristic and the lower bounds are equal, then the optimal solution is reached. In the other case, an exact procedure is proposed to find an optimal solution. Clearly, the heuristic and the lower bounds are helpful in narrowing the search interval for the exact procedure. In this study, the Branch and Bound (B&B) algorithm is the exact procedure adopted. The different components of the proposed B&B algorithm are detailed in the sequel.

5.1. Solutions Representation

The solution representation is the first step in the B&B algorithm, and the B&B efficiency is strongly related to this step. In this context, if $\sigma$ is a feasible schedule in the first stage $S_1$ then a parallel machine scheduling problem $P_{m_2}\left|r_j\right|C_{max}$ is systematically induced in the second stage. The parameters of this $P_{m_2}\left|r_j\right|C_{max}$ problem are the release dates, given by $r_j=c_{1,j}\left(\sigma \right)+t_j$ where $c_{1,j}\left(\sigma \right)$ is the completion time of job j relative to the feasible schedule $\sigma$ in the first stage. In addition, for the same problem, the processing times are expressed as $p_j=p_{2,j}+r{m}_{2,j}$ for each job $j\in J$. Clearly, the optimal solution ${\alpha }_{\sigma }^{*}$ of the $P_{m_2}\left|r_j\right|C_{max}$ problem allows obtaining a feasible solution for the studied problem $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$. This is performed by concatenating the two feasible solutions $\sigma$ and ${\alpha }_{\sigma }^{*}$. Therefore, solving the $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$ problem is equivalent to determining, in the first stage, a feasible schedule ${\sigma }^{*}$ satisfying $\stackrel{\_\_}{C}\left({\sigma }^{*}\right)={\displaystyle \underset{\sigma \in \mathsf{\Gamma }}{min}}$ $\stackrel{\_\_}{C}\left(\sigma \right),$ where $\mathsf{\Gamma }$ is the set of all feasible schedules in the first stage, and $\stackrel{\_\_}{C}\left(\sigma \right)$ the optimal makespan of the $P_{m_2}\left|r_j\right|C_{max}$ problem quoted above. In addition, a feasible schedule $\sigma \in \mathsf{\Gamma }$ is represented throughout a permutation $\left({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n\right)$ of n jobs, where the respective starting times $s_{{\sigma }_i}$ and $s_{{\sigma }_j}$ of the jobs ${\sigma }_i$ and ${\sigma }_j,$ respectively, satisfy $s_{{\sigma }_i}$≤$s_{{\sigma }_j}$ for $1\le i<j\le n.$ Thus, a feasible solution to the studied problem is represented by a permutation of the n jobs.

5.2. Branching Strategy

In the search tree associated with the B&B algorithm, any node at level k is denoted $N_k$. In this node, let $\sigma \left(N_k\right)$ be a partial schedule of k jobs in the first stage. It is worth mentioning that the partial schedule $\sigma \left(N_k\right)$ is explicitly represented throughout a partial permutation $\left({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_k\right)$ of the k scheduled jobs in node $N_k$. The $n-k$ remaining unscheduled jobs at node $N_k$ are considered the descendants. Therefore, from node $N_k$, the branching consists of selecting a job $j_0$ from the set of unscheduled jobs and creating a new node $N_{k+1}$ represented over the partial permutation $\left({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_k,j_0\right)$. Clearly, the branching process from node $N_k$ results in $n-k$ nodes at level $k+1$. Consequently, at level $n-1$, a feasible schedule is obtained in the first stage $S_1$. Naturally, a parallel machine scheduling problem with release dates $P_{m_2}\left|r_j\right|C_{max}$ is obtained in the second stage. For the latter problem, $r_j=c_{1,j}\left(\sigma \left(N_{n-1}\right)\right)+t_j$ where $c_{1,j}\left(\sigma \left(N_{n-1}\right)\right)$ is the completion time of job j relatively to the feasible schedule $\sigma \left(N_{n-1}\right)$. The exploration of the B&B search tree is performed using the first strategy.

5.3. Bounding Strategy

In this section, two lower bounds and a polynomial heuristic algorithm are proposed for each node. Useful notations and definitions are given as follows. A node in the search tree is denoted N with $N\ne N_0$, where $N_0$ is the root node. The set of the scheduled and removed jobs at node N is denoted as $J_S$, and the set of unscheduled job(s) is $J_{US}=J\backslash J_S$. Let $c_{1,j}$ be the completion time of job $j\in J_S$ and also let $u_i$ be the availability of machine $M_{1,i}$$\left(1\le i\le m_1\right)$ contained in the first stage after scheduling all $j\in J_S$. Without loss of generality, assume that the machines’ availabilities in the first stage are sorted in increasing order : $u_1\le u_2\le \dots \le u_{m_1}$.

5.3.1. First Stage Relaxed Capacity-Based Lower Bound

If the number of machines in the first stage is assumed to be infinite (capacity relaxation), then an unscheduled job finishes processing at time $u_1+p_{1,j}+r{m}_{1,j}+t_j$. This is the time for job j to start processing in the second stage. Clearly, a scheduled job j$\in J_S$ is ready to be processed in the second stage at time $r_j=c_{1,j}+t_j$. Consequently, in the second stage, a parallel machine scheduling problem $P_{m_2}\left|r_j\right|C_{max}$ with release dates is obtained. The processing times $p_j$ and the release dates $r_j$ for the latter problem are expressed as follows.

$$\left\{\begin{array}{cc}{p}_j=p_{2j}+r{m}_{2,j}\hfill & j\in J\hfill \\ r_j=u_1+p_{1j}+t_j\hfill & \mathrm{if}j\in J_{US}\hfill \\ r_j=c_{1j}+t_j\hfill & \mathrm{if}j\in J_S\hfill \end{array}\right.$$

(6)

Clearly, any lower bound for the latter problem $P_{m_2}\left|r_j\right|C_{max}$ is a lower bound at node N. The first lower bound is based on the following result.

Proposition 4.

If A is a subset of jobs $\left(A\subseteq J\right)$ such that $\left|A\right|\ge m_2$, and ${\overline{r}}_j\left(A\right)$ denotes the $jth$ release date in the increasing sorted order set $\left\{r_j,j\in A\right\}$ then

$$L{B}_N^1\left(A\right)=⌈\frac{{\displaystyle \sum _{k=1}^{m_2}}{\overline{r}}_j\left(A\right)+{\displaystyle \sum _{j\in A}}\left(p_{2,j}+r{m}_{2,j}\right)}{m_2}⌉,$$

is valid lower bound for the obtained sub-problem at node N.

Proof. 

Let $C_{max}^{*}$ be the optimal makespan for the problem $P_{m_2}\left|r_j\right|C_{max}$. For a machine $M_{2,i}$$\left(i=1,2,\dots ,m_2\right)$, let $t_{2,i}$ be the starting time of the first processed job. The time in each machine $M_{2,i}$ is subdivided into total processing and removing $P_i\left(A\right)$, and idle time $I_i\left(A\right)$. Clearly,

$$t_{2,i}+I_i\left(A\right)+P_i\left(A\right)\le C_{max}^{*}\mathrm{for}i=1\dots .m_2$$

(7)

Thus,

$${\displaystyle \sum _{k=1}^{m_2}}{t}_{2,i}+{\displaystyle \sum _{k=1}^{m_2}}{I}_i\left(A\right)+{\displaystyle \sum _{k=1}^{m_2}}{P}_i\left(A\right)\le m_2{C}_{max}^{*}$$

(8)

Since ${\displaystyle \sum _{k=1}^{m_2}}{\overline{r}}_j\left(A\right)\le$${\displaystyle \sum _{k=1}^{m_2}}{t}_{2,i}$, ${\displaystyle \sum _{k=1}^{m_2}}{P}_i\left(A\right)={\displaystyle \sum _{k=1}^n}\left(p_{2,j}+r{m}_{2,j}\right)$ and based on (8), the following inequality holds: ${\displaystyle \sum _{k=1}^{m_2}}{\overline{r}}_j\left(A\right)+{\displaystyle \sum _{k=1}^{m_2}}\left(p_{2,j}+r{m}_{2,j}\right)\le m_2{C}_{max}^{*}$. This ends the proof. □

If all the subsets $\left(A\subseteq J\right)$, such that $\left|A\right|\ge m_2$ are explored, then $L{B}_N^1\left(A\right)$ might be improved and $L{B}_N^1={\displaystyle \underset{A\subseteq J;\left|A\right|\ge m_2}{max}}L{B}_N^1\left(A\right)$ is a valid lower bound. In this case, an exponential number of subsets has to be explored, which is out of reach. However, only a polynomial number of subsets has to be explored according to the following proposition.

Proposition 5.

A valid lower bound at node N is given by $L{B}_N^1={\displaystyle \underset{A\subseteq J;\left|A\right|\ge m_2}{max}}L{B}_N^1\left(A\right)$. This lower bound has a complexity of $O(nlog{m}_2)$.

Proof. 

Trivially, ${\overline{r}}_{m_2}\left(A\right)\in \{r_{\left(m_2\right)},r_{\left(m_2+1\right)},\dots ,r_{\left(n\right)}\}$ with $r_{\left(i\right)}$ the $ith$ member of the increasing sorted list $\left\{r_j,j\in J\right\}$. If $A_k$$(k=m_2,\dots ,n)$ denotes a subset of J satisfying

$$L{B}_N^1\left(A_k\right)=\underset{A\subseteq J:{\overline{r}}_{m_2}\left(A\right)=r_{\left(k\right)}}{max}L{B}_N^1\left(A\right)$$

then clearly $L{B}_N^1={\displaystyle \underset{m_2\le k\le n}{max}}L{B}_N^1\left(A_k\right)$. Let $g(.)$ be a function on the job subsets defined by $g\left(A\right)={\displaystyle \sum _{k=1}^{m_2}}{\overline{r}}_j\left(A\right)+{\displaystyle \sum _{j\in A}}\left(p_{2,j}+r{m}_{2,j}\right)$ with $A\subseteq J$ and $\left|A\right|\ge m_2$. Thus, $g\left(A_{k+1}\right)=g\left(A_k\right)+r_{k+1}-r_{j_k}-\left(p_{2,j_k}+r{m}_{2,j_k}\right),k=m_2,\dots ,n-1$, and $j_k=arg{\displaystyle \underset{j\in A_k}{min}}(r_j+p_{2,j}+r{m}_{2,j})$. Based on the latter result, $g\left(A_{m_2}\right)$ needs $O\left(n\right)$ time to be computed. Knowing $g\left(A_k\right)$, the main effort for the computation of $g\left(A_{k+1}\right)$ lies on the determination of the job $j_k$. The determination of $j_k$ requires at most $O(log{m}_2)$ time. Based on the two previous observations, the computation of $g\left(A_k\right)$ for $k=m_2,\dots ,n$ is performed in $O(nlog{m}_2)$ time. □

5.3.2. Lower Bound Based on the Machines’ Availabilities

At node N of the search tree, some jobs are already scheduled, and then at the first stage, a parallel machine problem is induced. This parallel machine problem $P,N{C}_{inc}\left|q_j\right|C_{max}$ is defined on the set of unscheduled jobs $J_{US}$. In addition, the machines are subject to availabilities constraints and the jobs are characterized by their delivery times. The availability $v_i$ of machine $M_{1,i}$$\left(i=1,2,\dots ,m_2\right)$ is the completion time of the last scheduled job on it (if not, $v_i=0$). For a job $j\in J_{US}$, the delivery time is $q_j=t_j +$ $p_{2,j}+r{m}_{2,j}$ and the processing time is $p_j=p_{1,j}+r{m}_{1,j}$. Without loss of generality, the availabilities are assumed to satisfy $v_1\le v_2\le \dots \le v_{m_1}$. Clearly, any lower bound for the problem $P,N{C}_{inc}\left|q_j\right|C_{max}$ is a lower bound at node N. It is worth mentioning that, in some cases, less than $m_1$ machines are required in an optimal schedule to process the jobs. This is basically because of the the availability constraints. In order to bound the number of the utilized machines in an optimal schedule, the following result is recalled [33].

Proposition 6

([33]). Let $UB$ be an upper bound on the optimal makespan of the $P,N{C}_{inc}\left|q_j\right|C_{max}$ problem. Then, the number of utilized machines m in an optimal schedule is bounded as follows.

$$m_l\left(J_{US}\right)\le m\le m_u\left(J_{US}\right),$$

with:

• $m_l\left(J_{US}\right)=⌈{\displaystyle \frac{{\displaystyle \sum _{j\in J_{US}}}\left(p_{1,j}+r{m}_{1,j}\right)}{UB-v_1-{\overline{q}}_1\left(J_{US}\right)}}⌉$ where ${\overline{q}}_1\left(J_{US}\right)={\displaystyle \underset{j\in J_{US}}{min}}{q}_j$.
• $m_u\left(J_{US}\right)$ is the smallest k $(k=1,\dots ,m_1-1)$ satisfying $v_{k+1}+{\displaystyle \underset{j\in J_{US}}{min}}(p_{1,j}+r{m}_{1,j}+q_j)>UB$. Otherwise, $m_u\left(J_{US}\right)=m_1$.

At this stage, the second lower bound is presented in the following proposition.

Proposition 7.

Let $A\subseteq J_{US}$ be a subset of jobs and assume that m machines are used in an optimal schedule, then a valid lower bound is expressed as follows.

$$L{B}_N^2(A,m)=⌈\frac{{\displaystyle \sum _{1\le i\le m}}{v}_i+{\displaystyle \sum _{j\in A}}\left(p_{1,j}+r{m}_{1,j}\right)+{\displaystyle \sum _{1\le k\le m}}{\overline{q}}_k\left(A\right)}{m}⌉,$$

where ${\overline{q}}_k\left(A\right)$ is the $kth$ member of the set $\left\{q_j,j\in A\right\}$ sorted in increasing order.

Proof. 

For an optimal schedule with optimal makespan $C_{max}^{*}$ that uses m machines, the first processed jobs in each machine starts at $t_{1,i}\left(i=1,2,\dots ,m\right)$. The last scheduled jobs in each machine has a delivery time $q_{1,i}\left(A\right)$. If $P_i\left(A\right)$ is the total load in $M_{1,i}$, then $t_{1,i}+P_i\left(A\right)+q_{1,i}\left(A\right)\le C_{max}^{*}$ and ${\displaystyle \sum _{i=1,m}}{t}_{1,i}+{\displaystyle \sum _{i=1,m}}{P}_i\left(A\right)+{\displaystyle \sum _{i=1,m}}{q}_{1,i}\left(A\right)\le m{C}_{max}^{*}$. Since ${\displaystyle \sum _{1\le i\le m}}{v}_i\le {\displaystyle \sum _{1\le i\le m}}{t}_{1,i}$, ${\displaystyle \sum _{1\le i\le m}}{P}_i\left(A\right)={\displaystyle \sum _{j\in A}}\left(p_{1,j}+r{m}_{1,j}\right),$ and ${\displaystyle \sum _{1\le k\le m}}{\overline{q}}_k\left(A\right)\le {\displaystyle \sum _{1\le i\le m}}{q}_{1,i}\left(A\right)$, then ${\displaystyle \sum _{1\le i\le m}}{v}_i+{\displaystyle \sum _{j\in A}}\left(p_{1,j}+r{m}_{1,j}\right)+{\displaystyle \sum _{1\le k\le m}}{\overline{q}}_k\left(A\right)\le m{C}_{max}^{*}$, which ends the proof. □

Clearly, $L{B}_N^2\left(m\right)={\displaystyle \underset{A\subseteq J_{US}}{max}}L{B}_N^2(A,m)$ is a valid lower bound at node N. To compute $L{B}_N^2\left(m\right)$, a polynomial number of subsets A has to be explored. This is the content of the following result.

Proposition 8.

$L{B}_N^2\left(m\right)$ is a polynomial valid lower bound with a complexity $O(nlogm).$

Proof. 

The proof is conducted as in Proposition 5, where:

• ${\overline{q}}_k\left(A\right)$ replaces ${\overline{r}}_j\left(A\right)$
• $\left(p_{1,j}+r{m}_{1,j}\right)$ replaces $\left(p_{2,j}+r{m}_{2,j}\right)$
• ${\displaystyle \sum _{i=1,m}}{v}_i$ is a constant.

 □

An immediate consequence is the following result.

Corollary 4.

$$L{B}_N^2=\underset{m_l\left(J_{US}\right)\le m\le m_u\left(J_{US}\right)}{min}L{B}_N^2\left(m\right),$$

is a valid lower bound at node N with complexity $O(m_{1}nlog{m}_1).$

Proof. 

Immediate. □

Clearly,

$$L{B}_N=max\left(L{B}_N^1,L{B}_N^2\right),$$

(9)

is a lower bound at node N.

5.3.3. Upper Bounding Strategy

A greedy polynomial heuristic algorithm HL is computed at node $N\ne N_0$. This heuristic algorithm is based on a priority list. In this HL heuristic, the available unscheduled job with the largest $p_{2,j}+r{m}_{2,j}$ is scheduled in the most available machine in the first stage. The scheduling in the second stage is performed after all the jobs are scheduled in the first stage. In the second stage, among the unscheduled and available jobs, the one with the largest $p_{2,j}+r{m}_{2,j}$ is scheduled in the first available machine in the second stage.

The following pseudo-code presents the main steps of HL.

HL Heuristic

Phase 1—Scheduling in the first stage $S_1$

1.1. Set$V:=J_{US}$.

1.2.Schedule in the first stage the job$j\in J_{US}$with the largest$p_{2,j}+r{m}_{2,j}$in the most available machine.

1.3. Set$V:=V\backslash \left\{j\right\}$.

1.4. If  $V\ne Ø$  then   go to  Step  1.2.

Phase 2—Scheduling in the second stage $S_2$

2.1. Set  a release date  $r_j=c_{1,j}$for each job$j\in J$  ($c_{1,j}$ completion time of$j$in the first stage  $S_1$).

2.2.Set$V:=J$.

2.3.Schedule an available job$j\in V$with the largest$p_{2,j}+r{m}_{2,j}$ in the most available machine in the second stage.

2.4. Set$V:=V\backslash \left\{j\right\}$.

2.5. If$V=Ø$Thengo to Step2.6, Elsego to Step2.3.

2.6. STOP.

The main computational effort in HL is sorting the jobs according to their non-increasing order of $p_{2,j}+r{m}_{2,j}$, which requires $O(nlogn)$ time.

5.4. Additional Improvements

Additional improvements are proposed for the B&B algorithm in order to reduce the search tree size and, therefore, shorten the computational time. Among these improvements is a set of dominance rules. In addition, based on the symmetric propriety of the studied problem, the backward problem is systematically explored. In this context, the B&B algorithm is extended to the backward problem. These two main improvements are the respective topics of the two next subsections.

5.4.1. Dominance Rules

In order to eliminate additional nodes from the B&B search tree, dominance rules are proposed. Indeed, some nodes are shown to be dominated by others, and in this case, there is no need to explore them. In this work, the dominance rules presented in [34] are extended to the studied problem $F_2\left(P_{m_1},P_{m_2}\right)\left|r{m}_{i,j},t_j\right|C_{max}$. More precisely, the unscheduled jobs $J_{US}=\{j_1,j_2,...,j_K\}$ at node N are the candidates to be branched in the next step of exploration. In addition, if $\sigma \left(N\right)=\left({\sigma }_1,{\sigma }_2,...,{\sigma }_k\right)$ is the partial schedule at node N then,

• If there are two jobs $j_k\in$$J_{US}$ and $j_{k+1}\in$$J_{US}$ that have the same characteristics: $p_{1,j_k}=p_{1,j_{k+1}}$, $r{m}_{1,j_k}=r{m}_{1,j_{k+1}}$, $t_{j_k}=t_{j_{k+1}}$, $p_{2,j_k}=p_{2,j_{k+1}}$, and $r{m}_{2,j_k}=r{m}_{2,j_{k+1}}$, then the two nodes represented, respectively, by partial schedules $\left({\sigma }_1,{\sigma }_2,...,{\sigma }_k,j_k\right)$ and $\left({\sigma }_1,{\sigma }_2,...,{\sigma }_k,j_{k+1}\right)$ are the same and one of them should be eliminated.
• If $v_1=v_2$, then the two nodes represented, respectively, by partial schedules $\left({\sigma }_1,{\sigma }_2,...,{\sigma }_k,j_k,j_{k+1}\right)$ and $\left({\sigma }_1,{\sigma }_2,...,{\sigma }_k,j_{k+1},j_k\right)$ are the same, and one of them should be eliminated. This dominance rule is based on the symmetric availability of the two first machines ($v_1=v_2).$

5.4.2. Systematical Forward-Backward Procedure

Due to the symmetry of the studied problem (as mentioned in Proposition 1, the forward and the backward problems are investigated systematically. This is performed in order to obtain better results. In this context, the B&B algorithm is applied for the forward and the backward problems consecutively and iteratively. The obtained result for one of problems is the input for the other one. A time limit is set up for the B&B algorithm to find an optimal solution. If the B&B fails, then it moves to the other problem. This iterative procedure is cyclic, and it is halted if there is no improvement for the lower bounds and upper bounds or the optimal solution is not reached.

6. Computational Results

In order to evaluate the performance and the efficiency of the proposed procedures, an extensive experimental study on benchmark test problems was carried out. All the procedures were coded in C and implemented in a Pentium IV 2.8GHz Personal Computer with 1GBRAM.

6.1. Test Problems

In this study, the test problems are selected from an existing one for the hybrid flow shop environment [35]. These data are extended to include the transportation and removal times. Therefore, the number of jobs n and the number of machines in both stages $(m_1,m_2)$ are given as follows.

• The number of jobs n$\in \left\{10,20,30,40,50,100,150,200\right\}$.
• The number of machines in both stages $(m_1,m_2)$∈$\left\{(2,2),(2,4),(4,2),(4,4)\right\}$.

Recall that in this study the transportation and removal times are not neglected compared to the processing times. Two cases are considered: either the transportation and removal times are similar to the processing times or they are more important (double) than the processing times. To generate test problems satisfying the two previous cases, the processing times are set as:

• $p_{1,j}$ and $p_{2,j}$ are randomly and uniformly generated in $[1,20]$.

Three positive integers a, b, c are assigned, respectively, to removal time in the first stage $r{m}_{1,j}$, transportation time $t_j$, and removal time in the second stage $r{m}_{2,j}$. In addition, $a,b,c\in \{20,40\}$. Following the latter notations, the removal time in the first stage $r{m}_{1,j}$, transportation time $t_j$, and removal time in the second stage $r{m}_{2,j}$ are generated as follows.

• The removal times in the first stage $r{m}_{1,j}$ are randomly and uniformly generated in $[1,a]$.
• The transportation times $t_j$ are randomly and uniformly generated in $[1,b]$.
• The removal times in the second stage $r{m}_{2,j}$ are randomly and uniformly generated in $[1,c]$.

If, for example, $a=20$ then the removal time in the first stage is compared to the processing times, and if $a=40$, then the removal time in the first stage is more important than the processing times. This remark holds for $t_j$ and $r{m}_{2,j}$. For each combination, $n,$$m_1,$$m_2$, a, b, and c, 10 test problems are generated, and a set of 2560 test problems is obtained.

6.2. Performance of the Proposed Procedures

At this stage, it is worth recalling that three kinds of procedures are proposed in this work. These procedures are the lower bounds, the heuristic algorithm, and the B&B procedure. The roles of these procedures are complementary. Indeed, for each test problem, the lower bound $LB$ is computed first. After that, and in a second phase, the heuristic algorithm is executed, and a feasible solution with upper bound value’s $UB$ is obtained. If $LB=UB$, then an optimal solution is reached. In the other case where $LB<UB$, the B&B is executed with input $UB$. This means that the B&B algorithm takes advantage of the heuristic algorithm and does not start from scratch. Since the studied problem is NP-Hard, a time limit is set for the B&B algorithm. If an optimal solution is not reached within this time limit, then the lower bound is utilized to calculate the relative gap for a test problem. The expression of the relative gap is presented as follows.

$$rg={\displaystyle \frac{UB-LB}{LB}}\times 100$$

Consequently, the presented experimental results concern the three procedures simultaneously.

The utilized parameters to assess the performance of the proposed algorithms are:

• $[a:b:c]:$ The rate parameters, which means that $r{m}_{1,j}\in U[1,a]$, $t_j\in U[1,b]$, and $r{m}_{2,j}\in U[1,a]$.
• $SR:$ Number of test problems solved at the root node ($UB=LB$: (4), (5)).
• $SBB:$ Number of test problems solved by the B&B algorithm and not solved at the root node.
• $UN:$ Number of unsolved test problems by the heuristic algorithm and B&B procedure.
• $\%S:$ Percent of solved test problems.
• $MT:$ Mean computational time (in seconds) for solving the test problems.
• $MG:$ The average relative gap of unsolved instances.
• $MaxG:$ The maximum relative gap of the unsolved instances.

It is worth mentioning that the performance measure $SR$ assesses the performance of both the heuristic algorithm and the lower bound. Indeed, a test problem is optimally solved using the heuristic algorithm if $LB=UB$. If a test problem is not optimally solved using the heuristic algorithm, then the B&B algorithm is activated, and the performance measure $SBB$ assesses the efficiency of the B&B algorithm. The parameter $\%S$ measures the performance of the combined three procedures (lower bound, heuristic algorithm, and the B&B). The computational time solving the test problems is an important parameter that should be taken into account while evaluating the performance of an algorithm; this parameter is $MT$. For the unsolved test problems, the mean relative gap $MG$ is an interesting parameter showing the efficiency of the proposed procedures. Indeed, if $MG$ is relatively small, then the proposed procedure is not providing the optimal solution but a near-optimal solution, which is very close to the optimal solution.

The experimental results are reported in

Table 2. Performance of the proposed procedures.

$\mathit{SR}$	$\mathit{SBB}$	$\mathit{UN}$	$\%\mathit{S}$	$\mathit{MT}$	$\mathit{MG}$	$\mathit{MaxG}$
1690	605	265	89.65	47.44	2.40	10.97

,

Table 3. Performance of the proposed procedures according to the number of jobs.

n	$\mathit{SR}$	$\mathit{SBB}$	$\mathit{UN}$	$\%\mathit{S}$	$\mathit{MT}$	$\mathit{MG}$	$\mathit{MaxG}$
10	161	159	0	100.00	0.34	0.00	0.00
20	198	66	56	82.50	82.49	2.71	9.35
30	201	67	52	83.75	51.17	4.09	10.97
40	216	68	36	88.75	37.05	3.08	9.33
50	209	72	39	87.81	75.25	2.90	7.89
100	228	61	31	90.31	46.49	0.98	5.19
150	234	58	28	91.25	44.28	0.35	1.44
200	243	54	23	92.81	51.35	0.37	1.11

,

Table 4. Performance of the proposed procedures with respect to the number of machines.

$({\mathit{m}}_1,{\mathit{m}}_2)$	$\mathit{SR}$	$\mathit{SBB}$	$\mathit{UN}$	$\%\mathit{S}$	$\mathit{MT}$	$\mathit{MG}$	$\mathit{MaxG}$
(2,2)	332	238	70	89.06	75.93	2.35	10.97
(2,4)	537	99	4	99.38	7.43	0.39	0.54
(4,2)	545	87	8	98.75	26.81	2.05	6.60
(4,4)	276	181	183	71.41	96.15	2.48	9.35

,

Table 5. Performance of the proposed procedures according to $m_1$, $m_1$ and n.

n	$({\mathit{m}}_1,{\mathit{m}}_2)$	$\mathit{SR}$	$\mathit{SBB}$	$\mathit{UN}$	$\%\mathit{S}$	$\mathit{MT}$	$\mathit{MG}$	$\mathit{MaxG}$
10	(2,2)	21	59	0	100.00	0.97	0.00	0.00
10	(2,4)	61	19	0	100.00	0.09	0.00	0.00
10	(4,2)	63	17	0	100.00	0.07	0.00	0.00
10	(4,4)	16	64	0	100.00	0.20	0.00	0.00
20	(2,2)	31	32	17	78.75	145.08	1.55	6.38
20	(2,4)	74	4	2	97.50	0.16	0.43	0.45
20	(4,2)	71	5	4	95.00	2.70	3.43	6.60
20	(4,4)	22	25	33	58.75	264.27	3.36	9.35
30	(2,2)	35	29	16	80.00	73.38	4.35	10.97
30	(2,4)	69	11	0	100.00	7.71	0.00	0.00
30	(4,2)	72	7	1	98.75	25.08	2.19	2.19
30	(4,4)	25	20	35	56.25	142.68	4.02	8.99
40	(2,2)	41	27	12	85.00	85.54	2.90	7.97
40	(2,4)	70	10	0	100.00	3.81	0.00	0.00
40	(4,2)	73	6	1	98.75	10.58	0.23	0.23
40	(4,4)	32	25	23	71.25	62.54	3.29	9.33
50	(2,2)	42	26	12	85.00	121.42	2.23	5.95
50	(2,4)	66	12	2	97.50	12.35	0.36	0.54
50	(4,2)	66	14	0	100.00	67.06	0.00	0.00
50	(4,4)	35	20	25	68.75	119.27	3.43	7.89
100	(2,2)	54	21	5	93.75	51.59	0.83	3.35
100	(2,4)	67	13	0	100.00	10.72	0.00	0.00
100	(4,2)	63	16	1	98.75	39.79	0.19	0.19
100	(4,4)	44	11	25	68.75	101.18	1.04	5.19
150	(2,2)	56	19	5	93.75	62.46	0.29	0.61
150	(2,4)	65	15	0	100.00	4.46	0.00	0.00
150	(4,2)	64	15	1	98.75	38.04	0.06	0.06
150	(4,4)	49	9	22	72.50	84.17	0.37	1.44
200	(2,2)	52	25	3	96.25	87.50	0.52	0.79
200	(2,4)	65	15	0	100.00	20.04	0.00	0.00
200	(4,2)	73	7	0	100.00	29.99	0.00	0.00
200	(4,4)	53	7	20	75.00	75.18	0.35	1.11

,

Table 6. Performance of the proposed procedures for rates $[a:b:c]$.

a	b	c	$\mathit{SR}$	$\mathit{SBB}$	$\mathit{UN}$	$\%\mathit{S}$	$\mathit{MT}$	$\mathit{MG}$	$\mathit{MaxG}$
20	20	20	183	100	37	88.44	57.81	2.09	7.97
20	20	40	258	54	8	97.50	21.89	0.61	1.77
20	40	20	151	85	84	73.75	68.58	3.21	9.89
20	40	40	230	69	21	93.44	26.22	0.65	3.41
40	20	20	255	64	1	99.69	37.26	0.13	0.13
40	20	40	201	97	22	93.13	62.43	2.12	8.30
40	40	20	234	64	22	93.13	51.40	1.24	6.60
40	40	40	178	72	70	78.13	63.45	2.82	10.97

and

Table 7. Performance of the proposed procedures for rates $[20:40:20]$.

n	$({\mathit{m}}_1,{\mathit{m}}_2)$	$\mathit{SR}$	$\mathit{SBB}$	$\mathit{UN}$	$\%\mathit{S}$	$\mathit{MT}$	$\mathit{MG}$	$\mathit{MaxG}$
10	(2,2)	0	10	0	100.00	2.62	0.00	0.00
10	(2,4)	8	2	0	100.00	0.07	0.00	0.00
10	(4,2)	10	0	0	100.00	0.00	0.00	0.00
10	(4,4)	1	9	0	100.00	0.34	0.00	0.00
20	(2,2)	0	4	6	40.00	450.03	1.12	2.06
20	(2,4)	10	0	0	100.00	0.00	0.00	0.00
20	(4,2)	8	1	1	90.00	0.12	0.45	0.45
20	(4,4)	0	1	9	10.00	891.60	5.21	9.35
30	(2,2)	1	4	5	50.00	131.18	3.99	9.89
30	(2,4)	9	1	0	100.00	0.03	0.00	0.00
30	(4,2)	9	0	1	90.00	0.06	2.19	2.19
30	(4,4)	0	1	9	10.00	12.80	6.43	8.99
40	(2,2)	2	6	2	80.00	119.76	5.70	6.00
40	(2,4)	8	2	0	100.00	0.02	0.00	0.00
40	(4,2)	8	2	0	100.00	60.18	0.00	0.00
40	(4,4)	0	1	9	10.00	618.80	4.37	9.33
50	(2,2)	0	3	7	30.00	34.02	2.67	5.74
50	(2,4)	7	2	1	90.00	25.87	0.17	0.17
50	(4,2)	7	3	0	100.00	180.22	0.00	0.00
50	(4,4)	0	1	9	10.00	608.89	4.71	7.89
100	(2,2)	3	5	2	80.00	150.55	1.72	3.35
100	(2,4)	9	1	0	100.00	0.19	0.00	0.00
100	(4,2)	7	3	0	100.00	60.73	0.00	0.00
100	(4,4)	0	1	9	10.00	794.24	1.57	5.19
150	(2,2)	4	4	2	80.00	183.11	0.12	0.12
150	(2,4)	6	4	0	100.00	0.92	0.00	0.00
150	(4,2)	7	2	1	90.00	15.37	0.06	0.06
150	(4,4)	4	1	5	50.00	31.95	0.64	1.25
200	(2,2)	3	6	1	90.00	152.37	0.33	0.33
200	(2,4)	7	3	0	100.00	107.97	0.00	0.00
200	(4,2)	10	0	0	100.00	2.53	0.00	0.00
200	(4,4)	3	2	5	50.00	202.18	0.42	1.11

. More precisely, Table 2 is presenting the overall results. In Table 3, the impact of the number of jobs n on the performance of the proposed procedures is displayed. The effect of the machines’ distribution $(m_1,m_2)$ on the efficiency and performance of the developed algorithms is presented. Table 5 presents the results considering the simultaneous impact of n, $m_1$, and $m_2$ on the performance of the presented procedures. The effect of the rates $[a:b:c]$ on the behavior of the proposed procedures is presented in Table 6.

A summary of the general experimental results is displayed in Table 2.

Based on Table 2, one can observe that the percentage of solved test problems at the root node is $66.02\%$ (1960 out of 2560). This is evidence of the efficiency of the proposed lower bounds and the heuristic algorithm. Furthermore, the B&B procedure is able to solve $23.63\%$ (605 out of 2560) of the test problems and $77.56\%$ of the unsolved test problems (605 out of 870 unsolved test problems at the root node). Solving a test problem requires on average only $47.44$ s, which is a moderate computational time. In addition, the unsolved test problems present an average relative gap of $2.4\%$. All the presented results provide evidence of the efficiency and the effectiveness of the proposed procedure in solving even large size instances (up to 200 jobs) in a moderate CPU time.

The effect of the number of jobs on different results is presented in Table 3.

Based on Table 3 and as expected, for $n=10$, all the test problems were solved even if approximately $50\%$ (159 out of 320) were considered using the B&B algorithm. In addition, for $n=10$, the average time for solving the test problems reached its minimum with $MT=0.34$ s. The minimum solved percentage ($\%S$) is reached, respectively, for $n=20$ and $n=30$, with respective values $82.5\%$ and $83.75\%$. In addition, for $n=20$ and $n=30$, the maximum $MaxG$ (maximum gap) are reached with $MaxG=9.35$ and $MaxG=10.97$, respectively. For $n=20$, the maximum $MT$ is reached with $MT=82.49$ s. The percentage of solved test problems is increasing as the number of jobs is increasing from $n=40$ onward. Furthermore, the average relative gap is decreasing as the number of jobs increases from $n=40$ onward. Except for $n=10$, the highest percentage of solved test problems $92.81\%$ is reached for $n=200$. This means that the developed procedures perform well for the large size test problems.

The effect of the distribution of the machines in the two stages is reported in Table 4.

According to Table 4, the unbalanced $(m_1\ne m_2)$ distributions of the machines ($(m_1,m_2)=(2,4)$; $(4,2)$) present the easiest test problems to be solved. Indeed, for these latter distributions, almost all the test problems are solved, and the respective percentages of the solved problems are $99.38\%$ and $98.75\%$. In addition, for the unbalanced distributions, the maximum gap $MaxG$ as well as the average time $MT$ are reaching their minimum. The balanced $(m_1=m_2)$ distributions ($(2,2)$;$(4,4)$) are the hardest ones to be solved and the respective $\%S$ are $89.06\%$ and $71.41\%$. For the balanced distributions, one can observe that $\%S$ is decreasing as the number of machines increases. Therefore, the proposed procedures are favorable for the unbalanced distribution of machines.

Detailed results considering the number of jobs n and machines in the stages $m_1$ and $m_2$ are presented in Table 5.

Based on Table 5, the easiest test problems to be solved are the ones with unbalanced machine distribution and a large number of jobs ($n=200$, $(m_1,m_2)=(2,4);(4,2)$), where the percentage of solved problems reaches $100\%$. In addition, the hardest test problems are those with $n=30$ and $(m_1,m_2)=(4,4)$), where the $\%S$ reaches its minimum, which is $56.25\%$.

The effect of the rates [a: b: c] on the performance of the proposed procedures results is presented in Table 6.

Based on Table 6, the rates $[40:20:20]$, where the removal time in the first stage is more important compared to the other parameters (processing times, transportation times, and removal time in the first stage), presents the highest percentage of solved test problems, which is $99.69\%$. Since the studied problem is symmetric, a comparable behavior is expected for the rates $[20:20:40]$. For these rates $[20:20:40]$, the percentage of solved test problems is $97.5\%$. The least $\%S$ is reached for the rates $[20:40:20]$ with a value of $73.75\%$, which corresponds to the case where the transportation times are the most important parameter. In addition, the removal times are dominating the transportation times in terms of importance. Indeed, in the cases where $a=40$ or $c=40$, the value of the rate b is not affecting the results.

In order to identify the reasons behind the lowest percentage ($73.75\%$) of solved test problems for the rates $[20:40:20]$, the detailed results are presented for these rates in Table 7.

Based on Table 7, the lowest value of $\%S$ is reached for $(m_1,m_2)=(4,4)$, $n=20$, $n=30$, $n=40$, $n=50$, and $n=100$, where the percentage of solved test problems is only $10\%$. Even for $(m_1,m_2)=(4,4)$, $n=150$, and $n=200$, the percentage of solved test problems is $50\%$. Clearly for the rates $[20:40:20]$ and $[40:40:40]$, the hardest test problems to be solved are those with the highest balanced load: $a=c$, $m_1=m_2=4$, and the transportation times ($b=40$).

7. Conclusions

The two-stage hybrid flow shop scheduling problem with transportation and removal times is addressed in this work. A heuristic algorithm composed of two phases is proposed. In addition, two efficient lower bounds are presented. Furthermore, a Branch and Bound exact procedure is developed. The solution to the parallel machine scheduling problem with release dates and delivery times plays a key role in the development of the proposed algorithms.

Furthermore, a set of low complexity lower bounds are proposed within the Branch and Bound exact procedure in addition to several efficient dominance rules. All these procedures are evaluated over an extensive experimental study using benchmark test problems. The computational results show the efficiency and the performance of these procedures.

Future research could focus on solving extensions of the current studied problem by considering hybrid flow shop scheduling problems with more than two stages. In addition, several other restrictions might be included to the addressed problem by including, for example, the release dates and the delivery times.