Regularity and Travelling Wave Profiles for a Porous Eyring–Powell Fluid with Darcy–Forchheimer Law
Abstract
:1. Introduction
Fluid Model Principles
2. Existence and Uniqueness of Solutions
3. Travelling Waves Existence and Regularity
3.1. Geometric Perturbation Theory
3.2. Travelling Waves Profiles
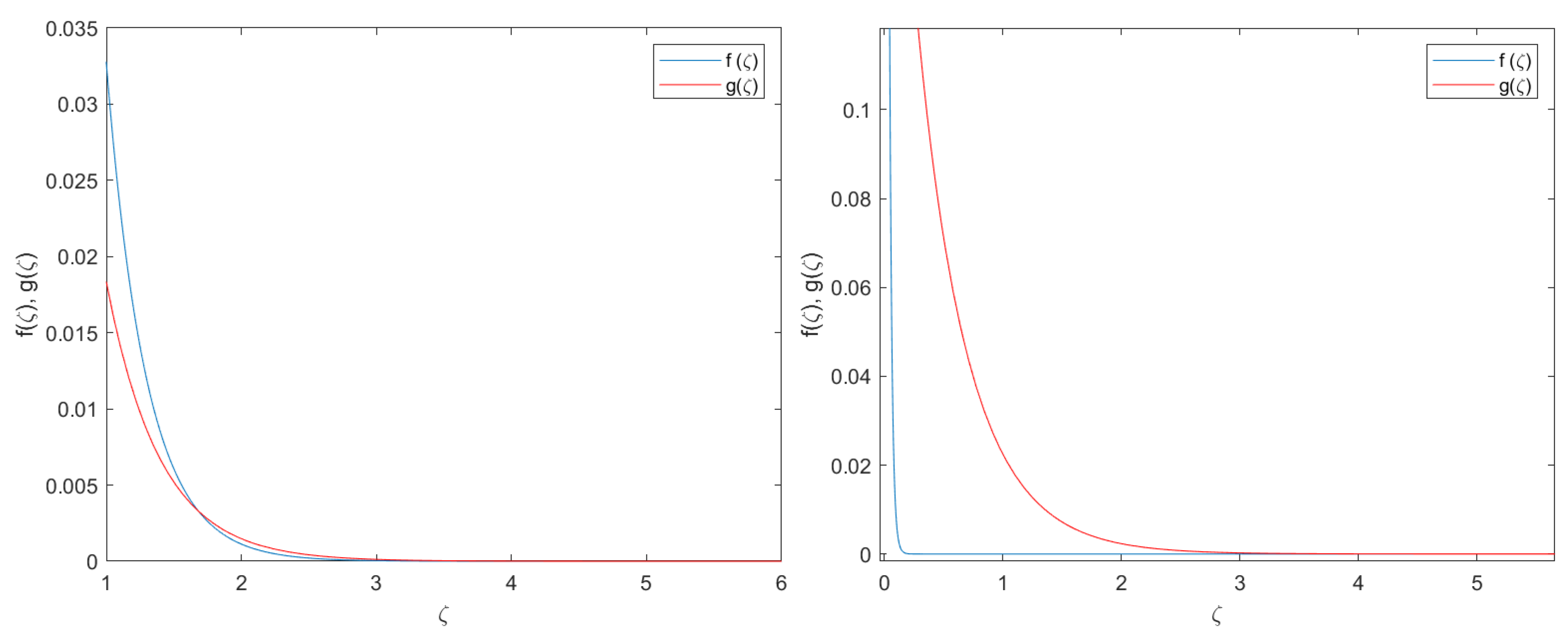
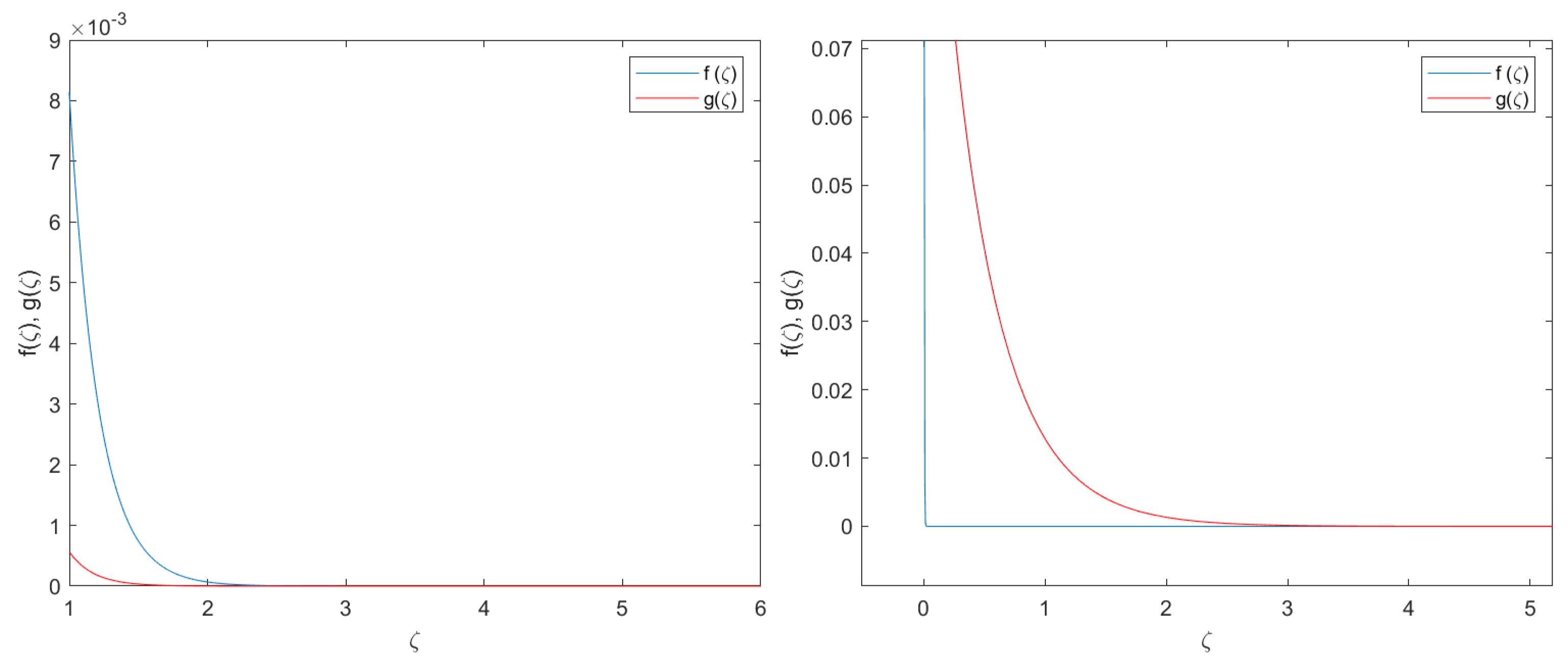
4. Numerical Validation
- The numerical approach is done with the Matlab function bvp4c. This function is based on a Runge–Kutta implicit approach with interpolant extensions [38]. The bvp4c has a collocation method at the pseudo-boundary conditions given by and .
- The influence of the pseudo-boundary conditions and the collocation method shall be minimized. To this end, the integration domain is sufficiently large .
- To make the problem tractable in terms of computational efforts, the integration domain has been split into 100,000 nodes with an absolute accumulated error of . With this level of discretization, the problem has been simulated with standard computers and with reasonable computational lead times.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Dalmont: Paris, France, 1856. [Google Scholar]
- Forchheimer, P. Wasserbewegung durch Boden. Z. Vereines Dtsch. Ingeneieure 1901, 45, 1782–1788. [Google Scholar]
- Jaeger, C. Engineering Fluid Mechanics; Blackie and Son: Edinburgh, UK, 1956. [Google Scholar]
- Mohapatra, S.C.; Fonseca, R.B.; Soares, C.G. Comparison of Analytical and Numerical Simulations of Long Nonlinear Internal Solitary Waves in Shallow Water. J. Coast. Res. 2018, 34, 928–938. [Google Scholar] [CrossRef]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; McGraw-Hill Book Company: New York, NY, USA, 1937. [Google Scholar]
- Ward, J.C. Flujo turbulento en medios porosos. Actas Div. Hidráulica Rev. ASCE 1964, 5, 1–12. [Google Scholar]
- Pal, D.; Mondal, H. Hydromagnetic convective diffusion of species in Darcy–Forchheimer porous medium with nonuniform heat source/sink and variable viscosity. Int. Commun. Heat Mass Transf. 2012, 39, 913–917. [Google Scholar] [CrossRef]
- Ganesh, N.A.; Hakeem, A.K.A.; Ganga, B. Darcy–Forchheimer flow of hydromagnetic nanofluid over a stretching/shrinking sheet in a thermally stratified porous medium with second order slip, viscous and ohmic dissipations effects. Ain Shams Eng. J. 2018, 9, 939–951. [Google Scholar] [CrossRef] [Green Version]
- Haq, R.U.; Soomro, F.A.; Mekkaouic, T.; Al-Mdallal, Q.M. MHD natural convection flow enclosure in a corrugated cavity filled with a porous medium. Int. J. Heat Mass Transf. 2018, 121, 1168–1178. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Al-Mezal, S.; Liao, S.J. Darcy–Forchheimer flow with variable thermal conductivity and Cattaneo-Christov heat flux. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2355–2369. [Google Scholar] [CrossRef]
- Abbas, W.; Megahed, A.M. Powell-Eyring fluid flow over a stratified sheet through porous medium with thermal radiation and viscous dissipation. AIMS Math. 2021, 6, 13464–13479. [Google Scholar] [CrossRef]
- Akbar, N.S.; Ebaid, A.; Khan, Z. Numerical analysis of magnetic field effects on Eyring–Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater. 2015, 382, 355–358. [Google Scholar] [CrossRef]
- Hina, S. MHD peristaltic transport of Eyring–Powell fluid with heat/mass transfer, wall properties and slip conditions. J. Magn. Magn. Mater. 2016, 404, 148–158. [Google Scholar] [CrossRef]
- Bhatti, M.; Abbas, T.; Rashidi, M.; Ali, M.; Yang, Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef] [Green Version]
- Ara, A.; Khan, N.A.; Khan, H.; Sultan, F. Radiation effect on boundary layer flow of an Eyring–Powell fluid over an exponentially shrinking sheet. Ain-Shams Eng. J. 2014, 5, 1337–1342. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Iqbal, Z.; Qasim, M.; Obaidat, S. Steady flow of an Eyring Powell fluid over a moving surface with convective boundary conditions. Int. J. Heat Mass Transf. 2012, 55, 1817–1822. [Google Scholar] [CrossRef]
- Hayat, T.; Awais, M.; Asghar, S. Radiative effects in a threedimensional flow of MHD Eyring–Powell fluid. J. Egypt Math. Soc. 2013, 21, 379–384. [Google Scholar] [CrossRef] [Green Version]
- Jalil, M.; Asghar, S.; Imran, S.M. Self similar solutions for the flow and heat transfer of Powell-Eyring fluid over a moving surface in parallel free stream. Int. J. Heat Mass Transf. 2013, 65, 73–79. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Farooq, M.A.; Alsaedi, A.; Liao, S.J. On model for three-dimensional flow of nanofluid: An application to solar energy. J. Mol. Liq. 2014, 194, 41–47. [Google Scholar] [CrossRef]
- Arshad, R.; Ellahi, R.; Sait, S.M. Role of hybrid nanoparticles in thermal performance of peristaltic flow of Eyring–Powell fluid model. J. Therm. Anal. Calorim. 2021, 143, 1021–1035. [Google Scholar]
- Díaz, J.L.; Rahman, S.; García-Haro, J.M. Heterogeneous Diffusion, Stability Analysis, and Solution Profiles for a MHD Darcy–Forchheimer Model. Mathematics 2022, 10, 20. [Google Scholar] [CrossRef]
- Murray, J. Mathematical Biology. In Biomathematics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Smolle, J. Shock Waves and Reactiondiffusion Equations; Springer Science Business Media: Berlin/Heidelberg, Germany, 2012; Volume 258. [Google Scholar]
- Champneys, A.; Hunt, G.; Thompson, J. Localization and Solitary Waves in Solid Mechanics; Advanced Series in Nonlinear Dynamics; World Scientific: Singapore, 1999. [Google Scholar]
- Kumar, R.N.; Jyothi, A.M.; Alhumade, H.; Gowda, R.J.P.; Alam, M.M.; Ahmad, I.; Gorji, M.R.; Prasannakumara, B.C. Impact of magnetic dipole on thermophoretic particle deposition in the flow of Maxwell fluid over a stretching sheet. J. Mol. Liq. 2021, 334, 116494. [Google Scholar] [CrossRef]
- Al-Mubaddel, F.S.; Farooq, U.; Al-Khaled, K.; Hussain, S.; Khan, S.U.; Aijaz, M.; Rahimi-Gorji, M.; Waqas, H. Double stratified analysis for bioconvection radiative flow of Sisko nanofluid with generalized heat/mass fluxes. Phys. Scr. 2021, 96, 5. [Google Scholar] [CrossRef]
- Dehghan, M.; Salehi, R. A meshfree weak-strong (MWS) form method for the unsteady magnetohydrodynamic (MHD) flow in pipe with arbitrary wall conductivity. Comput. Mech. 2013, 52, 1445–1462. [Google Scholar] [CrossRef]
- Dehghan, M.; Mirzaei, D. Meshless Local Petrov-Galerkin (MLPG) method for the unsteady magnetohydrodynamic (MHD) flow through pipe with arbitrary wall conductivity. Appl. Numer. Math. 2009, 59, 1043–1058. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. A finite volume spectral element method for solving magnetohydrodynamic (MHD) equations. Appl. Numer. Math. 2011, 61, 1–23. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M. Error analysis and numerical simulation of magnetohydrodynamics (MHD) equation based on the interpolating element free Galerkin (IEFG) method. Appl. Numer. Math. 2019, 137, 252–273. [Google Scholar] [CrossRef]
- Hosseinzadeh, H.; Dehghan, M.; Mirzaei, D. The boundary elements method for magneto-hydrodynamic (MHD) channel flows at high Hartmann. Appl. Math. Model. 2013, 37, 2337–2351. [Google Scholar] [CrossRef]
- Eldabe, N.; Hassan, A.; Mohamed, M.A. Effect of couple stresses on the MHD of a non-Newtonian unsteady flow between two parallel porous plates. Z. Fur Naturforschung A 2003, 58, 204–210. [Google Scholar] [CrossRef] [Green Version]
- De Pablo, A. Estudio de Una Ecuación de Reacción—Difusión. Ph.D. Thesis, Universidad Autónoma de Madrid, Madrid, Spain, 1989. [Google Scholar]
- De Pablo, A.; Vázquez, J.L. Travelling waves and finite propagation in a reactiondiffusion Equation. J. Differ. Equ. 1991, 93, 19–61. [Google Scholar] [CrossRef] [Green Version]
- Fenichel, N. Persistence and smoothness of invariant manifolds for flows. Indiana Univ. Math. J. 1971, 21, 193–226. [Google Scholar] [CrossRef]
- Akveld, M.E.; Hulshof, J. Travelling Wave Solutions of a Fourth-Order Semilinear Diffusion Equation. Appl. Math. Lett. 1998, 11, 115–120. [Google Scholar] [CrossRef] [Green Version]
- Jones, C.K.R.T. Geometric Singular Perturbation Theory in Dynamical Systems; Springer: Berlín, Germany, 1995. [Google Scholar]
- Enright, H.; Muir, P.H. A Runge-Kutta Type Boundary Value ODE Solver with Defect Control; Technical Reports; University of Toronto, Department of Computer Sciences: Toronto, ON, Canada, 1993; Volume 267, p. 93. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz Palencia, J.L.; Rahman, S.u.; Redondo, A.N.; Roa González, J. Regularity and Travelling Wave Profiles for a Porous Eyring–Powell Fluid with Darcy–Forchheimer Law. Symmetry 2022, 14, 1451. https://doi.org/10.3390/sym14071451
Díaz Palencia JL, Rahman Su, Redondo AN, Roa González J. Regularity and Travelling Wave Profiles for a Porous Eyring–Powell Fluid with Darcy–Forchheimer Law. Symmetry. 2022; 14(7):1451. https://doi.org/10.3390/sym14071451
Chicago/Turabian StyleDíaz Palencia, José Luis, Saeed ur Rahman, Antonio Naranjo Redondo, and Julián Roa González. 2022. "Regularity and Travelling Wave Profiles for a Porous Eyring–Powell Fluid with Darcy–Forchheimer Law" Symmetry 14, no. 7: 1451. https://doi.org/10.3390/sym14071451
APA StyleDíaz Palencia, J. L., Rahman, S. u., Redondo, A. N., & Roa González, J. (2022). Regularity and Travelling Wave Profiles for a Porous Eyring–Powell Fluid with Darcy–Forchheimer Law. Symmetry, 14(7), 1451. https://doi.org/10.3390/sym14071451






