Abstract
The automated manufacturing systems (AMS) can be regarded as a resource allocation system which can be abstracted as discrete event systems (DES) for analysis. Once an effective computational method is put forward to the DES, the corresponding real AMS, connected by networks or sensors, can be indirectly controlled. Supervisory control theory (SCT) of DES is developed with the intention of discovering the maximally permissible supervisor of AMS. The state-tree structure (STS) is an extension of SCT, whose application is mainly to solve the SCT state explosion of complicated AMS. The nonblocking supervisory control is investigated on the foundation of predicates in STS, of which the synthesis focuses on the states of the system but ignores the transition between events. In order to effectively solve the above problems, this paper puts forward a novel method based on state feedback control (SFBC) in the STS framework, by which the relation among events is discussed. First, following the definition of the SFBC for predicates, the algorithms to compute the SFBC under reachability, coreachability, and weak controllability are introduced. Second, it is proved that the nonblocking SFBC obtained by the proposed algorithm is equivalent to the one by computing predicates first, which ensures the satisfactory controllers for the supervisory control problems. To demonstrate the contribution of the proposed approach, which is designed considering the symmetry of the system behavior between the real system and its STS model, three examples are illustrated.
1. Introduction
As the Industrial 4.0 is developing rapidly, automated manufacturing systems (AMS) have been extensively employed to achieve managing and manufacturing process automation. In the AMS, the human intervention operation is eliminated, and the management process and technological process are fully automated. To realize the supervision and control of this process, the cooperation of software and hardware equipment is necessary. Therefore, an effective supervisory controller is of vital importance to achieve the smooth operation of the AMS.
The AMS can be regarded as a resource allocation system, and the supervisory controller is responsible for supervising the resource allocation in the control system [1,2,3,4]. The trajectories of such systems in space and time are discrete, so it is able to be extracted as a discrete-event system (DES) before investigation [5,6,7,8,9,10,11,12,13]. In the 1980s, Ramadge and Wonham put forward SCT in their research, which is also regarded as the Ramadge–Wonham (RW) framework [14,15,16] that offers a mathematical method with the intention of analyzing and controlling DES. On the other hand, for systems with high complexity, the completion of analysis work must be based on large-scale automated model. Based on this, a key obstacle faced by SCT is state explosion due to the sophistication of the controllers. For the purpose of effectively solving this problem, Ma and Wonham proposed a novel DES framework, which is named state-tree structures (STS) [17,18]. The research found a method that can make full use of STS to complete DES modeling. Hierarchical state-tree as well as the dynamic module, which is named holons (inspired by [19]), can be used to describe its concurrency and hierarchy. Both for the horizontal and vertical level, STS is equipped with the corresponding structure to model the system. In addition, in order to offer a compact representation of state-tree, a binary decision diagram (BDD) is proposed [20]. BDD can lay a good foundation for the optimization of supervisory control calculation. The application of BDD is conducive to the improvement of calculation efficiency, and can also have a positive impact on the representation of complex models in [21,22]. For predicates, in the case of displaying BDD, the number of nodes of BDD can directly determine the complexity of the method used in [17], rather than the state size of the model. In the actual operation process, the size of states is much larger than that of BDD nodes, so the utilization of BDD in the calculation of the supervisors can obtain more effective results.
In the last few years, many scholars have conducted a lot of research on the basis of STS. Some supervisory control (SC) problems with observation are analyzed and discussed, and several subpredicates such as the weakly controllable, coreachable, and observable (WCCO) subpredicate are calculated so as to settle the STS control problem under various situations in [23,24]. In [25], an STS with conditional-preemption matrices (STSM) is put forward, which is a new STS framework and used to solve various priority problems. At the same time, the optimal non-blocking supervisory control is arranged in the STSM framework. In [26], the symmetry of DES, which has parallel components as well as fixed buffer sizes, is studied with the purpose of extracting the invariance of abstract control functions. In order to ensure the solution of the SC problem of real-time systems (RTS) to the greatest extent, the reference [27] proposes a new RTS modeling framework based on STS to guarantee that tasks with multiple periods can be effectively solved. In this study, priority-free conditionally-preemptive scheduling is utilized with the intention of describing and defining the preemption relationship between different items in RTS. The authors in [28] propose a top-down supervisor localization procedure, which creates the pure distributed control architecture of DES, so it plays a unique role in the control design of large-scale systems. A control logic–failsafe mechanism based on STS is proposed in [29] to solve the problem that dangerous flight maneuvers might be executed when unexpected failures or command conflicts happen. Similarly, to solve the complex system, the studies [30,31,32] develop the decentralized SC of DES by use of STS to manage state explosion, and an independent optimal (maximally permissible) supervisor is prepared by decomposing the specification of the controlled system into several sub-specifications. In addition, the reference [33] gives full play to the role of the nesting method to decompose STS and forms a group of STS nests. So to equip all nests with supervisors, this reference also extends the boundary consistency attributed to ensure that it can cover the supervision control of STS, with the intention of reducing the computational complexity of optimal supervisors. All these conclusions come from the analysis and synthesis of predicates, and the control functions are given by computing the optimal subpredicate, which is represented by BDD. This is of high efficiency to solve the control problems of DES. These studies investigate the computation of supervisors based on predicates representing a suit of state-trees, but lack the discussion of the relation among events under certain constraints.
As is known to all, in [14], a DES is modeled by a controlled automaton, and the formal language, which is produced by the automaton over an alphabet of event, labels the conduction of the DES. The computation of the supervisor is proposed in view of the formal language, which specifies the control strategy. In [17], after standing for predicates by BDD, the specification is given by illegal state-trees, and the supervisor is computed by analyzing if a state-tree satisfies certain conditions. Though the computational complexity of the supervisor is reduced substantially, the relation among events is not discussed. In some cases, two events can occur at one state. In [17], if the state is illegal, the two events are disabled simultaneously, which is not conducive to the analysis of the control functions. To fix this, in this paper, we aim to construct the control functions of controllable events by the means of analyzing the property of the state-feedback control (SFBC) of events for a predicate which is given under reachability, coreachability, and weak controllability, respectively. First, the definition of the SFBC of events for a given predicate is proposed, and the property of the SFBC for predicates are discussed. Second, the definition and computation of the SFBC under reachability, coreachability, and weak controllability are introduced, respectively. Meanwhile, it is proved that the SFBC obtained by the proposed algorithms in this paper is equivalent to the one by computing the subpredicates first, which implies that the controllers obtained based on SFBC are also equivalent to the one on predicates. In summary, by comparison to the study [17], we provide an approach to achieve the aim of resolving the supervisory control problem based on SFBC, which makes the control strategy clearer while ensuring the computation efficiency. Moreover, this paper lays a foundation for the following work since the SFBC of events (indicating the relation between state-trees and events) is very important to the synthesis of the natural projection, and this leads to the development of other research, such as observability and decentralization. Finally, the contribution is demonstrated by two examples: Transfer Line and Small Factory. In addition, Small Factory, with the specification represented by the SFBC with one event disabled at a state-tree, is described with the intention of clarifying the devotion of this research.
The reminder of this study is structured as below. Section 2 is aimed at introducing the background of the STS model, and Section 3 explains the definition and properties of the SFBC of events for predicates. Section 4 emphatically studies the SFBC under reachability, coreachability, and weak controllability, respectively. Algorithms are introduced to compute the SFBC under certain constraints. Section 5 investigates the nonblocking SFBC for a given STS, which also shows the satisfactory solution for supervisory control problems. Section 6 presents three examples, which are Transfer Line, Small Factory, and Guide Way. Section 7 discusses the advantages and disadvantages of this paper. At last, Section 8 comes to a conclusion of this study.
2. Concepts and Terminologies
2.1. Sts Model
This chapter first analyzes and explains the state-tree structures (STS). The state-tree includes two structures, namely horizontal and vertical structure. Secondly, the holon is a local transition graph (see Section 2.1.2) and is assigned to state-tree or OR superstate. Then, the complete form of STS is described, which is the state-tree as well as its related set consisting of holons.
2.1.1. State-Tree
The four-tuple is considered to be a state-tree, where
- X is a structured state set, of which the number is limited;
- is a particular state which is named the root state;
- is the type function;
- is the expansion function, where , and ;
An AND superstate x is used to stand for the Cartesian product of its component, while the OR superstate is for the disjoint union. In fact, the AND superstate implies that its components can be reached simultaneously, while the OR superstate means the exclusion of its components. Shutting off the branches (but not all) which are rooted by OR superstates generates a sub-state-tree whose function is similar to a subset of states in a generator. Especially, a basic-sub-state-tree ensures that every OR superstate must own one component. stands for the basic-sub-state-tree set of . What is more, as the sub-state-tree can be regarded as a state-tree, “sub-state-tree” is able to be expressed as “state-tree”.
2.1.2. Holon
A Holon H is described as , where
- X is the non-null state set, organized as the nonintersecting combination of and , which are the external and internal state set;
- is the event set, which is structured as the nonintersecting combination of and , which are the boundary and internal event set, i.e., ; the event set can also be seen as , where is the uncontrollable event set and is the controllable event set;
- The transition structure is a partial function; this shows the transition between the states in the holon;
- is the initial state set;
- is the terminal state set.
2.1.3. State-Tree Structures
Definition 1.
The six-tuple is considered to be a state-tree structure, where
- is a state-tree.
- is a set of holons which can be matched to OR superstate of , in which a is an OR superstate and is the matching objective for holon, which is to say, portrays the dynamics among units of a as well as the transitions between the upper holon and .
- is the event set which consists of all events that happens in , in which represented the internal event set of .
- is the transition function, in which stands for the set of sub-state-trees of . This is the global transition function, which is different from δ.
- is the initial sub-state-tree.
- is the marker sub-state-tree set.
Similarly, represents a sub-state-tree of into another sub-state-tree. is the source-state-tree that, upon the occurrence of event , transforms to a sub-state-tree of T.
2.2. Predicate
Predicate P described on in [17] is regarded as a function . A predicate is able to be recognized by a set of basic-state-trees, named as , thus
or is stronger compared to indicates that . Quite the opposite, we can find that is weaker than . In other words, means that , where b satisfies only. Furthermore, P holds for , for example, iff .
What is more, is the reachability predicate [17], and it is proposed with the intention of indicating all the basic state-trees reachable form the initial basic state-tree via state-trees satisfying P.
is monotone, i.e., implies . Similarly, is the coreachablity predicate met with the basic state-trees that is able to reach the marker basic state-tree along state-trees satisfying P. As far as fixed G, is a predicate transformer. Clearly, and is monotone.
As is analyzed in [17], the weak controllability of predicates is defined instead of the controllability. By ignoring the condition of the controllability, the calculation expanse is much declined, which is proved to be reasonable since the weak controllability of a predicate P implies the controllability of .
Predicate P is weakly controllable if any event that cannot be controlled takes place at state-trees satisfying P, then the consequential state-trees also satisfy P [17]. This is able to be written as
Let represent the set of weakly controllable subpredicates which are stronger compared to P by
The weakest element sup exists, which indicates that the supremal weakly controllable subpredicate of P exists with sup.
Moreover, the nonblockingness of a predicate P is confirmed if is stronger compared to . P is coreachable if , which indicates the nonblockingness of P, as generally. Considering the coreachability and weakly controllability, as far as predicate P, let represent the set of the subpredicates of P that are weakly controllable, coreachable, and stronger than P [17], i.e.,
In particular, a (unique) supremal element sup exists in , which is given by
Notice that the reachability subpredicate of agrees on the reachability subpredicate of the optimal nonblocking controller, which shows the supremal controller of the supervisory control problems.
The control behavior of an STS is carried out by the utilization of state feedback control (SFBC) [17], and it is described by a set of predicates. Let be an SFBC for , in which . For , clarify a control function (a predicate) on the basis of iff . As a result, the synthesis of the supervisor is carried out by . In consideration of an event , (respectively, 0) indicates that event is allowed (respectively, not allowed) to occur at b. is defined to be equal to 1 for with .
The STS under f is depicted as , where , , and if . Or else, . If is stronger than , the SFBC f is nonblocking. Moreover, if P is weakly controllable and coreachable, it is proved that there does exist a nonblocking SFBC f with .
Example 1.
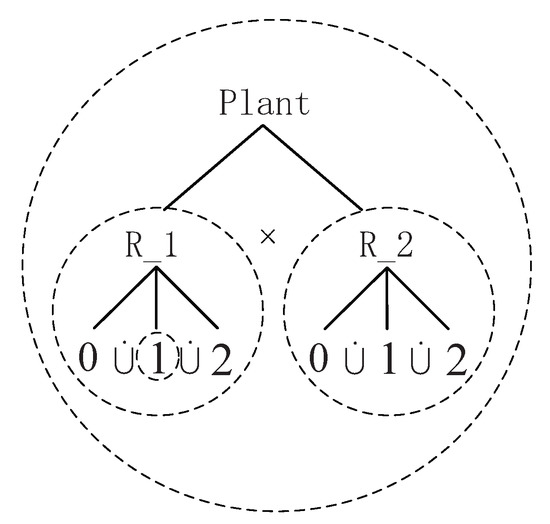
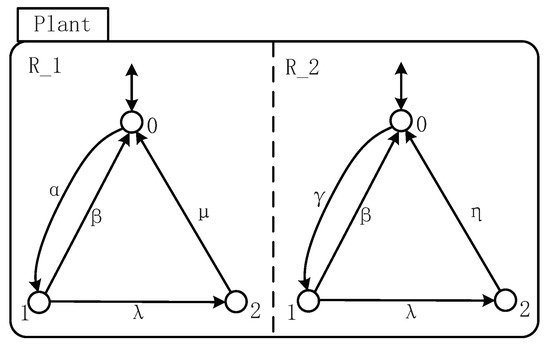
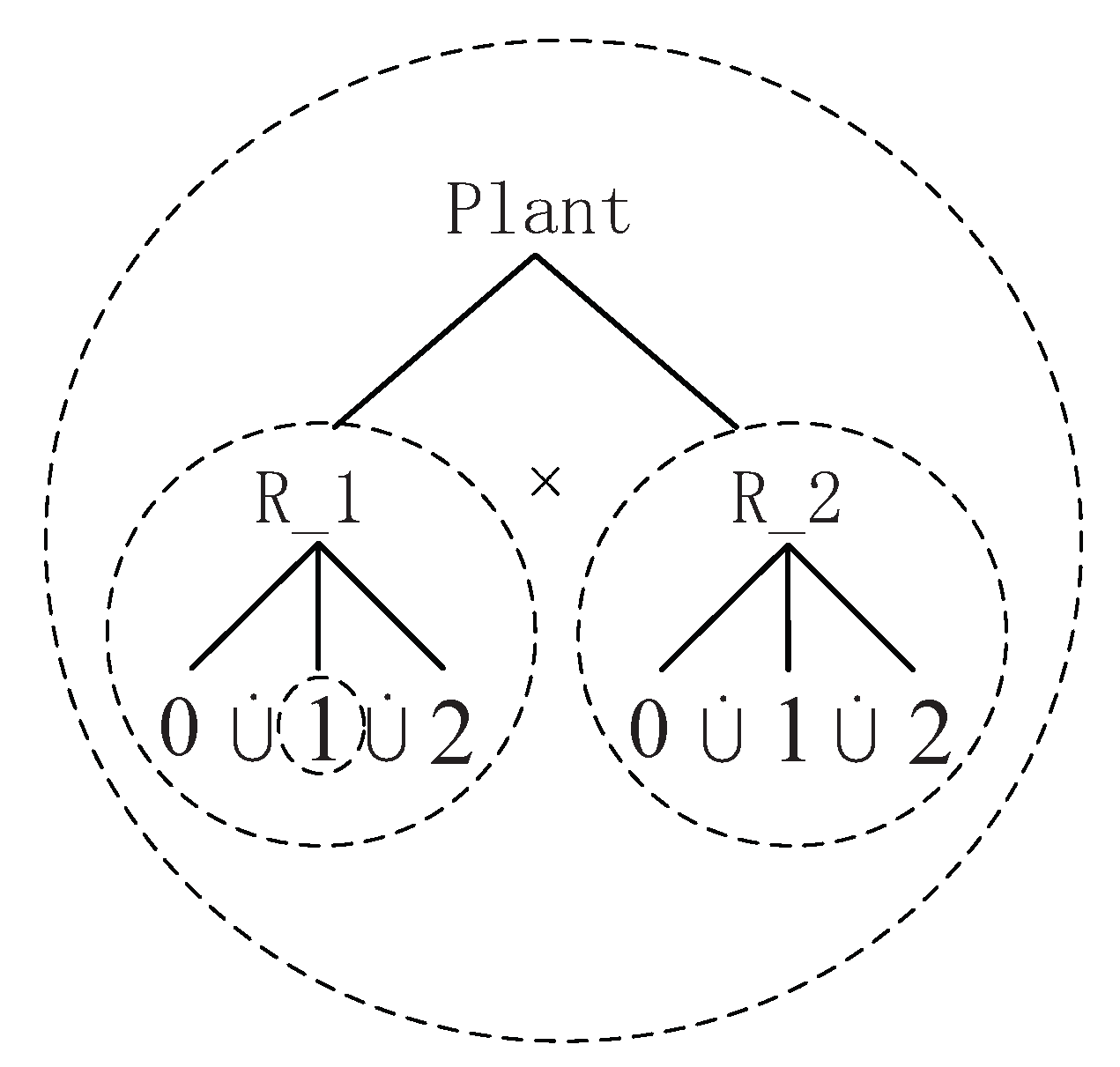
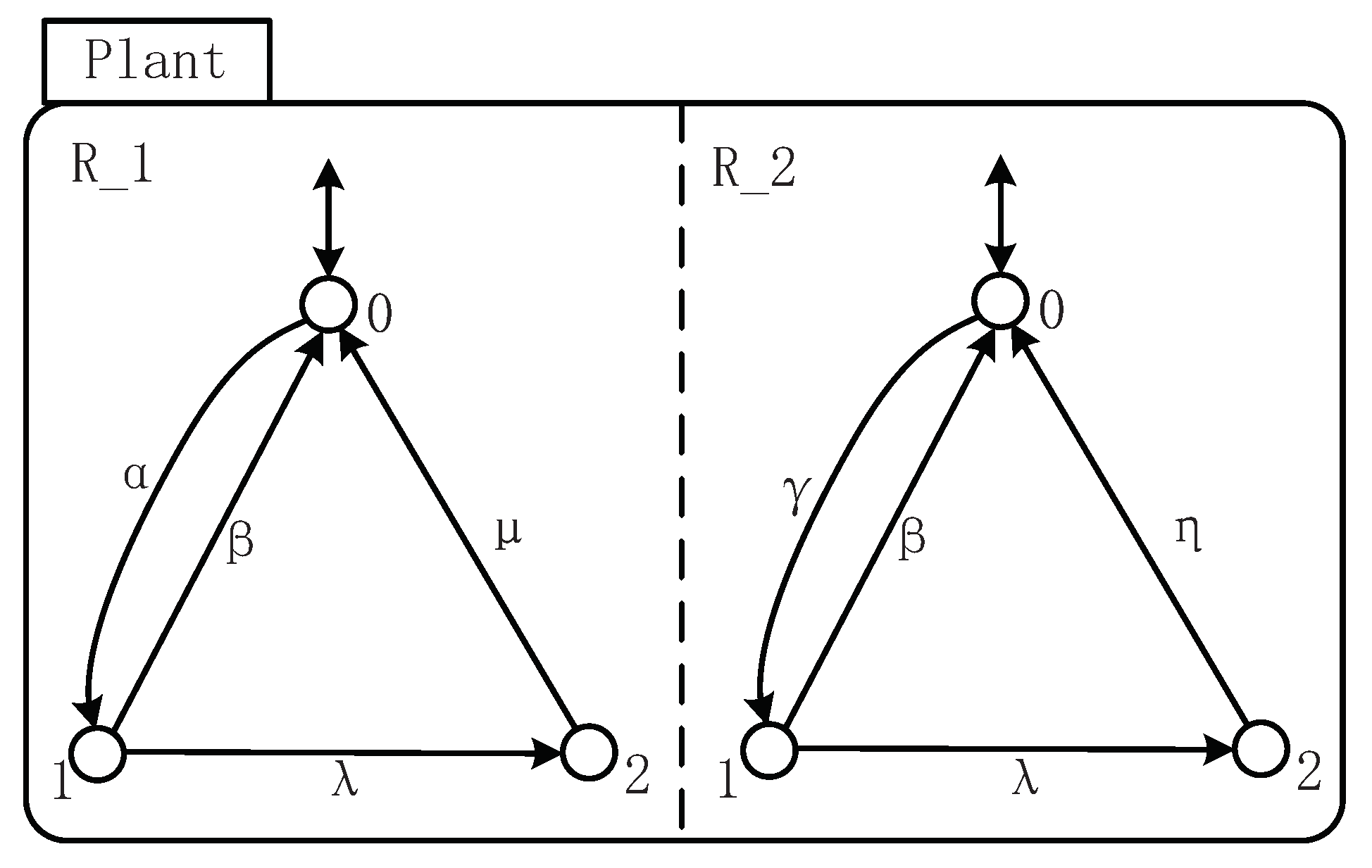
For a small task which must be performed by two machines and , each machine has three states “Idle”, “Work”, and “Breakdown”, and the transition between these states are represented by events α, γβ, λ, μ, and η. α stands for a workpiece arriving machine and γ for machine . The occurrence of β signifies the processing complete. λ is used to represent the damage of the machine, while μ (respectively, η) stands for the repair of machine (respectively, ). Its STS is depicted with the state-tree shown in Figure 1 and holons shown in Figure 2.

Figure 1.
State-tree of the given STS .

Figure 2.
The holons of the given STS .
For the state-tree shown in Figure 1,
- is the root state;
- ;, where , , and represent the components 0, 1, and 2 of , respectively. This means that there are three states in machine which represent the state “Idle”, “Work”, and “Breakdown”;, where , , and represent the components 0, 1, and 2 of , respectively, which represent the state “Idle”, “Work”, and “Breakdown” of machine .
- , implying that and work concurrently;, implying that the states , , and are mutually exclusive, i.e., the system can only reach one state at a time; and, which means the exact states for each machine.
For the holons shown in Figure 2, there are two holons and in this figure. Take as the example.
- The event set ;
- and ;
- ,,, and.
In this example, there is not an upper or lower holon for , which implies that the boundary event does not exist. Holon denotes the transition between the states in machine if one event occurs. Besides, since and are two components of an AND superstate, the holons and are parallel, which means that the shared event (β or λ) occurs simultaneously. For the system composed by two machines and , the system behavior can be described by the following explanation of the STS model.
- ,
- , which stands for the initial state-tree, that is, is at state 0 and is at 0;
- , and
- the transition function Δ is detailed by,,,,,,,, and….
3. Control Functions for Predicates
Since the synthesis of the given STS is proposed in view of a set of state-trees represented by a predicate, the computation complexity is greatly reduced. However, the relation between state-trees and events remains to be discussed. As for this part, with the intention of investigating this while ensuring the computation efficiency, the state feedback control (SFBC) f of controllable events is introduced on the basis of predicates instead of STS (as in [17,18,20]). A control function set is defined with respect to an individual predicate P, which is composed by SFBC f of all controllable events for P. To make the definitions clearer, an example is given in detail.
As known in [17,18,20], is proposed to define the SFBC for , in which
The event is allowed (respectively, not allowed) to occur at basic-state-tree b if (respectively, ). As far as event , the predicate is described by iff . In previous studies, the supervisory control problem is resolved by means of investigating the properties of predicates, which means that the state illegal implies that the related event is ineligible. To avoid this, in this chapter, the SFBC of each event is studied on the basis of a given predicate. First, Definition 2 is introduced.
Definition 2.
Suppose an STS with the controlled STS as for the closed system supervised by the SFBC f. As for the predicate P, an SFBC f of σ on P, denoted by , is defined by
Remark 1.
(1) Simply, the SFBC f of an event σ on P, denoted by , is a predicate and satisfied by any basic-state-tree b if σ is enabled at b and satisfies P, simultaneously. Notice that the event σ can be both controllable and uncontrollable since there might exist . In fact, is a predicate represented by BDD, which ensures the computational efficiency. Meanwhile, shows the relation between state-trees and events for P, which make the computation more fixable and accurate.
(2) represents the set of eligible events at P, i.e., .
(3) Let denote the SFBC for a predicate P with , which is also a predicate.
(4) For defined as a predicate, stands for the set of state-trees satisfying .
(5) means that σ is enabled at b and P is satisfied by the target state-tree.
For a predicate , the control function on over P can be denoted as
Thus, the following proposition is obtained.
Proposition 1.
For predicates and ,
Proof.
With the intention of demonstrating the equation, it is necessary for us to show that and .
- Show that . For , , which implies that . Thus, .
- Prove that . For , or . This means that .
Therefore, as required.
□
Remark 2.
(1) For predicates and , there might exist and with . Thus, , and , implying that is not always true.
(2) Since the SFBC f of σ is a predicate, propositional logic operators are also defined as
Example 2.
In consideration of an STS , which is depicted in Figure 2, suppose a predicate P with and . According to Definition 2, it is easy to know that
- with α is enabled at and satisfying P.
- since γ is eligible at but neither or satisfies P.
- Similarly, .
4. SFBC under Reachability, Coreachablity, and Weak Controllability
Aiming to discuss the supervisory control problem on the foundation of SFBC, better control strategies can be proposed since the control behavior obtained by SFBC is relatively flexible. On the other hand, the introduction of nonblocking supervisory control based on SFBC helps to decline the calculation complexity of controllers. In this section, the reachablity, coreachability, and weak controllability are defined in view of SFBC. Examples are given to explain the definitions.
4.1. The Reachability and Coreachablity
To solve the nonblocking supervisor, the definition and property of the SFBC f of events under reachability and coreachability are investigated, respectively, in this subsection.
is given to be a state-tree structure. The SFBC under reachability over a predicate P can be obtained by
- ;
- ;
- ;
- ;
- No other basic state-tree b satisfies .
Proposition 2.
A predicate P is reachable if
Proof.
To prove this proposition, we need to investigate if , .
It is easy to know that implies and . . And so forth, with , which means that . □
Proposition 3.
With a given STS and a predicate P, let be the SFBC under reachability. For the reachability predicate , the SFBC .
Proof.
To prove , two steps are necessary.
- Prove . If for any state-tree b, . This implies that there exists , and . Thus,…
- Prove . If for any state-tree b, . This implies that there exists with . Considering the definition of reachability predicate, , , , …, . Thus,Therefore, . is proved.
Then, the proposition is proved to be true. □
Besides, implies . According to Proposition 3, if , .
Let be a state-tree structure. The SFBC under reachability over with respect to can be obtained by Algorithm 1.
| Algorithm 1: The SFBC f under reachability. |
 |
Remark 3.
(1) According to this algorithm, any state-tree satisfying is reachable from the initial state-tree;
(2) .
Example 3.
As given in Example 1, suppose a predicate P with and . According to Definition 2, it is easy to know that
- ;
- ;
- There is no other basic-state-tree b that satisfy ;
Thus, and .
It is easy to know that the reachable predicate is satisfied by
and according to Definition 2, and
.
Thus, the SFBC f over any event σ obtained by computing first is equivalent to the .
Similarly, the SFBC f over under coreachablity with respect to a predicate P can be obtained by
- ;
- ;
- ;
- ;
- No other basic state-tree b satisfies .
Remark 4.
(1) According to this statement, any state-tree satisfying is coreachable from the marked state-tree;
(2) ;
(3) For any basic state-tree b, if there exists a string satisfying , then . This means that there must exist with , , …, . Whether a predicate is coreachable or not can be decided by discussing the SFBC as the following proposition.
Proposition 4.
A predicate P is coreachable if
Proof.
To prove this proposition, we need to investigate if , .
It is easy to know that implies and . . Further, with , which means that .
□
Proposition 5.
With a given STS and a predicate P, let be the SFBC under coreachability. For the coreachability predicate , the SFBC .
Proof.
To prove , two steps are necessary.
- Prove . If for any state-tree b, . This implies that there exists , . Thus,
- Prove . If for any state-tree b, . This implies that there exists with . According to the definition of coreachability predicate, , , , …, . Thus,Therefore, is proved.
□
Let be a state-tree structure. The SFBC under coreachability over with respect to can be obtained by Algorithm 2. An example is given to illustrate the algorithm.
| Algorithm 2: The SFBC f under coreachability. |
 |
Example 4.
As given in Example 1, suppose a predicate P with
and . According to the definition of coreachable SFBC, it is easy to know that
- ;
- ;
- ;
- ;
- Similarly, no other basic-state-tree b satisfies .
Thus, for any event σ, there is .
It is easy to know that the coreachable predicate is satisfied by and according to Definition 2, for any event σ, there is .
Thus, the SFBC f over any event σ obtained by computing first is equivalent to the .
4.2. Sfbc under Weakly Controllability
The weakest liberal precondition is the predicate transformer defined as follows:
A predicate is weakly controllable with respect to if
To achieve the aim of resolving the nonblocking control problem, the weak controllability should be investigated. Thus, the definition and property of SFBC under weak controllability are given in this part.
Proposition 6.
A predicate P is weakly controllable with respect to if
Proof.
Suppose an STS with the controlled STS as ,, , , for the closed system which is supervised and controlled by the SFBC f.
(IF) Assume that the predicate is weakly controllable. Thus, . According to the definition, . Therefore, is proved.
(ONLY IF) Assume that Thus, . Then, P is weakly controllable. □
For a predicate P, the family of weakly controllable subpredicates which are stronger compared to P is denoted by . As in [17], for each predicate , there exists SFBC f for to implement . The weak controllability of P ensures that its reachable subpredicate is controllable. As it is known that there exists a unique supremal element sup in , the is controllable and reachable. Thus, the SFBC f for is of vital importance. The SFBC f for , which is controllable and reachable, can be obtained by Algorithm 3.
| Algorithm 3: The SFBC of any event under controllability |
 |
Proposition 7.
For a predicate P, the SFBC f under controllability obtained by computing the predicate ) first is equivalent to by Algorithm 3, i.e., the diagram commutes.
Proof.
To prove that the diagram commutes, we need to show that obtained by Algorithm 3 is equivalent to the . Thus, if or any , the proposition is true. Since , and
Thus, it is easy to know , which means that . Additionally,
…
By the definition of the reachability predicate, , , …, , . Thus, is obvious. Until now, the proposition is proved. □
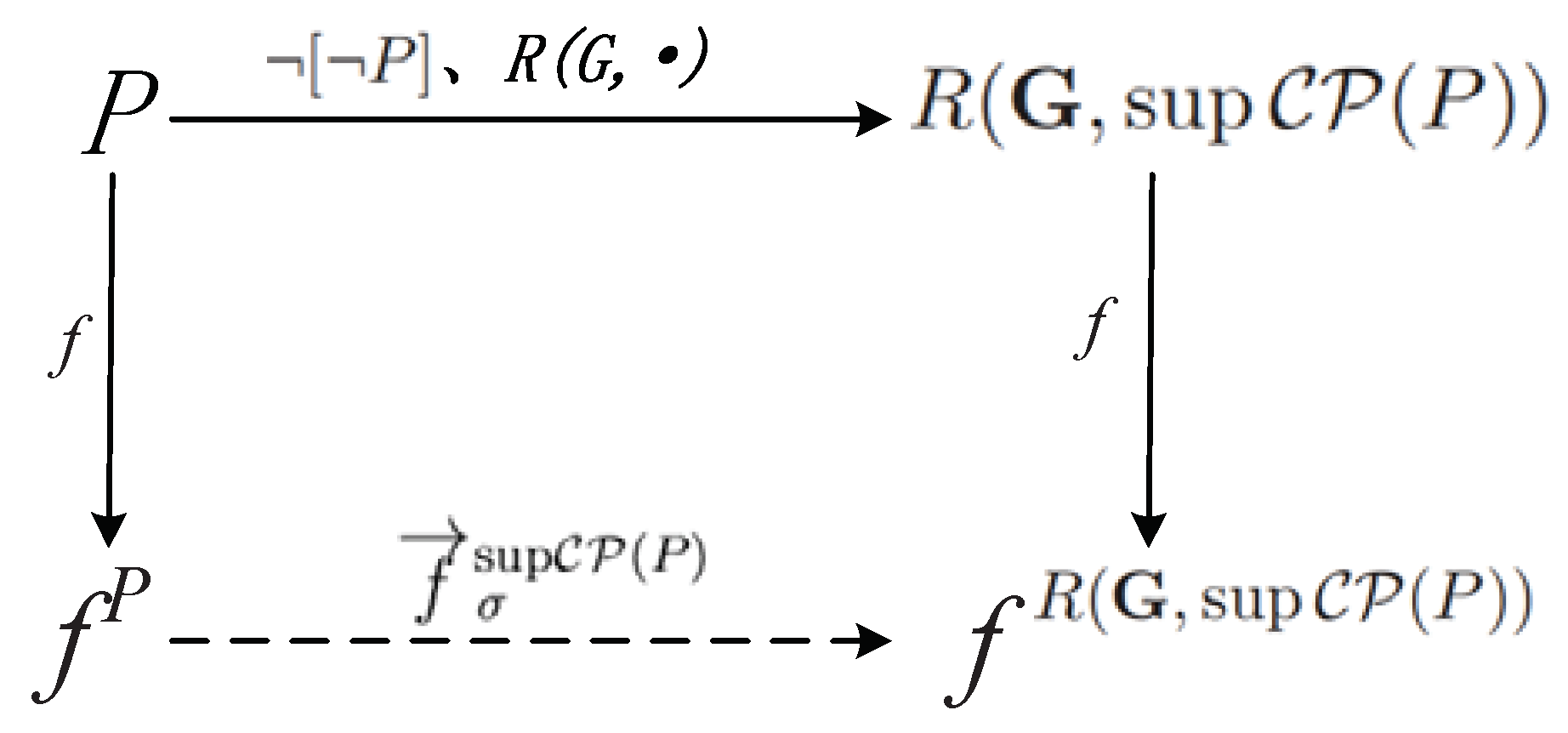
Note that the diagram in Figure 3 shows the relation between the predicate P and the SFBC over the reachability predicate . According to Proposition 7, for a predicate P, can be obtained by computing first and then SFBC over . Similarly, can also be obtained if is computed first. The proof of this diagram in Figure 3 shows the feasibility of Algorithm 3.
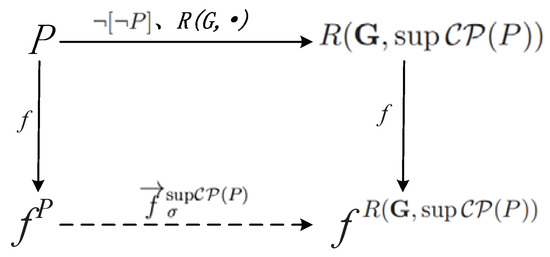
Figure 3.
The relationship between the SFBC and the weakly controllable predicate.
Example 5.
As given in Example 1, suppose a predicate P with
and . According to Algorithm 3, it is easy to know that for ,
- Since , ;
- For , , ;
- For , , ;
- And for , , ;
Thus, for any event σ, and .
It is easy to know that sup is satisfied by and is satisfied by . According to Definition 2, for any event σ, and .
Thus, the SFBC f over any event σ obtained by computing first is equivalent to the .
5. Nonblocking Sfbc for Sts
According to Theorem 3.3 in [17], a nonblocking SFBC f for with exists if P is weakly controllable and coreachable, where and . Notice that our sup is the optimal supervisor that is coreachable instead of nonblocking, where sup is the supremal element of . Furthermore, , where
This means that both controllers agree on their reachable subpredicates and is another optimal nonblocking controller. shows the final controlled behavior. Therefore, the control functions for are necessary to be discussed.
Proposition 8.
For a predicate P, if
- ; and
- .
Proof.
The proposition can be proved by the following two steps:
- 1.
- If , K is coreachable (i.e., ). For any , we need to prove .
- According to the definition of the coreachability predicate, if , , obviously.
- If , there must exists . This implies that and . Iteratively, a string can be obtained, which makes hold. Thus, .
It is proved that if , K is coreachable. - 2.
- If , K is weakly controllable. To prove this, should be discussed. For any , , which means that . Thus, . Thus, K is proved to be weakly controllable.
Therefore, the proposition is proved to be true. □
| Algorithm 4: The SFBC f under controllability and coreachability. |
 |
According to Theorem 3.3 in [17], a nonblocking SFBC f for with exists if P is weakly controllable and coreachable, where and . Since P is weakly controllable, is controllable. Thus, the nonblocking SFBC f under controllability and coreachability shows the control behaviors of the supervisor P, which can be computed according to Algorithm 4.
Remark 5.
According to this algorithm, the nonblocking SFBC f for with can be obtained by the following:
- 1.
- For predicate P, compute the SFBC f under weak controllability by analyzing the SFBC of the uncontrollable events, iteratively, to ensure that the uncontrollable event is not disabled;
- 2.
- Then, compute the SFBC under coreachability by revising the SFBC of any events which cannot lead the system to the marked state-tree;
- 3.
- If the SFBC of any event is not revised, go to Step 4; if not, back to Step 1;
- 4.
- Finally, compute the SFBC under reachability by revising the SFBC of any events which cannot reached by the initial state-tree.
So far, so good. However, we still need to answer an important question. Notice that the sup is the optimal supervisor with and a nonblocking f with exists. The nonblocking SFBC f of events can be obtained by
So the question is, does sup own the same control effect over G as sup?
Proposition 9.
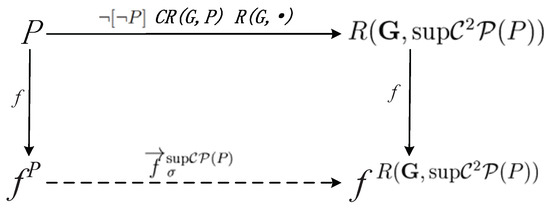
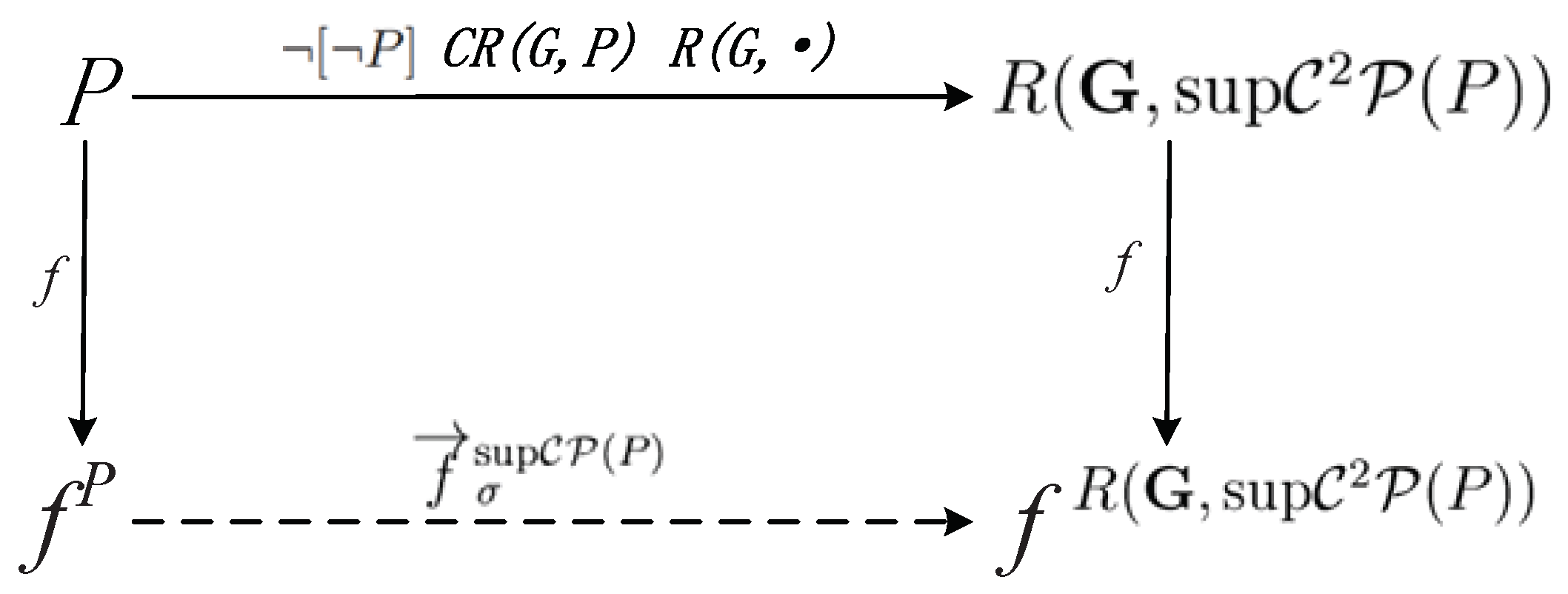
For a predicate P, the SFBC f wrt. obtained by computing the predicate first is equivalent to by Algorithm 4, i.e., the diagram in Figure 4 commutes.

Figure 4.
The relationship between and .
Proof.
To prove that the diagram commutes, we need to show that obtained by Algorithm 4 is equivalent to the . Thus, if for any , the proposition is true. Since , and
Thus, it is easy to know , which means that . Additionally,
…
By the definition of the reachability predicate, , , …, , . Thus, is obvious. Until now, the proposition is proved. □
Notice that the sup is the optimal supervisor that is coreachable instead of nonblocking. For , is proved, which implies that for any event , . Thus, the nonblocking SFBC f for with can be obtained by Algorithm 4.
Example 6.
As given in Example 1, suppose a predicate with
and . According to Algorithm 4, it is easy to know that for ,
- 1.
- Compute the SFBC according to Algorithm 3;
- For , ;
- .
- Compute the coreachable SFBC for each σ as follows:
- For , ;
- For , ;
- For ;
- For ;
- For ;
- ;
- No other state-tree satisfies ;
- 2.
- Compute the SFBC according to Algorithm 3;
- For , ;
- ;
- Compute the coreachable SFBC for each σ; it is obvious that . The iteration stops.
- 3.
- Compute the reachable SFBC f for each σ as follows:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- No other basic-state-tree b satisfies .
It is easy to know that is satisfied by , and according to Definition 2, for any event σ, .
Thus, the SFBC f over any event σ obtained by computing first is equivalent to the .
Overall, nine propositions and four algorithms are proposed, and the relation between these propositions and algorithms are displayed in Table 1. As shown in this table, we have the following:

Table 1.
Propositions, algorithms, and examples in this paper.
- Definition 1 is proposed to define the SFBC of an event for a predicate and Example 2 illustrates this definition;
- Proposition 1 shows the relation between the SFBC for two subpredicates of P;
- Propositions 2 and 3 show the reasonability of Algorithm 1, which is proposed to compute the SFBC under reachability, and Example 3 explains each step of Algorithm 1;
- Propositions 4 and 5 show the reasonability of Algorithm 2, which is proposed to compute the SFBC under coreachability, and Example 4 explains each step of Algorithm 2;
- Propositions 6 and 7 show the reasonability of Algorithm 3, which is proposed to compute the SFBC under weak controllability, and Example 5 explains each step of Algorithm 3;
- Propositions 8 and 9 show the reasonability of Algorithm 4, which is proposed to compute the SFBC under weak controllability and coreachability, and Example 6 explains each step of Algorithm 4; the computation of Algorithm 4 requires the results of Algorithms 1–3, and by Algorithm 4, the control functions of the supervisory control problem can be obtained.
6. Examples
6.1. Transfer Line
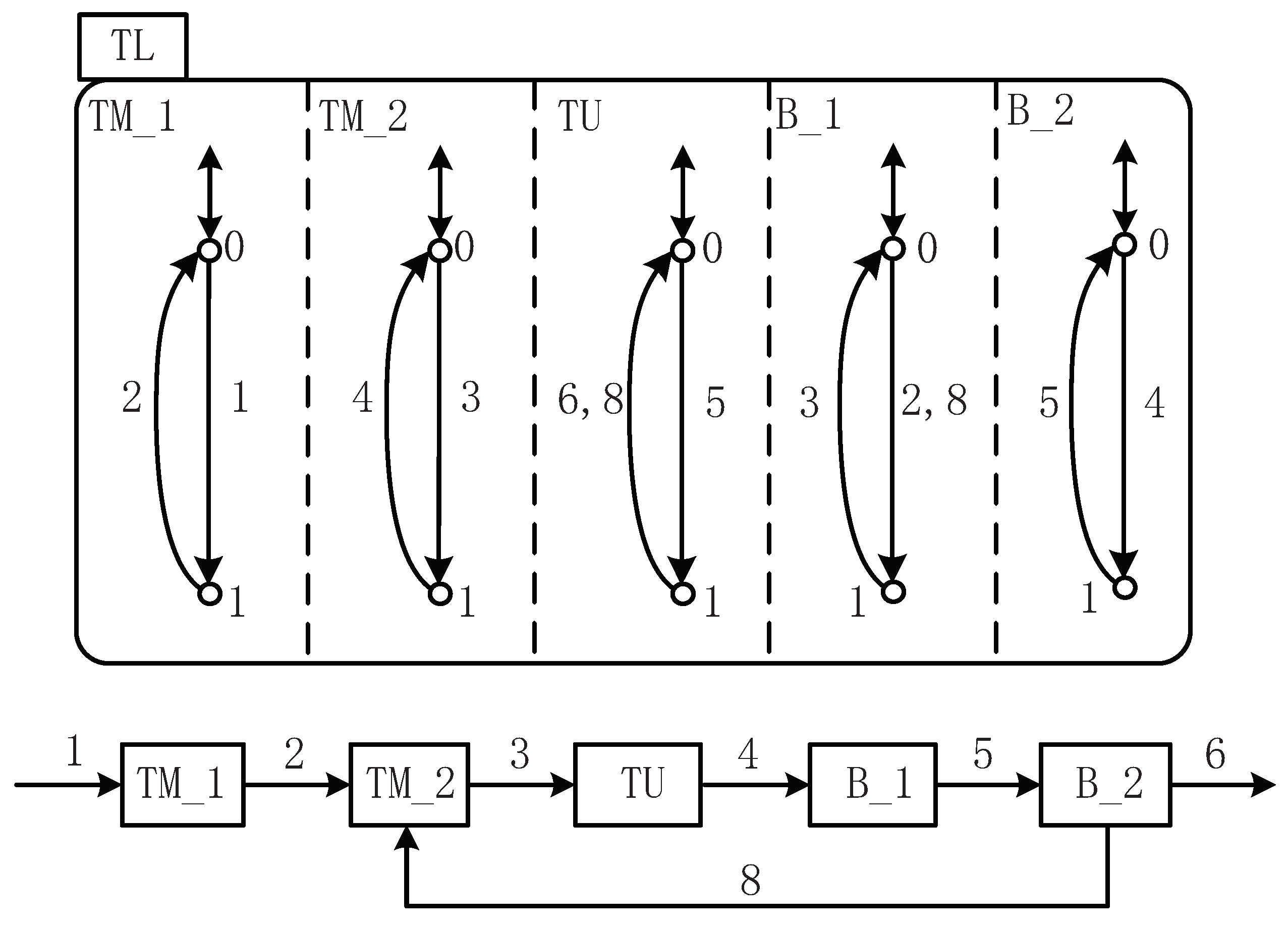
Chapter 4 in [14] proposes an industrial “transmission line” composed of two machines , , and a testing unit , which is connected by buffers and , as is depicted by Figure 5. If the workpiece is accepted after test, it can be released; otherwise, it will be returned to and reprocessed by . Because of this, the structure has the function of “material feedback”. The specification can help and avoid underflow as well as overflow, The capacities of and are assumed to be 1. The controlled events are 1, 3, and 5, while the uncontrolled events are 2, 4, 6, and 8.
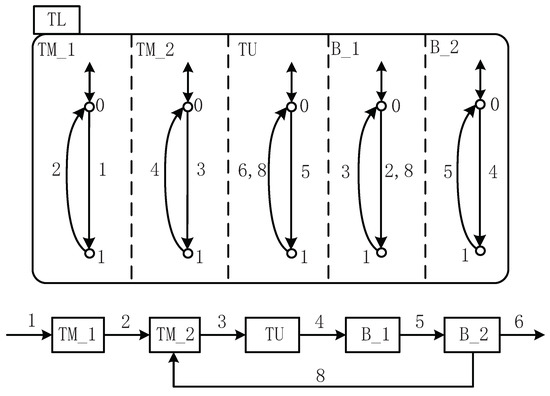
Figure 5.
STS model of the transfer line.
As its STS model is depicted in Figure 5, is an AND superstate and its components , , , , and are parallel, implying that the system work at these states simultaneously. is an OR superstate and its components and are exclusive, which means only one of and can be reached at a time. So as , , , and . The occurrence of events promotes the transition between these states. For the shared events, such as 2, if 2 occurs, the states and transfers to and simultaneously. Other events can always occur if the system reaches the trigger states. For example, event 1 can occur once stays at . Thus, to display the behavior of the system, can be given as follows:
…
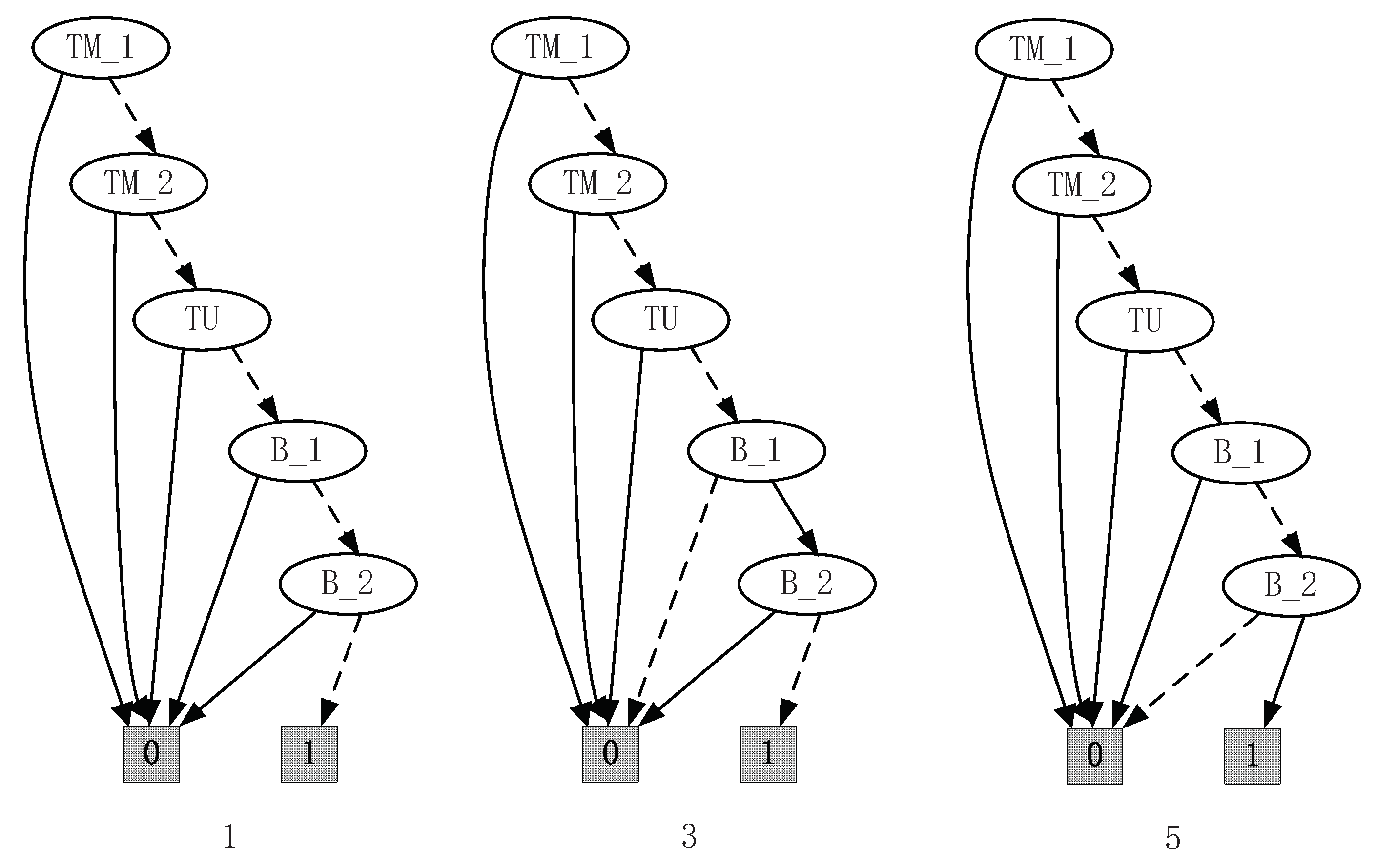
The specification of the transfer line is given by two holons ( and ). Based on the SFBC of each event, the control functions of 1, 3, and 5 can be given by Figure 6. For this example, , According to Algorithm 4, the nonblocking SFBC of the events can be obtained.
Figure 6.
Control functions of 1, 3, and 5.
Therefore, the control functions of the controllable events 1, 3, and 5 can be given by Figure 6.
Remark 6.
It is easy to find that the control functions obtained on the basis of SFBC are the same as the ones obtained on the predicates in Chapter 4 in [17]. In [17], the supremal weakly controllable and coreachable subpredicate needs to be calculated by analyzing the states of the system, and then the control functions are obtained in view of this subpredicate. For this example, the supremal subpredicate is . In view of the subpredicate and the transition function Δ, the control functions can be obtained by studying the enabled events of each states. However, by using Algorithm 4, we only need to focus on the SFBC of the uncontrollable events, which are disabled. Then, the control functions can be obtained directly, which helps to improve the calculation efficiency to a certain extent. The use of SFBC makes the computation process of the supervisory control problem more flexible since we can disable the event by letting , such as the following example.
6.2. Small Factory
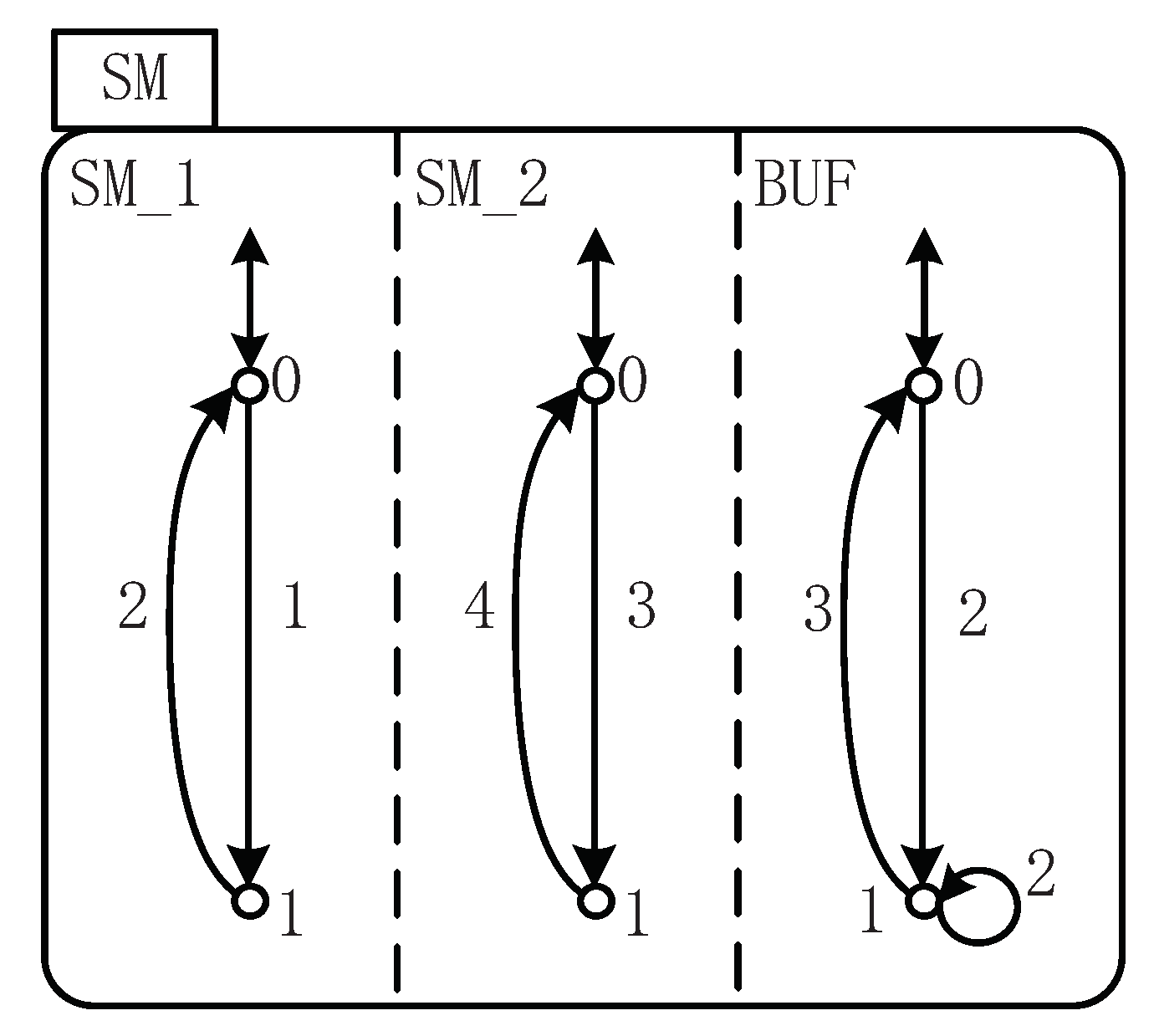
This example shows how to achieve the aim of resolving the control problem of the Small Factory based on SFBC. First, the STS model is shown in Figure 7, where the BUF contains a buffer with one slot. The two states of SM are represented as 0 and 1, where 0 stands for “idle” and 1 for “working”. In the initial state, the buffer is empty. SM can work from the infinite input bin (Event 1), after which M1 completes the work cycle (Event 2). The operation mechanism of SM is basically the same. Odd numbers represent controllable events and even numbers represent uncontrollable ones. After that, BUF needs to complete the following two tasks: first, when event 2 takes place, the workpiece will be placed in the buffer; secondly, when event 3 takes place, the workpiece is transferred to SM.
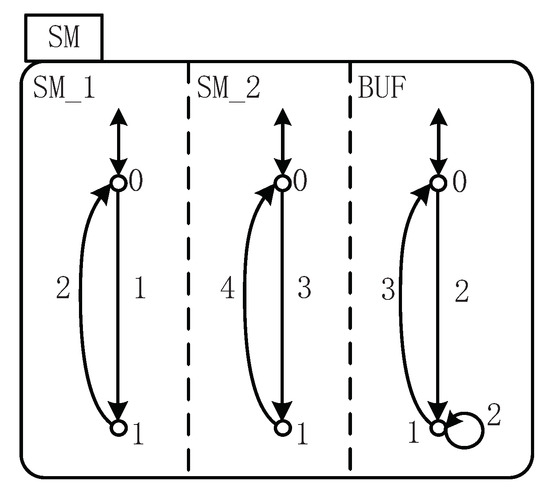
Figure 7.
STS model of Small Factory.
The overflow and underflow can be taken care of here. If the capacity of the buffer is one, to achieve this, we need to (1) disable event 3 at state 0 of the holon BUF and (2) disallow event 2 to occur at state 1 of the holon BUF. (1) is represented by the holon BUF, and (2) can be written as . The procedure to resolve this problem is displayed as follows.
- ;
- implies that and ;
- For event 1, , , , and ;For event 2, and ;For event 3, and ;For event 4, , , , and ;
- According to Algorithm 4, the nonblocking SFBC f can be got by
- -
- Under weak controllability, since , ;and for other event , ;
- -
- Under coreachability,and no other ;
- -
- It is easy to find that the SFBC satisfies the weakly controllability and coreachability. The iteration stops.
- -
- Under reachability, similar to the calculation of coreachability, can be computed.and no other ;
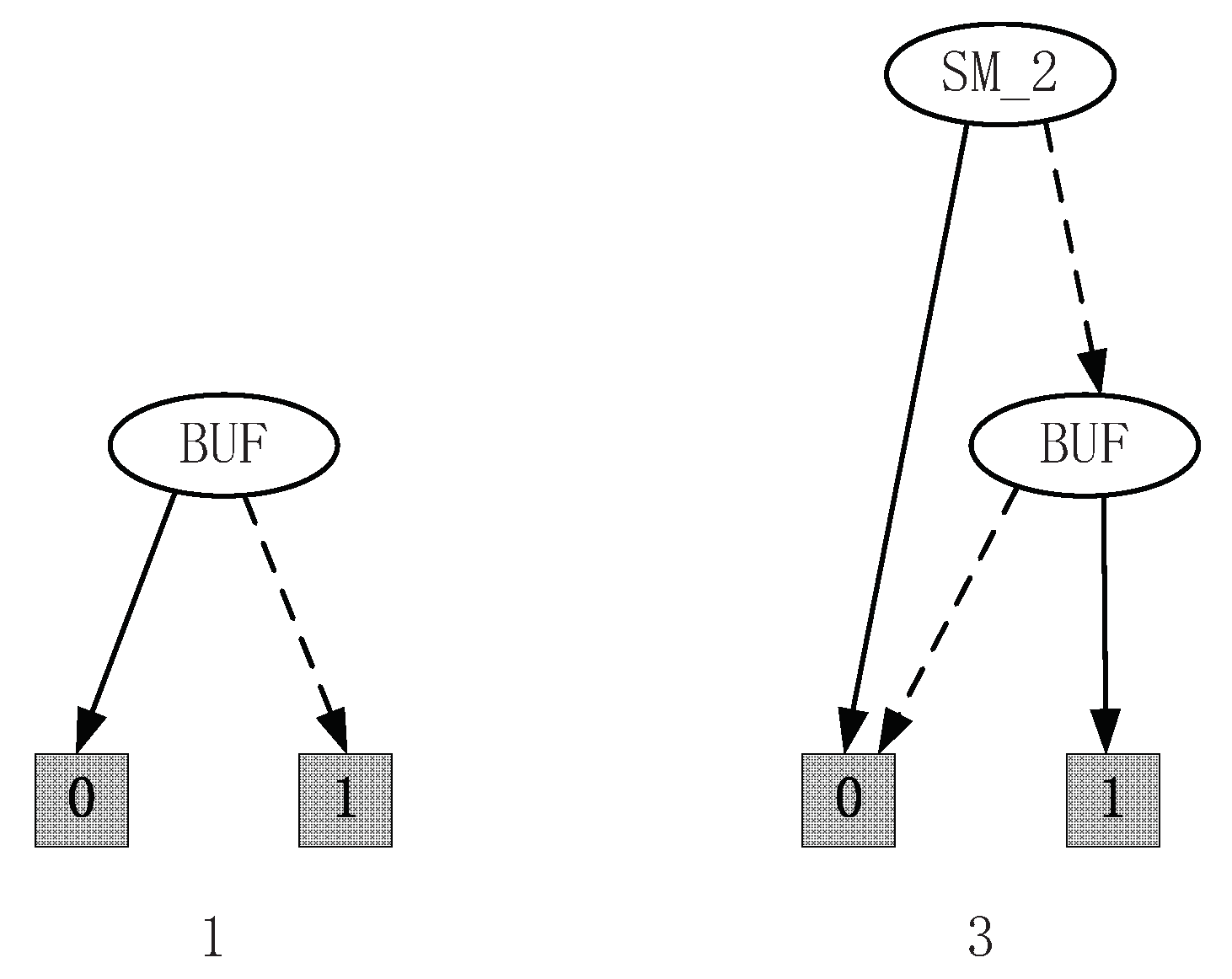
Therefore, the control functions of 1 and 3 can be given by and , which is depicted in Figure 8.
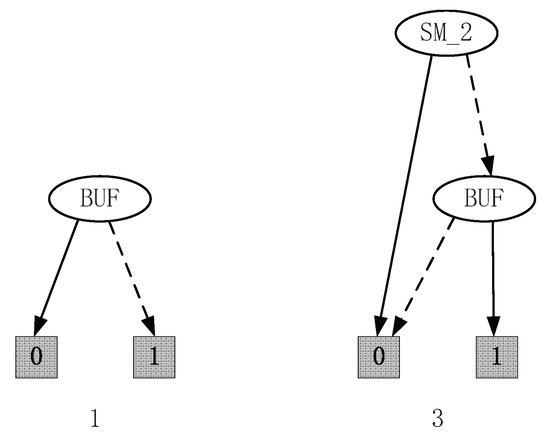
Figure 8.
Control functions of 1 and 3.
Remark 7.
The control functions of 1 and 3 obtained by Algorithm 4 are equivalent to the ones in Chapter 4 in [17], which shows that the solution based on SFBC is feasible. Since in [17], the specification is given by illegal state-trees, which means that all events related to the illegal state-trees are not allowed to occur. In this paper, the specification is given by SFBC, which makes the calculation easier since we can analyze the SFBC of the uncontrollable events instead of analyzing the exclusive states. For this example, the specification can be given by . The computation will focus on since the SFBC of the uncontrollable event 2 equals 0. Then, we can analyze the control functions with the transition function Δ. However, in [17], is deleted to ensure that the uncontrollable event will not occur. The calculation of the supremal subpredicate is given by keeping the reasonable states and deleting unreasonable ones. This will also narrow the system behavior. Such as for the supervisory control problem under partial observation, after the natural projection, the states are combined and thus one state might exists in different combination. Computing the supervisor only by deleting the states will reduce the permissive controlled behavior. In this paper, we can keep the states but delete the illegal events, which contributes to a more permissive supervisor.
6.3. Guide Way
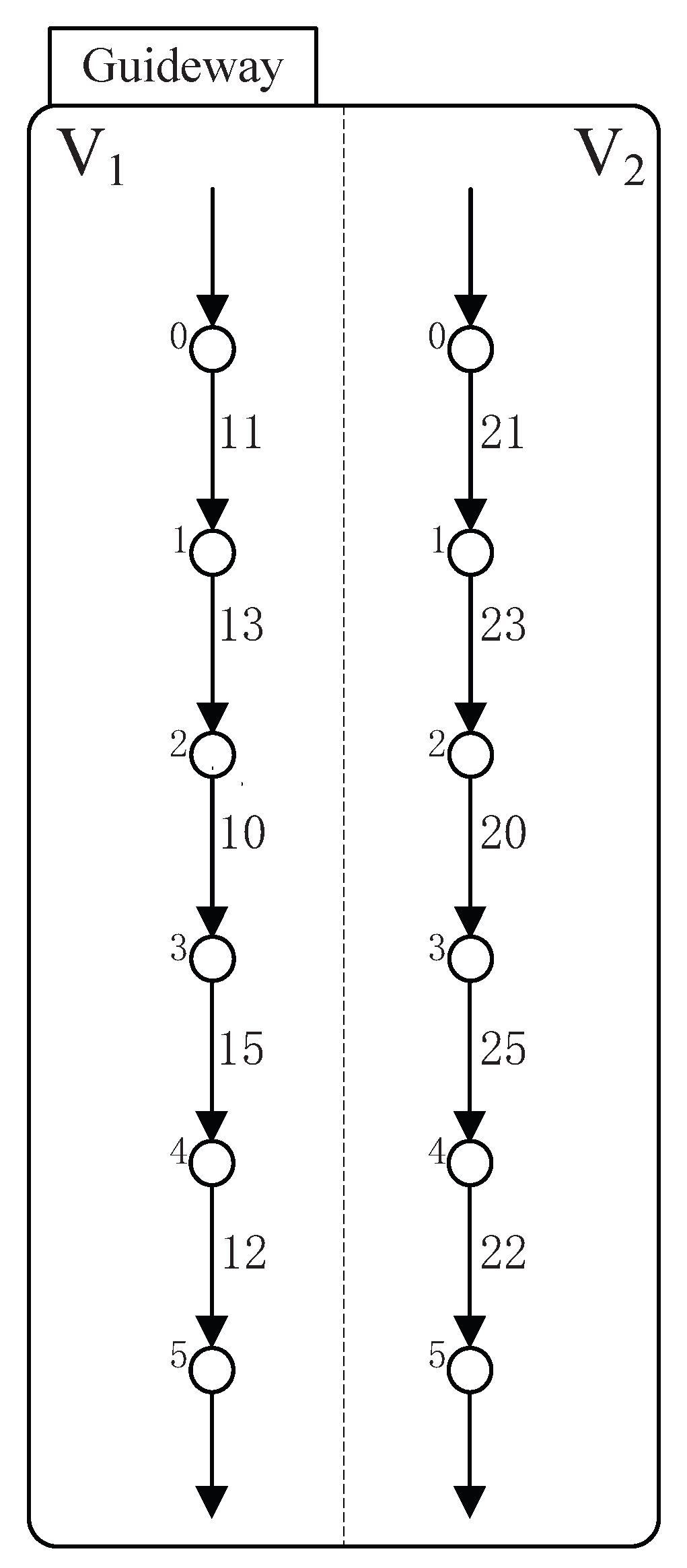
A and B are two stations on a single track guideway. There are four sections between A and B, as shown in Figure 9, with the symbol “·” representing the guideway between two sections and “*” showing that the section junctions install spotlights. If there are two vehicles and running on this guideway, the use of the spotlights prevents collision by ensuring that and never travels on the same section simultaneously.

Figure 9.
Guideway.
Its STS model is shown in Figure 10, with the odd number standing for the controllable events and the even number for the uncontrollable events. In Figure 10, holon (respectively, ) stands for the behavior of vehicle (respectively, ). Take as an example. Since there are four sections between A and B, six stations are represented by six states (0 to 5) in holon . Additionally, “·” implies the guideway between two sections, thus the five “·” can be represented as follows:
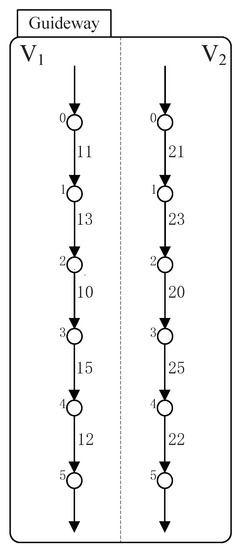
Figure 10.
Guideway.
- event 11 in Figure 10 stands for the first “·”, which means passing the guideway between A and station 1;
- event 13 in Figure 10 stands for the second “·”, which means passing the guideway between station 1 and 2;
- event 10 in Figure 10 stands for the third “·”, which means passing the guideway between station 2 and 3;
- event 15 in Figure 10 stands for the forth “·”, which means passing the guideway between station 3 and 4;
- event 12 in Figure 10 stands for the fifth “·”, which means passing the guideway between station 4 and B.
Thus, to prevent collision, the specification can be represented by the set of exclusive state-trees . This means that
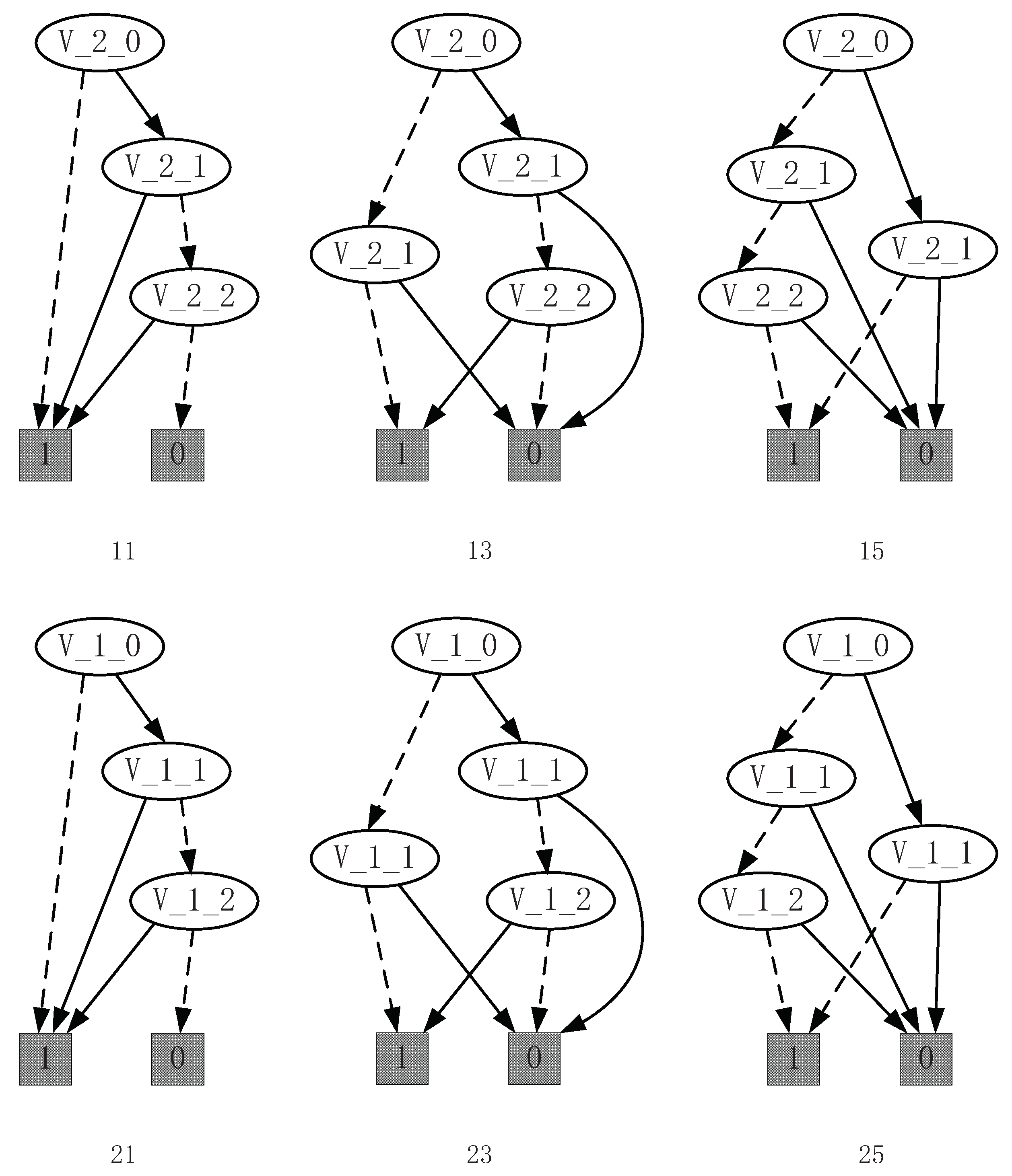
To compute the supervisor, we can focus on and since 20 and 10 are not allowed to be disabled. Thus, according to Algorithm 4, the control function is shown as Figure 11. This means that 1) event 11 occurs when is at state 0 and is at state 0, 2, 3, 4, or 5; 2) event 13 occurs when is at state 1 and is at state 0, 4, or 5; 3) event 15 occurs when is at state 3 and is at state 0, 1, or 5; 4) event 21 is allowed to occur when is at state 0 and is at state 0, 2, 3, 4, or 5; 5) event 23 is allowed to occur when is at state 1 and is at state 0, 4, or 5; and 6) event 25 is allowed to occur when is at state 3 and is at state 0, 1, or 5.

Figure 11.
Control functions of 11, 13, 15, 21, 23, and 25.
Remark 8.
The computation of the control functions in this paper is more efficient than that of [17]. In this paper, we only need to focus on the SFBC of the uncontrollable events since if there exists an SFBC equal to 0, the control functions must be not controllable. For this example, and . Since 20 and 10 are not allowed to be disabled, we need to make the SFBC of the controllable events (23 and 13) equal 0. Thus, just one step is needed to compute the control functions. However, in [17], the controllable predicate should be studied first by analyzing the uncontrollable events and then computing the control functions of the controllable events. The computation of the controllable predicate is omitted, which helps to improve the computational efficiency.
7. Discussion
In order to construct an efficient supervisor for complex automated manufacturing systems (AMS), supervisory control theory is put forward on the foundation of STS. STS can complete the control and modeling of hierarchy and concurrency of discrete-event systems (DES), and manage the state explosion encountered in the complex DES [14]. However, the relation between state-trees and events was not clearly defined during the course of investigating the supervisory control problem, which is of paramount significance in DES. In order to achieve this goal, an approach on the foundation of state feedback control (SFBC) is proposed in this paper, which constructs the control behavior directly by analyzing the SFBC of events. Thus, for a given AMS modeled by STS , the requirements of users denoted by the specification can be modeled as follows:
- The specification is explicitly saying that the dangerous situation (to be prohibited) is whenever the system is in a certain state. This specification can be denoted by the illegal state-trees. Such as, in Example 1, if the two machines, and , are not allowed to occur at the same time. The specification can be written as with , and the SFBC of events wrt. P can be obtained according to Definition 2. Then, the supervisor (shown by the control functions) can be computed by Algorithm 4.
- The specification can be put into the STS model as a holon. For example, in Small Factory, the specification is written as holon , which implicitly describes the control part: not allowing 3 to occur at state 0. Moreover, to avoid the buffer overflow, the event 2 is not allowed to occur at state 1. Thus, the illegal state-tree is and . The SFBC of events with respect to P can be obtained according to Definition 2. Then, the supervisor (shown by the control functions) can be computed by Algorithm 4.
- Moreover, the specification can be directly denoted by the SFBC which means some events disabled at state-trees. For example, in Small Factory, to avoid the buffer overflow, the event 2 is not allowed to occur at state 1. Thus, the SFBC of 2 can be written as . The SFBC of events with respect to P can be achieved according to Definition 2. Then, the control functions can be computed by Algorithm 4.
For the given specification P, the supervisory control problems can be solved by the proposed propositions and algorithms in this paper. By Algorithm 1, the SFBC for P under reachability can be computed and then, the SFBC under coreachability can be achieved by Algorithm 2. To solve the control problem, SFBC under controllability should be studied. Since the weak controllability implies controllability and the computation of the SFBC under weak controllability is more efficient, Algorithm 3 is proposed. As it is known that the controlled system should be nonblocking and controllable, Algorithm 4 is given to pursue the SFBC under coreachability and weak controllability since the nonblocking can be replaced by coreachability and controllability by weak controllability. As shown in examples, to compute the control functions, the SFBC under weak controllability and coreachability should be computed by using Algorithm 1 and Algorithm 2, iteratively. Then, the control functions can be obtained by using Algorithm 3. The reasonability of the algorithms can be proved by the nine propositions in this paper. During the computation process, only the SFBC of uncontrollable events needs to be considered, and the control functions can be obtained directly by analyzing the SFBC. This helps to improve the computational efficiency.
Moreover, this paper lays a foundation for the following work since the SFBC of events is very important to the development of other research. For example, the deployment of sensors and detectors to detect certain manufacturing processes may be too costly or difficult for technical reasons, which leads to the partial observability of AMS. To model and control these AMS, the definition of natural projection represented by predicates should be proposed. The SFBC of events with respect to predicates helps the analysis of the occurrence of events for the natural projection, which helps the achievement of more permissive system behavior under partial observation. Such as the example in Section 6.3, the symbol “!” represents detectors installed, implying that for (), the events 11, 10, 15, and 12 (resp, 21, 20, 25, and 22) are observable and event 13 (respectively, 23) is unobservable. To compute the control functions, the natural projections should be performed first. Therefore, some states will be combined, such as and can be seen as a new state, represented by , since 13 is unobservable as shown in [23]. The same is true for and , represented by . By using the proposed algorithms in this paper, does not imply that , which is different from the previous work. The state-tree is not deleted in this situation and only 13 is disabled. Thus, more permissive supervisor can be obtained under partial observation.
The above works are based on the relation between predicates and events and the supervisor is given by control functions that are represented by states that controllable event can occur. All these works ignore the structure of the STS model, which leads to a situation that all these results cannot be used in the next computation. If we can study the supervisory control problem by analyzing the STS model, the computation can focus on the holons related to the specification. The expected supervisor can be also represented by STS, which can be used directly in other computation if necessary. This helps to improve the efficiency of the computation and the practicality of the theory.
8. Conclusions
Considering that all behaviors in an automated manufacturing system (AMS) are discrete in space and time, the system can be seen as a discrete event system (DES), which ensures a valid representation of the AMS and effectively performs subsequent computations. In this study, to solve the control problem of AMS modeled by state-tree structures (STS), the supervisor of AMS is studied on the basis of state feedback control (SFBC). For the control requirements modeled by the specification, the supervisors can be computed by the proposed algorithms in this paper. First, after defining the SFBC of events for predicates, the properties of the SFBC are well investigated. Then, with the purpose of studying the supervisory problem on the foundation of SFBC, the algorithms to compute the SFBC under reachability, coreachability, and weak controllability are introduced. It is proved that the nonblocking SFBC obtained by the proposed algorithm is equivalent to the one obtained by computing predicates first, which ensures satisfactory controllers for the supervisory control problems. Finally, with the intention of demonstrating the contribution of the proposed approach, which is designed considering the symmetry of the system behavior between the real system and its STS model, three examples are illustrated. Consequently, for any specification, which can be represented by SFBC, the solution to the supervisory control problems is well investigated. However, since all these results are represented by predicates which cannot be used in the next computation, the future work will be devoted to solving the problem in view of the structure of STS models.
Author Contributions
Conceptualization, C.G.; Data curation, J.Z.; Formal analysis, C.G.; Funding acquisition, C.G.; Methodology, C.G.; Project administration, Z.H.; Software, J.Z.; Supervision, C.G.; Validation, Z.H.; Visualization, Z.H.; Writing—original draft, C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was sponsored in part by the National Natural Science Foundation of China Under Grant Nos. 62003201 and 61803246.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, Z.W.; Zhou, M.C. Deadlock Resolution in Automated Manufacturing Systems: A Novel Petri Net Approach; Springer Science Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Reveliotis, S.; Nazeem, A. Deadlock avoidance policies for automated manufacturing systems using finite state automata. Form. Methods Manuf. 2018, 169–196. [Google Scholar]
- Fanti, M.P.; Zhou, M.C. Deadlock control methods in automated manufacturing systems. IEEE Trans. Syst. Man Cyber. 2004, 34, 5–22. [Google Scholar] [CrossRef]
- Wu, N.Q.; Zhou, M.C. Deadlock resolution in automated manufacturing systems With robots. IEEE Trans. Autom. Sci. Eng. 2007, 4, 474–480. [Google Scholar] [CrossRef]
- He, Z.; Ma, Z.; Li, Z.W.; Giua, A. Parametric transformation of timed weighted marked graphs: Applications in optimal resource allocation. IEEE/CAA J. Autom. Sinica 2020, 8, 179–188. [Google Scholar] [CrossRef]
- He, Z.; Li, Z.W.; Giua, A. Performance optimization for timed weighted marked graphs under infinite server semantics. IEEE Trans. Autom. Control 2018, 63, 2573–2580. [Google Scholar] [CrossRef]
- He, Z.; Ma, Z.; Tang, W. Performance safety enforcement in strongly connected timed event graphs. Automatica 2021, 128, 109605. [Google Scholar] [CrossRef]
- He, Z.; Li, Z.W.; Giua, A. Cycle time optimization of deterministic timed weighted marked graphs by transformation. IEEE Trans. Control Syst. Technol. 2017, 25, 1318–1330. [Google Scholar] [CrossRef]
- He, Z.; Li, Z.W.; Giua, A. Optimization of deterministic timed weighted marked graphs. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1084–1095. [Google Scholar] [CrossRef]
- He, Z.; Ma, Z.Y. Performance safety enforcement in stochastic event graphs against boost and slow attacks. Nonlinear Anal. Hybrid Syst. 2021, 41, 101057. [Google Scholar] [CrossRef]
- Yan, L.Y. State-Based Control of Discrete-Event Systems with Observational Abstraction. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2011. [Google Scholar]
- Wang, X.; Li, Z.W.; Wonham, W.M. Dynamic multiple-period reconfiguration of real-time scheduling based on timed DES supervisory control. IEEE Trans. Ind. Inf. 2015, 12, 101–111. [Google Scholar] [CrossRef]
- Wang, X.; Khemaissia, I.; Khalgui, M.; Li, Z.W.; Wonham, W.M. Dynamic low-power reconfiguration of real-time systems with periodic and probabilistic tasks. IEEE Trans. Autom. Sci. Eng. 2014, 12, 258–271. [Google Scholar] [CrossRef]
- Wonham, W.M. Supervisory Control of Discrete-Event Systems. 2015. Available online: http://www.control.toronto.edu/DES (accessed on 1 July 2015).
- Wonham, W.M.; Ramadge, P.J. On the supremal controllable sublanguage of a given language. SIAM J. Control Optim. 1987, 25, 637–659. [Google Scholar] [CrossRef]
- Wonham, W.M.; Ramadge, P.J. Supervisory control of a class of discrete event processes. SIAM J. Control Optim. 1987, 25, 206–230. [Google Scholar]
- Ma, C.; Wonham, W.M. Nonblocking supervisory control of state tree structures. IEEE Trans. Autom. Control 2006, 51, 782–793. [Google Scholar] [CrossRef]
- Ma, C.; Wonham, W.M. Control of state tree structures. In Proceedings of the 11th Mediterranean Conference on Control and Automation, Rhodes, Greece, 18–20 June 2003. [Google Scholar]
- Harel, D. Statecharts: A visual formalism for complex systems. Sci. Comput. Program. 1987, 8, 231–274. [Google Scholar] [CrossRef]
- Ma, C.; Wonham, W.M. STSLib and its application to two benchmarks. In Proceedings of the 9th International Workshop on Discrete Event System (WODES’08), Gothenburg, Sweden, 28–30 May 2008; pp. 119–124. [Google Scholar]
- Mirenadi, S.; Lennartson, B. Symbolic on-the-fly synthesis in supervisory control theory. IEEE Trans. Control Syst. Technol. 2016, 24, 1705–1716. [Google Scholar] [CrossRef]
- Mirenadi, S.; Lennartson, B.; Akesson, K. A BDD-based approach for modelling plant and supervisor by extended finite automata. IEEE Trans. Control Syst. Technol. 2012, 20, 1421–1435. [Google Scholar] [CrossRef]
- Gu, C.; Wang, X.; Li, Z.W. Synthesis of supervisory control with partial observation on normal state-tree structures. IEEE Trans. Automa. Sci. Eng. 2018, 16, 984–997. [Google Scholar] [CrossRef]
- Gu, C.; Wang, X.; Li, Z.W.; Wu, N.Q. Supervisory control of state-tree structures with partial observation. Inf. Sci. 2018, 465, 523–544. [Google Scholar] [CrossRef]
- Wang, D.G.; Wang, X.; Li, Z.W. Nonblocking supervisory control of state-tree structures with conditional-preemption matrices. IEEE Trans. Ind. Inf. 2019, 16, 3744–3756. [Google Scholar] [CrossRef]
- Jiao, T.; Gan, T.; Xiao, G.; Wonham, W.M. Exploiting symmetry of state tree structures for discrete-event systems with parallel components. Int. J. Control 2017, 90, 1639–1651. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.W.; Wonham, W.M. Real-time scheduling based on nonblocking supervisory control of state-tree structures. IEEE Trans. Autom. Control 2020, 66, 4230–4237. [Google Scholar] [CrossRef]
- Cai, K.; Wonham, W.M. Supervisor localization of discrete-event systems based on state tree structure. IEEE Trans. Autom. Control 2013, 59, 1329–1335. [Google Scholar] [CrossRef]
- Dong, K.; Quan, Q.; Wonham, W.M. Failsafe mechanism design for autonomous aerial refueling using state tree structures. Unmanned Syst. 2019, 7, 261–279. [Google Scholar] [CrossRef]
- Chao, W.J.; Gan, Y.M.; Wang, Z.A.; Wonham, W.M. Decentralized supervisory control of discrete-event systems based on state tree structures. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 2184–2190. [Google Scholar]
- Chao, W.J.; Gan, Y.M.; Wang, Z.A.; Wonham, W.M. On computation of coordinator in blocking decentralized supervisory control of state tree structures. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 2157–2162. [Google Scholar]
- Chao, W.J.; Gan, Y.M.; Wang, Z.A.; Wonham, W.M. Modular supervisory control and coordination of state tree structures. Int. J. Control 2013, 86, 9–21. [Google Scholar] [CrossRef]
- Wang, X.; Moor, T.; Li, Z.W. Top-down nested supervisory control of state-tree structures based on state aggregations. IFAC-Papers OnLine 2020, 53, 11175–11180. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).