Learning Augmented Memory Joint Aberrance Repressed Correlation Filters for Visual Tracking
Abstract
:1. Introduction
- The AMRCF method is presented by simultaneously introducing adaptive spatial regularization, augmented memory regularization and aberrance repression regularization into the DCF framework. Combined with a dynamic appearance model update strategy, the overall tracking performance is improved in the case of partial/full occlusion, deformation and background clutter.
- Using the alternating direction method of multipliers (ADMM) [23] algorithm enables the model closure solution to be efficiently calculated.
- The overlap success and distance precision scores on four extensive benchmarks (i.e., OTB50, OTB100, TC128 and UAV123) verified that the proposed AMRCF has an excellent tracking performance comparable to state-of-the-art (SOTA) trackers.
2. Related Works
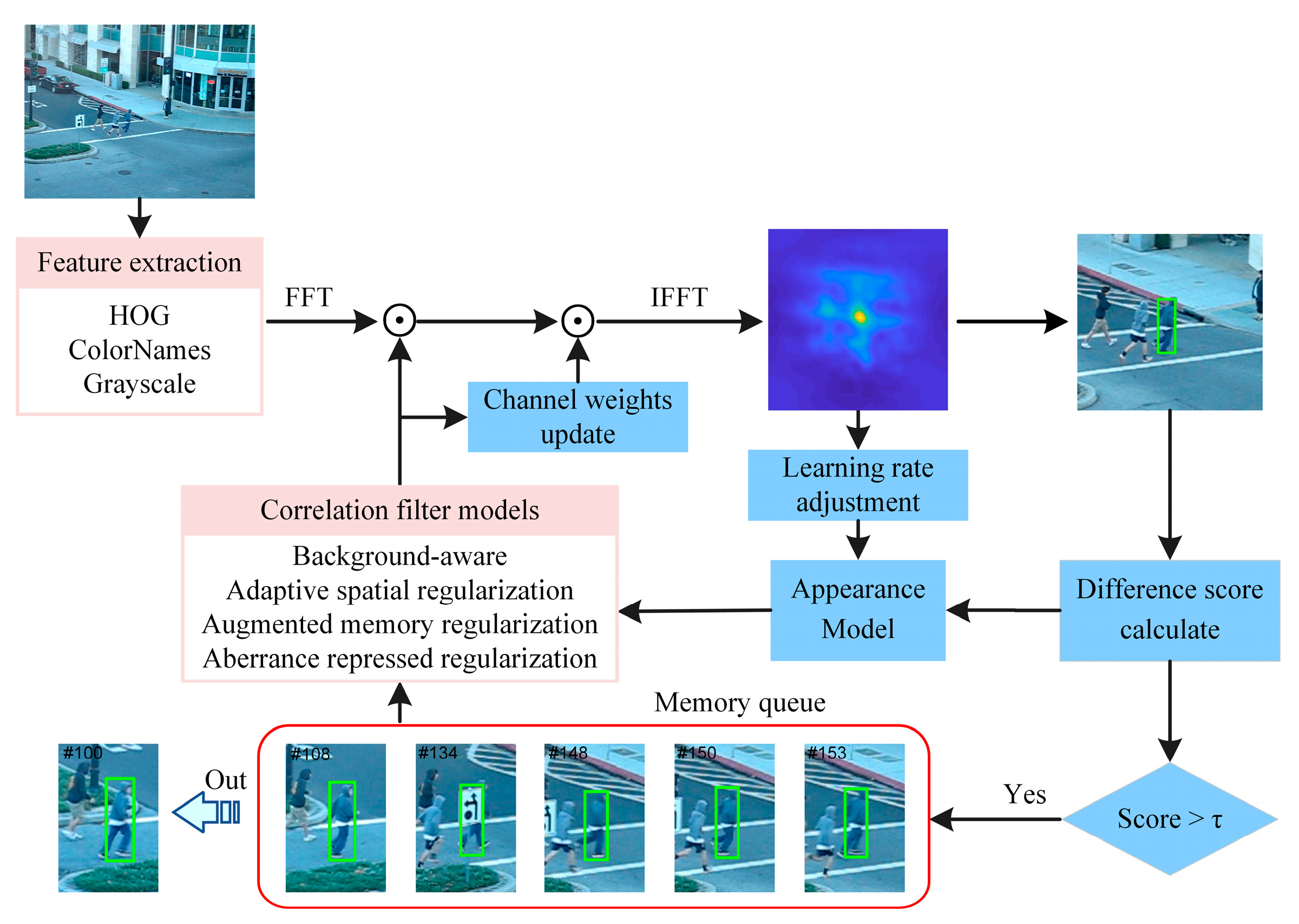
3. Proposed Method
3.1. Review the BACF Tracker
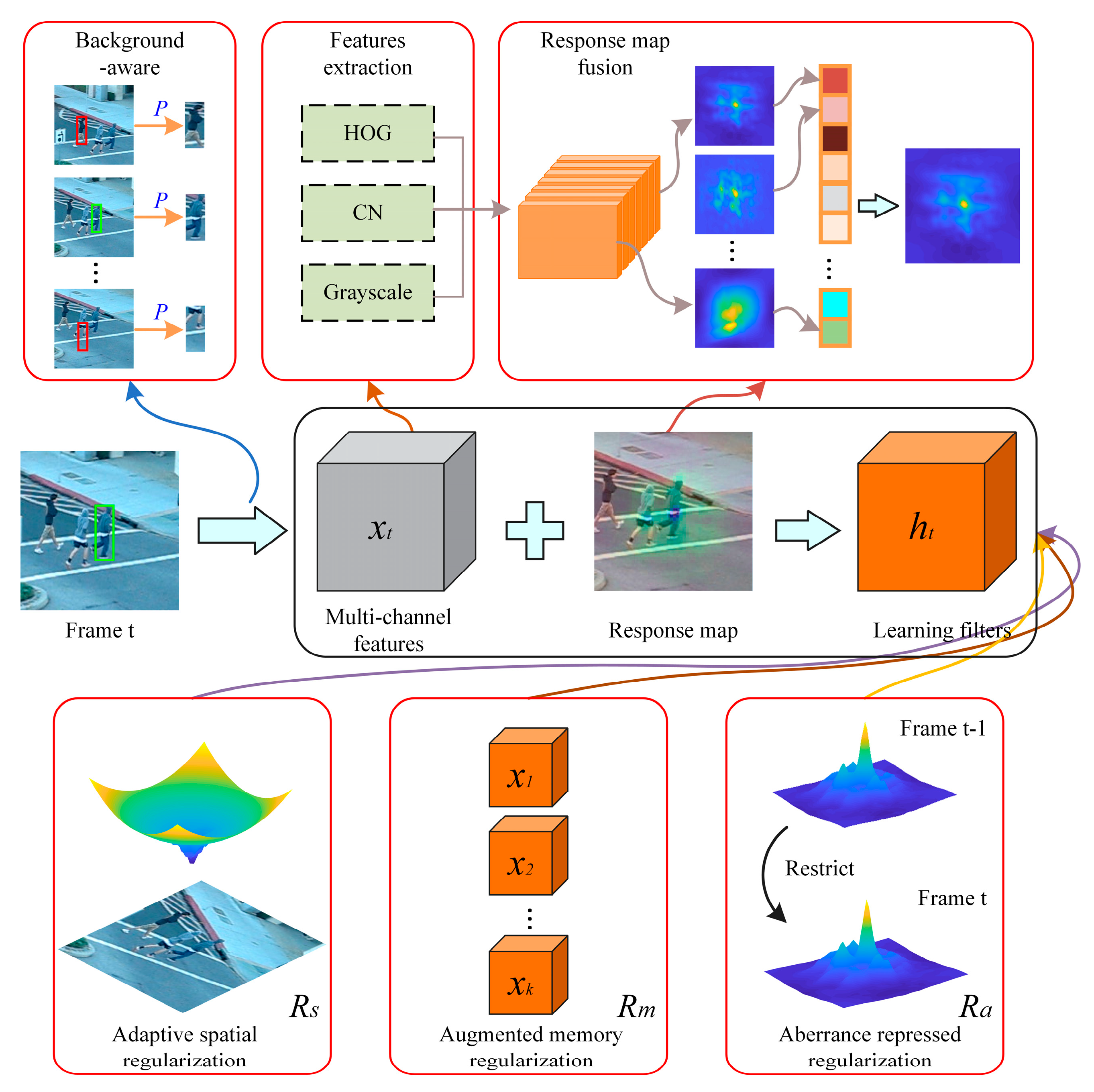
3.2. Objective Function of AMRCF
3.2.1. Adaptive Spatial Regularization
3.2.2. Augmented Memory Regularization
3.2.3. Aberrance Repression Regularization
3.3. Optimization
3.4. Detection
3.5. Model Update
| Algorithm 1: Augmented memory joint aberrance repressed correlation filter (AMRCF) |
| Input: First frame state of the sequence (i.e., target position and scale information); |
| Output: Target position at frame t; |
| Initialize tracker model hyperparameters. |
| for t = 1: end do |
| Training |
| Extract multi-channel feature maps |
| Calculate the hash matrix |
| if t = 1 then |
| Initialize the FIFO memory sequence. |
| Initialize the channel weight model |
| Initialize the appearance model. |
| else |
| Calculate the score between and . |
| if score > then |
| Update the FIFO memory queue. |
| end if |
| Store the hash matrix . |
| end if |
| Optimize the filter model via Equations (10) and (14)–(16) for L iterations |
| Detecting |
| Crop multi-scale search regions centered at with S scales based on the bounding box at frame t + 1. |
| Extract multi-channel feature maps |
| Use Equation (18) to final response output map . |
| Estimate the target position and scale from the maximum value of the response maps. |
| Updating |
| Use Equation (17) to update the channel weight model |
| Use Equation (20) to Calculate the learning rate . |
| Use Equation (21) to update the appearance model. |
| end for |
4. Experiments
4.1. Implementation Details
4.2. Evaluation of the OTB Benchmark
4.2.1. Overall Performance
4.2.2. Attribute Evaluation
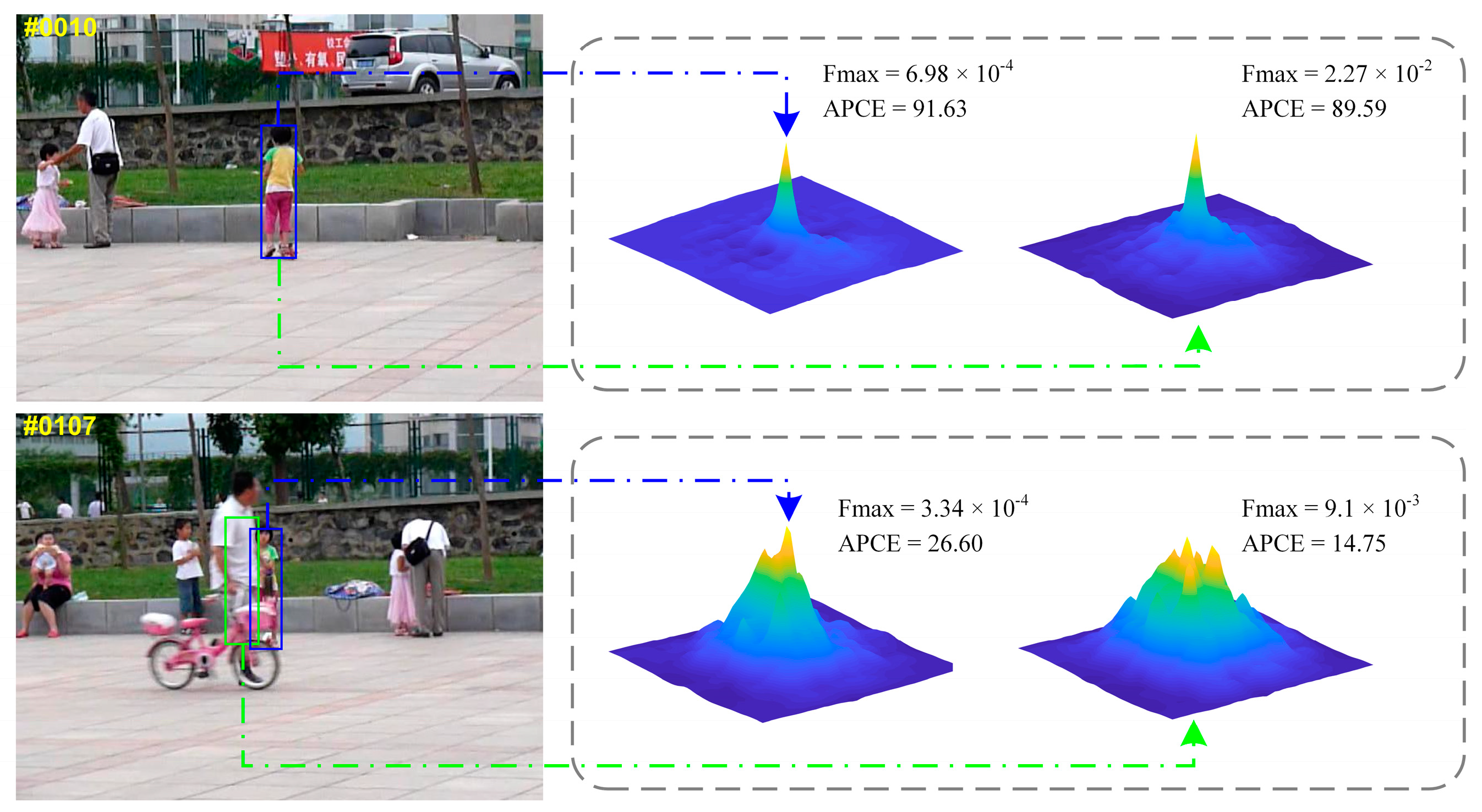
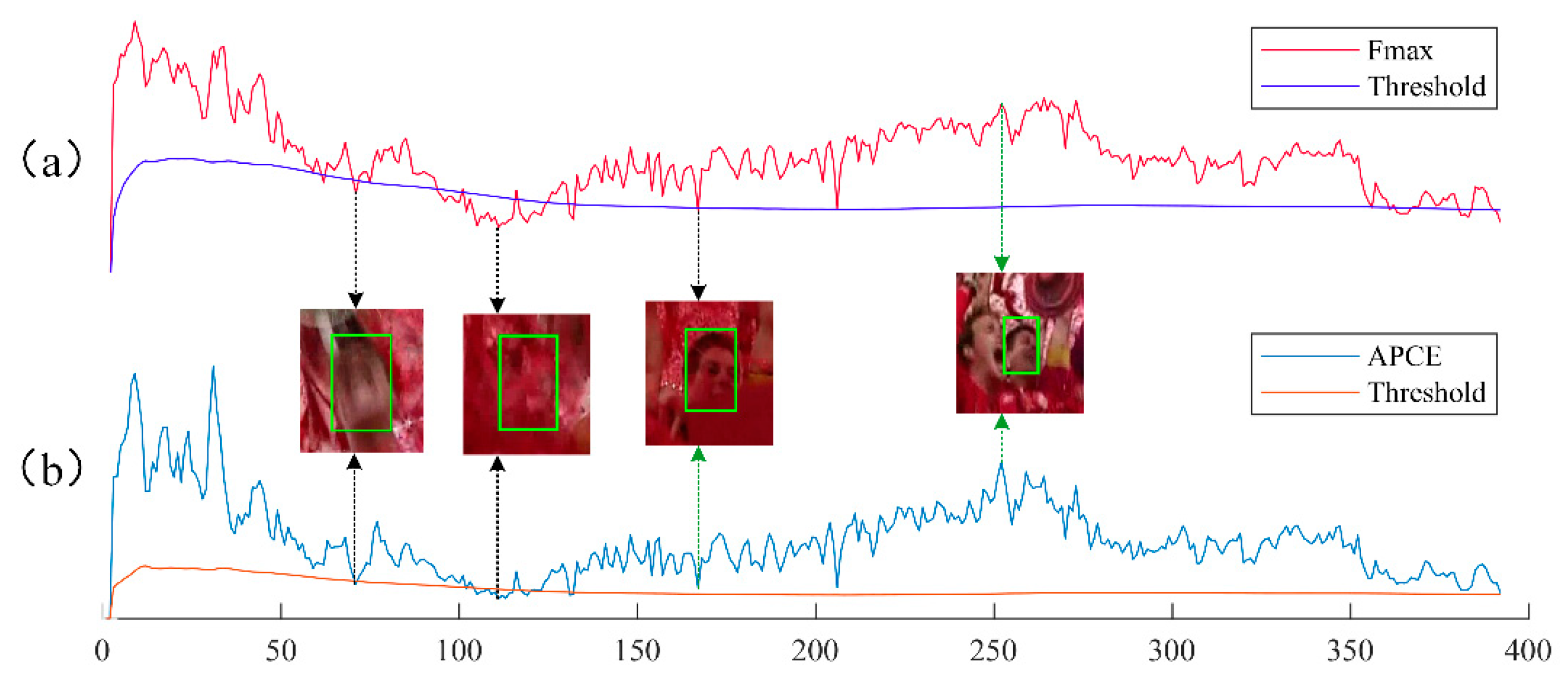
4.2.3. Qualitative Evaluation
4.3. Evaluation of the TC128 Benchmark
4.4. Evaluation of the UAV123 Benchmark
4.5. Compared with Deep Feature-Based Trackers
4.6. Ablation Studies and Effectiveness Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual object tracking using adaptive correlation filters. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. Exploiting the circulant structure of tracking-by-detection with kernels. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 702–715. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-speed tracking with kernelized correlation filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Zhu, J.; Hoi, S.C.; Song, W.; Wang, Z.; Liu, H. Robust estimation of similarity transformation for visual object tracking. Proc. AAAI Conf. Artif. Intell. 2019, 33, 8666–8673. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Luo, L.; Wen, M.; Chen, Z.; Zhang, C. Enable scale and aspect ratio adaptability in visual tracking with detection proposals. In Proceedings of the British Machine Vision Conference, Swansea, UK, 7–10 September 2015. [Google Scholar]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Discriminative scale space tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1561–1575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Danelljan, M.; Shahbaz Khan, F.; Felsberg, M.; Van de Weijer, J. Adaptive color attributes for real-time visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1090–1097. [Google Scholar]
- Ma, C.; Huang, J.; Yang, X.; Yang, M. Hierarchical convolutional features for visual tracking. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015; pp. 3074–3082. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Golodetz, S.; Miksik, O.; Torr, P.H. Staple: Complementary learners for real-time tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1401–1409. [Google Scholar]
- Lukežič, A.; Zajc, L.Č.; Kristan, M. Deformable parts correlation filters for robust visual tracking. IEEE Trans. Cybern. 2017, 48, 1849–1861. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Cheung, N.; Yao, H.; Guo, Y. Non-rigid object tracking via deformable patches using shape-preserved KCF and level sets. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5495–5503. [Google Scholar]
- Liu, T.; Wang, G.; Yang, Q. Real-time part-based visual tracking via adaptive correlation filters. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4902–4912. [Google Scholar]
- Danelljan, M.; Hager, G.; Shahbaz Khan, F.; Felsberg, M. Learning spatially regularized correlation filters for visual tracking. In Proceedings of the IEEE international Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015; pp. 4310–4318. [Google Scholar]
- Lukezic, A.; Vojir, T.; Cehovin Zajc, L.; Matas, J.; Kristan, M. Discriminative correlation filter with channel and spatial reliability. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6309–6318. [Google Scholar]
- Kiani Galoogahi, H.; Fagg, A.; Lucey, S. Learning background-aware correlation filters for visual tracking. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1135–1143. [Google Scholar]
- Li, F.; Tian, C.; Zuo, W.; Zhang, L.; Yang, M. Learning spatial-temporal regularized correlation filters for visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4904–4913. [Google Scholar]
- Gu, P.; Liu, P.; Deng, J.; Chen, Z. Learning Spatial–Temporal Background-Aware Based Tracking. Appl. Sci. 2021, 11, 8427. [Google Scholar] [CrossRef]
- Zhang, W.; Kang, B.; Zhang, S. Spatial-temporal aware long-term object tracking. IEEE Access 2020, 8, 71662–71684. [Google Scholar] [CrossRef]
- Huang, Z.; Fu, C.; Li, Y.; Lin, F.; Lu, P. Learning aberrance repressed correlation filters for real-time UAV tracking. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2891–2900. [Google Scholar]
- Fu, C.; Huang, Z.; Li, Y.; Duan, R.; Lu, P. Boundary effect-aware visual tracking for UAV with online enhanced background learning and multi-frame consensus verification. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4415–4422. [Google Scholar]
- Gan, L.; Ma, Y. Long-term correlation filter tracking algorithm based on adaptive feature fusion. In Proceedings of the Thirteenth International Conference on Graphics and Image Processing (ICGIP 2021), Kunming, China, 18–20 August 2021; Volume 12083, pp. 253–263. [Google Scholar]
- Hong, Z.; Chen, Z.; Wang, C.; Mei, X.; Prokhorov, D.; Tao, D. Multi-store tracker (muster): A cognitive psychology inspired approach to object tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 749–758. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Danelljan, M.; Robinson, A.; Shahbaz Khan, F.; Felsberg, M. Beyond correlation filters: Learning continuous convolution operators for visual tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 472–488. [Google Scholar]
- Danelljan, M.; Bhat, G.; Shahbaz Khan, F.; Felsberg, M. Eco: Efficient convolution operators for tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6638–6646. [Google Scholar]
- Bhat, G.; Johnander, J.; Danelljan, M.; Khan, F.S.; Felsberg, M. Unveiling the power of deep tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 483–498. [Google Scholar]
- Xu, L.; Gao, M.; Li, X.; Zhai, W.; Yu, M.; Li, Z. Joint spatiotemporal regularization and scale-aware correlation filters for visual tracking. J. Electron. Imaging 2021, 30, 043011. [Google Scholar] [CrossRef]
- Li, T.; Ding, F.; Yang, W. UAV object tracking by background cues and aberrances response suppression mechanism. Neural Comput. Appl. 2021, 33, 3347–3361. [Google Scholar] [CrossRef]
- Huang, B.; Xu, T.; Shen, Z.; Jiang, S.; Li, J. BSCF: Learning background suppressed correlation filter tracker for wireless multimedia sensor networks. Ad Hoc Netw. 2021, 111, 102340. [Google Scholar] [CrossRef]
- Elayaperumal, D.; Joo, Y.H. Aberrance suppressed spatio-temporal correlation filters for visual object tracking. Pattern Recognit. 2021, 115, 107922. [Google Scholar] [CrossRef]
- Dai, K.; Wang, D.; Lu, H.; Sun, C.; Li, J. Visual tracking via adaptive spatially-regularized correlation filters. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4670–4679. [Google Scholar]
- Mueller, M.; Smith, N.; Ghanem, B. Context-aware correlation filter tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1396–1404. [Google Scholar]
- Zha, Y.; Zhang, P.; Pu, L.; Zhang, L. Semantic-aware spatial regularization correlation filter for visual tracking. IET Comput. Vis. 2022, 16, 317–332. [Google Scholar] [CrossRef]
- Li, Y.; Fu, C.; Ding, F.; Huang, Z.; Pan, J. Augmented memory for correlation filters in real-time UAV tracking. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 1559–1566. [Google Scholar]
- Xu, T.; Feng, Z.; Wu, X.; Kittler, J. Learning adaptive discriminative correlation filters via temporal consistency preserving spatial feature selection for robust visual object tracking. IEEE Trans. Image Processing 2019, 28, 5596–5609. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, Y.; Chen, L.; He, H.; Liu, J.; Zhang, W.; Xu, G. Second-Order Spatial-Temporal Correlation Filters for Visual Tracking. Mathematics 2022, 10, 684. [Google Scholar] [CrossRef]
- Hu, Z.; Zou, M.; Chen, C.; Wu, Q. Tracking via context-aware regression correlation filter with a spatial–temporal regularization. J. Electron. Imaging 2020, 29, 023029. [Google Scholar] [CrossRef]
- Xu, L.; Kim, P.; Wang, M.; Pan, J.; Yang, X.; Gao, M. Spatio-temporal joint aberrance suppressed correlation filter for visual tracking. Complex Intell. Syst. 2021, 1–13. [Google Scholar] [CrossRef]
- Wang, M.; Liu, Y.; Huang, Z. Large margin object tracking with circulant feature maps. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4021–4029. [Google Scholar]
- Lin, F.; Fu, C.; He, Y.; Guo, F.; Tang, Q. BiCF: Learning bidirectional incongruity-aware correlation filter for efficient UAV object tracking. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2365–2371. [Google Scholar]
- Liu, L.; Feng, T.; Fu, Y. Learning Multifeature Correlation Filter and Saliency Redetection for Long-Term Object Tracking. Symmetry 2022, 14, 911. [Google Scholar] [CrossRef]
- Kozat, S.S.; Venkatesan, R.; Mihçak, M.K. Robust perceptual image hashing via matrix invariants. In Proceedings of the 2004 International Conference on Image Processing, 2004. ICIP’04., Singapore, 24–27 October 2004; pp. 3443–3446. [Google Scholar]
- Wu, Y.; Lim, J.; Yang, M. Online object tracking: A benchmark. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; Volume 5, pp. 2411–2418. [Google Scholar]
- Wu, Y.; Lim, J.; Yang, M.H. Object Tracking Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, P.; Blasch, E.; Ling, H. Encoding color information for visual tracking: Algorithms and benchmark. IEEE Trans. Image Processing 2015, 24, 5630–5644. [Google Scholar] [CrossRef] [PubMed]
- Mueller, M.; Smith, N.; Ghanem, B. A benchmark and simulator for uav tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 445–461. [Google Scholar]
- Li, Y.; Fu, C.; Ding, F.; Huang, Z.; Lu, G. AutoTrack: Towards high-performance visual tracking for UAV with automatic spatio-temporal regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11923–11932. [Google Scholar]
- Danelljan, M.; Hager, G.; Shahbaz Khan, F.; Felsberg, M. Adaptive decontamination of the training set: A unified formulation for discriminative visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1430–1438. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H. Fully-convolutional siamese networks for object tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 850–865. [Google Scholar]
- Wang, Q.; Gao, J.; Xing, J.; Zhang, M.; Hu, W. Dcfnet: Discriminant correlation filters network for visual tracking. arXiv 2017, arXiv:1704.04057. [Google Scholar]
- Valmadre, J.; Bertinetto, L.; Henriques, J.; Vedaldi, A.; Torr, P.H. End-to-end representation learning for correlation filter based tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2805–2813. [Google Scholar]

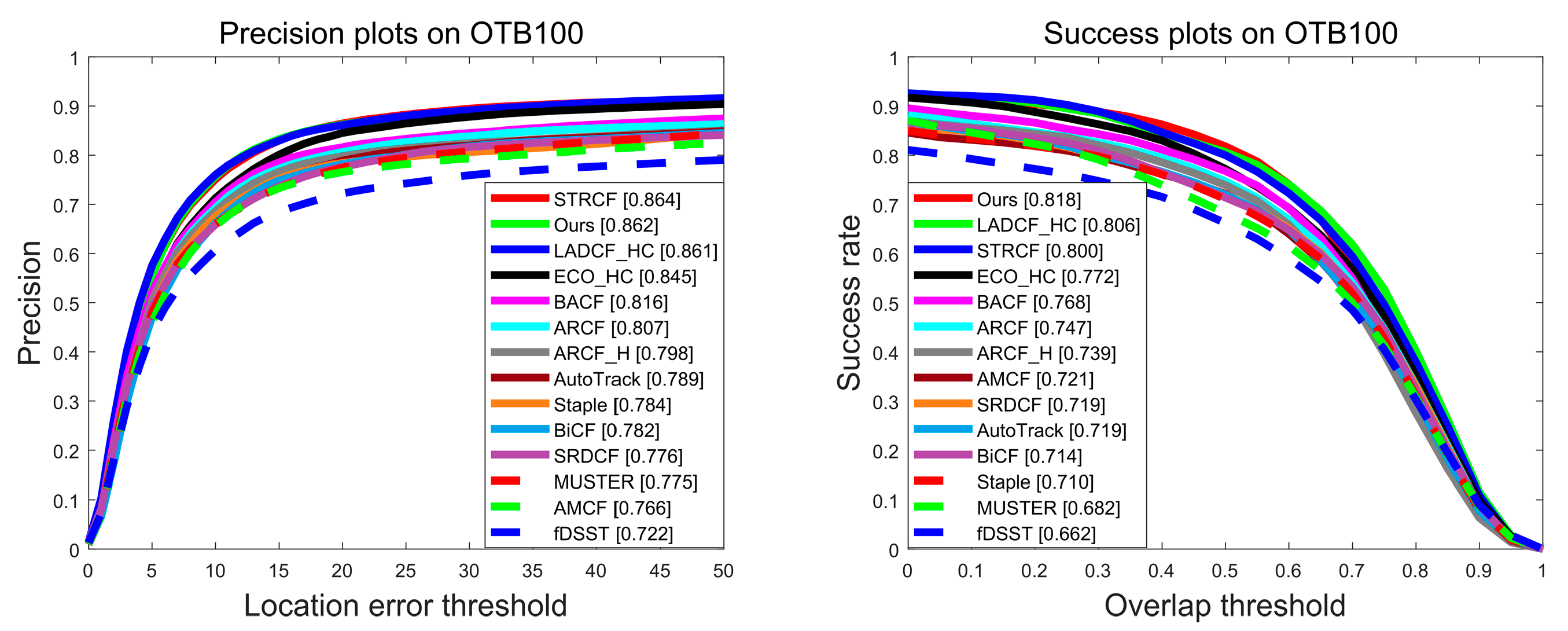


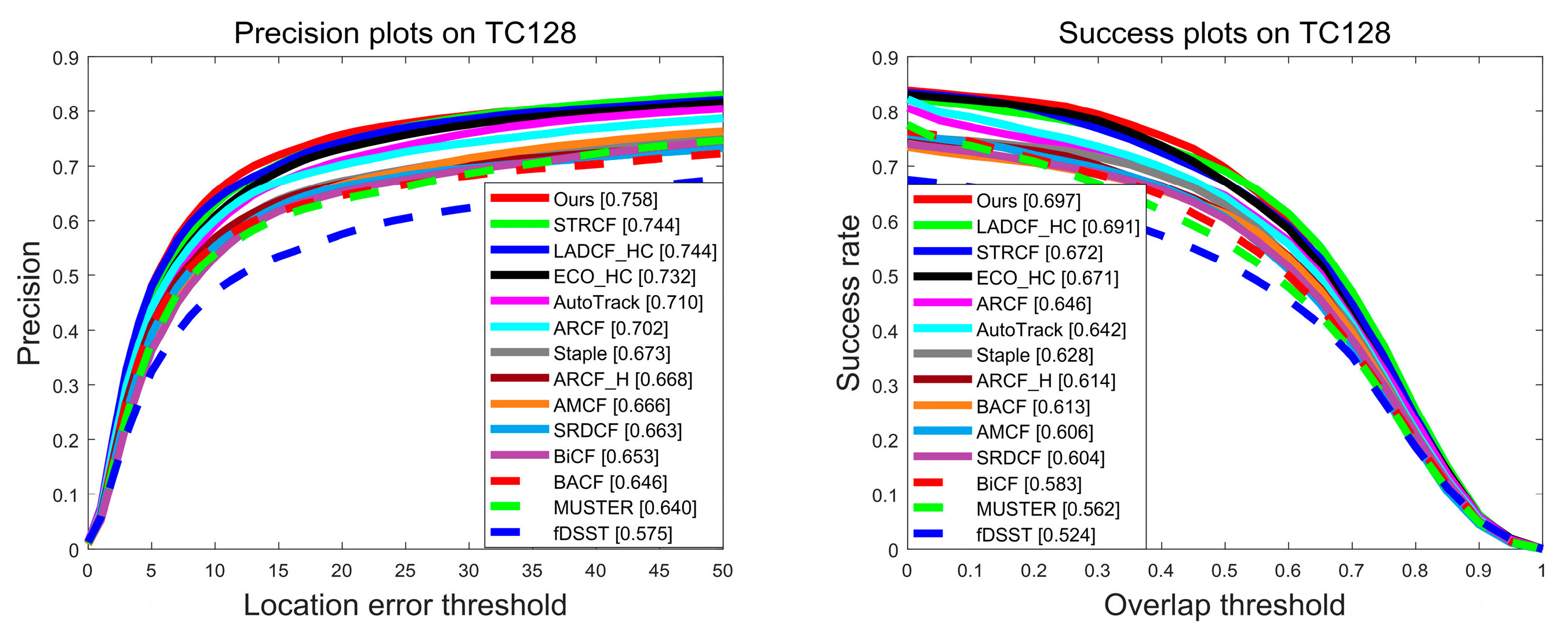
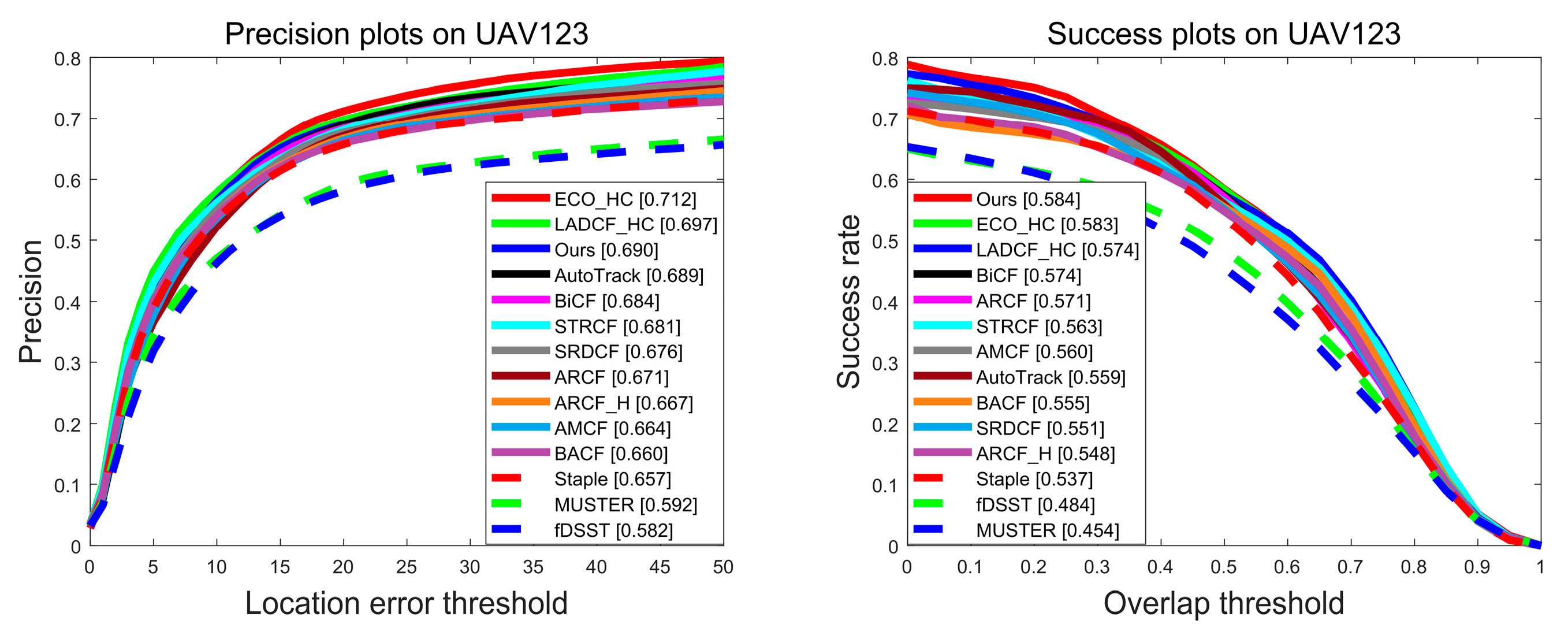
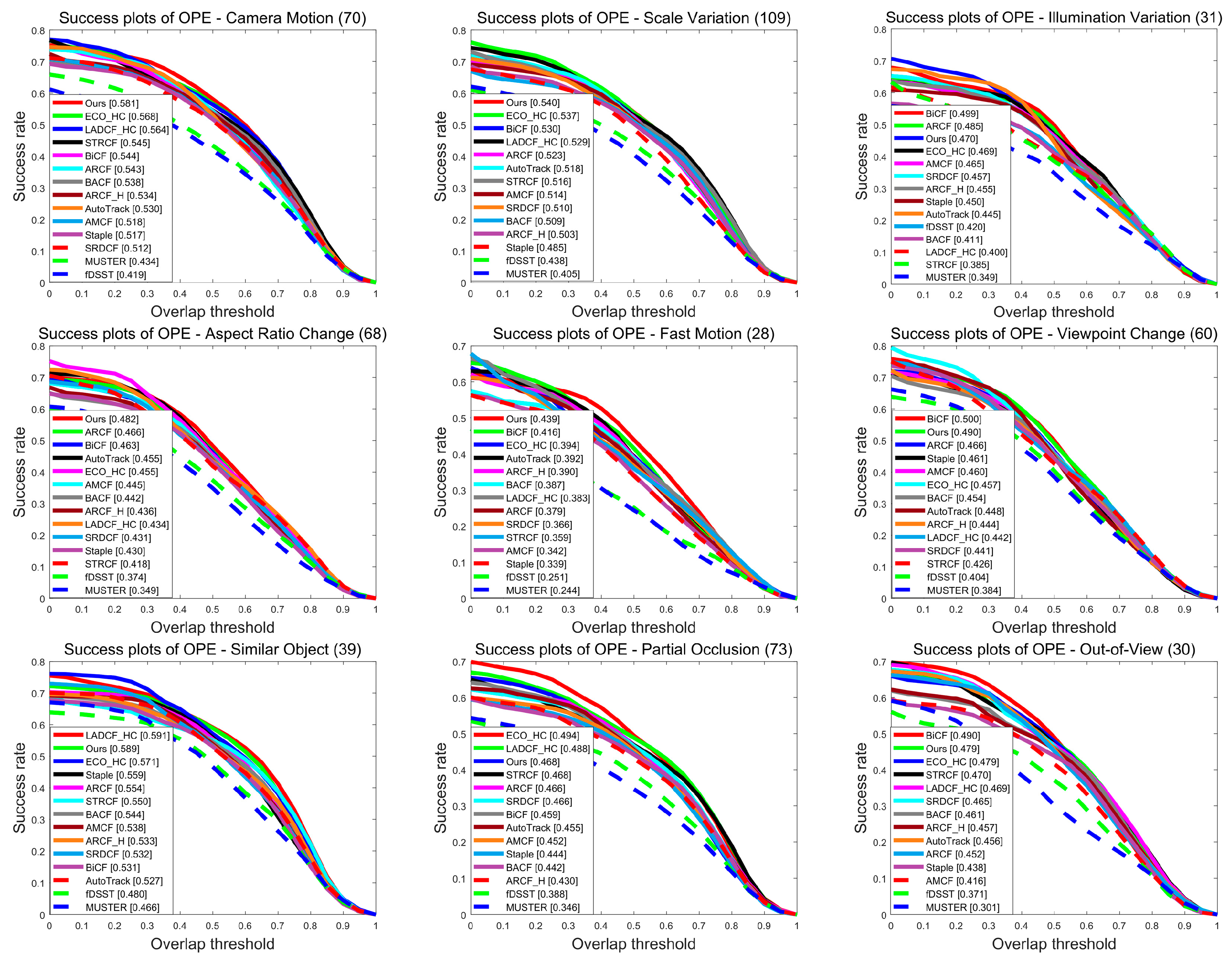
| Trackers | STRCF | ECO_HC | LADCF_HC | BACF | ARCF | AMCF | SRDCF | Ours |
|---|---|---|---|---|---|---|---|---|
| DP (%) | 86.4 | 84.5 | 86.1 | 81.6 | 80.7 | 76.6 | 77.6 | 86.2 |
| SR (%) | 80.0 | 77.2 | 80.6 | 76.8 | 74.7 | 72.1 | 71.9 | 81.8 |
| FPS | 25.57 | 51.06 | 20.23 | 39.49 | 17.07 | 34.44 | 7.22 | 12.56 |
| Trackers | LADCF | DeepSTRCF | SRDCFdecon | SiamFC3s | SiamFC | DCFNet | CFNet | Ours |
|---|---|---|---|---|---|---|---|---|
| DP (%) | 87.2 | 86.6 | 81.4 | 77.9 | 72.0 | 84.2 | 72.4 | 85.9 |
| SR (%) | 88.4 | 87.3 | 87.0 | 80.9 | 77.2 | 87.7 | 78.1 | 88.9 |
| FPS | 5.93 | 3.57 | 2.41 | 9.82 | 12.82 | 99.37 | 5.7 | 13.13 |
| IV | OPR | SV | OCC | DEF | MB | FM | IPR | OV | BC | LR | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LADCF | 79.0 | 87.6 | 84.9 | 89.8 | 87.3 | 74.8 | 79.2 | 81.5 | 79.4 | 81.4 | 55.4 |
| DeepSTRCF | 78.0 | 86.3 | 82.7 | 88.4 | 86.9 | 74.6 | 75.9 | 79.8 | 81.1 | 79.9 | 56.9 |
| SRDCFdecon | 81.8 | 85.8 | 83.3 | 86.1 | 84.2 | 79.0 | 78.3 | 80.6 | 78.5 | 84.6 | 52.7 |
| SiamFC3s | 70.9 | 78.8 | 79.6 | 80.2 | 74.3 | 69.8 | 72.3 | 74.3 | 78.0 | 73.2 | 65.9 |
| SiamFC | 67.6 | 74.7 | 77.3 | 68.0 | 70.1 | 52.5 | 66.9 | 71.7 | 64.3 | 72.3 | 48.9 |
| DCFNet | 82.7 | 86.7 | 88.3 | 87.0 | 83.4 | 74.3 | 77.4 | 83.9 | 80.3 | 82.8 | 64.2 |
| CFNet | 70.3 | 79.3 | 78.6 | 77.4 | 73.2 | 56.7 | 56.8 | 73.5 | 57.1 | 70.9 | 57.9 |
| Ours | 84.5 | 88.5 | 84.4 | 88.0 | 88.6 | 81.4 | 79.3 | 85.6 | 81.6 | 86.6 | 56.3 |
| Trackers | OTB100 Benchmark | UAV123 Benchmark | Average | |||
|---|---|---|---|---|---|---|
| Success (%) | Precision (%) | Success (%) | Precision (%) | Success (%) | Precision (%) | |
| BACF (Baseline) | 76.8 | 81.6 | 55.5 | 66.0 | 66.2 | 73.8 |
| AMRCF-AS | 79.3 | 83.4 | 57.3 | 68.0 | 68.3 | 75.7 |
| AMRCF-AM | 79.4 | 84.0 | 58.1 | 68.3 | 68.8 | 76.2 |
| AMRCF-CL | 81.4 | 85.7 | 58.0 | 70.1 | 69.7 | 77.9 |
| AMRCF-AR | 81.5 | 85.4 | 57.3 | 68.3 | 69.4 | 76.9 |
| AMRCF-AS-AM | 80.7 | 85.5 | 58.3 | 68.6 | 69.5 | 77.1 |
| AMRCF-AS-AM-CL | 81.6 | 85.9 | 58.2 | 69.3 | 69.9 | 77.6 |
| AMRCF | 81.8 | 86.2 | 58.4 | 69.0 | 70.1 | 77.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; He, J.; Sun, X.; Bai, Y.; Wei, Z.; Ghazali, K.H.b. Learning Augmented Memory Joint Aberrance Repressed Correlation Filters for Visual Tracking. Symmetry 2022, 14, 1502. https://doi.org/10.3390/sym14081502
Ji Y, He J, Sun X, Bai Y, Wei Z, Ghazali KHb. Learning Augmented Memory Joint Aberrance Repressed Correlation Filters for Visual Tracking. Symmetry. 2022; 14(8):1502. https://doi.org/10.3390/sym14081502
Chicago/Turabian StyleJi, Yuanfa, Jianzhong He, Xiyan Sun, Yang Bai, Zhaochuan Wei, and Kamarul Hawari bin Ghazali. 2022. "Learning Augmented Memory Joint Aberrance Repressed Correlation Filters for Visual Tracking" Symmetry 14, no. 8: 1502. https://doi.org/10.3390/sym14081502
APA StyleJi, Y., He, J., Sun, X., Bai, Y., Wei, Z., & Ghazali, K. H. b. (2022). Learning Augmented Memory Joint Aberrance Repressed Correlation Filters for Visual Tracking. Symmetry, 14(8), 1502. https://doi.org/10.3390/sym14081502






