2D Discrete Hodge–Dirac Operator on the Torus
Abstract
:1. Introduction
2. Discrete Model
3. Discrete Hodge Decomposition
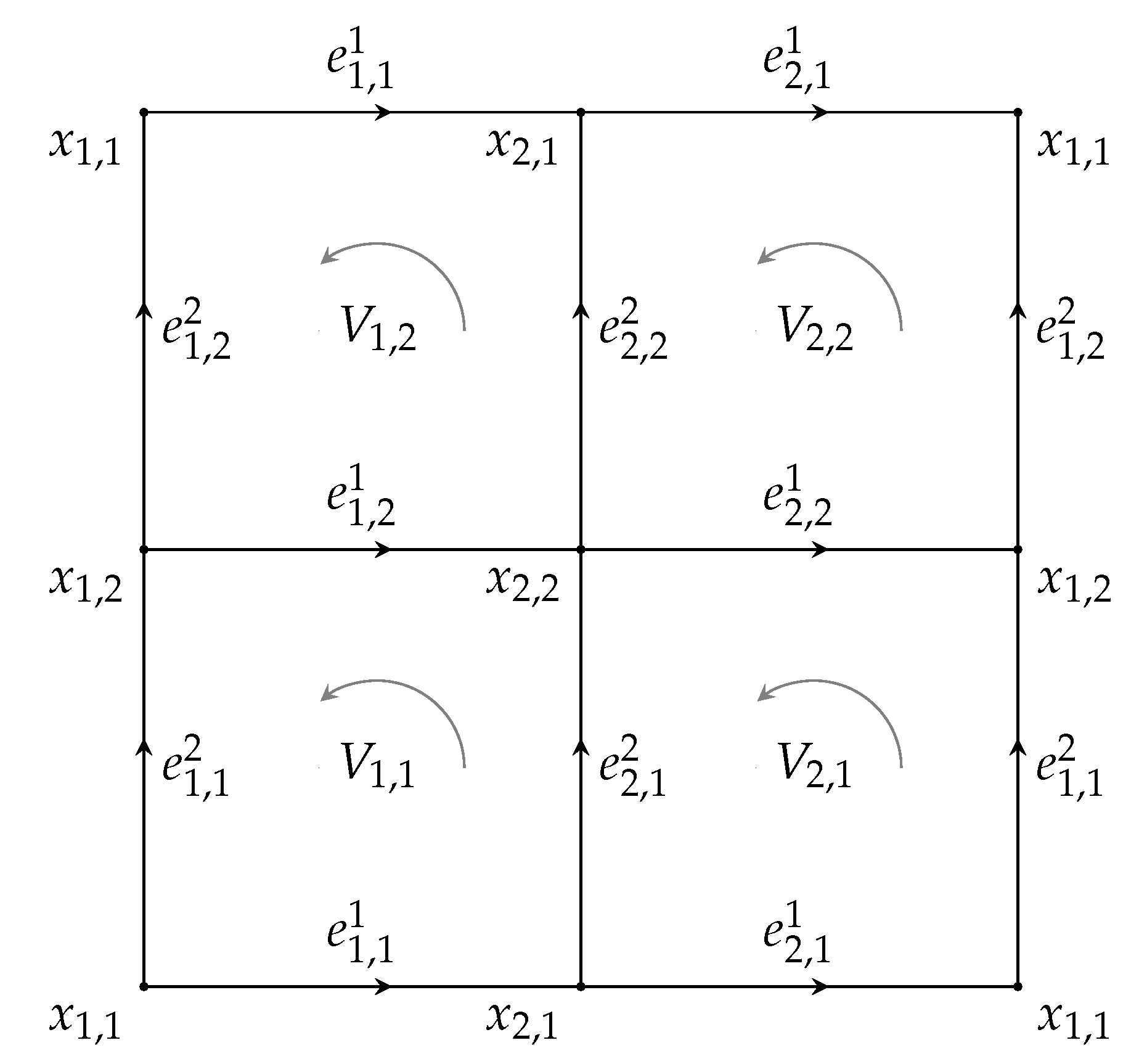
4. Combinatorial Torus
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arnold, D.N.; Falk, R.S.; Winther, R. Finite element exterior calculus, homological techniques, and applications. Acta Numer. 2006, 15, 1–155. [Google Scholar] [CrossRef] [Green Version]
- Arnold, D.N.; Falk, R.S.; Winther, R. Finite element exterior calculus: From Hodge theory to numerical stability. Bull. Amer. Math. Soc. 2010, 47, 281–354. [Google Scholar] [CrossRef] [Green Version]
- Ayoub, R.; Hamdouni, A.; Razafindralandy, D. A new Hodge operator in discrete exterior calculus. Application to fluid mechanics. Commun. Pure Appl. Anal. 2021, 20, 2155–2185. [Google Scholar] [CrossRef]
- Stern, A.; Leopardi, P. The abstract Hodge-Dirac operator and its stable discretization. SIAM J. Numer. Anal. 2016, 54, 3258–3279. [Google Scholar]
- Mohamed, M.S.; Hirani, A.N.; Samtaney, R. Discrete exterior calculus discretization of incompressible Navier–Stokes equations over surface simplicial meshes. J. Comput. Phys. 2016, 312, 175–191. [Google Scholar] [CrossRef] [Green Version]
- Dodziuk, J. Finite-difference approach to Hodge theory of harmonic forms. Am. J. Math. 1976, 98, 79–104. [Google Scholar] [CrossRef] [Green Version]
- Sen, S.; Sen, S.; Sexton, J.C.; Adams, D. A geometric discretisation scheme applied to the Abelian Chern-Simons theory. Phys. Rev. E 2000, 61, 3174–3185. [Google Scholar] [CrossRef] [Green Version]
- Wilson, S.O. Differential forms, fluids, and finite models. Proc. Am. Math. Soc. 2011, 139, 2597–2604. [Google Scholar] [CrossRef] [Green Version]
- Desbrun, M.; Hirani, A.N.; Leok, M.; Marsden, J.E. Discrete exterior calculus. arXiv 2005, arXiv:math/0508341v2. [Google Scholar]
- Desbrun, M.; Kanzo, E.; Tong, Y. Discrete differential forms for computational modeling. In Discrete Differential Geometry. Oberwolfach Seminars; Bobenko, A.I., Schroder, P., Sullivan, J.M., Ziegler, G.M., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2008; Volume 38, pp. 287–323. [Google Scholar]
- Teixeira, F.L. Differential forms in lattice field theories: An overview. ISRN Math. Phys. 2013, 2013, 487270. [Google Scholar] [CrossRef] [Green Version]
- Cerejeiras, P.; Kähler, U.; Sommen, F.; Vajiac, A. Script Geometry. In Modern Trends in Hypercomplex Analysis. Trends in Mathematics; Bernstein, S., Kähler, U., Sabadini, I., Sommen, F., Eds.; Birkhäuser: Cham, Switzerland, 2016; pp. 79–110. [Google Scholar]
- Dezin, A.A. Multidimensional Analysis and Discrete Models; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Sushch, V. Green function for a two-dimensional discrete Laplace-Beltrami operator. Cubo 2008, 10, 47–59. [Google Scholar]
- Sushch, V. A discrete model of the Dirac-Kähler equation. Rep. Math. Phys. 2014, 73, 109–125. [Google Scholar] [CrossRef] [Green Version]
- Sushch, V. A discrete Dirac-Kähler equation using a geometric discretisation scheme. Adv. Appl. Clifford Algebr. 2018, 28, 72. [Google Scholar] [CrossRef] [Green Version]
- Sushch, V. A discrete version of plane wave solutions of the Dirac equation in the Joyce form. Adv. Appl. Clifford Algebr. 2020, 30, 46. [Google Scholar] [CrossRef]
- Warner, F.W. Foundations of Differentiable Manifolds and Lie Groups; Springer: New York, NY, USA, 1983. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sushch, V. 2D Discrete Hodge–Dirac Operator on the Torus. Symmetry 2022, 14, 1556. https://doi.org/10.3390/sym14081556
Sushch V. 2D Discrete Hodge–Dirac Operator on the Torus. Symmetry. 2022; 14(8):1556. https://doi.org/10.3390/sym14081556
Chicago/Turabian StyleSushch, Volodymyr. 2022. "2D Discrete Hodge–Dirac Operator on the Torus" Symmetry 14, no. 8: 1556. https://doi.org/10.3390/sym14081556
APA StyleSushch, V. (2022). 2D Discrete Hodge–Dirac Operator on the Torus. Symmetry, 14(8), 1556. https://doi.org/10.3390/sym14081556





