Dynamic Analysis and Control for a Bioreactor in Fractional Order
Abstract
:1. Introduction
2. Mathematical Model
2.1. Mass Balance Equations
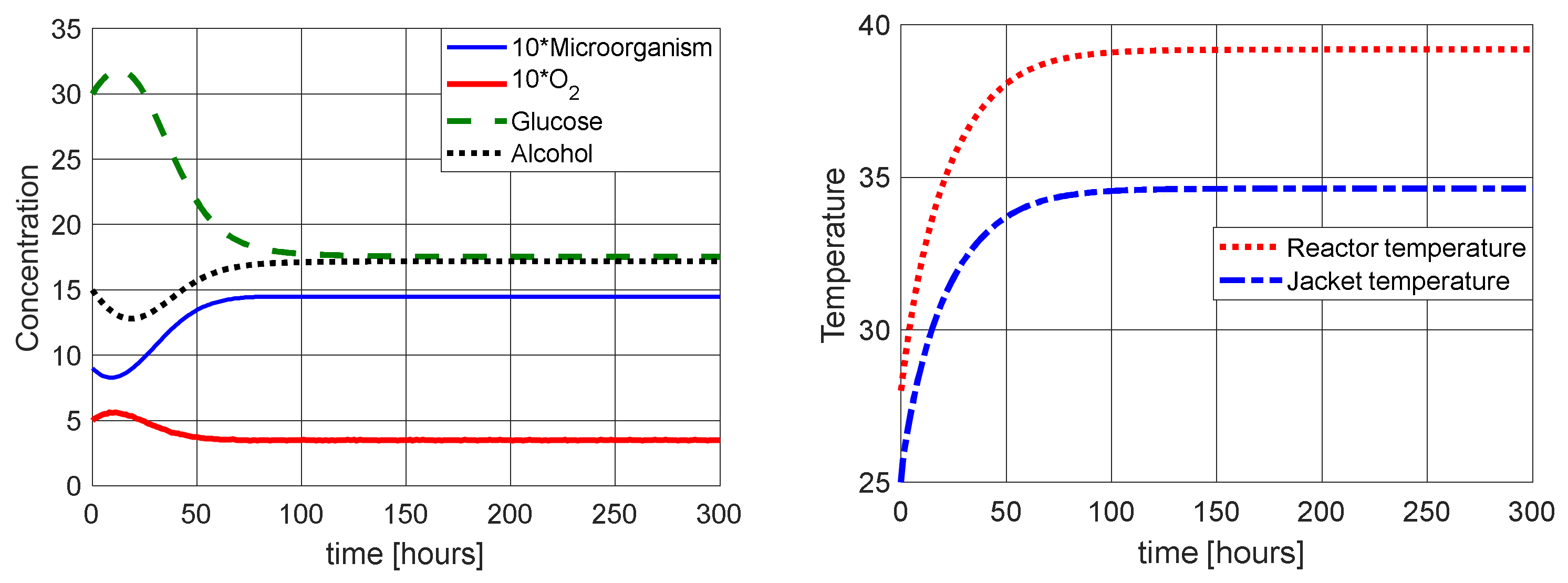
2.2. Numerical Simulations
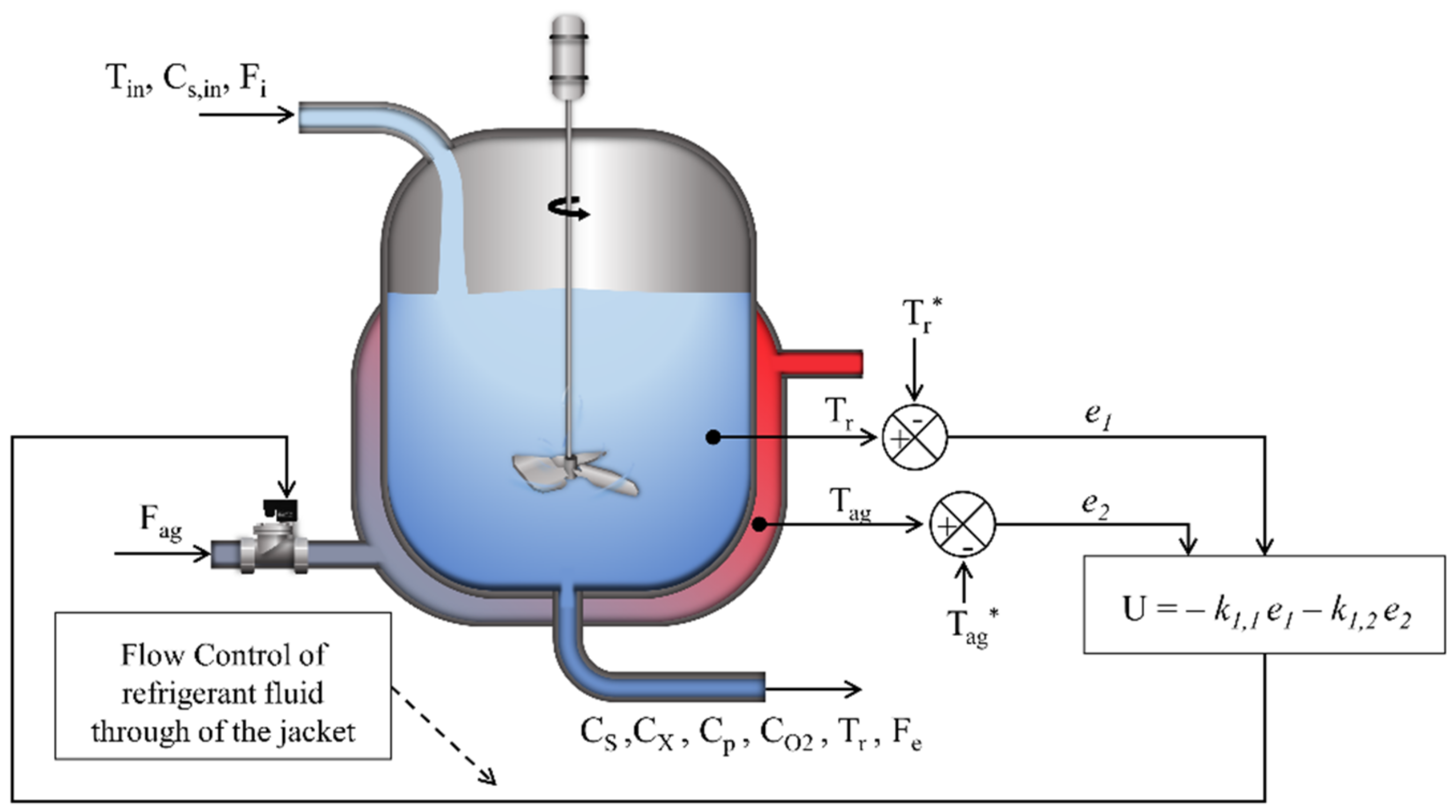
3. Temperature Control Strategy by LQR Control
4. Dynamic Analysis and Control for the Fractional-Order Case
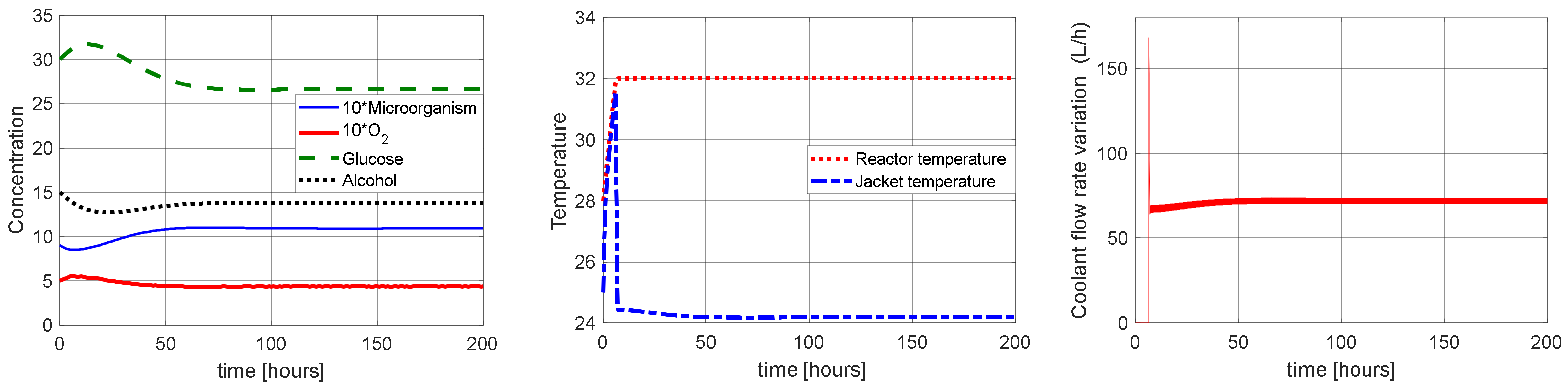
4.1. Proposal of the Temperature Control Strategy by LQR Control in Fractional Order Case
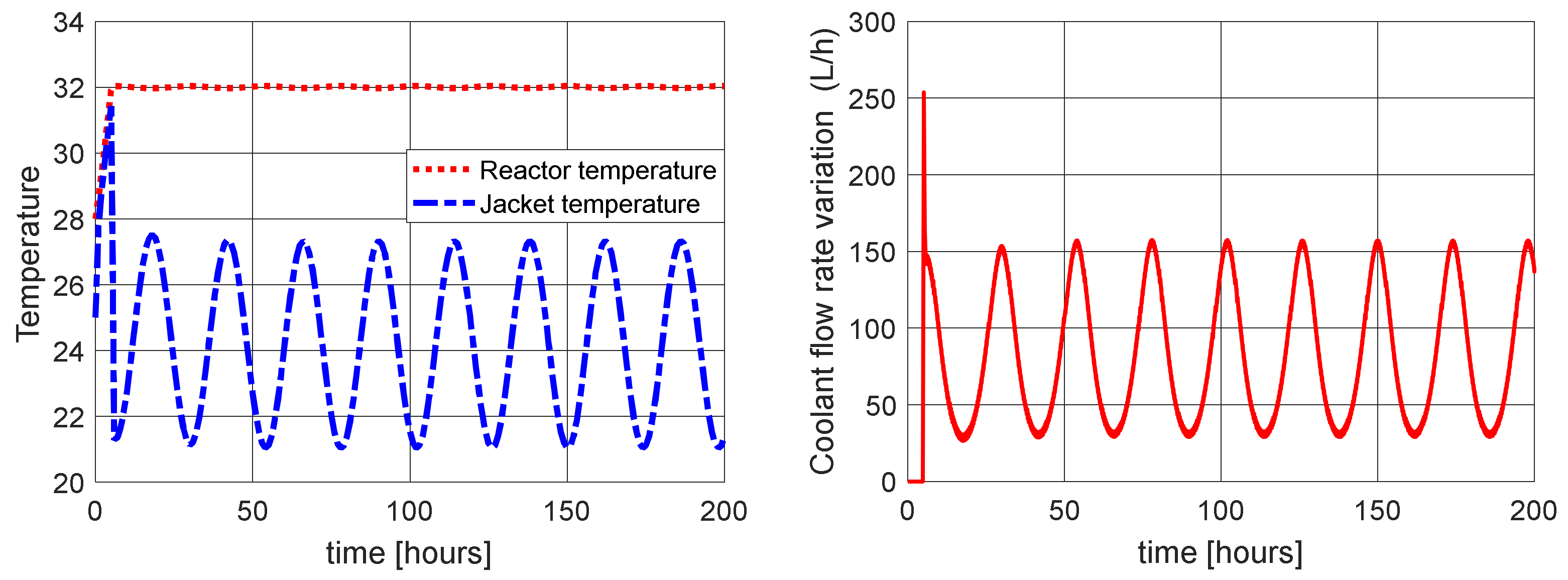
4.2. Proposed Control Sensitivity to Variations in the Reactor Inlet Temperature in Fractional Order Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | State matrix |
| B | Control matrix |
| Cs | Glucose concentration in the reactor |
| Cx | Biomass concentration |
| Cp | Ethanol concentration |
| CO2 | Oxygen concentration |
| Cs,in | Substrate concentration |
| Fag | Flow of the coolant |
| Fe | Fermenter outlet flow |
| FeV−1 | Dilution rate of the reactor |
| Fi | Fermentation vessel flow |
| Ks | Growth substrate constant |
| Kp | Growth inhibition constant by ethanol |
| Kla | Volumetric mass transfer coefficient |
| M | Controllability matrix |
| P | Pressure |
| P | Ricatti Equation |
| q | Derivative order |
| Q | Positive definite matrix |
| R | Positive definite matrix |
| T | Temperature |
| Tag | Temperature of the thermal jacket |
| T*ag | Desired temperature of the jacket |
| Tr | Outlet temperature |
| T*r | Desired temperature of the reactor |
| Tin | Reactor inlet temperature |
| U | Feedback control |
| V | Reactor volume |
| Vj | Jacket volume |
| Vr | Reagent flow |
| Vt | Tank volume |
| X | States vector |
| X* | Desired states vector |
| Specific growth rate | |
| Abbreviations | |
| ADALINE | Adaptive linear neural network |
| BOD | Biochemical oxygen demand |
| COD | Chemical oxygen demand |
| CSTR | Continuous stirred tank reactor |
| DOF | Degree of freedom |
| FOPID | Fractional order PID |
| IMC | Internal model control |
| LDPE | Low density polyethylene |
| LQR | Linear quadratic regulator |
| pH | Potential of hydrogen |
| PID | Proportional, integrative, derivative |
| SDRE | State-dependent Riccati equation |
References
- Ahmed, F.N.; Lan, C.Q. Treatment of landfill leachate using membrane bioreactors: A review. Desalination 2012, 287, 41–54. [Google Scholar] [CrossRef]
- Basso, T.O.; de Kok, S.; Dario, M.; Espirito-Santo, J.C.A.; Müller, G.; Schlölg, P.S.; Silva, C.P.; Tonso, A.; Daran, J.M.; Gombert, A.K.; et al. Engineering topology and kinetics of sucrose metabolism in Saccharomyces cerevisiae for improved ethanol yield. Metab. Eng. 2011, 13, 694–703. [Google Scholar] [CrossRef] [PubMed]
- Muniz, J.B.; Marcelino, M.; Motta, M.D.; Schuler, A.; Alves da Motta, M. Influence of static magnetic fields on S. cerevisae biomass growth. Braz. Arch. Biol. Technol. 2007, l50, 515–520. [Google Scholar] [CrossRef]
- Pachauri, N.; Singh, V.; Rani, A. Two degree of freedom PID based inferential control of continuous bioreactor for ethanol production. ISA Trans. 2017, 68, 235–250. [Google Scholar] [CrossRef]
- Schubert, J.; Simutis, R.; Dors, M.; Havlik, I.; Lübbert, A. Bioprocess optimization and control: Application of hybrid modelling. J. Biotechnol. 1994, 35, 51–68. [Google Scholar] [CrossRef]
- Sultana, S.; Jamil, N.M.; Saleh, E.A.M.; Yousuf, A.; Faizal, C.K.M. A mathematical model for ethanol fermentation from oil palm trunk sap using Saccharomyces cerevisiae. J. Phys. Conf. Ser. 2017, 890, 012050. [Google Scholar] [CrossRef]
- Pachauri, N.; Rani, A.; Singh, V. Bioreactor temperature control using modified fractional order IMC-PID for ethanol production. Chem. Eng. Res. Des. 2017, 122, 97–112. [Google Scholar] [CrossRef]
- Patnaik, P. Hybrid Models for Biological Reactors: Performance and Possibilities. IREPHY 2018, 12, 1–7. [Google Scholar]
- Ahmad, W.; Abdel-Jabbar, N. Modeling and Simulation of a Fractional Order Bioreactor System. IFAC Proc. 2006, 39, 260–264. [Google Scholar] [CrossRef]
- Mohcine, A.; Gueraoui, K.; Mzred, Z.G.; Men-La-Yakhaf, S. Mathematic and Numerical Modeling of Biogas Production in the Bioreactive Plant for Valorizing Domestic Waste. Int. Rev. Mech. Eng. 2017, 11, 249–255. [Google Scholar] [CrossRef]
- Von Stosch, M.; Oliveira, R.; Peres, J.; Azevedo, S.F. A general hybrid semi-parametric process control framework. J. Process. Control 2012, 22, 1171–1181. [Google Scholar] [CrossRef]
- Romero-Bustamante, J.A.; Moguel-Castañeda, J.G.; Puebla, H.; Hernandez-Martinez, E. Robust Cascade Control for Chemical Reactors: An Approach based on Modelling Error Compensation. Int. J. Chem. React. Eng. 2017, 15, 1–15. [Google Scholar] [CrossRef]
- Yao, F.Z.; Lohi, A.; Upreti, S.R.; Dhib, R. Modeling, simulation and optimal control of ethylene polymerization in non-isothermal, high-pressure tubular reactors. Int. J. Chem. React. Eng. 2004, 2, 1–15. [Google Scholar] [CrossRef]
- Fonseca, R.R.; Schmitz, J.; Fileti, A.M.F.; Silva, F. A fuzzy–split range control system applied to a fermentation process. Bioresour. Technol. 2013, 142, 475–482. [Google Scholar] [CrossRef]
- Rincón, A.; Hoyos, F.E.; Candelo-Becerra, J.E. Conditioned Adaptive Control for an Uncertain Bioreactor with Input Saturation and Steep Settling Desired Output. Symmetry 2022, 14, 1232. [Google Scholar] [CrossRef]
- Zhang, W.; Cui, Y.; Ding, X. An Improved Analytical Tuning Rule of a Robust PID Controller for Integrating Systems with Time Delay Based on the Multiple Dominant Pole-Placement Method. Symmetry 2020, 12, 1449. [Google Scholar] [CrossRef]
- Bressan, D.C.; Ribeiro, M.A.; Lenzi, G.G.; Balthazar, J.M.; Tusset, A.M. A Note on SDRE Control Applied in the Fermentation Reactor. Int. Rev. Mech. Eng. 2019, 13, 576–586. [Google Scholar] [CrossRef]
- Estakhrouiyeh, M.R.; Vali, M.; Gharaveisi, A. Application of fractional order iterative learning controller for a type of batch bioreactor. IET Control. Theory Appl. 2016, 10, 1374–1383. [Google Scholar] [CrossRef]
- Tan, H.L.; Wu, J.W.; Bao, H.B. Event-triggered impulsive synchronization of fractional-order coupled neural networks. Appl. Math. Comput. 2022, 429, 127244. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.N.; Zhang, J.; Ai, Z.Y.; Liu, F. Novel stability results of multivariable fractional-order system with time delay. Chaos Solitons Fractals 2022, 157, 111943. [Google Scholar] [CrossRef]
- Huang, C.D.; Wang, J.; Chen, X.P.; Cao, J.D. Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. 2021, 141, 344–354. [Google Scholar] [CrossRef]
- Xu, C.J.; Liao, M.X.; Li, P.L.; Yuan, S. Impact of leakage delay on bifurcation in fractional-order complex-valued neural networks. Chaos Solitons Fractals 2021, 142, 110535. [Google Scholar] [CrossRef]
- Borah, M.; Das, D.; Gayan, A.; Fenton, F.; Cherry, E. Control and anticontrol of chaos in fractional-order models of Diabetes, HIV, Dengue, Migraine, Parkinson’s and Ebola virus diseases. Chaos Solitons Fractals 2021, 153, 111419. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations to Methods of Their Solution and Some of Their Applications. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equation; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Shi, J.P.; He, K.; Fang, H. Chaos, Hopf bifurcation and control of a fractional-order delay financial system. Math. Comput. Simul. 2022, 194, 348–364. [Google Scholar] [CrossRef]
- Xu, C.J.; Zhang, W.; Aouiti, C.; Liu, Z.X.; Liao, M.X.; Li, P.L. Further investigation on bifurcation and their control of fractional order BAM neural networks involving four neurons and multiple delays. Math. Methods Appl. Sci. 2021, 2021, 1–24. [Google Scholar] [CrossRef]
- Xu, C.J.; Zhang, W.; Aouiti, C.; Liu, Z.X.; Yao, L.Y. Further analysis on dynamical properties of fractional-order bi-directional associative memory neural networks involving double delays. Math. Methods Appl. Sci. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Xue, G.M.; Lin, F.N.; Li, S.G.; Liu, H. Adaptive fuzzy finite-time backstepping control of fractional-order nonlinear systems with actuator faults via command-filtering and sliding mode technique. Inf. Sci. 2022, 600, 189–208. [Google Scholar] [CrossRef]
- Li, P.; Gao, R.; Xu, C.; Li, Y. Chaos Suppression of a Fractional-Order Modificatory Hybrid Optical Model via Two Different Control Techniques. Fractal Fract. 2022, 6, 359. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, J.; He, S. Fractional-Order Interval Observer for Multiagent Nonlinear Systems. Fractal Fract. 2022, 6, 355. [Google Scholar] [CrossRef]
- Liu, L.; Xue, D.; Zhang, S. General type industrial temperature system control based on fuzzy fractional-order PID controller. Complex Intell. Syst. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Mahto, T.; Kumar, R.; Malik, H.; Khan, I.A.; Al Otaibi, S.; Albogamy, F.R. Design and Implementation of Frequency Controller forWind Energy-Based Hybrid Power System Using Quasi-Oppositional Harmonic Search Algorithm. Energies 2021, 14, 6459. [Google Scholar] [CrossRef]
- Lan, Y.; Shi, J.; Fang, H. Hopf Bifurcation and Control of a Fractional-Order Delay Stage Structure Prey-Predator Model with Two Fear Effects and Prey Refuge. Symmetry 2022, 14, 1408. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Dubey, R.S.; Jain, M. A study of the fractional-order mathematical model of diabetes and its resulting complications. Math. Meth. Appl. Sci. 2019, 42, 4570–4583. [Google Scholar] [CrossRef]
- Kaewnimit, K.; Wannalookkhee, F.; Nonlaopon, K.; Orankitjaroen, S. The Solutions of Some Riemann–Liouville Fractional Integral Equations. Fractal Fract. 2021, 5, 154. [Google Scholar] [CrossRef]
- Baleanu, D.; Mustafa, O.G.; Agarwal, R.P. An existence result for a super linear fractional differential equation. Appl. Math. Lett. 2010, 23, 1129–1132. [Google Scholar] [CrossRef]
- Gosiewski, K.; Pawlaczyk-Kurek, A. Impact of Thermal Asymmetry on Efficiency of the Heat Recovery and Ways of Restoring Symmetry in the Flow Reversal Reactors. Int. J. Chem. React. Eng. 2019, 17, 20180021. [Google Scholar] [CrossRef]
- Atangana, A.; Secer, A. A Note on Fractional Order Derivatives and Table of Fractional Derivatives of Some Special Functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef]
- Moghadam, A.A. LQ control of coupled hyperbolic PDEs and ODEs: Application to a CSTR-PFR system. IFAC Proc. 2010, 43, 721–726. [Google Scholar] [CrossRef]
- Sundari, S.; Nachiappan, A. Design of optimal Linear Quadratic Regulator for the stabilization of Continuous Stirred Tank Reactor (CSTR) Process. Int. J. Pure Appl. Math. 2018, 118, 1–19. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College: Bologna, Italy, 2010. [Google Scholar]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer: Berlin/Heidelberg, Germany, 2011; Volume 84. [Google Scholar]
- Uchaikin, V. Fractional Derivatives for Physicists and Engineers, Background and Theory; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Battaglia, J.; Lay, L.L.; Batsale, J.C.; Oustaloup, A.; Cois, O. Heat flux estimation through inverted non integer identification models. Int. J. Therm. Sci. 2000, 39, 374–389. [Google Scholar] [CrossRef]
- Ouhsaine, L.; Boukal, Y.; Ganaoui, E.M.; Darouachc, M.; Zasadzinskic, M.; Mimetb, A.; Radhyd, N.E. A general fractional-order heat transfer model for photovoltaic/termal hybrid systems and its observer design. Energy Procedia 2017, 139, 49–50. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Bary, A.A. Effects of variable thermal conductivity and fractional order of heat transfer on a perfect conducting infinitely long hollow cylinder. Int. J. Therm. Sci. 2016, 108, 62–69. [Google Scholar] [CrossRef]
- Cecová, M.; Terpák, J. Fractional Heat Conduction Models and Thermal Diffusivity Determination. Math. Probl. Eng. 2015, 2015, 753936. [Google Scholar] [CrossRef]
- Tusset, A.M.; Piccirillo, V.; Balthazar, J.M.; Fonseca, R.M.L.R. On suppression of chaotic motions of a portal frame structure under non-ideal loading using a magneto-rheological damper. J. Theor. Appl. Mech. 2015, 53, 653–664. [Google Scholar] [CrossRef]
- Esfahanian, M.; Rad, A.S.; Khoshhal, S.; Najafpour, G. Mathematical modeling of continuous ethanol fermentation in a membrane bioreactor by pervaporation compared to conventional system: Genetic algorithm. Bioresour. Technol. 2016, 212, 62–71. [Google Scholar] [CrossRef]
- Amillastre, E.; Aceves-Lara, C.A.; Uribelarrea, J.L.; Alfenore, S.; Guillouet, S.E. Dynamic model of temperature impact on cell viability and major product formation during fed-batch and continuous ethanolic fermentation in Saccharomyces cerevisiae. Bioresour. Technol. 2012, 117, 242–250. [Google Scholar] [CrossRef]
- Tusset, A.M.; Balthazar, J.M.; Rocha, R.T.; Ribeiro, M.A.; Lenz, W.B. On suppression of chaotic motion of a nonlinear MEMS oscillator. Nonlinear Dyn. 2019, 99, 537–557. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ribeiro, M.A.; Balthazar, J.M.; Lenz, W.B.; Rocha, R.T.; Tusset, A.M. Numerical Exploratory Analysis of Dynamics and Control of an Atomic Force Microscopy in Tapping Mode with Fractional Order. Shock Vib. 2020, 2020, 4048307. [Google Scholar] [CrossRef]
- Tusset, A.M.; Ribeiro, M.A.; Lenz, W.B.; Rocha, R.T.; Balthazar, J.M. Time Delayed Feedback Control Applied in an Atomic Force Microscopy (AFM) Model in Fractional-Order. J. Vib. Eng. Technol. 2020, 8, 327–335. [Google Scholar] [CrossRef]

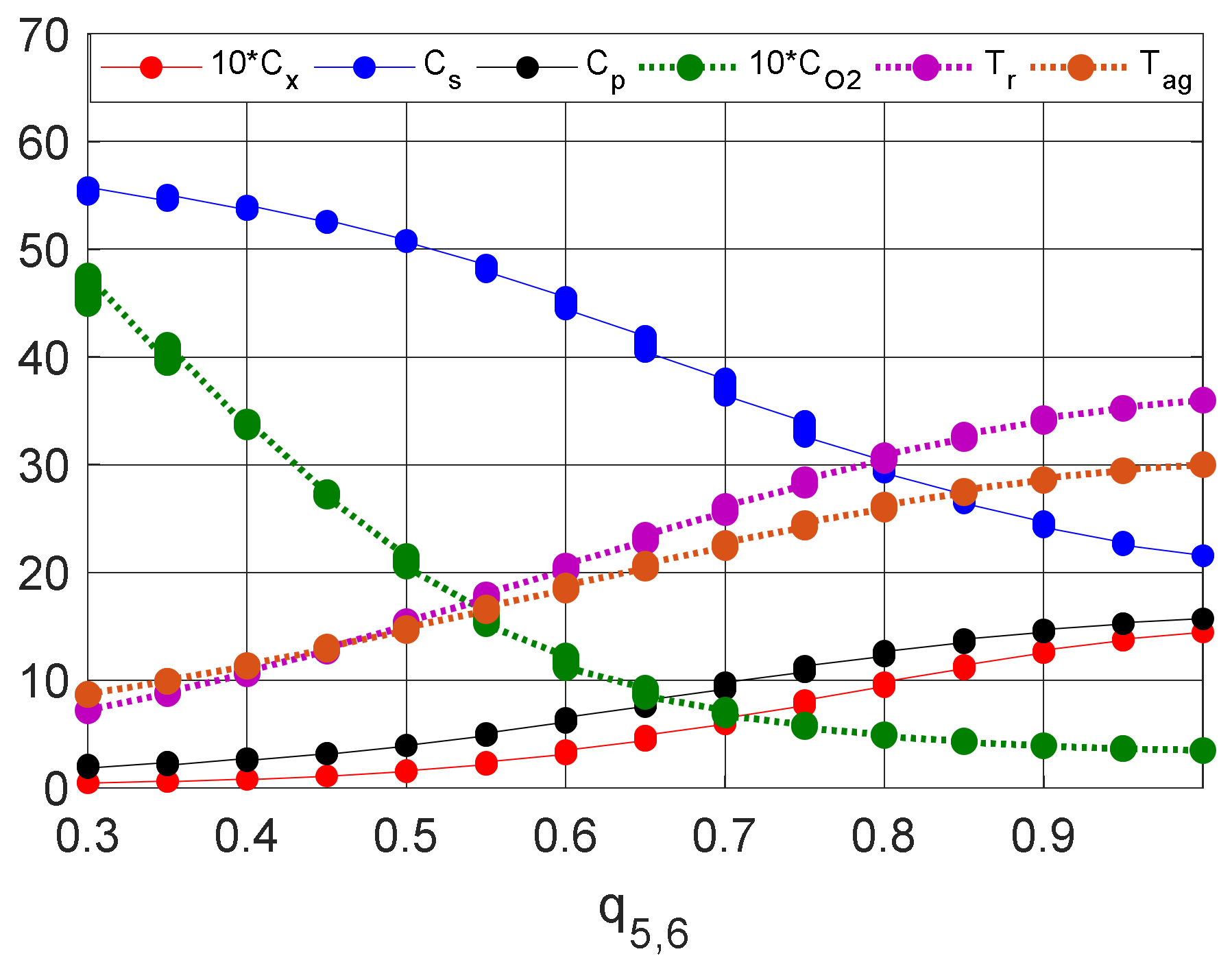

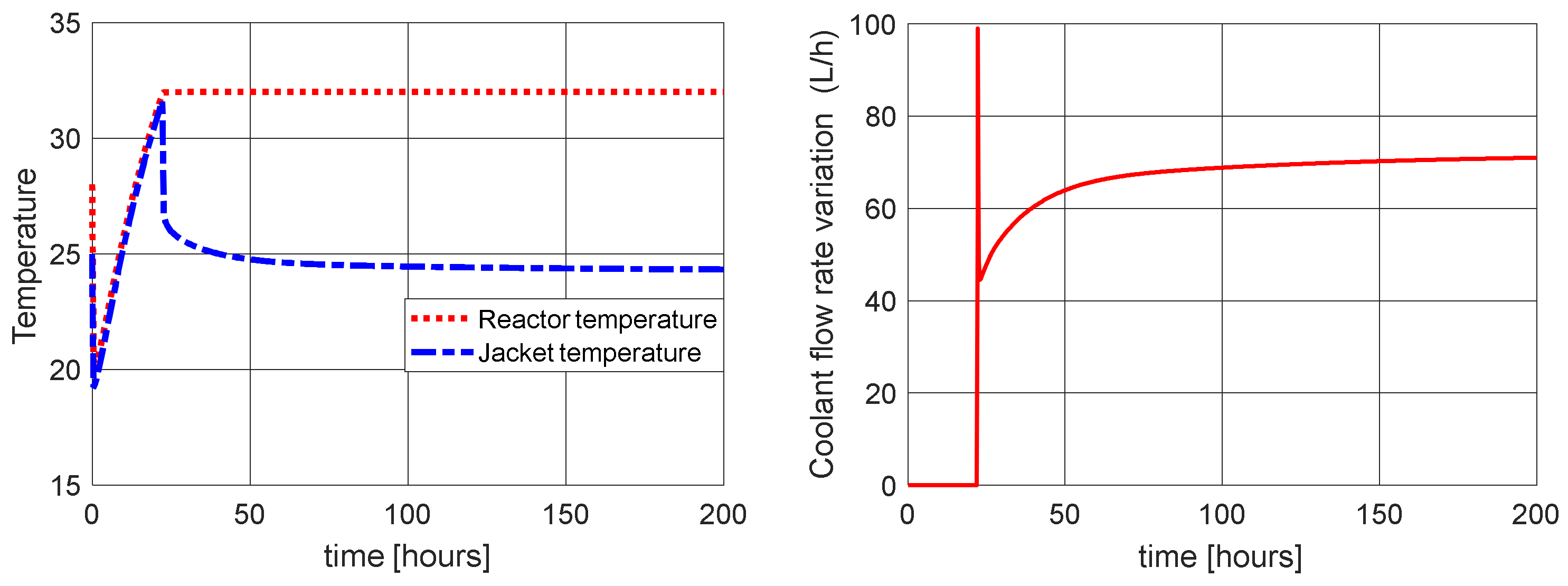
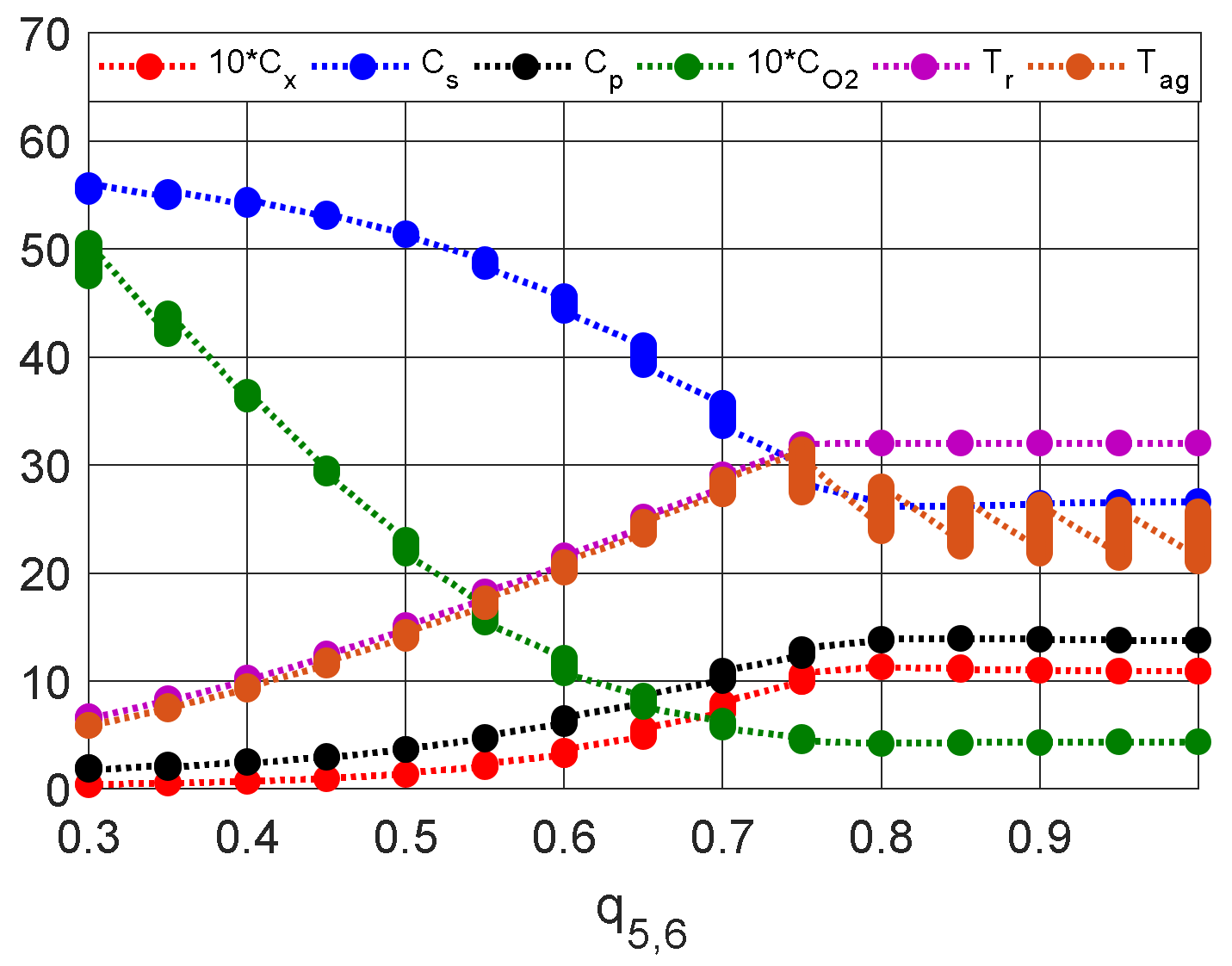
| Without control | 1.447 | 21.52 | 15.7 | 0.3484 | 36.01 | 30.01 |
| With control | 1.089 | 26.02 | 13.74 | 0.4371 | 32.01 | 24.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tusset, A.M.; Inacio, D.; Fuziki, M.E.K.; Costa, P.M.L.Z.; Lenzi, G.G. Dynamic Analysis and Control for a Bioreactor in Fractional Order. Symmetry 2022, 14, 1609. https://doi.org/10.3390/sym14081609
Tusset AM, Inacio D, Fuziki MEK, Costa PMLZ, Lenzi GG. Dynamic Analysis and Control for a Bioreactor in Fractional Order. Symmetry. 2022; 14(8):1609. https://doi.org/10.3390/sym14081609
Chicago/Turabian StyleTusset, Angelo M., Danilo Inacio, Maria E. K. Fuziki, Priscilla M. L. Z. Costa, and Giane G. Lenzi. 2022. "Dynamic Analysis and Control for a Bioreactor in Fractional Order" Symmetry 14, no. 8: 1609. https://doi.org/10.3390/sym14081609






