Einstein–Yang–Mills-Aether Theory with Nonlinear Axion Field: Decay of Color Aether and the Axionic Dark Matter Production

Abstract

We establish a nonlinear version of the SU(N)-symmetric theory, which describes self-consistently the interaction between the gravitational, gauge, vector and pseudoscalar (axion) fields. In the context of this theory the SU(N)-symmetric multiplet of vector fields is associated with the color aether, the decay of which in the early Universe produced the canonic dynamic aether and the axionic dark matter. The SU(N)-symmetric Yang–Mills field, associated with the color aether, forms the source, which transfers the energy of the decaying color aether to the axion field. The nonlinear modification of the model uses explicitly the requirement of discrete symmetry, prescribed by the axion field, and is based on the analogy with a nonlinear physical pendulum. We show that in the framework of this nonlinear regular model, the axion field can grow to an arbitrarily large value, thus explaining the abundance of the axionic dark matter in the Universe.

1. Introduction

Dark matter, the important element of the Universe structure, highly likely consists of axions and axion-like massive particles [1,2,3,4,5,6,7]. There is a number of scenarios according to which the relic axions could be produced in the early Universe [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. One of these scenarios is connected with the idea of contact coupling between the gauge and pseudoscalar fields. This idea arises naturally, when one sees the interaction term $\frac{1}{4}{g}_A\theta {}^{*}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}$ in the Lagrangian discussed in the classical works [24,25,26]. The term equal to the convolution of the Yang–Mills field strength $F_{\left(a\right)}^{mn}$ with its dual ${}^{*}{F}_{mn}^{\left(a\right)}$ multiplied by the pseudoscalar field $\theta$ and by the coupling constant $g_A$ indicates unambiguously that the evolutionary equation for the axion field itself has to have the pseudosource $-\frac{1}{4}{g}_A{}^{*}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}$ formed by the SU(N)-symmetric gauge field. In other words, when the Yang–Mills field configuration provides this pseudosource to be nonvanishing, we have the right to expect that the axion field can be produced due to such interaction. However, there are three questions in this reasoning.

I. The first question is connected with the origin of the SU(N)-symmetric gauge field. The multiplet of gauge field potentials $A_m^{\left(a\right)}$ can appear in the SU(N)-symmetric theory as the element of the extended covariant derivative acting on the scalar, vector, spinor, etc., fields. For instance, when we work with the multiplet of vector fields $U^{j\left(a\right)}$, the usage of the extended covariant derivative of the vector field multiplet $D_k{U}^{j\left(a\right)}={\nabla }_k{U}^{j\left(a\right)}+g{f}_{\left(b\right)\left(c\right)}^{\left(a\right)}{A}_k^{\left(b\right)}{U}^{j\left(c\right)}$ guarantees the theory to possess the SU(N) invariance, on the one hand, and provides the gauge field to become the inherent element of the theory, on the other hand. Thus, one can consider the following scenario of the axion production. Let us imagine that in the early Universe we deal with the SU(N)-symmetric multiplet of vector fields indicated in the works [27,28] as the SU(N)-symmetric dynamic aether, or the color aether, for short. The model of the color aether is considered to be a SU(N) extension of the model of the dynamic aether, introduced by Jacobson and colleagues (see, e.g., [29,30,31,32,33]); this color aether converts into the dynamic aether due to the spontaneous color polarization [28]. So if the gauge field, associated with the color aether, interacts with the pseudoscalar field, we could obtain the axion production, and these relic axions could now form the axionic dark matter.

II. The second question is connected with the energy transfer from the gauge field to the axion configuration. Clearly, a huge number of axions should be born as a result of interactions between the gauge and pseudoscalar fields in the early Universe, if now these particles form the dark matter, associated with 23% of the Universe’s energy density. In other words, we assume that in the course of its decay, the energy of the color aether was partially transferred to the canonic dynamic aether, and partially to the axion configuration, the gauge field being the mediator of this process. We assume that the theory, which could explain this phenomenon, has to be nonlinear (see, e.g., [34,35,36,37] for motivation and examples of modeling in the U(1)-symmetric theory).

III. The third question concerns the symmetry of the model, since it is the symmetry that guarantees the rigor of the theory formulations in the absence of a sufficient quantity of observational data. In the works [36,37], which dealt with nonlinear axion electrodynamics, we considered two special internal symmetries in addition to the standard requirements of a general relativistic approach and in addition to the standard U(1) symmetry of electrodynamics. First, we took into account that the nonlinear model had to be invariant with respect to the discrete transformation of the axion field $\theta \to \theta +2\pi n$ (n is an integer). Second, we assumed that the axion electrodynamics was also invariant with respect to Jackson’s symmetry, which also can be indicated as the SO(2) symmetry of classical electrodynamics [38]. This symmetry assumes that the Faraday–Maxwell equations hold the form, if we use the linear transformations of the electric and magnetic field four-vectors $E^k\to {\tilde{E}}^k=cos\phi E^k+sin\phi B^k$ and $B^k\to {\tilde{B}}^k=-sin\phi E^k+cos\phi B^k$ with some constant angle $\phi$. When we deal with the axion chromodynamics (SU(3) symmetric theory), or with general SU(N)-symmetric models involving the Yang–Mills fields coupled to the axion field, of course, we have to use again the discrete symmetry $\theta \to \theta +2\pi n$. As for Jackson’s symmetry, its generalization for the Yang–Mills theory bumps into one disputable moment. The Yang–Mills field strength tensor $F_{mn}^{\left(a\right)}={\nabla }_m{A}_n^{\left(a\right)}-{\nabla }_n{A}_m^{\left(a\right)}+g{f}_{\left(b\right)\left(c\right)}^{\left(a\right)}{A}_m^{\left(b\right)}{A}_n^{\left(c\right)}$ with the group index $\left(a\right)$ contains not only the potential $A_m^{\left(a\right)}$ with the same group index, but all other vector potentials as well, if the SU(N) group constants $f_{\left(b\right)\left(c\right)}^{\left(a\right)}$ are nonvanishing. In other words, for the non-Abelian Yang–Mills fields, the formal application of Jackson’s symmetry seems to be not sufficiently justified. That is why, in this work we suggest using the idea of generalization, which is associated with the model of physical pendulum in the classical mechanics. One can recall, that the equation $\ddot{x}+{\omega }_0^{2}sinx=0$, which describes the physical pendulum, converts into the equation of the harmonic oscillations of the mathematical pendulum $\ddot{x}+{\omega }_0^{2}x=0$, when x is small. For the physical pendulum, the constant ${\omega }_0$ can be eliminated by the time transformation $t\to \tau ={\omega }_{0}t$, i.e., the parameter $T_0=\frac{1}{{\omega }_0}$ defines the typical time scale of the evolution; in the case of a mathematical pendulum, ${\omega }_0$ relates to the frequency of the harmonic oscillations. Mention should be made that formally speaking, the equation of a physical pendulum is invariant with respect to discrete transformation $x\to x+2\pi n$ (n is an integer), while the equation of the mathematical pendulum does not possess this symmetry. As a result, the solutions to the second equation remain finite; however, the equation of the physical pendulum admits solutions, which grow with time quasi-periodically (see, e.g., [39] for details).

Keeping in mind the analogy with a physical pendulum and taking into account the discrete symmetry, which the theory of axions insists on, we consider below the nonlinear Lagrangian of the Yang–Mills field in the form $\mathcal{L}\left(\mathcal{I}\right)$ with the unified invariant $\mathcal{I}$ given by

$$\mathcal{I}=\frac{1}{4}\left[F_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}+sin\varphi {}^{*}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}\right].$$

(1)

Here, $\varphi$ denotes the dimensionless pseudoscalar field associated with the axionic dark matter. The function $\mathcal{L}\left(\mathcal{I}\right)$ is assumed to have at least two continuous derivatives and tends to $\mathcal{I}$ for small argument. The color aether coupled to the axion field is presented below using the extended constitutive tensor, nonlinear in the axion field, which also supports the discrete symmetry prescribed by the axion field.

To conclude, we would like to emphasize that the novelty of this work is associated with three items. First, based on the nonlinear version of the axion electrodynamics constructed in [36,37], we develop the generalized nonlinear axion chromodynamics, i.e., we use the SU(N)-symmetric Yang–Mills field instead of the U(1)-symmetric electromagnetic field. Second, we assume that the configuration of the coupled gauge and pseudoscalar fields possesses the symmetry indicated as the symmetry of physical pendulum, which replaces the Jackson symmetry of the nonlinear axion electrodynamics. Third, we consider the backreaction of the axion field on the color aether, which is encoded in the structure of the generalized Jacobson constitutive tensor; in this sense, the program of axionic extension of the dynamic aether fulfilled in [40] is now (partially) expanded on the model of the color aether with a gauge field.

The paper is organized as follows. In Section 2, the formalism of the theory is presented: starting from the nonlinearly extended Lagrangian of the coupled SU(N)-symmetric quartet, which includes the gravitational, gauge, vector and pseudoscalar fields, the self-consistent set of master equations is derived. In Section 3, based on the idea of the spontaneous color polarization, we reduce the master equations for the case of vector and gauge fields parallel in the group space, then we consider the application of this truncated model to the anisotropic cosmological model of the Bianchi-I type, and find the exact solutions to the equations for the gauge and vector fields. In Section 4, we focus on the solutions to the equation for the axion field and discuss the possibilities for the axion field growth. Section 5 contains conclusions.

2. The Formalism

2.1. Action Functional and Basic Definitions

The details of the interaction between the gravitational, gauge, vector and pseudoscalar fields are encoded in the action functional

$$S=\int d^{4}x\sqrt{-g}\left\{\frac{1}{2\kappa }\left[R+2\Lambda +\lambda \left(U_{\left(a\right)}^m{U}_m^{\left(a\right)}-1\right)+{\mathcal{K}}_{\left(a\right)\left(b\right)}^{ijmn}{D}_i{U}_m^{\left(a\right)}{D}_j{U}_n^{\left(b\right)}\right]+\right.$$

$$\left.+\mathcal{L}\left(\mathcal{I}\right)+\frac{1}{2}{\Psi }_0^2\left[V\left(\varphi \right)-{\nabla }_k\varphi {\nabla }^k\varphi \right]\right\}.$$

(2)

The gravitational field is described using the standard Einstein–Hilbert Lagrangian: $\sqrt{-g}$ is constructed using the determinant of the spacetime metric $g_{mn}$; R is the Ricci scalar; $\Lambda$ is the cosmological constant; $\kappa =8\pi G$ is the Einstein constant ($c=1$). Other elements of the total Lagrangian require more detailed definitions.

2.1.1. Multiplet of Vector Fields

We work with the multiplet of real vector fields $U^{j\left(a\right)}$, which appear in the adjoint representation of the SU(N) group [41]. We assume that the vector fields satisfy the condition $U^{m\left(a\right)}{U}^{n\left(b\right)}{g}_{mn}{G}_{\left(a\right)\left(b\right)}=1$. The group index a runs in the range $a=1,2,\dots N^2-1$. $G_{\left(a\right)\left(b\right)}$ is the metric in the group space; it is defined as follows

$$G_{\left(a\right)\left(b\right)}=\left({\mathbf{t}}_{\left(a\right)},{\mathbf{t}}_{\left(b\right)}\right)\equiv 2\mathrm{Tr}{\mathbf{t}}_{\left(a\right)}{\mathbf{t}}_{\left(b\right)}$$

(3)

via the SU(N) group generators ${\mathbf{t}}_{\left(a\right)}$, which satisfy the commutation relations

$$\left[{\mathbf{t}}_{\left(a\right)},{\mathbf{t}}_{\left(b\right)}\right]=i{f}_{\left(a\right)\left(b\right)}^{\left(c\right)}{\mathbf{t}}_{\left(c\right)}.$$

(4)

This formula involves the SU(N) group constants $f_{\left(b\right)\left(c\right)}^{\left(a\right)}$, which satisfy the Jacobi identity

$$f_{\left(b\right)\left(c\right)}^{\left(a\right)}{f}_{\left(e\right)\left(h\right)}^{\left(c\right)}+f_{\left(e\right)\left(c\right)}^{\left(a\right)}{f}_{\left(h\right)\left(b\right)}^{\left(c\right)}+f_{\left(h\right)\left(c\right)}^{\left(a\right)}{f}_{\left(b\right)\left(e\right)}^{\left(c\right)}=0.$$

(5)

The structure constants with three subscripts

$$f_{\left(c\right)\left(a\right)\left(b\right)}\equiv G_{\left(c\right)\left(d\right)}{f}_{\left(a\right)\left(b\right)}^{\left(d\right)}=-2i\mathrm{Tr}\left[{\mathbf{t}}_{\left(a\right)},{\mathbf{t}}_{\left(b\right)}\right]{\mathbf{t}}_{\left(c\right)}$$

(6)

are antisymmetric with respect to transposition of any two indices. The Lagrange multiplier $\lambda$ appearing in front of the term $\left(U_{\left(a\right)}^m{U}_m^{\left(a\right)}-1\right)$ stands to guarantee that this term is equal to zero. The SU(N)-symmetric extended covariant derivative [42] in the application to the vector field yields

$$D_k{U}^{j\left(a\right)}={\nabla }_k{U}^{j\left(a\right)}+g{f}_{\left(b\right)\left(c\right)}^{\left(a\right)}{A}_k^{\left(b\right)}{U}^{j\left(c\right)},$$

(7)

where ${\nabla }_k$ is the spacetime covariant derivative. It includes the coupling constant g and the multiplet of covector potentials $A_m^{\left(a\right)}$, describing the gauge field attributed to the SU(N) group. The metric $G_{\left(a\right)\left(b\right)}$ and the structure constants $f_{\left(a\right)\left(c\right)}^{\left(d\right)}$ satisfy the conditions

$$D_m{G}_{\left(a\right)\left(b\right)}=0,D_m{f}_{\left(b\right)\left(c\right)}^{\left(a\right)}=0,$$

(8)

i.e., they are the gauge covariant constant tensors in the group space.

2.1.2. Yang–Mills Tensors

The multiplet of tensors $F_{mn}^{\left(a\right)}$ is expressed via $A_m^{\left(a\right)}$ as follows:

$$F_{mn}^{\left(a\right)}={\nabla }_m{A}_n^{\left(a\right)}-{\nabla }_n{A}_m^{\left(a\right)}+g{f}_{\left(b\right)\left(c\right)}^{\left(a\right)}{A}_m^{\left(b\right)}{A}_n^{\left(c\right)}.$$

(9)

This multiplet of tensors describes the gauge field strength and is indicated by the Yang–Mills tensors. The dual tensors ${}^{*}{F}^{ik\left(a\right)}$

$${}^{*}{F}^{ik\left(a\right)}=\frac{1}{2}{ϵ}^{ikls}{F}_{ls}^{\left(a\right)},$$

(10)

are based on the universal Levi–Civita pseudotensor ${ϵ}^{ikls}=\frac{E^{ikls}}{\sqrt{-g}}$ ($E^{0123}=1$). When we use the definition (9), we obtain the identity

$$D_k{}^{*}{F}^{ik\left(a\right)}\equiv {\nabla }_k{}^{*}{F}^{ik\left(a\right)}+g{f}_{\left(b\right)\left(c\right)}^{\left(a\right)}{A}_k^{\left(b\right)}{}^{*}{F}^{ik\left(c\right)}=0.$$

(11)

2.1.3. Axion Field

The pseudoscalar (axion) field is described by the term $\varphi$ (here, we use the dimensionless quantity $\varphi$ instead of $\theta$). ${\Psi }_0$ is the coupling constant describing the interaction of the axions with the gauge field. According to the theory of axions, the Lagrangian of the axionically active system has to be invariant with respect to discrete symmetry $\varphi \to \varphi +2\pi n$ (n is an integer), that is why we consider the potential of the axion field $V\left(\varphi \right)$ to be of the periodic form

$$V\left(\varphi \right)=2m_A^2\left(1-cos\varphi \right).$$

(12)

The term $\frac{1}{4}sin\varphi {}^{*}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}$ in the unified invariant (1) also satisfies this discrete symmetry. In addition, the function $sin\varphi$ is odd, thus it changes the sign, when $t\to -t$, as the properties of the pseudoscalar field require. When $\varphi \to 0$ the mentioned term converts into $\frac{1}{4}\varphi {}^{*}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}$ recovering the original term introduced by Peccei and Quinn [24].

2.1.4. Extended Jacobson’s Constitutive Tensor

The structure of the constitutive tensor

$${\mathcal{K}}_{\left(a\right)\left(b\right)}^{ijmn}=cos\varphi \left[G_{\left(a\right)\left(b\right)}\left(C_1{g}^{ij}{g}^{mn}+C_2{g}^{im}{g}^{jn}+C_3{g}^{in}{g}^{jm}\right)+C_4{U}_{\left(a\right)}^i{U}_{\left(b\right)}^j{g}^{mn}\right]+$$

(13)

$$+sin\varphi \left\{C_5{G}_{\left(a\right)\left(b\right)}{ϵ}^{ijmn}+C_6\left[U_{s\left(a\right)}\left(U_{\left(b\right)}^i{ϵ}^{jsmn}+U_{\left(b\right)}^j{ϵ}^{isnm}\right)+U_{s\left(b\right)}\left(U_{\left(a\right)}^i{ϵ}^{jsmn}+U_{\left(a\right)}^j{ϵ}^{isnm}\right)\right]\right\},$$

which we use in the Lagrangian, can be explained as follows. First, when $\varphi =0$, and there is only one unit vector field $U^i$, this term recovers Jacobson’s constitutive tensor [29]. Second, this tensor holds the form when we use the transformation $i\to j$, $m\to n$, $a\to b$ simultaneously, i.e., it supports the internal symmetry of the kinetic term ${\mathcal{K}}_{\left(a\right)\left(b\right)}^{ijmn}{D}_i{U}_m^{\left(a\right)}{D}_j{U}_n^{\left(b\right)}$. Third, this constitutive tensor includes $\varphi$ as the argument of the trigonometric functions only, thus supporting the requirement of the discrete symmetry, prescribed by the axion field. Clearly, without the pseudoscalar field, i.e., when $\varphi =0$, Jacobson’s constitutive tensor could not contain the Levi–Civita pseudotensor ${ϵ}^{ijmn}$. In other words, the axionic extension of the Einstein–Yang–Mills-aether theory allows us to add, principally, new terms and new phenomenological constants $C_5$ and $C_6$. As it was mentioned in [27], there are also a lot of possibilities to introduce new coupling constants; however, we omit them, since after the decay of the color aether, when all the vector fields become parallel in the group space, the mentioned terms disappear, and the corresponding coupling constants become hidden. To conclude, in addition to the coupling constants $C_1$, $C_2$, $C_3$ and $C_4$ introduced in the classical work [29], we consider two new coupling constants $C_5$ and $C_6$, which are appropriate just for the axionic extension of the theory.

2.2. Master Equations of the Model

The total set of model equations can be obtained by the variation with respect to gauge potentials $A_i^{\left(a\right)}$, Lagrange multiplier $\lambda$, vector fields $U^{j\left(a\right)}$, pseudoscalar field $\varphi$ and the metric $g^{pq}$. This procedure gives the following results.

2.2.1. Equations for the Yang–Mills Fields

The variation of the action functional (2) with respect to $A_i^{\left(a\right)}$ gives the extended Yang–Mills equations

$$D_k\left\{{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left[F_{\left(a\right)}^{ik}+sin\varphi {}^{*}{F}_{\left(a\right)}^{ik}\right]\right\}={\Gamma }_{\left(a\right)}^i,$$

(14)

where the prime denotes the derivative with respect to the argument of the function. The color current ${\Gamma }_{\left(a\right)}^i$

$${\Gamma }_{\left(a\right)}^i=\frac{g}{\kappa }{f}_{\left(c\right)\left(a\right)}^{\left(d\right)}{U}_m^{\left(c\right)}{\mathcal{K}}_{\left(d\right)\left(b\right)}^{ijmn}{D}_j{U}_n^{\left(b\right)}$$

(15)

appears because of the variation of the second term in the right-hand side of (7) with respect to $A_i^{\left(a\right)}$. If we deal with the quasi-linear model, i.e., $\mathcal{L}=\mathcal{I}$, keeping in mind (11), we can rewrite (14) in the form

$${\nabla }_k{F}_{\left(a\right)}^{ik}+g{f}_{\left(b\right)\left(a\right)}^{\left(c\right)}{A}_k^{\left(b\right)}{F}_{\left(c\right)}^{ik}=$$

$$=-{}^{*}{F}_{\left(a\right)}^{ik}cos\varphi {\nabla }_k\varphi +\frac{g}{\kappa }{f}_{\left(c\right)\left(a\right)}^{\left(d\right)}{U}_m^{\left(c\right)}{\mathcal{K}}_{\left(d\right)\left(b\right)}^{ijmn}\left({\nabla }_j{U}_n^{\left(b\right)}+g{f}_{\left(h\right)\left(e\right)}^{\left(b\right)}{A}_j^{\left(h\right)}{U}_n^{\left(e\right)}\right).$$

(16)

The first term in the right-hand side of this equation for the gauge field can be interpreted as the source associated with the axion field, and the second term relates to the contribution of the color aether. In other words, we deal with two independent sources, which prescribe the details of the Yang–Mills field evolution.

2.2.2. Equations for the Vector Fields

The variation of the action functional (2) with respect to the Lagrange multiplier $\lambda$ gives the normalization condition $U_{\left(a\right)}^k{U}_k^{\left(a\right)}=1$. The variation with respect to the vector fields $U_m^{\left(a\right)}$ yields the balance equation

$$D_i{\mathcal{J}}_{\left(a\right)}^{im}=\lambda U_{\left(a\right)}^m+{\mathcal{I}}_{\left(a\right)}^m.$$

(17)

Here, the tensors ${\mathcal{J}}_{\left(a\right)}^{im}$ can be presented in the form

$${\mathcal{J}}_{\left(a\right)}^{im}\equiv {\mathcal{K}}_{\left(a\right)\left(b\right)}^{ijmn}{D}_j{U}_n^{\left(b\right)}=$$

(18)

$$=cos\varphi \left[C_1{D}^i{U}_{\left(a\right)}^m+C_2{g}^{im}{D}_n{U}_{\left(a\right)}^n+C_3{D}^m{U}_{\left(a\right)}^i+C_4{U}_{\left(a\right)}^i{U}_{\left(b\right)}^j{D}_j{U}^{m\left(b\right)}\right]-2C_{5}sin\varphi {\Omega }_{\left(a\right)}^{im}-$$

$$-C_{6}sin\varphi \left[2{\Omega }^{ms\left(b\right)}\left(U_{s\left(a\right)}{U}_{\left(b\right)}^i+U_{s\left(b\right)}{U}_{\left(a\right)}^i\right)+{ϵ}^{ismn}{D}_j{U}_n^{\left(b\right)}\left(U_{s\left(a\right)}{U}_{\left(b\right)}^j+U_{s\left(b\right)}{U}_{\left(a\right)}^j\right)\right].$$

In this formula, we used the new definition for the multiplet of pseudotensors

$${\Omega }^{lm\left(b\right)}\equiv \frac{1}{2}{ϵ}^{jlmn}{D}_j{U}_n^{\left(b\right)},$$

(19)

which are skew-symmetric with respect to the indices l and m, and play the roles of color vortex operators in our context. The term ${\mathcal{I}}_{\left(a\right)}^m$ in (17) appears due to the variation of the extended constitutive tensor with respect to the vector fields; its structure is the following:

$${\mathcal{I}}_{\left(d\right)}^l\equiv \frac{1}{2}{D}_i{U}_m^{\left(a\right)}{D}_j{U}_n^{\left(b\right)}\frac{\delta }{\delta U_l^{\left(d\right)}}{\mathcal{K}}_{\left(a\right)\left(b\right)}^{ijmn}=C_{4}cos\varphi D^l{U}_{\left(d\right)}^n{U}_{\left(b\right)}^j{D}_j{U}_n^{\left(b\right)}+$$

$$+2C_{6}sin\varphi \left[{\Omega }^{lm\left(b\right)}{U}_{\left(b\right)}^p{D}_p{U}_{m\left(d\right)}+{\Omega }_{\left(d\right)}^{lm}{U}_{\left(b\right)}^p{D}_p{U}_m^{\left(b\right)}+U_{s\left(b\right)}\left({\Omega }_{\left(d\right)}^{sm}{D}^l{U}_m^{\left(b\right)}+{\Omega }^{sm\left(b\right)}{D}^l{U}_{m\left(d\right)}\right)\right].$$

(20)

The Lagrange multiplier can be found as

$$\lambda =U_m^{\left(a\right)}\left[D_i{\mathcal{J}}_{\left(a\right)}^{im}-{\mathcal{I}}_{\left(a\right)}^m\right],$$

(21)

when the corresponding terms are already calculated.

2.2.3. Equation for the Axion Field

The variation of the action functional with respect to the pseudoscalar field $\varphi$ gives the equation

$${\nabla }^k{\nabla }_k\varphi +m_A^{2}sin\varphi =-\frac{1}{4{\Psi }_0^2}cos\varphi {\mathcal{L}}^{\prime }\left(\mathcal{I}\right){}^{*}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}+\mathcal{G},$$

(22)

where the first term in the right-hand side describes the source related to the gauge field, and the pseudoscalar $\mathcal{G}$ given by

$$\mathcal{G}=\frac{1}{2\kappa {\Psi }_0^2}\left\{sin\varphi \left[C_1{D}_n{U}_m^{\left(a\right)}{D}^n{U}_{\left(a\right)}^m+C_2{D}^m{U}_m^{\left(a\right)}{D}_n{U}_{\left(a\right)}^n+C_3{D}_n{U}_m^{\left(a\right)}{D}^m{U}_{\left(a\right)}^n+\right.\right.$$

(23)

$$\left.+C_4{U}_{\left(a\right)}^p{D}_p{U}_m^{\left(a\right)}{U}_{\left(b\right)}^q{D}_q{U}^{\left(b\right)m}\right]-$$

$$\left.-2cos\varphi \left[C_5{\Omega }_{\left(a\right)}^{pq}{D}_p{U}_q^{\left(a\right)}+2C_6{\Omega }^{qm\left(b\right)}{D}_p{U}_m^{\left(a\right)}\left(U_{q\left(a\right)}{U}_{\left(b\right)}^p+U_{q\left(b\right)}{U}_{\left(a\right)}^p\right)\right]\right\}$$

represents the source associated with the color aether contribution.

2.2.4. Equations for the Gravitational Field

The last variation procedure in our context relates to the variation with respect to the metric. The gravitational field is described by the following set of equations:

$$R_{pq}-\frac{1}{2}R{g}_{pq}-\Lambda g_{pq}=\lambda U_p^{\left(a\right)}{U}_{\left(a\right)q}+T_{pq}^{\left(\mathrm{U}\right)}+\kappa T_{pq}^{\left(\mathrm{YM}\right)}+\kappa T_{pq}^{\left(\mathrm{A}\right)}.$$

(24)

The effective stress–energy tensor of the color vector fields $T_{pq}^{\left(\mathrm{U}\right)}$ is of the following form:

$$T_{pq}^{\left(\mathrm{U}\right)}=\frac{1}{2}{g}_{pq}{\mathcal{K}}_{\left(a\right)\left(b\right)}^{ijmn}{D}_i{U}_m^{\left(a\right)}{D}_j{U}_n^{\left(b\right)}+D^m\left[U_{\left(a\right)(p}{\mathcal{J}}_{q)m}^{\left(a\right)}-{\mathcal{J}}_{m(p}^{\left(a\right)}{U}_{q\left)\right(a)}-{\mathcal{J}}_{\left(pq\right)}^{\left(a\right)}{U}_{\left(a\right)m}\right]+$$

(25)

$$+cos\varphi \left[C_1\left(D_m{U}_p^{\left(a\right)}{D}^m{U}_{q\left(a\right)}-D_p{U}^{m\left(a\right)}{D}_q{U}_{m\left(a\right)}\right)+C_4{U}_{\left(a\right)}^m{D}_m{U}_p^{\left(a\right)}{U}_{\left(b\right)}^n{D}_n{U}_q^{\left(b\right)}\right]+$$

$$+4C_{5}sin\varphi \left[\frac{1}{4}{g}_{pq}{D}_j{U}_{n\left(a\right)}{\Omega }^{jn\left(a\right)}-D_j{U}_{(p}^{\left(a\right)}{\Omega }_{q\left)\right(a)}^j\right]+$$

$$+4C_{6}sin\varphi \left[2D^j{U}_{\left(a\right)}^m{U}_j^{\left(\right(b)}{U}_{(p}^{\left(a\right))}{\Omega }_{q\left)m\right(b)}+2D^j{U}_{\left(a\right)(p}{\Omega }_{q\left)\right(b)}^m{U}_m^{\left(\right(a)}{U}_j^{\left(b\right))}+\right.$$

$$\left.+D_i{U}^{m\left(a\right)}{ϵ}_{jsm(p}{D}^j{U}_{q)}^{\left(b\right)}{U}_{\left(\right(b)}^i{U}_{\left(a\right))}^s-g_{pq}{D}_j{U}^{m\left(b\right)}{\Omega }_{sm}^{\left(a\right)}{U}_{\left(a\right)}^{(j}{U}_{\left(b\right)}^{s)}\right].$$

Here, the parentheses $\left(pq\right)$ denote the symmetrization with respect to the coordinate indices p and q, i.e., $a_{(p}{b}_{q)}=\frac{1}{2}(a_p{b}_q+a_q{b}_p)$. The symbol $T_{pq}^{\left(\mathrm{YM}\right)}$ relates to the effective stress–energy tensor of the nonlinear Yang–Mills field

$$T_{pq}^{\left(\mathrm{YM}\right)}={\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left[\frac{1}{4}{g}_{pq}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}-F_{pm}^{\left(a\right)}{F}_{\left(a\right)qn}{g}^{mn}\right]+g_{pq}\left[\mathcal{L}-\mathcal{I}{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\right].$$

(26)

The last term in (24)

$$T_{pq}^{\left(\mathrm{A}\right)}={\Psi }_0^2\left[{\nabla }_p\varphi {\nabla }_q\varphi +\frac{1}{2}{g}_{pq}\left(V\left(\varphi \right)-{\nabla }_n\varphi \nabla {\varphi }^n\right)\right]$$

(27)

describes the canonic effective stress–energy tensor of the pure axion field.

2.2.5. Short Summary

In this Section, we established the new self-consistent SU(N)-symmetric model of the nonlinear interaction between the gauge, vector, pseudoscalar and gravitational fields. The set of model master equations was derived for an arbitrary spacetime platform. This model as a whole deserves a detailed analysis and has a lot of potential applications. However, what do we plan to do now? Our purpose is to make the first step and to analyze the solutions to the equation for the axion field (22) with the sources corresponding to the decay of the color aether in the early Universe. We assume that this story can be described in the framework of the Bianchi-I spacetime model.

3. Decay of the Color Aether

3.1. Ansatz about Parallel Fields

In the work [28], we presented our version of the model of the color aether decay and of the transformation of the color aether into the canonic dynamic aether. The main idea was that a spontaneous color polarization took place, and the fields $U^{j\left(a\right)}$ happened to be parallel to one another in the group space. The idea of such parallelization is well known (see, e.g., [43,44,45]). Mathematically, we have $U^{j\left(a\right)}=q^{\left(a\right)}{U}^j$, where $U^j$ is the timelike unit vector field associated with the velocity four-vector of the dynamic aether [29]. We assume that $U_k{U}^k=1$, and thus the constant color vector $q^{\left(a\right)}$ is also unit, $G_{\left(a\right)\left(b\right)}{q}^{\left(a\right)}{q}^{\left(b\right)}=1$. At the decay moment, the tensor of color polarization $H^{\left(a\right)\left(b\right)}\equiv U_m^{\left(a\right)}{U}_n^{\left(b\right)}{g}^{mn}$ spontaneously transforms into $H^{\left(a\right)\left(b\right)}\equiv q^{\left(a\right)}{q}^{\left(b\right)}$ with a diagonal structure (see [28] for details). Now, we assume that in the epoch preceding the decay, the Yang–Mills fields were generated just by the SU(N)-symmetric aether, and thus, the decay of the color aether was accompanied by the decay of the gauge field. In other words, our second ansatz is that the multiplet of gauge field potentials $A_k^{\left(a\right)}$ also becomes parallel in the group space, i.e., $A_k^{\left(a\right)}=Q^{\left(a\right)}{A}_k$, and $Q^{\left(a\right)}$ is parallel to $q^{\left(a\right)}$, i.e., $Q^{\left(a\right)}=\nu q^{\left(a\right)}$ with some constant $\nu$. With the proposed ansatz, the master equations of the model simplify essentially.

3.1.1. Reduced Equations for the Gauge Fields

First of all, the Yang–Mills fields become quasi-Maxwellian, i.e.,

$$F_{mn}^{\left(a\right)}=\nu q^{\left(a\right)}{F}_{mn},F_{mn}={\nabla }_m{A}_n-{\nabla }_n{A}_m.$$

(28)

The terms $D_k{U}^{j\left(a\right)}$ and ${\Omega }^{pq\left(a\right)}$ convert, respectively, into

$$D_k{U}^{j\left(a\right)}=q^{\left(a\right)}{\nabla }_k{U}^j,{\Omega }^{pq\left(a\right)}=q^{\left(a\right)}{\Omega }^{pq},{\Omega }^{pq}=\frac{1}{2}{ϵ}^{pqmn}{\nabla }_m{U}_n.$$

(29)

The extended Yang–Mills equations (14) take now the Maxwell-type form

$${\nabla }_k\left[{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left(F^{ik}+sin\varphi {}^{*}{F}^{ik}\right)\right]=0,$$

(30)

and Equation (11) reads

$${\nabla }_k{}^{*}{F}^{ik}=0.$$

(31)

3.1.2. Reduced Equations for the Axion Field

With the proposed ansatz, we can transform the axion field Equation (22) as follows

$${\nabla }^k{\nabla }_k\varphi +m_A^{2}sin\varphi =-\frac{{\nu }^{2}cos\varphi }{4{\Psi }_0^2}{\mathcal{L}}^{\prime }\left(\mathcal{I}\right){}^{*}{F}_{mn}{F}^{mn}+\frac{cos\varphi }{\kappa {\Psi }_0^2}\left[2(C_5+2C_6){\omega }^{p}D{U}_p-C_5{\omega }^{pq}{\omega }_{pq}^{*}\right]+$$

(32)

$$+\frac{sin\varphi }{2\kappa {\Psi }_0^2}\left[(C_1+C_3){\sigma }_{mn}{\sigma }^{mn}+\frac{1}{3}{\Theta }^2(C_1+3C_2+C_3)+(C_1-C_3){\omega }_{mn}{\omega }^{mn}+(C_1+C_4)\mathcal{D}{U}_m\mathcal{D}{U}^m\right].$$

Here, we use the notations standard for the Einstein-aether theory, namely, the convective derivative $\mathcal{D}$, the scalar of the medium flow expansion $\Theta$, the projector ${\Delta }_m^p$, the skew-symmetric vortex tensor ${\omega }_{mn}$ and its dual ${\omega }^{*pq}$, the symmetric traceless shear tensor ${\sigma }_{mn}$ and the (pseudo) four-vector of the rotation velocity ${\omega }^p$:

$$\mathcal{D}\equiv U^p{\nabla }_p,\Theta \equiv {\nabla }_p{U}^p,{\omega }_{mn}\equiv \frac{1}{2}{\Delta }_m^p{\Delta }_n^q({\nabla }_p{U}_q-{\nabla }_q{U}_p),{\Delta }_m^p\equiv {\delta }_m^p-U^p{U}_m,$$

(33)

$${\sigma }_{mn}\equiv \frac{1}{2}{\Delta }_m^p{\Delta }_n^q({\nabla }_p{U}_q+{\nabla }_q{U}_p)-\frac{1}{3}{\Delta }_{mn}\Theta ,{\omega }^{*pq}\equiv \frac{1}{2}{ϵ}^{pqmn}{\omega }_{mn},$$

$${\omega }^p\equiv {\omega }^{*pq}{U}_q={\Omega }^{pq}{U}_q\equiv {\Omega }^p.$$

Equation (32) admits the equilibrium-type solutions $\varphi =2\pi n$ (n is an integer), introduced and advocated in [46,47,48,49], if and only if

$${\mathcal{L}}^{\prime }\left(\mathcal{I}\right){}^{*}{F}_{mn}{F}^{mn}=\frac{4}{\kappa {\nu }^2}\left[2(C_5+2C_6){\omega }^{p}D{U}_p-C_5{\omega }^{pq}{\omega }_{pq}^{*}\right],$$

(34)

otherwise, the axion production takes place inevitably in the course of the color aether decay.

3.1.3. Reduced Equation for the Vector Field

Since now ${\mathcal{J}}_{\left(a\right)}^{im}=q_{\left(a\right)}{\mathcal{J}}^{im}$ and ${\mathcal{I}}_{\left(a\right)}^m=q_{\left(a\right)}{\mathcal{I}}^m$, the balance equations (17) take the form

$${\nabla }_i{\mathcal{J}}^{im}=\lambda U^m+{\mathcal{I}}^m,$$

(35)

where the corresponding reduced quantities are

$${\mathcal{J}}^{im}=cos\varphi \left[C_1{\nabla }^i{U}^m+C_2{g}^{im}\Theta +C_3{\nabla }^m{U}^i+C_4{U}^i\mathcal{D}{U}^m\right]+$$

(36)

$$+sin\varphi \left[(2C_6-C_5)U_s{ϵ}^{imsn}\mathcal{D}{U}_n-8C_6{U}^i{\Omega }^m-2C_5{ϵ}^{impq}{\Omega }_{pq}\right],$$

$${\mathcal{I}}^l=C_{4}cos\varphi {\nabla }^l{U}^n\mathcal{D}{U}_n+4C_{6}sin\varphi \left[{\Omega }^{lm}D{U}_m-{\Omega }^m{\nabla }^l{U}_m\right].$$

(37)

The new coupling constant $C_5$ happens to be hidden in (37).

3.1.4. Modifications in the Equations for the Gravitational Field

Using the ansatz of parallel fields, we have to replace $\lambda U_p^{\left(a\right)}{U}_{\left(a\right)q}$ with $\lambda U_p{U}_q$ in (24), and to delete the group indices $\left(a\right)$ in the stress–energy tensor of the Yang–Mills field (26). The stress–energy tensor (25) converts now into

$$T_{pq}^{\left(\mathrm{U}\right)}={\nabla }^m\left[U_{(p}{\mathcal{J}}_{q)m}-{\mathcal{J}}_{m(p}{U}_{q)}-{\mathcal{J}}_{\left(pq\right)}{U}_m\right]+$$

(38)

$$+cos\varphi \left[C_1\left({\nabla }_m{U}_p{\nabla }^m{U}_q-{\nabla }_p{U}^m{\nabla }_q{U}_m\right)+C_4\mathcal{D}{U}_p\mathcal{D}{U}_q\right]+$$

$$+\frac{1}{2}{g}_{pq}cos\varphi \left[C_1{\nabla }^j{U}^m{\nabla }_j{U}_m+C_2{\Theta }^2+C_3{\nabla }_j{U}_m{\nabla }^m{U}^j+C_4\mathcal{D}{U}^m\mathcal{D}{U}_m\right]-$$

$$-2C_{5}sin\varphi {\nabla }_j{U}_{(p}{ϵ}_{q)mn}^j{\nabla }^m{U}^n+$$

$$+4C_{6}sin\varphi \left[\mathcal{D}{U}^m{U}_{(p}{ϵ}_{q)mls}{\nabla }^l{U}^s+\mathcal{D}{U}_{(p}{ϵ}_{q)mls}{U}^m{\nabla }^l{U}^s+\mathcal{D}{U}^m{U}^s{ϵ}_{jsm(p}{\nabla }^j{U}_{q)}\right].$$

The next simplification of the total set of master equations appears, when we choose the spacetime platform, which corresponds to the homogeneous Bianchi-I cosmological model.

3.2. Bianchi-I Spacetime Platform

Below, we consider the class of homogeneous spacetimes with the metric

$$d{s}^2=d{t}^2-a^2\left(t\right)d{x}^2-b^2\left(t\right)d{y}^2-c^2\left(t\right)d{z}^2.$$

(39)

We assume that all the unknown state functions inherit the spacetime symmetry and depend on the cosmological time only. It is reasonable to choose the global unit timelike vector $U^i$ in the form $U^i={\delta }_t^i$ and to check that the master equations for this vector are consistent. It is well known that for the metric (39) the covariant derivative is symmetric

$${\nabla }_m{U}_n={\nabla }_n{U}_m=\frac{1}{2}{\dot{g}}_{mn},$$

(40)

the vorticity tensor vanishes, ${\omega }_{mn}=0$, the acceleration four-vector also is vanishing, $\mathcal{D}{U}^m=0$, and the scalar of expansion $\Theta$ is of the form

$$\Theta \left(t\right)\equiv {\nabla }_k{U}^k=\frac{\dot{a}}{a}+\frac{\dot{b}}{b}+\frac{\dot{c}}{c}.$$

(41)

As usual, the dot denotes the ordinary derivative with respect to time.

An additional simplification is connected with the constraint, obtained due to observations of the events, encoded as GW170817 and GRB 170817A. Based on the observation of the binary neutron star merger [50], it was obtained that the ratio of the velocities of the gravitational and electromagnetic waves in vacuum satisfy the inequality $1-3\times {10}^{-15}<\frac{v_{\mathrm{gw}}}{c}<1+7\times {10}^{-16}$). The square of the velocity of the tensorial aether mode, calculated in [30], is equal to $S_{\left(2\right)}^2=\frac{1}{1-(C_1+C_3)}$, thus the sum of the parameters $C_1+C_3$ can be estimated as $-6\times {10}^{-15}<C_1+C_3<1.4\times {10}^{-15}$. Based on this fact, we can consider that $C_1+C_3=0$ with very high precision, and put $C_3=-C_1$ in the formulas below.

3.2.1. Solution to the Equation for the Gauge Field

Taking into account the symmetry of the reduced model, we can state that Equation (31) admits the solution $F_{12}=const$, and Equation (30) can be reduced to one equation

$$\frac{d}{dt}\left[{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left(abc{F}^{30}-F_{12}sin\varphi \right)\right]=0.$$

(42)

The solution to (42) is

$$F^{30}\left(t\right)=F^{30}\left(t_0\right)\frac{a\left(t_0\right)b\left(t_0\right)c\left(t_0\right)}{a\left(t\right)b\left(t\right)c\left(t\right)}·\frac{{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left(t_0\right)}{{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left(t\right)}+\frac{F_{12}}{a\left(t\right)b\left(t\right)c\left(t\right)}\left[sin\varphi \left(t\right)-sin\varphi \left(t_0\right)·\frac{{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left(t_0\right)}{{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\left(t\right)}\right],$$

(43)

where $t_0$ is some specific time moment. For illustration, we assume the following initial data: $F^{30}\left(t_0\right)=0$ and $\varphi \left(t_0\right)=\pi n$, so that below, we work with the exact solution

$$F^{30}\left(t\right)=\frac{F_{12}}{abc}sin\varphi \left(t\right),$$

(44)

which does not include the nonlinear function $\mathcal{L}\left(\mathcal{I}\right)$. For this elegant solution, the quadratic terms

$$\frac{1}{4}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}=\frac{{\nu }^2{F}_{12}^2}{2a^2{b}^2}{cos}^2\varphi ,\frac{1}{4}{}^{*}{F}_{mn}^{\left(a\right)}{F}_{\left(a\right)}^{mn}=\frac{{\nu }^2{F}_{12}^2}{a^2{b}^2}sin\varphi ,\mathcal{I}=\frac{{\nu }^2{F}_{12}^2}{2a^2{b}^2}(1+{sin}^2\varphi )$$

(45)

are also rather simple.

3.2.2. Solution to the Equation for the Vector Field

When we deal with the Bianchi-I model, for which $\mathcal{D}{U}_m=0$, ${\omega }_{mn}=0$, ${\Omega }^{pq}=0$ and $C_1+C_3=0$, we see that (37) gives ${\mathcal{I}}^l=0$, and one obtains from (36) that

$${\mathcal{J}}^{im}=C_2\Theta cos\varphi g^{im}.$$

(46)

Thus, Equation (35) admits a solution in the form $U^i={\delta }_0^i$. Indeed, three equations out of four are satisfied automatically, and the last equation gives the Lagrange multiplier $\lambda$:

$$\lambda =C_2\frac{d}{dt}\left(\Theta cos\varphi \right).$$

(47)

In other words, two subsets of the master equations, namely, the equations for the gauge and vector fields, happen to be solved analytically.

3.2.3. Key Equation for the Axion Field

The equation for the axion field is also simplified essentially in the Bianchi-I model with $C_1+C_3=0$, and it now takes the form

$$\ddot{\varphi }+\Theta \dot{\varphi }+sin\varphi \left[m_A^2+\frac{{\nu }^2{F}_{12}^2}{{\Psi }_0^2{a}^2{b}^2}cos\varphi {\mathcal{L}}^{\prime }\left(\mathcal{I}\right)-\frac{C_2}{2\kappa {\Psi }_0^2}{\Theta }^2\right]=0.$$

(48)

In this equation, the guiding functions $a\left(t\right)$, $b\left(t\right)$ and $\Theta \left(t\right)$ have to be found from the gravity field equations.

3.2.4. Evolutionary Equations for the Gravitational Field

For the Bianchi-I model, we obtain the simplified gravity field equations in the form

$$\frac{\dot{a}}{a}\frac{\dot{b}}{b}+\frac{\dot{a}}{a}\frac{\dot{c}}{c}+\frac{\dot{b}}{b}\frac{\dot{c}}{c}=\Lambda -\frac{1}{2}{C}_2{\Theta }^{2}cos\varphi +\frac{1}{2}{\Psi }_0^2\left[V\left(\varphi \right)+{\dot{\varphi }}^2\right]+\kappa \mathcal{L}\left(\mathcal{I}\right),$$

$$\frac{\ddot{b}}{b}+\frac{\ddot{c}}{c}+\frac{\dot{b}}{b}\frac{\dot{c}}{c}=\Lambda -C_2{\left(\Theta cos\varphi \right)}^{·}-\frac{1}{2}{C}_2{\Theta }^{2}cos\varphi +\frac{1}{2}{\Psi }_0^2\left[V\left(\varphi \right)-{\dot{\varphi }}^2\right]+\kappa \left[\mathcal{L}\left(\mathcal{I}\right)-2\mathcal{I}{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\right],$$

$$\frac{\ddot{a}}{a}+\frac{\ddot{c}}{c}+\frac{\dot{a}}{a}\frac{\dot{c}}{c}=\Lambda -C_2{\left(\Theta cos\varphi \right)}^{·}-\frac{1}{2}{C}_2{\Theta }^{2}cos\varphi +\frac{1}{2}{\Psi }_0^2\left[V\left(\varphi \right)-{\dot{\varphi }}^2\right]+\kappa \left[\mathcal{L}\left(\mathcal{I}\right)-2\mathcal{I}{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)\right],$$

$$\frac{\ddot{b}}{b}+\frac{\ddot{a}}{a}+\frac{\dot{b}}{b}\frac{\dot{a}}{a}=\Lambda -C_2{\left(\Theta cos\varphi \right)}^{·}-\frac{1}{2}{C}_2{\Theta }^{2}cos\varphi +\frac{1}{2}{\Psi }_0^2\left[V\left(\varphi \right)-{\dot{\varphi }}^2\right]+\kappa \mathcal{L}\left(\mathcal{I}\right).$$

(49)

When the aether is absent and thus $C_2=0$, these equations formally look similar to Equations (31)–(34) from [37], although now, the dependence of the function $\mathcal{I}$ on the axion field $\varphi$ is principally different. However, this similarity makes it easier for us to qualitatively monitor the behavior of the gravity field, if we take into account the corresponding numerical results from [37].

If the Bianchi-I model is characterized by the so-called local invariance, i.e., when $a\left(t\right)=b\left(t\right)$, one can introduce the auxiliary function $H=\frac{\dot{a}}{a}$ and exclude $c\left(t\right)$ from consideration using the relationship $\frac{\dot{c}}{c}=\Theta -2H$, then, keeping in mind that on the solutions of the master equations, the conservation law converts into identity, we obtain only two independent key equations for the gravity field with local invariance; in particular, for the quasi-linear model with $\mathcal{L}\left(\mathcal{I}\right)=\mathcal{I}$, this pair of key equations reads

$$2H\Theta -3H^2=\Lambda -\frac{1}{2}{C}_2{\Theta }^{2}cos\varphi +\frac{1}{2}{\Psi }_0^2\left[V\left(\varphi \right)+{\dot{\varphi }}^2\right]+\frac{{\nu }^2{F}_{12}^2}{2a^4}(1+{sin}^2\varphi ),$$

(50)

$$2\dot{H}+3H^2=\Lambda -C_2{\left(\Theta cos\varphi \right)}^{·}-\frac{1}{2}{C}_2{\Theta }^{2}cos\varphi +\frac{1}{2}{\Psi }_0^2\left[V\left(\varphi \right)-{\dot{\varphi }}^2\right]+\frac{{\nu }^2{F}_{12}^2}{2a^4}(1+{sin}^2\varphi ).$$

(51)

There is one interesting consequence from these equations:

$$\frac{d}{dt}\left(H+\frac{1}{2}{C}_2\Theta cos\varphi \right)=-3H\left(H-\frac{1}{3}\Theta \right).$$

(52)

In such a scheme, we deal with three key Equations (48), (50) and, say, (52) for three unknown functions $\varphi$, H and $\Theta$.

4. On the Solutions of the Equation for the Axion Field

4.1. Special Solutions with $\varphi =2\pi n$: Axions Are in the Equilibrium State

When $\varphi =2\pi n$, Equation (48) is satisfied identically for arbitrary functions $a\left(t\right)$, $b\left(t\right)$, $\Theta \left(t\right)$ and $\mathcal{L}\left(\mathcal{I}\right)$. For the values $\varphi =2\pi n$, the potential of the axion field (12) and its first derivative are equal to zero, $V\left(2\pi n\right)=0$, $V^{\prime }\left(2\pi n\right)=0$, i.e., the axion configuration is in the equilibrium state according to the terminology of [47]. This state is stable. We can choose the number n to be arbitrarily large, and such a solution can be considered as a final stable state of the axion field evolution.

The gravity field equations also become simplified. As an illustration, we consider Equations (50) and (52) for this case:

$$2H\Theta -3H^2=\Lambda -\frac{1}{2}{C}_2{\Theta }^2+\frac{{\nu }^2{F}_{12}^2}{2a^4},$$

(53)

$$\frac{d}{dt}\left(H+\frac{1}{2}{C}_2\Theta \right)=-3H\left(H-\frac{1}{3}\Theta \right).$$

(54)

In the asymptotic regime, when $\Lambda \ne 0$, $C_2\ne -\frac{2}{3}$ and $a\to \infty$, we obtain that

$$H\to H_{\infty }=\frac{1}{3}{\Theta }_{\infty },{\Theta }_{\infty }=\sqrt{\frac{6\Lambda }{2+3C_2}}.$$

(55)

This asymptotic regime corresponds to the isotropization of the Universe, and the behavior of the scale factors corresponds to the de Sitter type asymptote $\propto e^{H_{\infty }t}$. A typical method of solution of this system is the following: we find $\Theta$ from the quadratic Equation (53)

$$\Theta =-\frac{2}{C_2}H\pm \sqrt{\frac{4H^2}{C_2^2}+\frac{2}{C_2}\left(\Lambda +3H^2+\frac{B_0^2}{x^4}\right)},$$

(56)

put it into (54) and solve numerically the obtained nonlinear equation, keeping in mind that

$$B_0^2\equiv \frac{{\nu }^2{F}_{12}^2}{2a^4\left(t_0\right)},x\equiv \frac{a\left(t\right)}{a\left(t_0\right)},\frac{d}{dt}=xH\left(x\right)\frac{d}{dx}.$$

(57)

Here, we restrict ourselves to qualitative comments only.

When $\Lambda =0$, one can find the exact solutions to the system under discussion in the form

$$H\left(x\right)=\frac{\beta (1+C_2)}{x^2},\Theta \left(x\right)=\frac{\beta }{x^2},\beta =\frac{4\sqrt{3}{B}_0}{\sqrt{1-{(12C_2+7)}^2}}.$$

(58)

The solution is real, when Jacobson’s parameter satisfies the condition $-\frac{2}{3}<C_2<-\frac{1}{2}$. The scale factors $a\left(t\right)$ and $c\left(t\right)$, related to these $H\left(x\right)$ and $\Theta \left(x\right)$, have the form

$$\frac{a\left(t\right)}{a\left(t_0\right)}={\left[1+2\beta (1+C_2)(t-t_0)\right]}^{\frac{1}{2}},\frac{c\left(t\right)}{c\left(t_0\right)}={[1+2\beta (1+C_2)(t-t_0)]}^{-\frac{2C_2+1}{2C_2+2}}.$$

(59)

This regime cannot provide the asymptotic isotropization, i.e., this submodel is appropriate for the early Universe only.

4.2. Special Solutions with $\varphi =\pi (2n+1)$: Axions Are in the Unstable State

When $\varphi =\pi (2n+1)$, Equation (48) again is satisfied identically, but now we see that $V\left(\pi (2n+1)\right)=4m_A^2$, $V^{\prime }\left(\pi (2n+1)\right)=0$, i.e., the state of the axion configuration relates to the maximum of the axion potential. This state is unstable. Again, we can choose the number n to be arbitrarily large. The key equations for the gravity field happen to be modified as follows: first, we have to replace in (53) and (54) the cosmological constant $\Lambda \to {\Lambda }_{*}\equiv \Lambda +2{\Psi }_0^2{m}_A^2$; second, since $cos\pi (2n+1)=-1$, we can simply change the sign in front of $C_2$. The results of the previous subsection can be modified, respectively.

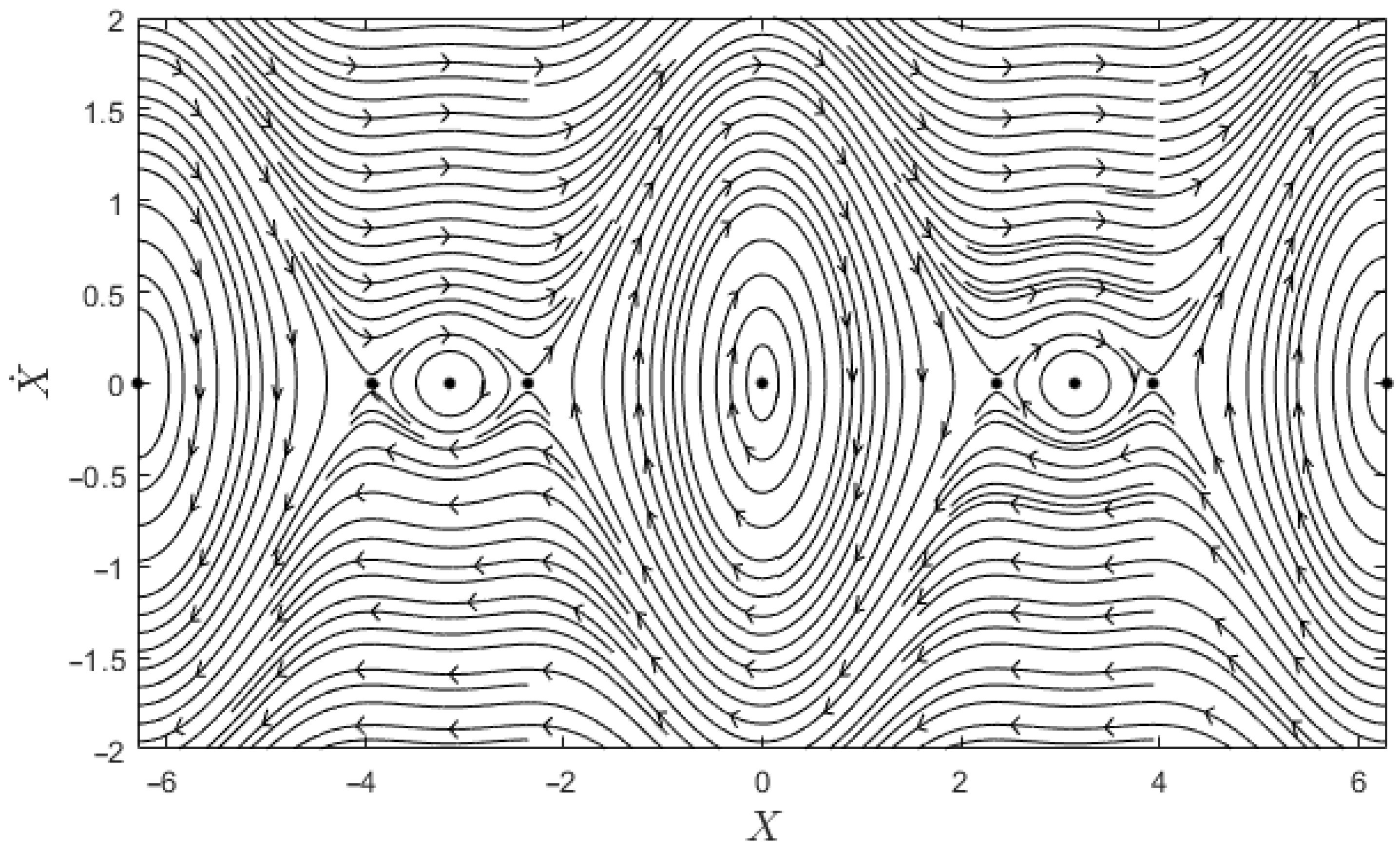
4.3. Dynamics of the Axion Field Growth

Let us focus on the qualitative analysis of Equation (48). Formally speaking, it can be indicated as a modified equation of a physical pendulum.

We would like to recall that for the canonic physical pendulum, the master equation $\ddot{x}+{\omega }_0^{2}sinx=0$ can be rewritten in the equivalent form $\dot{x}=y$, $\dot{y}=-{\omega }_0^{2}sin\varphi$. The phase portrait of this autonomous two-dimensional dynamic system has an infinite number of critical stationary points of two types: the saddle points at $y=0$, $x=\pm (2m+1)\pi$, and the centers at $y=0$, $x=\pm 2m\pi$. The saddle points are linked by separatrices, thus dividing the phase portrait into zones of finite and infinite motion (see [39] for details). In our context, it is important to stress that, when we consider the phase trajectory with noncritical initial data $y_0\ne 0$ for the starting points of both types: $x_0=\pm (2m+1)\pi$ and $x_0=\pm 2m\pi$, we can choose the value $y_0$ so that the pendulum motion is infinite, and the coordinate x grows with time.

Equation (48) can also be presented in terms of a two-dimensional dynamic system

$$\dot{\varphi }=y,\dot{y}=-\Theta y-\mathcal{H}sin\varphi ,$$

(60)

where

$$\mathcal{H}(t,\varphi )=\left[m_A^2+\frac{{\nu }^2{F}_{12}^2}{{\Psi }_0^2{a}^2\left(t\right)b^2\left(t\right)}cos\varphi {\mathcal{L}}^{\prime }\left(\mathcal{I}(t,\varphi )\right)-\frac{C_2}{2\kappa {\Psi }_0^2}{\Theta }^2\left(t\right)\right].$$

(61)

Again, the points $y=0$ and $\varphi =\pi n$ are critical and stationary and they do not move on the phase plane. However, there are a few novel details. First of all, this dynamic system is not autonomous, and its qualitative analysis is possible in time intervals, in which the functions $a\left(t\right)$, $b\left(t\right)$ and $\Theta \left(t\right)$ change slowly, so that in these time intervals, they can be approximately considered as constant. In this scheme, the type of critical points $y=0$ and $\varphi =\pi n$ depends on the sign of the term $\mathcal{H}(t,\varphi )$ on the fixed time interval. The second important detail is connected with possible new critical (nonstationary) points, which can appear, drift and disappear during different time intervals.

4.3.1. The First Case: The Function $\mathcal{H}$ Has No Zeros and $\mathcal{H}>0$

The function $\mathcal{H}$ is positive on the whole admissible time interval, when

$$cos\varphi {\mathcal{L}}^{\prime }\left(\mathcal{I}\right)>\frac{{\Psi }_0^2{a}^2{b}^2}{{\nu }^2{F}_{12}^2}\left[\frac{C_2}{2\kappa {\Psi }_0^2}{\Theta }^2-m_A^2\right].$$

(62)

In this situation, the critical points $y=0$ and $\varphi =\pm (2m+1)\pi$ and $y=0$ and $\varphi =\pm 2m\pi$ remain the saddle points and the centers, respectively, and the instantaneous phase portrait of the dynamic system looks like the one of the canonic physical pendulum. To illustrate the idea, we assume that $C_2=0$ and $\mathcal{L}=\mathcal{I}$. Then, the simplified requirement (62)

$$cos\varphi >-\frac{m_A^2{\Psi }_0^2{a}^2{b}^2}{{\nu }^2{F}_{12}^2}$$

(63)

is satisfied, when $m_A^2{\Psi }_0^2>\frac{{\nu }^2{F}_{12}^2}{a^2\left(t\right)b^2\left(t\right)}$.

4.3.2. The Second Case: The Function $\mathcal{H}$ Has No Zeros and $\mathcal{H}<0$

The function $\mathcal{H}$ is negative on the whole admissible time interval, when

$$cos\varphi {\mathcal{L}}^{\prime }\left(\mathcal{I}\right)<\frac{{\Psi }_0^2{a}^2{b}^2}{{\nu }^2{F}_{12}^2}\left[\frac{C_2}{2\kappa {\Psi }_0^2}{\Theta }^2-m_A^2\right].$$

(64)

For this situation, the critical points $y=0$ and $\varphi =\pm (2m+1)\pi$ become centers, and $y=0$ and $\varphi =\pm 2m\pi$ convert into the saddle points. The phase portrait seems to be the one for the physical pendulum shifted by the value $\pi$ along the horizontal axis. Incidentally, when $C_2=0$, $\mathcal{L}=\mathcal{I}$, this is not possible.

4.3.3. The Third Case: The Function $\mathcal{H}$ Has Zeros and Changes the Sign

If the solutions to the equation $\mathcal{H}=0$ exist, and we deal with the trigonometric equation

$$cos\varphi =\frac{{\Psi }_0^2{a}^2{b}^2}{{\nu }^2{F}_{12}^2{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)}\left[\frac{C_2}{2\kappa {\Psi }_0^2}{\Theta }^2-m_A^2\right],$$

(65)

one can write the roots of this equation as $\varphi =\pm {\varphi }_{*}+2\pi k$, where the solution ${\varphi }_{*}$ belongs to the interval $(0,\pi )$. We obtain now a new series of critical points, $y=0$ and $\varphi =\pm {\varphi }_{*}+2\pi k$, if

$$\left|\frac{{\Psi }_0^2{a}^2{b}^2}{{\nu }^2{F}_{12}^2{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)}\left(\frac{C_2}{2\kappa {\Psi }_0^2}{\Theta }^2-m_A^2\right)\right|<1.$$

(66)

In particular, when $C_2=0$ and $\mathcal{L}=\mathcal{I}$ and the product $a\left(t\right)b\left(t\right)$ grows, this requirement reads $m_A^2{\Psi }_0^2<\frac{{\nu }^2{F}_{12}^2}{a^2\left(t_0\right)b^2\left(t_0\right)}$, and it can be fulfilled for a rather strong magnetic component of the gauge field.

What is the type of these new critical nonstationary points? As usual, we put $\varphi =\pm {\varphi }_{*}+\xi$ and $y=\eta$ with small $\xi$ and $\eta$, and obtain the linearized system

$$\dot{\xi }=\eta ,\dot{\eta }=-\Theta \eta +\xi {sin}^2{\varphi }_{*}\frac{{\nu }^2{F}_{12}^2{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)}{{\Psi }_0^2{a}^2{b}^2}.$$

(67)

The corresponding characteristic equation has the roots

$${\lambda }_{1,2}=-\frac{1}{2}\Theta \pm \sqrt{\frac{1}{4}{\Theta }^2+{sin}^2{\varphi }_{*}\frac{{\nu }^2{F}_{12}^2{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)}{{\Psi }_0^2{a}^2{b}^2}}.$$

(68)

Keeping in mind that in the quasi-linear case ${\mathcal{L}}^{\prime }\left(\mathcal{I}\right)=1>0$, we assume that in the general nonlinear case we can choose the models with ${\mathcal{L}}^{\prime }\left(\mathcal{I}\right)>0$ only. With this assumption, we see that the roots of the characteristic equations ${\lambda }_1$ and ${\lambda }_2$ are real and have opposite signs; thus, the new critical points happen to be the saddle points. On the phase portrait of the dynamic system, the new saddle points appear between the old critical points (for instance, between $\varphi =0$ and $\varphi =\pi$, between $\varphi =\pi$ and $\varphi =2\pi$, etc.). This event reconstructs the phase portrait, since now all stationary points $\varphi =\pi k$ become centers, and the number of finite zones doubles. When the product $a^2\left(t\right)b^2\left(t\right)$ grows, there comes such a moment in time when the function $\mathcal{H}$ (61) loses the possibility to have zeros. The last possibility to have zeros takes place when $cos\varphi =1$ or $cos\varphi =-1$, depending on the values of the guiding parameters. This means that at that time moment, $+{\varphi }_{*}=-{\varphi }_{*}=0$ or $+{\varphi }_{*}=-{\varphi }_{*}=\pi$. On the phase portrait, two new saddle points, which harbor the points $\varphi =(2k+1)\pi$, are converging and finally coincide, thus removing additional zones of finite motion and recovering the old saddle points at $\varphi =(2m+1)\pi$. The illustration of a typical phase portrait is presented in Figure 1.

We have to stress that in this case, the zones of infinite motion exist, and the axion field can grow to an arbitrarily large value.

5. Conclusions and Outlook

The main idea we can conclude from this work is that the decay of the color aether, which took place in the early Universe, can be accompanied by intensive axion production. Why do we think so?

The evolutionary equation for the axion field (48), which we obtained in the framework of the nonlinear version of the self-consistent SU(N)-symmetric Einstein–Yang–Mills-aether axion model, is, in fact, the generalized master equation of a physical pendulum, and this equation admits the formal translational symmetry $\varphi \to \varphi +2\pi n$ with integer n. The typical instantaneous phase portrait of the corresponding nonautonomous dynamic system (60), depicted in Figure 1, shows that, as in the case of a classical physical pendulum, the phase portrait contains two zones of infinite motion (they are located above the upper line formed by the separatrices and below the lower one). The axionic system, which starts to evolve with the initial value $\varphi \left(t_0\right)=\pi n$ (see the requirement transforming the solution (43) to (44)) can enter the zones of infinite motion, if the initial value $\dot{\varphi }\left(t_0\right)$ is appropriate. Clearly, when $\varphi \left(t_0\right)=\pi$, i.e., the pendulum is in the inverted state, and the starting point is located on the phase plane near the saddle point, a small disturbance is enough to provide the infinite motion. For the starting point $\varphi \left(t_0\right)=0$, the corresponding value $\dot{\varphi }\left(t_0\right)$ should be big enough to provide the entrance to the zone of infinite motion.

What does this mean? In the described situation, the pseudoscalar field $\varphi$ grows quasi-periodically, and its final value can be estimated as $\varphi =2\pi n_{\infty }$. The final value $n_{\infty }$ is predetermined by the behavior of the function $\Theta \left(t\right)$ in the related model of the spacetime evolution. In this sense, it is interesting to analyze the term $\mathcal{H}$ (61) in different cosmological epochs. When the term $a^2{b}^2$ is small and $F_{12}^2$ is big, the second term in $\mathcal{H}$ is the leading one, so that the typical time scale for the axion field oscillations T relates to $T\to T_1=\frac{{\Psi }_{0}ab}{\nu |F_{12}|\sqrt{{\mathcal{L}}^{\prime }\left(\mathcal{I}\right)}}$. Thus, in the early Universe the typical time scale is predetermined by the gauge field strength, and it is rather small. For big values of the function $a^2\left(t\right)b^2\left(t\right)$, the second term in (61) is negligible, and the typical time scale is predetermined by the axion interaction with the aether, $T\to T_2=\sqrt{\frac{2\kappa }{\left|C_2\right|}}\frac{{\Psi }_0}{\Theta }$, or by the axion mass, $T\to T_3=\frac{1}{m_A}$, if $C_2=0$.

We agree that at this point some estimations are necessary, and we plan to consider them in a next letter. It might be especially interesting, since such estimations of the typical time scales could introduce new arguments into the debate about why there is so little baryonic matter compared to nonbaryonic (dark) matter in the observable Universe. Indeed, if the axions were born in a very early Universe due to the decay of a color aether, when the gauge field was large, the typical time scale $T_1$, proportional to $\frac{ab}{|F_{12}|}$, would be small. This means that the axion field, growing quasi-periodically, could reach its maximal value very quickly and in the epoch when the cosmic medium was extremely hot. Our hypothesis is that the color aether decay preceded other phase transitions in the early Universe; thus, these axions became relic at the time when baryons were not yet able to stand out as separate particles from the quark–gluon plasma. The Universe was rapidly expanding, the effective temperature of the cosmic medium was falling, and when the formation of stable baryons began, the most favorable time was lost, the cosmic medium became less energy-saturated and thus a smaller amount of energy was converted into the rest energy of baryons in comparison with the rest energy of axions. However, it is worth repeating that detailed assessments are needed to justify such a scheme of explanation.

There exists a rather delicate item in our discussion: how can the number of axions $n_A$ be connected with the value of the pseudoscalar field $\varphi$? When one deals with the early Universe and one works in quantum theory or in HEP phenomenology, the first term, $n_A$, appears as the eigenvalue of the particle number operator and happens to be expressed as an integral containing the square of $\varphi$. In this context, intuitively, we connect the growth of the axion number with the growth of the pseudoscalar field itself. When we apply this model to the late-time period of the Universe evolution, we use the classical approach and have to keep in mind three details. First, the Universe has to be considered as spatially isotropic, and the stress–energy tensor of the axion field contains isotropic Pascal pressure P and the energy density scalar W given by

$$W=\frac{1}{2}{\Psi }_0^2\left[{\dot{\varphi }}^2+V\left(\varphi \right)\right],P=\frac{1}{2}{\Psi }_0^2\left[{\dot{\varphi }}^2-V\left(\varphi \right)\right].$$

(69)

The second detail is that the axionic dark matter seems to be pressureless, $P\approx 0$; thus, we have to assume that $V\left(\varphi \right)\approx {\dot{\varphi }}^2$, and the energy density scalar takes the simplified form $W\approx {\Psi }_0^2{\dot{\varphi }}^2$. The third detail is that the dynamic variable $\varphi \left(t\right)$ turns out to be in the zone of finite motion indicated by the number $n_{\infty }$ and can be presented as $\varphi =2\pi n_{\infty }+\psi$ with $0<\psi <2\pi$. The evolutionary equation for this new variable $\psi$ is of the form

$$\ddot{\psi }+3H_0\dot{\psi }+m_A^{2}sin\psi =0,$$

(70)

where $H_0$ is the current value of the Hubble parameter. In particular, when $\left|\psi \right|$ is small, and if the second term is much smaller than the third one, we can work with the well-known solution

$$\psi \left(t\right)=\psi \left(t_{*}\right)cos\left[m_A(t-t_{*})\right]+\frac{\dot{\psi }\left(t_{*}\right)}{m_A}sin\left[m_A(t-t_{*})\right],$$

(71)

which describes the axionic oscillations. The time moment $t_{*}$ is chosen in the zone of finite motion indicated by the number $n_{\infty }$. Now, we can conclude that the amplitude of the oscillations of the energy density scalar can be estimated as follows:

$$W\left(t_{*}\right)={\Psi }_0^2\left[{\dot{\psi }}^2\left(t_{*}\right)+m_A^2{\psi }^2\left(t_{*}\right)\right].$$

(72)

Since in this representation the axion field enters the energy density scalar with a time derivative, and thus ${\dot{\varphi }}^2={\dot{\psi }}^2$, the parameter $n_{\infty }$ happens to be hidden. When we try to estimate the current density of cold axions in the Solar system, we can use the formula $n_A=\frac{W}{m_A}$, into which we can put the estimation for the dark matter energy density $W\to W_{\left(\mathrm{DM}\right)}\approx 0.45$ GeV/cm${}^3$. For instance, the estimation $m_A\approx 0.45\times {10}^{-15}$ GeV gives $n_A={10}^{15}$ axions in a cubic centimeter.

In order to formulate our further plans, we would like to make the following three comments.

1. In the paper [37], using the nonlinear axion electrodynamics, we showed that the interaction between the axionic dark matter and the global magnetic field could lead to the anomalous flares of the axionically induced electric field, but the axion field itself remained in the finite zone of evolution. In this work, we generalized the U(1)-symmetric axion electrodynamics and formulated the nonlinear SU(N)-symmetric generalized axion chromodynamics. In contrast to the mentioned result of [37], we showed that the axion field could grow to an arbitrarily large value, but the gauge field remained in the finite zone. Such a difference appeared because in [37], we used the internal Jackson SO(2) symmetry of classical electrodynamics, but here we assumed that the whole SU(N)-symmetric model could inherit the discrete symmetry of the physical pendulum.

2. In the paper [40], we considered the full-format generalization of the linear axion-aether theory; however, the electromagnetic field was not considered. In the work [51], we studied the general formalism of the U(1)-symmetric Einstein–Maxwell-aether theory, but the axion field was not considered. Now, we made the step to finish the proposed program, namely, we considered the model with SU(N) symmetry instead of U(1), i.e., we introduced the Yang–Mills fields instead of the Maxwell field, the color aether instead of the dynamic aether, and considered the coupling of the axion field to both of them.

3. In the papers [36,46,47], we studied the direct influence of the dynamic aether on the axionic dark matter by using the axion field potential, which depends on the invariants attributed to the dynamic aether. Now, we took into account the backreaction of the axion field on the color aether by using the generalization of Jacobson’s constitutive tensor.

Putting together all these finds, we hope in the nearest future to build a catalog of models, which predict the axionic dark matter production on the different stage of the Universe evolution.