The Effect of Linear Operators in Periodical Solutions of Ordinary Differential Equations
Abstract
:1. Introduction
2. The Method of Solution
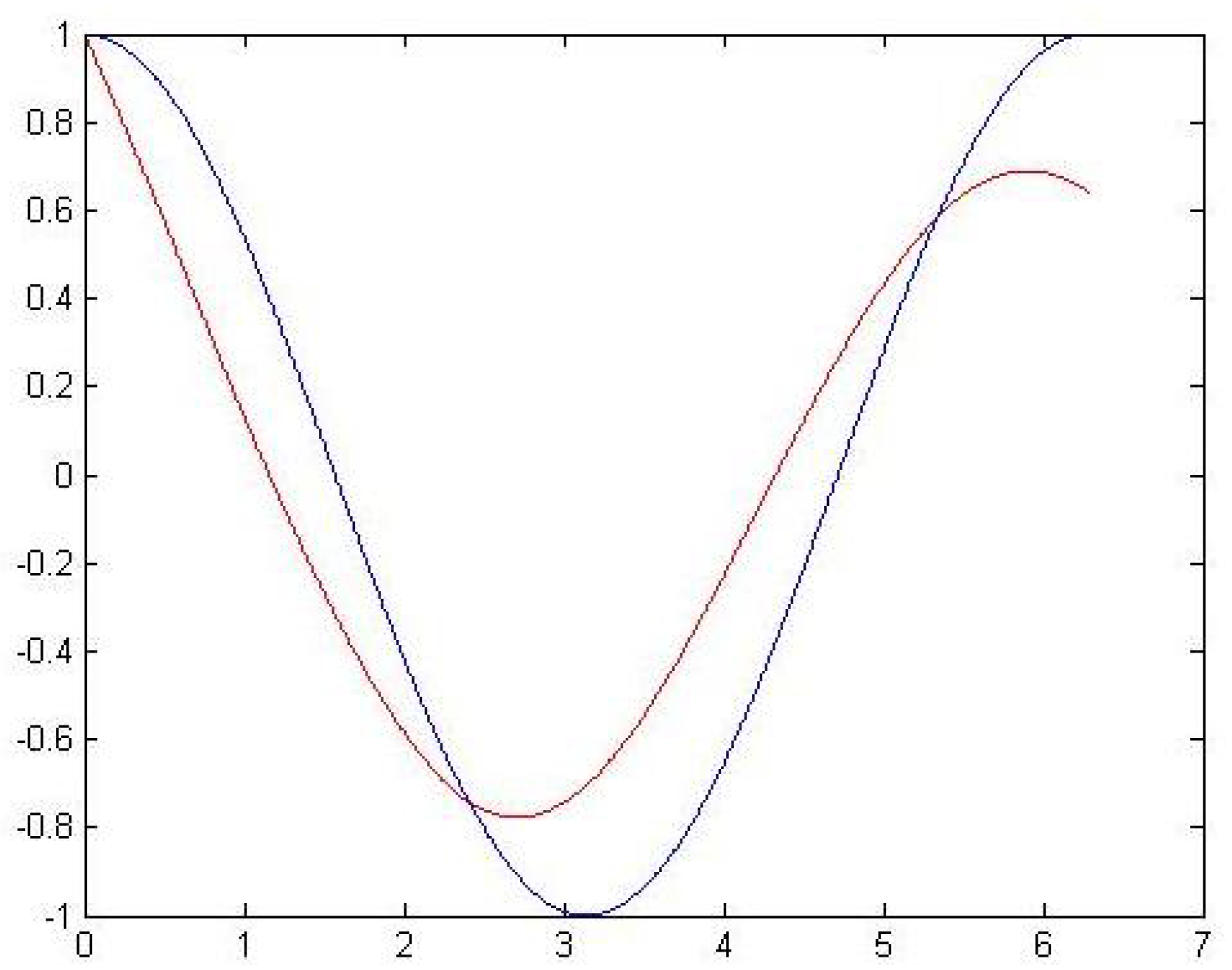
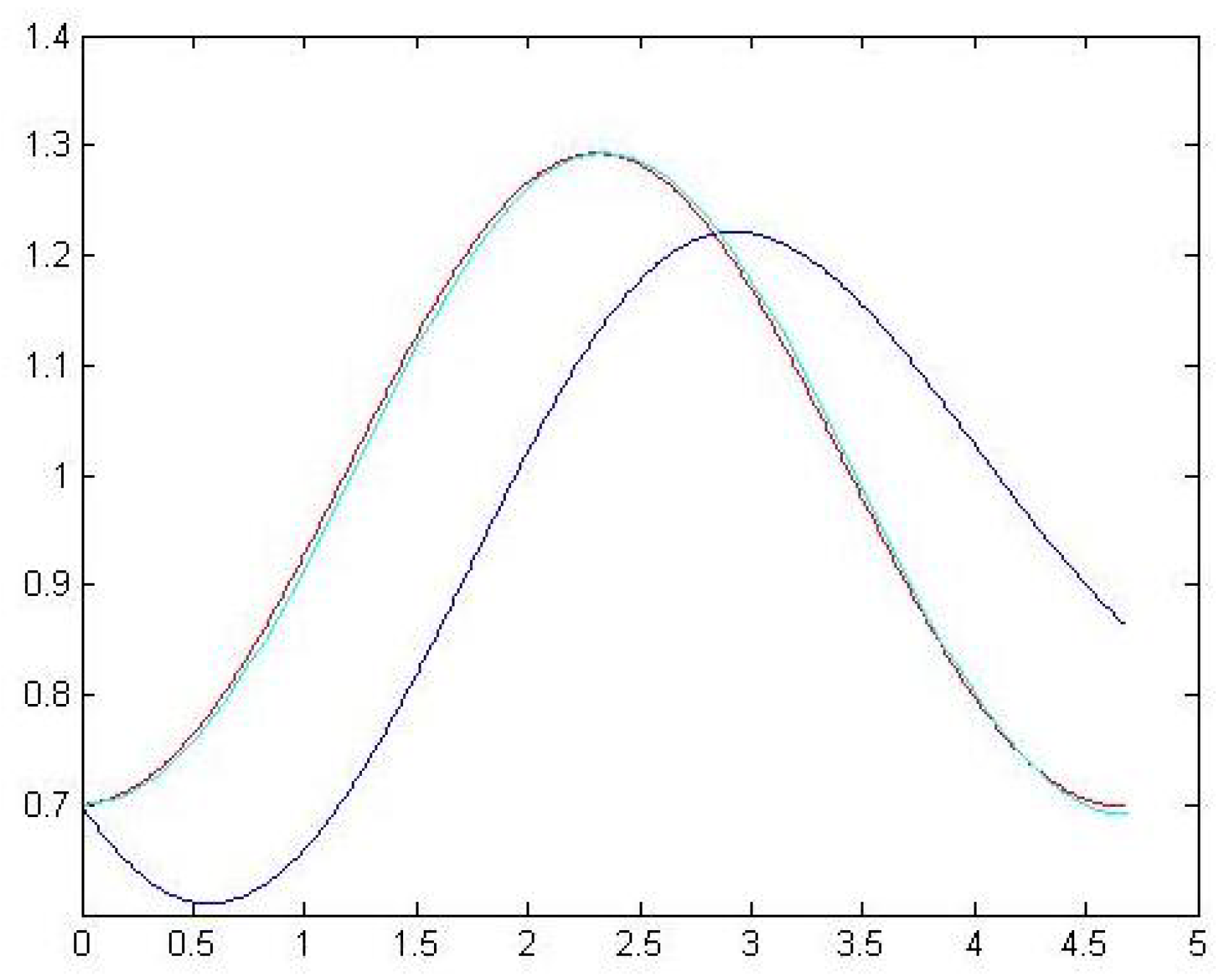
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shashkov, M.; Steinberg, S. Conservative Finite-Difference Methods on General Grids; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Rao, S.S. The Finite Element Method in Engineering; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Szabó, B.; Babuśka, I. Finite Element Analysis: Method, Verification and Validation; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Javeed, S.; Baleanu, D.; Waheed, A.; Shaukat Khan, M.; Affan, H. Analysis of homotopy perturbation method for solving fractional order differential equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Liao, S. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China, 2012; pp. 153–165. [Google Scholar]
- Nadeem, M.; He, J.H.; Islam, A. The homotopy perturbation method for fractional differential equations: Part 1 Mohand transform. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 3490–3504. [Google Scholar] [CrossRef]
- Kumar, M. Recent development of Adomian decomposition method for ordinary and partial differential equations. Int. J. Appl. Comput. Math. 2022, 8, 1–25. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y. Application of Adomian decomposition method to nonlinear systems. Adv. Differ. Equ. 2020, 2020, 67. [Google Scholar] [CrossRef]
- Ziane, D.; Belgacem, R.; Bokhari, A. A new modified Adomian decomposition method for nonlinear partial differential equations. Open J. Math. Anal. 2019, 3, 81–90. [Google Scholar] [CrossRef]
- Ziane, D.; Cherif, M.H.; Cattani, C.; Belghaba, K. Yang-Laplace Decomposition Method for Nonlinear System of Local Fractional Partial Differential Equations. Appl. Math. Nonlinear Sci. 2019, 4, 489–502. [Google Scholar] [CrossRef] [Green Version]
- Rehman, A.U.; Riaz, M.B.; Saeed, S.T.; Jarad, F.; Jasim, H.N.; Enver, A. An Exact and Comparative Analysis of MHD Free Convection Flow of Water-Based Nanoparticles via CF Derivative. Math. Probl. Eng. 2022, 2022, 9977188. [Google Scholar] [CrossRef]
- Big-Alabo, A. A simple cubication method for approximate solution of nonlinear Hamiltonian oscillators. Int. J. Mech. Eng. Educ. 2020, 48, 241–254. [Google Scholar] [CrossRef]
- Big-Alabo, A.; Ekpruke, E.O.; Ossia, C.V. Quasi-static quintication method for periodic solution of strong nonlinear oscillators. Sci. Afr. 2021, 11, e00704. [Google Scholar] [CrossRef]
- Firdous, H.; Saeed, S.T.; Ahmad, H.; Askar, S. Using Non-Fourier’s Heat Flux and Non-Fick’s Mass Flux Theory in the Radiative and Chemically Reactive Flow of Powell-Eyring Fluid. Energies 2021, 14, 6882. [Google Scholar] [CrossRef]
- Younesian, D.; Askari, H.; Saadatnia, Z.; Yildirim, A. Periodic solutions for the generalized nonlinear oscillators containing fraction order elastic force. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 1027–1032. [Google Scholar] [CrossRef]
- Liu, C.S.; Chang, C.W.; Chen, Y.W.; Chang, Y.S. Periodic Orbits of Nonlinear Ordinary Differential Equations Computed by a Boundary Shape Function Method. Symmetry 2022, 14, 1313. [Google Scholar] [CrossRef]
- Liu, C.S. Linearized homotopy perturbation method for two nonlinear problems of duffing equations. J. Math. Res. 2021, 13, 10. [Google Scholar] [CrossRef]
- Liu, C.S.; Chen, Y.W. A simplified Lindstedt-Poincaré method for saving computational cost to determine higher order nonlinear free vibrations. Mathematics 2021, 9, 3070. [Google Scholar] [CrossRef]
- Qian, D.; Li, X. Periodic solutions for ordinary differential equations with sublinear impulsive effects. J. Math. Anal. Appl. 2005, 303, 288–303. [Google Scholar] [CrossRef] [Green Version]
- Zu, J. Existence and uniqueness of periodic solution for nonlinear second-order ordinary differential equations. Bound. Value Probl. 2011, 2011, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Aksoy, N.Y. The Solvability of First Type Boundary Value Problem for a Schrödinger Equation. Appl. Math. Nonlinear Sci. 2020, 5, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Arslan, D. The Comparison Study of Hybrid Method with RDTM for Solving Rosenau-Hyman Equation. Appl. Math. Nonlinear Sci. 2020, 5, 267–274. [Google Scholar] [CrossRef] [Green Version]
- Burton, T.A. Stability and Periodic Solutions of Ordinary and Functional Differential Equations; Courier Corporation: Chelmsford, MA, USA, 2014. [Google Scholar]
- Chiu, K.S.; Li, T. Oscillatory and periodic solutions of differential equations with piecewise constant generalized mixed arguments. Math. Nachr. 2019, 292, 2153–2164. [Google Scholar] [CrossRef]
- Pankov, A.A. Bounded and Almost Periodic Solutions of Nonlinear Operator Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 55. [Google Scholar]
- Yokus, A.; Gulbahar, S. Numerical Solutions with Linearization Techniques of the Fractional Harry Dym Equation. Appl. Math. Nonlinear Sci. 2019, 4, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Cui, M.; Lin, Y. Anti-periodic solutions for Rayleigh-type equations via the reproducing kernel Hilbert space method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1754–1758. [Google Scholar] [CrossRef]
- De Jeu, M.; Jiang, X. Riesz representation theorems for positive linear operators. Banach J. Math. Anal. 2022, 16, 1–40. [Google Scholar] [CrossRef]
- Jäntschi, L. The eigenproblem translated for alignment of molecules. Symmetry 2019, 11, 1027. [Google Scholar] [CrossRef] [Green Version]
- North, G.R. Empirical orthogonal functions and normal modes. J. Atmos. Sci. 1984, 41, 879–887. [Google Scholar] [CrossRef] [Green Version]
- Abbasbandy, S.; Aslefallah, M. Reproducing Kernel Hilbert Space (RKHS) method for solving singular perturbed initial value problem. Theory Approx. Appl. 2016, 10, 1–12. [Google Scholar]
- Chen, S.B.; Soradi-Zeid, S.; Dutta, H.; Mesrizadeh, M.; Jahanshahi, H.; Chu, Y.M. Reproducing kernel Hilbert space method for nonlinear second order singularly perturbed boundary value problems with time-delay. Chaos Solitons Fractals 2021, 144, 110674. [Google Scholar] [CrossRef]
- Farzaneh Javan, S.; Abbasbandy, S.; Araghi, F.; Ali, M. Application of reproducing kernel Hilbert space method for solving a class of nonlinear integral equations. Math. Probl. Eng. 2017, 2017, 7498136. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Azarnavid, B.; Alhuthali, M.S. A shooting reproducing kernel Hilbert space method for multiple solutions of nonlinear boundary value problems. J. Comput. Appl. Math. 2015, 279, 293–305. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Azarnavid, B. Some error estimates for the reproducing kernel Hilbert spaces method. J. Comput. Appl. Math. 2016, 296, 789–797. [Google Scholar] [CrossRef]
- Azarnavid, B.; Parvaneh, F.; Abbasbandy, S. Picard-reproducing kernel hilbert space method for solving generalized singular nonlinear Lane-Emden type equations. Math. Model. Anal. 2015, 20, 754–767. [Google Scholar] [CrossRef]
- Linz, P. Theoretical Numerical Analysis; Courier Dover Publications: Mineola, NY, USA, 2019. [Google Scholar]
- Han, B. Framelets and Wavelets. Algorithms, Analysis, and Applications, Applied and Numerical Harmonic Analysis; Birkhäuser Cham: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Papageorgiou, N.S.; Rädulescu, V.D.; Repovš, D.D. Nonlinear Analysis-Theory and Methods; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Zhou, R.; Shi, S.; Li, W. Renormalization group approach to boundary layer problems. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 220–230. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Liang, S.; Liu, S. An open problem on the optimality of an asymptotic solution to Duffing’s nonlinear oscillation problem. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 4189–4195. [Google Scholar] [CrossRef]
- Van Gorder, R.A. Solutions to a novel Casimir equation for the Ito system. Commun. Theor. Phys. 2011, 56, 801. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Van Gorder, R.A.; Hajiketabi, M.; Mesrizadeh, M. Existence and numerical simulation of periodic traveling wave solutions to the Casimir equation for the Ito system. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 254–262. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soradi-Zeid, S.; Mesrizadeh, M.; Cattani, C. The Effect of Linear Operators in Periodical Solutions of Ordinary Differential Equations. Symmetry 2022, 14, 1645. https://doi.org/10.3390/sym14081645
Soradi-Zeid S, Mesrizadeh M, Cattani C. The Effect of Linear Operators in Periodical Solutions of Ordinary Differential Equations. Symmetry. 2022; 14(8):1645. https://doi.org/10.3390/sym14081645
Chicago/Turabian StyleSoradi-Zeid, Samaneh, Mehdi Mesrizadeh, and Carlo Cattani. 2022. "The Effect of Linear Operators in Periodical Solutions of Ordinary Differential Equations" Symmetry 14, no. 8: 1645. https://doi.org/10.3390/sym14081645





