Symmetry Reductions, Cte Method and Interaction Solutions for Sharma-Tasso-Olver-Burgers Equation

Abstract

In this paper, the Sharma-Tasso-Olver-Burgers (STOB) system is analyzed by the Lie point symmetry method. The hypergeometric wave solution of the STOB equation is derived by symmetry reductions. In the meantime, the consistent tanh expansion (CTE) method is applied to the STOB equation. An nonauto-Bäcklund (BT) theorem that includes the over-determined equations and the consistent condition is obtained by the CTE method. By using the nonauto-BT theorem, the interactions between one-soliton and the cnoidal wave, and between one-soliton and the multiple resonant soliton solutions, are constructed. The dynamics of these novel interaction solutions are shown both in analytical and graphical forms. The results are potentially useful for explaining ocean phenomena.

1. Introduction

The study of exact solutions of integrable systems has been extensively investigated. A number of mathematical physical equations have been investigated by various classical methods, such as the inverse scattering transformation [1], the Painlevé property [2], the Darboux transformation [3], the Bäcklund transformation (BT) [4], the Hirota bilinear method [5], and the variable separation method [6], etc. [7,8,9,10,11,12,13,14]. Among these methods, the Lie point symmetry approach plays key roles in studying the nonlinear partial differential equation (NPDE) [13,14]. It can reduce the number of variables for the NPDE and the order of the ordinary differential equation (ODE). One can use the symmetry to obtain the explicit solutions. The group invariant solutions are obtained by the symmetry reduction equation.

On the other hand, in order to construct various interaction solutions between different types of excitations, it is necessary to develop some methods for studying nonlinear systems. The soliton solutions on a cnoidal waves background, which can treated as a nonautonomous soliton solution, have been extensively investigated [15]. The interaction between solitons and the cnoidal waves can be obtained by the Darboux transformation [16], the symmetry reductions related by the nonlocal symmetry and the consistent tanh expansion (CTE) method [17,18,19,20,21,22,23]. The CTE method is a relatively simple method to obtain various interaction solutions between different types of excitations. The exploration of the Lie point symmetry method and the CTE method for the NPDE is an interesting topic [17]. These methods have been not applied to the Sharma-Tasso-Olver-Burgers (STOB) equation. In this paper, the purpose of this study is mainly to apply the Lie point symmetry approach and the CTE method to the STOB equation.

The STOB equation has the following form:

$$u_t-\alpha (2u{u}_x+u_{xx})-\beta (3u^2{u}_x+3u_x^2+3u{u}_{xx}+u_{xxx})=0,$$

(1)

where $\alpha$ and $\beta$ are arbitrary constants. It is obvious that (1) will degenerate to the usual Burgers system with $\beta =0$ and the STO system with $\alpha =0$, respectively. The integrability properties and the nonlinear waves of these three integrable systems have been investigated by using different approaches. Super extension of the Burgers equation is studied by the bosonization approach [24,25]. The soliton fission and fusion of the STO equation is studied by the symmetry reduction procedure [26]. The nonlocal symmetry and the CTE method are applied to the STO equation [27,28]. Non-topological, topological and rogue waves for the STO equation are constructed by the solitary wave ansatz approach [29]. For the STOB equation, lump and diverse interaction solutions are obtained by means of the corresponding bilinear form [30]. Soliton molecules of the STOB equation are constructed by means of the velocity resonant mechanism [31]. Conservation laws and the kink solitons are studied by the formal Lagrangian, the Kudryashov and exponential methods [32].

The paper is organized as follows. The preliminaries of the Lie point symmetry and the CTE method are introduced in Section 2. In Section 3, the STOB equation is studied by the Lie point symmetry method. In Section 4, the CTE method is applied to the STOB equation. Some novel interaction solutions are constructed using the nonauto-BT theorem. Section 5 is a simple summary and discussion.

2. Preliminaries of Lie Point Symmetry and CTE Method

2.1. Method of Lie Point Symmetry

One supposes the form of a derivative nonlinear polynomial equation as

$$\overrightarrow{\mathbf{P}}(\overrightarrow{\mathbf{x}},t,\overrightarrow{\mathbf{u}})=0,\overrightarrow{\mathbf{x}}=\{x_1,x_2,\dots ,x_n\},\overrightarrow{\mathbf{P}}=\{P_1,P_2,\dots ,P_m\},\overrightarrow{\mathbf{u}}=\{u_1,u_2,\dots ,u_m\}.$$

(2)

A one-parameter Lie group of infinitesimal transformations on the system (2) reads

$${\overrightarrow{\mathbf{x}}}^{\prime }\to \overrightarrow{\mathbf{x}}+ϵ\overrightarrow{\mathbf{X}}+o\left({ϵ}^2\right),t^{\prime }\to t+ϵ\tau +o\left({ϵ}^2\right),{\overrightarrow{\mathbf{u}}}^{\prime }\to \overrightarrow{\mathbf{u}}+ϵ\overrightarrow{\mathbf{U}}+o\left({ϵ}^2\right),$$

(3)

where $ϵ$ is the parameter of the transformation and $\overrightarrow{\mathbf{X}},\tau$ and $\overrightarrow{\mathbf{U}}$ are the infinitesimals of the transformations, respectively. A symmetry of (2) is defined as a solution of its linearized equation

$${\overrightarrow{\mathbf{P}}}^{\prime }(\overrightarrow{\mathbf{x}},t,\overrightarrow{\mathbf{u}}){\sigma }^{\overrightarrow{\mathbf{u}}}=\underset{ϵ=0}{lim}\frac{d\overrightarrow{\mathbf{P}}({\overrightarrow{\mathbf{x}}}^{\prime },t^{\prime },{\overrightarrow{\mathbf{u}}}^{\prime })}{dϵ}=0.$$

(4)

The general Lie point symmetry has the form

$${\sigma }^{\overrightarrow{\mathbf{u}}}=\overrightarrow{\mathbf{X}}{u}_x+\tau u_t-\overrightarrow{\mathbf{U}}.$$

(5)

The corresponding vector with the group of transformations can be written as

$$\begin{array}{c}\hfill V=\overrightarrow{\mathbf{X}}\frac{\partial }{\partial \overrightarrow{\mathbf{x}}}+\tau \frac{\partial }{\partial t}+\overrightarrow{\mathbf{U}}\frac{\partial }{\partial \overrightarrow{\mathbf{u}}}.\end{array}$$

(6)

Substituting Equation (5) into the linearized Equation (4) and making the field $\overrightarrow{\mathbf{u}}$ to satisfy Equation (2), we can obtain the infinitesimals $\overrightarrow{\mathbf{X}},\tau$ and $\overrightarrow{\mathbf{U}}$. By using these infinitesimals, some group invariant solutions can be constructed by the symmetry reductions.

2.2. Method of CTE Method

According to the CTE method [17], the expansion form of Equation (2) reads as

$$\begin{array}{c}\hfill \overrightarrow{\mathbf{u}}=u_i=\sum _{j=0}^{J_i}{u}_{i,j}{tanh}^j\left(\chi \right),\end{array}$$

(7)

where the positive integer $J_i,i=1,2,\dots ,m$ is determined by the leading order analysis, and $\chi$ is an arbitrary function of $\overrightarrow{\{\mathbf{x}},t\}$. Substituting Equation (7) into Equation (2) leads to

$$\begin{array}{c}\hfill P_j(\overrightarrow{\mathbf{x}},t,\overrightarrow{\mathbf{u}})=\sum _{i=0}^{N_j}{P}_{j,i}(\overrightarrow{\mathbf{x}},t,u_{l,k},\chi ){tanh}^i\left(\chi \right)=0,j=1,2,\dots ,m,\end{array}$$

(8)

where $N_j,j=1,2,\dots ,m$ are dependent on the models, and $P_{j,i}(\overrightarrow{\mathbf{x}},t,u_{l,k},\chi )$ are functions of $\{\overrightarrow{\mathbf{x}},t,u_{l,k},\chi \}$ and their derivatives. By vanishing different powers of ${tanh}^i\left(\chi \right)$, we obtain the over-determined system

$$\begin{array}{c}\hfill P_{j,i}(\overrightarrow{\mathbf{x}},t,u_{l,k},\chi )=0,i=0,1,\dots ,N_j,j=1,2,\dots ,m.\end{array}$$

(9)

The nonlinear system (2) is called a CRE solvable system while system (9) is consistent. In the following two sections, we apply the Lie point symmetry and CRE method to study the STOB equation.

3. Lie Point Symmetry and Similarity Reductions of STOB Equation

Based on the Lie symmetry method [13], the STOB equation is invariant under transformation

$$\begin{array}{c}\hfill u\to u+ϵ{\sigma }^u.\end{array}$$

(10)

The general vector field is given as

$$\begin{array}{c}\hfill V=X\frac{\partial }{\partial x}+T\frac{\partial }{\partial t}+U\frac{\partial }{\partial u},\end{array}$$

(11)

where $X,T$ and U are the functions of $x,t$ and u. The symmetry equation for ${\sigma }^u$ is expressed as a solution of the linearized system (1)

$$\begin{array}{c}\hfill {\sigma }_t^u-\alpha [2{\left({\sigma }^{u}u\right)}_x+{\sigma }_{xx}^u]-\beta [3{\left({\sigma }^{u}u\right)}_{xx}+3{\left({\sigma }^u{u}^2\right)}_x+{\sigma }_{xxx}^u]=0.\end{array}$$

(12)

The symmetry ${\sigma }^u$ has the form

$$\begin{array}{c}\hfill {\sigma }^u=X{u}_x+T{u}_t-U.\end{array}$$

(13)

Over-determined equations of the STOB system can be obtained by substituting Equation (13) into the symmetry Equation (12) and letting u satisfy the STOB system. Solving the over-determined equations leads to the infinitesimals

$$\begin{array}{c}\hfill X=\frac{C_1}{3}x+\frac{2C_1{\alpha }^2}{9\beta }t+C_3,T=C_{1}t+C_2,U=-\frac{C_1}{3}u-\frac{C_1\alpha }{9\beta },\end{array}$$

(14)

where $C_i(i=1,2,3)$ are arbitrary constants. We can find the group invariant solutions by solving the characteristic equation [25]

$$\begin{array}{c}\hfill \frac{dx}{X}=\frac{dt}{T}=\frac{du}{U}.\end{array}$$

(15)

The general symmetry reductions related with Equation (14) are studied in detail. There are three cases for symmetry reductions.

Case I. By solving the characteristic Equation (15), the similarity solution is given as the following form

$$\begin{array}{c}\hfill u=\frac{1}{\sqrt[3]{C_{1}t+C_2}}U\left(\xi \right)+\frac{\alpha }{3\beta },\end{array}$$

(16)

with the similarity variable $\xi =\frac{1}{\sqrt[3]{C_{1}t+C_2}}\left(x-\frac{{\alpha }^2}{3\beta }t-\frac{C_2{\alpha }^2-3C_3\beta }{C_1\beta }\right)$ and the group invariant function $U\left(\xi \right)$. By substituting Equation (16) into the system (1), the invariant function $U\left(\xi \right)$ satisfies the variable coefficient of the ODE

$$\frac{d^{3}U\left(\xi \right)}{d{\xi }^3}+3U\left(\xi \right)\frac{d^{2}U\left(\xi \right)}{d{\xi }^2}+3U^2\left(\xi \right)\frac{dU\left(\xi \right)}{d\xi }+3{\left(\frac{dU\left(\xi \right)}{d\xi }\right)}^2+\frac{C_1}{3\beta }\xi \frac{dU\left(\xi \right)}{d\xi }+\frac{C_1}{3\beta }U\left(\xi \right)=0.$$

(17)

It is obvious that once the solution $U\left(\xi \right)$ is solved by Equation (17), the the similarity solution is given by using Equation (16).

By means of the MAPLE technique, the hypergeom solution of $U\left(\xi \right)$ can be obtained by solving Equation (17) directly

$$\begin{array}{cc}\hfill & U\left(\xi \right)=[C_6\mathrm{H}\left(\left[\frac{C_4\beta }{C_1}+\frac{1}{3}\right],\left[\frac{2}{3},\frac{4}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)+2\xi \mathrm{H}\left(\left[\frac{\beta C_4}{C_1}+\frac{2}{3}\right],\left[\frac{4}{3},\frac{5}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)-(\frac{C_4}{20}+\frac{C_1}{30\beta })\hfill \\ \hfill & {\xi }^4\mathrm{H}\left(\left[\frac{\beta C_4}{C_1}+\frac{5}{3}\right],\left[\frac{7}{3},\frac{8}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)-C_6(\frac{C_1}{24\beta }+\frac{C_4}{8}){\xi }^3\mathrm{H}\left(\left[\frac{\beta C_4}{C_1}+\frac{4}{3}\right],\left[\frac{5}{3},\frac{7}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)\hfill \\ \hfill & -\frac{C_4{C}_5}{2}{\xi }^2\mathrm{H}\left(\left[\frac{\beta C_4}{C_1}+1\right],\left[\frac{4}{3},\frac{5}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)]/[C_5\mathrm{H}\left(\left[\frac{C_4\beta }{C_1}\right],\left[\frac{1}{3},\frac{2}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)\hfill \\ \hfill & +C_6\xi \mathrm{H}\left(\left[\frac{\beta C_4}{C_1}+\frac{1}{3}\right],\left[\frac{2}{3},\frac{4}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)+{\xi }^2\mathrm{H}\left(\left[\frac{3\beta C_4}{C_1}+\frac{2}{3}\right],\left[\frac{4}{3},\frac{5}{3}\right],-\frac{C_1{\xi }^3}{27\beta }\right)],\hfill \end{array}$$

(18)

where H denotes the generalized hypergeometric function. The solution of the STOB Equation (1) can be obtained by using Equations (16) and (18). The type solution of the hypergeometric function can be also obtained by means of the Hopf–Cole transformation [33].

Case II. $C_1=0$. The group invariant solution reads as the following form after solving the characteristic Equation (15)

$$\begin{array}{c}\hfill u=U\left(\eta \right),\end{array}$$

(19)

with the similarity variable $\eta =-\frac{C_2}{C_3}x+t$ and the group invariant function $U\left(\eta \right)$. Substituting Equation (19) into Equation (1), the invariant function $U\left(\eta \right)$ satisfies the reduction system

$$\begin{array}{c}\hfill \frac{d^{3}U\left(\eta \right)}{d{\eta }^3}-\left(\frac{3C_3}{C_2}U\left(\eta \right)+\frac{C_3\alpha }{C_2\beta }\right)\frac{d^{2}U\left(\eta \right)}{d{\eta }^2}+\frac{C_3^2}{C_2^2}\left(3U^2\left(\eta \right)+\frac{2}{\beta }U\left(\eta \right)+\frac{C_3}{C_2\beta }\right)\frac{dU\left(\eta \right)}{d\eta }-\frac{3C_3}{C_2}{\left(\frac{dU\left(\eta \right)}{d\eta }\right)}^2=0.\end{array}$$

(20)

As a similar procedure, the solution of the STOB equation can be derived by solving the reduction system (20).

Case III. $C_1=C_3=0$. The group invariant solution reads as the following form after solving out the characteristic Equation (15),

$$\begin{array}{c}\hfill u=U\left(x\right).\end{array}$$

(21)

The group invariant function $U\left(x\right)$ satisfies the following reduction system

$$\begin{array}{c}\hfill \alpha \left(\frac{d^{2}U\left(x\right)}{d{x}^2}+2U\left(x\right)\frac{dU\left(x\right)}{dx}\right)+\beta \left(3U^2\left(x\right)\frac{dU\left(x\right)}{dx}+3U\left(x\right)\frac{d^{2}U\left(x\right)}{d{x}^2}+3{\left(\frac{dU\left(x\right)}{dx}\right)}^2+\frac{d^{3}U\left(x\right)}{d{x}^3}\right)=0.\end{array}$$

(22)

The field of u can be obtained by solving the above reduction system.

4. CTE Solvability and Interaction Solutions of STOB Equation

Based on the CTE method [17], the generalized truncated tanh expansion of the STOB equation is

$$\begin{array}{c}\hfill u=u_0+u_{1}tanh\left(w\right),\end{array}$$

(23)

where $u_0$, $u_1$ and w are arbitrary functions of x and t. By substituting Equation (23) into the STOB system (1) and vanishing the coefficients of the powers of $tanh\left(f\right)$, one obtains two classes solutions.

Case I. The functions $u_0$ and $u_1$ read as

$$\begin{array}{c}\hfill u_1=2w_x,u_0=-\frac{w_{xx}}{w_x}-\frac{\alpha }{3\beta },\end{array}$$

(24)

and w satisfies the following over-determined equations

$$\begin{array}{c}\hfill C+2\beta K-4\beta w_x^2+\frac{{\alpha }^2}{3\beta }=0,\end{array}$$

(25)

$$\begin{array}{c}\hfill K_{xx}-4K{w}_x^2-10w_{xx}^2=0,\end{array}$$

(26)

where $C=\frac{w_t}{w_x}$ and K satisfies the Schwarzian derivative $K=\{w;x\}=-\frac{3w_{xx}^2}{2w_x^2}+\frac{w_{xxx}}{w_x}$ [19].

Case II. The solutions of $u_0$ and $u_1$ are

$$\begin{array}{c}\hfill u_0=w_x,u_1=w_x,\end{array}$$

(27)

and the consistent condition is

$$\begin{array}{c}\hfill w_t-\alpha (w_{xx}+2w_x^2)-\beta (w_{xxx}+4w_x^3+6w_x{w}_{xx})=0.\end{array}$$

(28)

From the above detailed calculations, an nonauto-BT theorem can be constructed.

Nonauto-BT theorem. One finds the solution w of the over-determined Equations (25) and (26) or the consistent condition (28); then, the following forms of u are also a solution of the STOB system

$$\begin{array}{c}\hfill u=2w_{x}tanh\left(w\right)-\frac{w_{xx}}{w_x}-\frac{\alpha }{3\beta },\end{array}$$

(29)

and

$$\begin{array}{c}\hfill u=w_{x}tanh\left(w\right)+w_x,\end{array}$$

(30)

respectively.

By using the above nonauto-BT theorem, some interactions between solitons and other types of nonlinear waves are derived. One lists some novel interactions as follows. The interaction between one-soliton and the cnoidal wave for the over-determined Equations (25) and (26) is assumed

$$\begin{array}{c}\hfill f=k_{0}x+{\omega }_{0}t+c_0+a_{0}F\left(\varsigma \right),\varsigma =k_{1}x+{\omega }_{1}t+c_1,\end{array}$$

(31)

where $k_0$, ${\omega }_0,c_0,a_0$, $k_1,{\omega }_1$ and $c_1$ are all free constants. Substituting Equation (31) into Equation (25), one obtains the over-determined equations of $F_1\left(\varsigma \right)$:

$$\begin{array}{c}\hfill F_{1\varsigma }^2-4a_0^2{F}_1^4-a_0{a}_1{F}_1^3-a_2{F}_1^2-a_3{F}_1-a_4=0,F_1=F_{\varsigma },\end{array}$$

(32)

$$\begin{array}{c}\hfill (k_0{\omega }_1-k_1{\omega }_0)(a_0^3{b}_1{F}_1^4+a_0^2{b}_2{F}_1^3+a_0{b}_3{F}_1^2+k_0{b}_4{F}_1+k_0^2{b}_5)=0,\end{array}$$

(33)

with

$$\begin{array}{cc}\hfill & a_1=C_1{a}_0^2{k}_1^3+\frac{12k_0}{k_1},a_2=3C_1{k}_0{a}_0^2{k}_1^2+\frac{12k_0^2}{k_1^2}+\frac{{\alpha }^2}{3{\beta }^2{k}_1^2}+\frac{{\omega }_1}{\beta k_1^3},\hfill \\ \hfill & a_3=3C_1{k}_1{a}_0{k}_0^2+\frac{4k_0^3}{a_0{k}_1^3}+\frac{2{\alpha }^2{k}_0}{3a_0{\beta }^2{k}_1^3}+\frac{3k_0{\omega }_1}{2a_0\beta k_1^4}+\frac{{\omega }_0}{2a_0\beta k_1^3},a_4=6C_1{k}_0^3+\frac{2k_0^2{\alpha }^2}{a_0^2{k}_1^4{\beta }^2}+\frac{3k_0^2{\omega }_1}{a_0^2{k}_1^5\beta }+\frac{3k_0{\omega }_0}{a_0^2{k}_1^4\beta },\hfill \\ \hfill & b_1=\frac{C_2{a}_0^2{k}_1^4}{4\beta }-\frac{k_0}{\beta },b_2=\frac{C_2{a}_0^2{k}_0{k}_1^3}{\beta }-\frac{4k_0^2}{k_1\beta }+\frac{{\alpha }^2}{6k_1{\beta }^3}+\frac{{\omega }_1}{2{\beta }^2{k}_1^2},\hfill \\ & b_3=\frac{3C_2{k}_0^2{a}_0^2{k}_1^2}{2\beta }-\frac{6k_0^3}{k_1^2\beta }+\frac{{\alpha }^2{k}_0}{2k_1^2{\beta }^3}+\frac{9{\omega }_1{k}_0}{8{\beta }^2{k}_1^3}+\frac{3{\omega }_0}{8k_1^2{\beta }^2},b_4=\frac{C_2{k}_1{a}_0^2{k}_0^2}{\beta }-\frac{4k_0^3}{\beta k_1^3}+\frac{{\alpha }^2{k}_0}{2k_1^3{\beta }^3}+\frac{3k_0{\omega }_1}{4{\beta }^2{k}_1^4}+\frac{3{\omega }_0}{4{\beta }^2{k}_1^3},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & b_5=\frac{C_2{a}_0{k}_0^2}{4\beta }-\frac{k_0^3}{k_1^4{a}_0\beta }+\frac{{\alpha }^2{k}_0}{6a_0{k}_1^4{\beta }^3}+\frac{k_0{\omega }_1}{8a_0{\beta }^2{k}_1^5}+\frac{3{\omega }_0}{8a_0{\beta }^2{k}_1^4},\hfill \end{array}$$

where $C_1$ and $C_2$ are arbitrary constants. Equation (32) is the standard elliptic function equation, while Equation (33) becomes the identical equation with the constraint as

$$\begin{array}{c}\hfill {\omega }_0=\frac{k_0{\omega }_1}{k_1}.\end{array}$$

(34)

It indicates that the interaction between one soliton and the cnoidal wave is obtained by solving the over-determined equations. This type of interaction solution is discussed via the CTE method [34,35].

Besides solving over-determined equations, the interaction between one-soliton and the cnoidal wave can be obtained by solving the consistent condition (28). The corresponding solution form assumes

$$\begin{array}{c}\hfill w=k_{0}x+{\omega }_{0}t+c_0+\mathrm{EllipticPi}\left[\mathrm{JacobiSN}(k_{1}x+{\omega }_{1}t+c_1,m),n,m\right],\end{array}$$

(35)

where $\mathrm{EllipticPi}$ and $\mathrm{JacobiSN}$ are the third kind of elliptic integral and the Jacobi elliptic function, respectively. Substituting Equation (35) into Equation (28), one obtains

$$\begin{array}{cc}\hfill & n^2(2\beta k_1^3{m}^2+n{\omega }_0-4\beta n{k}_0^3-2\alpha n{k}_0^2){\mathrm{Sn}}^6\left(\zeta \right)+n(6\beta k_1^3{m}^2-4\beta k_1^3{m}^{2}n+12\beta k_0^{3}n+12\beta k_0^2{k}_{1}n\hfill \\ \hfill & -4\beta k_1^{3}n+6\alpha k_0^{2}n+4\alpha k_0{k}_{1}n-3n{\omega }_0-n{\omega }_1){\mathrm{Sn}}^4\left(\zeta \right)-2k_1^2{n}^2(6\beta k_0+\alpha ){\mathrm{Sn}}^3\left(\zeta \right)\mathrm{Cn}\left(\zeta \right)\mathrm{Dn}\left(\zeta \right)\hfill \\ \hfill & -n(4\beta k_1^3{m}^2-6\beta k_1^{3}n+12\beta k_0^3+24\beta k_0^2{k}_1+12\beta k_0{k}_1^2+4\beta k_1^3+6\alpha k_0^2+8\alpha k_0{k}_1+2\alpha k_1^2\hfill \\ \hfill & -3{\omega }_0-2{\omega }_1){\mathrm{Sn}}^2\left(\zeta \right)+2k_1^{2}n(6\beta k_0+6\beta k_1+\alpha )\mathrm{Sn}\left(\zeta \right)\mathrm{Cn}\left(\zeta \right)\mathrm{Dn}\left(\zeta \right)+2\beta k_1^{3}n+4\beta k_0^3\hfill \\ \hfill & +12\beta k_0^2{k}_1+12\beta k_0{k}_1^2+4\beta k_1^3+2\alpha k_0^2+4\alpha k_0{k}_1+2\alpha k_1^2-{\omega }_0-{\omega }_1=0,\hfill \end{array}$$

(36)

where $\mathrm{Sn}\left(\zeta \right),\mathrm{Cn}\left(\zeta \right)$ and $\mathrm{Dn}\left(\zeta \right)$ represent the Jacobi elliptic functions of $\mathrm{JacobiSN}(k_{1}x+{\omega }_{1}t+c_1,m),\mathrm{JacobiCN}(k_{1}x+{\omega }_{1}t+c_1,m)$ and $\mathrm{JacobiDN}(k_{1}x+{\omega }_{1}t+c_1,m)$, respectively. Vanishing the coefficients of the powers of $\mathrm{S}\mathrm{n}$, the non-trivial constants are

$$\begin{array}{c}\hfill n=0,{\omega }_0=2\alpha {(k_0+k_1)}^2+4\beta {(k_0+k_1)}^3-{\omega }_1.\end{array}$$

(37)

Substituting (35) and (37) into (30), the interaction solution of the STOB Equation (1) reads

$$\begin{array}{cc}\hfill & u=(k_0+k_1)tanh\{2{(k_0+k_1)}^2(\alpha +2\beta k_0+2\beta k_1)t+k_{0}x-{\omega }_{1}t+c_0+\hfill \\ \hfill & \mathrm{EllipticPi}\left[\mathrm{JacobiSN}(k_{1}x+{\omega }_{1}t+c_1,m),n,m\right]\}+k_0+k_1.\hfill \end{array}$$

(38)

By selecting the parameters as

$$\begin{array}{c}\hfill m=\frac{49}{50},k_1=-\frac{1}{2},{\omega }_1=\frac{1}{2},k_0=1,c_0=2,c_1=2,\alpha =1,\beta =1,\end{array}$$

(39)

the interaction solution (38) becomes

$$\begin{array}{c}\hfill u=\frac{1}{2}tanh\left[x+\frac{t}{2}+2+\mathrm{EllipticF}\left(\mathrm{JacobiSN}\left(-\frac{x}{2}+\frac{t}{2}+2,\frac{49}{50}\right),\frac{49}{50}\right)\right]+\frac{1}{2},\end{array}$$

(40)

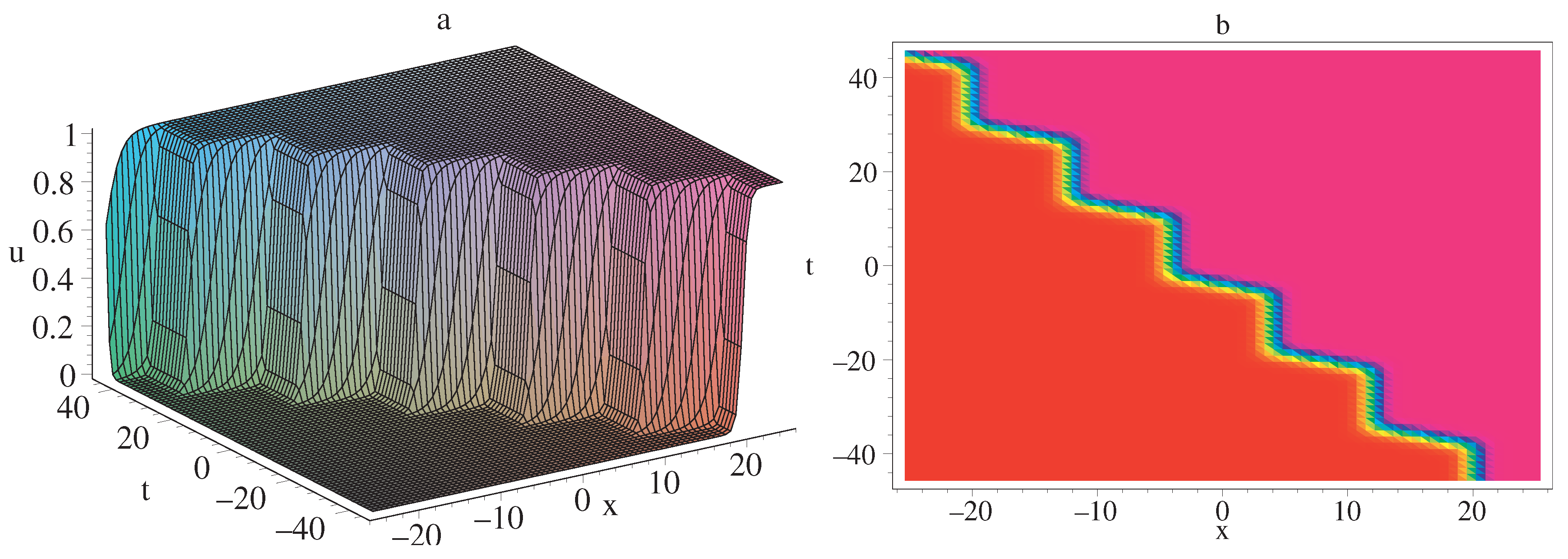
with the first kind of incomplete elliptic integral of $\mathrm{EllipticF}$. Figure 1 displays the three-dimensional and the density plots of interaction solution (40).

The interaction between one soliton and multiple resonant soliton solutions of the consistent condition (28) has the form

$$\begin{array}{c}\hfill w=k_{0}x+{\omega }_{0}t+c_0+a_{0}ln\left(1+\sum _{i=1}^{n}exp(k_{i}x+{\omega }_{i}t+c_i)\right),\end{array}$$

(41)

where $k_0,k_i,c_0$ and $c_i$ are arbitrary constants and $a_0,{\omega }_0$ and ${\omega }_i$ satisfy the relations

$$\begin{array}{c}\hfill a_0=\frac{1}{2},{\omega }_0=2\alpha k_0^2+4\beta k_0^3,{\omega }_i=\alpha k_i(4k_0+k_i)+\beta k_i(12k_0^2+6k_0{k}_i+k_i^2).\end{array}$$

(42)

By substituting Equations (41) and (42) into Equation (30), the interaction between one-soliton and the multiple resonant soliton solutions can be written as

$$\begin{array}{c}\hfill u=\frac{k_0+k_0{\sum }_{i=1}^{n}exp\left({\vartheta }_i\right)+\frac{1}{2}{\sum }_{i=1}^n{k}_{i}exp\left({\vartheta }_i\right)}{1+{\sum }_{i=1}^{n}exp\left({\vartheta }_i\right)}\left(1+tanh\left(w\right)\right),\end{array}$$

(43)

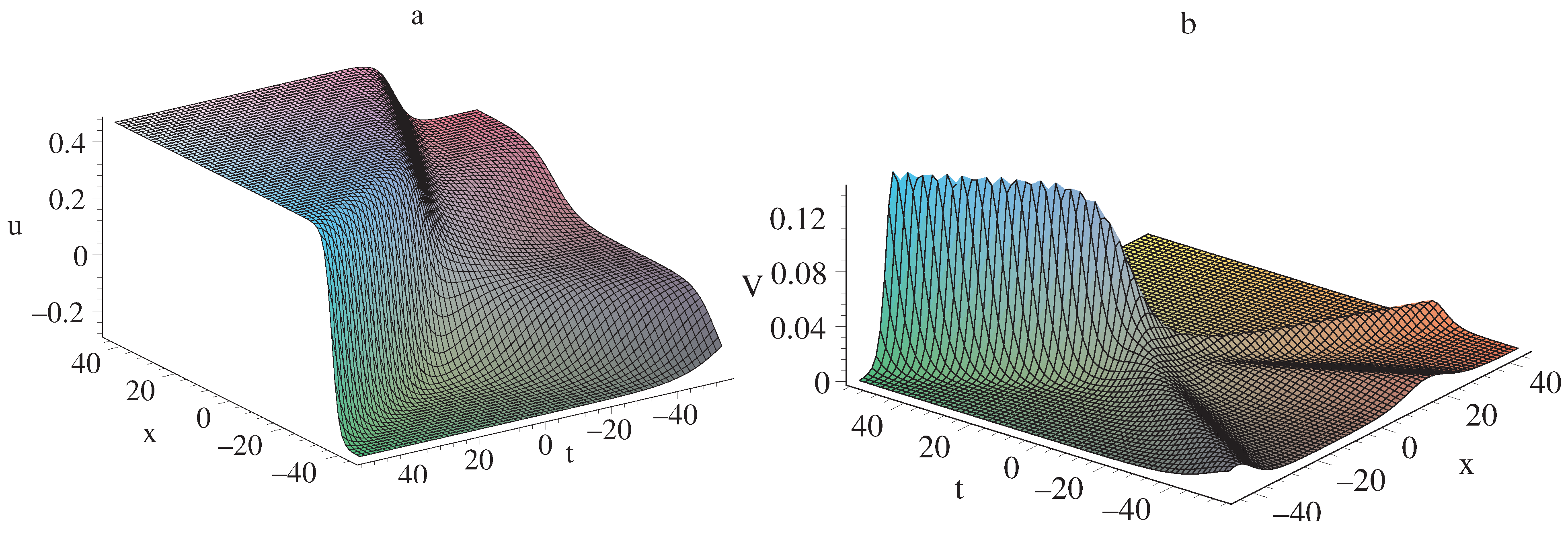
with ${\vartheta }_i=k_{i}x+k_i\left(\beta (12k_0^2+6k_0{k}_i+k_i^2)+\alpha (4k_0+k_i)\right)t+c_i$. We show this type of solution in Figure 2 by selecting the parameters as

$$n=2,k_0=\frac{1}{9},k_1=\frac{1}{4},k_2=-\frac{1}{2},c_0=1,c_1=\frac{1}{2},c_2=-6,\alpha =2,\beta =\frac{1}{2}.$$

(44)

Figure 2a,b plot the solution of u and the potential of u, i.e., $V=u_x$, respectively. It is obvious that three solitary waves become a single wave with the time evolution. This is called the fusion phenomena of the solitary waves, which have been studied both theoretically and experimentally [36].

These types of interaction between solitons and the cnoidal periodic waves, and interaction between solitons and the multiple resonant soliton solutions, may happen in the ocean [18]. The results are useful for explaining ocean phenomena.

5. Conclusions and Discussion

In summary, the Lie point symmetry approach and the CTE method are applied for solving the STOB equation. One obtains three classes of symmetry reduction equations based on the infinitesimal generators. Some explicit solutions are derived by solving the symmetry reduction equations. In addition, a nonauto-BT theorem that includes the types of the over-determined Equations (25) and (26) and the consistent condition (28) is obtained by the CTE method. The interaction between one-soliton and the cnoidal wave can be obtained by solving the over-determined equations and the consistent condition. The interaction between one-soliton and the multiple resonant soliton solutions is derived by means of the consistent condition. These novel solutions are studied both in analytical and graphical ways. The fusion phenomena of the solitary waves are shown in Figure 2. The results are helpful in understanding some physical phenomena including fluid dynamics, oceanography and related disciplines.

Besides the Lie point symmetry, the nonlocal symmetry is widely studied by the Painlevé analysis, the Lax pair and so on [17,18,19]. Based on the the Painlevé analysis, the solution of the STOB equation can be expanded as the following form about the singularity manifold $f(x,t)$

$$\begin{array}{c}\hfill u=\frac{u_0}{f}+u_1,\end{array}$$

(45)

where $u_0$ and $u_1$ are functions with respect to x and t. By substituting Equation (45) into Equation (1) and vanishing the coefficients of the powers of $f(x,t)$ independently. We obtain

$$\begin{array}{c}\hfill u_0=f_x,u_1=f_x.\end{array}$$

(46)

This type of nonlocal symmetry, which is named the residual symmetry, can be read out by the residual of the singularity manifold $f(x,t)$ [17]. The nonlocal symmetry of the STOB equation is written as ${\sigma }^u=f_x$ from the expression (46). The field of f satisfies the following equation

$$\begin{array}{c}\hfill f_t-\alpha (f_{xx}+2f_x^2)-\beta (f_{xxx}+3f_x^3+6f_x{f}_{xx})=0.\end{array}$$

(47)

The symmetry reductions related tp the nonlocal symmetry and the infinite many nonlocal symmetries are worth studying.