Decay Conditions for Antiplane Shear of a High-Contrast Multi-Layered Semi-Infinite Elastic Strip
Abstract
:1. Introduction
2. Statement of the Problem
3. Classical Decay Condition
4. Additional Decay Conditions
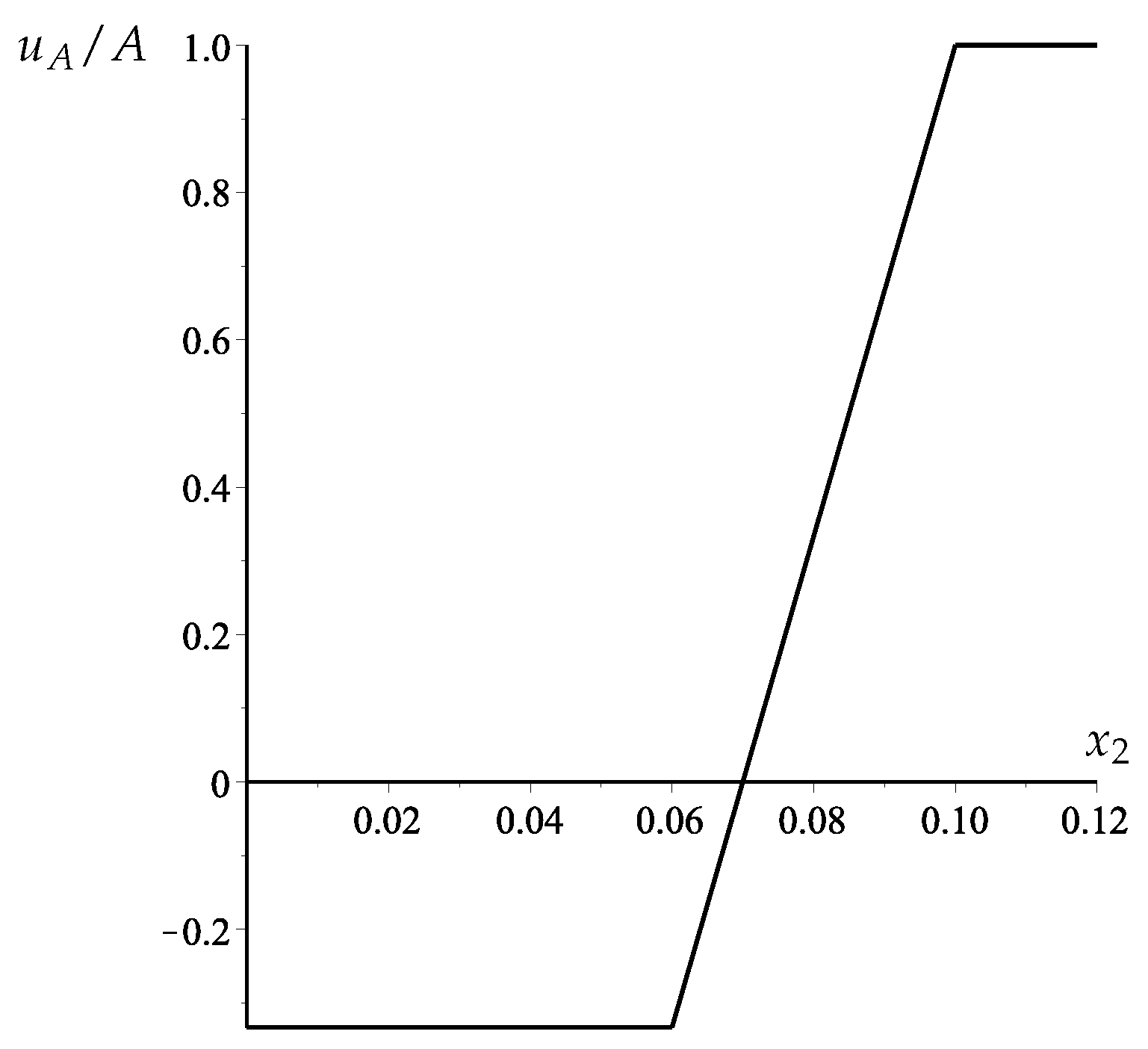
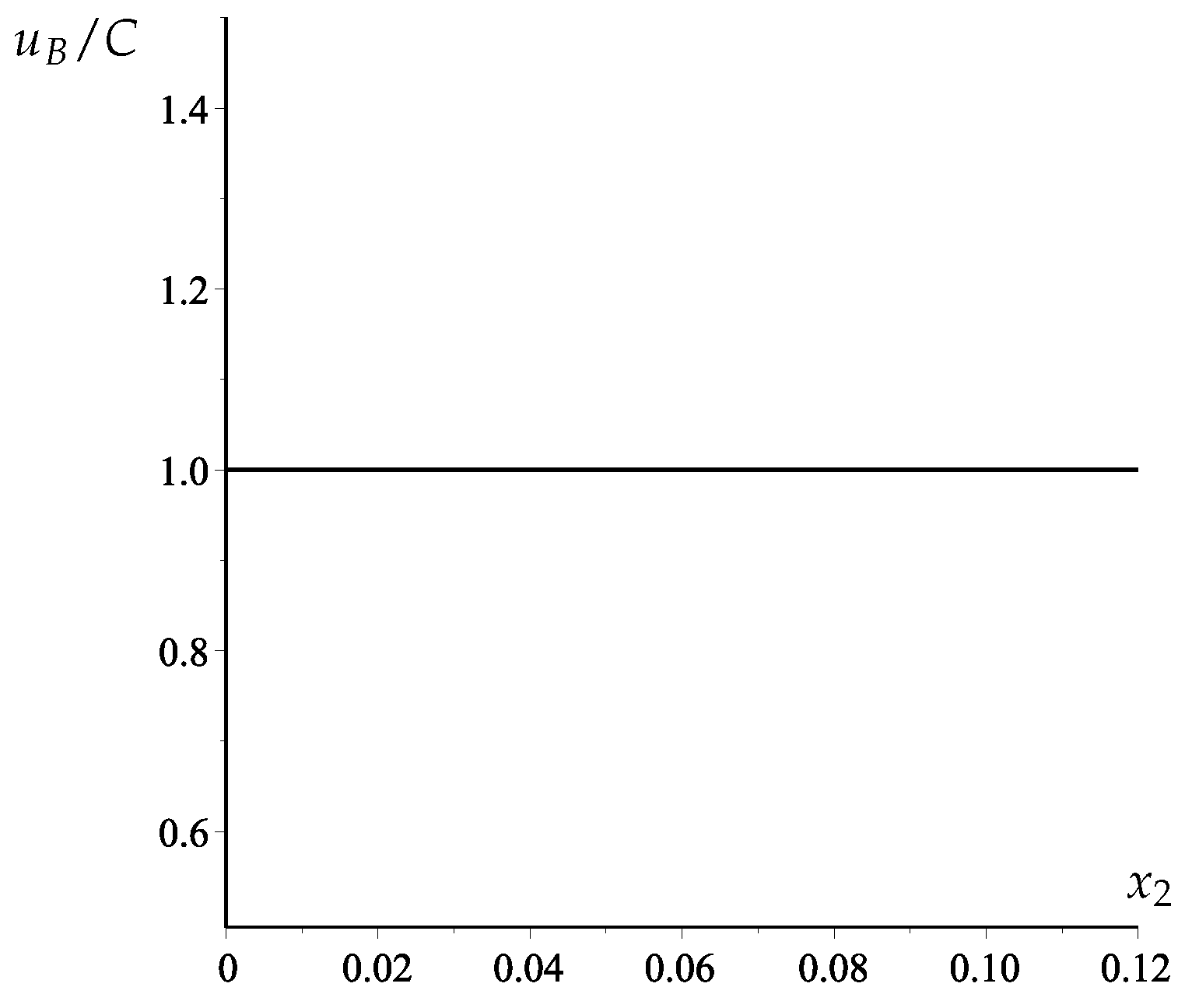
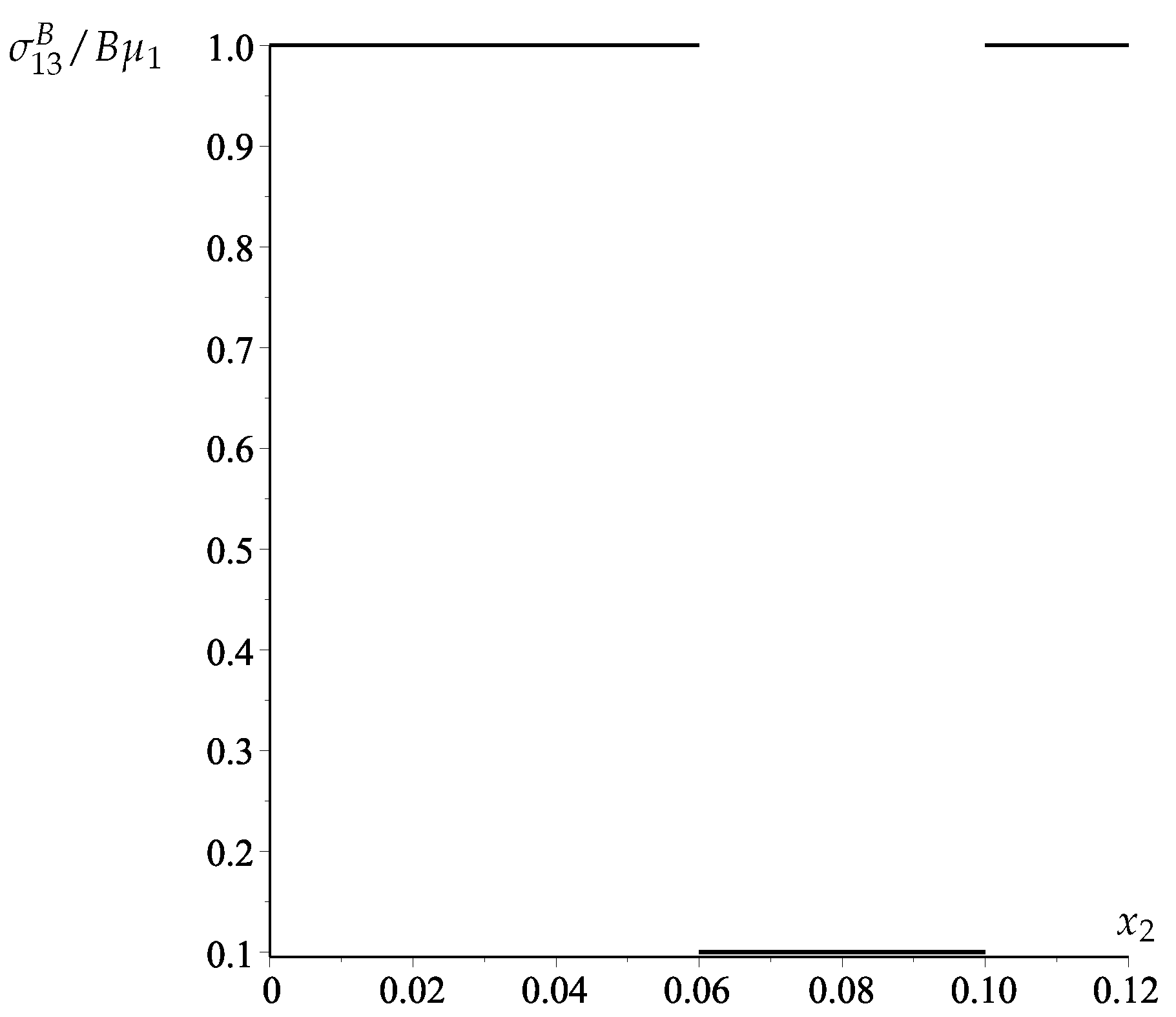
5. Example
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Gusein-Zade, M. On necessary and sufficient conditions for the existence of decaying solutions of the plane problem of the theory of elasticity for a semistrip. J. Appl. Math. Mech. 1965, 29, 892–901. [Google Scholar] [CrossRef]
- Gol’denveizer, A.; Kolos, A. On the derivation of two-dimensional equations in the theory of thin elastic plates. J. Appl. Math. Mech. 1965, 29, 151–166. [Google Scholar] [CrossRef]
- Goldenveizer, A. Theory of Thin Elastic Shells; Izdatel’stvo Nauka: Moscow, Russian, 1976. (In Russian) [Google Scholar]
- Wilde, M.V.; Surova, M.Y.; Sergeeva, N.V. Asymptotically correct boundary conditions for the higher-order theory of plate bending. Math. Mech. Solids 2022. [Google Scholar] [CrossRef]
- Gregory, R.D.; Wan, F.Y. Decaying states of plane strain in a semi-infinite strip and boundary conditions for plate theory. J. Elast. 1984, 14, 27–64. [Google Scholar] [CrossRef]
- Gregory, R.D.; Wan, F.Y. On plate theories and Saint-Venant’s principle. Int. J. Solids Struct. 1985, 21, 1005–1024. [Google Scholar] [CrossRef]
- Babenkova, E.; Kaplunov, J. The two-term interior asymptotic expansion in the case of low-frequency longitudinal vibrations of an elongated elastic rectangle. In IUTAM Symposium on Asymptotics, Singularities and Homogenisation in Problems of Mechanics; Springer: Dordrecht, The Netherlands, 2003; pp. 137–145. [Google Scholar] [CrossRef]
- Babenkova, E.; Kaplunov, J. Low-frequency decay conditions for a semi-infinite elastic strip. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 460, 2153–2169. [Google Scholar] [CrossRef]
- Horgan, C. Saint-Venant end effects for sandwich structures. In Fourth International Conference on Sanwich Construction; EMAS Publishing UK: London, UK, 1998; Volume 1, pp. 191–200. [Google Scholar]
- Kaplunov, J.; Prikazchikov, D.; Sergushova, O. Multi-parametric analysis of the lowest natural frequencies of strongly inhomogeneous elastic rods. J. Sound Vib. 2016, 366, 264–276. [Google Scholar] [CrossRef]
- Kaplunov, J.; Prikazchikov, D.; Prikazchikova, L. Dispersion of elastic waves in a strongly inhomogeneous three-layered plate. Int. J. Solids Struct. 2017, 113, 169–179. [Google Scholar] [CrossRef]
- Prikazchikova, L.; Ece Aydın, Y.; Erbaş, B.; Kaplunov, J. Asymptotic analysis of an anti-plane dynamic problem for a three-layered strongly inhomogeneous laminate. Math. Mech. Solids 2020, 25, 3–16. [Google Scholar] [CrossRef]
- Kaplunov, J.; Prikazchikova, L.; Alkinidri, M. Antiplane shear of an asymmetric sandwich plate. Contin. Mech. Thermodyn. 2021, 33, 1247–1262. [Google Scholar] [CrossRef]
- Goldenveizer, A. The boundary conditions in the two-dimensional theory of shells. The mathematical aspect of the problem. J. Appl. Math. Mech. 1998, 62, 617–629. [Google Scholar] [CrossRef]

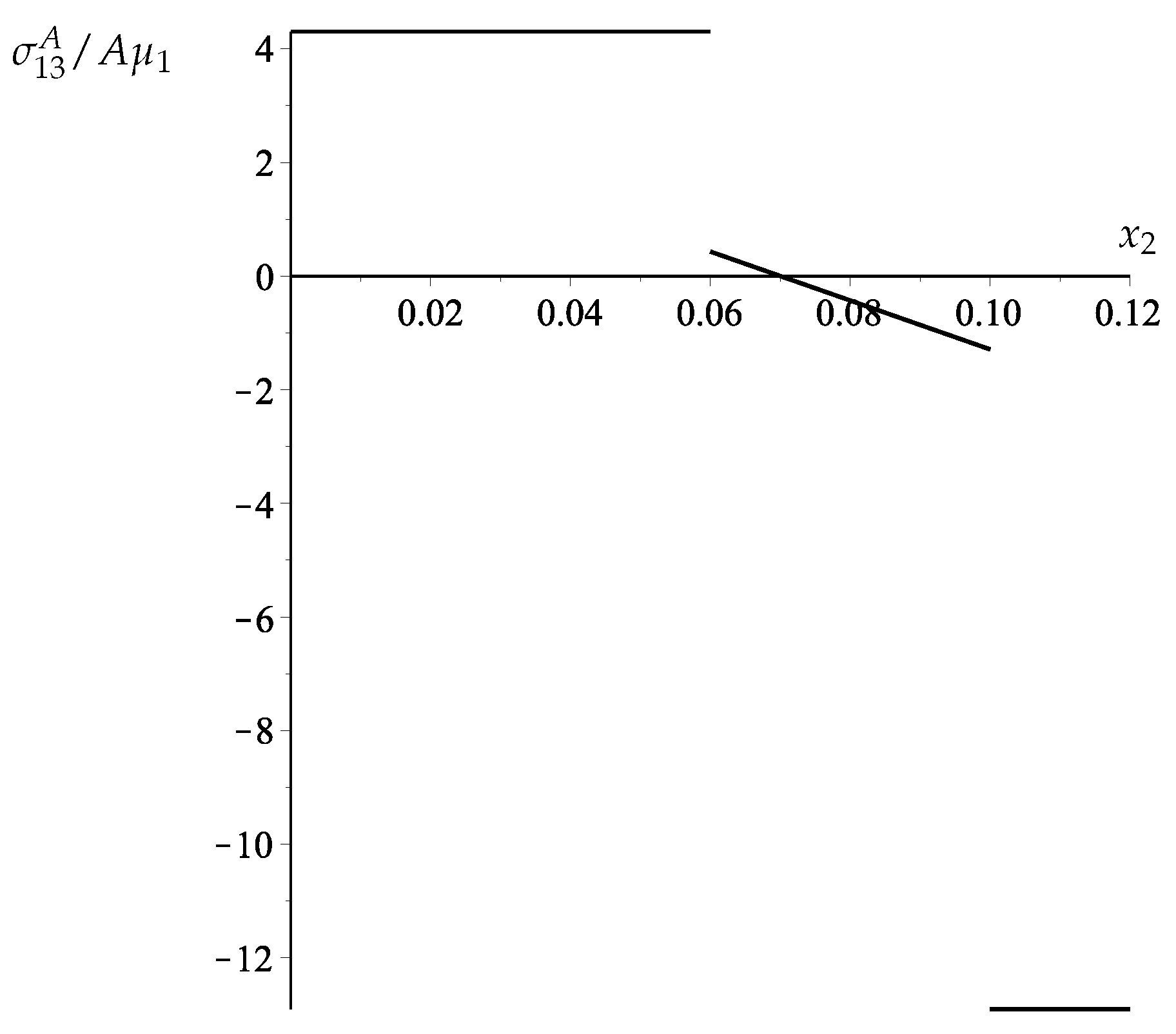
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prikazchikova, L. Decay Conditions for Antiplane Shear of a High-Contrast Multi-Layered Semi-Infinite Elastic Strip. Symmetry 2022, 14, 1697. https://doi.org/10.3390/sym14081697
Prikazchikova L. Decay Conditions for Antiplane Shear of a High-Contrast Multi-Layered Semi-Infinite Elastic Strip. Symmetry. 2022; 14(8):1697. https://doi.org/10.3390/sym14081697
Chicago/Turabian StylePrikazchikova, Ludmila. 2022. "Decay Conditions for Antiplane Shear of a High-Contrast Multi-Layered Semi-Infinite Elastic Strip" Symmetry 14, no. 8: 1697. https://doi.org/10.3390/sym14081697
APA StylePrikazchikova, L. (2022). Decay Conditions for Antiplane Shear of a High-Contrast Multi-Layered Semi-Infinite Elastic Strip. Symmetry, 14(8), 1697. https://doi.org/10.3390/sym14081697





