Review of Model Predictive Control of Distributed Energy Resources in Microgrids
Abstract
1. Introduction
2. Overview of DG Sources in Microgrids
2.1. Low Voltage AC Networks
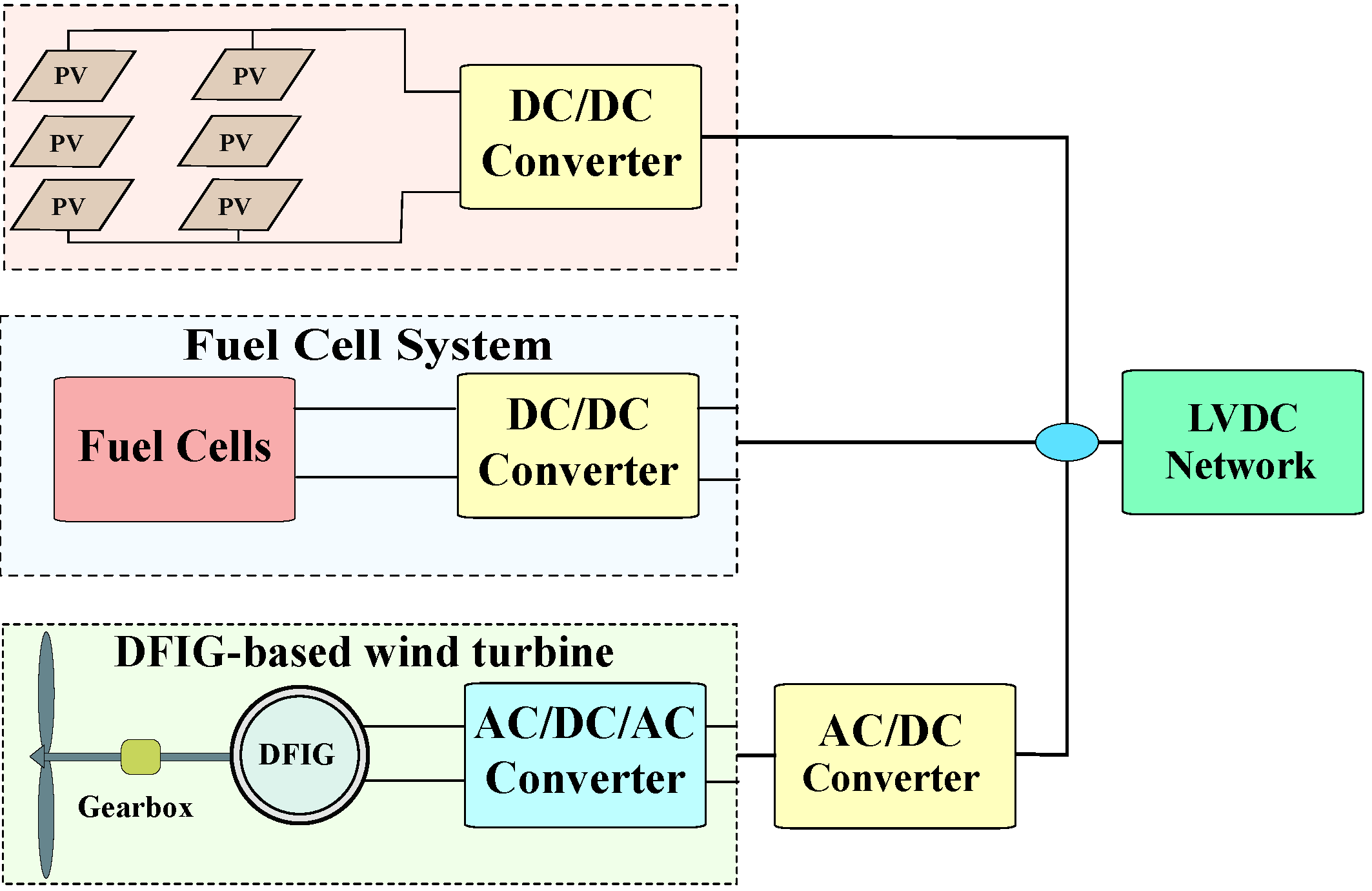
2.2. Low Voltage DC Networks
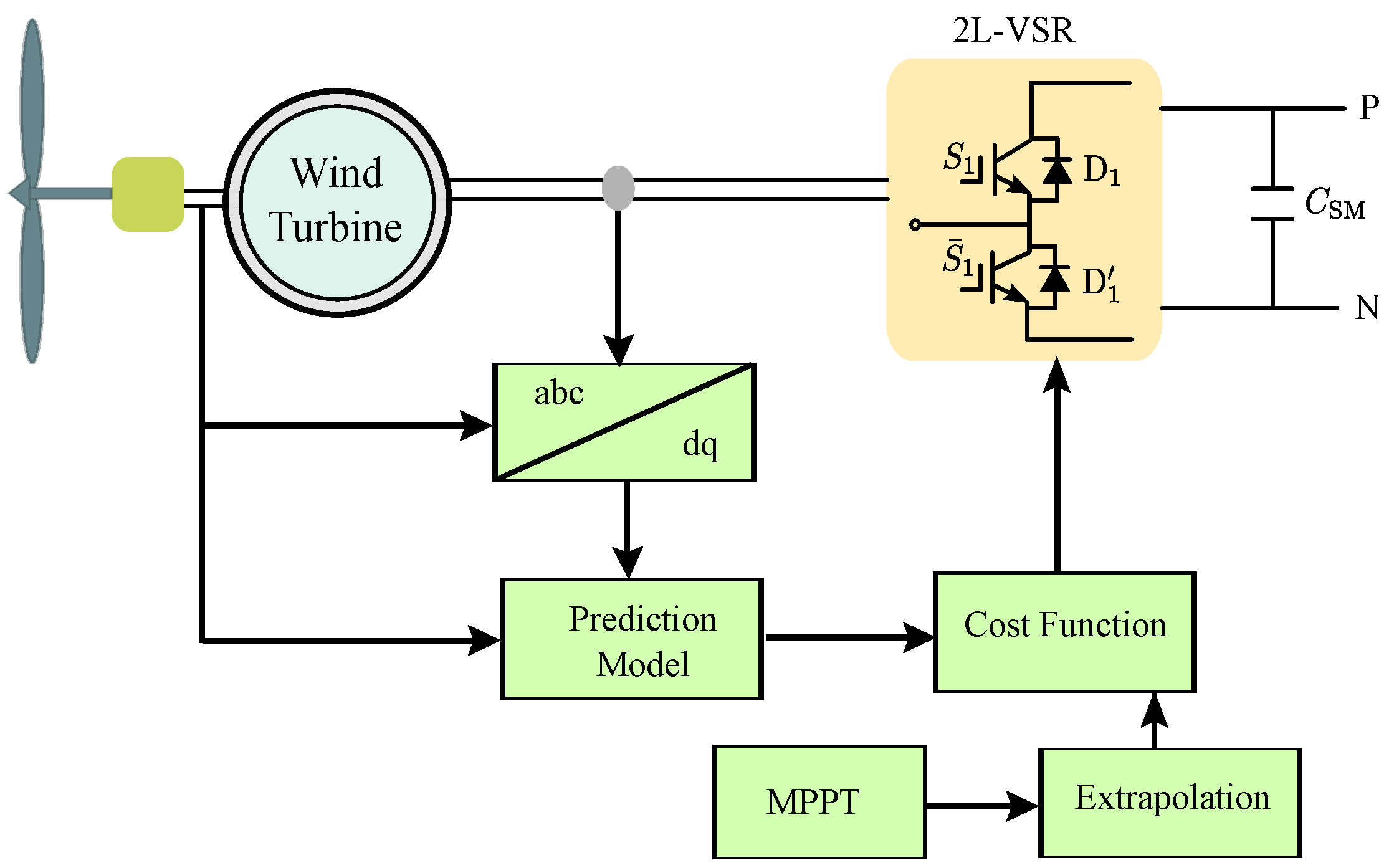
2.3. Wind Turbines
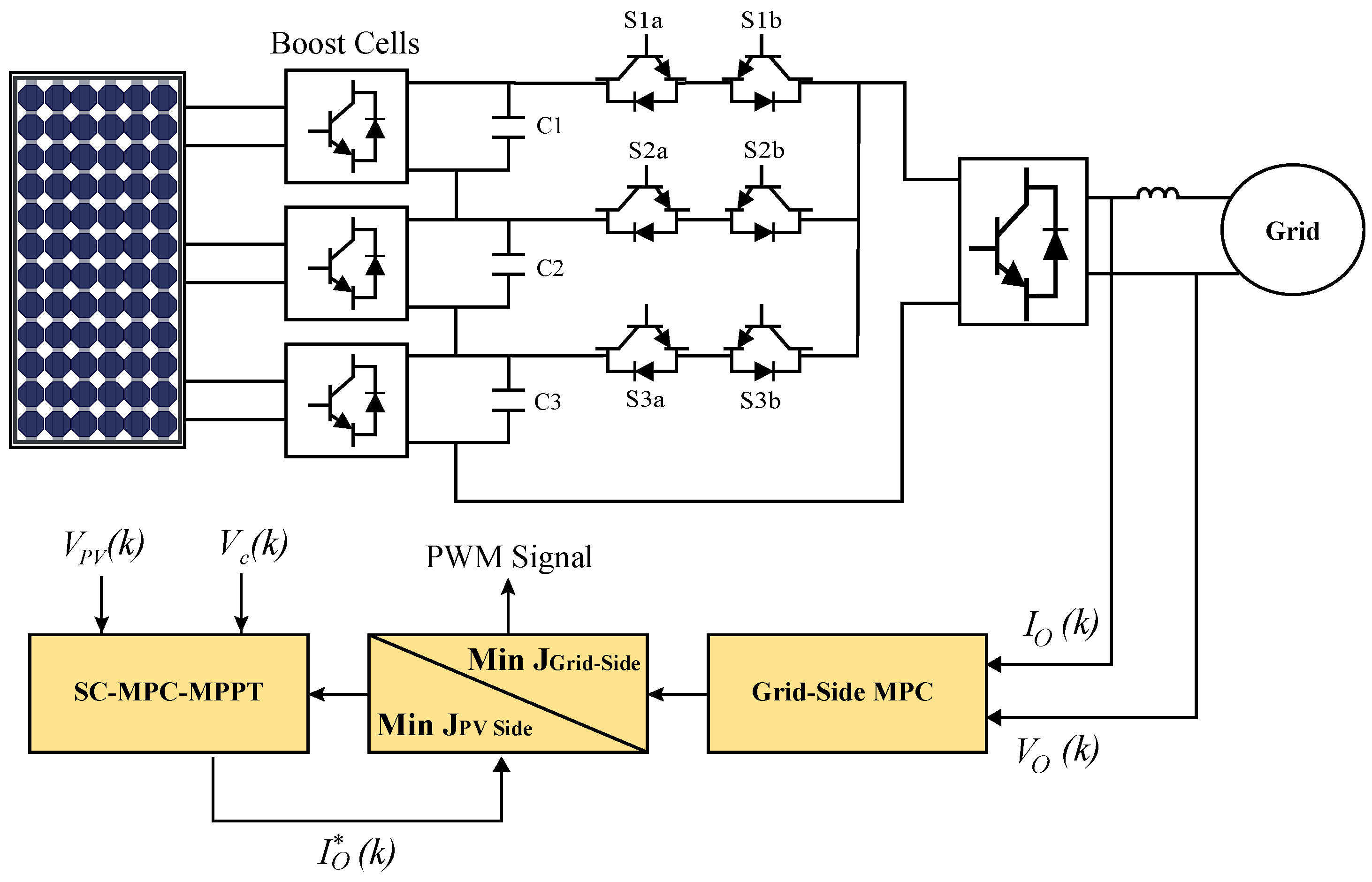
2.4. Photovoltaic (PV) Units
2.5. Energy Storage Systems
2.6. Microgrid Operation Modes
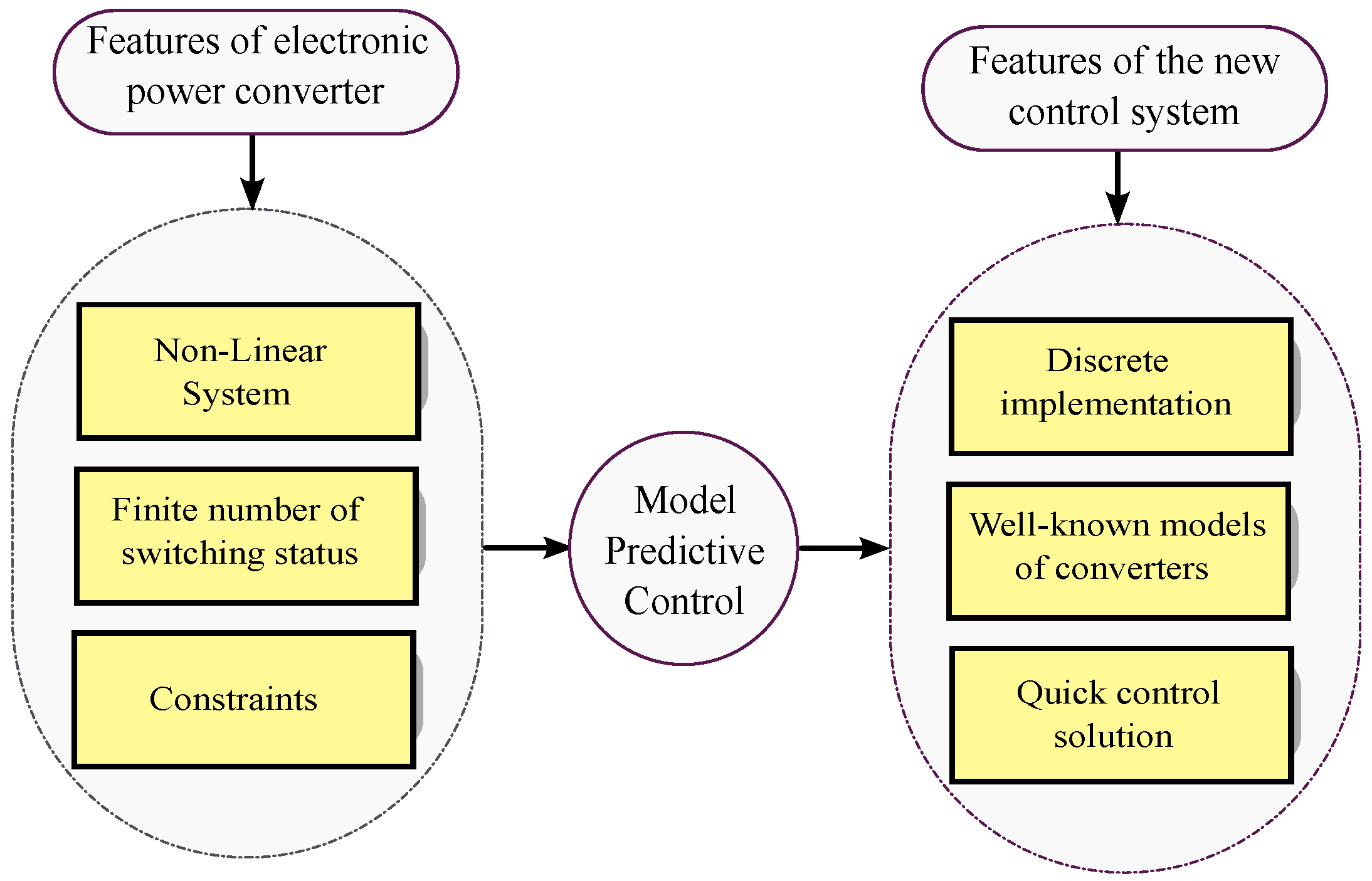
3. Model Predictive Control Strategies for DER-Based Microgrid
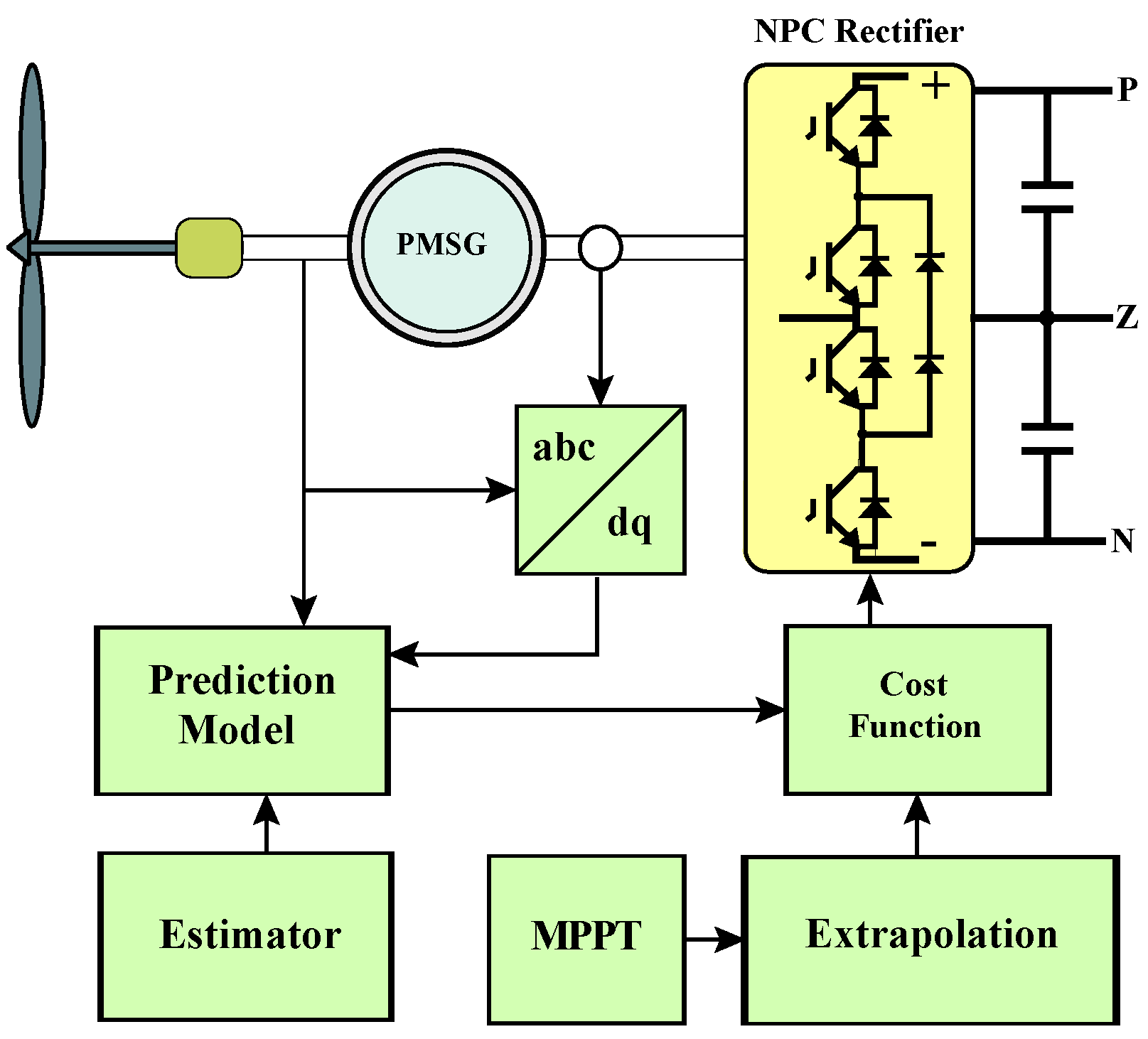
3.1. MPC for Wind Conversion
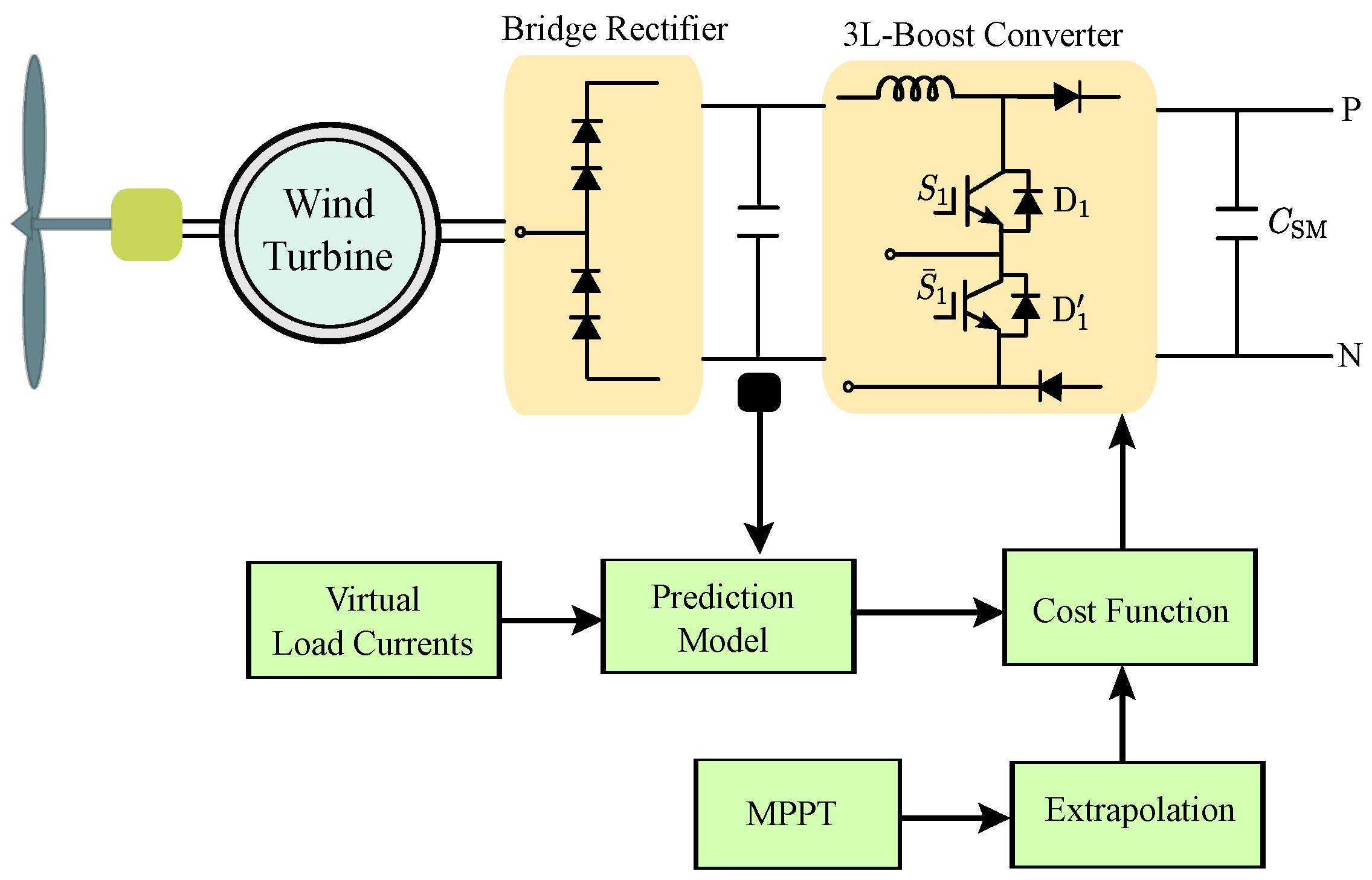
3.2. MPC for Solar PV Conversion

4. MPC for Frequency Regulation
5. Reliability
6. Challenges and Future Perspectives
6.1. Trends in Integration to Power Systems
6.2. MPC Challenges in Terms of Solutions for DERs
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haddad, R.J.; Guha, B.; Kalaani, Y.; El-Shahat, A. Smart distributed generation systems using artificial neural network-based event classification. IEEE Power Energy Technol. Syst. J. 2018, 5, 18–26. [Google Scholar] [CrossRef]
- Krishan, O.; Suhag, S. An updated review of energy storage systems: Classification and applications in distributed generation power systems incorporating renewable energy resources. Int. J. Energy Res. 2019, 43, 6171–6210. [Google Scholar] [CrossRef]
- Bahramara, S.; Mazza, A.; Chicco, G.; Shafie-khah, M.; Catalão, J.P. Comprehensive review on the decision-making frameworks referring to the distribution network operation problem in the presence of distributed energy resources and microgrids. Int. J. Electr. Power Energy Syst. 2020, 115, 105466. [Google Scholar] [CrossRef]
- Sarangi, S.; Sahu, B.K.; Rout, P.K. Distributed generation hybrid AC/DC microgrid protection: A critical review on issues, strategies, and future directions. Int. J. Energy Res. 2020, 44, 3347–3364. [Google Scholar] [CrossRef]
- Bajaj, M.; Singh, A.K. An analytic hierarchy process-based novel approach for benchmarking the power quality performance of grid-integrated renewable energy systems. Electr. Eng. 2020, 102, 1153–1173. [Google Scholar] [CrossRef]
- Akhavan, A.; Vasquez, J.; Guerrero, J. Stability Evaluation of Grid-Connected Microgrid Clusters in Asymmetrical Grids. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022. [Google Scholar] [CrossRef]
- Han, J.; Zhao, P.; Yao, G.; Chen, H.; Wang, Y.; Benbouzid, M.; Tang, T. Model predictive current control of asymmetrical hybrid cascaded multilevel inverter. J. Power Electron. 2022, 22, 580–592. [Google Scholar] [CrossRef]
- Justo, J.J.; Mwasilu, F.; Lee, J.; Jung, J.W. AC-microgrids versus DC-microgrids with distributed energy resources: A review. Renew. Sustain. Energy Rev. 2013, 24, 387–405. [Google Scholar] [CrossRef]
- Igwemezie, V.; Mehmanparast, A.; Kolios, A. Current trend in offshore wind energy sector and material requirements for fatigue resistance improvement in large wind turbine support structures—A review. Renew. Sustain. Energy Rev. 2019, 101, 181–196. [Google Scholar] [CrossRef]
- Akinyele, D.; Olabode, E.; Amole, A. Review of fuel cell technologies and applications for sustainable microgrid systems. Inventions 2020, 5, 42. [Google Scholar] [CrossRef]
- Ranjbaran, P.; Yousefi, H.; Gharehpetian, G.; Astaraei, F.R. A review on floating photovoltaic (FPV) power generation units. Renew. Sustain. Energy Rev. 2019, 110, 332–347. [Google Scholar] [CrossRef]
- Lee, J.; Shepley, M.M. Benefits of solar photovoltaic systems for low-income families in social housing of Korea: Renewable energy applications as solutions to energy poverty. J. Build. Eng. 2020, 28, 101016. [Google Scholar] [CrossRef]
- Khalid, M. A review on the selected applications of battery-supercapacitor hybrid energy storage systems for microgrids. Energies 2019, 12, 4559. [Google Scholar] [CrossRef]
- Hajiaghasi, S.; Salemnia, A.; Hamzeh, M. Hybrid energy storage system for microgrids applications: A review. J. Energy Storage 2019, 21, 543–570. [Google Scholar] [CrossRef]
- Haron, A.R.; Mohamed, A.; Shareef, H. A review on protection schemes and coordination techniques in microgrid system. J. Appl. Sci. 2012, 12, 101–112. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T.; Kennel, R. Reformulation of the long-horizon direct model predictive control problem to reduce the computational effort. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 3512–3519. [Google Scholar]
- Jupin, S.; Vechiu, I.; Tapia-Otaegui, G. Universal switched state-space representation for model predictive control of power converters. Electr. Power Syst. Res. 2020, 180, 106120. [Google Scholar] [CrossRef]
- Donoso, F.; Mora, A.; Cardenas, R.; Angulo, A.; Saez, D.; Rivera, M. Finite-set model-predictive control strategies for a 3L-NPC inverter operating with fixed switching frequency. IEEE Trans. Ind. Electron. 2017, 65, 3954–3965. [Google Scholar] [CrossRef]
- Novak, M.; Dragicevic, T. Supervised imitation learning of finite-set model predictive control systems for power electronics. IEEE Trans. Ind. Electron. 2020, 68, 1717–1723. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Peng, Z. A computationally efficient FCS-MPC method without weighting factors for NNPCs with optimal duty cycle control. IEEE/ASME Trans. Mechatron. 2018, 23, 2503–2514. [Google Scholar] [CrossRef]
- Kang, S.W.; Soh, J.H.; Kim, R.Y. Symmetrical three-vector-based model predictive control with deadbeat solution for IPMSM in rotating reference frame. IEEE Trans. Ind. Electron. 2019, 67, 159–168. [Google Scholar] [CrossRef]
- Yang, W.; Yang, F.; Chen, J. Distributed predictive control of grid-connected solar PV generation based on data-driven subspace approach. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 1087–1092. [Google Scholar]
- Khan, H.S.; Aamir, M.; Kauhaniemi, K.; Mumtaz, M.; Hassan, M.W.; Ali, M. Improved finite control set model predictive control for distributed energy resource in islanded microgrid with fault-tolerance capability. Eng. Sci. Technol. Int. J. 2021, 24, 694–705. [Google Scholar] [CrossRef]
- Mosa, M.; Balog, R.S.; Abu-Rub, H.; Elbuluk, M. A modified symmetric and asymmetric multilevel power inverter with reduced number of power switches controlled by MPC. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 488–493. [Google Scholar]
- Korniejenko, K.; Kozub, B.; Bąk, A.; Balamurugan, P.; Uthayakumar, M.; Furtos, G. Tackling the Circular Economy Challenges—Composites Recycling: Used Tyres, Wind Turbine Blades, and Solar Panels. J. Compos. Sci. 2021, 5, 243. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.; Kennel, R. Robust predictive control scheme for permanent-magnet synchronous generators based modern wind turbines. Electronics 2021, 10, 1596. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.; Kennel, R. Model predictive control of permanent magnet synchronous generators in variable-speed wind turbine systems. In Proceedings of the Power and Energy Student Summit (PESS 2016), Aachen, Germany, 19–20 January 2016. [Google Scholar]
- Qudaih, Y.S.; Bernard, M.; Mitani, Y.; Mohamed, T. Model predictive based load frequency control design in the presence of DFIG wind turbine. In Proceedings of the 2011 2nd International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 15–17 November 2011; pp. 1–5. [Google Scholar]
- Zhang, Z.; Li, Z.; Kazmierkowski, M.P.; Rodríguez, J.; Kennel, R. Robust predictive control of three-level NPC back-to-back power converter PMSG wind turbine systems with revised predictions. IEEE Trans. Power Electron. 2018, 33, 9588–9598. [Google Scholar] [CrossRef]
- Zhang, Z.; Fang, H.; Gao, F.; Rodríguez, J.; Kennel, R. Multiple-vector model predictive power control for grid-tied wind turbine system with enhanced steady-state control performance. IEEE Trans. Ind. Electron. 2017, 64, 6287–6298. [Google Scholar] [CrossRef]
- Dehghani Arani, Z.; Taher, S.; Karimi, M.; Rahimi, M. Coordinated Model Predictive DC-Link Voltage, Current, and Electromagnetic Torque Control of Wind Turbine with DFIG under Grid Faults. J. Electr. Comput. Eng. Innov. (JECEI) 2020, 8, 201–218. [Google Scholar]
- Huang, S.; Wu, Q.; Guo, Y.; Rong, F. Optimal active power control based on MPC for DFIG-based wind farm equipped with distributed energy storage systems. Int. J. Electr. Power Energy Syst. 2019, 113, 154–163. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Alepuz, S.; Kouro, S. Predictive control for low-voltage ride-through enhancement of three-level-boost and NPC-converter-based PMSG wind turbine. IEEE Trans. Ind. Electron. 2014, 61, 6832–6843. [Google Scholar] [CrossRef]
- Jiang, H.; Jiao, X.; Ren, L. MPC-based power tracking control for a wind energy conversion system with PM synchronous generator. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 4079–4083. [Google Scholar]
- Wang, X.; Sun, D. Three-vector-based low-complexity model predictive direct power control strategy for doubly fed induction generators. IEEE Trans. Power Electron. 2016, 32, 773–782. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Model Predictive Control of Wind Energy Conversion Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Faulstich, A.; Stinke, J.; Wittwer, F. Medium voltage converter for permanent magnet wind power generators up to 5 MW. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005; p. 9. [Google Scholar]
- Liserre, M.; Cardenas, R.; Molinas, M.; Rodriguez, J. Overview of multi-MW wind turbines and wind parks. IEEE Trans. Ind. Electron. 2011, 58, 1081–1095. [Google Scholar] [CrossRef]
- Wei, J.; Li, C.; Wu, Q.; Zhou, B.; Xu, D.; Huang, S. MPC-based DC-link voltage control for enhanced high-voltage ride-through of offshore DFIG wind turbine. Int. J. Electr. Power Energy Syst. 2021, 126, 106591. [Google Scholar] [CrossRef]
- Omidi, A.; Kalantar, M. Improved Fault Ride Through Strategy Of Doubly Fed Induction Generator based Wind Turbine Using Model Predictive Control. In Proceedings of the 7th Iran Wind Energy Conference (IWEC2021), Shahrood, Iran, 17–18 May 2021; pp. 1–6. [Google Scholar]
- Hosseini, S.H.; Farakhor, A.; Haghighian, S.K. Novel algorithm of maximum power point tracking (MPPT) for variable speed PMSG wind generation systems through model predictive control. In Proceedings of the 2013 8th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2013; pp. 243–247. [Google Scholar]
- Aguirre, M.; Kouro, S.; Rodriguez, J.; Abu-Rub, H. Model predictive control of interleaved boost converters for synchronous generator wind energy conversion systems. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 2295–2301. [Google Scholar]
- Hassine, I.M.B.; Naouar, M.; Mrabet-Bellaaj, N. Model based predictive control strategies for wind turbine system based on PMSG. In Proceedings of the IREC2015: The Sixth International Renewable Energy Congress, Sousse, Tunisia, 24–26 March 2015; pp. 1–6. [Google Scholar]
- Yaramasu, V.; Wu, B.; Chen, J. Model-predictive control of grid-tied four-level diode-clamped inverters for high-power wind energy conversion systems. IEEE Trans. Power Electron. 2013, 29, 2861–2873. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Predictive control of a three-level boost converter and an NPC inverter for high-power PMSG-based medium voltage wind energy conversion systems. IEEE Trans. Power Electron. 2013, 29, 5308–5322. [Google Scholar] [CrossRef]
- Chirapongsananurak, P.; Hoonchareon, N. Design of a controller for DFIG-based wind power generation using model predictive control. In Proceedings of the ECTI-CON2010: The 2010 ECTI International Confernce on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Chiang Mai, Thailand, 19–21 May 2010; pp. 833–837. [Google Scholar]
- Jia, Y.; Liu, X. Distributed model predictive control of wind and solar generation system. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 7795–7799. [Google Scholar]
- Shadmand, M.B.; Li, X.; Balog, R.S.; Rub, H.A. Model predictive control of grid-tied photovoltaic systems: Maximum power point tracking and decoupled power control. In Proceedings of the 2015 First Workshop on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 22–23 March 2015; pp. 1–6. [Google Scholar]
- Saxena, V.; Kumar, N.; Singh, B.; Panigrahi, B.K. An MPC Based Algorithm for a Multipurpose Grid Integrated Solar PV System With Enhanced Power Quality and PCC Voltage Assist. IEEE Trans. Energy Convers. 2021, 36, 1469–1478. [Google Scholar] [CrossRef]
- Metry, M.; Shadmand, M.B.; Balog, R.S.; Abu-Rub, H. MPPT of photovoltaic systems using sensorless current-based model predictive control. IEEE Trans. Ind. Appl. 2016, 53, 1157–1167. [Google Scholar] [CrossRef]
- Bayhan, S.; Abu-Rub, H.; Balog, R.S. Model predictive control of quasi-Z-source four-leg inverter. IEEE Trans. Ind. Electron. 2016, 63, 4506–4516. [Google Scholar] [CrossRef]
- Sadabadi, M.S.; Shafiee, Q.; Karimi, A. Plug-and-play robust voltage control of DC microgrids. IEEE Trans. Smart Grid 2017, 9, 6886–6896. [Google Scholar] [CrossRef]
- Alhasheem, M.; Abdelhakim, A.; Blaabjerg, F.; Mattavelli, P.; Davari, P. Model Predictive Control of Grid Forming Converters with Enhanced Power Quality. Appl. Sci. 2020, 10, 6390. [Google Scholar] [CrossRef]
- Narender Reddy, N.; Chandrashekar, O.; Srujana, A. Power quality enhancement by MPC based multi-level control employed with improved particle Swarm optimized selective harmonic elimination. Energy Sources Part A Recover. Util. Environ. Eff. 2019, 41, 2396–2414. [Google Scholar] [CrossRef]
- Zhou, D.; Quan, Z.; Li, Y. Hybrid model predictive control of ANPC converters with decoupled low-frequency and high-frequency cells. IEEE Trans. Power Electron. 2019, 35, 8569–8580. [Google Scholar] [CrossRef]
- Metry, M.; Bayhan, S.; Shadmand, M.B.; Balog, R.S.; Rub, H.A. Sensorless current model predictive control for maximum power point tracking of single-phase subMultilevel inverter for photovoltaic systems. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar]
- Alhosaini, W.; Zhao, Y. A model predictive voltage control using virtual space vectors for grid-forming energy storage converters. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1466–1471. [Google Scholar]
- Prabhakar, P.; Vennila, H. Improvement of power quality in microgrids using predictive controller. Int. J. Intell. Syst. Technol. Appl. 2018, 17, 109–122. [Google Scholar]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Rodriguez, J.; Leon, J.I. Switching frequency regulation for FCS-MPC based on a period control approach. IEEE Trans. Ind. Electron. 2017, 65, 5764–5773. [Google Scholar] [CrossRef]
- Narender Reddy, N.; Chandrasheker, O.; Srujana, A. Power quality enhancement in micro grids by employing MPC-EKF. Int. J. Eng. Technol. (UAE) 2018, 7, 996–999. [Google Scholar] [CrossRef][Green Version]
- Samuel, O.; Javaid, N.; Khalid, A.; Khan, W.Z.; Aalsalem, M.Y.; Afzal, M.K.; Kim, B.S. Towards real-time energy management of multi-microgrid using a deep convolution neural network and cooperative game approach. IEEE Access 2020, 8, 161377–161395. [Google Scholar] [CrossRef]
- Cortes, P.; Kouro, S.; Barrios, F.; Rodriguez, J. Predictive control of a single-phase cascaded h-bridge photovoltaic energy conversion system. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; Volume 2, pp. 1423–1428. [Google Scholar]
- Majstorović, M.; Abarca, M.E.R.; Ristic, L. Review of MPC techniques for MMCs. In Proceedings of the 2019 20th International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 23–26 October 2019; pp. 1–7. [Google Scholar]
- Maalandish, M.; Hosseini, S.H.; Sabahi, M.; Asgharian, P. Modified MPC based grid-connected five-level inverter for photovoltaic applications. Compel- Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 971–985. [Google Scholar] [CrossRef]
- Zaouche, K.; Benmerabet, S.M.; Talha, A.; Berkouk, E.M. Finite-set model predictive control of an asymmetric cascaded h-bridge photovoltaic inverter. Appl. Surf. Sci. 2019, 474, 102–110. [Google Scholar] [CrossRef]
- Abbasi, Z.; Farahani, H.F. Open-Delta Three-Phase Inverter Current Control Using Predictive Control For PV System Connected To The Grid. Cumhuriyet Üniversitesi Fen Edebiyat Fakültesi Fen Bilimleri Dergisi 2015, 36, 121–134. [Google Scholar]
- Yaramasu, V.; Rivera, M.; Wu, B.; Rodriguez, J. Model predictive current control of two-level four-leg inverters—Part I: Concept, algorithm, and simulation analysis. IEEE Trans. Power Electron. 2012, 28, 3459–3468. [Google Scholar] [CrossRef]
- Trabelsi, M.; Ben-Brahim, L. A New Design of dSpace Microcontroller-based Real-Time Digital Predictive Controller for Grid Connected Photovoltaic Power Conditioning System. Int. J. Adv. Res. Comput. Commun. Eng. 2013, 2, 4049–4055. [Google Scholar]
- Sebaaly, F.; Vahedi, H.; Kanaan, H.Y.; Moubayed, N.; Al-Haddad, K. Finite control set model predictive controller for grid connected inverter design. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 1208–1213. [Google Scholar]
- Jain, S.; Shadmand, M.B.; Balog, R.S. Decoupled active and reactive power predictive control for PV applications using a grid-tied quasi-Z-source inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1769–1782. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Chen, X.; Christofides, P.D. Supervisory predictive control of standalone wind/solar energy generation systems. IEEE Trans. Control Syst. Technol. 2010, 19, 199–207. [Google Scholar] [CrossRef]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. MPC-controlled virtual synchronous generator to enhance frequency and voltage dynamic performance in islanded microgrids. IEEE Trans. Smart Grid 2020, 12, 953–964. [Google Scholar] [CrossRef]
- Ekanayake, J.B.; Jenkins, N.; Liyanage, K.; Wu, J.; Yokoyama, A. Smart Grid: Technology and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Chakrabortty, A.; Ilić, M.D. Control and Optimization Methods for Electric Smart Grids; Springer: Berlin/Heidelberg, Germany, 2011; Volume 3. [Google Scholar]
- Chowdhury, S.; Chowdhury, S.P.; Crossley, P. Microgrids and Active Distribution Networks; The Institution of Engineering and Technology: London, UK, 2021. [Google Scholar]
- Hartono, B.; Budiyanto, Y.; Setiabudy, R. Review of microgrid technology. In Proceedings of the 2013 International Conference on QiR, Yogyakarta, Indonesia, 25–28 June 2013; pp. 127–132. [Google Scholar]
- Mahmoud, M.S.; Rahman, M.S.U.; Fouad, M.S. Review of microgrid architectures—A system of systems perspective. IET Renew. Power Gener. 2015, 9, 1064–1078. [Google Scholar] [CrossRef]
- Jayachandran, M.; Ravi, G. Decentralized model predictive hierarchical control strategy for islanded AC microgrids. Electr. Power Syst. Res. 2019, 170, 92–100. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172. [Google Scholar] [CrossRef]
- Aminu, M.; Solomon, K. A Review of Control Strategies for Microgrids. Adv. Res. 2016, 7, 1–9. [Google Scholar] [CrossRef]
- Rezaei, N.; Kalantar, M. Smart microgrid hierarchical frequency control ancillary service provision based on virtual inertia concept: An integrated demand response and droop controlled distributed generation framework. Energy Convers. Manag. 2015, 92, 287–301. [Google Scholar] [CrossRef]
- Soni, N.; Doolla, S.; Chandorkar, M.C. Improvement of transient response in microgrids using virtual inertia. IEEE Trans. Power Deliv. 2013, 28, 1830–1838. [Google Scholar] [CrossRef]
- Faria, P.; Vale, Z. Demand response in electrical energy supply: An optimal real time pricing approach. Energy 2011, 36, 5374–5384. [Google Scholar] [CrossRef]
- Gbadega, P.A.; Saha, A.K. Load Frequency Control of a Two-Area Power System With a Stand-Alone Microgrid Based on Adaptive Model Predictive Control. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 7253–7263. [Google Scholar] [CrossRef]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. Enhancement of Frequency Regulation in AC Microgrid: A Fuzzy-MPC Controlled Virtual Synchronous Generator. IEEE Trans. Smart Grid 2021, 12, 3138–3149. [Google Scholar] [CrossRef]
- Wang, H.; Yang, J.; Chen, Z.; Ge, W.; Ma, Y.; Xing, Z.; Yang, L. Model predictive control of PMSG-based wind turbines for frequency regulation in an isolated grid. IEEE Trans. Ind. Appl. 2018, 54, 3077–3089. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Tzamalis, G.; Glielmo, L. Use of model predictive control for experimental microgrid optimization. Appl. Energy 2014, 115, 37–46. [Google Scholar] [CrossRef]
- Verma, A.K.; Gooi, H.; Ukil, A.; Tummuru, N.R.; Kollimalla, S.K. Microgrid frequency stabilization using model predictive controller. In Proceedings of the 2016 IEEE PES Transmission & Distribution Conference and Exposition-Latin America (PES T&D-LA), Morelia, Mexico, 20–24 September 2016; pp. 1–6. [Google Scholar]
- Cominesi, S.R.; Farina, M.; Giulioni, L.; Picasso, B.; Scattolini, R. A two-layer stochastic model predictive control scheme for microgrids. IEEE Trans. Control Syst. Technol. 2017, 26, 1–13. [Google Scholar] [CrossRef]
- Salazar, M.; Balerna, C.; Elbert, P.; Grando, F.P.; Onder, C.H. Real-time control algorithms for a hybrid electric race car using a two-level model predictive control scheme. IEEE Trans. Veh. Technol. 2017, 66, 10911–10922. [Google Scholar] [CrossRef]
- Pahasa, J.; Ngamroo, I. PHEVs bidirectional charging/discharging and SoC control for microgrid frequency stabilization using multiple MPC. IEEE Trans. Smart Grid 2014, 6, 526–533. [Google Scholar] [CrossRef]
- Namerikawa, T.; Kato, T. Distributed load frequency control of electrical power networks via iterative gradient methods. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 7723–7728. [Google Scholar]
- Zhao, C.; Topcu, U.; Low, S.H. Frequency-based load control in power systems. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 4423–4430. [Google Scholar]
- Guo, J.; Zhao, T.; Liu, W.; Zhang, J. Reliability modeling and assessment of isolated microgrid considering influences of frequency control. IEEE Access 2019, 7, 50362–50371. [Google Scholar] [CrossRef]
- Ding, C.; Chen, Y.; Nie, T. LVRT Control Strategy for Asymmetric Faults of DFIG Based on Improved MPCC Method. IEEE Access 2021, 9, 165207–165218. [Google Scholar] [CrossRef]
- Kamel, R.M. Distributed generators as reactive power providers and their impacts on standalone micro-grid performance during both symmetrical and unsymmetrical faults. Renew. Energy Focus 2020, 35, 159–170. [Google Scholar] [CrossRef]
- Das, T.K.; Chattopadhyay, S.; Das, A. Load Bus Symmetrical Fault Analysis in Microgrid System. Lectures on Modelling and Simulation (AMSE). 4–5 November 2017, pp. 151–162. Available online: https://amsemodelling.com/publications/lectures_on_modeling_and_simulation/calcutta_15.pdf (accessed on 28 June 2022).
- Khoun Jahan, H.; Eskandari, R.; Rahimi, T.; Shalchi Alishah, R.; Ding, L.; Bertilsson, K.; Sabahi, M.; Blaabjerg, F. A limited common-mode current switched-capacitor multilevel inverter topology and its performance and lifetime evaluation in grid-connected photovoltaic applications. Energies 2021, 14, 1915. [Google Scholar] [CrossRef]
- Ghiasi, M. Detailed study, multi-objective optimization, and design of an AC-DC smart microgrid with hybrid renewable energy resources. Energy 2019, 169, 496–507. [Google Scholar] [CrossRef]
- Ghiasi, M.; Niknam, T.; Dehghani, M.; Siano, P.; Haes Alhelou, H.; Al-Hinai, A. Optimal multi-operation energy management in smart microgrids in the presence of ress based on multi-objective improved de algorithm: Cost-emission based optimization. Appl. Sci. 2021, 11, 3661. [Google Scholar] [CrossRef]
- Dehghani, M.; Ghiasi, M.; Niknam, T.; Rouzbehi, K.; Wang, Z.; Siano, P.; Alhelou, H.H. Control of LPV Modeled AC-Microgrid Based on Mixed H2/H∞ Time-Varying Linear State Feedback and Robust Predictive Algorithm. IEEE Access 2021, 10, 3738–3755. [Google Scholar] [CrossRef]
- Moghateli, F.; Taher, S.A.; Karimi, A.; Shahidehpour, M. Multi-objective design method for construction of multi-microgrid systems in active distribution networks. IET Smart Grid 2020, 3, 331–341. [Google Scholar] [CrossRef]
- Merabet, A.; Labib, L.; Ghias, A.M. Robust model predictive control for photovoltaic inverter system with grid fault ride-through capability. IEEE Trans. Smart Grid 2017, 9, 5699–5709. [Google Scholar] [CrossRef]
- Easley, M.; Jain, S.; Shadmand, M.; Abu-Rub, H. Autonomous model predictive controlled smart inverter with proactive grid fault ride-through capability. IEEE Trans. Energy Convers. 2020, 35, 1825–1836. [Google Scholar] [CrossRef]
- Druant, J.; Vyncke, T.; De Belie, F.; Sergeant, P.; Melkebeek, J. Adding inverter fault detection to model-based predictive control for flying-capacitor inverters. IEEE Trans. Ind. Electron. 2014, 62, 2054–2063. [Google Scholar] [CrossRef]
- Marquez, J.; Zafra-Cabeza, A.; Bordons, C.; Ridao, M.A. A fault detection and reconfiguration approach for MPC-based energy management in an experimental microgrid. Control Eng. Pract. 2021, 107, 104695. [Google Scholar] [CrossRef]
- Lunardi, A.; Conde D, E.R.; de Assis, J.; Fernandes, D.A.; Sguarezi Filho, A.J. Model predictive control with modulator applied to grid inverter under voltage distorted. Energies 2021, 14, 4953. [Google Scholar] [CrossRef]
- Jin, N.; Guo, L.; Yao, G. Model predictive direct power control for nonredundant fault tolerant grid-connected bidirectional voltage source converter. Energies 2017, 10, 1133. [Google Scholar] [CrossRef]
- Gonçalves, P.F.; Cruz, S.M.; Abadi, M.B.; Caseiro, L.M.; Mendes, A.M. Fault-tolerant predictive power control of a DFIG for wind energy applications. IET Electr. Power Appl. 2017, 11, 969–980. [Google Scholar] [CrossRef]
- Novak, M.; Ferreira, V.; Andresen, M.; Dragicevic, T.; Blaabjerg, F.; Liserre, M. FS-MPC based thermal stress balancing and reliability analysis for NPC converters. IEEE Open J. Power Electron. 2021, 2, 124–137. [Google Scholar] [CrossRef]
- Peng, T.; Xu, Y.; Yang, C.; Xie, F.; Tao, H.; Yang, C. Equivalent temperature estimation-based FCS-MPC for thermal stress balance of 3L-NPC traction inverter. IET Power Electron. 2021, 14, 2314–2323. [Google Scholar] [CrossRef]
- Baier, C.R.; Ramirez, R.O.; Marciel, E.I.; Hernández, J.C.; Melín, P.E.; Espinosa, E.E. FCS-MPC without steady-state error applied to a grid-connected cascaded H-Bridge multilevel inverter. IEEE Trans. Power Electron. 2021, 36, 11785–11799. [Google Scholar] [CrossRef]
- Babaie, M.; Mehrasa, M.; Sharifzadeh, M.; Al-Haddad, K. Floating weighting factors ANN-MPC based on Lyapunov stability for seven-level modified PUC active rectifier. IEEE Trans. Ind. Electron. 2021, 69, 387–398. [Google Scholar] [CrossRef]
- Kaymanesh, A.; Chandra, A. Computationally Efficient MPC Technique for PUC-Based Inverters Without Weighting Factors. In Proceedings of the 2021 IEEE Industry Applications Society Annual Meeting (IAS), Vancouver, BC, Canada, 10–14 October 2021; pp. 1–5. [Google Scholar]
- Liu, B.; Wang, H.; Yang, Y.; Zhang, X.; Guo, B. Improved Model Predictive Control for Single-Phase Grid-Tied Inverter with Virtual Vectors in the Compacted Solution-Space. IEEE Trans. Ind. Electron. 2021, 69, 9673–9678. [Google Scholar] [CrossRef]
- Liu, B.; Li, G.; He, D.; Chen, Y. DC and AC power quality control for single-phase grid-tied PEMFC systems with low DC-link capacitance by solution-space-reduced MPC. IEEE Trans. Ind. Electron. 2021, 69, 5625–5636. [Google Scholar] [CrossRef]
- Tsili, M.; Papathanassiou, S. A review of grid code technical requirements for wind farms. IET Renew. Power Gener. 2009, 3, 308–332. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Taher, S.A.; Karimi, M.H.; Arani, Z.D. Improving fault ride through capability of full-Scale WRSG wind turbines using MPC-based DVR. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 863–867. [Google Scholar]
- Sebaaly, F.; Kanaan, H.Y.; Rodriguez, J.; Al-Haddad, K. Direct predictive control for a nine-level packed E-Cell (PEC9) converter based shunt active power filter (SAPF). In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–7. [Google Scholar]
- Andino, J.; Ayala, P.; Llanos-Proaño, J.; Naunay, D.; Martinez, W.; Arcos-Aviles, D. Constrained Modulated Model Predictive Control for a Three-Phase Three-Level Voltage Source Inverter. IEEE Access 2022, 10, 10673–10687. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Z.; Wang, S.; Zhang, Z. Predictive current control of three-phase three-wire APF with error feedback correction. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 5748–5752. [Google Scholar]



| Energy Generation | Energy Storage | |||||
|---|---|---|---|---|---|---|
| Application | Fuel Cell | PV | Wind Turbine | UPS | Battery | Flywheel |
| Stand-Alone System | ✔ | ✔ | ✔ | Not applicable | ||
| Power quality | Not applicable | ✔ | ✔ | ✔ | ||
| Combined Heat and Power | ✔ | Not applicable | Not applicable | |||
| Connection with network | DC/AC Converter | AC/DC Converter | Asynchronous Generator | Power Converter | ||
| Size Range (kW) | 100–250 | 0.01–8 | 0.2–5000 | 40 | 1–1000 | 2–1600 |
| Application | Control Objective | Optimized Parameter | Operating Mode | Ref. |
|---|---|---|---|---|
| Boost Converter Inverter MPPT | MPPT | Voltage, Current | Island | [42] |
| Rectifier Boost Converter | Generator Control at Low Speeds | Voltage, Current | Grid-Connected | [43] |
| Back-to-Back Converter | Wind Turbine Control | Voltage, Current | Grid-Connected | [44] |
| Four Level Diode Clamped Inverter | Grid-tied Inverter Control | Voltage, Current | Grid-Connected | [45] |
| NPC Inverter Three level Boost FCS-MPC | Control of NPC Inverter at High Power | Voltage, Current | Island | [46] |
| Voltage Source Inverter | Reduction of Frequency Fluctuations | Active/Reactive Power | Island | [47] |
| Rectifier DC-DC Converter Inverter | To develop model MPC for hybrid system | Power/Torque/ Speed | Island | [48] |
| Proposed Structure | Control Purpose | Outcome Specifications | Ref. |
|---|---|---|---|
| MPC-PWM | Reduce the circulating current of the inverter, regulation of the currents injected into the grid | Increase system reliability | [59] |
| FCS-MPC | Switching frequency control and power quality improvement | Reduction of losses by decreasing variable switching frequency | [60] |
| MPC-DSTATCOM | Reactive power compensation and harmonic reduction | Increase stability | [61] |
| MDSOGI-MPC | Optimal management of the power transmission | Optimal performance of VSC by estimator SOGI | [62] |
| MPC-REKF-IPSO | Improvement of power quality | Reduction of harmonic | [63] |
| MPC-EKF | Increase reliability | Reduction of the computational time | [64] |
| Configuration | Main Purpose | The Optimized Parameters | Operating Mode | Ref. |
|---|---|---|---|---|
| Three Phase Inverter | Microgrid Optimization | Inverter Output Current | Grid-Connected | [67] |
| Three Phase Two Level Four Leg Inverter | DC link Voltage Control for Balanced/Unbalanced Condition | Inverter Output Voltage | Island | [68] |
| Grid-Connected Solar PV Inverter | The Proper Dynamic Response | Inverter Output Current | Grid-Connected | [22] |
| Flying Capacitors Inverter, DC-DC Boost | MPPT | Inverter Output Current | Grid-Connected | [69] |
| Impedance Source Inverter | Regulation of the inverter current | Inverter Output Current | Grid-Connected | [70] |
| The Grid-tied Inverter | Improved Predictive Method for Inverter Current Control | Inverter Output Current | Grid-Connected | [71] |
| Load Connected PV/Wind Inverter | The Solar/Wind Power Control | Inverter Output Current | Island | [72] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razmi, D.; Babayomi, O.; Davari, A.; Rahimi, T.; Miao, Y.; Zhang, Z. Review of Model Predictive Control of Distributed Energy Resources in Microgrids. Symmetry 2022, 14, 1735. https://doi.org/10.3390/sym14081735
Razmi D, Babayomi O, Davari A, Rahimi T, Miao Y, Zhang Z. Review of Model Predictive Control of Distributed Energy Resources in Microgrids. Symmetry. 2022; 14(8):1735. https://doi.org/10.3390/sym14081735
Chicago/Turabian StyleRazmi, Darioush, Oluleke Babayomi, Alireza Davari, Tohid Rahimi, Yuntao Miao, and Zhenbin Zhang. 2022. "Review of Model Predictive Control of Distributed Energy Resources in Microgrids" Symmetry 14, no. 8: 1735. https://doi.org/10.3390/sym14081735
APA StyleRazmi, D., Babayomi, O., Davari, A., Rahimi, T., Miao, Y., & Zhang, Z. (2022). Review of Model Predictive Control of Distributed Energy Resources in Microgrids. Symmetry, 14(8), 1735. https://doi.org/10.3390/sym14081735







