Combining Two Exponentiated Families to Generate a New Family of Distributions
Abstract
:1. Introduction
- (1)
- (2)
- as and as
- (3)
- is differentiable and monotonically non-decreasing.
2. Exponentaited Exponentiated T-X Family
3. Exponentiated Exponentiated Weibull Exponential Distribution
3.1. Exponentiated Exponentiated Weibull-X Family
3.2. CDF and PDF of EEWE Distribution
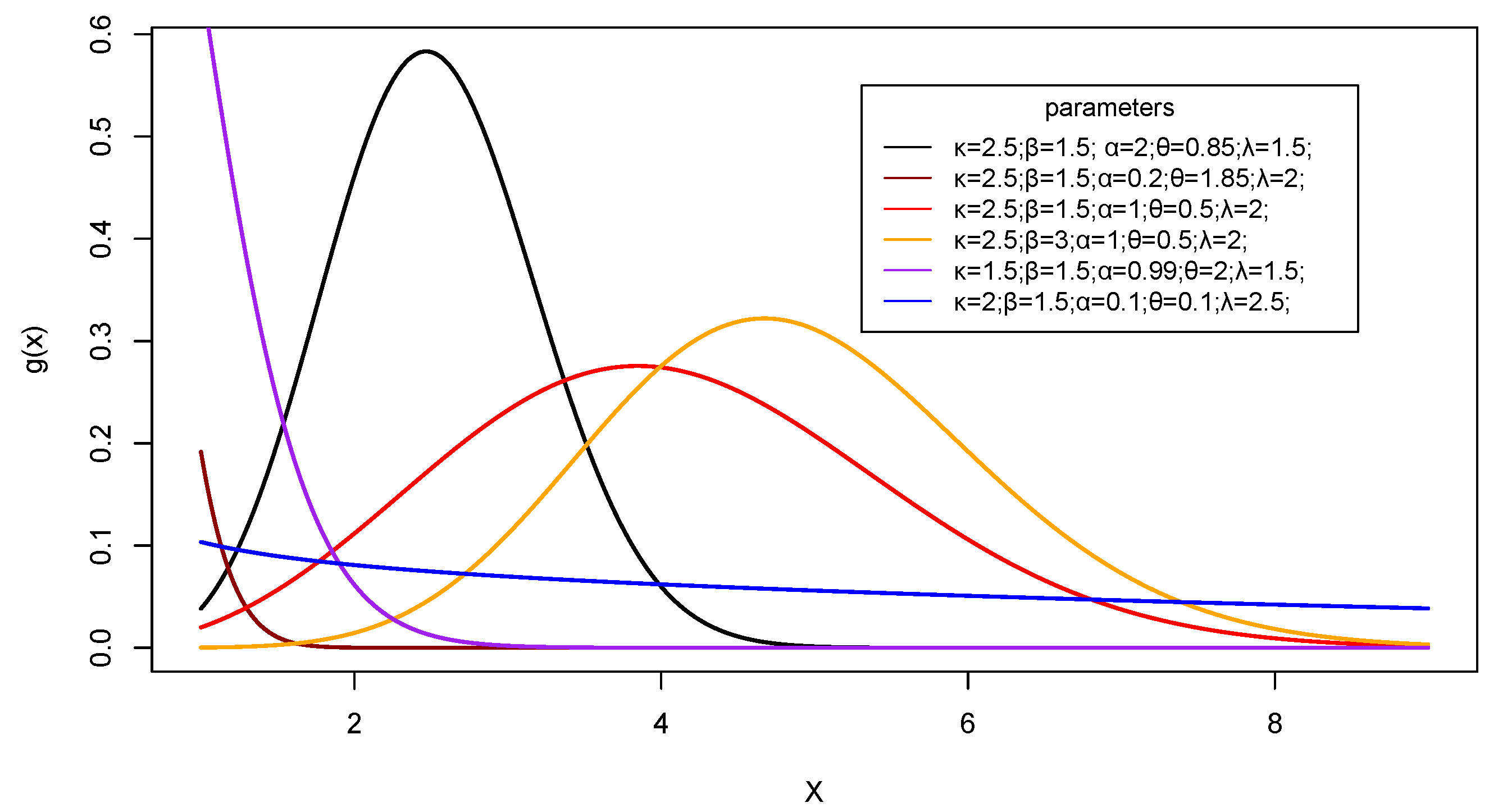
3.3. Some Special Cases of EEWE Distribution
- When , the EEWE distribution converts to the generalized Weibull exponential (GWE) distribution with parameters , , , and .
- When , , the EEWE distribution converts to the Weibull exponential (WE) distribution with parameters , , and .
- When , the EEWE distribution converts to the exponentiated Weibull exponential (EWE) distribution with parameters , , , and .
- When , , , , the EEWE distribution converts to the exponential (E) with one parameter .
- When , the EEWE distribution converts to the exponentiated Weibull exponential (EWE) distribution with parameters , and , as presented in [11].
3.4. Some of EEWE Distribution Properties
3.4.1. The Quantile Function and the Median
Useful Expansions
3.4.2. Moments
3.4.3. Moment Generating Function and Characteristic Function
3.4.4. Rényi Entropy
3.4.5. Order Statistics
3.5. Parameter Estimation for EEWE Distribution
4. Simulation Study
5. Application
- (1)
- Exponential distribution
- (2)
- Weibull exponential distribution
- (3)
- Generalized Weibull exponential distribution presented by [16]
- (4)
- Exponentiated Weibull exponential distribution
- (5)
- Generalized transmuted generalized exponential distribution
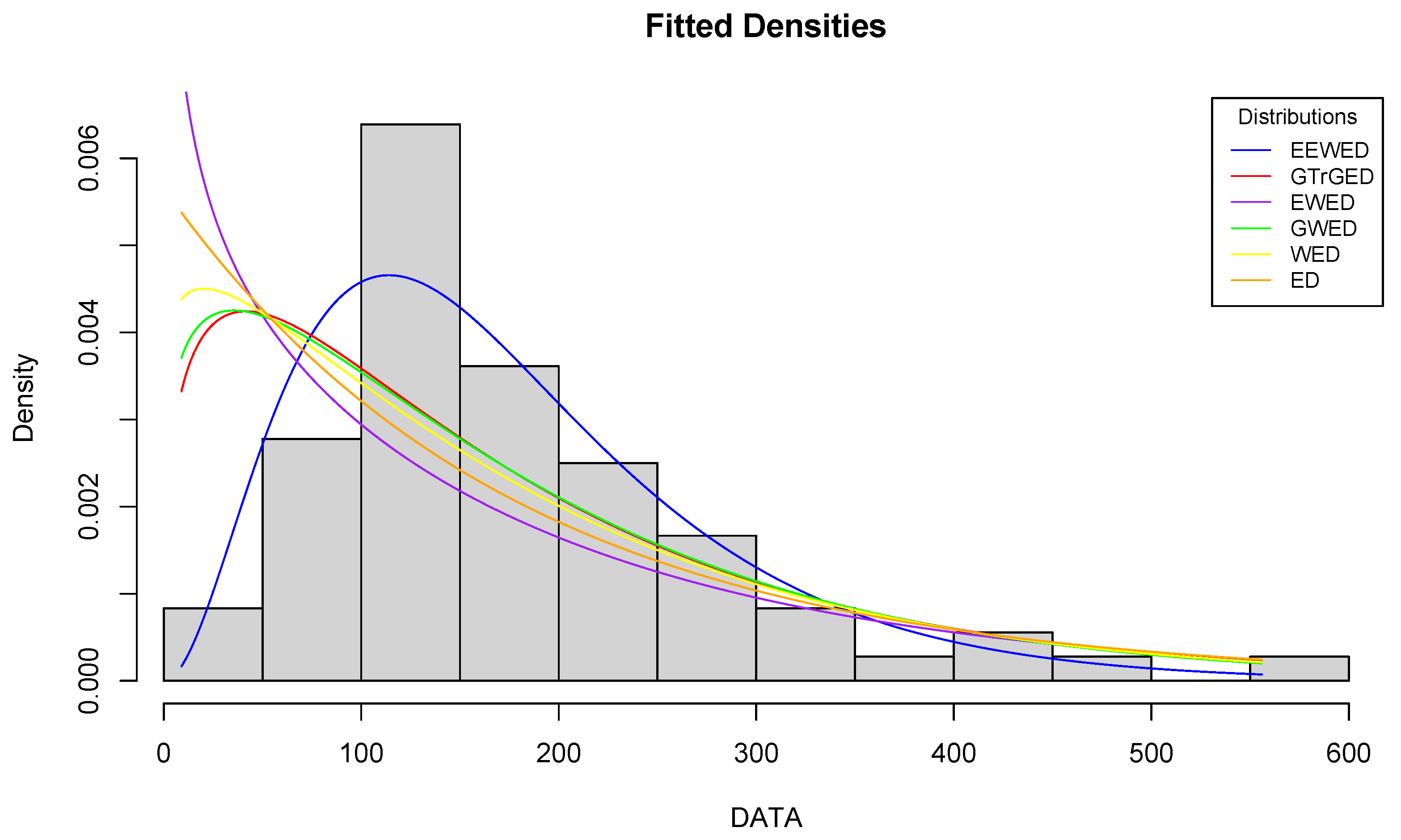
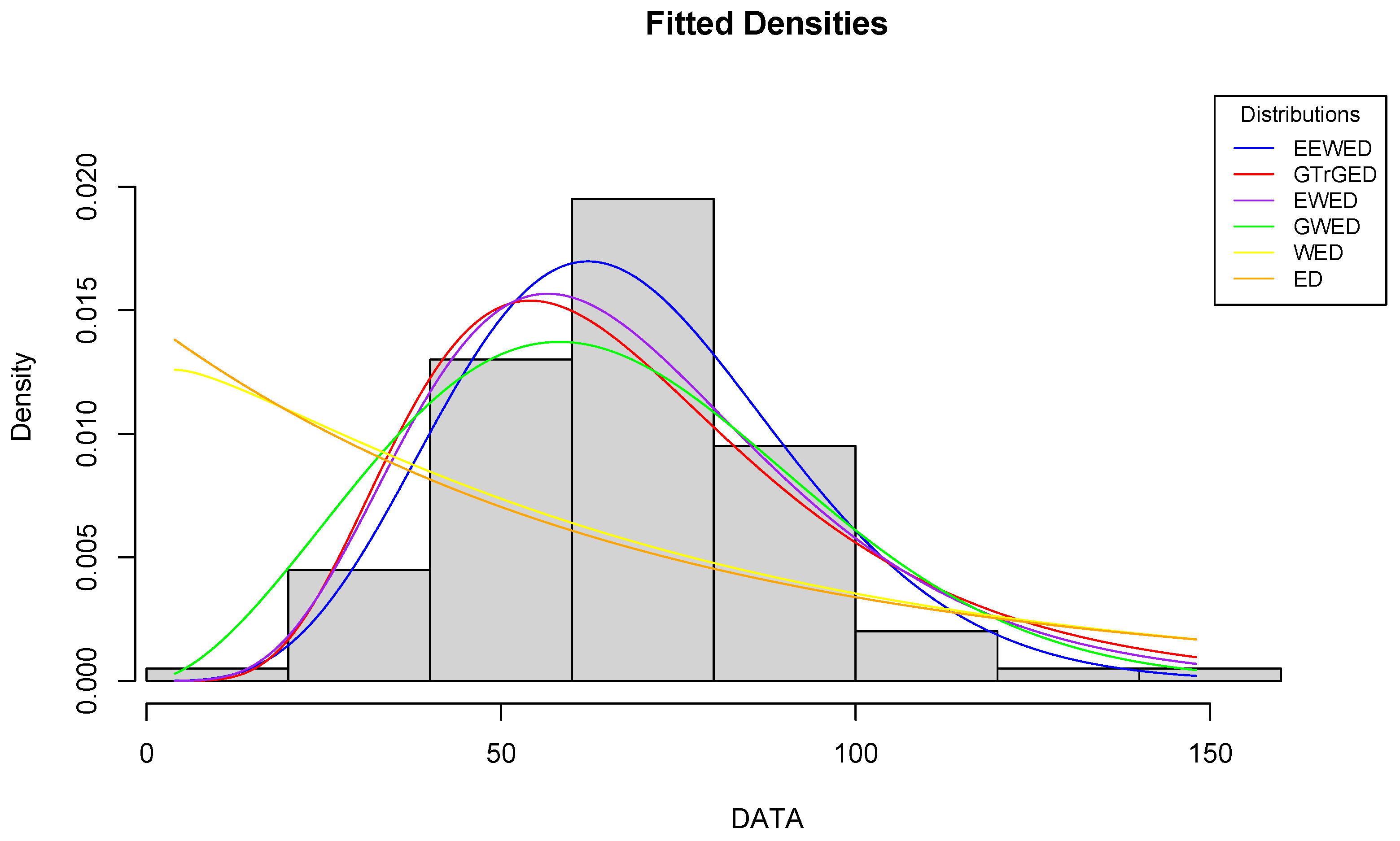
5.1. First Dataset
5.2. Second Dataset
5.3. Third Dataset
6. Conclusions
7. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling Failure Time Data by Lehman Alternatives. Commun. Stat.-Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Ali, M.M.; Pal, M.; Woo, J.S. Some Exponentiated Distributions. Commun. Stat. Appl. Methods 2007, 14, 93–109. [Google Scholar] [CrossRef]
- Nadarajah, S.; Gupta, A.K. The Exponentiated Gamma Distribution with Application to Drought Data. Calcutta Stat. Assoc. Bull. 2007, 59, 29–54. [Google Scholar] [CrossRef]
- Shawky, A.; Abu-Zinadah, H.H. Exponentiated Pareto Distribution: Different Method of Estimations. Int. J. Contemp. Math. Sci. 2009, 4, 677–693. [Google Scholar]
- Abu-Zinadah, H.H.; Aloufi, A.S. Some characterizations of the exponentiated Gompertz distribution. Int. Math. Forum 2014, 9, 1427–1439. [Google Scholar] [CrossRef]
- Salem, H.M. The Exponentiated Lomax Distribution: Different Estimation Methods. Am. J. Appl. Math. Stat. 2014, 2, 364–368. [Google Scholar] [CrossRef]
- Rather, A.A.; Subramanian, C. Exponentiated Mukherjee-Islam Distribution. J. Stat. Appl. Probab. 2018, 7, 357–361. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Famoye, F.; Lee, C. A New Method for Generating Families of Continuous Distributions. METRON 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Famoye, F.; Lee, C. Weibull-Pareto Distribution and its Applications. Commun. Stat.-Theory Methods 2013, 42, 1673–1691. [Google Scholar] [CrossRef]
- Klakattawi, H.S. The Weibull-Gamma Distribution: Properties and Applications. Entropy 2019, 21, 438. [Google Scholar] [CrossRef]
- Alzaghal, A.; Famoye, F.; Lee, C. Exponentiated T-X Family of Distributions with Some Applications. Int. J. Stat. Probab. 2013, 2, 31–49. [Google Scholar] [CrossRef]
- Jabeen, S.; Para, B. Exponentiated Gamma Exponential Distribution. Sohag J. Math. 2018, 5, 79–84. [Google Scholar]
- Nadarajah, S.; Cordeiro, G.M.; Ortega, E.M. The Zografos–Balakrishnan-G family of distributions: Mathematical properties and applications. Commun. Stat.-Theory Methods 2015, 44, 186–215. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; M Ortega, E.M.; Ramires, T.G. A new generalized Weibull family of distributions: Mathematical properties and applications. J. Stat. Distrib. Appl. 2015, 2, 1–25. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, Berkeley, CA, USA, 20 June–30 July 1960; The Regents of the University of California: Oakland, CA, USA, 1961. [Google Scholar]
- Salem, H.M.; Selim, M. The Generalized Weibull-Exponential Distribution: Properties and Applications. Int. J. Stat. Appl. 2014, 4, 102–112. [Google Scholar]
- Bjerkedal, T. Acquisition of Resistance in Guinea Pies infected with Different Doses of Virulent Tubercle Bacilli. Am. J. Hyg. 1960, 72, 130–148. [Google Scholar] [PubMed]
- Xu, K.; Xie, M.; Tang, L.C.; Ho, S. Application of neural networks in forecasting engine systems reliability. Appl. Soft Comput. 2003, 2, 255–268. [Google Scholar] [CrossRef]
- Birnbaum, Z.W.; Saunders, S.C. Estimation for a family of life distributions with applications to fatigue. J. Appl. Probab. 1969, 6, 328–347. [Google Scholar] [CrossRef]


| Sample Size | Parameter | Case I | Case II | Case III | |||
|---|---|---|---|---|---|---|---|
| MLE | MSE | MLE | MSE | MLE | MSE | ||
| 1.76213618 | 0.129651982 | 9.99999859 | 6.954299 | 1.74599329 | 0.039682607 | ||
| 0.70181142 | 0.376492237 | 0.69998767 | 4.283840 | 4.96089997 | 0.038061954 | ||
| 1.19264764 | 0.124722840 | 0.39993911 | 7.877924 | 0.49491032 | 0.009612482 | ||
| 0.63184321 | 0.004721838 | 0.01003896 | 2.259842 | 0.06848698 | 0.043138538 | ||
| 0.06247869 | 0.001296300 | 0.29997104 | 1.193325 | 0.18147413 | 0.186045347 | ||
| 1.74879729 | 0.0449915708 | 9.99999963 | 1.076094 | 1.70939431 | 0.006057104 | ||
| 0.54529106 | 0.0828786328 | 0.69999617 | 9.621094 | 4.99155636 | 0.005188604 | ||
| 1.14668157 | 0.0507040578 | 0.39997500 | 2.988855 | 0.49763442 | 0.001341771 | ||
| 0.63752005 | 0.0002359174 | 0.01000043 | 7.295098 | 0.02243868 | 0.007344277 | ||
| 0.06777658 | 0.0005551312 | 0.29998489 | 8.749173 | 0.09581724 | 0.035992660 | ||
| 1.72037501 | 0.0199463651 | 9.99999977 | 3.979467 | 1.70018095 | 4.287554 | ||
| 0.52909388 | 0.0304618773 | 0.69999751 | 3.975560 | 4.99994003 | 6.777741 | ||
| 1.11148820 | 0.0232369786 | 0.39998275 | 1.094464 | 0.50049358 | 2.552080 | ||
| 0.63848830 | 0.0001331668 | 0.01000066 | 3.239753 | 0.01043817 | 4.765273 | ||
| 0.07083394 | 0.0002764211 | 0.29998902 | 3.205238 | 0.07072449 | 1.246056 | ||
| 1.71516169 | 0.0082627191 | 9.999999975 | 4.400126 | 1.70000095 | 2.189370 | ||
| 0.50519590 | 0.0099628342 | 0.699999507 | 6.021973 | 5.00000030 | 7.631066 | ||
| 1.10662718 | 0.0096392748 | 0.399992036 | 4.053356 | 0.50001427 | 8.525506 | ||
| 0.63743595 | 0.0000782145 | 0.009995108 | 1.321479 | 0.01001696 | 5.476000 | ||
| 0.07094053 | 0.0001238495 | 0.299993643 | 2.002551 | 0.07003131 | 2.155901 | ||
| Distributions | EEWE | GTrGE | EWE | GWE | WE | E |
|---|---|---|---|---|---|---|
| Parameters estimation | = 0.0103 | = 0.006 | = 0.0023 | = 0.0065 | = 0.0061 | = 0.0057 |
| = 1.1 | = 1.1062 | = 1.1 | = 1.1 | = 1.1 | ||
| = 1.1 | = 0.0471 | = 0.5 | = 1.1 | = 1.1 | ||
| = 1.1 | = 1.2058 | = 0.7 | = 1.1 | |||
| = 2.5 | = 0.4997 | |||||
| Log-likelihood | −425.7619 | −437.7061 | −450.4563 | −437.9455 | −440.1889 | −444.6093 |
| AICc | 862.4329 | 886.3213 | 909.5096 | 884.4880 | 886.7306 | 891.2757 |
| AIC | 861.5238 | 885.4122 | 908.9126 | 883.8910 | 886.3777 | 891.2186 |
| p-value | 4.3706 | 3.2755 | 1.0452 | 1.9622 | 5.5284 | 7.5031 |
| Distributions | EEWE | GTrGE | EWE | GWE | WE | E |
|---|---|---|---|---|---|---|
| Parameters estimation | = 0.0349 | = 0.4499 | = 0.0368 | = 0.0243 | = 0.0501 | = 0.1599 |
| = 4.1813 | = 3.1014 | = 4.8742 | = 2.8551 | = 3.8584 | ||
| = 0.0442 | = −0.0061 | = 0.275 | = 0.0753 | = 0.3468 | ||
| = 2.2543 | = 3.0681 | =0.6589 | = 1.4053 | |||
| = 0.329 | = −0.0014 | |||||
| Log-likelihood | −79.6825 | −90.1427 | −81.2893 | −82.6434 | −82.4759 | −113.3193 |
| AICc | 171.1297 | 192.0500 | 171.7215 | 174.4297 | 171.6184 | 228.7438 |
| AIC | 169.3650 | 190.2853 | 170.5787 | 173.2868 | 170.9518 | 228.6385 |
| p-value | 8.5019 | 2.9757 | 7.6829 | 7.3139 | 7.4037 | 5.2504 |
| Distributions | EEWE | GTrGE | EWE | GWE | WE | E |
|---|---|---|---|---|---|---|
| Parameters estimation | = 0.0173 | = 0.0393 | = 0.017 | = 0.0117 | = 0.0043 | = 0.0146 |
| = 1.8712 | = 2.9796 | = 1.318 | = 1.8748 | = 1.0524 | ||
| = 0.8063 | = −0.0244 | = 0.6616 | = 0.5594 | = 0.2944 | ||
| = 1.3978 | = 2.8173 | = 4.5336 | = 1.5371 | |||
| = 1.889 | = 0.0358 | |||||
| Log-likelihood | −454.6378 | −464.1941 | −459.8019 | −459.9742 | −517.9904 | −522.4495 |
| AICc | 919.9140 | 939.0264 | 928.0248 | 928.3694 | 1042.2296 | 1046.9399 |
| AIC | 919.2757 | 938.3881 | 927.6038 | 927.9483 | 1041.9796 | 1046.8991 |
| p-value | 4.2979 | 1.2058 | 1.4214 | 2.6729 | 1.9496 | 4.2664 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsolami, E.; Alsulami, D. Combining Two Exponentiated Families to Generate a New Family of Distributions. Symmetry 2022, 14, 1739. https://doi.org/10.3390/sym14081739
Alsolami E, Alsulami D. Combining Two Exponentiated Families to Generate a New Family of Distributions. Symmetry. 2022; 14(8):1739. https://doi.org/10.3390/sym14081739
Chicago/Turabian StyleAlsolami, Eatemad, and Dawlah Alsulami. 2022. "Combining Two Exponentiated Families to Generate a New Family of Distributions" Symmetry 14, no. 8: 1739. https://doi.org/10.3390/sym14081739
APA StyleAlsolami, E., & Alsulami, D. (2022). Combining Two Exponentiated Families to Generate a New Family of Distributions. Symmetry, 14(8), 1739. https://doi.org/10.3390/sym14081739






