Numerical Contrivance for Kawahara-Type Differential Equations Based on Fifth-Kind Chebyshev Polynomials
Abstract
:1. Introduction
- Establishing some results concerned with fifth-kind Chebyshev polynomials, including a new formula that linearizes the product of the Chebyshev polynomials of the fifth kind and their first derivative.
- Developing a new numerical algorithm on the basis of the application of the Tau method to solve Kawahara-type differential equations.
- Investigating theoretically and numerically the convergence of the proposed algorithm.
- An innovative strategy is provided in this article for solving Kawahara-type equations.
- Other classes of nonlinear differential equations are amenable to treatment with the proposed approach.
2. Some Properties of the Fifth-Kind Chebyshev Polynomials and Their Shifted Ones
3. New Linearization Formula of the Fifth-Kind Chebyshev Polynomials and Their First-Order Derivative
4. Numerical Treatment of Kawahara Equation
4.1. Tau Algorithm for the Numerical Treatment of the Kawahara Equation
4.2. Convergence and Error Analysis
5. Numerical Examples
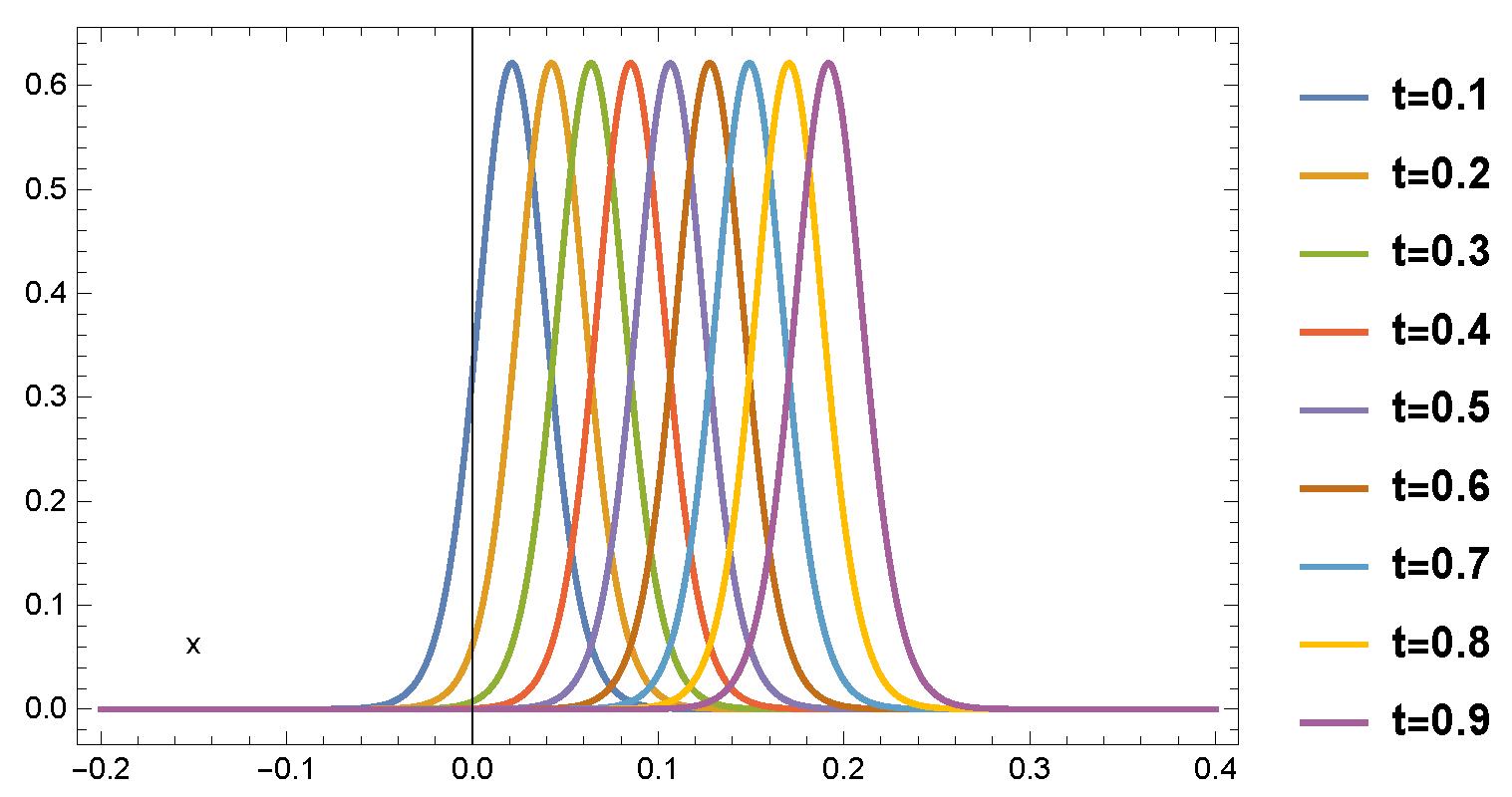
- Figure 1 presents the numerical solution of Example 1 for various spatial values. From the results in this figure, we can see the moving behavior of the solution wave as x changes.
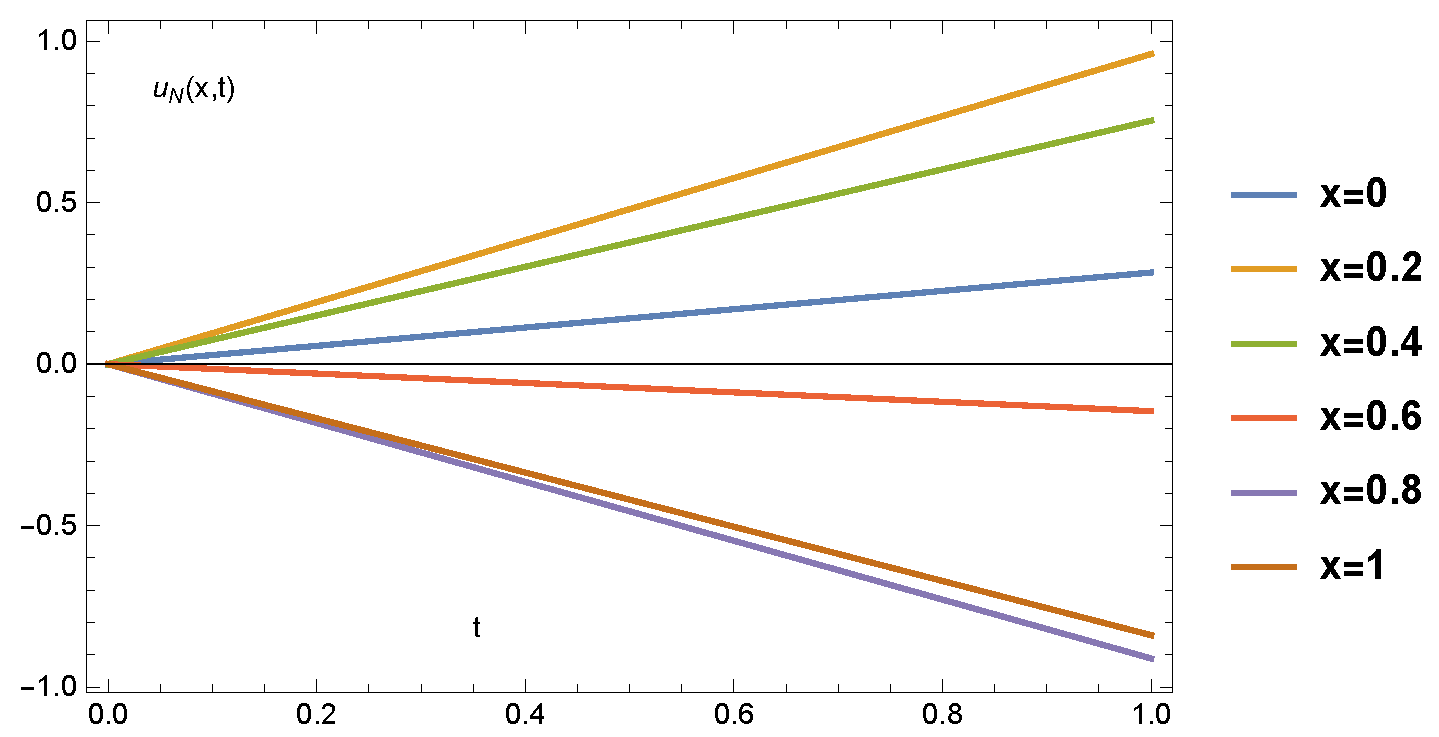
- Figure 2 presents the numerical solution of Example 1 for various temporal values. From the results in this figure, we can see the infinitesimal change of the solution wave as time goes on for fixed values of x.
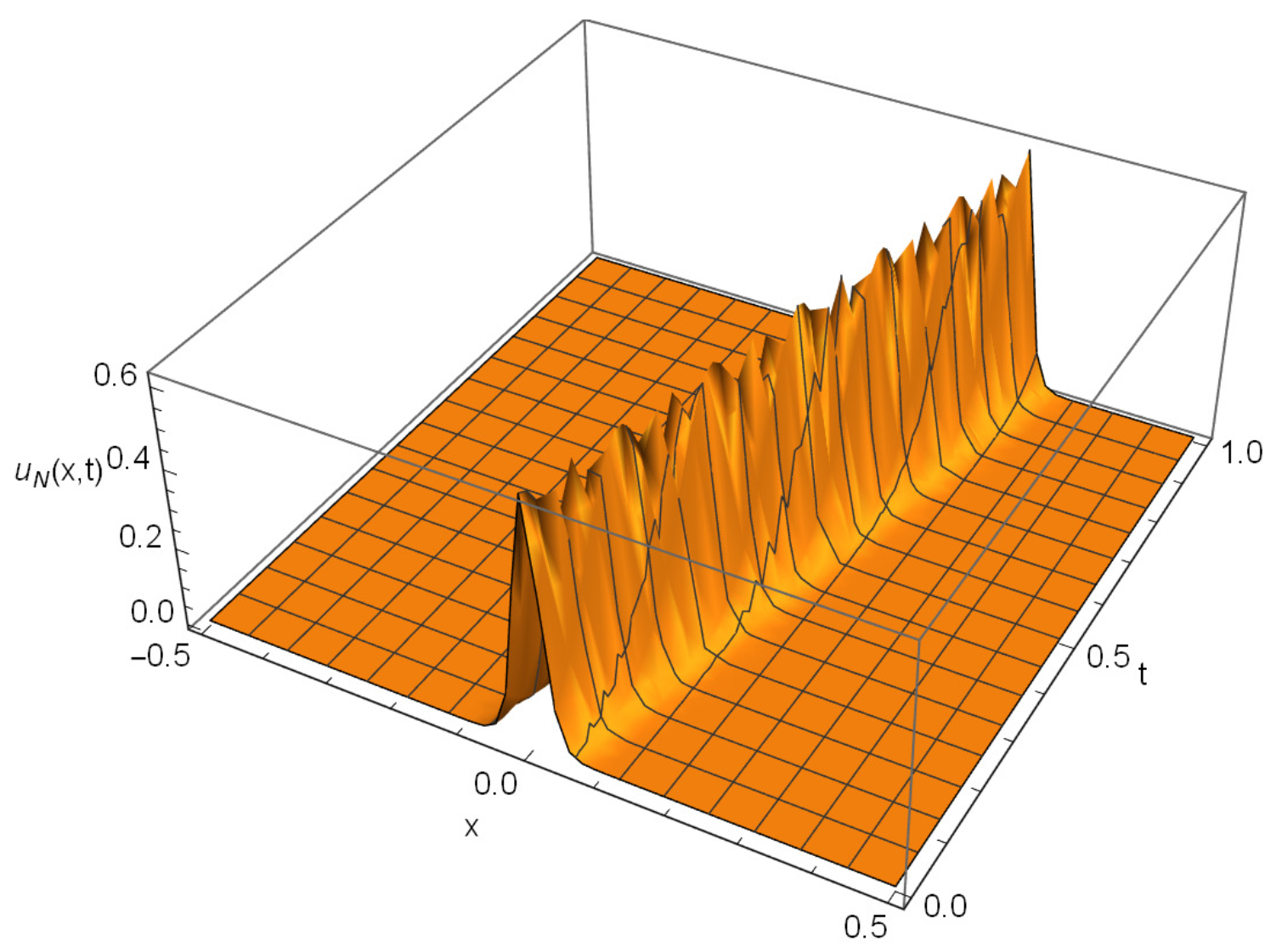
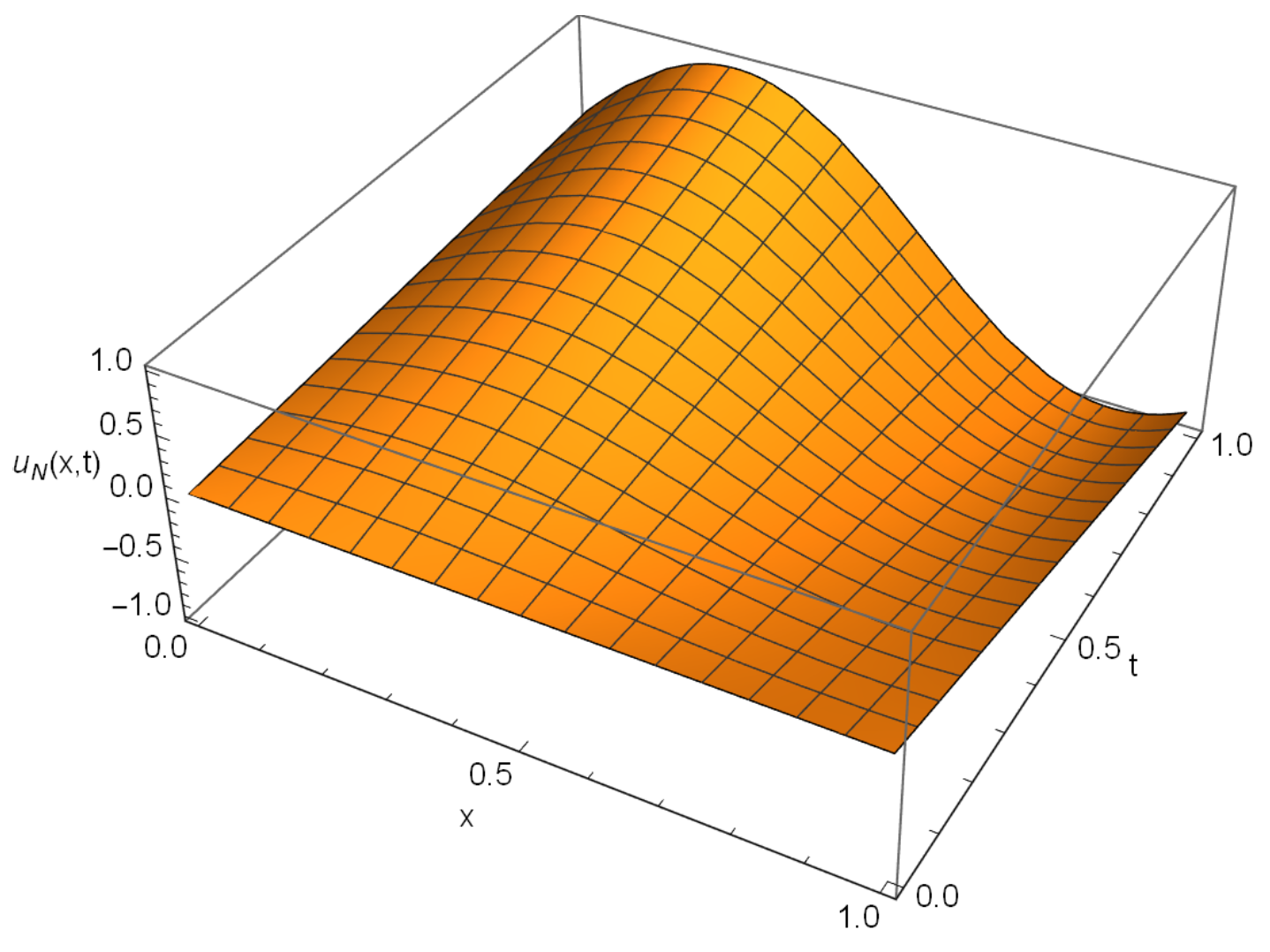
- Figure 3 presents the numerical solution of Example 1 at any point . From the results in this figure, we see the whole solution when both temporal and space variable changes, and this wave coincides with the two previous figures.
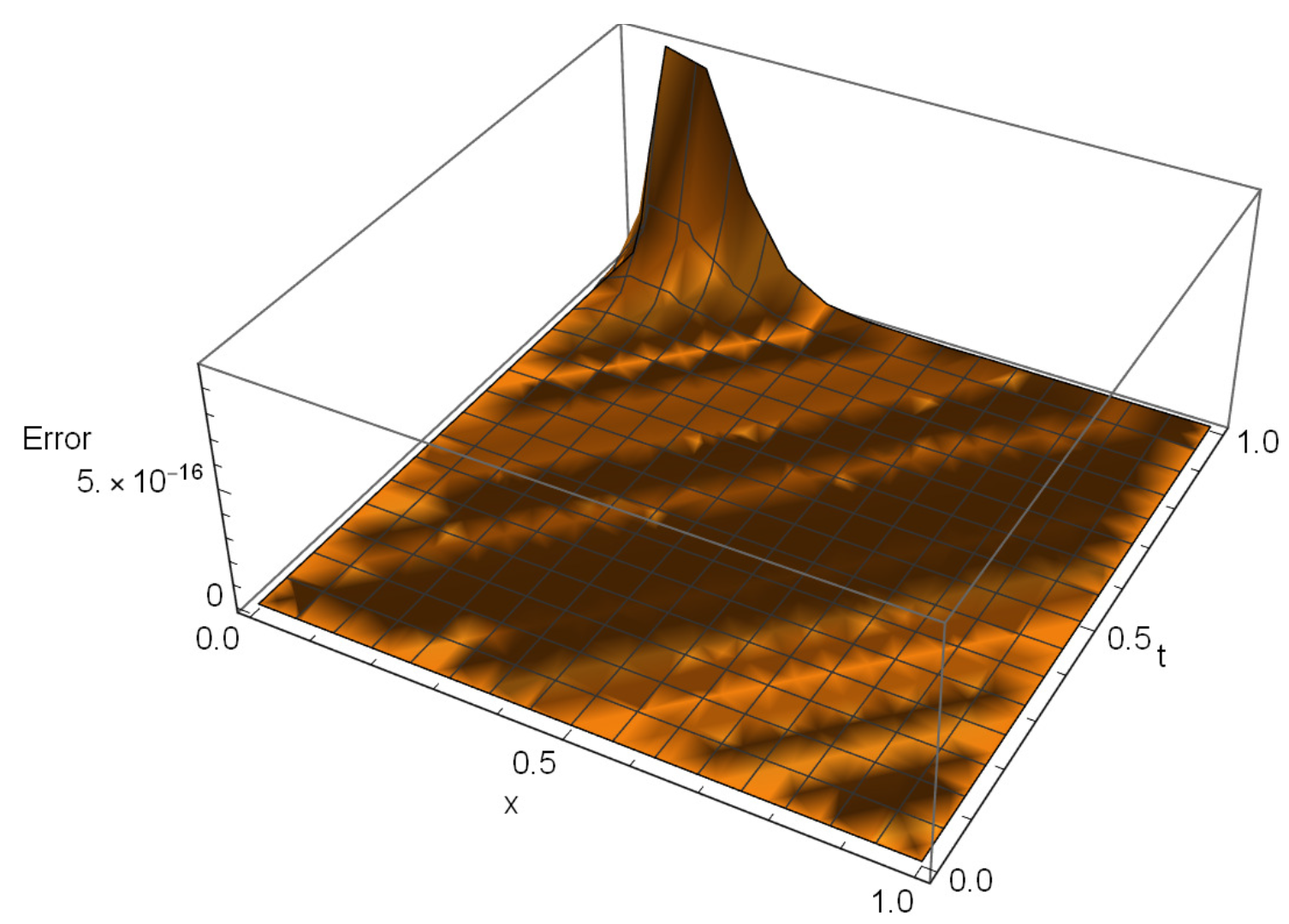
- Figure 4 presents the absolute error of Example 1 at any point . From the results in this figure, we ascertain the exponential convergence of the method as the error is of order .
- Figure 6 presents the numerical solution of Example 3 for various spatial values. From the results in this figure, we can track the spatial change of the solution at a fixed instant.
- Figure 7 presents the numerical solution of Example 3 for various temporal values. From the results in this figure, we can track the temporal change of the solution at a fixed x.
- Figure 8 presents the numerical solution of Example 3 at any point . From the results in this figure we can see the whole solution at any point in the plane.
- Figure 9 presents the absolute error of Example 3 at any point . From the results in this figure, we can clearly verify the accuracy of the method.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods; Springer Science & Business Media: New York, NY, USA, 2013; Volume 22. [Google Scholar]
- Smith, G. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Hesthaven, J.S.; Gottlieb, S.; Gottlieb, D. Spectral Methods for Time-Dependent Problems; Cambridge University Press: Cambridge, MA, USA, 2007; Volume 21. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Abd-Elhameed, W.M. Novel expressions for the derivatives of sixth-kind Chebyshev polynomials: Spectral solution of the non-linear one-dimensional Burgers’ equation. Fractal Fract. 2021, 5, 53. [Google Scholar] [CrossRef]
- Singh, H. Jacobi collocation method for the fractional advection-dispersion equation arising in porous media. Numer. Methods Part. Differ. Equ. 2022, 38, 636–653. [Google Scholar] [CrossRef]
- Khader, M.; Saad, K.; Hammouch, Z.; Baleanu, D. A spectral collocation method for solving fractional KdV and KdV-Burgers equations with non-singular kernel derivatives. Appl. Numer. Math. 2021, 161, 137–146. [Google Scholar] [CrossRef]
- Atta, A.G.; Youssri, Y.H. Advanced shifted first-kind Chebyshev collocation approach for solving the nonlinear time-fractional partial integro-differential equation with a weakly singular kernel. Comput. Appl. Math. 2022, 41, 381. [Google Scholar] [CrossRef]
- Canıvar, A.; Sari, M.; Dag, I. A Taylor–Galerkin finite element method for the KdV equation using cubic B-splines. Phys. B Cond. Matter 2010, 405, 3376–3383. [Google Scholar] [CrossRef]
- Shen, J. A new dual-Petrov-Galerkin method for third and higher odd-order differential equations: Application to the KDV equation. SIAM J. Numer. Anal. 2003, 41, 1595–1619. [Google Scholar] [CrossRef]
- Turgut, A.K.; Karakoç, S.B.G.; Biswas, A. Application of Petrov-Galerkin finite element method to shallow water waves model: Modi ed Korteweg-de Vries equation. Sci. Iran. B 2017, 24, 1148–1159. [Google Scholar]
- Noor, M.A.; Noor, K.I.; Waheed, A.; Al-Said, E.A. Some new solitonary solutions of the modified Benjamin–Bona–Mahony equation. Comput. Math. Appl. 2011, 62, 2126–2131. [Google Scholar] [CrossRef] [Green Version]
- Yokus, A.; Sulaiman, T.A.; Bulut, H. On the analytical and numerical solutions of the Benjamin–Bona–Mahony equation. Opt. Quantum Electron. 2018, 50, 31. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G.D. Solitary and periodic wave solutions of the generalized fourth-order Boussinesq equation via He’s variational methods. Math. Methods Appl. Sci. 2021, 44, 5617–5625. [Google Scholar] [CrossRef]
- Kawahara, T. Oscillatory solitary waves in dispersive media. J. Phys. Soc. Jpn. 1972, 33, 260–264. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dağ, I. Crank-Nicolson–differential quadrature algorithms for the Kawahara equation. Chaos Solitons Fractals 2009, 42, 65–73. [Google Scholar] [CrossRef]
- Haq, S.; Uddin, M. RBFs approximation method for Kawahara equation. Eng. Anal. Bound. Elem. 2011, 35, 575–580. [Google Scholar] [CrossRef]
- Yuan, J.; Shen, J.; Wu, J. A dual-Petrov-Galerkin method for the Kawahara-type equations. J. Sci. Comput. 2008, 34, 48–63. [Google Scholar] [CrossRef] [Green Version]
- Kaya, D. An explicit and numerical solutions of some fifth-order KdV equation by decomposition method. Appl. Math. Comput. 2003, 144, 353–363. [Google Scholar] [CrossRef]
- Yusufoğlu, E.; Bekir, A. Symbolic computation and new families of exact travelling solutions for the Kawahara and modified Kawahara equations. Comput. Math. Appl. 2008, 55, 1113–1121. [Google Scholar] [CrossRef] [Green Version]
- Jin, L. Application of variational iteration method and homotopy perturbation method to the modified Kawahara equation. Math. Comput. Model. 2009, 49, 573–578. [Google Scholar] [CrossRef]
- Yusufoğlu, E.; Bekir, A.; Alp, M. Periodic and solitary wave solutions of Kawahara and modified Kawahara equations by using Sine–Cosine method. Chaos Solitons Fractals 2008, 37, 1193–1197. [Google Scholar] [CrossRef]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials; Chapman and Hall: New York, NY, USA; CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover: New York, NY, USA, 2000. [Google Scholar]
- Öztürk, Y. Numerical solution of systems of differential equations using operational matrix method with Chebyshev polynomials. J. Taibah Univ. Sci. 2018, 12, 155–162. [Google Scholar] [CrossRef]
- Heydari, M.H.; Atangana, A.; Avazzadeh, Z. Chebyshev polynomials for the numerical solution of fractal–fractional model of nonlinear Ginzburg–Landau equation. Eng. Comput. 2021, 37, 1377–1388. [Google Scholar] [CrossRef]
- Öztürk, Y.; Gülsu, M. An operational matrix method to solve linear Fredholm–Volterra integro-differential equations with piecewise intervals. Math. Sci. 2021, 15, 189–197. [Google Scholar] [CrossRef]
- Öztürk, Y. An efficient numerical algorithm for solving system of Lane–Emden type equations arising in engineering. Nonlinear Eng. 2019, 8, 429–437. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Alaa-Eldeen, T.; Baleanu, D.; Alshehri, M.G.; El-Kady, M. Approximating real-life BVPs via Chebyshev polynomials’ first derivative pseudo-Galerkin method. Fractal Frac. 2021, 5, 165. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Ahmed, H.M. Tau and Galerkin operational matrices of derivatives for treating singular and Emden–Fowler third-order-type equations. Int. J. Mod. Phys. 2022, 33, 2250061. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Abd-Elhameed, W.M.; Ahmed, H.M. New fractional derivative expression of the shifted third-kind Chebyshev polynomials: Application to a type of nonlinear fractional pantograph differential equations. J. Funct. Spaces 2022, 2022, 3966135. [Google Scholar] [CrossRef]
- Duangpan, A.; Boonklurb, R.; Juytai, M. Numerical solutions for systems of fractional and classical integro-differential equations via finite integration method based on shifted Chebyshev polynomials. Fractal Frac. 2021, 5, 103. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Malikan, M. Application of shifted Chebyshev polynomial-based Rayleigh–Ritz method and Navier’s technique for vibration analysis of a functionally graded porous beam embedded in Kerr foundation. Eng. Comput. 2021, 37, 3569–3589. [Google Scholar] [CrossRef]
- Öztürk, Y.; Gülsu, M. An operational matrix method for solving Lane–Emden equations arising in astrophysics. Math. Methods Appl. Sci. 2014, 37, 2227–2235. [Google Scholar] [CrossRef]
- Öztürk, Y.; Demir, A.İ. A spectral collocation matrix method for solving linear Fredholm integro-differential–difference equations. Comput. Appl. Math. 2021, 40, 218. [Google Scholar] [CrossRef]
- Draux, A.; Sadik, M.; Moalla, B. Markov–Bernstein inequalities for generalized Gegenbauer weight. Appl. Numer. Math. 2011, 61, 1301–1321. [Google Scholar] [CrossRef]
- Xu, Y. An integral formula for generalized Gegenbauer polynomials and Jacobi polynomials. Adv. Appl. Math. 2002, 29, 328–343. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alkhamisi, S.O. New results of the fifth-kind orthogonal Chebyshev polynomials. Symmetry 2021, 13, 2407. [Google Scholar] [CrossRef]
- Atta, A.G.; Abd-Elhameed, W.M.; Moatimid, G.M.; Youssri, Y.H. Modal shifted fifth-kind Chebyshev tau integral approach for solving heat conduction equation. Fractal Frac. 2022, 6, 619. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. Fifth-kind orthonormal Chebyshev polynomial solutions for fractional differential equations. Comput. Appl. Math. 2018, 37, 2897–2921. [Google Scholar] [CrossRef]
- Masjed-Jamei, M. Some New Classes of Orthogonal Polynomials and Special Functions: A Symmetric Generalization of Sturm-Liouville Problems and Its Consequences. Ph.D. Thesis, Department of Mathematics, University of Kassel, Kassel, Germany, 2006. [Google Scholar]
- Abd-Elhameed, W.M.; Youssri, Y.H. New formulas of the high-order derivatives of fifth-kind Chebyshev polynomials: Spectral solution of the convection–diffusion equation. In Numerical Methods for Partial Differential Equations; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Koepf, W. Hypergeometric Summation, 2nd ed.; Springer Universitext Series; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Bagherzadeh, A.S. B-spline collocation method for numerical solution of nonlinear Kawahara and modified Kawahara equations. TWMS J. App. Eng. Math. 2017, 7, 188–199. [Google Scholar]
- Goswami, A.; Singh, J.; Kumar, D. Numerical simulation of fifth order KdV equations occurring in magneto-acoustic waves. Ain Shams Eng. J. 2018, 9, 2265–2273. [Google Scholar] [CrossRef]




| t | Method in [18] | Present Method |
|---|---|---|
| 0.5 | ||
| 1 |
| t | Method in [44] | Present Method |
|---|---|---|
| 5 | ||
| 15 | ||
| 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-Elhameed, W.M.; Alkhamisi, S.O.; Amin, A.K.; Youssri, Y.H. Numerical Contrivance for Kawahara-Type Differential Equations Based on Fifth-Kind Chebyshev Polynomials. Symmetry 2023, 15, 138. https://doi.org/10.3390/sym15010138
Abd-Elhameed WM, Alkhamisi SO, Amin AK, Youssri YH. Numerical Contrivance for Kawahara-Type Differential Equations Based on Fifth-Kind Chebyshev Polynomials. Symmetry. 2023; 15(1):138. https://doi.org/10.3390/sym15010138
Chicago/Turabian StyleAbd-Elhameed, Waleed Mohamed, Seraj Omar Alkhamisi, Amr Kamel Amin, and Youssri Hassan Youssri. 2023. "Numerical Contrivance for Kawahara-Type Differential Equations Based on Fifth-Kind Chebyshev Polynomials" Symmetry 15, no. 1: 138. https://doi.org/10.3390/sym15010138
APA StyleAbd-Elhameed, W. M., Alkhamisi, S. O., Amin, A. K., & Youssri, Y. H. (2023). Numerical Contrivance for Kawahara-Type Differential Equations Based on Fifth-Kind Chebyshev Polynomials. Symmetry, 15(1), 138. https://doi.org/10.3390/sym15010138






