Nanoscale Bending Dynamics in Mixed-Chain Lipid Membranes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Vesicle Preparation
2.3. Small Angle Neutron Scattering (SANS)
2.4. Dynamic Light Scattering (DLS)
2.5. Neutron Spin Echo Spectroscopy (NSE)
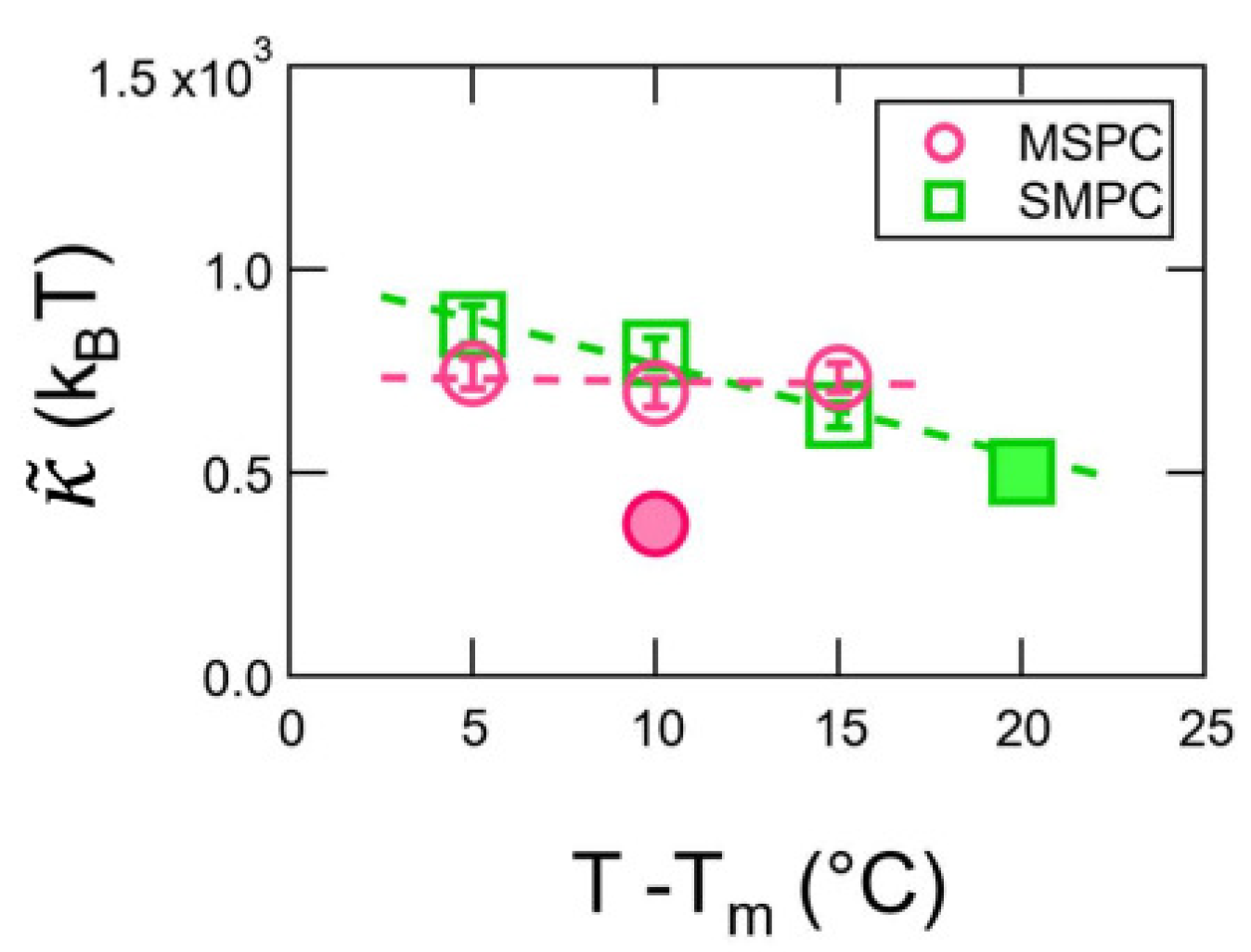
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DLS | Dynamic Light Scattering |
| DMPC | 1,2-dimyrisotoyl-sn-glycerco-3-phosphocholine (di 14:0 PC) |
| DOPC | 1,2-dioleoyl-sn-glycero-3-phosphocholine (di 18:1 PC) |
| DPPC | 1,2-dipalmitoyl-sn-glycerco-3-phosphocholine (di 16:0 PC) |
| DSPC | 1,2-distearoyl-sn-glycerco-3-phosphocholine (di 18:0 PC) |
| MSPC | 1-myrisotyl-2-stearoyl-sn-glycerol-3-phosphocholine (14:0-18:0 PC) |
| NSE | Neutron Spin Echo Spectroscopy |
| SANS | Small Angle Neutron Scattering |
| SAXS | Small Angle X-ray Scattering |
| SMPC | 1-stearoyl-2-myristoyl-sn-glycero-3-phosphocholine (18:0-14:0 PC) |
References
- Kučerka, N.; Nieh, M.P.; Katsaras, J. Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature. Biochim. Biophys. Acta (BBA)-Biomembr. 2011, 1808, 2761–2771. [Google Scholar] [CrossRef] [PubMed]
- Kučerka, N.; Heberle, F.A.; Pan, J.; Katsaras, J. Structural significance of lipid diversity as studied by small angle neutron and X-ray scattering. Membranes 2015, 5, 454–472. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rawicz, W.; Olbrich, K.C.; McIntosh, T.; Needham, D.; Evans, E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000, 79, 328–339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woodka, A.C.; Butler, P.D.; Porcar, L.; Farago, B.; Nagao, M. Lipid bilayers and membrane dynamics: Insight into thickness fluctuations. Phys. Rev. Lett. 2012, 109, 058102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagao, M.; Kelley, E.G.; Ashkar, R.; Bradbury, R.; Butler, P.D. Probing elastic and viscous properties of phospholipid bilayers using neutron spin echo spectroscopy. J. Phys. Chem. Lett. 2017, 8, 4679–4684. [Google Scholar] [CrossRef] [PubMed]
- Faizi, H.A.; Dimova, R.; Vlahovska, P.M. A vesicle microrheometer for high-throughput viscosity measurements of lipid and polymer membranes. Biophys. J. 2022, 121, 910–918. [Google Scholar] [CrossRef]
- Nagle, J.F.; Tristram-Nagle, S. Structure of lipid bilayers. Biochim. Biophys. Acta (BBA)-Rev. Biomembr. 2000, 1469, 159–195. [Google Scholar] [CrossRef] [Green Version]
- Lorent, J.; Levental, K.; Ganesan, L.; Rivera-Longsworth, G.; Sezgin, E.; Doktorova, M.; Lyman, E.; Levental, I. Plasma membranes are asymmetric in lipid unsaturation, packing and protein shape. Nat. Chem. Biol. 2020, 16, 644–652. [Google Scholar] [CrossRef]
- Goñi, F.M.; Alonso, A. Biophysics of sphingolipids I. Membrane properties of sphingosine, ceramides and other simple sphingolipids. Biochim. Biophys. Acta (BBA)-Biomembr. 2006, 1758, 1902–1921. [Google Scholar] [CrossRef] [Green Version]
- Jimenez-Rojo, N.; Garcia-Arribas, A.B.; Sot, J.; Alonso, A.; Goni, F.M. Lipid bilayers containing sphingomyelins and ceramides of varying N-acyl lengths: A glimpse into sphingolipid complexity. Biochim. Biophys. Acta (BBA)-Biomembr. 2014, 1838, 456–464. [Google Scholar] [CrossRef]
- Fujimoto, T.; Parmryd, I. Interleaflet coupling, pinning, and leaflet asymmetry—Major players in plasma membrane nanodomain formation. Front. Cell Dev. Biol. 2017, 4, 155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makarova, M.; Peter, M.; Balogh, G.; Glatz, A.; MacRae, J.I.; Mora, N.L.; Booth, P.; Makeyev, E.; Vigh, L.; Oliferenko, S. Delineating the rules for structural adaptation of membrane-associated proteins to evolutionary changes in membrane lipidome. Curr. Biol. 2020, 30, 367–380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reinhard, J.; Mattes, C.; Väth, K.; Radanović, T.; Surma, M.A.; Klose, C.; Ernst, R. A quantitative analysis of cellular lipid compositions during acute proteotoxic ER stress reveals specificity in the production of asymmetric lipids. Front. Cell Dev. Biol. 2020, 8, 756. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Mason, J.; Levin, I. Raman spectroscopic study of saturated mixed-chain phosphatidylcholine multilamellar dispersions. Biochemistry 1983, 22, 2775–2780. [Google Scholar] [CrossRef]
- McIntosh, T.; Simon, S.; Ellington Jr, J.; Porter, N. New structural model for mixed-chain phosphatidylcholine bilayers. Biochemistry 1984, 23, 4038–4044. [Google Scholar] [CrossRef]
- Hui, S.; Mason, J.; Huang, C. Acyl chain interdigitation in saturated mixed-chain phosphatidylcholine bilayer dispersions. Biochemistry 1984, 23, 5570–5577. [Google Scholar] [CrossRef] [PubMed]
- Halladay, H.N.; Stark, R.E.; Ali, S.; Bittman, R. Magic-angle spinning NMR studies of molecular organization in multibilayers formed by 1-octadecanoyl-2-decanoyl-sn-glycero-3-phosphocholine. Biophys. J. 1990, 58, 1449–1461. [Google Scholar] [CrossRef] [Green Version]
- Zhu, T.; Caffrey, M. Thermodynamic, thermomechanical, and structural properties of a hydrated asymmetric phosphatidylcholine. Biophys. J. 1993, 65, 939–954. [Google Scholar] [CrossRef] [Green Version]
- Frewein, M.P.; Doktorova, M.; Heberle, F.A.; Scott, H.L.; Semeraro, E.F.; Porcar, L.; Pabst, G. Structure and interdigitation of chain-asymmetric phosphatidylcholines and milk sphingomyelin in the fluid phase. Symmetry 2021, 13, 1441. [Google Scholar] [CrossRef]
- Lewis, R.; McElhaney, R.N.; Monck, M.A.; Cullis, P.R. Studies of highly asymmetric mixed-chain diacyl phosphatidylcholines that form mixed-interdigitated gel phases: Fourier transform infrared and 2H NMR spectroscopic studies of hydrocarbon chain conformation and orientational order in the liquid-crystalline state. Biophys. J. 1994, 67, 197–207. [Google Scholar]
- Mason, J.T. Properties of phosphatidylcholine bilayers as revealed by mixed-acyl phospholipid fluorescent probes containing n-(9-anthroyloxy) fatty acids. Biochim. Biophys. Acta (BBA)-Biomembr. 1994, 1194, 99–108. [Google Scholar] [CrossRef]
- Schram, V.; Thompson, T.E. Interdigitation does not affect translational diffusion of lipids in liquid crystalline bilayers. Biophys. J. 1995, 69, 2517–2520. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali, S.; Smaby, J.M.; Momsen, M.M.; Brockman, H.L.; Brown, R.E. Acyl chain-length asymmetry alters the interfacial elastic interactions of phosphatidylcholines. Biophys. J. 1998, 74, 338–348. [Google Scholar] [CrossRef] [Green Version]
- Illya, G.; Lipowsky, R.; Shillcock, J. Effect of chain length and asymmetry on material properties of bilayer membranes. J. Chem. Phys. 2005, 122, 244901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dan, N. Lipid tail chain asymmetry and the strength of membrane-induced interactions between membrane proteins. Biochim. Biophys. Acta (BBA)-Biomembr. 2007, 1768, 2393–2399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- den Otter, W.K.; Shkulipa, S. Intermonolayer friction and surface shear viscosity of lipid bilayer membranes. Biophys. J. 2007, 93, 423–433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seifert, U.; Langer, S.A. Viscous modes of fluid bilayer membranes. EPL (Europhys. Lett.) 1993, 23, 71. [Google Scholar] [CrossRef] [Green Version]
- Shkulipa, S.; den Otter, W.K.; Briels, W.J. Thermal undulations of lipid bilayers relax by intermonolayer friction at submicrometer length scales. Phys. Rev. Lett. 2006, 96, 178302. [Google Scholar] [CrossRef] [Green Version]
- Anthony, A.A.; Sahin, O.; Yapici, M.K.; Rogers, D.; Honerkamp-Smith, A.R. Systematic measurements of interleaflet friction in supported bilayers. Biophys. J. 2022, 121, 2981–2993. [Google Scholar] [CrossRef]
- Kelley, E.G.; Blick, E.E.; Prabhu, V.M.; Butler, P.D.; Nagao, M. Interactions, Diffusion, and Membrane Fluctuations in Concentrated Unilamellar Lipid Vesicle Solutions. Front. Phys. 2022, 10, 866024. [Google Scholar] [CrossRef]
- Scott, H.L.; Skinkle, A.; Kelley, E.G.; Waxham, M.N.; Levental, I.; Heberle, F.A. On the Mechanism of Bilayer Separation by Extrusion, or Why Your LUVs Are Not Really Unilamellar. Biophys. J. 2019, 117, 1381–1386. [Google Scholar] [CrossRef] [PubMed]
- Barker, J.; Moyer, J.; Kline, S.; Jensen, G.; Cook, J.; Gagnon, C.; Kelley, E.; Chabot, J.P.; Maliszewskyj, N.; Parikh, C.; et al. The very small angle neutron scattering instrument at the National Institute of Standards and Technology. J. Appl. Crystallogr. 2022, 55, 271–283. [Google Scholar] [CrossRef] [PubMed]
- Kline, S.R. Reduction and analysis of SANS and USANS data using IGOR Pro. J. Appl. Crystallogr. 2006, 39, 895–900. [Google Scholar] [CrossRef]
- Rosov, N.; Rathgeber, S.; Monkenbusch, M. Neutron Spin Echo Spectroscopy at the NIST Center for Neutron Research. ACS Symp. Ser. 1999, 739, 103–116. [Google Scholar]
- Azuah, R.T.; Kneller, L.R.; Qiu, Y.; Tregenna-Piggott, P.L.; Brown, C.M.; Copley, J.R.; Dimeo, R.M. DAVE: A comprehensive software suite for the reduction, visualization, and analysis of low energy neutron spectroscopic data. J. Res. Natl. Inst. Stand. Technol. 2009, 114, 341. [Google Scholar] [CrossRef]
- Schleger, P.; Alefeld, B.; Barthelemy, J.; Ehlers, G.; Farago, B.; Giraud, P.; Hayes, C.; Kollmar, A.; Lartigue, C.; Mezei, F.; et al. The long-wavelength neutron spin-echo spectrometer IN15 at the Institut Laue-Langevin. Phys. B Condens. Matter 1997, 241, 164–165. [Google Scholar] [CrossRef]
- Kelley, E.G.; Butler, P.D.; Nagao, M. 4. Collective dynamics in model biological membranes measured by neutron spin echo spectroscopy. In Characterization of Biological Membranes; de Gruyter: Berlin, Germany, 2019; pp. 131–176. [Google Scholar]
- Gupta, S.; De Mel, J.U.; Schneider, G.J. Dynamics of liposomes in the fluid phase. Curr. Opin. Colloid Interface Sci. 2019, 42, 121–136. [Google Scholar] [CrossRef]
- Kinnun, J.J.; Scott, H.L.; Ashkar, R.; Katsaras, J. Biomembrane Structure and Material Properties Studied With Neutron Scattering. Front. Chem. 2021, 9, 203. [Google Scholar] [CrossRef]
- Gupta, S.; Ashkar, R. The dynamic face of lipid membranes. Soft Matter 2021, 17, 6910–6928. [Google Scholar] [CrossRef]
- Zilman, A.; Granek, R. Undulations and dynamic structure factor of membranes. Phys. Rev. Lett. 1996, 77, 4788. [Google Scholar] [CrossRef]
- Watson, M.C.; Peng, Y.; Zheng, Y.; Brown, F.L. The intermediate scattering function for lipid bilayer membranes: From nanometers to microns. J. Chem. Phys. 2011, 135, 194701. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, I. Data Analysis and Background Subtraction in Neutron Spin Echo Spectroscopy. Front. Phys. 2021, 8, 602. [Google Scholar] [CrossRef]
- Liu, Y. Intermediate scattering function for macromolecules in solutions probed by neutron spin echo. Phys. Rev. E 2017, 95, 020501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zilman, A.G.; Granek, R. Membrane dynamics and structure factor. Chem. Phys. 2002, 284, 195–204. [Google Scholar] [CrossRef]
- Gapinski, J.; Wilk, A.; Patkowski, A.; Häussler, W.; Banchio, A.; Pecora, R.; Nägele, G. Diffusion and microstructural properties of solutions of charged nanosized proteins: Experiment versus theory. J. Chem. Phys. 2005, 123, 054708. [Google Scholar] [CrossRef] [Green Version]
- Banchio, A.J.; Nägele, G. Short-time transport properties in dense suspensions: From neutral to charge-stabilized colloidal spheres. J. Chem. Phys. 2008, 128, 104903. [Google Scholar] [CrossRef] [Green Version]
- Watson, M.C.; Brown, F.L. Interpreting membrane scattering experiments at the mesoscale: The contribution of dissipation within the bilayer. Biophys. J. 2010, 98, L9–L11. [Google Scholar] [CrossRef] [Green Version]
- Nagle, J.F. Measuring the bending modulus of lipid bilayers with cholesterol. Phys. Rev. E 2021, 104, 044405. [Google Scholar] [CrossRef]
- Gupta, S.; De Mel, J.U.; Perera, R.M.; Zolnierczuk, P.; Bleuel, M.; Faraone, A.; Schneider, G.J. Dynamics of Phospholipid Membranes beyond Thermal Undulations. J. Phys. Chem. Lett. 2018, 9, 2956–2960. [Google Scholar] [CrossRef]
- Rickeard, B.W.; Nguyen, M.H.; DiPasquale, M.; Yip, C.G.; Baker, H.; Heberle, F.A.; Zuo, X.; Kelley, E.G.; Nagao, M.; Marquardt, D. Transverse lipid organization dictates bending fluctuations in model plasma membranes. Nanoscale 2020, 12, 1438–1447. [Google Scholar] [CrossRef]
- Winterhalter, M.; Helfrich, W. Effect of surface charge on the curvature elasticity of membranes. J. Phys. Chem. 1988, 92, 6865–6867. [Google Scholar] [CrossRef]
- Winterhalter, M.; Helfrich, W. Bending elasticity of electrically charged bilayers: Coupled monolayers, neutral surfaces, and balancing stresses. J. Phys. Chem. 1992, 96, 327–330. [Google Scholar] [CrossRef]
- Dimova, R. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 2014, 208, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Monkenbusch, M.; Holderer, O.; Frielinghaus, H.; Byelov, D.; Allgaier, J.; Richter, D. Bending moduli of microemulsions; comparison of results from small angle neutron scattering and neutron spin-echo spectroscopy. J. Phys. Condens. Matter 2005, 17, S2903. [Google Scholar] [CrossRef]
- Meyer, F.; Bloch, K. Metabolism of stearolic acid in yeast. J. Biol. Chem. 1963, 238, 2654–2659. [Google Scholar] [CrossRef]
- Ballweg, S.; Ernst, R. Control of membrane fluidity: The OLE pathway in focus. Biol. Chem. 2017, 398, 215–228. [Google Scholar] [CrossRef]
- Budin, I.; de Rond, T.; Chen, Y.; Chan, L.J.G.; Petzold, C.J.; Keasling, J.D. Viscous control of cellular respiration by membrane lipid composition. Science 2018, 362, 1186–1189. [Google Scholar] [CrossRef] [Green Version]
- Koynova, R.; Caffrey, M. Phases and phase transitions of the phosphatidylcholines. Biochim. Biophys. Acta (BBA)-Rev. Biomembr. 1998, 1376, 91–145. [Google Scholar] [CrossRef]
- Nanda, H.; Sakai, V.G.; Khodadadi, S.; Tyagi, M.S.; Schwalbach, E.J.; Curtis, J.E. Relaxation dynamics of saturated and unsaturated oriented lipid bilayers. Soft Matter 2018, 14, 6119–6127. [Google Scholar] [CrossRef] [Green Version]
- Marsh, D. Analysis of the bilayer phase transition temperatures of phosphatidylcholines with mixed chains. Biophys. J. 1992, 61, 1036–1040. [Google Scholar] [CrossRef] [Green Version]
- Helfrich, W. Steric interaction of fluid membranes in multilayer systems. Z. Naturforschung A 1978, 33, 305–315. [Google Scholar] [CrossRef]
- Arriaga, L.; Rodriguez-Garcia, R.; López-Montero, I.; Farago, B.; Hellweg, T.; Monroy, F. Dissipative curvature fluctuations in bilayer vesicles: Coexistence of pure-bending and hybrid curvature-compression modes. Eur. Phys. J. E 2010, 31, 105–113. [Google Scholar] [CrossRef] [PubMed]
- Mell, M.; Moleiro, L.H.; Hertle, Y.; López-Montero, I.; Cao, F.J.; Fouquet, P.; Hellweg, T.; Monroy, F. Fluctuation dynamics of bilayer vesicles with intermonolayer sliding: Experiment and theory. Chem. Phys. Lipids 2015, 185, 61–77. [Google Scholar] [CrossRef] [PubMed]
- Hirn, R.; Bayerl, T.M.; Rädler, J.O.; Sackmann, E. Collective membrane motions of high and low amplitude, studied by dynamic light scattering and micro-interferometry. Faraday Discuss. 1999, 111, 17–30. [Google Scholar] [CrossRef] [PubMed]
- Monzel, C.; Schmidt, D.; Kleusch, C.; Kirchenbüchler, D.; Seifert, U.; Smith, A.; Sengupta, K.; Merkel, R. Measuring fast stochastic displacements of bio-membranes with dynamic optical displacement spectroscopy. Nat. Commun. 2015, 6, 8162. [Google Scholar] [CrossRef] [Green Version]
- Falus, P.; Borthwick, M.; Mochrie, S. Fluctuation dynamics of block copolymer vesicles. Phys. Rev. Lett. 2005, 94, 016105. [Google Scholar] [CrossRef]
- Gupta, S.; Schneider, G.J. Modeling the dynamics of phospholipids in the fluid phase of liposomes. Soft Matter 2020, 16, 3245–3256. [Google Scholar] [CrossRef] [Green Version]
- Granek, R. Comment on “Dynamics of Phospholipid Membranes beyond Thermal Undulations”. J. Phys. Chem. B 2019, 123, 5665–5666. [Google Scholar] [CrossRef] [Green Version]
- Nagle, J.F. Introductory lecture: Basic quantities in model biomembranes. Faraday Discuss. 2013, 161, 11–29. [Google Scholar] [CrossRef] [Green Version]
- Doktorova, M.; Harries, D.; Khelashvili, G. Determination of bending rigidity and tilt modulus of lipid membranes from real-space fluctuation analysis of molecular dynamics simulations. Phys. Chem. Chem. Phys. 2017, 19, 16806–16818. [Google Scholar] [CrossRef]
- Kelley, E.G.; Butler, P.D.; Ashkar, R.; Bradbury, R.; Nagao, M. Scaling relationships for the elastic moduli and viscosity of mixed lipid membranes. Proc. Natl. Acad. Sci. USA 2020, 117, 23365–23373. [Google Scholar] [CrossRef] [PubMed]
- Meleard, P.; Gerbeaud, C.; Pott, T.; Fernandez-Puente, L.; Bivas, I.; Mitov, M.D.; Dufourcq, J.; Bothorel, P. Bending elasticities of model membranes: Influences of temperature and sterol content. Biophys. J. 1997, 72, 2616–2629. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tristram-Nagle, S.; Kučerka, N.; Nagle, J.F. Temperature dependence of structure, bending rigidity, and bilayer interactions of dioleoylphosphatidylcholine bilayers. Biophys. J. 2008, 94, 117–124. [Google Scholar] [CrossRef] [PubMed]


| Sample | (C) | c (mg/mL) | (nm) | |
|---|---|---|---|---|
| MSPC | 40 | 20 | 54 | 0.089 |
| 50 | 39 | 0.15 | ||
| SMPC | 30 | 20 | 58 | 0.095 |
| 50 | 44 | 0.17 | ||
| DPPC | 41 | 50 | 36 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelley, E.G.; Frewein, M.P.K.; Czakkel, O.; Nagao, M. Nanoscale Bending Dynamics in Mixed-Chain Lipid Membranes. Symmetry 2023, 15, 191. https://doi.org/10.3390/sym15010191
Kelley EG, Frewein MPK, Czakkel O, Nagao M. Nanoscale Bending Dynamics in Mixed-Chain Lipid Membranes. Symmetry. 2023; 15(1):191. https://doi.org/10.3390/sym15010191
Chicago/Turabian StyleKelley, Elizabeth G., Moritz P. K. Frewein, Orsolya Czakkel, and Michihiro Nagao. 2023. "Nanoscale Bending Dynamics in Mixed-Chain Lipid Membranes" Symmetry 15, no. 1: 191. https://doi.org/10.3390/sym15010191
APA StyleKelley, E. G., Frewein, M. P. K., Czakkel, O., & Nagao, M. (2023). Nanoscale Bending Dynamics in Mixed-Chain Lipid Membranes. Symmetry, 15(1), 191. https://doi.org/10.3390/sym15010191





