Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations
Abstract
:1. Introduction
2. Preliminaries
- (i)
- (ii)
- (iii)
3. LRPSM Idea
- (i)
- and for each ;
- (ii)
- If , then
- (iii)
- for and
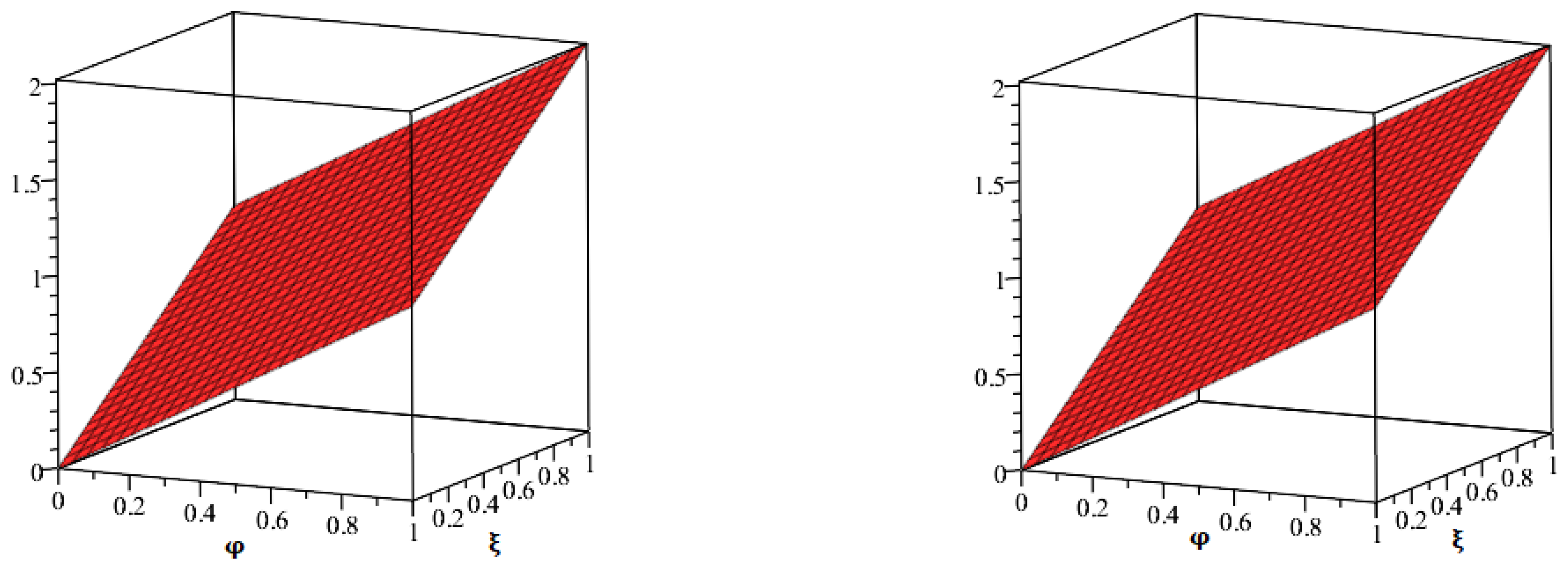
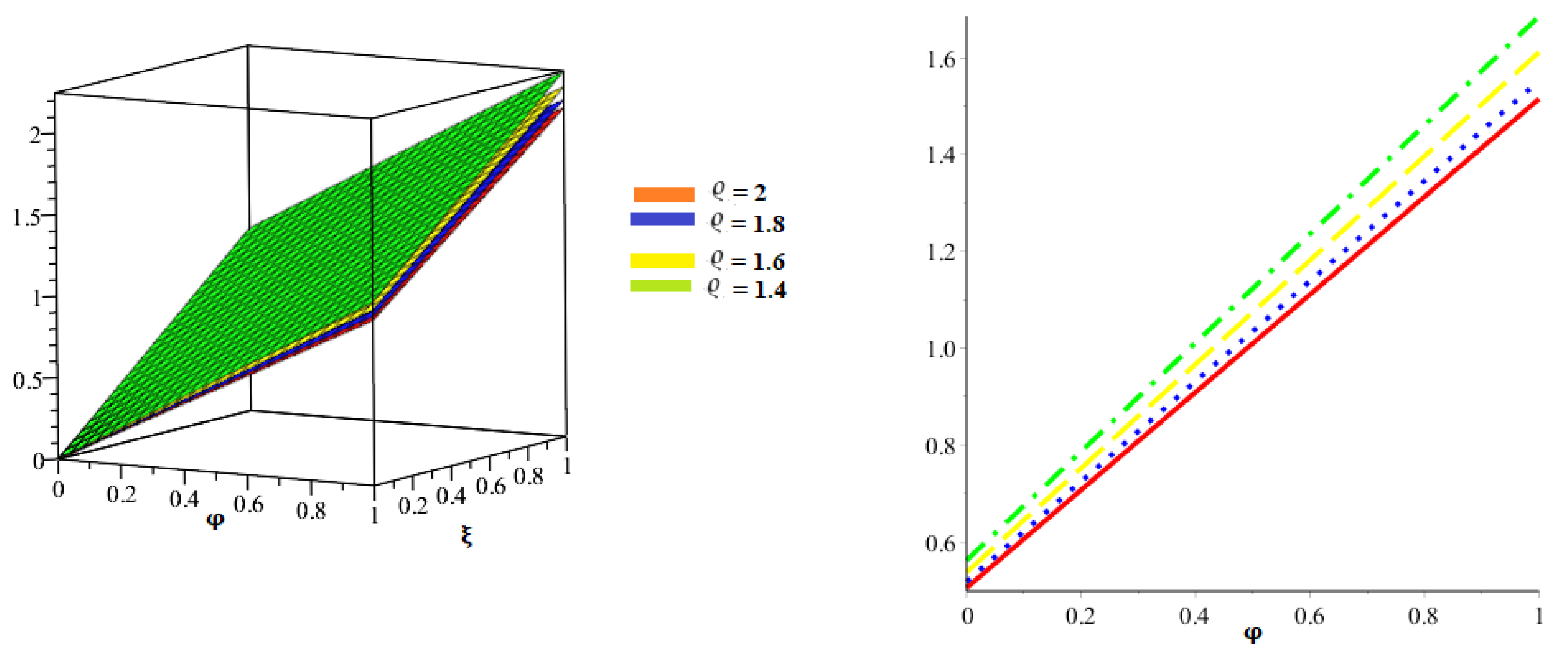
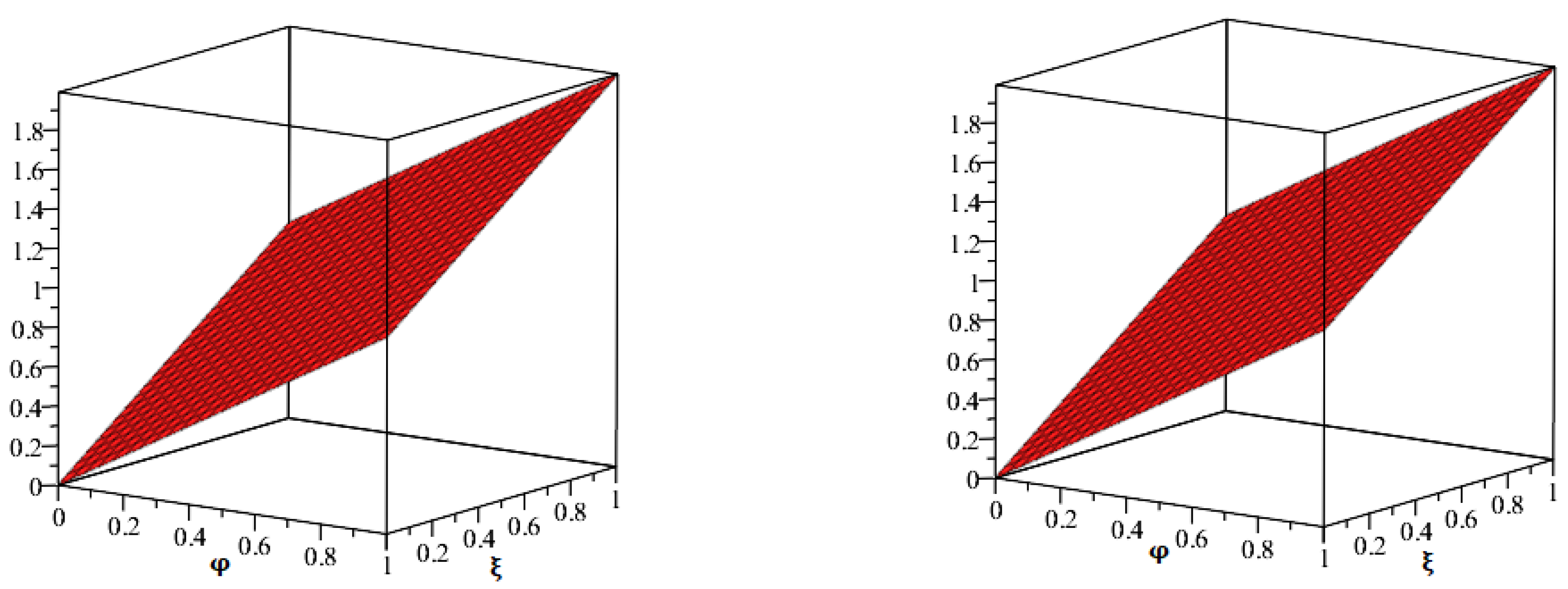
4. Numerical Problems
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Milici, C.; Draganescu, G.; Machado, J.T. Introduction to Fractional Differential Equations; Springer: Cham, Switzerland, 2018; Volume 25. [Google Scholar]
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 54, 3442. [Google Scholar] [CrossRef] [Green Version]
- Batiha, I.M.; Oudetallah, J.; Ouannas, A.; Al-Nana, A.A.; Jebril, I.H. Tuning the Fractional-order PID-Controller for Blood Glucose Level of Diabetic Patients. Int. J. Adv. Soft Comput. Appl. 2021, 13, 1–10. [Google Scholar]
- Atangana, A.; Secer, A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley-Interscience: New York, NY, USA, 1993. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Lu, S.; Guo, J.; Liu, S.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. An Improved Algorithm of Drift Compensation for Olfactory Sensors. Appl. Sci. 2022, 12, 9529. [Google Scholar] [CrossRef]
- Bai, Z.; Zhang, S.; Sun, S.; Yin, C. Monotone iterative method for fractional differential equations. Electron. J. Differ. Equ. 2016, 6, 1–8. [Google Scholar]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. Aims Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Garrappa, R. Trapezoidal methods for fractional differential equations: Theoretical and computational aspects. Math. Comput. Simul. 2015, 110, 96–112. [Google Scholar] [CrossRef] [Green Version]
- Demir, A.; Bayrak, M.A.; Ozbilge, E. A new approach for the approximate analytical solution of space-time fractional differential equations by the homotopy analysis method. Adv. Math. Phys. 2019, 2019, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Tian, X.; Yang, B.; Liu, S.; Ding, Y.; Tian, J.; Yin, L. A Few Shot Classification Methods Based on Multiscale Relational Networks. Appl. Sci. 2022, 12, 4059. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Shah, R.; Baleanu, D. An efficient analytical approach for the solution of certain fractional-order dynamical systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Akbulut, A.; Kaplan, M. Auxiliary equation method for time-fractional differential equations with conformable derivative. Comput. Math. Appl. 2018, 75, 876–882. [Google Scholar] [CrossRef]
- Ban, Y.; Liu, M.; Wu, P.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Depth Estimation Method for Monocular Camera Defocus Images in Microscopic Scenes. Electronics 2022, 11, 2012. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abdl-Rahim, H.R.; Ahmad, H.; Chu, Y.M. Fractional residual power series method for the analytical and approximate studies of fractional physical phenomena. Open Phys. 2020, 18, 799–805. [Google Scholar] [CrossRef]
- Chen, S.B.; Jahanshahi, H.; Abba, O.A.; Solis-Perez, J.E.; Bekiros, S.; Gomez-Aguilar, J.F.; Yousefpour, A.; Chu, Y.M. The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization. Chaos Solitons Fractals 2020, 140, 110223. [Google Scholar] [CrossRef]
- Zhou, J.C.; Salahshour, S.; Ahmadian, A.; Senu, N. Modeling the dynamics of COVID-19 using fractal-fractional operator with a case study. Results Phys. 2022, 33, 105103. [Google Scholar] [CrossRef]
- Hendy, M.H.; Amin, M.M.; Ezzat, M.A. Two-dimensional problem for thermoviscoelastic materials with fractional order heat transfer. J. Therm. Stress. 2019, 42, 1298–1315. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, Y. Variational Formulation Of The Stress-Strain Problem In Capillary-Porous Materials With Fractal Structure. In Proceedings of the 2020 IEEE 15th International Conference on Computer Sciences and Information Technologies (CSIT), Zbarazh, Ukraine, 23–26 September 2020; Volume 1, pp. 1–4. [Google Scholar]
- Hoan, L.V.C.; Korpinar, Z.; Inc, M.; Chu, Y.M.; Almohsen, B. On convergence analysis and numerical solutions of local fractional Helmholtz equation. Alex. Eng. J. 2020, 59, 4335–4341. [Google Scholar] [CrossRef]
- Abuasad, S.; Yildirim, A.; Hashim, I.; Karim, S.A.A.; Gómez-Aguilar, J. Fractional multi-step differential transformed method for approximating a fractional stochastic SIS epidemic model with imperfect vaccination. Int. J. Environ. Res. Public Health 2019, 16, 973. [Google Scholar] [CrossRef] [PubMed]
- Abuasad, S.; Moaddy, K.; Hashim, I. Analytical treatment of two-dimensional fractional Helmholtz equations. J. King Saud Univ.-Sci. 2019, 31, 659–666. [Google Scholar] [CrossRef]
- Ghaffar, F.; Badshah, N.; Islam, S. Multigrid method for solution of 3d helmholtz equation based on hoc schemes. Abstr. Appl. Anal. 2014, 2014, 954658. [Google Scholar] [CrossRef]
- Gupta, P.K.; Yildirim, A.; Rai, K. Application of he’s homotopy perturbation method for multi-dimensional fractional helmholtz equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 424–435. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Fedorov, R.V.; Generalov, D.A.; Chukalin, A.V.; Katsikis, V.N.; Mourtas, S.D.; Simos, T.E. Portfolio Insurance through Error-Correction Neural Networks. Mathematics 2022, 10, 3335. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Kornilova, M.I.; Khakhalev, Y.A.; Generalov, D.A.; Simos, T.E.; Tsitouras, C. Fitted modifications of Runge-Kutta-Nystrom pairs of orders7(5) for addressing oscillatory problems. Math. Meth. Appl. Sci. 2022, 46, 273–282. [Google Scholar] [CrossRef]
- Xie, X.; Wang, T.; Zhang, W. Existence of solutions for the (p,q)-Laplacian equation with nonlocal Choquard reaction. Appl. Math. Lett. 2023, 135, 108418. [Google Scholar] [CrossRef]
- Nguyen, S.; Delcarte, C. A spectral collocation method to solve Helmholtz problems with boundary conditions involving mixed tangential and normal derivatives. J. Comput. Phys. 2004, 200, 34–49. [Google Scholar] [CrossRef]
- Yang, X.-J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press (Elsevier Science Publishers): Amsterdam, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2016. [Google Scholar]
- Srivastava, H.M.; Hasanov, A.; Choi, J. Double-layer potentials for a generalized bi-axially symmetric Helmholtz equation. Sohag J. Math. 2015, 2, 1–10. [Google Scholar]
- Benamou, J.D.; Desprès, B. A domain decomposition method for the Helmholtz equation and related optimal control problems. J. Comput. Phys. 1997, 136, 68–82. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.-J.; Srivastava, H.M.; Jafari, H.; Yang, X.-J. Helmholtz and diffusion equations associated with local fractional derivative operators involving the Cantorian and Cantor-type cylindrical coordinates. Adv. Math. Phys. 2013, 2013, 754248. [Google Scholar] [CrossRef] [Green Version]
- Arqub, O.A. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- Ahmad, E.-A. Adapting the Laplace transform to create solitary solutions for the nonlinear time-fractional dispersive PDEs via a new approach. Eur. Phys. J. Plus 2021, 136, 1–22. [Google Scholar]
- Arqub, O.A.; El-Ajou, A.; Momani, S. Construct and predicts solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J. Comput. Phys. 2015, 293, 385–399. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Dang, W.; Guo, J.; Liu, M.; Liu, S.; Yang, B.; Yin, L.; Zheng, W. A Semi-Supervised Extreme Learning Machine Algorithm Based on the New Weighted Kernel for Machine Smell. Appl. Sci. 2022, 12, 9213. [Google Scholar] [CrossRef]
- Albalawi, W.; El-Tantawy, S.A.; Salas, A.H. On the rogue wave solution in the framework of a Korteweg–de Vries equation. Results Phys. 2021, 30, 104847. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; El-Sherif, L.S.; Bakry, A.M.; Weaam, A.; Abdul-Majid, W. On the analytical approximations to the nonplanar damped Kawahara equation: Cnoidal and solitary waves and their energy. Phys. Fluids 2022, 34, 113103. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alyousef, H.A.; Alharthi, M.R. Novel approximations to a nonplanar nonlinear Schrodinger equation and modeling nonplanar rogue waves/breathers in a complex plasma. Chaos Solitons Fractals 2022, 163, 112612. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Alharthi, M.R. Novel solutions to the (un)damped Helmholtz-Duffing oscillator and its application to plasma physics: Moving boundary method. Phys. Scr. 2021, 96, 104003. [Google Scholar]
- El-Tantawy, S.A.; Salas; Alvaro, H.; Alharthi, M.R. On the Analytical Solutions of the Forced Damping Duffing Equation in the Form of Weierstrass Elliptic Function and its Applications. Math. Probl. Eng. 2021, 2021, 6678102. [Google Scholar] [CrossRef]
- Aljahdaly Noufe, H.; El-Tantawy, S.A. On the multistage differential transformation method for analyzing damping Duffing oscillator and its applications to plasma physics. Mathematics 2021, 9, 432. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas Alvaro, H.; Alharthi, M.R. A new approach for modelling the damped Helmholtz oscillator: Applications to plasma physics and electronic circuits. Commun. Theor. Phys. 2021, 73, 035501. [Google Scholar] [CrossRef]
- Alhejaili, W.; Salas, A.H.; El-Tantawy, S.A. Novel Approximations to the (Un)forced Pendulum–Cart System: Ansatz and KBM Methods. Mathematics 2022, 10, 2908. [Google Scholar] [CrossRef]



| at | at | at | Exact Solution | |
|---|---|---|---|---|
| (0.2, 0.01) | 0.2102371 | 0.2100072 | 0.2100000 | 0.2100000 |
| (0.4, 0.01) | 0.4104630 | 0.4100141 | 0.4100000 | 0.4100000 |
| (0.6, 0.01) | 0.6106889 | 0.6100209 | 0.6100000 | 0.6100000 |
| (0.2, 0.02) | 0.2103355 | 0.2100121 | 0.2100000 | 0.2100000 |
| (0.4, 0.02) | 0.4106550 | 0.4100237 | 0.4100000 | 0.4100000 |
| (0.6, 0.02) | 0.6109746 | 0.6100353 | 0.6100000 | 0.6100000 |
| (0.2, 0.03) | 0.2104110 | 0.2100164 | 0.2100000 | 0.2100000 |
| (0.4, 0.03) | 0.4108025 | 0.4100321 | 0.4100000 | 0.4100000 |
| (0.6, 0.03) | 0.6111940 | 0.6100478 | 0.6100000 | 0.6100000 |
| (0.2, 0.04) | 0.2104747 | 0.2100204 | 0.2100000 | 0.2100000 |
| (0.4, 0.04) | 0.4109269 | 0.4100399 | 0.4100000 | 0.4100000 |
| (0.6, 0.04) | 0.6113790 | 0.6100593 | 0.6100000 | 0.6100000 |
| (0.2, 0.05) | 0.2105309 | 0.2100241 | 0.2100000 | 0.2100000 |
| (0.4, 0.05) | 0.4110365 | 0.4100471 | 0.4100000 | 0.4100000 |
| (0.6, 0.05) | 0.6115421 | 0.6100701 | 0.6100000 | 0.6100000 |
| at | at | at | Exact Solution | |
|---|---|---|---|---|
| (0.2, 0.01) | 0.2088204 | 0.2099810 | 0.2099994 | 0.2099994 |
| (0.4, 0.01) | 0.4076970 | 0.4099466 | 0.4099989 | 0.4099989 |
| (0.6, 0.01) | 0.6065736 | 0.6099392 | 0.6099984 | 0.6099984 |
| (0.2, 0.02) | 0.2083348 | 0.2099813 | 0.2099989 | 0.2099989 |
| (0.4, 0.02) | 0.4067490 | 0.4099235 | 0.4099979 | 0.4099979 |
| (0.6, 0.02) | 0.6051632 | 0.6099176 | 0.6099969 | 0.6099969 |
| (0.2, 0.03) | 0.2079635 | 0.2099392 | 0.2099984 | 0.2099984 |
| (0.4, 0.03) | 0.4060240 | 0.4099608 | 0.4099969 | 0.4099969 |
| (0.6, 0.03) | 0.6040845 | 0.6099978 | 0.6099954 | 0.6099954 |
| (0.2, 0.04) | 0.2076512 | 0.2098978 | 0.2099979 | 0.2099979 |
| (0.4, 0.04) | 0.4054143 | 0.4099005 | 0.4099959 | 0.4099959 |
| (0.6, 0.04) | 0.6031774 | 0.6099032 | 0.6099939 | 0.6099939 |
| (0.2, 0.05) | 0.2073767 | 0.2099792 | 0.2099973 | 0.2099973 |
| (0.4, 0.05) | 0.4048784 | 0.4099642 | 0.4099948 | 0.4099948 |
| (0.6, 0.05) | 0.6023800 | 0.6099492 | 0.6099923 | 0.6099923 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albalawi, W.; Shah, R.; Nonlaopon, K.; El-Sherif, L.S.; El-Tantawy, S.A. Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations. Symmetry 2023, 15, 194. https://doi.org/10.3390/sym15010194
Albalawi W, Shah R, Nonlaopon K, El-Sherif LS, El-Tantawy SA. Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations. Symmetry. 2023; 15(1):194. https://doi.org/10.3390/sym15010194
Chicago/Turabian StyleAlbalawi, Wedad, Rasool Shah, Kamsing Nonlaopon, Lamiaa S. El-Sherif, and Samir A. El-Tantawy. 2023. "Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations" Symmetry 15, no. 1: 194. https://doi.org/10.3390/sym15010194
APA StyleAlbalawi, W., Shah, R., Nonlaopon, K., El-Sherif, L. S., & El-Tantawy, S. A. (2023). Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations. Symmetry, 15(1), 194. https://doi.org/10.3390/sym15010194










