Innovative CODAS Algorithm for q-Rung Orthopair Fuzzy Information and Cancer Risk Assessment

Abstract

Due to insufficient healthcare facilities for the fight against cancer, a large percentage of individuals die. Utilizing computational tools inside the health and medical system helps to minimize fatalities. Timely cancer detection enhances the likelihood of effective therapy. Cancer risk assessment is important for legal and regulatory reasons, for cancer prevention, and to avoid the risks. The approach for assessing cancer risk based on the q-rung orthopair fuzzy set (q-ROFS) is described. The technique is predicated on a multifactor evaluation of the likelihood of a cancerous. q-ROFS is a robust approach for modeling uncertainties in multicriteria decision making (MCDM). The combinative distance-based assessment (CODAS) technique integrates two separate approaches, namely the “simple additive weighting” (SAW) method and the “weighted product method (WPM)”. In this study, the CODAS approach is extended to the q-rung orthopair fuzzy framework with application to cancer risk assessment. Additionally, the symmetry of the optimal decision in cancer risk assessment is carried out by a comparison analysis of the suggested model with some existing models.

1. Introduction

Cancer is a widespread killer, despite the large amount of examinations and rapid research progress in recent decades. Current data show that cancer accounts for 23% of deaths in the USA, the second highest cause of death after cardiovascular disorders [1]. Deaths from cardiopathy have been steadily declining in the U.S. population from 1975 to 2002. As of 2020, the world populace has reached seven billion. Fifteen million new cancer cases have been identified, and twelve million cancer patients died [2]. These tendencies in cancer occurrence and the loss of life recall Bailer’s 1985 judgement of the U.S. cancer response as a “certified failure”, a plan created fourteen years prior through President Nixon’s declaration of a “war on cancer”. Several decades later, researchers continue to research whether or not or how cancers may be preventable and ask, “Why are we losing the war on most cancers?” We tend to answer this question through examining the risks for cancer and exploring how to modulate those risks [3].

Decision making is a crucial aspect of many medical fields, as healthcare professionals are often required to make complex and difficult decisions in a time-sensitive manner. Some of the areas in which decision making is particularly important include:

• Diagnosis: Healthcare professionals must consider a range of factors when making a diagnosis, including the patient’s symptoms, medical history, and test results. Making an accurate diagnosis is crucial for determining the most appropriate course of treatment.
• Treatment: Healthcare professionals must consider the potential benefits and risks of different treatment options and choose the one that is most likely to be effective and safe for the patient. This can involve weighing the potential benefits and risks of different medications, therapies, or procedures.
• Management of chronic conditions: For patients with chronic conditions, such as diabetes or heart disease, healthcare professionals must make ongoing decisions about the management of the condition. This can involve determining the most appropriate treatment plan, adjusting the treatment plan as needed, and monitoring the patient’s progress.
• Palliative care: Healthcare professionals working in palliative care must make decisions about the care of patients who are nearing the end of life. This can involve determining the most appropriate treatment and care options, as well as addressing issues related to end-of-life planning, such as advance care directives.

Proper decision making is crucial for ensuring the best possible outcomes for patients.

Uncertainty is a vital element of any choice-making method, especially MCDM. Numerous techniques and procedures for reducing the uncertainty in choice making have been advanced. An expert weighs the advantages, features, and boundaries of the typical elements as a way to make an informed selection. To address uncertainty, Zadeh [4] introduced a prominent notion, called a “fuzzy set” (FS), which has been used in several sectors of technology. Each alternative in an FS is assigned a value between zero and 1. The definition of a membership feature is fundamental to the improvement in the fuzzy logic and modeling. Researchers continue to discuss the way to effectively describe a membership function so as to ensure good choice strategies. Nevertheless, in real-world demanding situations, selection makers decide based on membership degree (MSD) and non-membership degree (NMSD). Atanassov [5] advanced a generalization of FS, termed the Intuitionist Fuzzy Set (IFS), which includes membership and non-membership functions that may express satisfactory and unsatisfactory levels, respectively. Yager [6,7] provided a Pythagorean fuzzy set (PFS) with the constraint that the rectangular of the sum of its MSD and NMSD was less than or equal to one. PFS is better than IFS at modeling the uncertainty in demanding MCDM situations. Yager [8] also developed q-ROFSs to represent selection records in which the sum of the qth energy of the MSD and NMSD was less than or equal to one. As “q” increases, so does the distance of the desirable orthopairs, and more orthopairs fulfill the boundary requirement. We can exploit more fuzzy records using q-ROFSs. In other words, we can change the ‘q’ to determine the information range, making q-ROFS more flexible and desirable for uncertainty.

In 2016, Ghorabaee et al. [9] proposed the combinative distance-based assessment (CODAS) technique for integrating two separate scoring processes, namely the “simple additive weighting” (SAW) method and the “weighted product method” (WPM). Over the past few decades, the CODAS technique has been utilized in numerous fields. Ghorabaee et al. [10] also extended the CODAS approach to a fuzzy set. Badi et al. [11] presented the CODAS approach to solve MCDM issues for a Libyan steel manufacturer. Bolturk [12] presented Pythagorean fuzzy CODAS and its application to the supplier selection process in a manufacturer. Bolturk and Kahraman [13] presented the Interval-valued intuitionistic fuzzy CODAS approach and its implementation to the subject of wave-energy plant selection. Mathew and Sahu [14] compared CODAS to several MCDM approaches. Pamucar et al. [15] devised the linguistic neutrosophic CODAS approach to select power-generation technologies. Peng and Garg [16] developed a strategy with novel similarities to CODAS. Roy et al. [17] presented an adaptation of the CODAS methodology utilizing an interval-valued intuitionistic fuzzy (IVIF) set for the efficient selection of metals in building projects with imperfect weight data. Seker [18] suggested an IVIF trapezoidal CODAS algorithm. Liu and Liu [19] proposed novel Bonferroni mean AOs for q-ROFS with applications to MCDM. Liu et al. [20] introduced q-ROF Heronian mean AOs, their properties, and their applications. Joshi and Gegov [21] presented the concept of confidence level q-ROF AOs for the MCDM technique and demonstrated it with a real-world problem of customer selection. Garg [22] introduced the connection numbers-based q-ROFSs with applications to MCDM. Liu and Wang [23] proposed some basic AOs (averaging and geometric) for q-ROFSs with applications. Garg et al. [24] initiated the concept of exponential operation-based AOs for q-ROFSs with some new score functions. Jana et al. [25] conceptualized some Dombi AOs for q-ROFSs with applications to real-life problems. Wei et al. [26] also conceptualized Heronian mean AOs. Lin et al. [27] proposed linguistic q-ROFSs and interactional partitioned Heronian mean AOs for linguistic q-ROFSs. Khan et al. [28] proposed the idea of a knowledge base for q-ROFSs. Zeng et al. [29] proposed weighted induced logarithmic distance measures for q-ROFSs with MCDM. Sitara et al. [30] produced graph structures related to q-ROFS with decision-making analysis. Farid and Riaz [31] proposed generalized q-ROF Einstein interactive geometric AOs. Saha et al. [32] proposed the idea of hybrid hesitant fuzzy weighted AOs. Feng et al. [33] gave the score functions of a generalized orthopair fuzzy set. Mahmood et al. [34] proposed the spherical fuzzy set and T-spherical fuzzy set with applications for medical diagnosis. Ashraf and Abdullah [35] proposed a mathematical approach for MCDM in COVID-19 by utilizing spherical fuzzy information. Attaullah et al. [36] introduced the concept of q-rung orthopair hesitant fuzzy rough AOs. Extensive work related to decision making can be seen in [37,38,39]. Zararsız and Riaz proposed Bipolar fuzzy metric spaces and their application [40]. Alcantud [41] presented extensive results related to soft sets. Karaaslan and Ozlu [42] developed work related to dual type-2 hesitant FSs. Senapati et al. [43] proposed Aczel–Alsina geometric AOs for interval-valued IFSs.

1.1. Motivation and Objectives

Multicriteria decision making (MCDM) is a useful tool for cancer risk assessment, as it allows for the evaluation and comparison of multiple criteria in order to make informed decisions about the cancer risk. One of the main motivations for using fuzzy MCDM in cancer risk assessment is the complexity of the decision-making process. Cancer risk assessment involves the evaluation of a wide range of factors that can influence an individual’s risk of developing cancer, including genetic factors, environmental exposures, and lifestyle behaviors. MCDM methods allow for the systematic and transparent evaluation of these factors, which can help to improve the accuracy and reliability of the risk assessment process. Another motivation for using fuzzy MCDM in cancer risk assessment is the need to balance multiple conflicting objectives. For example, an individual may be concerned about their risk of developing cancer but may also have other priorities, such as their quality of life or the cost of risk reduction measures. MCDM methods allow for the integration of multiple objectives and the explicit consideration of the tradeoffs between them.

Finally, MCDM can be used to engage stakeholders in the decision-making process. In the context of cancer risk assessment, stakeholders may include healthcare professionals, policymakers, and the general public. By using MCDM methods, these stakeholders can be involved in the decision-making process, and their preferences and values can be taken into account. MCDM is a useful tool for cancer risk assessment due to the complexity of the decision-making process, the need to balance multiple conflicting objectives, and the ability to engage stakeholders in the decision-making process.

The objectives of this paper are as follows:

1.

An improved q-rung orthopair fuzzy CODAS is discussed in detail. The CODAS technique integrates two separate approaches, namely the “simple additive weighting” (SAW) method and the “weighted product method (WPM)”.

2.

A case study related to cancer risk assessment is provided as an application of the q-rung orthopair fuzzy CODAS approach.

3.

The optimal decision for cancer risk assessment is carried out by a comparison analysis of the suggested model with some existing models.

1.2. Organization of Paper

The remainder of the article is structured as follows. In Section 2, we introduce some of the fundamental characteristics associated with q-ROFSs. The q-ROF CODAS method is presented in Section 3. The case study, cancer risk factors, and related example are provided in Section 4. The conclusion is drawn in Section 5.

2. Preliminaries

We introduce a few important elements of the q-ROFS, the operational laws of the q-ROFS, and the score and accuracy functions in this section.

Definition  1 ([8]).

Let $q\ge 1$. A q-rung orthopair fuzzy set $\mathbb{O}$ in $S$ is defined as

$$\mathbb{O}=\{\langle \varkappa ,{\mathcal{L}}_{\mathbb{O}}(\varkappa ),{\mathcal{M}}_{\mathbb{O}}(\varkappa )\rangle :\varkappa \in S\},$$

where ${\mathcal{L}}_{\mathbb{O}},{\mathcal{M}}_{\mathbb{O}}:S\to [0,1]$ defines the membership and non-membership of the alternative $\varkappa \in S$, and for every ϰ, we have

$$0\le {\mathcal{L}}_{\mathbb{O}}^q(\varkappa )+{\mathcal{M}}_{\mathbb{O}}^q(\varkappa )\le 1.$$

Furthermore, ${\pi }_{\mathbb{O}}(\varkappa )={(1-{\mathcal{L}}_{\mathbb{O}}^q(\varkappa )-{\mathcal{M}}_{\mathbb{O}}^q(\varkappa ))}^{1/q}$ is called the indeterminacy degree of ϰ to $\mathbb{O}$.

Liu and Wang suggested combining the q-ROFN information with the following operational rules.

Definition  2 ([23]).

Let ${\mathcal{H}}_1=\langle {\mathcal{L}}_1,{\mathcal{M}}_1\rangle$ and ${\mathcal{H}}_2=\langle {\mathcal{L}}_2,{\mathcal{M}}_2\rangle$ be q-ROFN. Then,

(1) $\overline{{\mathcal{H}}_1}=\langle {\mathcal{M}}_1,{\mathcal{L}}_1\rangle$;

(2) ${\mathcal{H}}_1\vee {\mathcal{H}}_2=\langle max\{{\mathcal{L}}_1,{\mathcal{M}}_1\},min\{{\mathcal{L}}_2,{\mathcal{M}}_2\}\rangle$;

(3) ${\mathcal{H}}_1\wedge {\mathcal{H}}_2=\langle min\{{\mathcal{L}}_1,{\mathcal{M}}_1\},max\{{\mathcal{L}}_2,{\mathcal{M}}_2\}\rangle$;

(4) ${\mathcal{H}}_1\oplus {\mathcal{H}}_2=\langle {({\mathcal{L}}_1^q+{\mathcal{L}}_2^q-{\mathcal{L}}_1^q{\mathcal{L}}_2^q)}^{1/q},{\mathcal{M}}_1{\mathcal{M}}_2\rangle$;

(5) ${\mathcal{H}}_1\otimes {\mathcal{H}}_2=\langle {\mathcal{L}}_1{\mathcal{L}}_2,{({\mathcal{M}}_1^q+{\mathcal{M}}_2^q-{\mathcal{M}}_1^q{\mathcal{M}}_2^q)}^{1/q}\rangle$;

(6) $\sigma {\mathcal{H}}_1=\langle {(1-{(1-{\mathcal{L}}_1^q)}^{\sigma })}^{1/q},{\mathcal{M}}_1^{\sigma }\rangle$;

(7)${\mathcal{H}}_1^{\sigma }=\langle {\mathcal{L}}_1^{\sigma },{(1-{(1-{\mathcal{M}}_1^q)}^{\sigma })}^{1/q}\rangle$.

Definition  3 ([23]).

Assume that ${\breve{\mathcal{H}}}_k=\langle {\mathcal{L}}_k,{\mathcal{M}}_k\rangle$ is the family of q-ROFN and q-ROFWG: ${\Lambda }^n\to \Lambda$, if

$$\begin{array}{cc}\hfill \mathit{\text{q-ROFWG}}({\breve{\mathcal{H}}}_1,{\breve{\mathcal{H}}}_2,\dots {\breve{\mathcal{H}}}_n)& =\sum _{k=1}^n{\breve{\mathcal{H}}}_k^{{\mathfrak{F}}_k}\hfill \\ \hfill & ={\breve{\mathcal{H}}}_1^{{\mathfrak{F}}_1}\otimes {\breve{\mathcal{H}}}_2^{{\mathfrak{F}}_2}\otimes \dots ,{\breve{\mathcal{H}}}_n^{{\mathfrak{F}}_n},\hfill \end{array}$$

where ${\Lambda }^n$ is the set of all q-ROFN, and $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\breve{\mathcal{H}}}_1,{\breve{\mathcal{H}}}_2,\dots ,{\breve{\mathcal{H}}}_n)$, such that $0⩽{\mathfrak{F}}_k⩽1$, and ${\sum }_{k=1}^n{\mathfrak{F}}_k=1$. Then, the q-ROFWG is called the q-rung orthopair fuzzy weighted geometric operator.

Based on the q-ROF operational rules, we can also consider q-ROFWG by the theorem below.

Theorem  1 ([23]).

Let ${\breve{\mathcal{H}}}_k=\langle {\mathcal{L}}_k,{\mathcal{M}}_k\rangle$ be the family of q-ROFN, we can find q-ROFWG by

$$\mathit{\text{q-ROFWG}}({\breve{\mathcal{H}}}_1,{\breve{\mathcal{H}}}_2,\dots {\breve{\mathcal{H}}}_n)=〈\prod _{k=1}^n{\mathcal{L}}_k^{{\mathfrak{F}}_k},\sqrt[q]{(1-\prod _{k=1}^n{(1-{\mathcal{M}}_k^q)}^{{\mathfrak{F}}_k})}〉.$$

Definition  4 ([23]).

Consider $\widehat{\Re }=\langle \mathcal{L},\mathcal{M}\rangle$ as a q-ROFN; then, the score function $\mathcal{V}$ of $\widehat{\Re }$ will be given as

$$\mathcal{V}(\widehat{\Re })={\mathcal{L}}^q-{\mathcal{M}}^q,$$

with $\mathcal{V}(\widehat{\Re })\in [-1,1]$. The rating of a q-ROFN defines its ranking i.e., a high score defines a strong choice of the q-ROFN. However, the score characteristic is not useful in several instances. Consequently, to examine q-ROFNs, it is important to not always rely on the score function. We add a further technique, the accuracy characteristic, to solve this problem.

Definition  5 ([23]).

Suppose $\widehat{\Re }=\langle \mathcal{L},\mathcal{M}\rangle$ is a q-ROFN; then, the accuracy function $\mathcal{G}$ of $\widehat{\Re }$ is defined as

$$\mathcal{G}(\widehat{\Re })={\mathcal{L}}^q+{\mathcal{M}}^q,$$

where $\mathcal{G}(\widehat{\Re })\in [0,1]$. The high value of the accuracy degree $\mathcal{G}(\widehat{\Re })$ defines the high preference of $\widehat{\Re }$.

Theorem  2.

Let $\mathcal{Z}=\langle {\mathcal{L}}_{\mathcal{Z}},{\mathcal{M}}_{\mathcal{Z}}\rangle$ and $\mathfrak{J}=\langle {\mathcal{L}}_{\mathfrak{J}},{\mathcal{M}}_{\mathfrak{J}}\rangle$ be any two q-ROFN, $\mathcal{V}(\mathcal{Z}),\mathcal{V}(\mathfrak{J})$ be the score function of $\mathcal{Z}$ and $\mathfrak{J}$, and $\mathcal{G}(\mathcal{Z}),\mathcal{G}(\mathfrak{J})$ be the accuracy function of $\mathcal{Z}$ and $\mathfrak{J}$, respectively; then,

(1) If $\mathcal{V}(\mathcal{Z})>\mathcal{V}(\mathfrak{J})$, then $\mathcal{Z}>\mathfrak{J}$;

(2) If $\mathcal{G}(\mathcal{Z})>\mathcal{G}(\mathfrak{J})$ then $\mathcal{Z}>\mathfrak{J}$.

The value of the score feature is between –1 and 1. We introduce every other score feature to assist subsequent studies, $\mathcal{H}(\Re )=\frac{1+{\mathcal{L}}_{\Re }^q-{\mathcal{M}}_{\Re }^q}{2}$. We can see that $0\le \mathcal{H}(\Re )\le 1$. This new score function satisfies all the properties of a score function.

3. q-Rung Fuzzy CODAS Approach

The main assignment in preferred multicriteria decision making (MCDM) issues is to choose one or more options from a set of options primarily based on the criteria. The “combinative distance-based evaluation” (CODAS) approach is a relatively new MCDM method introduced by Ghorabaee et al. [9] in 2016. Ghorabaee et al. [10] also extended the CODAS approach to a fuzzy set. We extended the CODAS approach to q-ROFNs, and we present its application as an assessment tool to assess cancer risk. To start, in comparison to the large amount of current methods, which give identical weight to experts or a known reputation vector, specialists’ should have an impact on the criteria and their weights, based on their qualifications and reputation. Second, the q-rung direct rating approach is used to set up the relations and relevance of the criteria primarily based on the professional group’s evaluation of the alternatives. Third, the q-rung fuzzy CODAS approach is used to construct alternative orderings based on their assessment scores. Assume that there are n alternatives given as ${\mathcal{A}}^{⊢}=\left\{{\mathcal{A}}_1^{⊢},\dots ,{\mathcal{A}}_i^{⊢},\dots ,{\mathcal{A}}_n^{⊢}\right\}(n\ge 2)$ and ${\mathcal{A}}^{⊣}=\left\{{\mathcal{A}}_1^{⊣},\dots ,{\mathcal{A}}_j^{⊣},\dots ,{\mathcal{A}}_m^{⊣}\right\}$$(m\ge 2)$ that comprise the finite set of m criteria. Suppose that ${\zeta }^{\mho }=\left\{{\zeta }_1^{\mho },\dots ,{\zeta }_e^{\mho },\dots ,{\zeta }_z^{\mho }\right\}$$(z\ge 2)$ are the assemblage of invited DMs. The q-ROF-CODAS approach consists of the following steps (Algorithm 1, q-rung fuzzy CODAS approach).

Step 1: The reputation of the decision makers is evaluated first:

The notations used are ${\widehat{\Psi }}_x$, which indicates the q-ROFN average reputation of the invited DM ${\mathcal{L}}_x^{⊢}$, and ${\mathcal{M}}_x^{(1)}$ and ${\Psi }_x^{(2)}$ are the q-ROF that express the invited DM ${\zeta }_x^{⊢}$ in terms of education and expertise, respectively.

$${\widehat{\Psi }}_e=\mathrm{avg}\left({\Psi }_e^{(1)},{\Psi }_e^{(2)}\right)=\left(\frac{{\mathcal{L}}_{{\Psi }_e^{(1)}}+{\mathcal{L}}_{{\Psi }_e^{(2)}}}{2},\frac{{\mathcal{M}}_{{\Psi }_e^{(1)}}+{\mathcal{M}}_{{\Psi }_e^{(2)}}}{2}\right),e=1,2,\dots ,x.$$

(1)

Table 1. q-ROF linguistic scale to distinguish the DMs.

Qualifications	Experience (Years)	Working in Cancer Hospital	q-ROF
General physician	$[5,8)$	$[1,2)$	$(0.820,0.840)$
Cancer specialist	$[8,11.5)$	$[2,5)$	$(0.900,0.460)$
Cancer surgeon	$[12,20)$	$[5,10)$	$(0.940,0.350)$
Ph.D. in cancer research	$\ge 20$	$\ge 10$	$(0.890,0.160)$

shows a q-ROF linguistic scale that can be used to distinguish specialists based on their credentials and expertise.

Step 2: Normalize the importance of the DMs:

$$\begin{array}{cc}\hfill {\mathcal{D}}^{⊢}=& \frac{{score}^P\left({\widehat{\Delta }}_e\right)}{{\sum }_{t=1}^z{score}^P\left({\widehat{\Delta }}_t\right)}=\frac{1+{\mathcal{L}}_{{\widehat{\Delta }}_e}^q-{\mathcal{M}}_{{\widehat{\Delta }}_e}^q}{{\sum }_{t=1}^z\left(1+{\mathcal{L}}_{{\widehat{\Delta }}_t}^q-{\mathcal{M}}_{{\widehat{\Delta }}_t}^q\right)},e=1,\dots ,z;\hfill \end{array}$$

(2)

here, ${\mathcal{D}}^{⊢}=$${\left({\mathcal{D}}_1^{⊢},\dots ,{\mathcal{D}}^{⊢},\dots ,{\mathcal{D}}_z^{⊢}\right)}^T$ is the importance vector of the DMs, with ${\mathcal{D}}^{⊢}\in [0,1]$ and ${\sum }_{e=1}^z{\mathcal{D}}_e^{⊢}=1$.

Step 3: Evaluate the criteria of the importance matrices $V^e={\left[V_j^e\right]}_{m\times 1}$:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathcal{A}}_1^{⊣}\\ {\mathcal{A}}_2^{⊣}\\ ⋮\\ ⋮\\ {\mathcal{A}}_m^{⊣}\end{array}\left[\begin{array}{c}({\mathcal{L}}_{V_1}^e,{\mathcal{M}}_{V_1}^e)\hfill \\ ({\mathcal{L}}_{V_2}^e,{\mathcal{M}}_{V_2}^e)\hfill \\ ⋮\\ ⋮\\ ({\mathcal{L}}_{V_m}^e,{\mathcal{M}}_{V_m}^e)\hfill \end{array}\right]\end{array}$$

here, $V_j^e=\left({\mathcal{L}}_{V_j}^e,{\mathcal{M}}_{V_j}^e\right)(j=1,\dots ,m;e=1,\dots ,z)$ is an q-ROFNs representing the important assessment of the criterion ${\mathcal{A}}_j^{⊣}$ provided by the DM ${\zeta }_e^{\mho }$.

Step 4: Compute the consolidated criterion significance matrix:

$$\begin{array}{cc}\hfill \widehat{\mathrm{W}}& ={\left[{\mathcal{W}}_j\right]}_{m\times 1}:\hfill \\ \hfill {\mathcal{W}}_j& =\left({\mathcal{L}}_{{\mathcal{W}}_j},{\mathcal{M}}_{{\mathcal{W}}_j}\right)\hfill \\ & =q-ROFW{G}_{⊢}\left(V_j^1,\dots ,V_j^e,\dots ,V_j^z\right)=\underset{e=1}{\overset{z}{⨂}}{\left(V_j^e\right)}^{{\mathcal{D}}_e^{⊢}}\hfill \end{array}$$

$$=\left(\prod _{e=1}^z{\mathcal{L}}_{V_j^e}^{{\mathcal{D}}_e^{⊢}},\sqrt[q]{1-\prod _{e=1}^z{\left(1-{\mathcal{M}}_{V_j^e}^q\right)}^{{\mathcal{D}}_e^{⊢}}}\right),j=1,\dots ,m;$$

(3)

here, ${\mathcal{W}}_j=\left({\mathcal{L}}_{{\mathcal{W}}_j},{\mathcal{M}}_{{\mathcal{W}}_j}\right)$ is the q-ROF aggregated importance assessment of the criterion ${\mathcal{A}}_j^{⊣}$ given by the DMs.

Step 5: Normalize the aggregated criteria importance:

$$\begin{array}{cc}\hfill {\daleth }_j& =\frac{{score}^P\left({\mathcal{W}}_j\right)}{{\sum }_{l=1}^m{score}^P\left({\mathcal{W}}_l\right)}=\frac{1+{\mathcal{L}}_{{\mathcal{W}}_j}^q-{\mathcal{M}}_{{\mathcal{W}}_j}^q}{{\sum }_{l=1}^m\left(1+{\mathcal{L}}_{{\mathcal{W}}_l}^q-{\mathcal{M}}_{{\mathcal{W}}_l}^q\right)},\hfill \end{array}$$

where $\daleth ={\left(\daleth 1,\dots ,\daleth j,\dots ,\daleth m\right)}^T$ is the importance vector of the criteria, with $\daleth j\in [0,1](j=1,\dots ,n)$ and ${\sum }_{j=1}^n\daleth j=1.$

Step 6: Obtain the decision matrices ${\Psi }^e={\left[{\Psi }_{ij}^e\right]}_{n\times m}:$

$$\begin{array}{}& \hspace{1em}{\mathcal{A}}_1^{⊣}\hspace{1em}& \hspace{1em}\hspace{1em}\hspace{1em}{\mathcal{A}}_2^{⊣}\hspace{1em}& & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathcal{A}}_m^{⊣}\hspace{1em}\begin{array}{cc}\begin{array}{c}{\mathcal{A}}_1^{⊢}\\ {\mathcal{A}}_2^{⊢}\\ \\ {\mathcal{A}}_n^{⊢}\end{array}& \left[\begin{array}{cccc}({\mathcal{L}}_{11}^1,{\mathcal{M}}_{11}^1)& ({\mathcal{L}}_{12}^1,{\mathcal{M}}_{12}^1,)& \cdots \cdots & ({\mathcal{L}}_{1m}^1,{\mathcal{M}}_{1m}^1)\\ ({\mathcal{L}}_{21}^1,{\mathcal{M}}_{21}^1)& ({\mathcal{L}}_{22}^1,{\mathcal{M}}_{22}^1,)& \cdots \cdots & ({\mathcal{L}}_{2m}^1,{\mathcal{M}}_{2m}^1)\\ ⋮& ⋮& \ddots \ddots & ⋮\\ ({\mathcal{L}}_{n1}^1,{\mathcal{M}}_{n1}^1)& ({\mathcal{L}}_{n2}^1,{\mathcal{M}}_{n2}^1)& \cdots \cdots & ({\mathcal{L}}_{nm}^1,{\mathcal{M}}_{nm}^1)\end{array}\right]\end{array}\end{array}$$

where ${\Psi }_{ij}^e=\left({\mathcal{L}}_{{\Psi }_{ij}^e},{\mathcal{M}}_{{\Psi }_{ij}^e}\right)(i=1,\dots ,n;j=1,\dots ,m;e=1,\dots ,z$ ) is a q-ROFN that represents the assessment of the alternative ${\mathcal{A}}_i^{⊢}$ with respect to the criterion ${\mathcal{A}}_j^{⊣}$ given by the invited expert ${\zeta }_e^{\mho }$. It is defined by utilizing the q-rung fuzzy set.

Step 7: Determine the aggregated decision matrix $\mathrm{G}={\left[{\mathrm{G}}_{ij}\right]}_{n\times m}:$

$$\begin{array}{ccc}\hfill {\mathrm{G}}_{ij}& =& {\text{q-ROFWG}}_{⊢}\left({\Psi }_{ij}^1,\dots ,{\widehat{\Psi }}_{ij}^e,\dots ,{\Psi }_{ij}^k\right)\hfill \\ \hfill \\ & =& \left(\prod _{e=1}^z{\mathcal{L}}_{{\Psi }_{ij}^e}^{\mathcal{D}{⊢}_e},\sqrt[4]{1-\prod _{e=1}^z{\left(1-{\mathcal{M}}_{{\Psi }_{ij}^e}\right)}^{\mathcal{D}{⊢}_e}}\right),\hfill \end{array}$$

(4)

where the aggregation is determined by applying the “q-rung fuzzy geometric (q-ROFWG) operator”, and ${\mathrm{G}}_{ij}=\left({\mathcal{L}}_{{\mathrm{G}}_{ij}},{\mathcal{M}}_{{\mathrm{G}}_{ij}}\right)$ is the q-rung fuzzy aggregated calculation of the possible options or alternatives ${\mathcal{A}}_i^{⊢}$ with respect to the criterion ${\mathcal{A}}_j^{⊣}$ given by the experts.

Step 8: Determine the normalized decision matrix $\widehat{\mathcal{G}}={\left[{\tilde{R}}_{ij}\right]}_{n\times m}$:

$${\tilde{R}}_{ij}=\left\{\begin{array}{cc}{\left({\mathrm{G}}_{ij}\right)}^c;\hfill & \mid {\mathcal{A}}_j^{⊣}\in {\mathrm{CR}}^{-}\hfill \\ {\mathrm{G}}_{ij};\hfill & \mid {\mathcal{A}}_j^{⊣}\in {\mathrm{CR}}^{+},\hfill \end{array}\right.$$

(5)

where ${\tilde{R}}_{ij}=\left({\mathcal{L}}_{{\tilde{R}}_{ij}},{\mathcal{M}}_{{\tilde{R}}_{ij}}\right)$ denotes the q-ROF normalized assessment of the alternative ${\mathcal{A}}_i^{⊢}$ with respect to the criterion ${\mathcal{A}}_j^{⊣}$ given by the experts, ${\mathrm{CR}}^{-}\subseteq \mathrm{CR}$ is the set of benefit criteria, ${\mathrm{CR}}^{-}\subseteq \mathrm{CR}$ is the set of cost criteria, and ${\mathrm{CR}}^{+}\cup {\mathrm{CR}}^{-}=\mathrm{CR}$. Only alternative assessments with respect to the cost criteria are transformed by utilizing the complement operation.

Step 9: Determine the q-rung fuzzy negative-ideal solution (q-ROFNsIS).

$$\begin{array}{cc}\hfill {\widehat{S}}_j^{-}& =\left({\mathcal{L}}_{{\widehat{S}}_j^{-}},{\mathcal{M}}_{{\widehat{S}}_j^{-}}\right)=\widehat{R_j^{-}}\mid score\left(\widehat{R_j^{-}}\right)\hfill \\ & =\underset{1\le i\le n}{min}\left[score\left(R_{ij}\right)\right],j=1,\dots ,m,\hfill \end{array}$$

where $\widehat{S^{-}}=$$\left\{\widehat{S_1^{-}},\dots ,\widehat{S_j^{-}},\dots ,{\widehat{S}}_m^{-}\right\}$ is a collection of q-ROFNs that represent the q-ROFNsIS, and ${\tilde{R}}_j^{-}$ is a q-ROFN with the lowest score function value of alternatives with respect to the criterion ${\mathcal{A}}_j^{⊣}$.

Step 10: Find the weighted Euclidean distance $({\mathcal{V}}_i)$ and weighted Hamming distance $(H_i)$ of the alternatives from the q-ROFNIS given in Equations (6) and (7), respectively.

$${\mathcal{H}}_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)=\frac{1}{2}\sum _{j=1}^n{\daleth }_j\left(\left|{\mathcal{L}}_{{\tilde{R}}_{ij}}^q-{\mathcal{L}}_{{\tilde{R}}_j^{-}}^q\right|+\left|{\mathcal{M}}_{{\tilde{R}}_{ij}}^q-{\mathcal{M}}_{{\widehat{S}}_j^{-}}^q\right|\right)$$

(6)

$${\mathcal{V}}_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)=\sqrt{\frac{1}{2}\sum _{j=1}^n{\daleth }_j\left[{\left({\mathcal{L}}_{{\tilde{R}}_{ij}}^q-{\mathcal{L}}_{{\tilde{R}}_j^{-}}^q\right)}^2+{\left({\mathcal{M}}_{{\tilde{R}}_{ij}}^q-{\mathcal{M}}_{{\widehat{S}}_j^{-}}^q\right)}^2\right]}.$$

(7)

Step 11: Construct the relative assessment matrix $\mathcal{P}={\left[{\mathcal{P}}_{it}\right]}_{n\times n}:$

$${\mathcal{P}}_{it}={\mathbf{E}}_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)-{\mathbf{E}}_t\left({\mathcal{A}}_t^{⊢},{\widehat{S}}^{-}\right)+{\Phi }_{it}\left({\mathbf{E}}_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)-{\mathbf{E}}_t\left({\mathcal{A}}_t^{⊢},{\widehat{S}}^{-}\right)\right)·\left[H_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)-H_t\left({\mathcal{A}}_t^{⊢},{\widehat{S}}^{-}\right)\right],$$

with $i,t=1,\dots ,n$, where $\Phi$ is a threshold function to recognize the equality of the Euclidean distance measures of the two alternatives. It is defined as follows

$${\Phi }_{it}\left({\mathbf{E}}_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)-{\mathbf{E}}_t\left({\mathcal{A}}_t^{⊢},{\widehat{S}}^{-}\right)\right)=\left\{\begin{array}{cc}1\hfill & \varphi \le |{\mathbf{E}}_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)-{\mathbf{E}}_t\left({\mathcal{A}}_t^{⊢},{\widehat{S}}^{-}\right)\mid \hfill \\ \\ 0\hfill & \varphi >|{\mathbf{E}}_i\left({\mathcal{A}}_i^{⊢},{\widehat{S}}^{-}\right)-{\mathbf{E}}_t\left({\mathcal{A}}_t^{⊢},{\widehat{S}}^{-}\right)\mid \hfill \end{array}\right.,$$

(8)

where $\varphi$ is the threshold parameter.

Step 12: Calculate the evaluation scores and rank the alternatives:

$${\mathcal{G}}_j=\sum _{t=1}^n{\mathcal{P}}_{jt},j=1,2,\dots ,n,$$

(9)

where ${\mathcal{G}}_j$ represents the evaluation scores of the alternative ${\mathcal{A}}_j^{⊢}$. The alternatives are ranked consistent with the reducing values of their assessment score. The best score is the most ideal opportunity.

Algorithm 1: Q-Rung CODAS

4. Case Study

Decision making regarding cancer—especially regarding cancer treatments—might appear to be an easy matter: select the choice that extends life the longest. If treatments are equivalent in prolonging life, then select the one that maximizes the quality of life (e.g., has fewer side effects). However, analysis has shown that cancer treatment choices are not straightforward. This analysis illuminates how people determine the high-stakes choices and a way to help people to create choices that improve their physical and psychological state.

A cancer risk assessment helps a person to discover their risk factors for hereditary cancer. These conditions are usually passed down in families. Cancer risk assessments take some of the uncertainty out of a person’s current health standing and help one to make decisions about the future. The substantial decline in the cancer-related mortality rate over the past two decades is attributable, in part, to advances in screening that have led to earlier and more curable cancer discovery. In order to maintain this trend, it is imperative to conduct a comprehensive study of cancer risk within the framework of medical care and to implement targeted screening techniques. Typically, the assessment of cancer risk is divided into two primary categories: the examination of familial or genetic risk and the study of environmental factors causally linked to cancer. When performing research into familial risk, it is essential to consider both maternal and paternal lineages and to focus on malignancies that frequently occur in tandem in well-known hereditary cancer syndromes. It is essential, while conducting an analysis of environmental factors, to evaluate well-known modifiable factors such as smoking, obesity, diet, and the degree of physical activity.

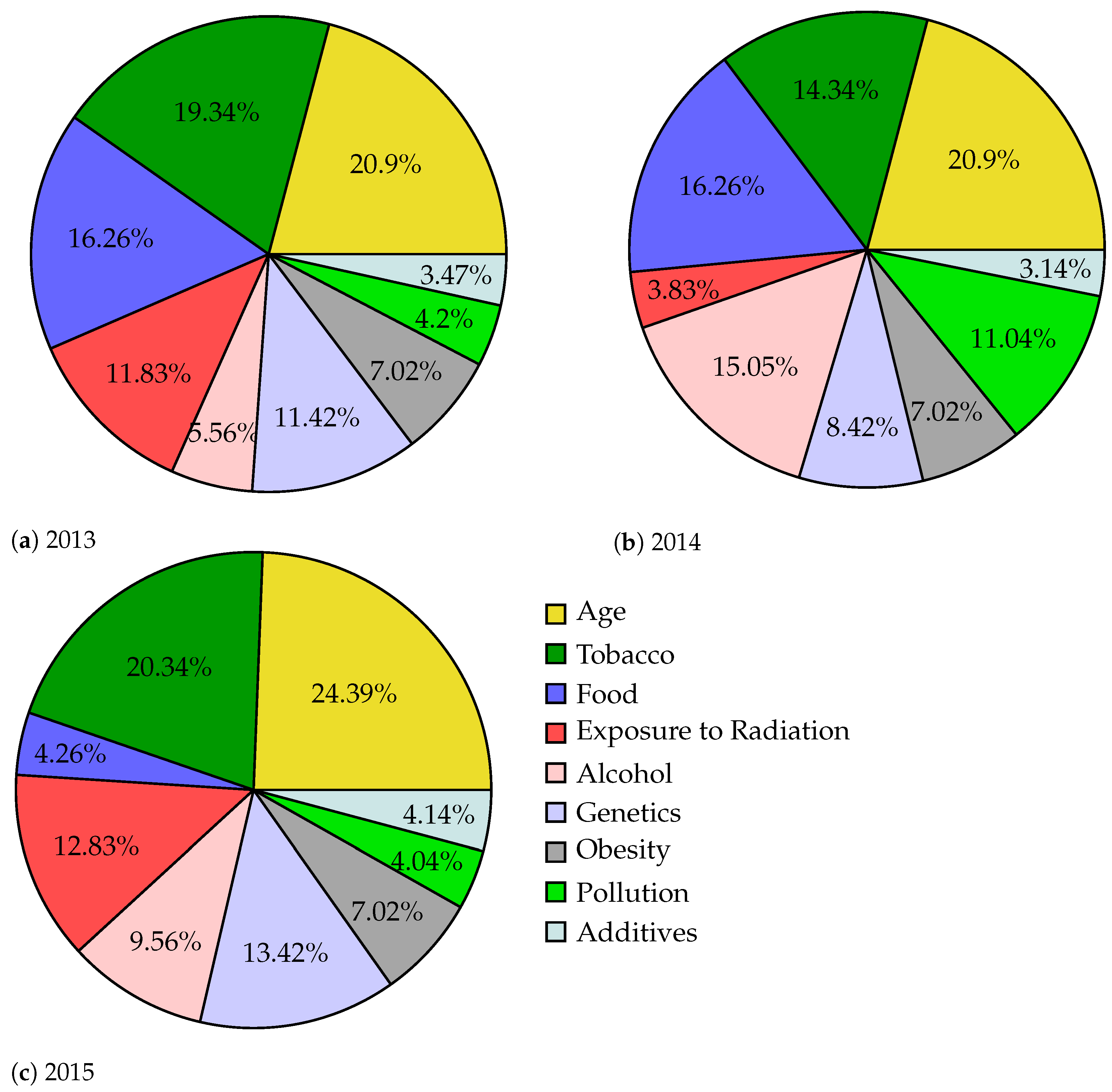
4.1. Risk Factors for Cancer

Among all ailments, a tumor can result in despair, with people assuming they will live only a short time. A North American study found that that patients worried about the beginning, progression, and expansion of cancer inside the body.

Risk evaluation is a way to understand the risks that have the opportunity to be avoided, reduced, or managed. A risk evaluation is largely about the ability to change; hence, the idea of chance is particularly difficult to understand. Numerous research has attempted to produce analysis strategies for tumor risks. The final purpose is to provide information to people about the chance of cancer, to monitor the situation, and provide a survivability prediction. Notwithstanding the large amount of research, few studies have been carried out in situations of the middle stages in between a past diagnosis and a current diagnosis. Existing research has not addressed the chance of recurrence. Yet, this research query is of tremendous importance, as it enables the patient to think and plan ahead, not only about healthcare but also about the state of their affairs and duties [3]. For risk analysis, it is important to determine which of the major sources of cancer can be labeled risk factors.

Figure 1 shows that 90–95% of the risk factors for cancer are environmental factors, whereas 90–95% is due to genes. Here, we focus on the environmental risk factors.

An increase in a tumor risk increases a person’s likelihood of malignancy. However, most risk factors do not cause malignancy in a straightforward manner. Some tumors from risk factors never become malignant, and others with no known risk factors do.

4.2. Using Tobacco

During the 1950s, the evidence began to accrue for the carcinogenicity of tobacco smoking. By the end of the 1950s, convincing evidence linking smoking with respiratory organ cancers and other cancers was shown from case-control studies and cohort research; cancer-causing agents were recognized in tobacco smoke, and cigarette smoke in the atmosphere was shown to cause tumors in mice. The sharp increase in the number of deaths as a result of tobacco smoking reflects the smoking styles in previous years. Smoking tobacco causes nearly half of cancer deaths, and if smoking persists in developing nations, these cancers are predicted to increase. Additionally, smoking causes death from vascular, metastasis, and other diseases; so in general, tobacco smoking is estimated to account for about four–five million deaths each year worldwide [44]. This is projected to rise to 10 million each year by 2030. As a consequence, if current smoking patterns continue, there will be over a billion deaths resulting from tobacco smoking in the 21st century in comparison with 100 million deaths in the 20th century. Figure 1 shows that smoking is one of the main causes of cancer.

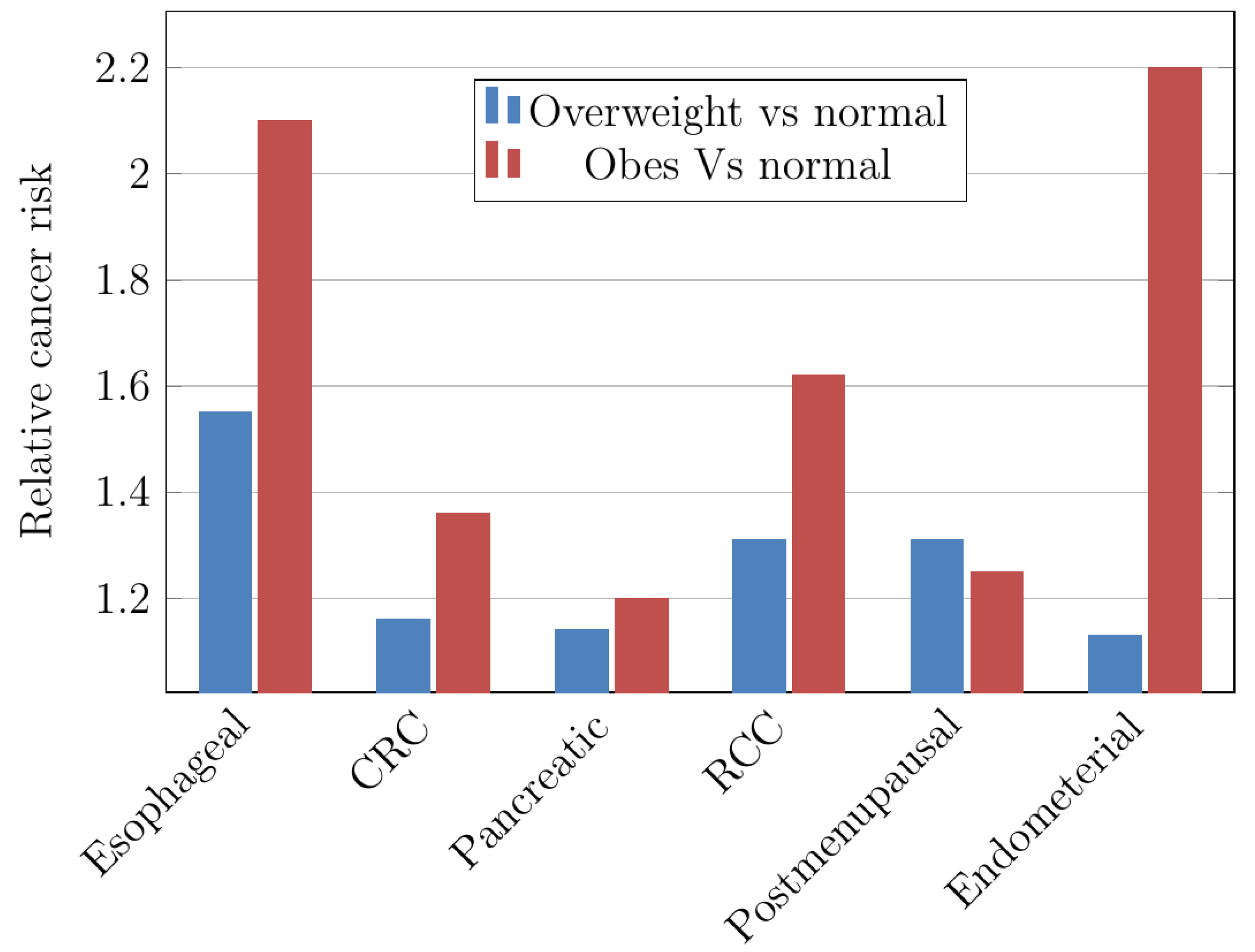
4.3. Obesity

Recent research has emphasized the significance of the trio of obesity/corpulence, insulin resistance, and adipocytokines in cancer. Although the role of obesity in the etiopathogenesis of tumors is not fully understood, the key pathways connecting obesity and adiposopathy to tumors comprise adipocytokines and insulin resistance [45].

1:

Hyperinsulinemia/IR and abnormalities of the insulin-like development determinant-I (IGF-I) system and indicators;

2:

Sex hormones’ biogenesis and pathway;

3:

Subclinical chronic inferior swelling and oxidative stress;

4:

Changes in the pathophysiology of adipocytokine synthesis;

5:

Determinants of fat deposition;

6:

Microenvironment and natural perturbations;

7:

Determinants of obesity and malignancy such as digestive minerals;

8:

Altered intestinal microbiome; and

9:

Mechanistic determinants of obesity.

Figure 2 depicts the mechanisms associating obesity with cancer.

4.4. Genetic

Researchers have long known that some cancers are hereditary; familial genetics are vital for some tumors and less so for others. Researchers have shed light on the hereditary components of twelve types of cancer—showing a familial link particularly to abdomenal cancer and providing some clarity on the types of mutations in well-known carcinoma-susceptible genes.

4.5. Older Age

Age is a substantial risk factor for the disease. People over the age of 74 make up 28% of those with new tumors. Researchers are not sure why this is. It maybe that the passing decades give the cells longer to mutate or grow into malignancy. It may be that a younger age means a person has been exposed for a shorter time to cigarettes, chemical compounds, and alternative cancer-precipitating agents. Figure 3 shows that the risk of cancer increases with age; so, age is an important factor in the analysis of an individual’s cancer risk [46].

4.6. Exposure to Radiation

Energy travels and disseminates. Radiation takes place in atoms through nuclei decay and unharnessed particles. Ionized dissemination takes place before the fragment loses its associated lepton. Unstable atoms can have greater strength or mass. The diffusion of the surplus strength or mass determines the radiation. Radiation doses are calculated in mrem. Radiation can cause burns and cancers. Forms of fallout include the initial force, coarse particles, and their dispersion. There can be dissemination from many areas, which can be referred to as background radiation. The amount of radiation a person absorbs depends on the distance from and the height of the fallout [47]. The development of cancer due to radiation is shown in Figure 4.

4.7. Decision-Making Process

To save human lives, people need to know their risk of cancer. Timely action against cancer is very important. For that purpose, six candidates (${\mathcal{A}}_1^{⊢},{\mathcal{A}}_2^{⊢},{\mathcal{A}}_3^{⊢},{\mathcal{A}}_4^{⊢},{\mathcal{A}}_5^{⊢}$, and ${\mathcal{A}}_6^{⊢}$ ) were evaluated further. In order to assess who was at the highest risk of cancer, a committee of three DMs, ${\zeta }_1^{\mho }$, ${\zeta }_2^{\mho }$, and ${\zeta }_3^{\mho },$ was constituted. Five criteria (factors) were taken into account, as shown in

Table 2. Criterion for the assessment.

	Criteria
${\mathcal{A}}_1^{⊣}$	Age
${\mathcal{A}}_2^{⊣}$	Genetics
${\mathcal{A}}_3^{⊣}$	Using tobacco
${\mathcal{A}}_4^{⊣}$	Obesity
${\mathcal{A}}_5^{⊣}$	Radiation

.

• Step 1: Three DMs participated in the provided case study. The q-ROF linguistic scale was applied to the various DMs shown in

  Table 3. Information about the DMs.

  DMs	Qualifications	Experience (Years)	Experience (Working in Cancer Hospital)
  ${\zeta }_1^{\mho }$	Ph.D. in cancer research	11	10
  ${\zeta }_2^{\mho }$	Cancer specialist	9	3
  ${\zeta }_3^{\mho }$	General physician	7	1.5

  . The table contained q-ROFNs that denoted the experts’ credentials and expertise. Then, we utilized Equation (1) and the associated q-ROFNs.

The fuzzy average distinction of each expert using the q-rung fuzzy sets for an expert is shown in

Table 4. Information about the DMs in terms of the q-ROF.

DMs	Qualifications	Experience (Years)	Experience (Working in Cancer Hospital)	Average
${\zeta }_1^{\mho }$	(0.450, 0.910)	(0.250, 0.700)	( 0.250, 0.700)	(0.350, 0.805)
${\zeta }_2^{\mho }$	(0.550, 0.970)	(0.500, 0.500)	(0.250, 0.700)	(0.350, 0.980)
${\zeta }_3^{\mho }$	(0.900, 0.150 )	(0.700, 0.250)	(0.700, 0.250)	(0.775, 0.540)

.

Furthermore, the aggregated q-ROFNs for the DMs are shown in

Table 5. Aggregated FFNs for the criterion.

DMs	Importance
	Average q-ROFNs	Positive Score	Normalized
${\zeta }_1^{\mho }$	(0.350, 0.805)	0.6585	0.2861
${\zeta }_1^{\mho }$	$(0.350,0.980)$	0.5360	0.2329
${\zeta }_1^{\mho }$	$(0.775,0.540)$	1.1070	0.4810

.

• Step 2: The q-ROF average reputations of the DMs were normalized using Equation (2). Because a DM cannot have a negative reputation value, the positive score algorithm was employed to obtain a crisp average result. The obtained reputation vector of the DMs was

  $${\mathcal{D}}^{⊢}=(0.2861,0.2329,0.4810)$$
• Step 3: The DMs examined the predefined factors that estimate the risk of cancer.

  Table 6. DMs’ evaluations of each criterion in terms of the corresponding q-ROFNs.

  Criterion	DMs
  	${\mathbf{\zeta }}_{\mathbf{1}}^{\mho }$	${\mathbf{\zeta }}_{\mathbf{2}}^{\mho }$	${\mathbf{\zeta }}_{\mathbf{3}}^{\mho }$
  ${\mathcal{A}}_1^{⊣}$	$(0.9881,0.1012)$	$(0.8500,0.3100)$	$(0.6501,0.5012)$
  ${\mathcal{A}}_2^{⊣}$	$(0.2031,0.7401)$	$(0.7101,0.5501)$	$(0.8501,0.3010)$
  ${\mathcal{A}}_3^{⊣}$	$(0.4001,0.7501)$	$(0.5501,0.5081)$	$(0.6501,0.2104)$
  ${\mathcal{A}}_4^{⊣}$	$(0.8501,0.3001)$	$(0.7501,0.4001)$	$(0.5501,0.5101)$
  ${\mathcal{A}}_5^{⊣}$	$(0.3501,0.5003)$	$(0.7004,0.3501)$	$(0.6501,0.8003)$

  contains the DMs’ evaluations of each criterion in terms of the corresponding q-ROFNs.
• Step 4: Equation (3) aggregated the q-ROF significance ratings of the parameters by taking into account the DMs’ reputation vector.

  Table 7. Aggregated FFNs for the criterion.

  Criterion	Importance
  	Aggregated q-ROFNs	Positive Score	Normalized
  ${\mathcal{A}}_1^{⊣}$	(0.7800, 0.4262)	1.3373	0.2500
  ${\mathcal{A}}_2^{⊣}$	(0.5412, 0.5892)	0.9653	0.1805
  ${\mathcal{A}}_3^{⊣}$	(0.5442, 0.5865)	0.9694	0.1812
  ${\mathcal{A}}_4^{⊣}$	(0.6697, 0.4506)	1.1599	0.2169
  ${\mathcal{A}}_5^{⊣}$	(0.6304, 0.7006)	0.9170	0.1714

  contains the calculated value.
• Step 5: Now, the q-ROF aggregated significance of the criterion was normalized. Due to the fact that a criterion cannot have negative significance, the positive score function was used to evaluate crisp aggregated values. The normalized values are given in Table 7.
• Step 6: The three decision matrices shown in

  Table 8. DM evaluations of the alternative terms of the corresponding q-ROFNs.

  Experts	Alternatives	Criterion
  		${\mathcal{A}}_{\mathbf{1}}^{⊣}$	${\mathcal{A}}_{\mathbf{2}}^{⊣}$	${\mathcal{A}}_{\mathbf{3}}^{⊣}$	${\mathcal{A}}_{\mathbf{4}}^{⊣}$	${\mathcal{A}}_{\mathbf{5}}^{⊣}$
  ${\zeta }_1^{\mho }$	${\mathcal{A}}_1^{⊢}$	(0.3220, 0.9600)	(0.3210, 0.9200)	(0.4130, 0.9600)	(0.5120, 0.6300)	(0.8100, 0.2540)
  	${\mathcal{A}}_2^{⊢}$	(0.1120, 0.9700)	(0.1320, 0.9700)	(0.4320, 0.9400)	(0.5120, 0.6900)	(0.2320, 0.9800)
  	${\mathcal{A}}_3^{⊢}$	(0.2120, 0.9200)	(0.2110, 0.9300 )	(0.1120, 0.6300)	(0.6120, 0.9500 )	(0.8120, 0.8600)
  	${\mathcal{A}}_4^{⊢}$	(0.9120, 0.7400)	(0.9820, 0.4000)	(0.9600, 0.6000)	(0.8820, 0.6000 )	(0.8720, 0.3000 )
  	${\mathcal{A}}_5^{⊢}$	(0.3000, 0.8000 )	(0.4000, 0.6500)	(0.8000, 0.3000)	(0.9000, 0.2000)	(0.5500, 0.5000)
  	${\mathcal{A}}_6^{⊢}$	(0.6500, 0.4000)	(0.1000, 0.9750)	(0.8000, 0.3000)	(0.4000, 0.6500 )	(0.5500, 0.5000 )
  ${\zeta }_1^{\mho }$	${\mathcal{A}}_1^{⊢}$	(0.9920, 0.3400)	(0.3310, 0.2410)	(0.7720, 0.3680)	(0.9820, 0.4400)	(0.3400, 0.9120)
  	${\mathcal{A}}_2^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_3^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_4^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_5^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_6^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  ${\zeta }_1^{\mho }$	${\mathcal{A}}_1^{⊢}$	(0.9920, 0.3400)	(0.3310, 0.2410)	(0.7720, 0.3680)	(0.9820, 0.4400)	(0.3400, 0.9120)
  	${\mathcal{A}}_2^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_3^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_4^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_5^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)
  	${\mathcal{A}}_6^{⊢}$	(0.5340, 0.9720)	(0.8720, 0.5140)	(0.5340, 0.9320)	(0.1340, 0.9920)	(0.7820, 0.4130)

  were aggregated using the q-ROFWG operator specified in Equation (4), taking the DMs’ reputational vectors into consideration.

  Table 9. Normalized assessment matrix.

  Criterion	Alternatives
  	${\mathcal{A}}_{\mathbf{1}}^{⊢}$	${\mathcal{A}}_{\mathbf{2}}^{⊢}$	${\mathcal{A}}_{\mathbf{3}}^{⊢}$	${\mathcal{A}}_{\mathbf{4}}^{⊢}$	${\mathcal{A}}_{\mathbf{5}}^{⊢}$	${\mathcal{A}}_{\mathbf{6}}^{⊢}$
  ${\mathcal{A}}_1^{⊣}$	(0.7189, 0.8068)	(0.3415, 0.9714)	(0.1883, 0.9170)	(0.8785, 0.7637)	(0.3186, 0.9572)	(0.6903, 0.3573)
  ${\mathcal{A}}_2^{⊣}$	(0.3281, 0.7428)	(0.5081, 0.8362)	(0.2605, 0.8343)	(0.6447, 0.7076)	(0.3538, 0.7410)	(0.2986, 0.9158)
  ${\mathcal{A}}_3^{⊣}$	(0.6455, 0.8078)	(0.5026, 0.9344)	(0.4772, 0.4860 )	(0.6784, 0.6371)	(0.7615, 0.4660)	(0.7903, 0.7763)
  ${\mathcal{A}}_4^{⊣}$	(0.8150, 0.5206)	(0.1966, 0.9797)	(0.7524, 0.7995)	(0.6364, 0.6000)	(0.9096, 0.3714)	(0.4703, 0.6278)
  ${\mathcal{A}}_5^{⊣}$	(0.4359, 0.8685)	(0.5523, 0.8527)	(0.7092, 0.6846)	(0.7056, 0.4757)	(0.4886, 0.7266)	(0.6903, 0.5958)

  contains the derived q-rung aggregated assessments of the alternatives in relation to the criteria specified by the three DMs.
• Step 7: Table contains the normalized decision matrix. Equation (5) was used to determine it based on the aggregated decision matrix. The complement operation is used solely for the cost type attributes. Here, we had no such attributes; therefore, the values in Table 9 were used for further evaluations.
• Step 8: To begin, the values of the q-ROF normalized assessments’ score functions were determined using the formulation of the q-ROFNs’ score function. Then, the q-ROFNIS was calculated and provided as {(0.3145, 0.9714) (0.3538, 0.7410) (0.5026, 0.9344) (0.1966, 0.9797) (0.0.4359, 0.8685)}.
• Step 9: We evaluated the weighted Euclidean distances and weighted Hamming distances using Equations (6) and (7).

The weighted Euclidean distances and weighted Hamming distances are listed in

Table 10. Weighted Euclidean distances and weighted Hamming distances.

Distance Measure	Alternatives
	${\mathcal{A}}_{\mathbf{1}}^{⊢}$	${\mathcal{A}}_{\mathbf{2}}^{⊢}$	${\mathcal{A}}_{\mathbf{3}}^{⊢}$	${\mathcal{A}}_{\mathbf{4}}^{⊢}$	${\mathcal{A}}_{\mathbf{5}}^{⊢}$	${\mathcal{A}}_{\mathbf{6}}^{⊢}$
Weighted Euclidean	0.3818	0.0618	0.3263	0.4639	0.4466	0.4871
Weighted Hamming	0.2712	0.0304	0.2453	0.3943	0.2945	0.4036

.

• Step 10 and Step 11: We constructed the relative assessment matrix, which is given in

  Table 11. Relative assessment matrix.

  Alternatives	${\mathcal{A}}_1^{⊢}$	${\mathcal{A}}_2^{⊢}$	${\mathcal{A}}_3^{⊢}$	${\mathcal{A}}_4^{⊢}$	${\mathcal{A}}_5^{⊢}$	${\mathcal{A}}_5^{⊢}$
  ${\mathcal{A}}_1^{⊢}$	0	−0.3200	−0.0555	0.0821	0.0648	0.1053
  ${\mathcal{A}}_2^{⊢}$	0.3200	0	0.2645	0.4020	0.3848	0.4253
  ${\mathcal{A}}_3^{⊢}$	0.0554	−0.2645	0	0.1375	0.1203	0.1607
  ${\mathcal{A}}_4^{⊢}$	−0.0821	−0.4020	−0.1375	0	−0.0172	0.0232
  ${\mathcal{A}}_5^{⊢}$	−0.0648	−0.3848	−0.1203	0.0172	0	0.0405
  ${\mathcal{A}}_6^{⊢}$	−0.1053	−0.4253	−0.1607	−0.0232	−0.0405	0

  . In the base case scenario, the threshold parameter $\varphi >0$ was set to 0.40.
• Step 12: We calculated the assessment scores and ranked the alternatives using Equation (9).

Table 12. Assessment scores and final ranking.

Alternatives	Assessment Score	Rank
${\mathcal{A}}_1^{⊢}$	0.1232	4
${\mathcal{A}}_2^{⊢}$	−1.7966	6
${\mathcal{A}}_3^{⊢}$	−0.2095	5
${\mathcal{A}}_4^{⊢}$	0.6156	2
${\mathcal{A}}_5^{⊢}$	0.5123	3
${\mathcal{A}}_6^{⊢}$	0.7550	1

gives the assessment scores and the final ranking.

The ranking of alternatives was ${\mathcal{A}}_6^{⊢}\succ {\mathcal{A}}_4^{⊢}\succ {\mathcal{A}}_5^{⊢}\succ {\mathcal{A}}_1^{⊢}\succ {\mathcal{A}}_3^{⊢}\succ {\mathcal{A}}_2^{⊢}$.

The ranking shown in Table 12 for the cancer risk of the alternatives is displayed in Figure 5 graphically.

4.8. Comparison Analysis

A comparison analysis is presented in

Table 13. Comparison analysis.

Reference	Model	Top Alternative
Bolturk [12]	Pythagorean fuzzy CODAS	${\mathcal{A}}_6^{⊢}$
Karagoz [48]	intuitionistic fuzzy CODAS	${\mathcal{A}}_6^{⊢}$
Yeni [49]	Interval valued intuitionistic fuzzy CODAS	${\mathcal{A}}_6^{⊢}$
Proposed method	Q-rung CODAS	${\mathcal{A}}_6^{⊢}$

with our proposed method. The symmetry of the optimal decision can be seen in the sense that all the techniques evaluated ${\mathcal{A}}_6^{⊢}$ as an optimal choice. Obtaining the same optimal solution demonstrates the robustness, strength, and consistency of our proposed model.

5. Conclusions

Cancer is the second largest cause of death in the USA, after heart disease. The evaluation of cancer risk can be divided into two primary categories: the evaluation of inherited risk and the number of incidental variables that may have a causal relationship with cancer. The discovery of a potentially inherited tumor condition can lead to further evaluation and measures that can considerably minimize the probability of acquiring cancer. Our team employed a q-rung orthopair fuzzy combinative distance-based evaluation approach to identify whether a person is at risk for acquiring cancer and, if so, to what extent this risk exists. In contrast to the vast majority of the existing systems for collective decision making, which assume either a known reputation vector or assign equal weights for each expert, the reputation of experts was established by their qualifications and experience in the topic area. In the second part of the procedure, the q-rung fuzzy direct rating method was used to calculate the relative weight that should be assigned to each of the evaluation criteria based on the preferences of the expert panel. Thirdly, the q-rung fuzzy CODAS approach was employed to generate alternative orderings based on the item assessment scores. In addition, a number of important q-ROFS-related ideas were studied throughout the course of this research. A comparison analysis was conducted to analyze the symmetry and efficiency of the suggested method as compared to the existing models.