Pythagorean Fuzzy Partial Correlation Measure and Its Application
Abstract
1. Introduction
- enhancement of an existing PFCC approach to be used for the development of PFPCC,
- development of PFPCC using the enhanced PFCC,
- theoretical descriptions of the PFPCC for the sake of validation, and
- the application of the developed PFPCC in pattern recognition.
2. Preliminaries
2.1. Pythagorean Fuzzy Sets
- (i)
- iff for every .
- (ii)
- iff , for every .
- (iii)
- , .
- (iv)
- .
- (v)
- .
2.2. Simple Correlation Measures in Pythagorean Fuzzy Domain
- (i)
- ,
- (ii)
- ,
- (iii)
- iff .
2.2.1. Thao’s Technique
2.2.2. Liu et al.’s Technique
2.2.3. Thao et al.’s Technique
2.2.4. Modified Technique
2.2.5. Comparison for the PFCMs
3. Partial Correlation Coefficient of PFSs
3.1. First-Order PFPCC
- (i)
- If , thenFurthermore, if , then
- (ii)
- If , and , then
3.2. nth-Order PFPCC
4. Applicative Example in Pattern Recognitions and Classifications
Case Study
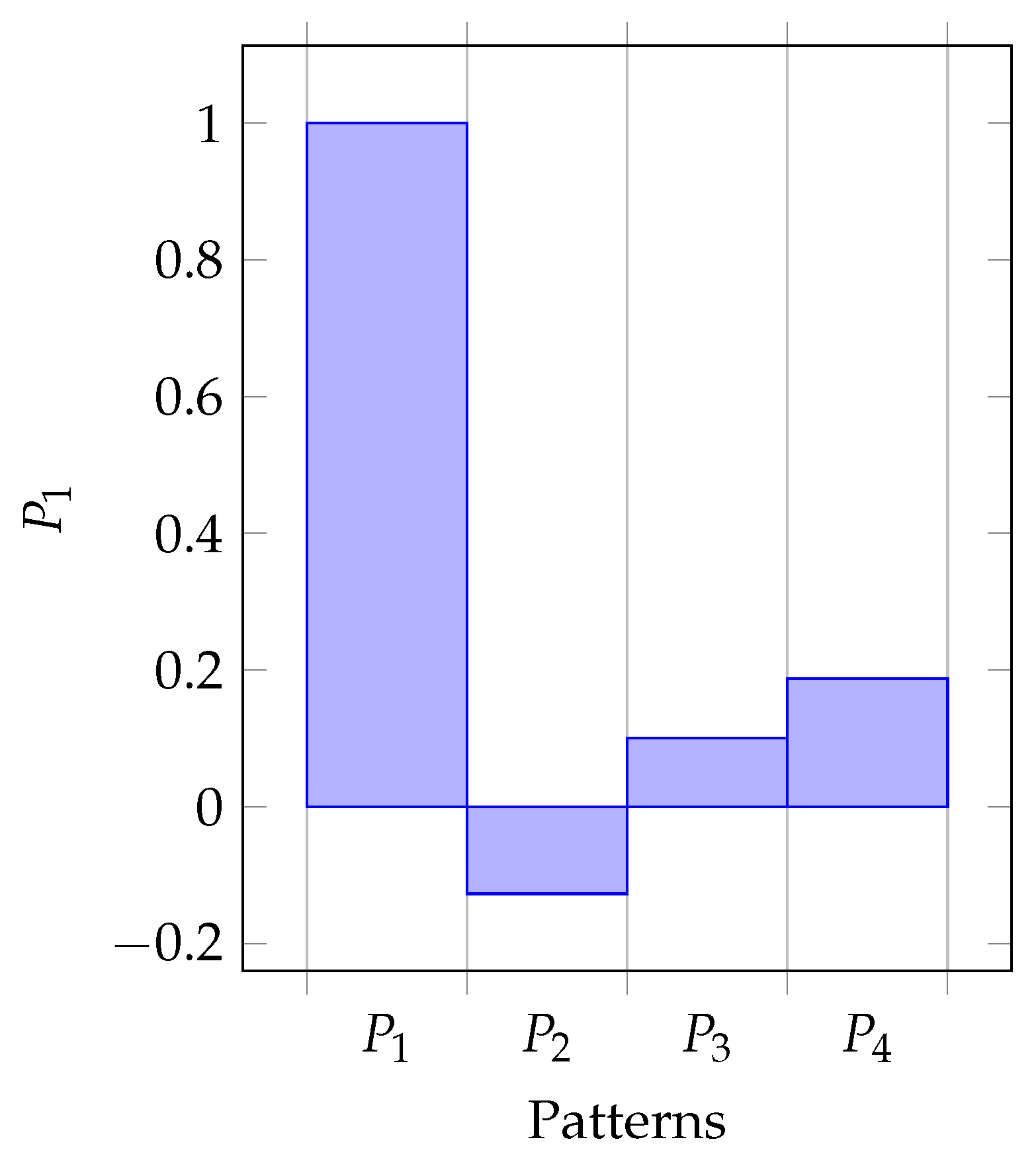
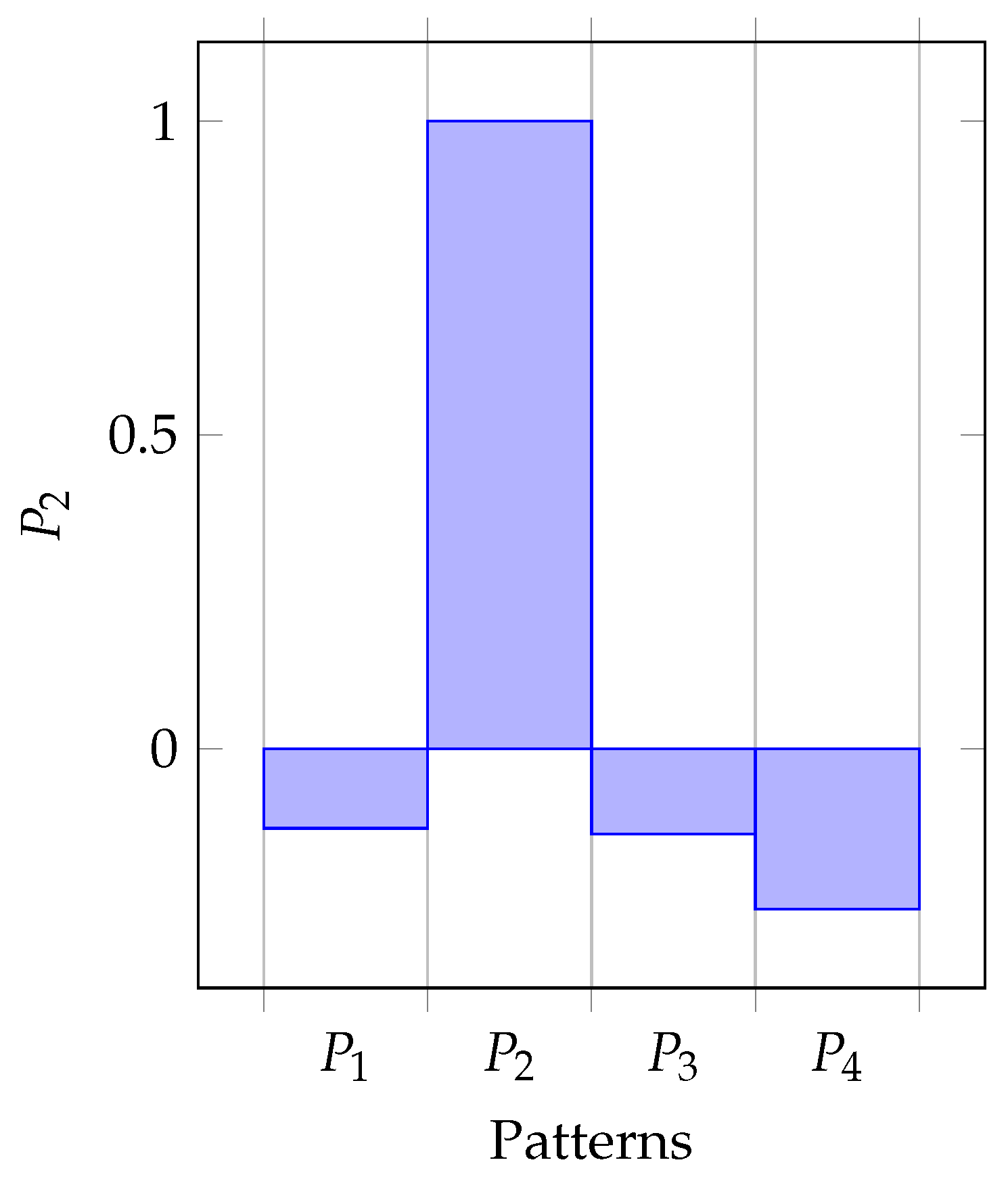
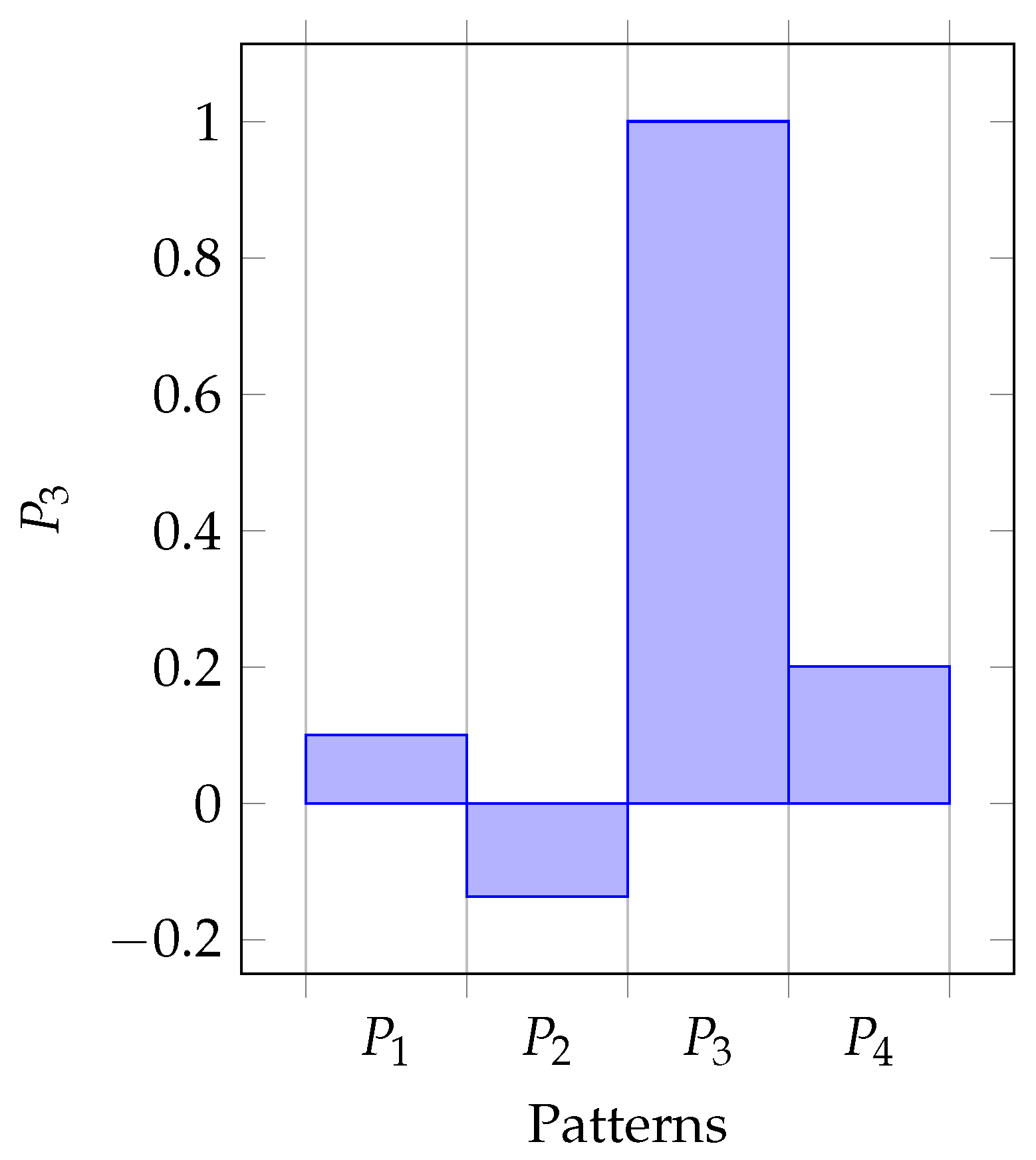
- (i)
- Pattern has a negative sway on the correlation between patterns , and a positive effect on the correlation of .
- (ii)
- Pattern only has a positive sway on the correlation between patterns , and .
- (iii)
- Pattern has a negative effect on the correlation between patterns , and a positive effect on the correlation of .
- (iv)
- Pattern has a negative influence on the correlation between patterns , and a positive effect on the correlation of .
- (i)
- Pattern has a negative effect on the first-order partial correlations , and a positive effect on .
- (ii)
- Pattern only has a positive effect on the first-order partial correlations , and .
- (iii)
- Pattern has a negative impact on the first-order partial correlations , and a positive effect on .
- (iv)
- Pattern has a negative effect on the first-order partial correlation coefficients , and a positive impact on .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 15, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Ejegwa, P.A. Intuitionistic fuzzy sets approach in appointment of positions in an organization via max-min-max rule. Glob. J. Sci. Front. Res. Math. Decis. Sci. 2015, 15, 1–5. [Google Scholar]
- Ejegwa, P.A.; Ahemen, S. Enhanced intuitionistic fuzzy similarity operators with applications in emergency management and pattern recognition. Granul. Comput. 2022, 2022. [Google Scholar] [CrossRef]
- Boran, F.E.; Akay, D. A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition. Inf. Sci. 2014, 225, 45–57. [Google Scholar] [CrossRef]
- De, S.K.; Biswas, R.; Roy, A.R. An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets Syst. 2001, 117, 209–213. [Google Scholar] [CrossRef]
- Liu, P.; Chen, S.M. Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans. Cybern. 2017, 47, 2514–2530. [Google Scholar] [CrossRef]
- Wang, W.; Xin, X. Distance measure between intuitionistic fuzzy sets. Pattern Recognit. Lett. 2005, 26, 2063–2069. [Google Scholar] [CrossRef]
- Xu, S.; Chen, J.; Wu, J.J. Cluster algorithm for intuitionistic fuzzy sets. Inf. Sci. 2008, 178, 3775–3790. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Onyeke, I.C.; Terhemen, B.T.; Onoja, M.P.; Ogiji, A.; Opeh, C.U. Modified Szmidt and Kacprzyk’s intuitionistic fuzzy distances and their applications in decision-making. J. Niger. Soc. Phys. Sci. 2022, 4, 175–182. [Google Scholar] [CrossRef]
- Atanassov, K.T. Geometrical Interpretation of the Elements of the Intuitionistic Fuzzy Objects; Preprint IM-MFAIS-1-89; IM-MFAIS: Sofia, Bulgaria, 1989. [Google Scholar]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers and decision making. J. Intell. Fuzzy Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- He, X.; Du, Y.; Liu, W. Pythagorean fuzzy power average operators. Fuzzy Syst. Math. 2016, 30, 116–124. [Google Scholar]
- Gou, X.; Xu, Z.; Ren, P. The properties of continuous Pyhagorean fuzzy information. Int. J. Intell. Syst. 2016, 31, 401–424. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Adah, V.; Onyeke, I.C. Some modified Pythagorean fuzzy correlation measures with application in determining some selected decision-making problems. Granul. Comput. 2022, 7, 381–391. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Zhang, X. A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. Int. J. Intell. Syst. 2016, 31, 593–611. [Google Scholar] [CrossRef]
- Wu, K.; Ejegwa, P.A.; Feng, Y.; Onyeke, I.C.; Johnny, S.E.; Ahemen, S. Some Enhanced Distance Measuring Approaches Based on Pythagorean Fuzzy Information with Applications in Decision Making. Symmetry 2022, 14, 2669. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Neural Comput. Appl. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Ejegwa, P.A. Novel correlation coefficient for intuitionistic fuzzy sets and its application to multi-criteria decision-making problems. Int. J. Fuzzy Syst. Appl. 2021, 10, 39–58. [Google Scholar]
- Zeng, W.; Li, D.; Yin, Q. Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int. J. Intell. Syst. 2018, 33, 2236–2254. [Google Scholar] [CrossRef]
- Ejegwa, P.A. Modified Zhang and Xu’s distance measure of Pythagorean fuzzy sets and its application to pattern recognition problems. Neural Comput. Appl. 2020, 32, 10199–10208. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Wen, S.; Feng, W.; Tang, N. Novel Pythagorean fuzzy correlation measures via Pythagorean fuzzy deviation, variance and covariance with applications to pattern recognition and career placement. IEEE Trans. Fuzzy Syst. 2022, 30, 1660–1668. [Google Scholar] [CrossRef]
- Debnath, P.; Mohiuddine, S.A. Soft Computing Techniques in Engineering, Health, Mathematical and Social Sciences; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Ejegwa, P.A.; Wen, S.; Feng, Y.; Zhang, W. Determination of pattern recognition problems based on a Pythagorean fuzzy correlation measure from statistical viewpoint. In Proceedings of the 13th International Conference Advanced Computational Intelligence, Wanzhou, China, 14–16 May 2021; pp. 132–139. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Feng, Y.; Tang, S.; Agbetayo, J.M.; Dai, X. New Pythagorean fuzzy-based distance operators and their applications in pattern classification and disease diagnostic analysis. Neural Comput. Appl. 2022, 2022. [Google Scholar] [CrossRef]
- Ejegwa, P.A. Improved composite relation for Pythagorean fuzzy sets and its application to medical diagnosis. Granul. Comput. 2020, 5, 277–286. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Siddique, I.; El-Morsy, S. Einstein-ordered weighted geometric operator for Pythagorean fuzzy soft set with its application to solve MAGDM problem. Math. Probl. Eng. 2022, 2022, 5199427. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Siddique, I.; Ahmad, S.; Iampan, A.; Jovanov, G.; Vranjes, D.; Vasiljevic, J. Pythagorean fuzzy soft Einstein ordered weighted average operator in sustainable supplier selection problem. Math. Probl. Eng. 2021, 2021, 2559979. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Siddique, I.; Jarad, F.; Hamed, Y.S.; Abualnaja, K.M.; Iampan, A. Einstein aggregation operators for Pythagorean fuzzy soft sets with their application in multiattribute group decision-making. J. Funct. Spaces 2022, 2022, 1358675. [Google Scholar] [CrossRef]
- Dumitrescu, D. Fuzzy correlation. Stud. Univ.-Babes-Bolyai Math. 1978, 23, 41–44. [Google Scholar]
- Chiang, D.A.; Lin, N.P. Correlation of fuzzy sets. Fuzzy Sets Syst. 1999, 102, 221–226. [Google Scholar] [CrossRef]
- Gerstenkorn, T.; Manko, J. Correlation of intuitionistic fuzzy sets. Fuzzy Sets Syst. 1991, 8, 39–43. [Google Scholar] [CrossRef]
- Hung, W.L. Using statistical viewpoint in developing correlation of intuitionistic fuzzy sets. Int. Uncertain. Fuzziness -Knowl.-Based Syst. 2001, 9, 509–516. [Google Scholar] [CrossRef]
- Liu, B.; Shen, L.; Mu, L.; Chen, X.; Chen, L. A new correlation measure of the intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2016, 30, 1019–1028. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. A novel correlation coefficient of intuitionistic fuzzy sets based on the connection number of set pair analysis and its application. Sci. Iran 2018, 25, 2373–2388. [Google Scholar] [CrossRef]
- Thao, N.X.; Ali, M.; Smarandache, F. An intuitionistic fuzzy clustering algorithm based on a new correlation coefficient with application in medical diagnosis. J. Intell. Fuzzy Syst. 2019, 36, 189–198. [Google Scholar] [CrossRef]
- Garg, H. A novel correlation coefficients between Pythagorean fuzzy sets and its applications to decision making processes. Int. J. Intell. Syst. 2016, 31, 1234–1252. [Google Scholar] [CrossRef]
- Thao, N.X. A new correlation coefficient of the Pythagorean fuzzy sets and its applications. Soft Comput. 2020, 24, 9467–9478. [Google Scholar] [CrossRef]
- Ejegwa, P.A. Generalized triparametric correlation coefficient for Pythagorean fuzzy sets with application to MCDM problems. Granul. Comput. 2021, 6, 557–566. [Google Scholar] [CrossRef]
- Singh, S.; Ganie, A.H. On some correlation coefficients in Pythagorean fuzzy environment with applications. Int. J. Intell. Syst. 2020, 35, 682–717. [Google Scholar] [CrossRef]
- Chiang, D.A.; Lin, N.P. Partial correlation of fuzzy sets. Int. J. Intell. Syst. 2000, 110, 209–215. [Google Scholar] [CrossRef]
- Hung, W.L.; Wu, J.J. Multiple and partial correlation coefficients of fuzzy sets. Qual. Quant. 2007, 41, 333–340. [Google Scholar] [CrossRef]
- Hung, W.L. Partial correlation coefficients of intuitionistic fuzzy sets. Int. Uncertain. Fuzziness-Knowl.-Based Syst. 2002, 10, 105–112. [Google Scholar] [CrossRef]

| PFCCs | ||||
|---|---|---|---|---|
| Example 1 | ||||
| Example 2 |
| Feature Space | |||||
|---|---|---|---|---|---|
| PFS | |||||
| 0.8000 | 0.7000 | 0.9000 | 0.6000 | 0.8000 | |
| 0.1000 | 0.2000 | 0.0000 | 0.3000 | 0.1000 | |
| 0.9000 | 0.8000 | 0.8000 | 0.5000 | 0.7000 | |
| 0.1000 | 0.1000 | 0.1000 | 0.3000 | 0.2000 | |
| 0.5000 | 0.5000 | 0.9000 | 0.5000 | 0.7000 | |
| 0.3000 | 0.2000 | 0.0000 | 0.4000 | 0.1000 | |
| 0.7000 | 0.5000 | 0.9000 | 0.6000 | 0.8000 | |
| 0.2000 | 0.4000 | 0.1000 | 0.3000 | 0.0000 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, D.; Wu, K.; Ejegwa, P.A.; Xie, X.; Feng, Y. Pythagorean Fuzzy Partial Correlation Measure and Its Application. Symmetry 2023, 15, 216. https://doi.org/10.3390/sym15010216
Yan D, Wu K, Ejegwa PA, Xie X, Feng Y. Pythagorean Fuzzy Partial Correlation Measure and Its Application. Symmetry. 2023; 15(1):216. https://doi.org/10.3390/sym15010216
Chicago/Turabian StyleYan, Dongfang, Keke Wu, Paul Augustine Ejegwa, Xianyang Xie, and Yuming Feng. 2023. "Pythagorean Fuzzy Partial Correlation Measure and Its Application" Symmetry 15, no. 1: 216. https://doi.org/10.3390/sym15010216
APA StyleYan, D., Wu, K., Ejegwa, P. A., Xie, X., & Feng, Y. (2023). Pythagorean Fuzzy Partial Correlation Measure and Its Application. Symmetry, 15(1), 216. https://doi.org/10.3390/sym15010216






