Analysis of a Productive Topological Index Correlated to Fullerenes’ Physical Properties
Abstract
:1. Introduction
2. Methodology
- Step 1:
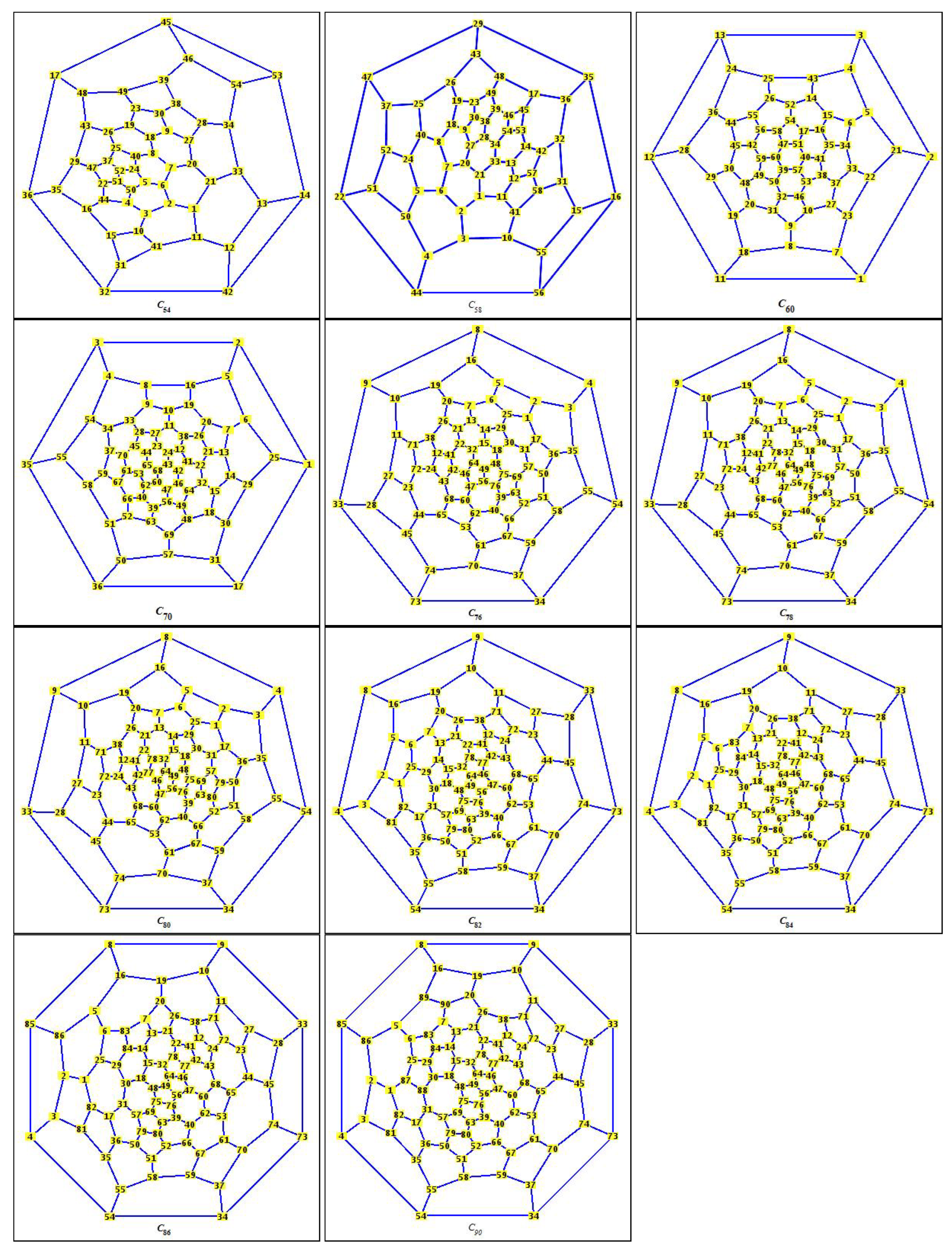
- Considering each of the molecular graph of the specific fullerene structures: , , , , , , , , , , .
- Step 2:
- The vertices and their degrees would be calculated.
- Step 3:
- The and indices would be derived using their specific formulae.
- Step 4:
- The linear regression relation between each of the mentioned sum based index and the sum based index would be computed. The coefficient of determination and the correlation coefficient would also be computed.
- Step 5:
- The linear regression relation between each of the physical properties including BE, RT minima, SRs and Hof depending on the sum based GA index are analyzed. The coefficient of determination and the correlation coefficient would also be computed to judge the productivity of the sum based index.
3. Computational Details
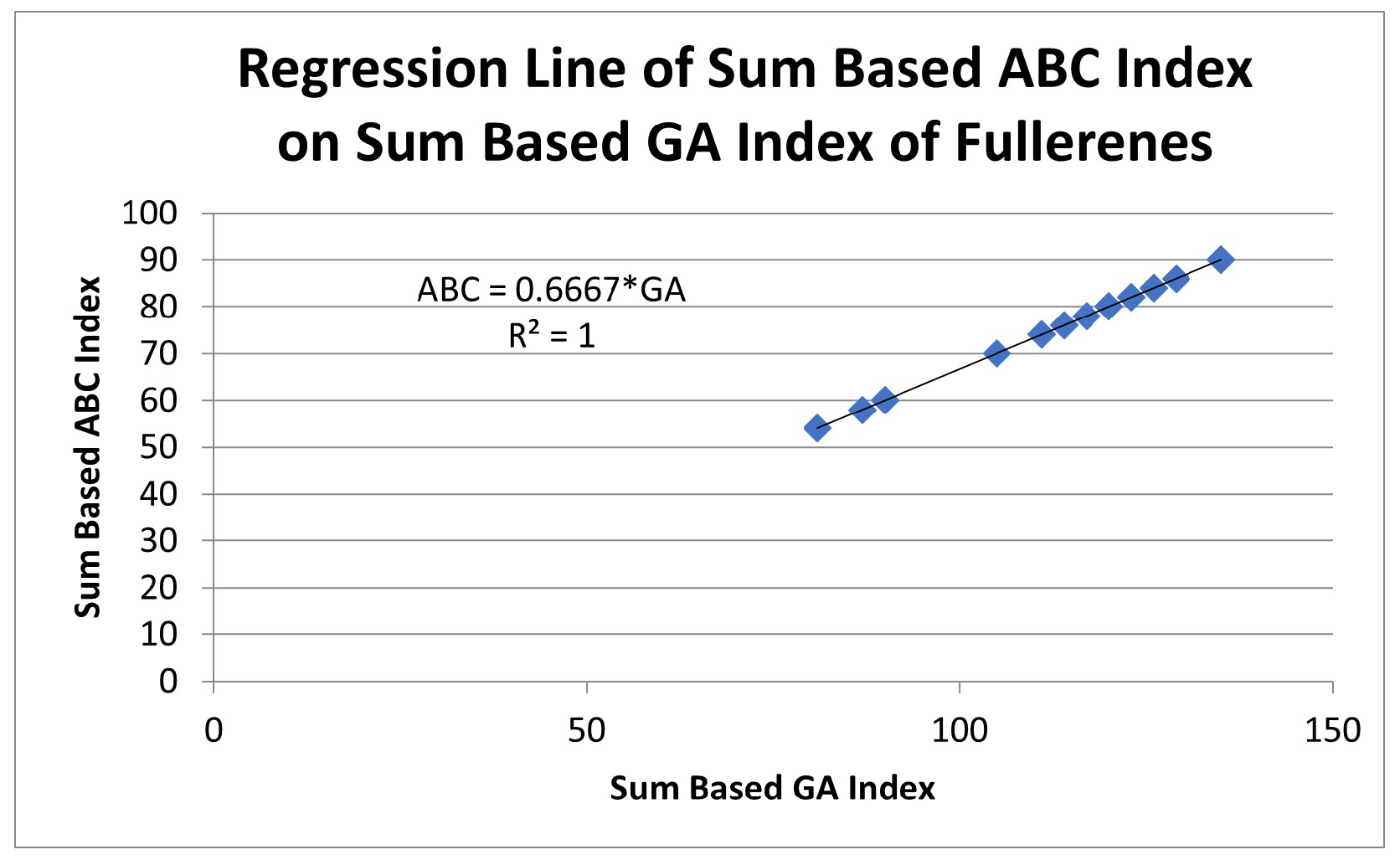
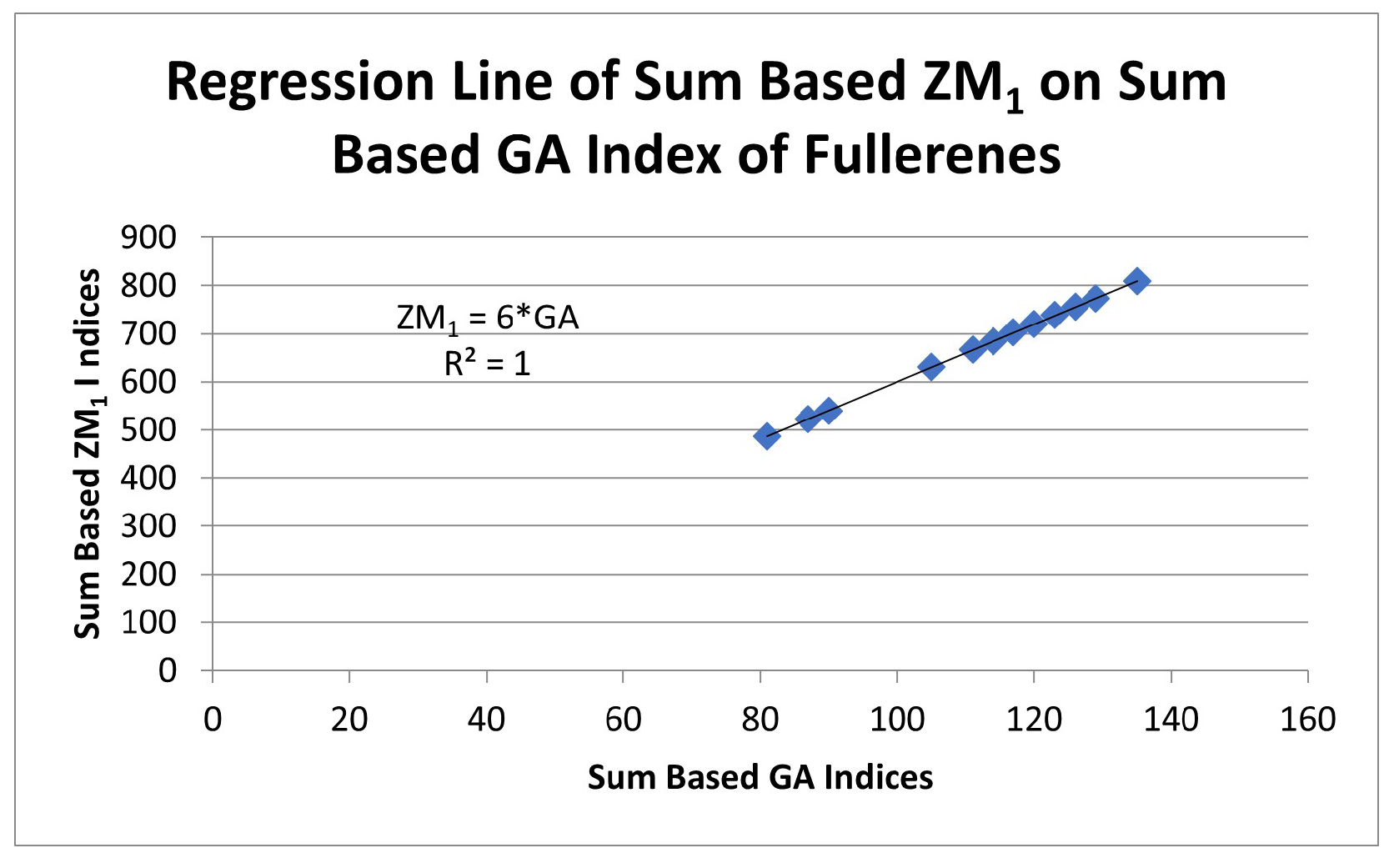
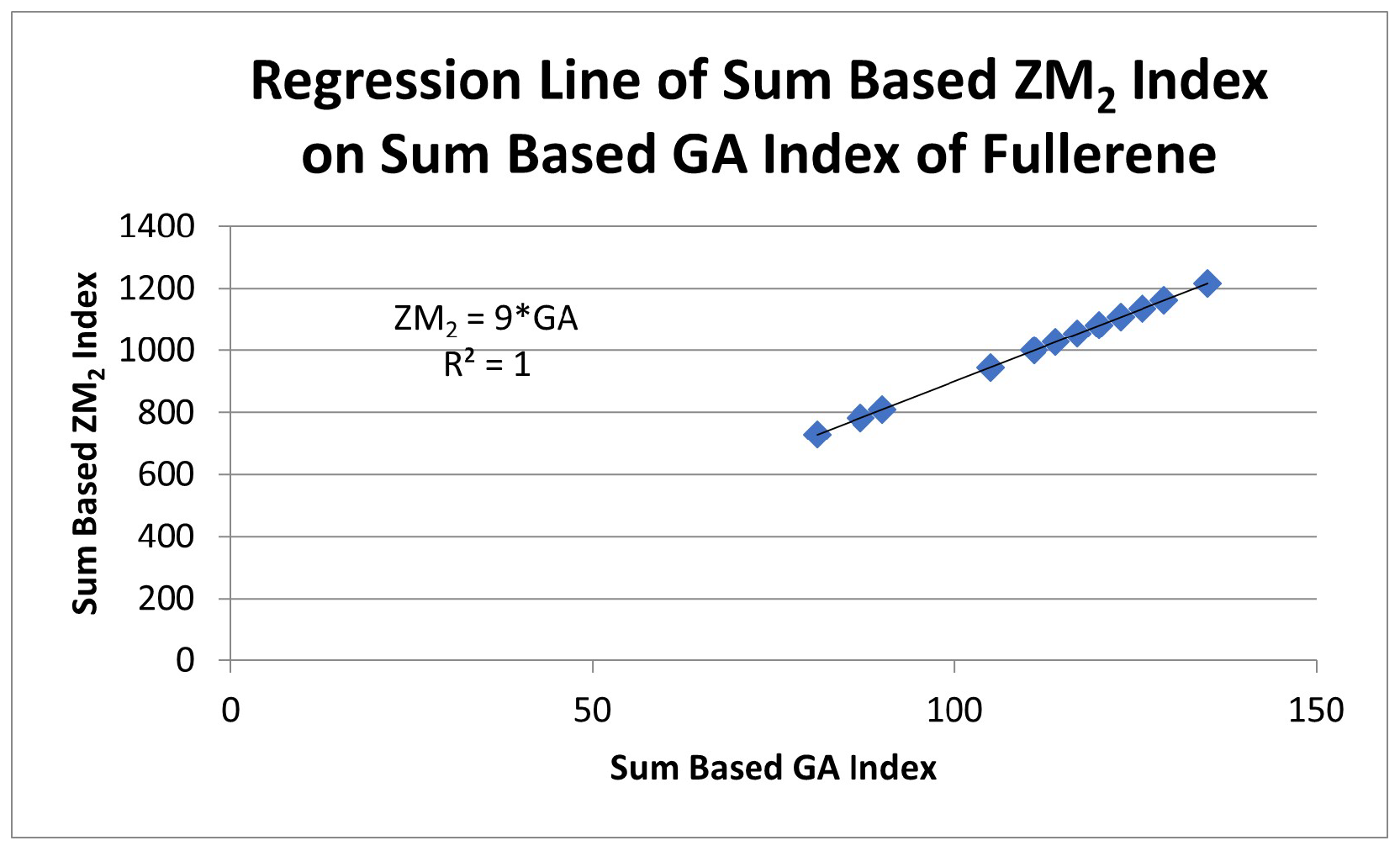
4. Analyzing Relationship of Sum Based and Indices with Sum Based Index
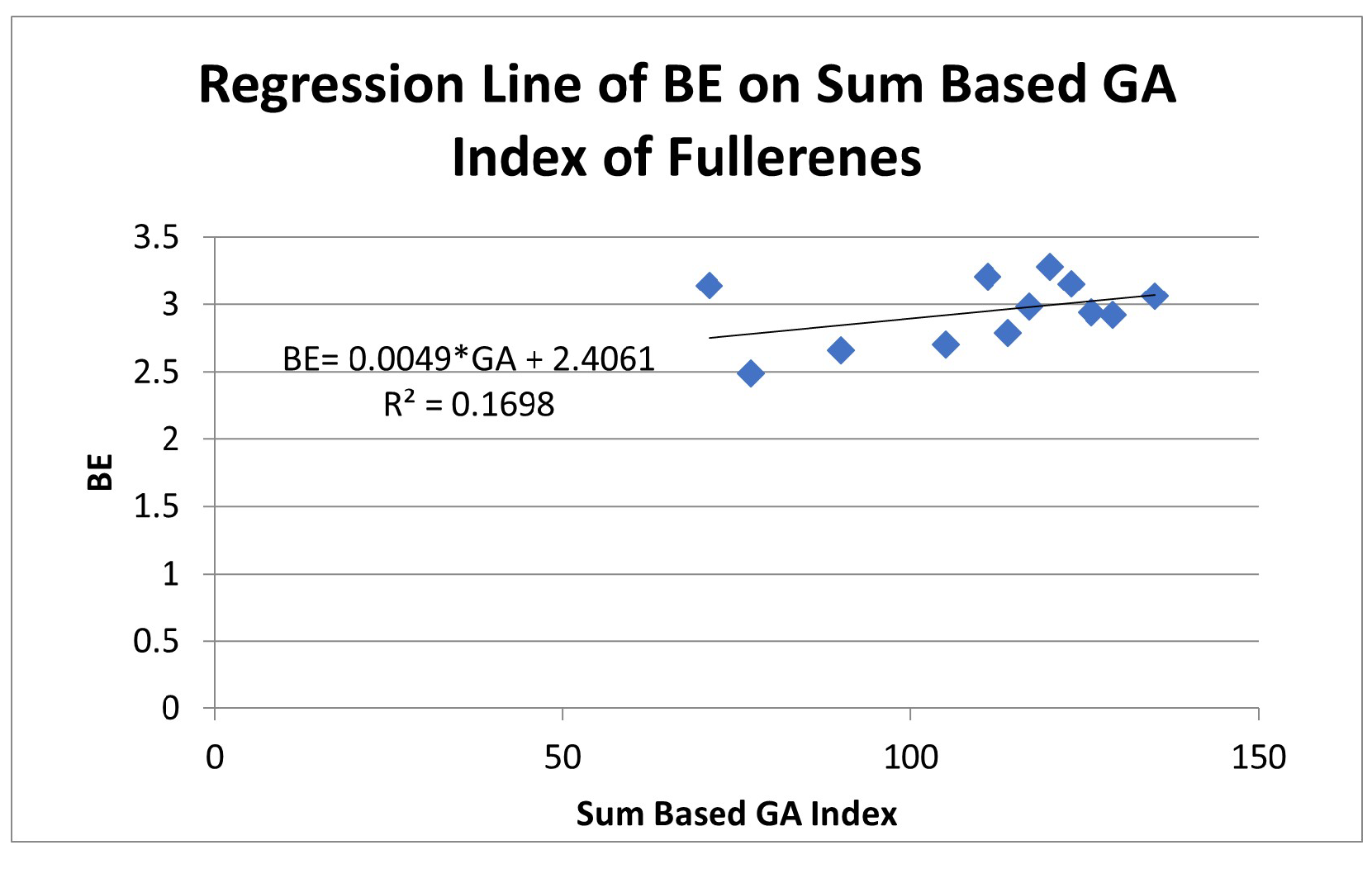
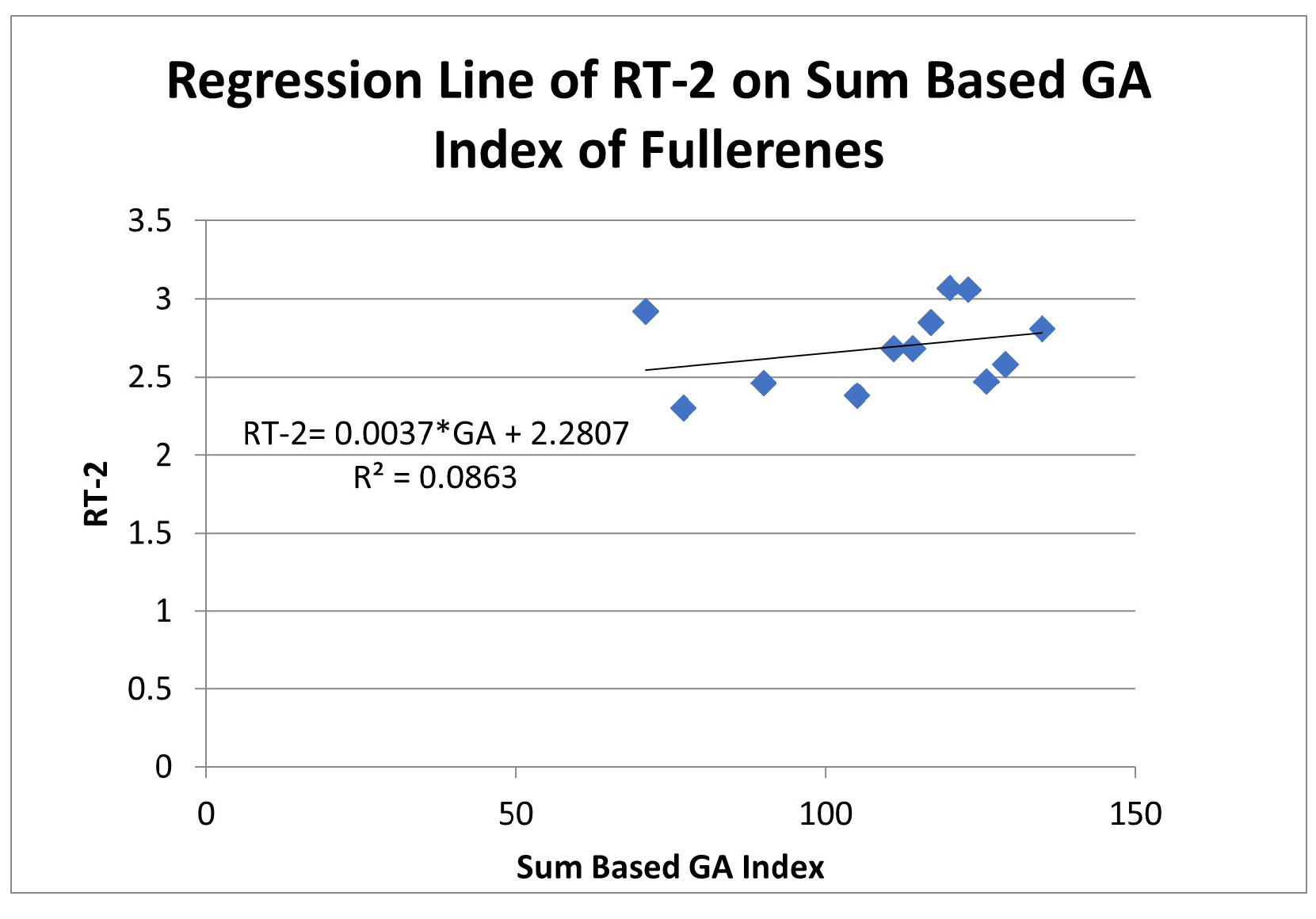
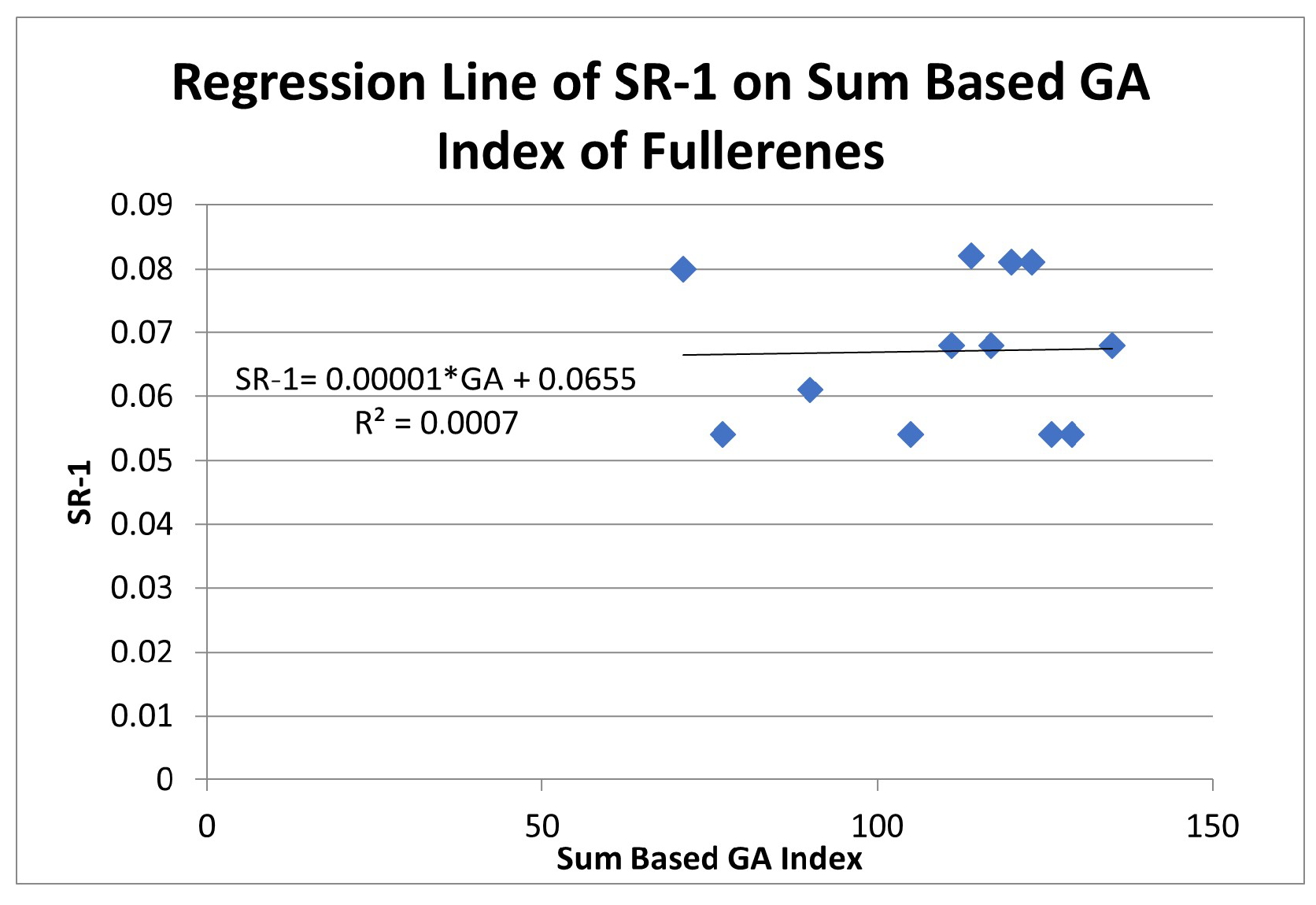
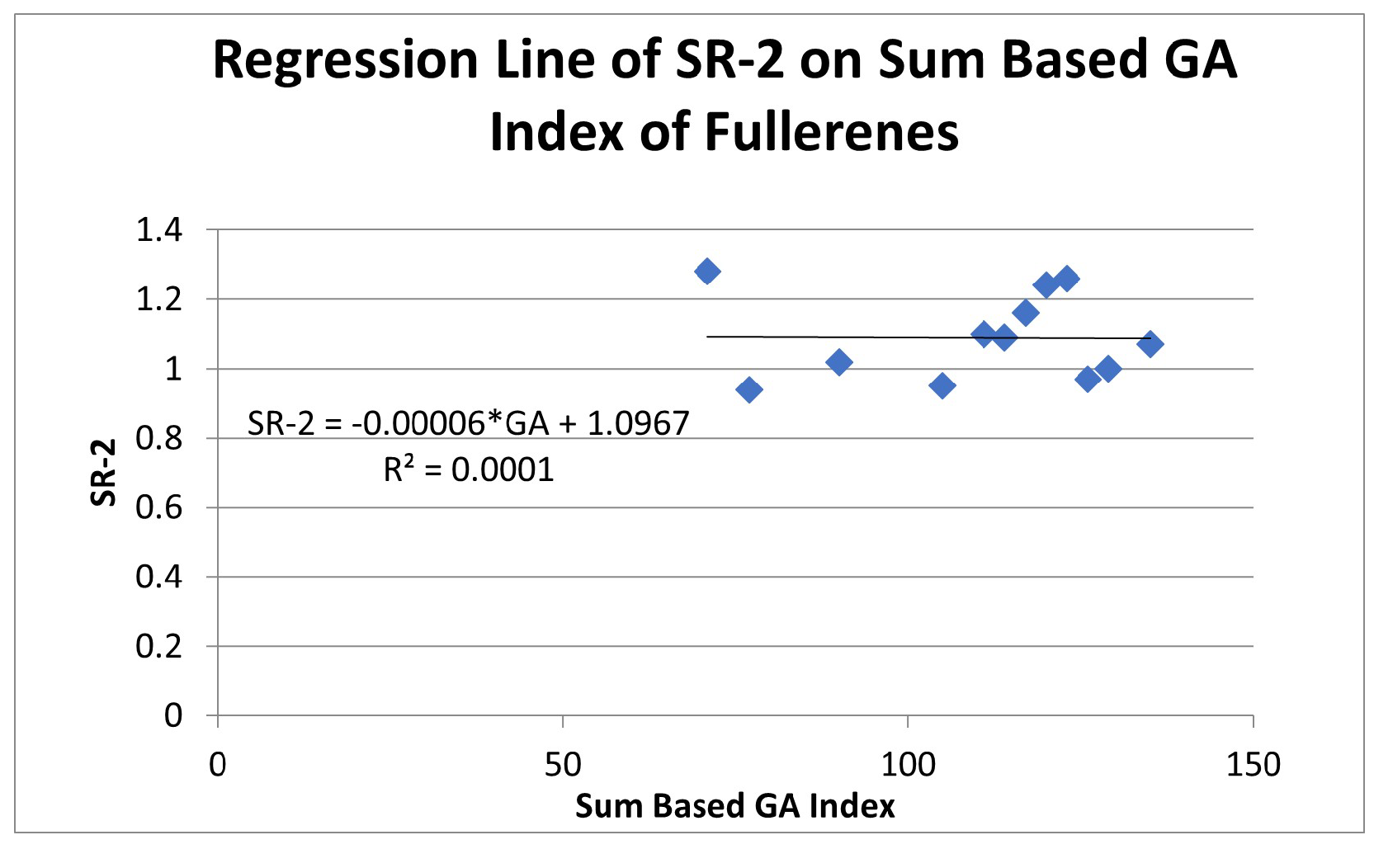
5. Analyzing the Relationship of Physical Properties with Sum Based Index
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deza, M.; Fowler, P.W.; Rassat, A.; Rogers, K.M. Fullerenes as tilings of surfaces. J. Chem. Inf. Comput. Sci. 2000, 40, 550–558. [Google Scholar] [CrossRef] [PubMed]
- Mehboob, M.Y.; Adnan, M.; Hussain, R.; Irshad, Z. Quantum chemical designing of banana-shaped acceptor materials with outstanding photovoltaic properties for high-performance non-fullerene organic solar cells. Synth. Met. 2021, 277, 116800. [Google Scholar] [CrossRef]
- Joshi, G.; Mehta, K.P. Fabrication and applications of fullerene-based metal nanocomposites: A review. J. Mater. Res. 2021, 36, 114–128. [Google Scholar]
- Zhang, J.; Zhou, Q.; Cao, J.; Wu, W.; Zhang, H.; Shi, Y.; Mao, Q.; Ma, H. Flexible textile ion sensors based on reduced graphene oxide/fullerene and their potential applications of sweat characterization. Cellulose 2021, 28, 3123–3133. [Google Scholar] [CrossRef]
- Kepley, C.L. Fullerenes in medicine; Will it ever occur? J. Nanomed. Nanotechnol. 2012, 3, e111. [Google Scholar] [CrossRef]
- Shunaev, V.V.; Pincak, R.; Glukhova, O.E. The energetical, electronic and optical properties of the intermetallic fullerene Fe@ C60. Comput. Theor. Chem. 2022, 1214, 113784. [Google Scholar] [CrossRef]
- Bosi, S.; Ros, T.D.; Spalluto, G.; Prato, M. Fullerene derivatives: An attractive tool for biological applications. Eur. J. Med. Chem. 2003, 38, 913–923. [Google Scholar] [CrossRef]
- Cataldo, F.; Da Ros, T. (Eds.) Medicinal Chemistry and Pharmacological Potential of Fullerenes and Carbon Nanotubes; Springer Science and Business Media: New York, NY, USA, 2008; Volume 1. [Google Scholar]
- Krishna, V.; Singh, A.; Sharma, P.; Iwakuma, N.; Wang, Q.; Zhang, Q.; Knapik, J.; Jiang, H.; Grobmyer, S.R.; Koopman, B.; et al. Polyhydroxy fullerenes for non-invasive cancer imaging and therapy. Small 2010, 6, 2236–2241. [Google Scholar] [CrossRef]
- Sheikh, U.; Rashid, S.; Ozel, C.; Pincak, R. On Hosoya Polynomial and Subsequent Indices of C4C8(R) and C4C8(S) Nanosheets. Symmetry 2022, 14, 1349. [Google Scholar] [CrossRef]
- Sheikh, U.; Rashid, S.; Ozel, C.; Pincak, R. On Hosoya Polynomial and Subsequent Indices of Pent-Heptagonal Carbon Nanosheets. Int. J. Geom. Methods Mod. Phys. 2022. [Google Scholar] [CrossRef]
- Babar, U.; Ali, H.; Arshad, S.H.; Sheikh, U. Multiplicative topological properties of graphs derived from honeycomb structure. Aims Math. 2020, 5, 1562–1587. [Google Scholar] [CrossRef]
- Mondal, S.; De, N.; Pal, A. Multiplicative degree based topological indices of nanostar dendrimers. Biointerface Res. Appl. Chem. 2021, 11, 7700–7711. [Google Scholar]
- Estrada, E. Atom-bond connectivity and the energetic of branched alkanes. Chem. Phys. Lett. 2008, 463, 422–425. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodriguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Shanmukha, M.C.; Usha, A.; Siddiqui, M.K.; Fufa, S.A.; Praveen, B.M. Degree-Based Molecular Descriptors of Guar Gum and Its Chemical Derivatives. J. Chem. 2022, 2022, 7371538. [Google Scholar] [CrossRef]
- Turaci, T.; Durgut, R. On topological properties of some molecular cactus chain networks and their subdivisions by using line operator. J. Discret. Math. Sci. Cryptogr. 2021, 1–18. [Google Scholar] [CrossRef]
- Naeem, M.; Rauf, A.; Maqbool, S.; Aslam, A. Degree-based topological indices of geranyl and farnesyl penicillin G bioconjugate structure. Eur. Phys. J. Plus 2022, 137, 303. [Google Scholar] [CrossRef]
- Bokhary, S.A.H.; Adnan Siddiqui, M.K.; Cancan, M. On Topological Indices and QSPR Analysis of Drugs Used for the Treatment of Breast Cancer. Polycycl. Aromat. Compd. 2022, 42, 6233–6253. [Google Scholar] [CrossRef]
- Malik, M.Y.H.; Binyamin, M.A.; Hayat, S. Correlation Ability of Degree-Based Topological Indices for Physicochemical Properties of Polycyclic Aromatic Hydrocarbons with Applications. Polycycl. Aromat. Compd. 2022, 42, 6267–6281. [Google Scholar] [CrossRef]
- Ke, X.; Wei, S.; Huang, J. The atom-bond connectivity and geometric-arithmetic indices in random polyphenyl chains. Polycycl. Aromat. Compd. 2021, 41, 1873–1882. [Google Scholar] [CrossRef]
- Shanmukha, M.C.; Usha, A.; Basavarajappa, N.S.; Shilpa, K.C. Graph entropies of porous graphene using topological indices. Comput. Theor. Chem. 2021, 1197, 113142. [Google Scholar] [CrossRef]
- Hussain, A.; Numan, M.; Naz, N.; Butt, S.I.; Aslam, A.; Fahad, A. On topological indices for new classes of Benes network. J. Math. 2021, 2021, 6690053. [Google Scholar] [CrossRef]
- Havare, O.C. Quantitative Structure Analysis of Some Molecules in Drugs Used in the Treatment of COVID-19 with Topological Indices. Polycycl. Aromat. Compd. 2021, 42, 5249–5260. [Google Scholar] [CrossRef]
- Rosary, M.S. Topological Study of Line Graph of Remdesivir Compound Used in the Treatment of Corona Virus. Polycycl. Aromat. Compd. 2021, 42, 5731–5747. [Google Scholar] [CrossRef]
- Zuo, X.; Rather, B.A.; Imran, M.; Ali, A. On Some Topological Indices Defined via the Modified Sombor Matrix. Molecules 2022, 27, 6772. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A. Simple method for determining binding energies of fullerene and complex atomic negative ions. In APS Division of Atomic, Molecular and Optical Physics Meeting Abstracts; American Physical Society: Sacramento, CA, USA, 2017; Volume 2017, pp. Q1–Q144. [Google Scholar]


| Index Name | Abbreviation | Formula |
|---|---|---|
| Index | ||
| Index | ||
| R Index | R(G) | |
| Index | ||
| Index |
| Fullerene Structure | R | ||||
|---|---|---|---|---|---|
| 81 | 54 | 27 | 486 | 729 | |
| 87 | 58 | 29 | 522 | 783 | |
| 90 | 60 | 30 | 540 | 810 | |
| 105 | 70 | 35 | 630 | 945 | |
| 111 | 74 | 37 | 666 | 999 | |
| 114 | 76 | 38 | 684 | 1026 | |
| 117 | 78 | 39 | 702 | 1053 | |
| 120 | 80 | 40 | 720 | 1080 | |
| 123 | 82 | 41 | 738 | 1107 | |
| 126 | 84 | 42 | 756 | 1134 | |
| 129 | 86 | 43 | 774 | 1161 | |
| 135 | 90 | 45 | 810 | 1215 |
| Relation | Expression | Formula |
|---|---|---|
| Regression Line | The coefficients a and b can be calculated from: | |
| Coefficient of Determination | ||
| Coefficient of Correlation | R |
| Sum Based Index | Regression Relation with Sum Based Index | Coefficient of Determination | Correlation Coefficient |
|---|---|---|---|
| 1 | 1 | ||
| R | 1 | 1 | |
| 1 | 1 | ||
| 1 | 1 |
| Fullerene Structure | BE (eV) | RT-1 (eV) | RT-2 (eV) | SR-1 (eV) | SR-2 (eV) | Hof (kcal/mol) |
|---|---|---|---|---|---|---|
| 3.14 | 0.94 | 2.92 | 0.08 | 1.28 | 642.0 | |
| 2.49 | 0.71 | 2.30 | 0.054 | 0.94 | 648.1 | |
| 2.66 | 0.76 | 2.46 | 0.061 | 1.02 | 618.1 | |
| 2.70 | 0.71 | 2.38 | 0.054 | 0.95 | 657.7 | |
| 3.21 | 0.82 | 2.68 | 0.068 | 1.1 | 694.6 | |
| 2.79 | 0.82 | 2.68 | 0.082 | 1.09 | 699.1 | |
| 2.98 | 0.87 | 2.85 | 0.068 | 1.16 | 712.5 | |
| 3.28 | 0.92 | 3.07 | 0.081 | 1.24 | 727.2 | |
| 3.15 | 0.95 | 3.06 | 0.081 | 1.26 | 727.8 | |
| 2.94 | 0.72 | 2.47 | 0.054 | 0.97 | 768.1 | |
| 2.92 | 0.75 | 2.58 | 0.054 | 1.0 | 745.7 | |
| 3.06 | 0.82 | 2.81 | 0.068 | 1.07 | 763.7 |
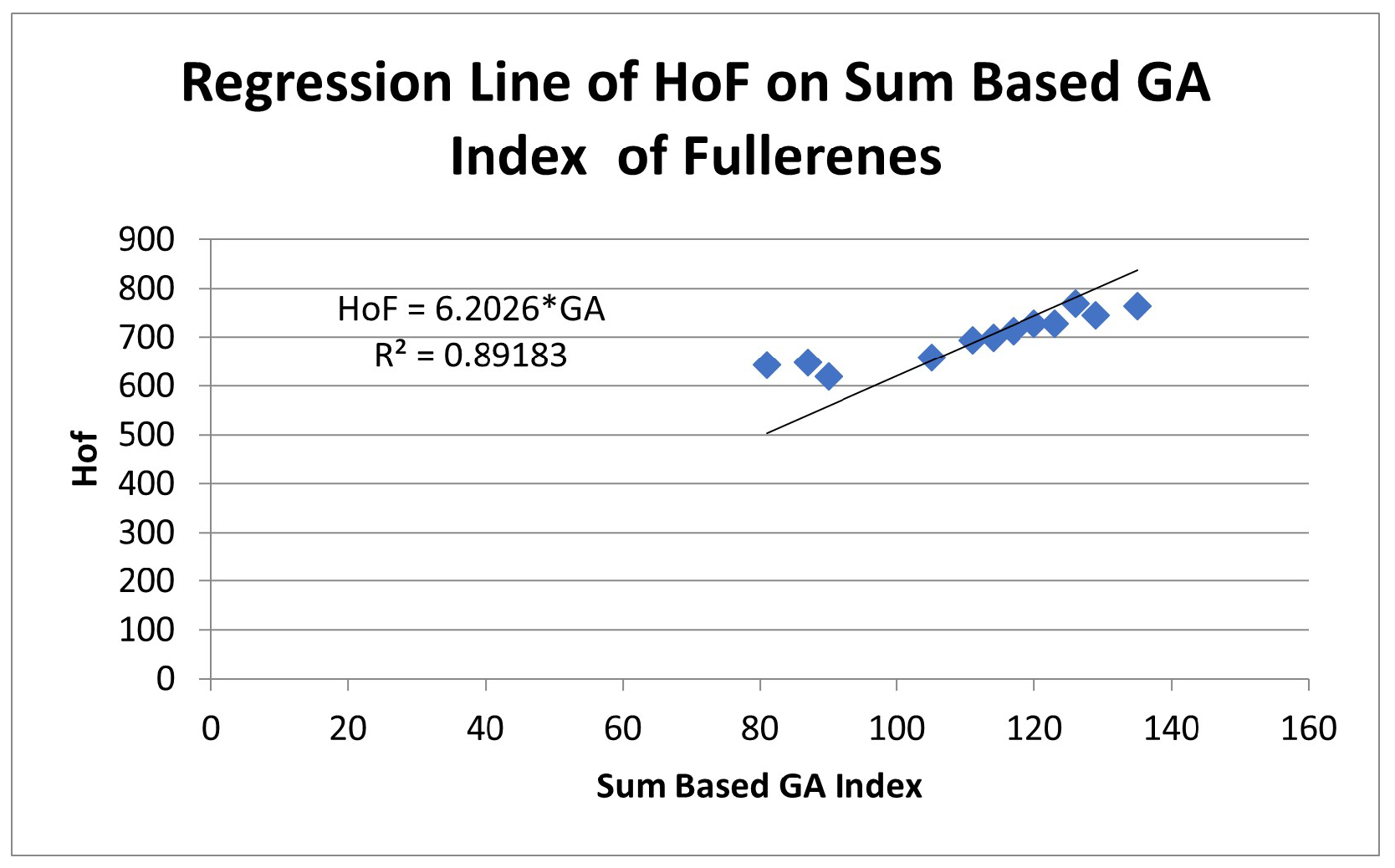
| Sum Based Index | Regression Relation with Sum Based Index | Coefficient of Determination | Correlation Coefficient |
|---|---|---|---|
| BEs | 0.1698 | 0.412035 | |
| RT-1 | 0.001615 | 0.040187 | |
| RT-2 | 0.086322 | 0.293806 | |
| SR-1 | 0.0007 | 0.02553 | |
| SR-2 | 0.000105 | 0.010231 | |
| Hof | 0.89183 | 0.94437 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheikh, U.; Tahir, Q.u.A.; Anjam, Y.N.; Pincak, R. Analysis of a Productive Topological Index Correlated to Fullerenes’ Physical Properties. Symmetry 2023, 15, 58. https://doi.org/10.3390/sym15010058
Sheikh U, Tahir QuA, Anjam YN, Pincak R. Analysis of a Productive Topological Index Correlated to Fullerenes’ Physical Properties. Symmetry. 2023; 15(1):58. https://doi.org/10.3390/sym15010058
Chicago/Turabian StyleSheikh, Umber, Qurrat ul Ain Tahir, Yasir Nadeem Anjam, and Richard Pincak. 2023. "Analysis of a Productive Topological Index Correlated to Fullerenes’ Physical Properties" Symmetry 15, no. 1: 58. https://doi.org/10.3390/sym15010058
APA StyleSheikh, U., Tahir, Q. u. A., Anjam, Y. N., & Pincak, R. (2023). Analysis of a Productive Topological Index Correlated to Fullerenes’ Physical Properties. Symmetry, 15(1), 58. https://doi.org/10.3390/sym15010058







