Observable Properties of Thin Accretion Disk in the γ Spacetime

Abstract

We study matter accretion in a static, axially symmetric and vacuum geometry describing the exterior gravitational field of a black hole mimicker called the $\gamma$ metric. We evaluate the thermal and optical properties of thin accretion disks, including the emission rate, luminosity and shadow, in the $gamma$ spacetime. Also, we explore the radial accretion of polytropic matter fields onto the central source and evaluate the thermal and optical properties of the infalling gas, such as temperature and luminosity. The results are discussed in the context of evaluating the possibility that the true nature of astrophysical black hole candidates may not be a black hole but some exotic compact object possessing a non-vanishing mass quadrupole moment.

1. Introduction

This paper explores the application of Noether’s theorem and spacetime symmetries in the field of relativistic astrophysics, particularly focusing on the dynamics of accretion disks around compact objects. Noether’s theorem, a fundamental principle in modern physics, relates symmetries to conservation laws, providing insights into the fundamental nature of astrophysical systems. Spacetime symmetries, in turn, involve transformations that leave the underlying spacetime structure invariant, enabling a deeper understanding of the behavior of accretion disks in various astrophysical contexts which are observed around objects such as black holes, neutron stars etc. and play an important role in energy transfer, matter accretion, and electromagnetic X-ray radiation emission. Understanding their dynamics requires a comprehensive theoretical framework that incorporates both Noether’s theorem and spacetime symmetries.

The study of accretion disks benefits from analyzing various symmetries present in the spacetime geometry that correspond to the conserved quantities, such as angular momentum, energy, the Carter constant and mass accretion rate. Spacetime symmetries involve coordinate transformations that preserve the geometric structure of spacetime. These symmetries lead to the discovery of conserved quantities, such as and the energy–angular momentum relation. The interplay between spacetime symmetries and accretion disk dynamics is thoroughly discussed.

Understanding the symmetries and conservation laws associated with accretion disks has practical implications for astrophysical observations. By analyzing observational data, one can infer the properties of accretion disks and the objects they surround.

The recent observation of the shadow of the supermassive black hole (SMBH) candidate in the galaxy M87 [1] has been followed by renewed interest in probing the nature of extreme gravitational compact objects (see, for example, [2,3,4]). This can be done by devising ways to obtain information regarding the object’s mass and spin from observations while imposing constraints on the possible values of additional parameters related to black hole mimickers, such as, for example, NUT charges (see, for example, [5]) or mass quadrupole moments (see, for example, [6]). Such observations may include the orbital motion of stars in the vicinity of an SMBH candidate, the spectra of accretion disks surrounding the compact object and the object’s ‘shadow’, such as that observed for the SMBH candidate in M87. For example, the mass of the SMBH candidate at the center of the Milky Way galaxy can be measured through the Newtonian motion of S2 stars as observed in infrared (IR) wavelengths [7,8]. Similarly, the inner edge of the shadow of the SMBH candidate in M87 provides information about the angular momentum of the central object [9]. Other parameters of gravitational compact objects can be estimated through detailed analysis of the thermal spectrum of accretion disks and fluorescent iron lines in low mass X-ray binaries (LMXBs) [10,11]. An overlap of different observations and different methods may, in principle, allow to constrain the values of additional parameters and determine the nature of the geometry surrounding the compact object.

In this paper, we shall consider accretion onto a specific class of static black hole mimickers and focus the attention on three main features, namely (i) the spectrum of the accretion disk, (ii) the shadow of the disk and (iii) radial accretion. An accretion disk is a complex structure formed by diffuse matter being in orbital motion in the close environment of a massive central compact object, where gravitational and frictional forces compress and raise the temperature of the orbiting matter, producing the thermal emission of highly energetic electromagnetic radiation. The frequency range of the produced electromagnetic radiation strongly depends on the total mass of a central gravitational object. The accretion rate may be sub-Eddington with extremely high opacity, forming a thin accretion disk, which is geometrically thin in the vertical direction and has a disk-like shape for the orbiting. Radiation pressure in the disk may be neglected and therefore the orbiting gas descends towards the central object following very tight spirals, resembling almost free Keplerian circular orbits. Thin disks are relatively luminous and generate thermal electromagnetic black body radiation. Following the pioneering paper by Shakura and Sunyaev [12] on thin accretion disks, the key properties of thin disks were elaborated by numerous authors (see for example [13,14]).

A general relativistic treatment is necessary for the description of the inner part of the accretion disk when the central gravitational object is a black hole. This was first developed by Novikov, Page and Thorne [15,16,17]. Simulated optical images of the accretion disk around the black hole were first elaborated by Luminet [18] and showed that an intrinsically symmetric black hole produces asymmetric images. This is due to the fact that the Doppler beaming of the emission by the particles required for centrifugal equilibrium in the strong gravitational field regime near the black hole produces a strong Doppler redshift on the receding side of the disk and a strong blueshift on the approaching side. Also, due to light bending, the disk appears distorted and is nowhere hidden by the black hole. Simulations, with fully relativistic models for the accretion disk, of the imaging of various massive candidates for the central gravitational compact object at the core of M87 were recently developed by Mizuno et al. [19] with the aim of constraining the possible existence of exotic compact objects.

In the present article, we consider matter accretion onto the Zipoy–Voorhees spacetime [20,21], also known as $\gamma$ metric [22] or q metric [23,24,25,26,27,28,29,30], which is a static and axially symmetric solution of the field equations in vacuum describing the gravitational field of a deformed compact object. This spacetime belongs to Weyl’s class of static vacuum solutions [31,32,33] and, due to its simplicity and its straightforward relation to the Schwarzschild solution, has been widely investigated in the past. The structure of the solution was explored in [34]. Interior solutions for the exterior metric were discussed in [35,36,37]. Several studies of the observable properties of the $\gamma$ metric can be found in the recent literature, including its optical appearance [38], the properties of thin accretion disks [22,39], shadows and light bending [40,41], geodesics motion [42,43], spinning particle motion [44], harmonic oscillations of test particles [45] and neutrino lensing [46,47]. Particle motion in the $\gamma$ spacetime in the presence of a scalar field was discussed in Ref. [48], while the motion of charged particles in the presence of a magnetic field was studied in [49,50]. The collision of massive particles in the vicinity of the singularity was studied in [51]. Its connection to other spacetimes such as wormholes was discussed in [52,53]. In this article, we build upon the previous results and investigate the luminosity and shadow of thin accretion disks in the $\gamma$ metric while developing, for the first time, a model of perfect fluid radial accretion based on [54].

The article is organized as follows. In Section 2, we review the general formalism to study geodesics in the $\gamma$ spacetime. In Section 3, we consider the thermal properties of thin accretion disks in the $\gamma$ metric following the Novikov–Thorne model [15] for black holes. In particular, we simulate the thermal spectrum of the disk and the optical image of the shadow. In Section 4, we study the thermal properties of matter radially falling onto the naked singularity in the $\gamma$-metric and elaborate on its contribution to the luminosity of the source. Finally, the last Section 5 summarizes the main results and their potential implications for astrophysical black hole candidates.

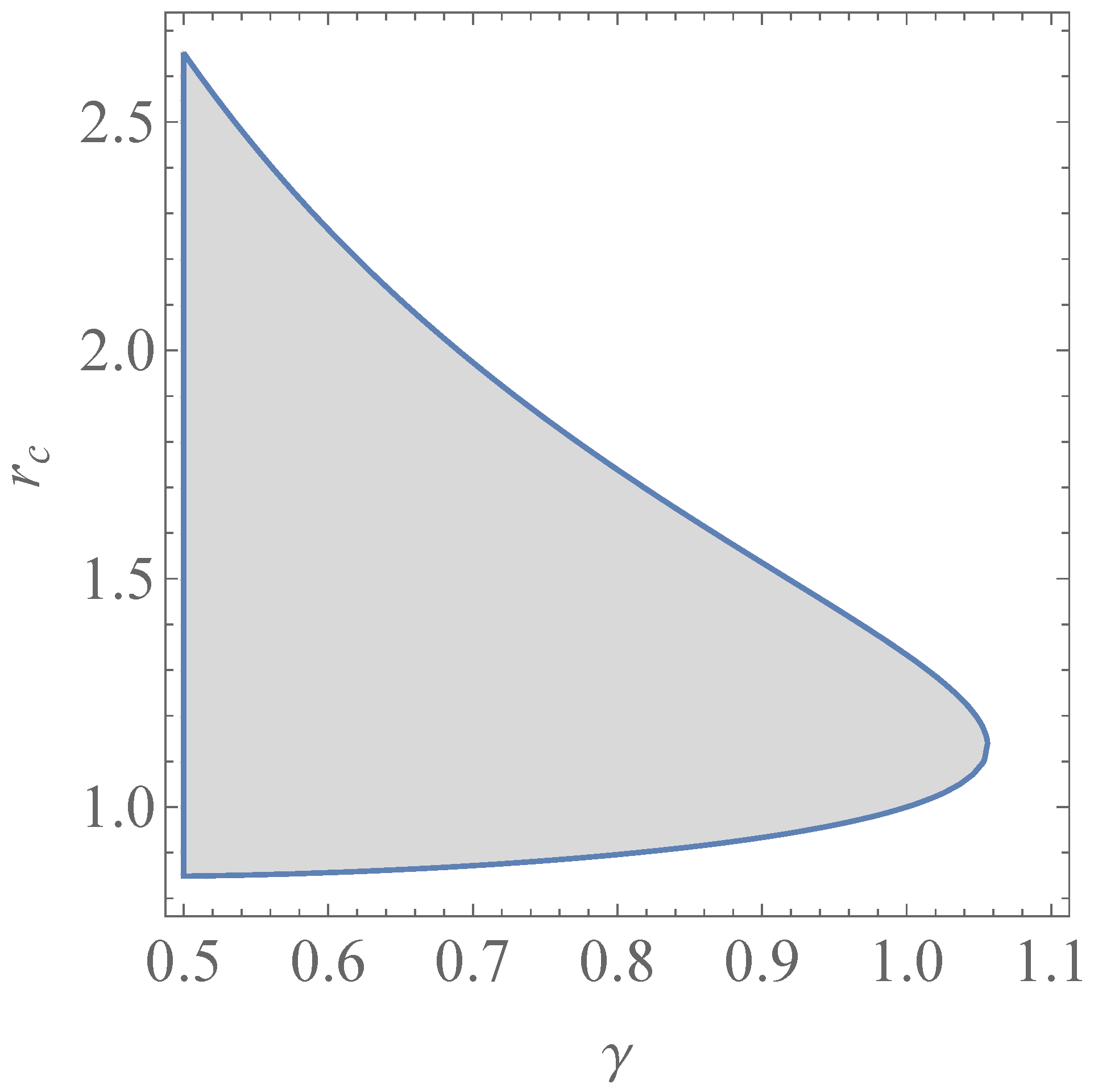
2. Geodesics in the $\gamma$-Metric

In spherical coordinates $x^{\alpha }=(t,r,\theta ,\varphi )$, the $\gamma$ spacetime is given by the line element [20,21]

$$\begin{array}{cc}\hfill d{s}^2=& -f^{\gamma }d{\left(ct\right)}^2+\frac{f^{{\gamma }^2-\gamma }}{h^{{\gamma }^2-1}}\left(\frac{d{r}^2}{f}+r^{2}d{\theta }^2\right)+f^{1-\gamma }{r}^2{sin}^2\theta d{\varphi }^2,\hfill \end{array}$$

(1)

with

$$\begin{array}{cc}\hfill & f\left(r\right)=1-\frac{2M_{\ast }}{\gamma r},h(r,\theta )=1-\frac{2M_{\ast }}{\gamma r}+\frac{M_{\ast }^2{sin}^2\theta }{{\gamma }^2{r}^2}.\hfill \end{array}$$

(2)

The line element depends on two parameters, namely $M_{\ast }$ and $\gamma$, restoring the units G and c, being the gravitational constant and the speed of light. In the first, we see that $M_{\ast }=GM/c^2$ represents the total gravitational mass of the compact object, which is exactly the mass monopole. The second $\gamma$ is the deformation parameter, which determines the departure of the geometry from spherical symmetry and is related to the mass quadrupole $M_2=(1-{\gamma }^2)M_{\ast }^3/\left(3{\gamma }^2\right)$. The geometry reduces to the Schwarzschild metric with a horizon of $r_{\ast }=2M_{\ast }$ for $\gamma =1$. Therefore, the $\gamma$ metric possesses a naked singularity located at $r_{\ast }$ for every value of $\gamma \ne 1$. Usually, the mass parameter is taken as $m=M_{\ast }/\gamma$ due to the fact that the function $f\left(r\right)$ assumes the more common form $f\left(r\right)=1-2m/r$. However, the total mass as measured by far away observers, i.e., the mass monopole, is given by $M_{\ast }=m\gamma$, and therefore it is useful and interesting to recast the line element using the gravitational mass $M_{\ast }$ in the place of m as done in Equation (1).

The $\gamma$ metric is a member of Weyl’s class of static and asymptotically flat vacuum solutions of the field equations that possess axial symmetry, and it is related to other interesting spacetimes besides Schwarzschild through the values of the two parameters. In Ref. [42], it was shown how the line element reduces to the Levi–Civita metric for $m\to \infty$, while for a large value of $\gamma$, i.e., for $\gamma \to \infty$, the metric reduces to the Curzon solution [55], which is the limit of an extremely oblate source. This is immediately visible with the line element given in the form of Equation (1) as

$$\begin{array}{cc}\hfill d{s}^2=& -e^{-2M_{\ast }/r}d{\left(ct\right)}^2+e^{2M_{\ast }/r}{r}^2{sin}^2\theta d{\varphi }^2+e^{2M_{\ast }/r-M_{\ast }^2{sin}^2\theta /r^2}\left(d{r}^2+r^{2}d{\theta }^2\right).\hfill \end{array}$$

(3)

To study accretion in the $\gamma$ metric, we must consider the motion of massive and massless particles in the exterior geometry. The geodesic equation is given by

$$\begin{array}{c}\hfill {\ddot{x}}^{\alpha }+{\mathrm{\Gamma }}_{\mu \nu }^{\alpha }{\dot{x}}^{\mu }{\dot{x}}^{\nu }=0,{\dot{x}}_{\alpha }{\dot{x}}^{\alpha }=ϵ,\end{array}$$

(4)

where ${\dot{x}}^{\alpha }=d{x}^{\alpha }/d\lambda$ is the four-velocity of the test particle, depending on the affine parametrization $\lambda$, ${\mathrm{\Gamma }}_{\mu \nu }^{\alpha }$ are the Christoffel symbols symmetric to the lower index, and $ϵ=0,-1$ determines whether the particle is massless ($ϵ=0$) or massive ($ϵ=-1$), respectively.

It is important to emphasize that in this geometry, it is impossible to separate the variables in the equation of motion, in general [56]. However, for simplicity, one can consider photon motion in the equatorial plane $\theta =\pi /2$, which is also the relevant case for astrophysical situations since accretion disks are expected to settle on the equatorial plane of the central object. Also, since the line element is static and axially symmetric, we always have two conserved quantities associated with time translations, namely the energy of particle $\mathcal{E}$, and rotations about the symmetry axis, namely the component of the angular momentum of the particle along the axis $\mathcal{L}$. These two constant of motion are related to Killing vector $\zeta$ and formulated as $\mathcal{E}={\partial }_t$ and $\mathcal{L}={\partial }_{\varphi }$. We first focus on the motion of massless particles (i.e., photons) in the $\gamma$ spacetime. From a standard textbook algebraic calculation, one can find that the orbit of the photon in the $\gamma$-metric is determined by the following equation:

$$\begin{array}{c}\hfill {\left[\frac{f^{\gamma -1}}{r^2}{\left(1-\frac{M_{\ast }}{\gamma r}\right)}^{1-{\gamma }^2}\left(\frac{dr}{d\varphi }\right)\right]}^2=\frac{1}{b^2}-\frac{f^{2\gamma -1}}{r^2}=U\left(r\right).\end{array}$$

(5)

where b is the impact parameter of the photon defined as $b=\mathcal{L}/\mathcal{E}$, with $\mathcal{L}$ being its angular momentum and $\mathcal{E}$ its energy as measured from infinity. The function $U\left(r\right)$ describes the effective potential for massless particles. The radius of the photon capture surface $r_{\mathrm{ph}}$ and the critical value of the impact parameter $b_{\mathrm{cr}}$ are found from the conditions $U^{\prime }\left(r\right)=U\left(r\right)=0$, which give

$$\begin{array}{cc}\hfill & r_{\mathrm{ph}}=M_{\ast }\left(2+\frac{1}{\gamma }\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & b_{\mathrm{cr}}=M_{\ast }\sqrt{4-\frac{1}{{\gamma }^2}}{\left(\frac{2\gamma +1}{2\gamma -1}\right)}^{\gamma }.\hfill \end{array}$$

(7)

It is evident from the outset that the parameter $\gamma$ must be at least one half, specifically $\gamma \ge 1/2$, to ensure the existence of a photon capture radius. Nonetheless, in certain references, such as [38,57,58], the lower values of $\gamma <1/2$ were discussed, which does not have physical meaning. As expected, for the case when $\gamma =1$, $b_{\mathrm{cr}}=3\sqrt{3}{M}_{\ast }$ reproduces the critical impact parameter in the Schwarzschild case. For $\gamma \to 1/2$, we have $b_{\mathrm{cr}}\to 4M_{\ast }$, while the asymptotic behavior of the critical impact parameter for $\gamma \to \infty$ is given by $b_{\mathrm{cr}}\to 2e{M}_{\ast }$ (where $e\simeq 2.7$ is the Euler number).

From the critical impact parameter, one can immediately calculate the capture cross section of photons, i.e., the area of the shadow, as $\sigma =\pi b_{\mathrm{cr}}^2$. The top panel in Figure 1 shows the dependence of the capture cross section $\sigma$ on the parameter $\gamma$. As one can see, the minimum value of the capture cross section is $\sigma =16\pi M_{\ast }^2\simeq 50M_{\ast }^2$, which is obtained for $\gamma =1/2$, while the maximum value is obtained asymptotically as $\gamma \to \infty$ and is $\sigma =4\pi e^2{M}_{\ast }^2\simeq 90M_{\ast }^2$. The bottom panel of Figure 1 shows the capture cross section of photons in the equatorial plane $\{x,y\}$. The inner ring represents $\sigma$ for $\gamma =1/2$, while the outer ring is $\sigma$ for $\gamma \to \infty$. This shows the interesting, though somewhat obvious, feature that even as $\gamma$ tends to infinity, the size of the shadow of the object will remain finite as long as the total mass of the object remains finite.

Now, we focus on the motion of massive particles. As mentioned, the symmetry of the line element (1) implies the conservation of energy and angular momentum of the test particles. To describe particles on accretion disks, we restrict our attention to circular orbits in the equatorial plane so that the particle’s four-velocity is ${\dot{x}}^{\alpha }=(\dot{t},0,0,\dot{\varphi })$. The explicit expressions for the specific energy $\mathcal{E}$, specific angular momentum $\mathcal{L}$, and angular velocity $\mathrm{\Omega }$ of the test particles at a radius r as measured by a distant observer can be obtained from

$$\begin{array}{cc}\hfill & \mathcal{E}=-\frac{g_{tt}}{\sqrt{-g_{tt}-{\mathrm{\Omega }}^2{g}_{\varphi \varphi }}},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \mathcal{L}=\frac{g_{\varphi \varphi }\mathrm{\Omega }}{\sqrt{-g_{tt}-{\mathrm{\Omega }}^2{g}_{\varphi \varphi }}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \mathrm{\Omega }=\frac{d\varphi }{dt}=\sqrt{-\frac{g_{tt,r}}{g_{\varphi \varphi ,r}}}.\hfill \end{array}$$

(10)

Our aim is to study the stability of circular motion and find the location of the marginally stable orbit, also known as the innermost stable circular orbit (ISCO), around the source. The radius of the marginally stable orbit is responsible for the stationary point of the specific energy and specific angular momentum of test particles, which can be found from the conditions $d\mathcal{E}/dr=d\mathcal{L}/dr=0$. In the $\gamma$ spacetime, this takes the form [49,50]

$$\begin{array}{c}\hfill r_{\pm }=M_{\ast }\left(3+\frac{1}{\gamma }\pm \sqrt{5-\frac{1}{{\gamma }^2}}\right).\end{array}$$

(11)

The two radii coincide at $r_{+}=r_{-}=M_{\ast }(3+\sqrt{5})$ for $\gamma =1/\sqrt{5}$; for $\gamma <1/\sqrt{5}$, there are no marginally stable circular orbits, and stable circular orbits are allowed at every distance from the singularity $r_{\ast }$. Notice that, in general, for $\gamma >1/\sqrt{5}$, there are two radii for marginally stable orbits. The physically relevant one for the description of the inner edge of an accretion disk is the outer radius $r_{+}=r_{\mathrm{ms}}$, which has maximum value $r_{+}^{\max }=(3+\sqrt{10})M_{\ast }$ at $\gamma =\sqrt{2/5}$. Finally, the asymptotic behavior of the marginally stable orbit is found as $r_{\mathrm{ms}}\to (3+\sqrt{5})M_{\ast }$ for $\gamma \to \infty$. See Figure 2 for details.

Note that there is another type of circular orbit for test particle particles usually called the marginally bound orbit (MBO). In this orbit, the energy of the test particle should be equal to its rest energy i.e., $\mathcal{E}=1$. The MBO radius $r_{\mathrm{mb}}$ in the $\gamma$-metric is found as the solution to the following equation:

$$\begin{array}{c}\hfill {\left(1-\frac{2M_{\ast }}{\gamma r}\right)}^{\gamma }=\frac{\gamma r-M_{\ast }-2\gamma M_{\ast }}{\gamma r-M_{\ast }-\gamma M_{\ast }}.\end{array}$$

(12)

It is impossible to find such a solution in analytical form; however, one can find the dependence of the MBO radius from the parameter $\gamma$ numerically as can be seen in Figure 2. Keep in mind that the MBO is always located closer to the compact object than the marginally stable orbit. In the case when $\gamma =1$, the solution of Equation (12) reduces to $r_{\mathrm{mb}}=4M_{\ast }$, which is the known value for the Schwarzschild spacetime, while for the large value of $\gamma$ (i.e., in the limit of the Curzon spacetime), the MBO radius goes to the asymptotic value of $r_{\mathrm{mb}}=3.16M_{\ast }$.

Figure 2 illustrates the dependence on $\gamma$ of the characteristic radii, namely, singularity $r_{\ast }$, marginally stable $r_{\mathrm{ms}}$, marginally bound $r_{\mathrm{mb}}$, photon capture $r_{\mathrm{ph}}$ and critical impact parameter for photons $b_{\mathrm{cr}}$. As one can see, with the exception of the critical impact parameter, all radii decrease with $\gamma$ for oblate sources, i.e., when $\gamma >1$. Also, the radius of the marginally stable orbit for prolate sources, namely when $\gamma <1$, grows to the maximum value $(3+\sqrt{10})M_{\ast }$ for $\gamma =\sqrt{2/5}$ and then decreases up to asymptotical value $(3+\sqrt{5})M_{\ast }$ as shown in Figure 2. In principle, this behavior of the marginally stable orbit can be explained as follows: test particles follow geodesic trajectories which are determined by the gravitational and centrifugal forces. In the range $1/2<\gamma <\sqrt{2/5}$, the gravitational force dominates, while in the range $\sqrt{2/5}<\gamma <\infty$, the centrifugal force prevails. Another interesting feature of the $\gamma$-metric is that photonsphere decreases while impact parameters increase with the increasing of the $\gamma$ parameter. It also indicates the difference of the $\gamma$ spacetime from other spherical symmetrical spacetimes. This effect arises due to the specific properties of the spacetime. It is well known that the gravitational force is mainly described through the zero-th component of the metric tensor, i.e., $g_{tt}$. In contrast, the centrifugal force is described by $g_{\varphi \varphi }$, which depends on the $\gamma$ parameter. Therefore, the critical impact parameter of the photon monotonically increases with the increase in the $\gamma$ parameter, unlike the photosphere, and even it can be greater than the radius of marginal orbit in the case when $\gamma \simeq 5$. Note that the asymptotics of the critical impact parameter is located at $b_{\mathrm{cr}}=2e{M}_{\ast }$, which can be easily found in Figure 2.

It is also interesting to consider the orbital velocity of the test particles as measured by a local frame. In Ref. [59], it was shown that the orbital velocity of test particles in the $\gamma$ metric is given by

$$\begin{array}{c}\hfill v=c\sqrt{\frac{\gamma M_{\ast }}{\gamma r-M_{\ast }-\gamma M_{\ast }}}.\end{array}$$

(13)

In the Schwarzschild spacetime, the above expression reduces to $v=c\sqrt{M_{\ast }/(r-2M_{\ast })}$, while for the Curzon spacetime (i.e., $\gamma \to \infty$), it becomes $v=c\sqrt{M_{\ast }/(r-M_{\ast })}$. Figure 3 shows the radial dependence of the orbital velocity for different values of $\gamma$ (top panel). As expected, the orbital velocity of the test particle will become equal to the speed of light at the photon capture radius. Also, it is easy to check that in the Schwarzschild case, the orbital velocity of a test particle on the marginally stable orbit $r_{\mathrm{ms}}$ equals half the speed of light, i.e., $v_{\mathrm{ms}}=c/2$, while in the Curzon case, it becomes $v_{\mathrm{ms}}=c\sqrt{\sqrt{5}-2}\sim 0.25c$. The maximum orbital velocity for a particle at $r_{\mathrm{ms}}$ is $v_{\max }=c/\sqrt{3}\simeq 0.58c$, and it is obtained for $\gamma =1/2$. The bottom panel of Figure 3 shows the dependence of the orbital velocity of test particles at the marginally stable orbit on the parameter $\gamma$.

3. Accretion onto the $\gamma$-Metric: Thin Disks

We now consider the thermal properties of thin accretion disks following the framework originally developed for black holes by Novikov–Thorne [15] and extend the treatment to the $\gamma$ spacetime. The Novikov–Thorne accretion disk is a theoretical model of an accretion disk around a massive black hole. However, this model is based on the principles of general relativity, and it provides a detailed description of how matter spirals into a black hole. However, this model can be applied to the exotic object, such as that given by $\gamma$ spacetime. The Novikov–Thorne model incorporates the effects of general relativity, which describes the curvature of spacetime around massive objects. In the vicinity of a black hole and exotic objects, the spacetime is highly curved, leading to phenomena such as gravitational time dilation and frame dragging. The accretion process around a black hole or an extremely compact object is possible in the region $r>r_{\mathrm{ms}}$, where $r_{\mathrm{ms}}$ is the radius of the ISCO of the test particles. This means that the radius of the marginally stable orbit can be taken as the inner edge of the thin accretion disk $r_{\mathrm{in}}=r_{\mathrm{ms}}$, while the outer edge $r_{\mathrm{out}}$ can be chosen freely. For our calculation, we fixed it as $r_{\mathrm{out}}=30M_{\ast }>>r_{\mathrm{in}}$. When particles falling from rest at infinity accrete onto the central object, they heat up, and their gravitational energy is converted into radiation and released back into space.

The Novikov–Thorne model has been influential in the field of astrophysics and has been used to interpret observations of black hole X-ray binaries and active galactic nuclei (AGN). It provides a theoretical framework for understanding how matter accretes onto black holes and how the release of energy in the form of radiation can be used to study these extreme cosmic objects. Therefore, in order to model the thin accretion disk, one needs to make the following assumptions:

(i)

Matter in the accretion disk loses energy as it spirals inward toward the central object due to friction and gravitational forces. This energy loss results in the emission of radiation, primarily in the form of X-rays and other high-energy photons.

(ii)

The accretion disk is envisioned as a flattened, rotating structure composed of gas, dust, and other matter. As matter falls inward, it follows nearly circular orbits within the disk, gradually losing angular momentum and spiraling closer to the black hole. The disk is assumed to be geometrically thin and optically thick, which means that the radial extension $\Delta r=r_{\mathrm{out}}-r_{\mathrm{in}}$ of the disk is much larger than its thickness $h<<\Delta r$.

(iii)

According to the Novikov–Thorne model, there is an innermost stable circular orbit where matter can orbit the black hole or exotic object without rapidly falling in. The radius of this orbit depends on the black hole’s mass and angular momentum. Inside the ISCO, matter rapidly plunges into the central object.

(iv)

The innermost part of the accretion disk lies very close to the black hole’s event horizon—the point beyond which nothing can escape the black hole’s gravitational pull. Radiation emitted by matter near the event horizon is greatly redshifted, making it difficult to detect.

(v)

The motion of gas particles in the disk approximately follows a circular Keplerian orbit, and therefore it is well described by test particles on circular orbits.

(vi)

The torque in the zone near the inner edge of the accretion disk is negligible.

(iv)

The mass accretion rate of the thin disk can be considered constant and it should be less than the Eddington mass rate. More precisely, $\dot{\mathcal{M}}\simeq (0.03-0.5){\dot{\mathcal{M}}}_{\mathrm{Edd}}$, where the Eddington mass rate is defined as

$${\dot{\mathcal{M}}}_{\mathrm{Edd}}=\frac{4\pi GM{m}_p}{c{\sigma }_T},$$

where M is the mass of the gravitational object, $m_p$ is the proton mass and ${\sigma }_T$ is the Thompson cross section of the electron. In units of solar mass, we have ${\dot{\mathcal{M}}}_{\mathrm{Edd}}\simeq 2.33\times {10}^{18}\left(M/M_{\odot }\right)\mathrm{g}·{\mathrm{s}}^{-1}$.

(vii)

The model predicts that the radiation emitted by the accretion disk will have a characteristic spectrum. The spectrum is influenced by factors such as the black hole’s mass and spin, and it includes a distinctive peak in the X-ray part of the electromagnetic spectrum.

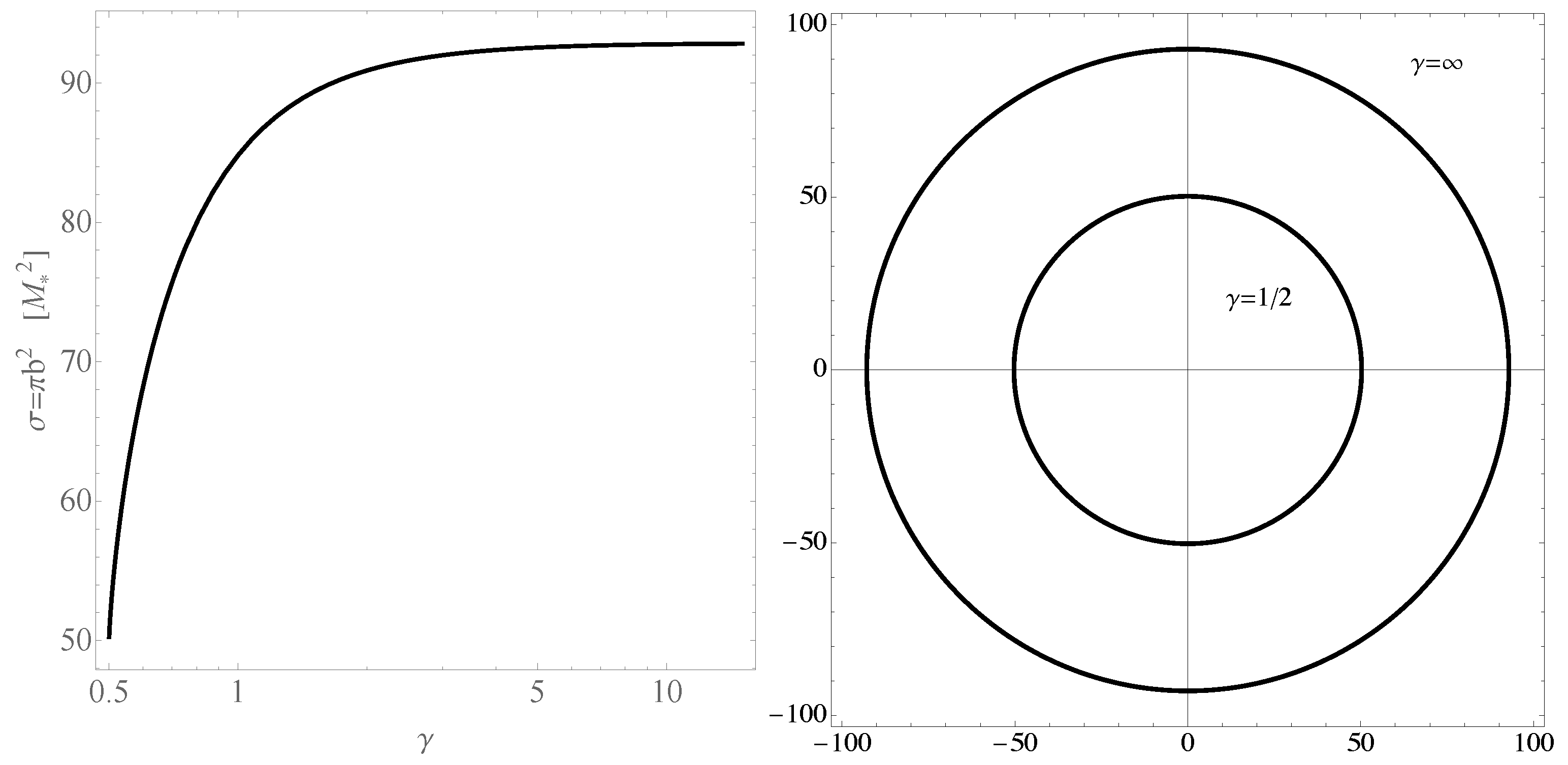
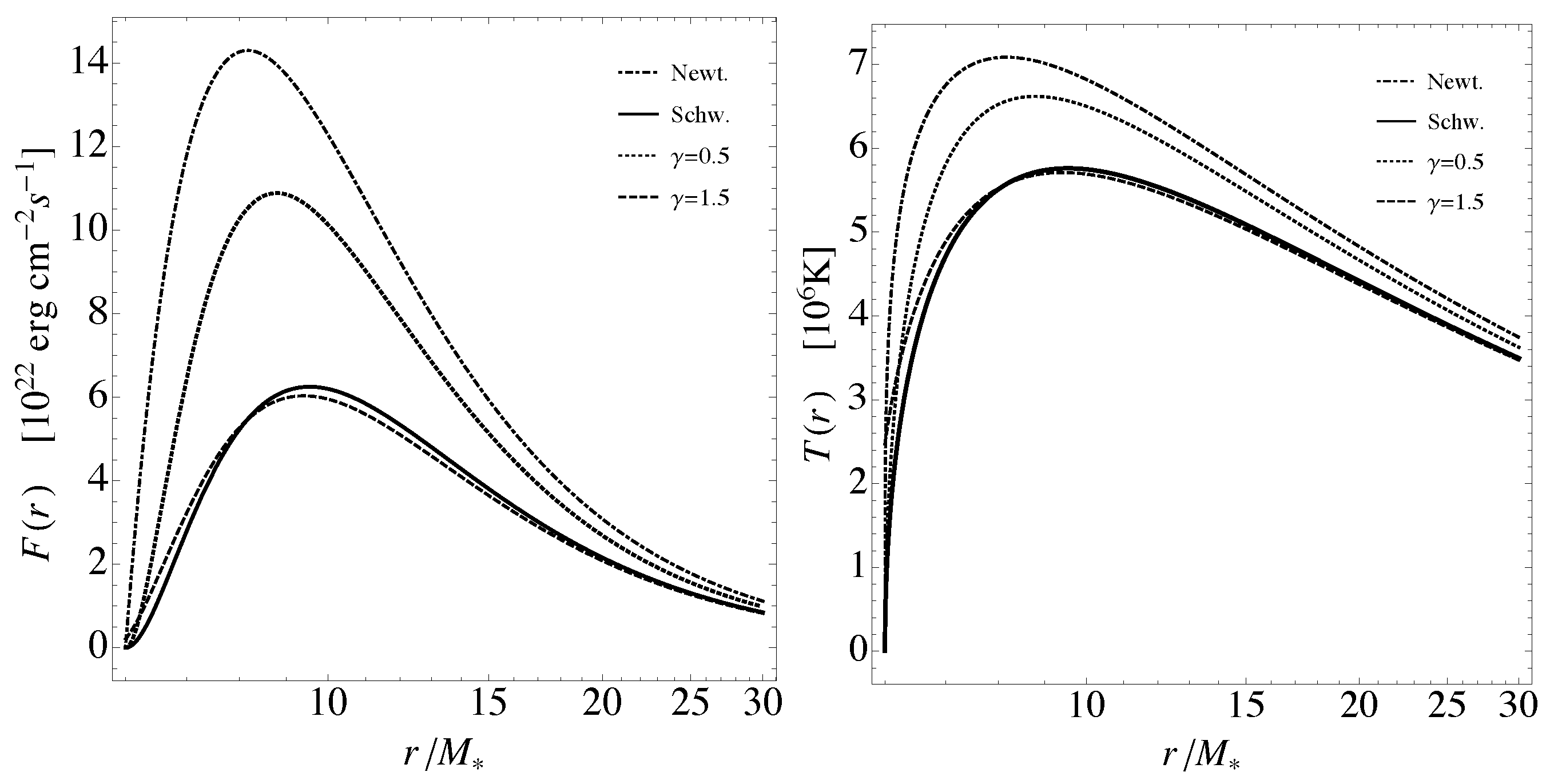
3.1. Temperature Profile of the Disk

To model the spectrum of the light emitted by the accretion disk, we also need to make an assumption about the spectral profile. The most natural choice, which is also accurate enough as a first approximation, is of course to assume that the disk emits with the black body spectrum. According to the Boltzmann law, the energy emission rate is proportional to the fourth power of the temperature of the disk i.e., $\mathcal{F}\left(r\right)\sim T^4\left(r\right)$. So, the effective temperature of the thin disk is determined as

$$\begin{array}{c}\hfill T\left(r\right)=\sqrt[4]{\frac{\mathcal{F}\left(r\right)}{{\sigma }_B}},\end{array}$$

(14)

where ${\sigma }_B$ is the Stefan–Boltzmann constant. The flux of the radiant energy of the disk can then be expressed as [16,17]

$$\begin{array}{c}\hfill \mathcal{F}\left(r\right)=-\frac{\dot{\mathcal{M}}}{4\pi \sqrt{-\tilde{g}}}\frac{{\mathrm{\Omega }}^{\prime }}{{(\mathcal{E}-\mathrm{\Omega }\mathcal{L})}^2}{\int }_{r_{\mathrm{ms}}}^{r}dr(\mathcal{E}-\mathrm{\Omega }\mathcal{L}){\mathcal{L}}^{\prime },\end{array}$$

(15)

where a prime ${(}^{\prime })$ denotes the derivative with respect to radial coordinate r and $\tilde{g}=\sqrt{-g_{tt}{g}_{rr}{g}_{\varphi \varphi }}$ is the determinant of the spacetime metric at the equatorial plane. After some algebraic manipulations, the energy flux emitted by the disk in the $\gamma$-metric can be found as

$$\begin{array}{cc}\hfill \mathcal{F}\left(r\right)& =-\frac{\dot{\mathcal{M}}{c}^2}{8\pi }\frac{\gamma \sqrt{M_{\ast }}\left(3{\gamma }^2{r}^2-6\gamma (\gamma +1)M_{\ast }+2(\gamma +1)(2\gamma +1)M_{\ast }^2\right)}{r^{3/2}{(\gamma r-2M_{\ast })}^{3/2}\sqrt{\gamma r-M_{\ast }-\gamma M_{\ast }}(\gamma r-M_{\ast }-2\gamma M_{\ast })}\hfill \\ \hfill & \times \{\sqrt{\left(\frac{r}{M_{\ast }}-\frac{2}{\gamma }\right)\left(1-\frac{M_{\ast }}{r}-\frac{M_{\ast }}{\gamma r}\right)}+\sqrt{1+\frac{1}{\gamma }}\left[F\left(\varphi |k\right)+E\left(\varphi |k\right)\right]+\frac{1-2\gamma }{\sqrt{\gamma (\gamma +1)}}\mathrm{\Pi }\left(n;-\varphi |k\right)\hfill \\ & -\sqrt{\left(\frac{r_{\mathrm{ms}}}{M_{\ast }}-\frac{2}{\gamma }\right)\left(1-\frac{M_{\ast }}{r_{\mathrm{ms}}}-\frac{M_{\ast }}{\gamma r_{\mathrm{ms}}}\right)}-\sqrt{1+\frac{1}{\gamma }}\left[F\left({\varphi }_{\mathrm{ms}}|k\right)+E\left({\varphi }_{\mathrm{ms}}|k\right)\right]-\frac{1-2\gamma }{\sqrt{\gamma (\gamma +1)}}\mathrm{\Pi }\left(n;-{\varphi }_{\mathrm{ms}}|k\right)\}.\hfill \end{array}$$

(16)

where $F\left(\varphi |k\right)$, $E\left(\varphi |k\right)$, and $\mathrm{\Pi }\left(n;\varphi |\alpha \right)$ are, respectively, the incomplete elliptic integrals of the first, second and third kinds defined as [60]

$$\begin{array}{cc}\hfill & F\left(\varphi |k\right)={\int }_0^{\varphi }\frac{d\theta }{\sqrt{1-k^2{sin}^2\theta }},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & E\left(\varphi |k\right)={\int }_0^{\varphi }d\theta \sqrt{1-k^2{sin}^2\theta },\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & \mathrm{\Pi }\left(n;\varphi |k\right)={\int }_0^{\varphi }\frac{d\theta }{(1-n^2{sin}^2\theta )\sqrt{1-k^2{sin}^2\theta }}.\hfill \end{array}$$

(19)

with

$$\varphi ={sin}^{-1}\sqrt{\frac{M_{\ast }}{r}\left(1+\frac{1}{\gamma }\right)},k=\frac{2}{\gamma +1},n=\frac{2\gamma +1}{\gamma +1}.$$

In the limiting case $\gamma =1$, the energy emission rate reduces to that of the Schwarzschild spacetime as [16,18]

$$\begin{array}{cc}\hfill & \mathcal{F}\left(r\right)=\frac{3\dot{\mathcal{M}}{c}^2}{8\pi M_{\ast }^2}{\left(\frac{M_{\ast }}{r}\right)}^3{\left(1-\frac{3M_{\ast }}{r}\right)}^{-1}\left[1-\sqrt{\frac{6M_{\ast }}{r}}+\sqrt{\frac{3M_{\ast }}{r}}log\sqrt{\frac{\sqrt{r}+\sqrt{3M_{\ast }}}{\sqrt{r}-\sqrt{3M_{\ast }}}\frac{\sqrt{2}-1}{\sqrt{2}+1}}\right],\hfill \end{array}$$

(20)

while in the classical limit, the energy emission rate reduces to the expression obtained by Shakura–Sunyaev in the form [12,61]:

$$\begin{array}{c}\hfill \mathcal{F}\left(r\right)=\frac{3\dot{\mathcal{M}}{c}^2}{8\pi M_{\ast }^2}{\left(\frac{M_{\ast }}{r}\right)}^3\left(1-\sqrt{\frac{6M_{\ast }}{r}}\right).\end{array}$$

(21)

From the above, we can determine the energy emission rate and the effective temperature of the thin disk in the $\gamma$ spacetime and consider whether they may be used to distinguish it from the Schwarzschild spacetime. The energy emission rate and the effective temperature as given by Equations (16) and (14) are shown in Figure 4.

Another important feature of the accretion disk is related to the radiative efficiency $\eta$ of the disk. This is an important quantity that does not depend on the coordinate system, and it can be expressed as the difference between the specific energies of the particle at infinity and at the marginally stable orbit, i.e., $\eta ={\mathcal{E}}_{\infty }-{\mathcal{E}}_{\mathrm{ms}}$. Since the specific energy of the particle at infinity is set to one, i.e., ${\mathcal{E}}_{\infty }=1$, then $\eta$ for the accretion disk in the $\gamma$-metric takes the form

$$\begin{array}{c}\hfill \eta =1-\sqrt{\frac{2\gamma +\sqrt{5{\gamma }^2-1}}{\gamma +\sqrt{5{\gamma }^2-1}}{\left(\frac{3\gamma -1+\sqrt{5{\gamma }^2-1}}{3\gamma +1+\sqrt{5{\gamma }^2-1}}\right)}^{\gamma }}.\end{array}$$

(22)

The dependence of the energy efficiency $\eta$ on the parameter $\gamma$ is illustrated in Figure 5. The maximum value of the radiative efficiency in the $\gamma$ spacetime is approximately $\simeq 7\%$, and is obtained for $\gamma =1/2$, while the minimum value is around $5.5\%$, slightly smaller than the Schwarzschild case, and is obtained asymptotically as $\gamma \to \infty$. Notice that the energy efficiency in the Schwarzschild spacetime is around $\simeq 5.7\%$, which suggests that it may be difficult to distinguish oblate sources from black holes by measuring $\eta$.

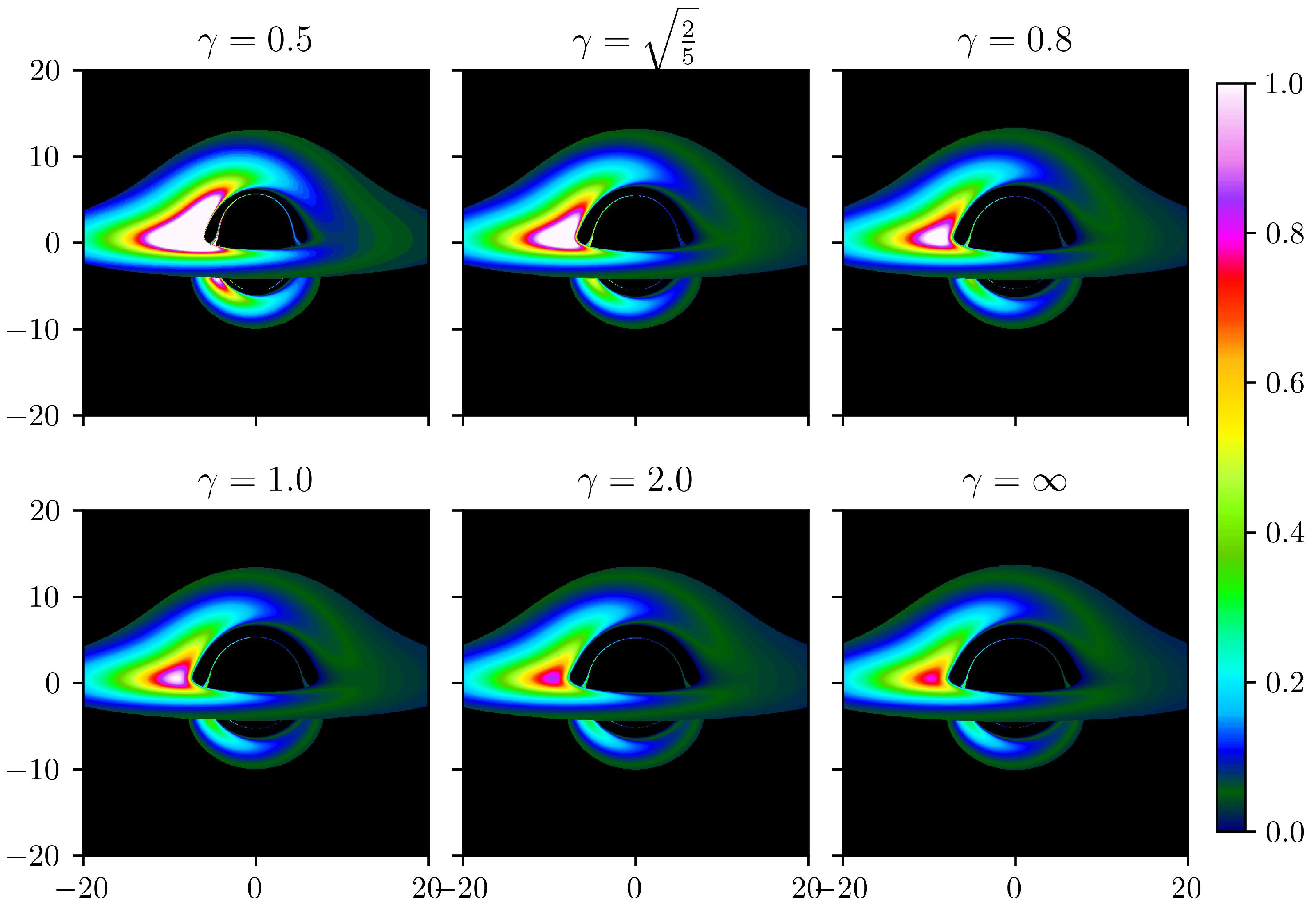
3.2. Thermal Spectrum and Image of the Disk

Using the expression for the temperature profile on the disk T in Equation (14) and assuming thermal black body emission from the disk, we can obtain the spectral luminosity $L\left(\nu \right)$ of the disk as a function of the frequency of the emitted radiation, which takes the following form:

$$\begin{array}{c}\hfill L\left(\nu \right)=\frac{8\pi hcos\chi }{c^2}{\int }_{r_{\mathrm{in}}}^{r_{\mathrm{out}}}{\int }_0^{2\pi }\frac{{\nu }_e^{3}rdrd\varphi }{exp\left(\frac{h{\nu }_e}{k_{B}T}\right)-1},\end{array}$$

(23)

where $\chi$ is the inclination angle relative to the symmetry axis, and $r_{\mathrm{in}}$ and $r_{\mathrm{out}}$ are the locations of the inner and outer edges of the disk. The frequency $\nu$ is measured by a distant observer, while ${\nu }_e$ is the frequency of photons emitted from the accretion disk. These two frequencies are related to each other through the red-shift factor, i.e., $g={\nu }_e/\nu$, which can be expressed as

$$\begin{array}{cc}\hfill g=& \left(1+\mathrm{\Omega }rsin\varphi sin\chi \right)\sqrt{\frac{\gamma r-M_{\ast }-\gamma M_{\ast }}{\gamma r-M_{\ast }-2\gamma M_{\ast }}{\left(1-\frac{2M_{\ast }}{\gamma r}\right)}^{-\gamma }}.\hfill \end{array}$$

(24)

Figure 6 shows the total spectral luminosity emitted by the thin accretion disk for the different values of the inclination angle $\chi$ as well as the deformation parameter $\gamma$. Notice that at $\chi =\pi /2$ the spectral luminosity is zero because of the $cos\chi$ factor in Equation (23). As one can see in each panel of Figure 6, in the low-frequency region (infrared (IR), optical and ultraviolet (UV) band), there are almost no differences between the spectra of the different cases; however, for the high-frequency region, in particular, the X-ray band, there is a measurable difference between each curve. Also, the frequency corresponding to the maximum depends on the value of $\gamma$, suggesting that it could be possible in principle to test the nature of the geometry via such kinds of observations.

In order to better understand the optical properties of the geometry in the $\gamma$ metric and investigate its viability as the description of the exterior of an astrophysical exotic compact source, it is useful to consider its shadow, simulating the image of the thin accretion as pictured by a distant observer. It is assumed that the distant observer is static relative to the coordinates ($r,\theta ,\varphi$), i.e., observing the compact object from a fixed distance much larger than the characteristic radii of the spacetime and at a fixed inclination angle, while the emitters, i.e., the particles on the disk, follow Keplerian orbits. To evaluate the frequency shift of the photons emitted from the accretion disk and received by the observer, one can easily use the redshift factor g, which is given in Equation (24). As we mentioned before, the inner edge of the disk is located as the marginally stable orbit $r_{\mathrm{ms}}$, while the outer edge is to be chosen arbitrarily. Figure 7, Figure 8 and Figure 9 show the shadow of the thin disk in the $\gamma$-metric for the different values of $\gamma$ and different inclination angles. As previously indicated, it is important to note that the distortion parameter must exceed one half for meaningful results ($\gamma \ge 1/2$). If this condition is not met, the impact parameter of the photon will yield complex values. Consequently, the cross section of the photon interaction with a $\gamma$ object is well defined only when $\gamma \ge 1/2$. As one can see from each figure, the temperature of the disk (as well as energy emission rate) becomes large for small values of the $\gamma$ parameter, while for the largest value of the $\gamma$ parameter, in particular, in Curzon spacetime (i.e., $\gamma \to \infty$), the temperature of the disk will be low.

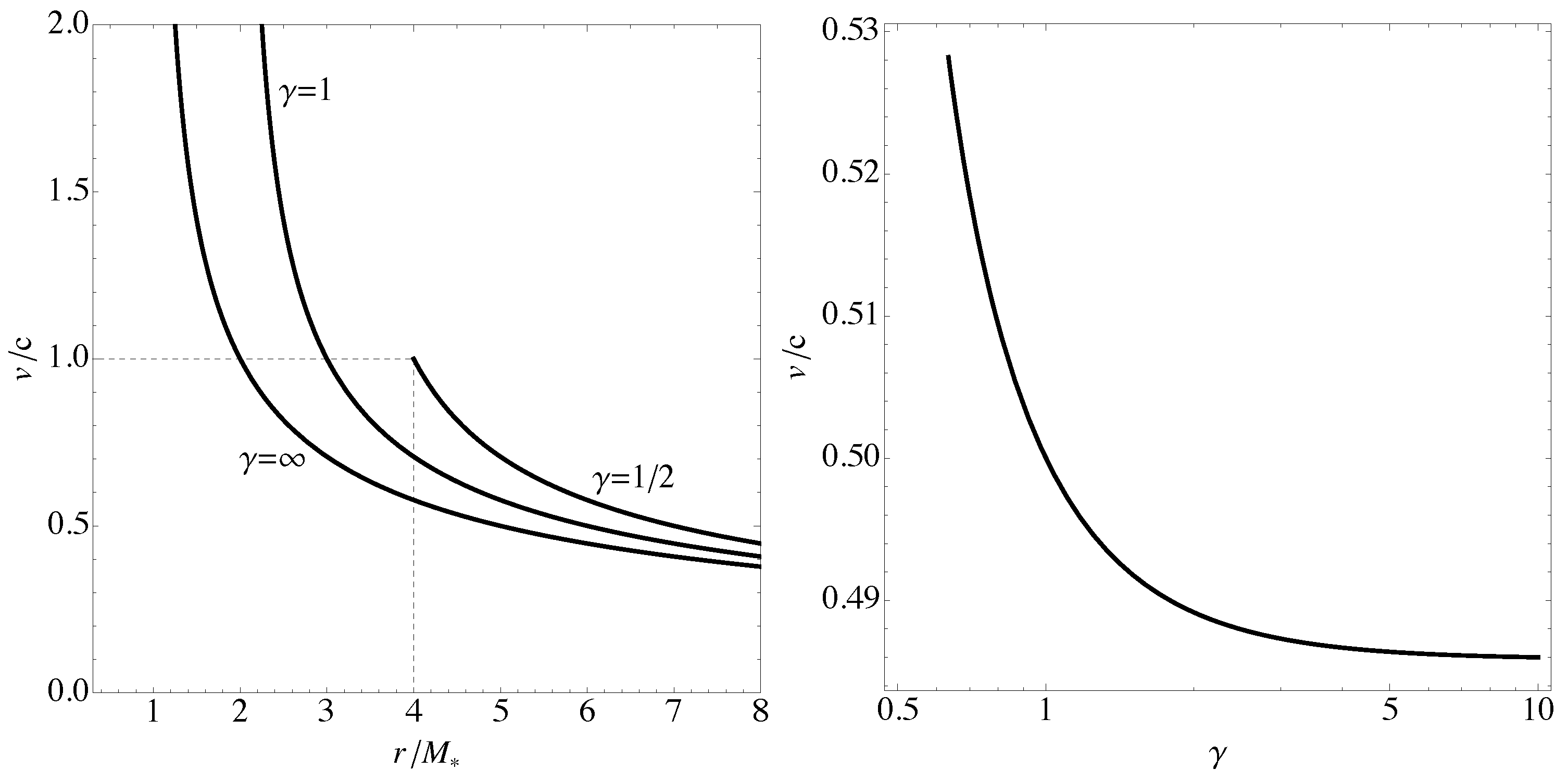
4. Accretion onto the $\gamma$ Metric: Radial Infall

In this section, we discuss the radiation emitted by radially infalling matter onto the naked singularity of the $\gamma$ metric. This is another aspect of matter accretion onto compact objects that may be relevant for observations of astrophysical black hole candidates and has not been thoroughly investigated in theoretical models of black hole mimickers. Following [54], the mass flux and energy momentum tensor of the infalling matter are given by

$$\begin{array}{c}\hfill J^{\alpha }=\rho u^{\alpha },T_{\alpha \beta }=(P+\rho )u_{\alpha }{u}_{\beta }+P{g}_{\alpha \beta },\end{array}$$

(25)

where $\rho$ and P are, respectively, the mass density and pressure of the matter, and $u^{\alpha }={\dot{x}}^{\alpha }$ is its normalized four velocity. According to the Noether theorem, the conservation of mass flux and energy flux can be expressed as

$$\begin{array}{c}\hfill {\nabla }_{\alpha }{J}^{\alpha }=0,{\nabla }_{\alpha }{T}_{\beta }^{\alpha }=0,\end{array}$$

(26)

where ${\nabla }_{\alpha }$ stands for the covariant derivative. For simplicity, we consider radially infalling matter onto the naked singularity in the equatorial plane ($\theta =\pi /2$) and the four-velocity of matter reduces to $u^{\alpha }=(u^t,u^r,0,0)$. In general, even for a spherically symmetric gravitating object, the matter in the accretion disk will move in an azimuthal direction. However, for simplicity in the Bondi accretion model, it is negligible (see, e.g., [54]). By integrating Equation (26), we obtain

$$\begin{array}{c}\hfill \rho u^r\sqrt{-g}=\mathrm{const},(P+\rho )u_t{u}^r\sqrt{-g}=\mathrm{const},\end{array}$$

(27)

and using the normalization of the four-velocity, hereafter simple algebraic manipulations, we obtain the following expressions:

$$\begin{array}{c}\hfill u_t^2=f^{\gamma }+u^2{\left(\frac{f}{h}\right)}^{{\gamma }^2-1},h={\left(1-\frac{M_{\ast }}{\gamma r}\right)}^2,\end{array}$$

(28)

where $u_t=-f^{\gamma }dt/d\lambda$ and $u=u^r=dr/d\lambda$. Note that in the Schwarzschild spacetime, (i.e., $\gamma =1$), Equation (28) takes the simple form $u_t^2=1-2M_{\ast }/r+u^2$ as written in Ref. [54].

Taking into account Equation (28), Equation (27) is rewritten as follows:

$$\begin{array}{cc}\hfill C_1& =\rho u{r}^{2}G\left(r\right),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill C_2& ={\left(1+\frac{P}{\rho }\right)}^2\left(f^{\gamma }+u^{2}H\left(r\right)\right),\hfill \end{array}$$

(30)

where

$$\begin{array}{c}\hfill G\left(r\right)=f^{{\gamma }^2-\gamma }{h}^{1-{\gamma }^2},H\left(r\right)={\left(\frac{f}{h}\right)}^{{\gamma }^2-1}.\end{array}$$

(31)

Hereafter differentiating Equations (29) and (30) and eliminating $d\rho$ from the final expression, one can obtain

$$\begin{array}{c}\hfill \left[V^2\frac{d}{dr}ln\left(r^{2}G\left(r\right)\right)-\frac{\gamma f^{\prime }{f}^{\gamma -1}+u^2{H}^{\prime }\left(r\right)}{2\left(f^{\gamma }+u^{2}H\left(r\right)\right)}\right]dr+\frac{du}{u}\left[V^2-\frac{u^{2}H\left(r\right)}{f^{\gamma }+u^{2}H\left(r\right)}\right]=0,\end{array}$$

(32)

which can be satisfied only if the expressions in both brackets are zero. Now we focus on finding the critical distance $r_c$ at which matter can start to fall onto a central object. Of course, the radial velocity u and function V depend on the critical distance. Hereafter performing simple algebraic manipulations, the critical radial velocity $u_c$ and function $V_c$ can be found as

$$\begin{array}{cc}\hfill u_c^2& =\frac{M_{\ast }{f}^{\gamma -1}}{r^{2}H\left(r\right)\frac{d}{dr}ln\left(\frac{r^{2}G\left(r\right)}{\sqrt{H\left(r\right)}}\right)}{|}_{r=r_c},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill V_c^2& =\frac{1}{1+\frac{f{r}^2}{M_{\ast }}\frac{d}{dr}ln\left(\frac{r^{2}G\left(r\right)}{\sqrt{H\left(r\right)}}\right)}{|}_{r=r_c}.\hfill \end{array}$$

(34)

The quantities $u_c$ and $V_c$ indicate radial velocity and radial function, which are measured at the position of the critical distance. One can see from Equations (33) and (34) that in the case when $\gamma =1$, we obtain $u_c^2=M_{\ast }/2r_c$ and $V_c^2=u_c^2/(1-3u_c^2)$, which is shown in Ref. [54]. Here, $u_c^2$ must be less than $1/3$, which leads to $r_c>1.5M_{\ast }$. Since the left-hand side of Equation (34) is positive, then the right-hand side also should be positive, which means

$$\begin{array}{c}\hfill 1+\frac{f{r}^2}{M_{\ast }}\frac{d}{dr}ln\left(\frac{r^{2}G\left(r\right)}{\sqrt{H\left(r\right)}}\right){|}_{r=r_c}>0.\end{array}$$

(35)

The above expression represents the dependence of the critical distance that matter starts to flow onto the central object from the $\gamma$ parameter. In the presence of the $\gamma$ parameter, the critical distance $r_c$ will be slightly different. The dependence of the critical distance at which matter starts to flow onto compact objects from the $\gamma$ parameter is shown in Figure 10.

$$\begin{array}{c}\hfill r_c>\frac{4+\gamma \pm \sqrt{8-7{\gamma }^2}}{4\gamma },\end{array}$$

(36)

Here we examine the accreting of polytropic gas onto the black hole. To do this, we consider the polytropic equation of state

$$\begin{array}{c}\hfill P=K{\rho }^{\mathrm{\Gamma }}=K{\rho }^{1+\frac{1}{n}}\end{array}$$

(37)

where $\mathrm{\Gamma }$ is the Poisson adiabatic index, n is the polytropic index and K is a dimensional constant. It is important to note that the polytropic equation of state is an approximation that assumes certain idealized conditions, such as the absence of phase transitions and chemical reactions. It provides a simplified representation of the behavior of a system under specific circumstances and is often used as a starting point for more detailed analyses or simulations.

The speed of sound in the polytropic medium can be determined as $c_{\mathrm{s}}=dP/d\rho =\sqrt{K\mathrm{\Gamma }{\rho }^{\mathrm{\Gamma }-1}}$, while the temperature of matter is defined as $T=P/\rho$. Then constants in Equations (29) and (30) can be rewritten as

$$\begin{array}{cc}\hfill C_1& =T^{n}u{r}^{2}F\left(r\right),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill C_2& ={\left(1+(n+1)T\right)}^2\left(f^{\gamma }+u^{2}H\left(r\right)\right),\hfill \end{array}$$

(39)

and

$$\begin{array}{cc}\hfill V^2& =\frac{(n+1)T}{n\left[1+(1+n)T\right]}.\hfill \end{array}$$

(40)

At infinity, the radial velocity should be zero $u=0$ and the temperature will take some non-zero value $T_{\infty }\simeq {10}^4\mathrm{K}$ of the local interstellar medium. We cannot find constant $C_1$, and the other constant $C_2$ can be found

$$\begin{array}{c}\hfill C_2\simeq {\left[1+(n+1)T_{\infty }\right]}^2,\end{array}$$

(41)

and on the other hand, taking into account Equation (40), Equation (39) can be rewritten as

$$\begin{array}{c}\hfill C_2\simeq \frac{{\left(f^{\gamma }\left(r_c\right)+u_c^{2}H\left(r_c\right)\right)}^3}{{\left(f^{\gamma }\left(r_c\right)+(1-n)u_c^{2}H\left(r_c\right)\right)}^2},\end{array}$$

(42)

which allows one to write

$$\begin{array}{c}\hfill T_{\infty }=\frac{1}{n+1}\left[\frac{{\left(f^{\gamma }\left(r_c\right)+u_c^{2}H\left(r_c\right)\right)}^{3/2}}{f^{\gamma }\left(r_c\right)+(1-n)u_c^{2}H\left(r_c\right)}-1\right],\end{array}$$

(43)

The critical temperature $T_c$ can be found as

$$\begin{array}{c}\hfill T_c=\frac{1}{n+1}{\left[\frac{f^{\gamma }\left(r_c\right)+u_c^{2}H\left(r_c\right)}{n{u}_c^{2}H\left(r_c\right)}-1\right]}^{-1},\end{array}$$

(44)

The ratio of temperature is

$$\begin{array}{cc}\hfill \frac{T_c}{T_{\infty }}& ={\left[\frac{f^{\gamma }\left(r_c\right)+u_c^{2}H\left(r_c\right)}{n{u}_c^{2}H\left(r_c\right)}-1\right]}^{-1}{\left[\frac{{\left(f^{\gamma }\left(r_c\right)+u_c^{2}H\left(r_c\right)\right)}^{3/2}}{f^{\gamma }\left(r_c\right)+(1-n)u_c^{2}H\left(r_c\right)}-1\right]}^{-1},\hfill \end{array}$$

(45)

The ratio of the matter density can approximately be found as $\rho /{\rho }_{\infty }={\left(T/T_{\infty }\right)}^3$. The dependence of the temperature and density of the falling matter onto compact objects are illustrated in Figure 11 and Figure 12. As one can see, the effect of the $\gamma$ spacetime on non-relativistic polytropic gas is valuable in comparison with that on the relativistic one at the small values of the $\gamma$ parameter. On the other hand, our analyses demonstrate that both the temperature and density of relativistic polytropic gas are always greater than non-relativistic polytropic gas. Hereafter making simple algebraic manipulations, another constant $C_1$ can be found as

$$\begin{array}{cc}\hfill C_1& =u_c{r}_c^2{T}_c^n=u_c{r}_c^2{\left[\frac{f^{\gamma }\left(r_c\right)+u_c^{2}H\left(r_c\right)}{n{u}_c^{2}H\left(r_c\right)}-1\right]}^{-n},\hfill \end{array}$$

which is useful to estimate the luminosity of polytropic gas. Here, we discuss the luminosity of the polytropic gas in two cases: relativistic and non-relativistic. The expressions for the luminosity are given by [54]

$$\begin{array}{c}\hfill \mathcal{L}\left(\gamma \right)\le \frac{3}{2}{m}_p{c}^2{T}_s\left(4\pi C_1\right)\left(\frac{n_{\infty }}{{10}^5{\mathrm{cm}}^{-3}}\right){\left(\frac{T_{\infty }}{{10}^4\mathrm{K}}\right)}^{-3/2},\end{array}$$

(46)

where $n_{\infty }$ is the concentration of matter at infinity. We already found the temperature at infinity $T_{\infty }$, the temperature at a given surface $T_s$ and the constant $C_1$. To see the effects arising from the $\gamma$ metric, the fractional expression of the luminosity of the falling matter in the $\gamma$ spacetime and Schwarzschild spacetime can be expressed as

$$\begin{array}{c}\hfill \frac{\mathcal{L}\left(\gamma \right)}{\mathcal{L}\left(1\right)}\simeq \left(\frac{C_1\left(\gamma \right)}{C_1\left(1\right)}\right)\left(\frac{T_s\left(\gamma \right)}{T_s\left(1\right)}\right){\left(\frac{T_{\infty }\left(\gamma \right)}{T_{\infty }\left(1\right)}\right)}^{-3/2}.\end{array}$$

(47)

Figure 13 draws the dependence of fractional luminosity on the $\gamma$ parameter. It is evident that the $\gamma$ spacetime has the potential to alter the luminosity of falling matter. Specifically, in the region $0.5<\gamma <1$, the luminosity of both relativistic and non-relativistic gases in the $\gamma$ spacetime is lower than that in the Schwarzschild spacetime. Conversely, when $\gamma >1$, the luminosity of falling matter exceeds that in the Schwarzschild spacetime. It is also apparent that non-relativistic polytropic gas is flexible for the $\gamma$ parameter in comparison with the relativistic one.

5. Conclusions

We discussed the motion of massive and massless particles around the gravitational compact object described by the $\gamma$ spacetime. Using standard analytical calculations, the characteristic radii around the gravitational compact object, namely marginally stable and marginally bound orbits for massive particles, photonsphere and impact parameter of the photon, and the position of singularity in the $\gamma$ spacetime are explicitly discussed.

We examined the properties of thin accretion disks surrounding a compact object described by the $\gamma$ spacetime. Due to the generally chaotic nature of particle motion, our analysis is focused exclusively on the equatorial plane to ensure integrability. By employing the Novikov–Thorne model, we initially determined the energy emission rate from the disk’s surface. The temperature profile of the accretion disk was obtained using the standard Stefan–Boltzmann law. Subsequently, we evaluated the total spectral luminosity of this disk for various observer positions and different values of the $\gamma$ parameter. Our findings reveal that spacetime deformation can potentially affect the high-frequency region of the emission originating from the thin accretion disk. To further investigate these effects, we utilized a ray-tracing code to generate an image of the thin accretion disk in the $\gamma$ spacetime. By performing this, we were able to test the impact of spacetime deformation on the disk’s appearance.

Lastly, we investigated the accretion of matter onto an exotic compact object described by the Zipoy–Voorhees metric, also known as the $gamma$ metric. We discussed how spacetime deformation affects the properties of accretion onto the compact object. Specifically, we examined the temperature and density of the infalling matter, which were described by the polytropic equation of state for the $\gamma$ object. We determined the ratio of the luminosity of infalling matter in the $\gamma$ metric to that in the Schwarzschild spacetime. However, all obtained results were compared to those that are valid in the Schwarzschild spacetime.

The exploration of Noether’s theorem and spacetime symmetries in the context of accretion disks opens up avenues for further research. It opens avenues for future directions, such as extending the analysis to magnetohydrodynamic effects, incorporating quantum gravity effects, and studying more complex accretion scenarios. We conclude by summarizing the importance of Noether’s theorem and spacetime symmetries in enhancing our understanding of accretion disk dynamics in astrophysical environments. By revealing the underlying conservation laws, these principles provide a powerful tool for deciphering the complex behavior of matter and energy flow in accretion disks.