Observable Properties of Thin Accretion Disk in the γ Spacetime
Abstract
:1. Introduction
2. Geodesics in the -Metric
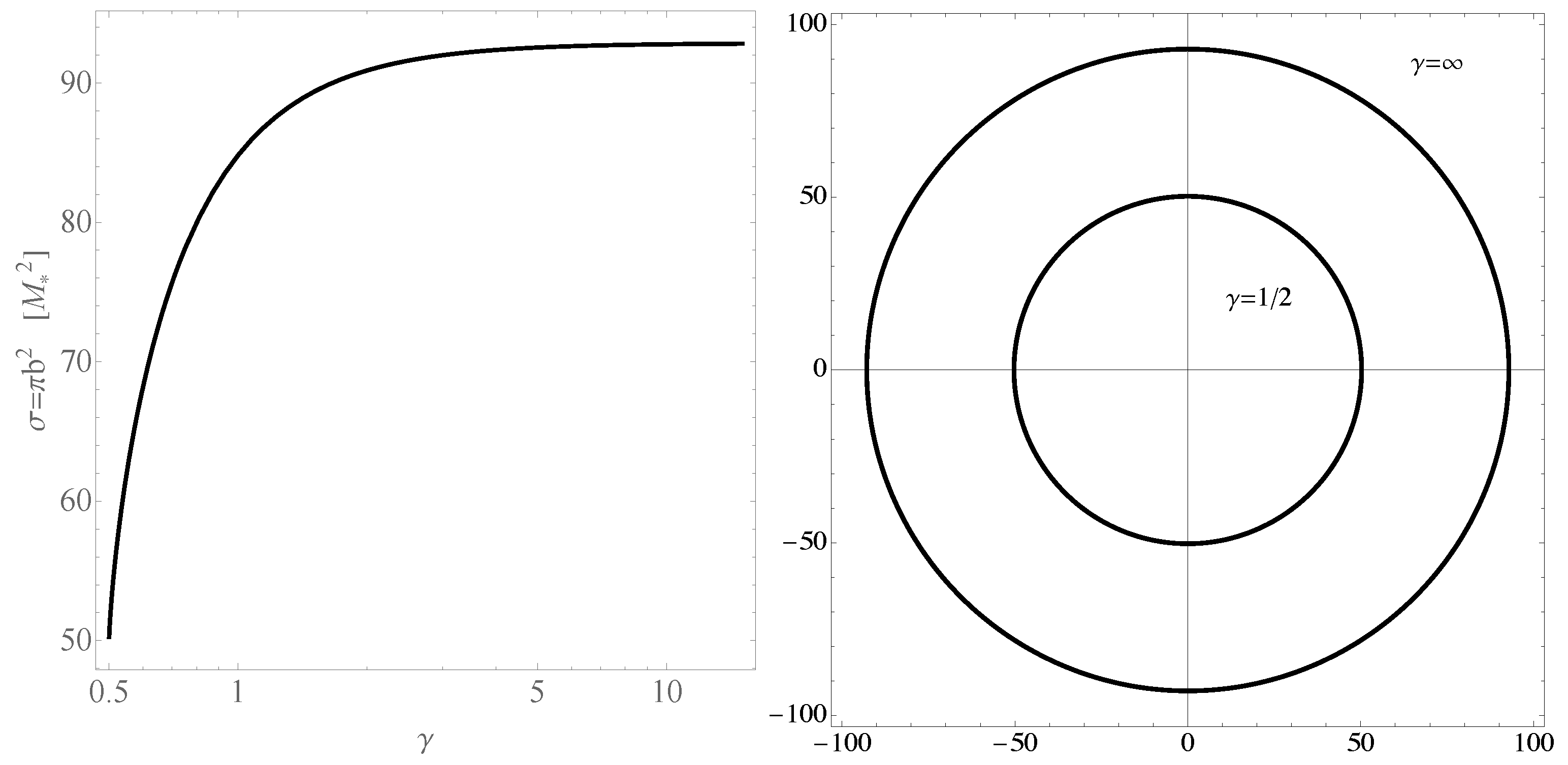
3. Accretion onto the -Metric: Thin Disks
- (i)
- Matter in the accretion disk loses energy as it spirals inward toward the central object due to friction and gravitational forces. This energy loss results in the emission of radiation, primarily in the form of X-rays and other high-energy photons.
- (ii)
- The accretion disk is envisioned as a flattened, rotating structure composed of gas, dust, and other matter. As matter falls inward, it follows nearly circular orbits within the disk, gradually losing angular momentum and spiraling closer to the black hole. The disk is assumed to be geometrically thin and optically thick, which means that the radial extension of the disk is much larger than its thickness .
- (iii)
- According to the Novikov–Thorne model, there is an innermost stable circular orbit where matter can orbit the black hole or exotic object without rapidly falling in. The radius of this orbit depends on the black hole’s mass and angular momentum. Inside the ISCO, matter rapidly plunges into the central object.
- (iv)
- The innermost part of the accretion disk lies very close to the black hole’s event horizon—the point beyond which nothing can escape the black hole’s gravitational pull. Radiation emitted by matter near the event horizon is greatly redshifted, making it difficult to detect.
- (v)
- The motion of gas particles in the disk approximately follows a circular Keplerian orbit, and therefore it is well described by test particles on circular orbits.
- (vi)
- The torque in the zone near the inner edge of the accretion disk is negligible.
- (iv)
- The mass accretion rate of the thin disk can be considered constant and it should be less than the Eddington mass rate. More precisely, , where the Eddington mass rate is defined aswhere M is the mass of the gravitational object, is the proton mass and is the Thompson cross section of the electron. In units of solar mass, we have .
- (vii)
- The model predicts that the radiation emitted by the accretion disk will have a characteristic spectrum. The spectrum is influenced by factors such as the black hole’s mass and spin, and it includes a distinctive peak in the X-ray part of the electromagnetic spectrum.
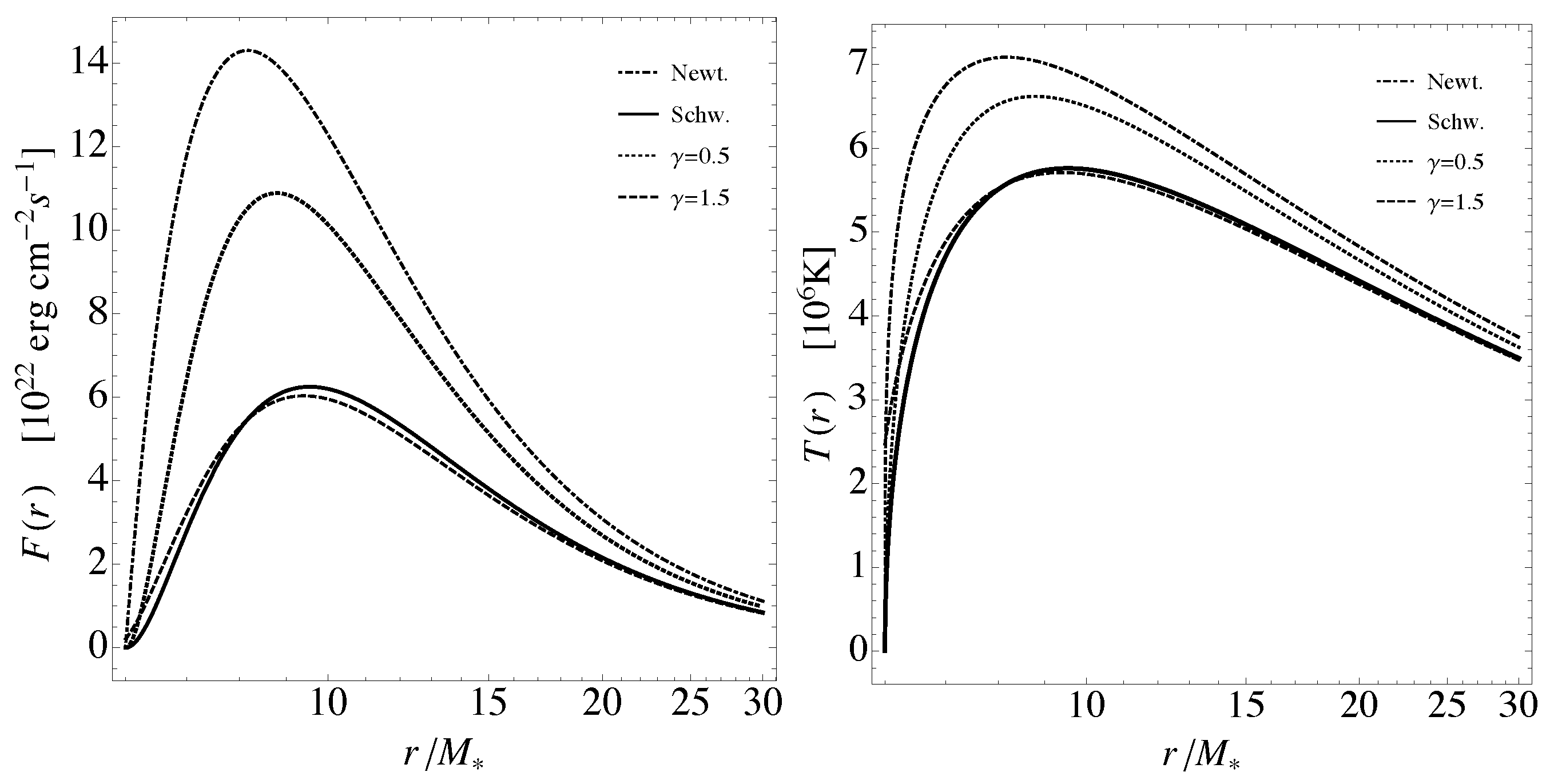
3.1. Temperature Profile of the Disk
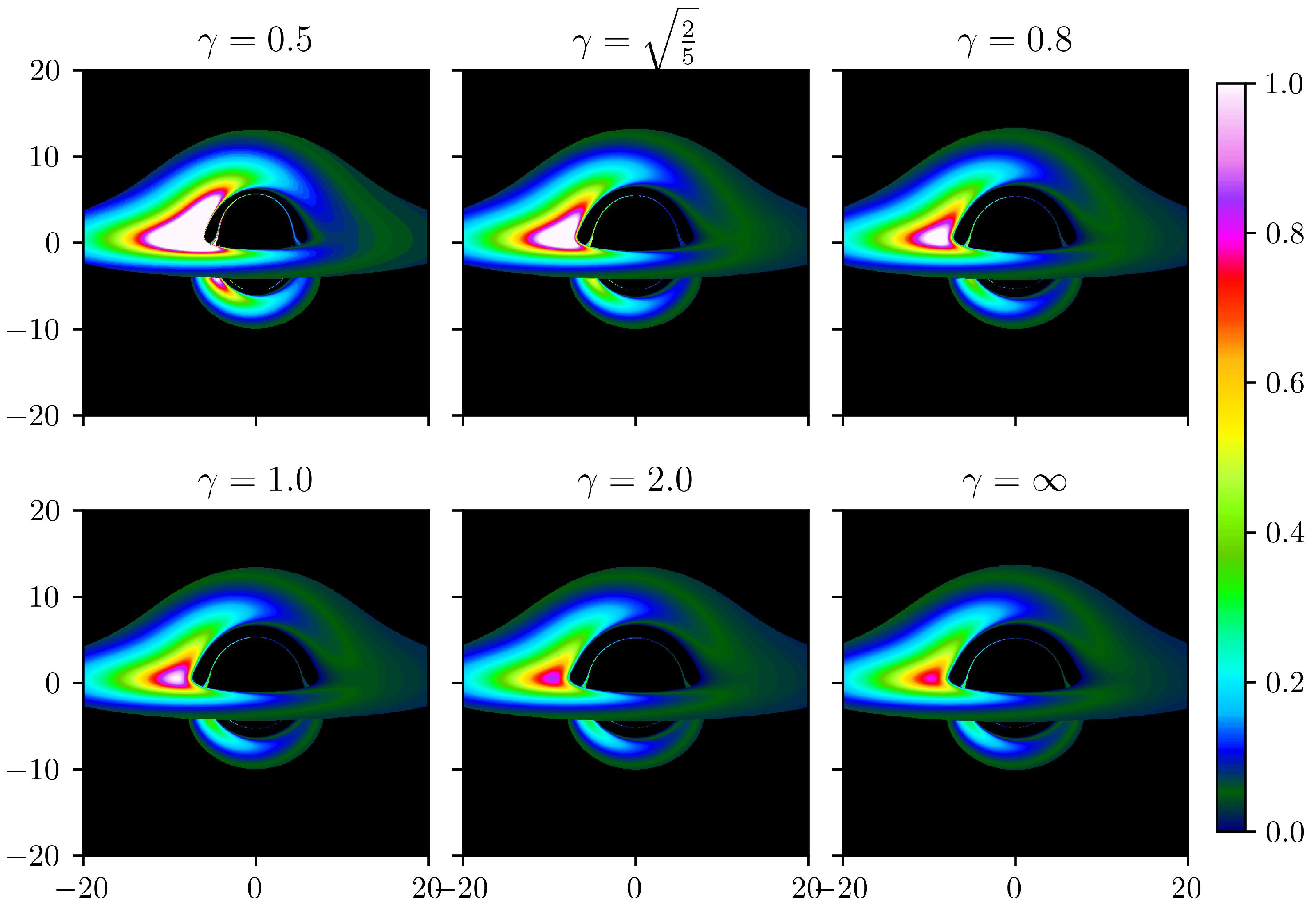
3.2. Thermal Spectrum and Image of the Disk
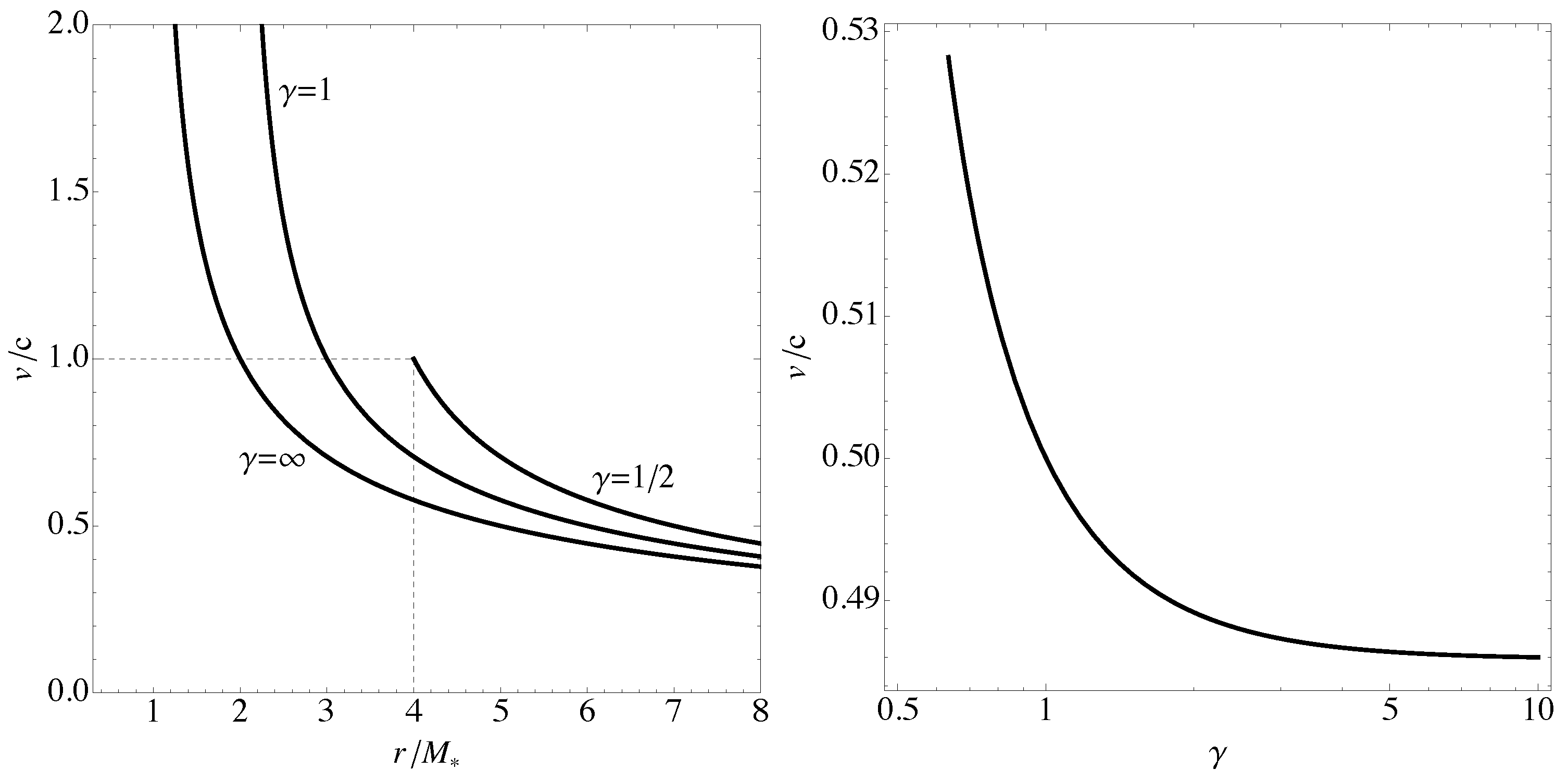
4. Accretion onto the Metric: Radial Infall
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ball, D.; Chan, C.K.; Christian, P.; Jannuzi, B.T.; Kim, J.; Marrone, D.P.; Medeiros, L.; Ozel, F.; Psaltis, D.; Rose, M.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Bambi, C.; Freese, K.; Vagnozzi, S.; Visinelli, L. Testing the rotational nature of the supermassive object M87* from the circularity and size of its first image. Phys. Rev. D 2019, 100, 044057. [Google Scholar] [CrossRef]
- Bambi, C. Testing black hole candidates with electromagnetic radiation. Rev. Mod. Phys. 2017, 89, 025001. [Google Scholar] [CrossRef]
- Bambi, C. Testing the Kerr Black Hole Hypothesis. Mod. Phys. Lett. A 2011, 26, 2453–2468. [Google Scholar] [CrossRef]
- Ghasemi-Nodehi, M.; Chakraborty, C.; Yu, Q.; Lu, Y. Investigating the existence of gravitomagnetic monopole in M87*. Eur. Phys. J. C 2021, 81, 939. [Google Scholar] [CrossRef]
- Erez, G.; Rosen, N. The gravitational field of a particle possessing a multipole moment. Bull. Res. Counc. Isr. 1959, 8F, 47. [Google Scholar]
- Genzel, R.; Eisenhauer, F.; Gillessen, S. The Galactic Center massive black hole and nuclear star cluster. Rev. Mod. Phys. 2010, 82, 3121–3195. [Google Scholar] [CrossRef]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E.; et al. Measuring Distance and Properties of the Milky Way’s Central Supermassive Black Hole with Stellar Orbits. Astrophys. J. 2008, 689, 1044–1062. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Della Valle, M. Measurement of the spin of the M87 black hole from its observed twisted light. MNRAS 2020, 492, L22–L27. [Google Scholar] [CrossRef]
- Bambi, C. A Code to Compute the Emission of Thin Accretion Disks in Non-Kerr Spacetimes and Test the Nature of Black Hole Candidates. Astrophys. J. 2012, 761, 17. [Google Scholar] [CrossRef]
- Bambi, C. Testing the space-time geometry around black hole candidates with the analysis of the broad Kα iron line. Phys. Rev. D 2013, 87, 023007. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Pringle, J.E. Accretion discs in astrophysics. Ann. Rev. Astron. Astrophys. 1981, 19, 137–162. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Fragile, P.C. Foundations of Black Hole Accretion Disk Theory. Living Rev. Relativ. 2013, 16, 1. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Université de Grenoble: Les Houches, France, 1973; pp. 343–450. [Google Scholar]
- Page, D.N.; Thorne, K.S. Disk-Accretion onto a Black Hole. Time-Averaged Structure of Accretion Disk. Astrophys. J. 1974, 191, 499–506. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophys. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Porth, O.; De Laurentis, M.; Olivares, H.; Falcke, H.; Kramer, M.; Rezzolla, L. The current ability to test theories of gravity with black hole shadows. Nat. Astron. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Zipoy, D.M. Topology of Some Spheroidal Metrics. J. Math. Phys. 1966, 7, 1137–1143. [Google Scholar] [CrossRef]
- Voorhees, B.H. Static Axially Symmetric Gravitational Fields. Phys. Rev. D 1970, 2, 2119–2122. [Google Scholar] [CrossRef]
- Chowdhury, A.N.; Patil, M.; Malafarina, D.; Joshi, P.S. Circular geodesics and accretion disks in the Janis-Newman-Winicour and gamma metric spacetimes. Phys. Rev. D 2012, 85, 104031. [Google Scholar] [CrossRef]
- Papadopoulos, D.; Stewart, B.; Witten, L. Some properties of a particular static, axially symmetric space-time. Phys. Rev. D 1981, 24, 320–326. [Google Scholar] [CrossRef]
- Quevedo, H. Multipole Moments in General Relativity—Static and Stationary Vacuum Solutions. Fortschritte Der Phys. 1990, 38, 733–840. [Google Scholar] [CrossRef]
- Hernández-Pastora, J.L.; Martín, J. Monopole-quadrupole static axisymmetric solutions of Einstein field Equations. Gen. Relativ. Gravit. 1994, 26, 877–907. [Google Scholar] [CrossRef]
- Toktarbay, S.; Quevedo, H. A stationary q-metric. Gravit. Cosmol. 2014, 20, 252–254. [Google Scholar] [CrossRef]
- Quevedo, H.; Toktarbay, S. Generating static perfect-fluid solutions of Einstein’s Equations. J. Math. Phys. 2015, 56, 052502. [Google Scholar] [CrossRef]
- Hernandez-Pastora, J.L.; Herrera, L.; Martin, J. Axially symmetric static sources of gravitational field. Class. Quantum Gravity 2016, 33, 235005. [Google Scholar] [CrossRef]
- Frutos-Alfaro, F.; Quevedo, H.; Sanchez, P.A. Comparison of vacuum static quadrupolar metrics. R. Soc. Open Sci. 2018, 5, 170826. [Google Scholar] [CrossRef]
- Arrieta-Villamizar, J.A.; Velásquez-Cadavid, J.M.; Pimentel, O.M.; Lora-Clavijo, F.D.; Gutiérrez-Piñeres, A.C. Shadows around the q-metric. Class. Quantum Gravity 2021, 38, 015008. [Google Scholar] [CrossRef]
- Weyl, H. Zur Gravitationstheorie. Ann. Der Phys. 1917, 359, 117–145. [Google Scholar] [CrossRef]
- Weyl, H. Bemerkung über die axialsymmetrischen Lösungen der Einsteinschen Gravitationsgleichungen. Ann. Der Phys. 1919, 364, 185–188. [Google Scholar] [CrossRef]
- Weyl, H. Ausbreitung elektromagnetischer Wellen über einem ebenen Leiter. Ann. Der Phys. 1919, 365, 481–500. [Google Scholar] [CrossRef]
- Kodama, H.; Hikida, W. Global structure of the Zipoy Voorhees Weyl spacetime and the dgr = 2 Tomimatsu Sato spacetime. Class. Quantum Gravity 2003, 20, 5121–5140. [Google Scholar] [CrossRef]
- Stewart, B.W.; Papadopoulos, D.; Witten, L.; Berezdivin, R.; Herrera, L. An interior solution for the gamma metric. Gen. Relativ. Gravit. 1982, 14, 97–103. [Google Scholar] [CrossRef]
- Herrera, L.; Magli, G.; Malafarina, D. Non-spherical sources of static gravitational fields: Investigating the boundaries of the no-hair theorem. Gen. Relativ. Gravit. 2005, 37, 1371–1383. [Google Scholar] [CrossRef]
- Bonnor, W.B. An interior solution for Curzon spacetime. Gen. Relativ. Gravit. 2013, 45, 1403–1410. [Google Scholar] [CrossRef]
- Shaikh, R.; Paul, S.; Banerjee, P.; Sarkar, T. Shadows and thin accretion disk images of the γ-metric. Eur. Phys. J. C 2022, 82, 696. [Google Scholar] [CrossRef]
- Boshkayev, K.; Konysbayev, T.; Kurmanov, E.; Luongo, O.; Malafarina, D.; Quevedo, H. Luminosity of accretion disks in compact objects with a quadrupole. Phys. Rev. D 2021, 104, 084009. [Google Scholar] [CrossRef]
- Abdikamalov, A.B.; Abdujabbarov, A.A.; Ayzenberg, D.; Malafarina, D.; Bambi, C.; Ahmedov, B. Black hole mimicker hiding in the shadow: Optical properties of the γ metric. Phys. Rev. D 2019, 100, 024014. [Google Scholar] [CrossRef]
- Gal’tsov, D.V.; Kobialko, K.V. Photon trapping in static axially symmetric spacetime. Phys. REv. D 2019, 100, 104005. [Google Scholar] [CrossRef]
- Herrera, L.; Paiva, F.M.; Santos, N.O.; Ferrari, V. Geodesics in the γ Spacetime. Int. J. Mod. Phys. D 2000, 9, 649–659. [Google Scholar] [CrossRef]
- Boshkayev, K.; Gasperín, E.; Gutiérrez-Piñeres, A.C.; Quevedo, H.; Toktarbay, S. Motion of test particles in the field of a naked singularity. Phys. Rev. D 2016, 93, 024024. [Google Scholar] [CrossRef]
- Toshmatov, B.; Malafarina, D. Spinning test particles in the γ spacetime. Phys. Rev. D 2019, 100, 104052. [Google Scholar] [CrossRef]
- Toshmatov, B.; Malafarina, D.; Dadhich, N. Harmonic oscillations of neutral particles in the γ metric. Phys. Rev. D 2019, 100, 044001. [Google Scholar] [CrossRef]
- Boshkayev, K.; Luongo, O.; Muccino, M. Neutrino oscillation in the q-metric. Eur. Phys. J. C 2020, 80, 964. [Google Scholar] [CrossRef]
- Chakrabarty, H.; Borah, D.; Abdujabbarov, A.; Malafarina, D.; Ahmedov, B. Effects of gravitational lensing on neutrino oscillation in γ -spacetime. Eur. Phys. J. C 2022, 82, 24. [Google Scholar] [CrossRef]
- Turimov, B.; Ahmedov, B.; Kološ, M.; Stuchlík, Z. Axially symmetric and static solutions of Einstein Equations with self-gravitating scalar field. Phys. Red. D 2018, 98, 084039. [Google Scholar] [CrossRef]
- Benavides-Gallego, C.A.; Abdujabbarov, A.; Malafarina, D.; Ahmedov, B.; Bambi, C. Charged particle motion and electromagnetic field in γ spacetime. Phys. Rev. D 2019, 99, 044012. [Google Scholar] [CrossRef]
- Benavides-Gallego, C.A.; Abdujabbarov, A.; Malafarina, D.; Bambi, C. Quasiharmonic oscillations of charged particles in static axially symmetric space-times immersed in a uniform magnetic field. Phys. Rev. D 2020, 101, 124024. [Google Scholar] [CrossRef]
- Malafarina, D.; Sagynbayeva, S. What a difference a quadrupole makes? Gen. Relativ. Gravit. 2021, 53, 112. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Volkov, M.S. Weyl metrics and wormholes. J. Cosmol. Astropart. Phys. 2017, 2017, 039. [Google Scholar] [CrossRef]
- Narzilloev, B.; Malafarina, D.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Particle motion around a static axially symmetric wormhole. Phys. Rev. D 2021, 104, 064016. [Google Scholar] [CrossRef]
- Michel, F.C. Accretion of Matter by Condensed Objects. Astrophys. Space Sci. 1972, 15, 153–160. [Google Scholar] [CrossRef]
- Curzon, H.E.J. Cylindrical Solutions of Einstein’s Gravitation equations. Proc. Lond. Math. Soc. 1925, s2–s23, 477–480. [Google Scholar] [CrossRef]
- Lukes-Gerakopoulos, G. Nonintegrability of the Zipoy-Voorhees metric. Phys. Rev. D 2012, 86, 044013. [Google Scholar] [CrossRef]
- Gyulchev, G.; Kunz, J.; Nedkova, P.; Vetsov, T.; Yazadjiev, S. Observational signatures of strongly naked singularities: Image of the thin accretion disk. Eur. Phys. J. C 2020, 80, 1017. [Google Scholar] [CrossRef]
- Guerrero, M.; Olmo, G.J.; Rubiera-Garcia, D.; Gómez, D.S.C. Multiring images of thin accretion disk of a regular naked compact object. Phys. Rev. D 2022, 106, 044070. [Google Scholar] [CrossRef]
- Turimov, B.; Ahmedov, B. Zipoy-Voorhees Gravitational Object as a Source of High-Energy Relativistic Particles. Galaxies 2021, 9, 59. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Shakura, N.I.; Sunyaev, R.A. A theory of the instability of disk accretion on to black holes and the variability of binary X-ray sources, galactic nuclei and quasars. Mon. N. R. Astron. Soc. 1976, 175, 613–632. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turimov, B.; Ahmedov, B. Observable Properties of Thin Accretion Disk in the γ Spacetime. Symmetry 2023, 15, 1858. https://doi.org/10.3390/sym15101858
Turimov B, Ahmedov B. Observable Properties of Thin Accretion Disk in the γ Spacetime. Symmetry. 2023; 15(10):1858. https://doi.org/10.3390/sym15101858
Chicago/Turabian StyleTurimov, Bobur, and Bobomurat Ahmedov. 2023. "Observable Properties of Thin Accretion Disk in the γ Spacetime" Symmetry 15, no. 10: 1858. https://doi.org/10.3390/sym15101858
APA StyleTurimov, B., & Ahmedov, B. (2023). Observable Properties of Thin Accretion Disk in the γ Spacetime. Symmetry, 15(10), 1858. https://doi.org/10.3390/sym15101858







