Exact Solutions of M-Fractional Kuralay Equation via Three Analytical Schemes
Abstract
:1. Introduction
2. Classical Kuralay-II Equations
2.1. Kuralay-IIA Equation
- Case
2.2. Kuralay-IIB Equation
2.2.1. Case
2.2.2. Case
3. Truncated M-Fractional Derivative and Its Properties
4. Methodologies
4.1. Function Scheme
4.2. Extended Sinh–Gordon Equation Expansion Scheme (EShGEES)
4.3. Generalized Kudryashov Scheme
5. Model Description
5.1. Kuralay-IIA Equation (K-IIAE)
5.2. Kuralay-IIB Equation (K-IIBE)
6. Mathematical Treatment of the Model
6.1. K-IIAE
6.2. K-IIBE
7. Analytical Wave Solutions of K-IIAE
7.1. By Function Scheme
7.2. By the Extended Sinh-Gordon Equation Expansion Scheme
7.3. By the Generalized Kudryashov Scheme
8. Solutions of K-IIBE
8.1. By the Function Scheme
8.2. By the Extended Sinh-Gordon Equation Expansion Scheme
8.3. By the Generalized Kudryashov Scheme
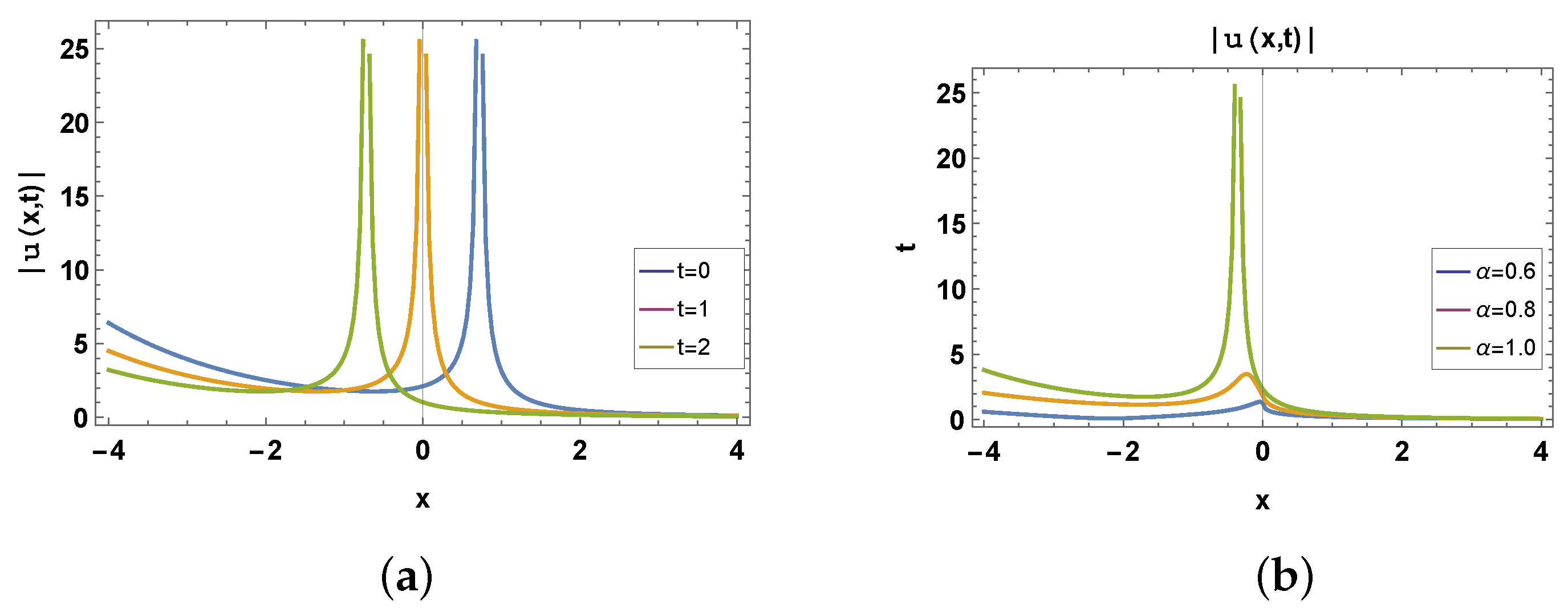
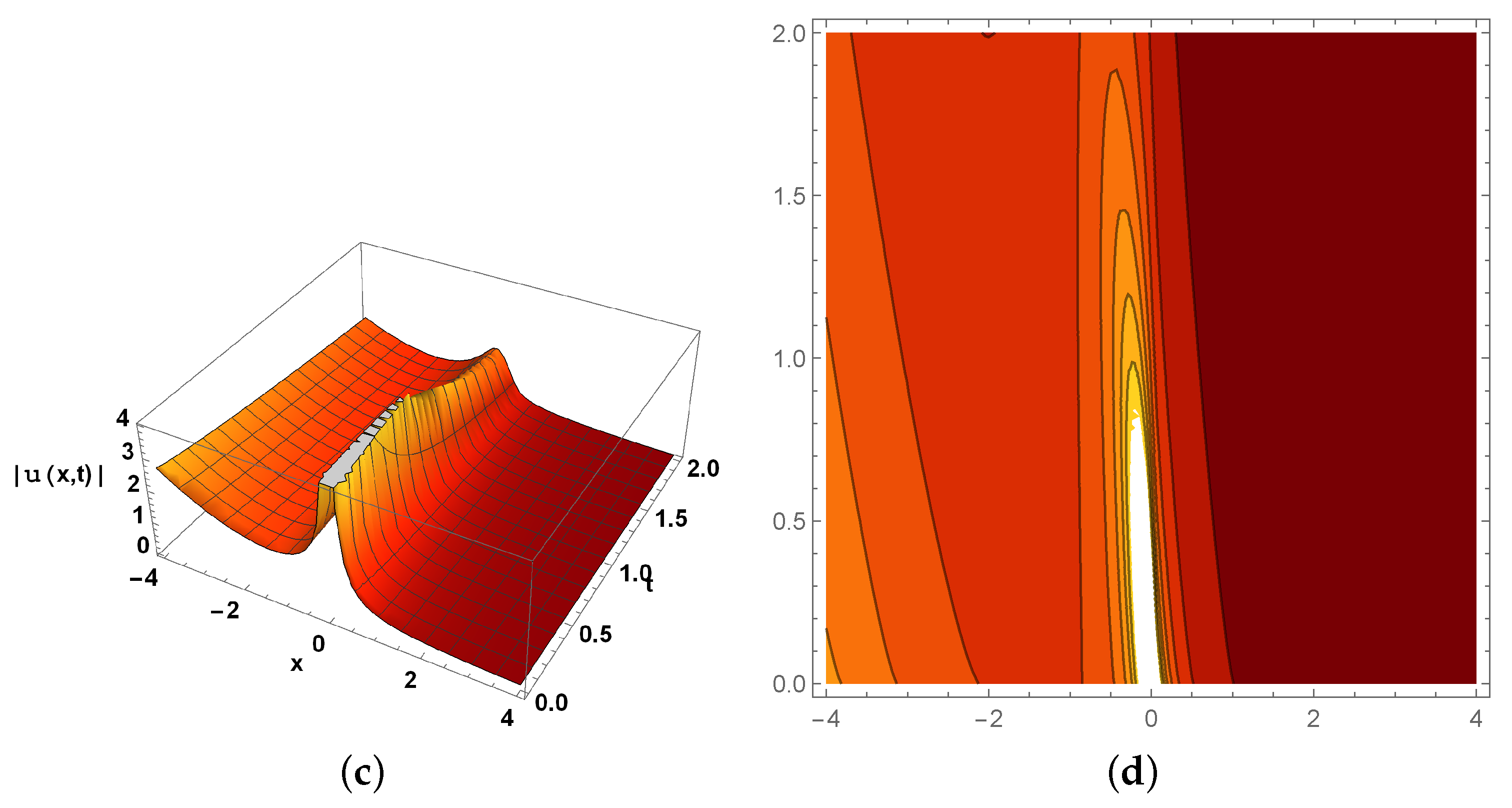
9. Physical Description of Solutions
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghanbari, B.; Osman, M.S.; Baleanu, D. Generalized exponential rational function method for extended Zakharov–Kuzetsov equation with conformable derivative. Mod. Phys. Lett. A 2019, 34, 1950155. [Google Scholar] [CrossRef]
- Akbulut, A.; Taşcan, F.; Özel, E. Trivial conservation laws and solitary wave solution of the fifth order Lax equation. Partial Differ. Equ. Appl. Math. 2021, 4, 100101. [Google Scholar] [CrossRef]
- Khatri, H.; Gautam, M.S.; Malik, A. Localized and complex soliton solutions to the integrable (4 + 1)-dimensional Fokas equation. SN Appl. Sci. 2019, 1, 1070. [Google Scholar] [CrossRef]
- Alam, M.N.; İlhan, O.A.; Uddin, M.S.; Rahim, M.A. Regarding on the Results for the Fractional Clannish Random Walker’s Parabolic Equation and the Nonlinear Fractional Cahn-Allen Equation. Adv. Math. Phys. 2022, 2022, 5635514. [Google Scholar] [CrossRef]
- Alam, M.N.; Islam, S.; İlhan, O.A.; Bulut, H. Some new results of nonlinear model arising in incompressible visco-elastic Kelvin–Voigt fluid. Math. Methods Appl. Sci. 2022, 45, 10347–10362. [Google Scholar] [CrossRef]
- Younas, U.; Seadawy, A.R.; Younis, M.; Rizvi, S.T.R. Optical solitons and closed form solutions to the (3 + 1)-dimensional resonant Schrödinger dynamical wave equation. Int. J. Mod. Phys. B 2020, 34, 2050291. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Ahmed, S.; Younis, M.; Ali, K. Study of multiple lump and rogue waves to the generalized unstable space time fractional nonlinear Schrödinger equation. Chaos Solitons Fractals 2021, 151, 111251. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Iqbal, M.; Lu, D. Applications of propagation of long-wave with dissipation and dispersion in nonlinear media via solitary wave solutions of generalized Kadomtsev–Petviashvili modified equal width dynamical equation. Comput. Math. Appl. 2019, 78, 3620–3632. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.; Lu, D.; Wang, J. Travelling wave solutions of generalized coupled Zakharov–Kuznetsov and dispersive long wave equations. Results Phys. 2016, 6, 1136–1145. [Google Scholar] [CrossRef]
- Rani, M.; Ahmed, N.; Dragomir, S.S.; Mohyud-Din, S.T.; Khan, I.; Nisar, K.S. Some newly explored exact solitary wave solutions to nonlinear inhomogeneous Murnaghan’s rod equation of fractional order. J. Taibah Univ. Sci. 2021, 15, 97–110. [Google Scholar] [CrossRef]
- Kumar, S.; Nisar, K.S.; Niwas, M. On the dynamics of exact solutions to a (3 + 1)-dimensional YTSF equation emerging in shallow sea waves: Lie symmetry analysis and generalized Kudryashov method. Results Phys. 2023, 48, 106432. [Google Scholar] [CrossRef]
- Irshad, A.; Ahmed, N.; Nazir, A.; Khan, U.; Mohyud-Din, S.T. Novel exact double periodic Soliton solutions to strain wave equation in micro structured solids. Phys. Stat. Mech. Appl. 2020, 550, 124077. [Google Scholar] [CrossRef]
- Ellahi, R.; Mohyud-Din, S.T.; Khan, U. Exact traveling wave solutions of fractional order Boussinesq-like equations by applying Exp-function method. Results Phys. 2018, 8, 114–120. [Google Scholar]
- Bibi, S.; Mohyud-Din, S.T.; Khan, U.; Ahmed, N. Khater method for nonlinear Sharma Tasso-Olever (STO) equation of fractional order. Results Phys. 2017, 7, 4440–4450. [Google Scholar] [CrossRef]
- Irshad, A.; Mohyud-Din, S.T.; Ahmed, N.; Khan, U. A new modification in simple equation method and its applications on nonlinear equations of physical nature. Results Phys. 2017, 7, 4232–4240. [Google Scholar] [CrossRef]
- Dahiya, S.; Kumar, H.; Kumar, A.; Gautam, M.S. Optical solitons in twin-core couplers with the nearest neighbor coupling. Partial. Differ. Equ. Appl. Math. 2021, 4, 100136. [Google Scholar]
- El-Ganaini, S.; Ma, W.-X.; Kumar, H. Modulational instability, optical solitons and travelling wave solutions to two nonlinear models in birefringent fibres with and without four-wave mixing terms. Pramana 2023, 97, 119. [Google Scholar] [CrossRef]
- El-Ganaini, S.; Kumar, H. A variety of new soliton structures and various dynamical behaviors of a discrete electrical lattice with nonlinear dispersion via variety of analytical architectures. Math. Methods Appl. Sci. 2023, 46, 2746–2772. [Google Scholar] [CrossRef]
- Alam, M.N. An analytical method for finding exact solutions of a nonlinear partial differential equation arising in electrical engineering. Open J. Math. Sci. 2023, 7, 10–18. [Google Scholar] [CrossRef]
- Ali, A.T.; Hassan, E.R. General expa function method for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 451–459. [Google Scholar] [CrossRef]
- Yan, C. A simple transformation for nonlinear waves. Phys. Lett. A 1996, 22, 77–84. [Google Scholar] [CrossRef]
- Zafar, A.; Bekir, A.; Raheel, M.; Rezazadeh, H. Investigation for optical soliton solutions of two nonlinear Schrödinger equations via two concrete finite series methods. Int. J. Appl. Comput. Math. 2020, 6, 65. [Google Scholar] [CrossRef]
- Chen, Z.; Manafian, J.; Raheel, M.; Zafar, A.; Alsaikhan, F.; Abotaleb, M. Extracting the exact solitons of time-fractional three coupled nonlinear Maccari’s system with complex form via four different methods. Results Phys. 2022, 36, 105400. [Google Scholar] [CrossRef]
- Aljoudi, S. Exact solutions of the fractional Sharma-Tasso-Olver equation and the fractional Bogoyavlenskii’s breaking soliton equations. Appl. Math. Comput. 2021, 405, 126237. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations, Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Gaber, A.A.; Aljohani, A.F.; Ebaid, A.; Machado, J.T. The generalized Kudryashov method for nonlinear space–time fractional partial differential equations of burgers type. Nonlinear Dyn. 2019, 95, 361–368. [Google Scholar] [CrossRef]
- Barman, H.K.; Roy, R.; Mahmud, F.; Akbar, M.A.; Osman, M.S. Harmonizing wave solutions to the Fokas-Lenells model through the generalized Kudryashov method. Optik 2021, 229, 166294. [Google Scholar] [CrossRef]
- Pandir, Y.; Sahragül, E.R.E.N. Exact solutions of the two dimensional KdV-Burger equation by generalized Kudryashov method. J. Inst. Sci. Technol. 2021, 11, 617–624. [Google Scholar] [CrossRef]
- Sagidullayeva, Z.; Nugmanova, G.; Myrzakulov, R.; Serikbayev, N. Integrable Kuralay equations: Geometry, solutions and generalizations. Symmetry 2022, 14, 1374. [Google Scholar] [CrossRef]
- Faridi, W.A.; Bakar, M.A.; Myrzakulova, Z.; Myrzakulov, R.; Akgül, A.; El Din, S.M. The formation of solitary wave solutions and their propagation for Kuralay equation. Results Phys. 2023, 52, 106774. [Google Scholar] [CrossRef]
- Mathanaranjan, T. Optical soliton, linear stability analysis and conservation laws via multipliers to the integrable Kuralay equation. Optik 2023, 290, 171266. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota–Maccari system. Mod. Phys. Lett. B 2019, 33, 1950052. [Google Scholar] [CrossRef]
- Sousa, J.V.D.A.C.; De Oliveira, E.C. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Zayed, E.M.E.; Al-Nowehy, A.G. Generalized kudryashov method and general expa function method for solving a high order nonlinear schrödinger equation. J. Space Explor. 2017, 6, 120. [Google Scholar]
- Hosseini, K.; Ayati, Z.; Ansari, R. New exact solutions of the Tzitzéica-type equations in non-linear optics using the expa function method. J. Mod. Opt. 2018, 65, 847–851. [Google Scholar] [CrossRef]
- Yang, X.L.; Tang, J.S. Travelling wave solutions for Konopelchenko-Dubrovsky equation using an extended sinh-Gordon equation expansion method. Commun. Theor. Phys. 2008, 50, 10471051. [Google Scholar]
- Gómez, C.A.; Salas, A.H. Special symmetries to standard Riccati equations and applications. Appl. Math. Comput. 2010, 216, 3089–3096. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, A.; Raheel, M.; Ali, M.R.; Myrzakulova, Z.; Bekir, A.; Myrzakulov, R. Exact Solutions of M-Fractional Kuralay Equation via Three Analytical Schemes. Symmetry 2023, 15, 1862. https://doi.org/10.3390/sym15101862
Zafar A, Raheel M, Ali MR, Myrzakulova Z, Bekir A, Myrzakulov R. Exact Solutions of M-Fractional Kuralay Equation via Three Analytical Schemes. Symmetry. 2023; 15(10):1862. https://doi.org/10.3390/sym15101862
Chicago/Turabian StyleZafar, Asim, Muhammad Raheel, Mohamed R. Ali, Zhaidary Myrzakulova, Ahmet Bekir, and Ratbay Myrzakulov. 2023. "Exact Solutions of M-Fractional Kuralay Equation via Three Analytical Schemes" Symmetry 15, no. 10: 1862. https://doi.org/10.3390/sym15101862





