Estimation of Multiple Breaks in Panel Data Models Based on a Modified Screening and Ranking Algorithm
Abstract
:1. Introduction
2. The Model and Assumption
3. Method
3.1. SaRa for a Time Series Model
3.2. SaRa for a Panel Data Model
- Given a set of bandwidths , . For each bandwidth , we compute the scan statistic for , .
- We find the local maximizers for each bandwidth and form a set called ., where is an estimator of the number of break points under the bandwidth .
- Under the bandwidth , we utilize the threshold criterion to filter out the break points on the collection of local maximizers,and then we collect together the break points obtained under each bandwidth and denote them as .
- We remove duplicate break points in the set , i.e., if the distance between two break points obtained from different bandwidths is less than the shorter bandwidth, we remove the break points obtained from the shorter bandwidth and keep the breakpoints obtained from the longer bandwidth, and denote the set of break points finally obtained as .
- We obtain the final break point estimation by the best subset selection on the set using the minimization information criterionwhere .
3.3. Statistical Properties
4. Numerical Result
- (i)
- , , ;
- (ii)
- , where , , , ;
- (iii)
- , , , ;
- (iv)
- , where , , , , .
5. Empirical Example
5.1. The GDP Data
5.2. The Real Effective Exchange Rate Index Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Csörgö, M.; Horváth, L. Limit Theorems in Change-Point Analysis; John Wiley & Sons Inc.: New York, NY, USA, 1997. [Google Scholar]
- Bai, J.; Perron, P. Estimating and Testing Linear Models with Multiple Structural Changes. Econometrica 1998, 66, 47–78. [Google Scholar] [CrossRef]
- Perron, P. Dealing with structural breaks. Palgrave Handb. Econ. 2006, 1, 278–352. [Google Scholar]
- Gombay, E. Change detection in autoregressive time series. J. Multivar. Anal. 2008, 99, 451–464. [Google Scholar] [CrossRef]
- Chen, Z.; Tian, Z. Modified procedures for change point monitoring in linear models. Math. Comput. Simulat. 2010, 81, 62–75. [Google Scholar] [CrossRef]
- Chen, H. Sequential change-point detection based on nearest neighbors. Ann. Stat. 2019, 47, 1381–1407. [Google Scholar] [CrossRef]
- Zou, C.; Yin, G.; Feng, L.; Wang, Z. Nonparametric maximum likelihood approach to multiple change-point problems. Ann. Stat. 2014, 42, 970–1002. [Google Scholar] [CrossRef]
- Zou, C.; Wang, G.; Li, R. Consistent selection of the number of change-points via sample-splitting. Ann. Stat. 2020, 48, 413–439. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, G.; Yang, J.; Lai, H.; Liu, S.; Chen, C.; Xu, W. Change Point Detection with Mean Shift Based on AUC from Symmetric Sliding Windows. Symmetry 2020, 12, 599. [Google Scholar] [CrossRef]
- Tveten, M.; Eckley, I.A.; Fearnhead, P. Scalable change-point and anomaly detection in cross-correlated data with an application to condition monitoring. Ann. Appl. Stat. 2022, 16, 721–743. [Google Scholar] [CrossRef]
- Bai, J. Common breaks in means and variances for panel data. J. Econ. 2010, 157, 78–92. [Google Scholar] [CrossRef]
- Kim, D. Estimating a common deterministic time trend break in large panels with cross sectional dependence. J. Econ. 2011, 164, 310–330. [Google Scholar] [CrossRef]
- Kim, D. Common local breaks in time trends for large panels. Econ. J. 2014, 17, 301–337. [Google Scholar]
- Peštová, B.; Pešta, M. Testing structural changes in panel data with small fixed panel size and bootstrap. Metrika 2015, 78, 665–689. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Feng, Q.; Kao, C. Estimation of heterogeneous panels with structural breaks. J. Econ. 2016, 191, 176–195. [Google Scholar] [CrossRef]
- Xu, M.; Zhong, P.; Wang, W. Detecting variance change-points for blocked time series and dependent panel data. J. Bus. Econ. Stat. 2016, 34, 213–226. [Google Scholar] [CrossRef]
- Horváth, L.; Hušková, M.; Rice, G.; Wang, J. Asymptotic properties of the CUSUM estimator for the time of change in linear panel data models. Econ. Theor. 2017, 33, 366–412. [Google Scholar] [CrossRef]
- Lumsdaine, R.L.; Okui, R.; Wang, W. Estimation of panel group structure models with structural breaks in group memberships and coefficients. J. Econ. 2023, 233, 45–65. [Google Scholar] [CrossRef]
- Feng, Q.; Kao, C.; Lazarova, S. Estimation of Change Points in Panels; Working Paper; Syracuse University: New York, NY, USA, 2009. [Google Scholar]
- Li, D.; Qian, J.; Su, L. Panel data models with interactive fixed effects and multiple structural breaks. J. Am. Stat. Assoc. 2016, 111, 1804–1819. [Google Scholar] [CrossRef]
- Qian, J.; Su, L. Shrinkage estimation of common breaks in panel data models via adaptive group fused lasso. J. Econ. 2016, 191, 86–109. [Google Scholar] [CrossRef]
- Okui, R.; Wang, W. Heterogeneous structural breaks in panel data models. J. Econ. 2020, 220, 447–473. [Google Scholar]
- Kaddoura, Y.; Westerlund, J. Estimation of panel data models with random interactive effects and multiple structural breaks when T is Fixed. J. Bus. Econ. Stat. 2022, 41, 1–38. [Google Scholar] [CrossRef]
- Cho, H. Change-point detection in panel data via double CUSUM statistic. Electron. J. Stat. 2016, 10, 2000–2038. [Google Scholar] [CrossRef]
- Song, C.; Min, X.; Zhang, H. The screening and ranking algorithm for change-points detection in multiple samples. Ann. Appl. Stat. 2016, 10, 2102–2129. [Google Scholar] [CrossRef] [PubMed]
- Niu, Y.S.; Zhang, H. The screening and ranking algorithm to detect DNA copy number variations. Ann. Appl. Stat. 2012, 6, 1306–1326. [Google Scholar] [CrossRef]
- Hao, N.; Niu, Y.S.; Zhang, H. Multiple change-point detection via a screening and ranking algorithm. Statist. Sin. 2013, 23, 1553–1572. [Google Scholar] [CrossRef]
- Xiao, F.; Min, X.; Zhange, H. Modified screening and ranking algorithm for copy number variation detection. Bioinformatics 2015, 31, 1341–1348. [Google Scholar] [CrossRef]
- Horváth, L.; Hušková, M. Change-point detection in panel data. J. Time Ser. Anal. 2012, 33, 631–648. [Google Scholar] [CrossRef]
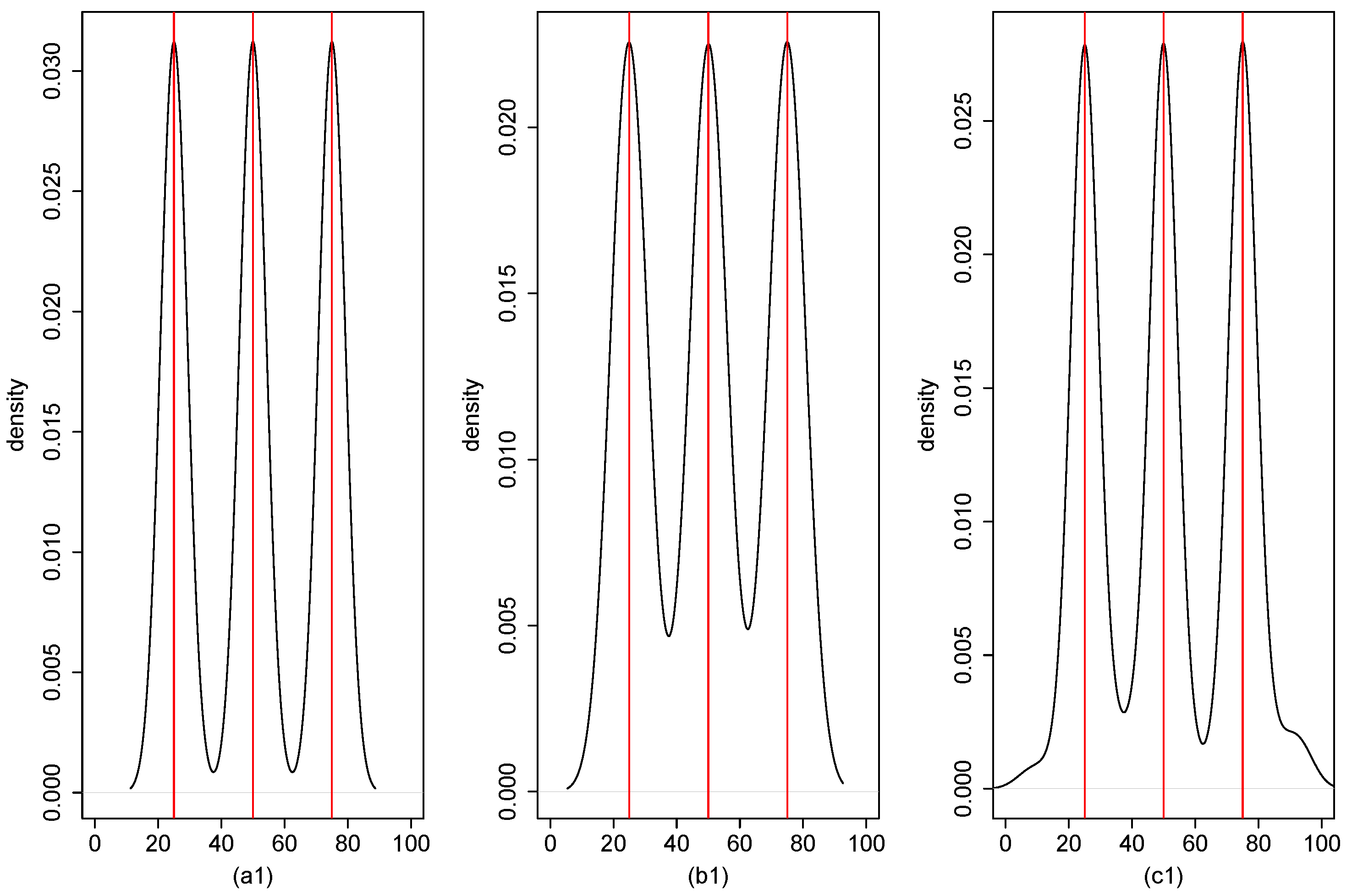
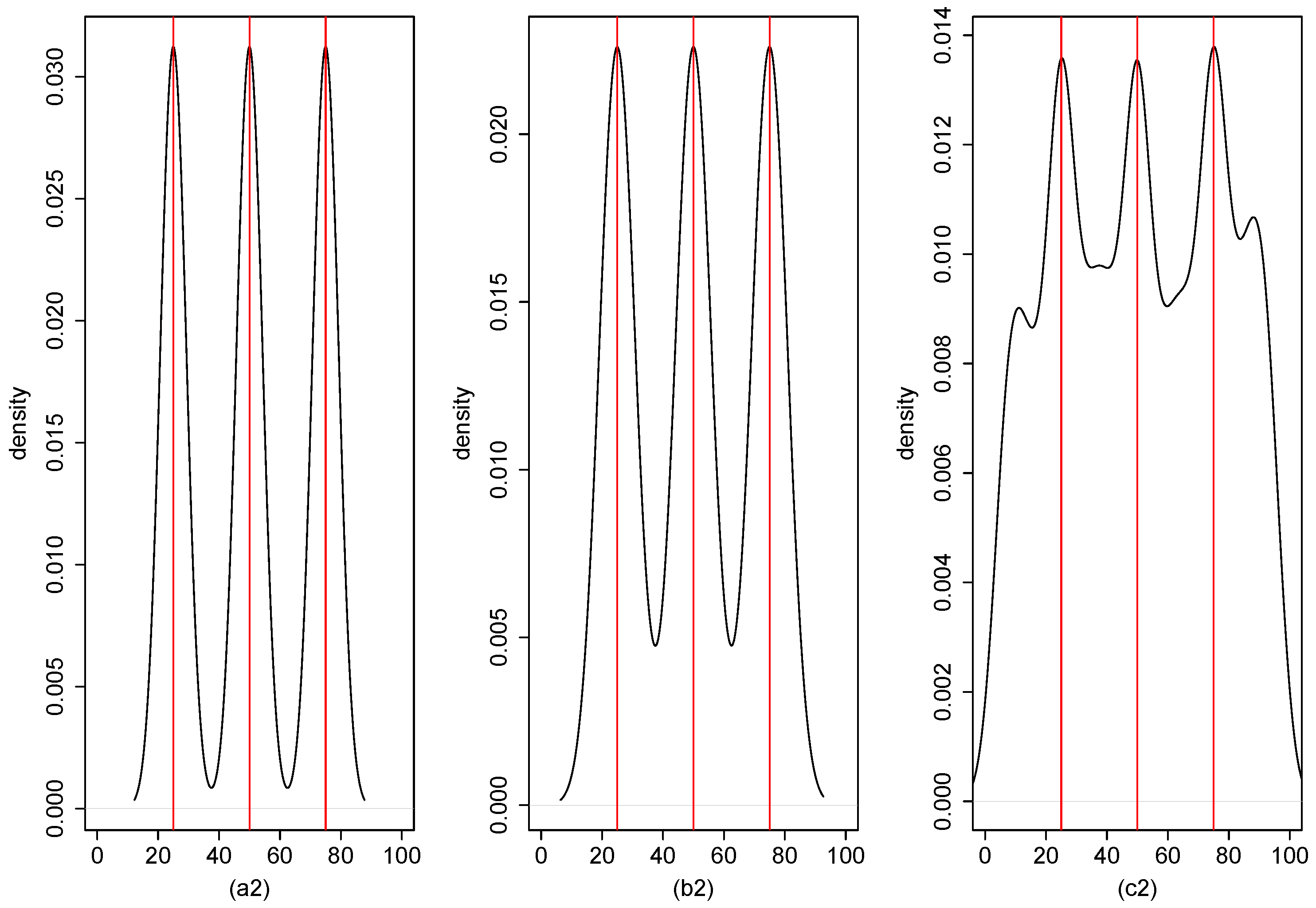

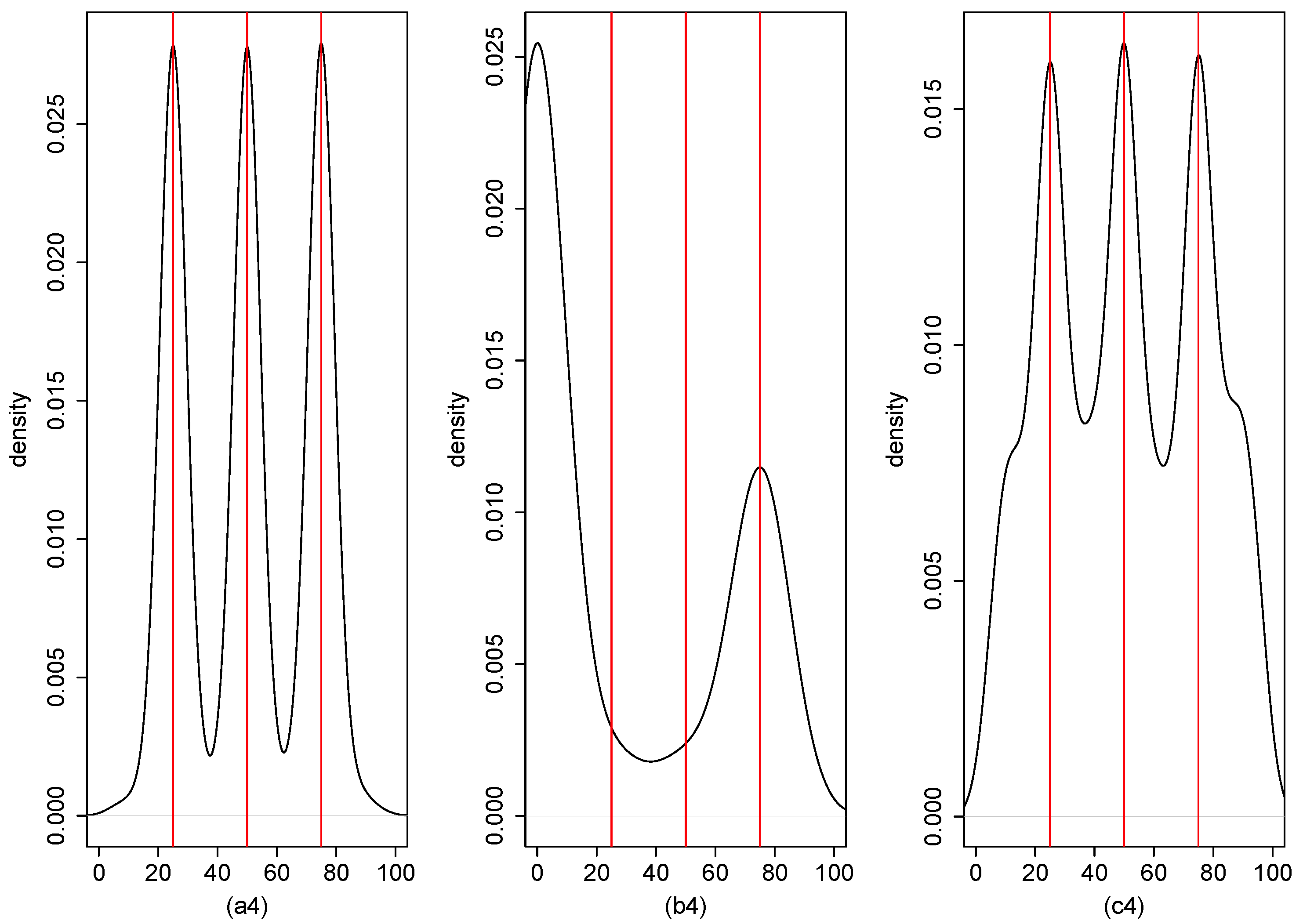
| Single Break Point | Three Break Points | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N/T | < 1 | = 1 | > 1 | MHD | Location Accuracy | < 3 | = 3 | > 3 | MHD | Location Accuracy | |||
| SaRa-M | 50/50 | 0 | 100 | 0 | 0.416 | 99 | 6.2 | 93.8 | 0 | 1.752 | 94 | 94 | 99.8 |
| 50/100 | 0 | 100 | 0 | 0.446 | 99.6 | 0 | 100 | 0 | 0.336 | 100 | 100 | 100 | |
| 100/50 | 0 | 100 | 0 | 0.122 | 100 | 0 | 100 | 0 | 0.062 | 100 | 100 | 100 | |
| 100/100 | 0 | 100 | 0 | 0.122 | 100 | 0 | 100 | 0 | 0.056 | 100 | 100 | 100 | |
| DCUSUM | 50/50 | 0 | 99.5 | 0.5 | 0.315 | 99 | 65.5 | 34.5 | 0 | 16.291 | 36.5 | 35 | 98.5 |
| 50/100 | 0 | 99.5 | 0.5 | 0.21 | 100 | 0 | 100 | 0 | 0.5 | 99.5 | 99.5 | 100 | |
| 100/50 | 0 | 100 | 0 | 0.07 | 100 | 31.5 | 68.5 | 0 | 8.055 | 68.5 | 68.5 | 100 | |
| 100/100 | 0 | 100 | 0 | 0.035 | 100 | 0 | 100 | 0 | 0.16 | 100 | 100 | 100 | |
| MSSaRa | 50/50 | 0.8 | 97 | 2.2 | 0.744 | 97.8 | 3 | 92.8 | 4.2 | 0.966 | 100 | 97.6 | 98.8 |
| 50/100 | 1.8 | 81 | 17.2 | 4.798 | 96.8 | 0 | 77.6 | 22.4 | 2.812 | 100 | 100 | 100 | |
| 100/50 | 0 | 98.4 | 1.6 | 0.344 | 99.8 | 0 | 97.6 | 2.4 | 0.212 | 100 | 100 | 100 | |
| 100/100 | 0 | 83 | 17 | 4.968 | 100 | 0 | 74.4 | 25.6 | 2.974 | 100 | 100 | 100 | |
| Single Break Point | Three Break Points | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N/T | < 1 | = 1 | > 1 | MHD | Location Accuracy | < 3 | = 3 | > 3 | MHD | Location Accuracy | |||
| SaRa-M | 50/50 | 0 | 100 | 0 | 0.074 | 99.8 | 0.2 | 99.8 | 0 | 0.06 | 100 | 100 | 99.6 |
| 50/100 | 0 | 100 | 0 | 0.092 | 99.8 | 0 | 100 | 0 | 0.042 | 100 | 100 | 100 | |
| 100/50 | 0 | 100 | 0 | 0.024 | 99.8 | 0 | 100 | 0 | 0.002 | 100 | 100 | 100 | |
| 100/100 | 0 | 100 | 0 | 0.01 | 100 | 0 | 100 | 0 | 0.01 | 100 | 100 | 100 | |
| DCUSUM | 50/50 | 0 | 99 | 1 | 0.135 | 100 | 15 | 85 | 0 | 3.9 | 85 | 85 | 100 |
| 50/100 | 0 | 99 | 1 | 0.15 | 100 | 0 | 100 | 0 | 0.04 | 100 | 100 | 100 | |
| 100/50 | 0 | 100 | 0 | 0 | 100 | 0 | 100 | 0 | 0.01 | 100 | 100 | 100 | |
| 100/100 | 0 | 100 | 0 | 0 | 100 | 0 | 100 | 0 | 0.02 | 100 | 100 | 100 | |
| MSSaRa | 50/50 | 0.2 | 94.6 | 5.2 | 0.822 | 99.2 | 0 | 56.4 | 43.6 | 2.93 | 99.9 | 100 | 100 |
| 50/100 | 0.6 | 81 | 18.4 | 4.99 | 98.8 | 0 | 24.5 | 75.5 | 9.381 | 99.9 | 100 | 100 | |
| 100/50 | 0 | 70.8 | 29.2 | 4.098 | 100 | 0 | 34.2 | 65.8 | 4.501 | 99.9 | 99.9 | 100 | |
| 100/100 | 0 | 15.3 | 84.7 | 25.637 | 99.8 | 0 | 0 | 100 | 17.058 | 100 | 100 | 100 | |
| Single Break Point | Three Break Points | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N/T | < 1 | = 1 | > 1 | MHD | Location Accuracy | < 3 | = 3 | > 3 | MHD | Location Accuracy | |||
| SaRa-M | 50/50 | 0 | 82 | 18 | 3.718 | 79.2 | 25 | 75 | 0 | 5.436 | 83 | 81.4 | 91.8 |
| 50/100 | 0 | 100 | 0 | 1.606 | 89.2 | 61 | 39 | 0 | 29.35 | 43.2 | 43.6 | 93.2 | |
| 100/50 | 0 | 81 | 19 | 2.864 | 91.8 | 0.4 | 93.4 | 6.2 | 0.78 | 99.6 | 98.2 | 99.6 | |
| 100/100 | 0 | 98.2 | 1.8 | 1.238 | 95.8 | 0.2 | 99.6 | 0.2 | 0.586 | 99.6 | 99.2 | 99.6 | |
| DCUSUM | 50/50 | 19 | 81 | 0 | 1.253 | 85 | 100 | 0 | 0 | 22.485 | 12.5 | 17.5 | 65.5 |
| 50/100 | 0 | 97 | 3 | 1.66 | 92.5 | 63 | 37 | 0 | 31.673 | 35.5 | 34.5 | 93 | |
| 100/50 | 1 | 99 | 0 | 0.576 | 94.5 | 99 | 1 | 0 | 23.052 | 11.5 | 11.5 | 83.5 | |
| 100/100 | 0 | 95.5 | 4.5 | 1.39 | 98.5 | 20.5 | 79.5 | 0 | 10.78 | 78 | 77 | 99 | |
| MSSaRa | 50/50 | 0 | 59.2 | 40.8 | 6.916 | 72.4 | 1.2 | 45.4 | 53.4 | 4.328 | 98.8 | 95.8 | 97.8 |
| 50/100 | 0 | 0 | 100 | 35.628 | 81.2 | 0 | 0 | 100 | 17.568 | 97.2 | 98 | 97.6 | |
| 100/50 | 0 | 67.6 | 32.4 | 5.254 | 89 | 0.4 | 58.2 | 41.4 | 3.222 | 99.4 | 98.8 | 99.6 | |
| 100/100 | 0 | 0 | 100 | 35.61 | 90 | 0 | 0 | 100 | 17.678 | 100 | 99.8 | 99.8 | |
| Single Break Point | Three Break Points | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N/T | < 1 | = 1 | > 1 | MHD | Location Accuracy | < 3 | > 3 | MHD | Location Accuracy | ||||
| SaRa-M | 50/50 | 0 | 85.4 | 14.6 | 3.574 | 82.6 | 33.8 | 65.2 | 1 | 8.29 | 70.4 | 70.4 | 91.2 |
| 50/100 | 0 | 98.2 | 1.8 | 2.266 | 90 | 15.6 | 83.2 | 1.2 | 9.832 | 79.4 | 80 | 93.8 | |
| 100/50 | 0 | 61.8 | 38.2 | 5.96 | 86.6 | 6.8 | 84.4 | 8.8 | 3.062 | 93.8 | 90.4 | 97.2 | |
| 100/100 | 0 | 89 | 11 | 4.256 | 91.4 | 0.4 | 91.8 | 7.8 | 3.15 | 95.4 | 96.4 | 96.6 | |
| DCUSUM | 50/50 | 53 | 47 | 0 | 2.319 | 83 | 100 | 0 | 0 | 23.846 | 48 | 13 | 49 |
| 50/100 | 9 | 90 | 1 | 2.527 | 86 | 98 | 2 | 0 | 43.383 | 13 | 22 | 75 | |
| 100/50 | 49 | 51 | 0 | 2.157 | 75 | 100 | 0 | 0 | 20.304 | 19 | 31 | 45 | |
| 100/100 | 0 | 95 | 5 | 2.22 | 95 | 87 | 13 | 0 | 39.892 | 20 | 21 | 85 | |
| MSSaRa | 50/50 | 2.3 | 82.5 | 15.2 | 3.953 | 76.2 | 0.2 | 75.9 | 23.9 | 1.489 | 99.4 | 99.7 | 99.3 |
| 50/100 | 1.1 | 23.8 | 75.1 | 23.481 | 79.5 | 0.1 | 7.1 | 92.8 | 12.941 | 95 | 94.4 | 95.1 | |
| 100/50 | 0.1 | 80 | 19.9 | 4.352 | 80.5 | 3.6 | 70 | 26.4 | 3.292 | 96.7 | 93.7 | 96.5 | |
| 100/100 | 0 | 9 | 91 | 28.908 | 93.4 | 0 | 2.5 | 97.5 | 14.155 | 97.3 | 97 | 96.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Xiao, Y.; Chen, Z. Estimation of Multiple Breaks in Panel Data Models Based on a Modified Screening and Ranking Algorithm. Symmetry 2023, 15, 1890. https://doi.org/10.3390/sym15101890
Li F, Xiao Y, Chen Z. Estimation of Multiple Breaks in Panel Data Models Based on a Modified Screening and Ranking Algorithm. Symmetry. 2023; 15(10):1890. https://doi.org/10.3390/sym15101890
Chicago/Turabian StyleLi, Fuxiao, Yanting Xiao, and Zhanshou Chen. 2023. "Estimation of Multiple Breaks in Panel Data Models Based on a Modified Screening and Ranking Algorithm" Symmetry 15, no. 10: 1890. https://doi.org/10.3390/sym15101890
APA StyleLi, F., Xiao, Y., & Chen, Z. (2023). Estimation of Multiple Breaks in Panel Data Models Based on a Modified Screening and Ranking Algorithm. Symmetry, 15(10), 1890. https://doi.org/10.3390/sym15101890








