Kinetic Axion f(R) Gravity Phase Space
Abstract
:1. Introduction
2. Essential Features of Kinetic Axion Gravity with and without Chern–Simons Corrections
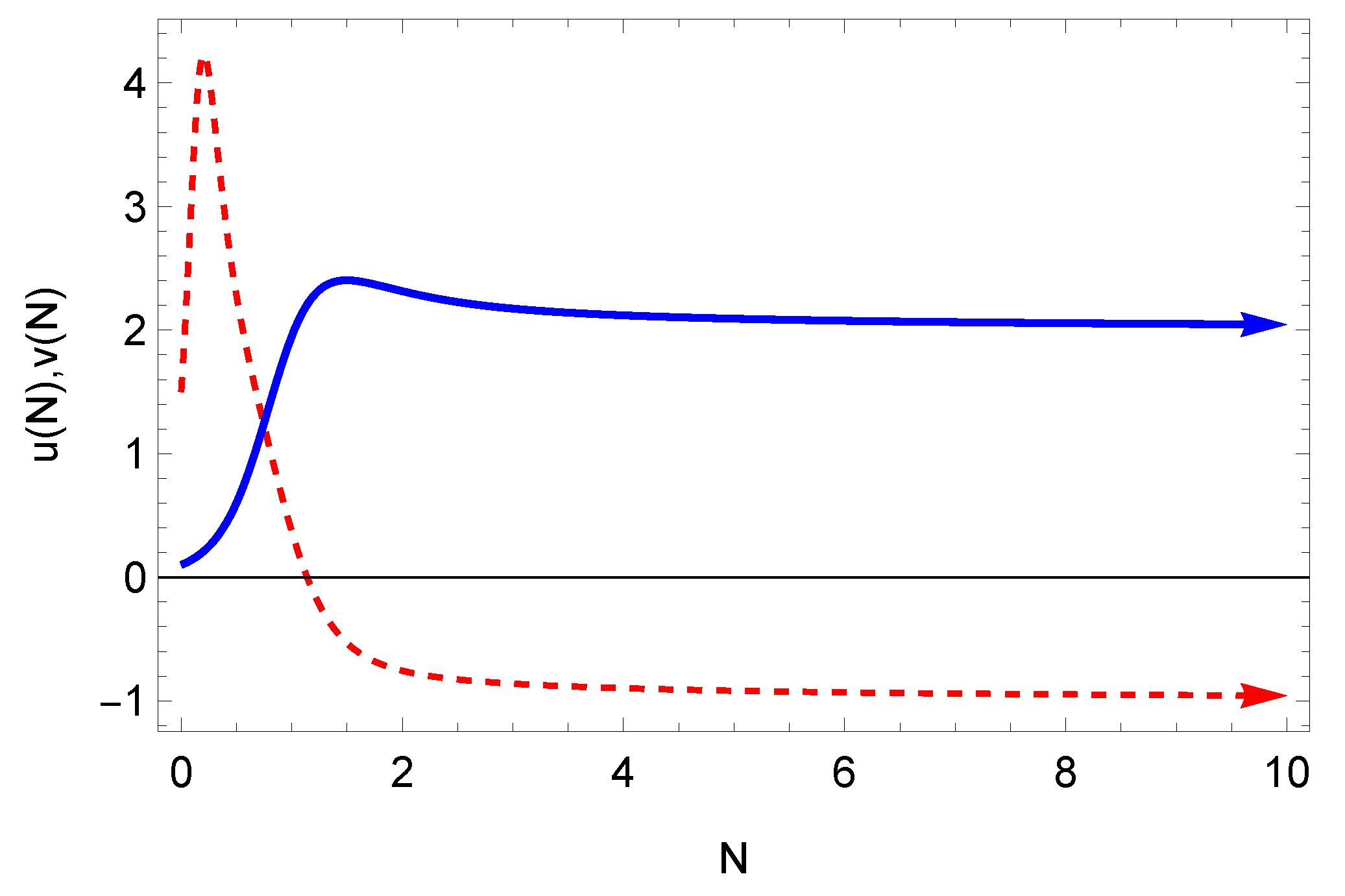
3. Phase Space Analysis of the Chern–Simons-Corrected Kinetic Axion Gravity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic Inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of Phase Transition in the New Inflationary Universe Scenario and Generation of Perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Linde, A.D. Inflationary Cosmology. arXiv 2008, arXiv:0705.0164. [Google Scholar]
- Gorbunov, D.S.; Rubakov, V.A. Introduction to the Theory of the Early Universe: Cosmological Perturbations and Inflationary Theory; World Scientific: Hackensack, CA, USA, 2011; 489p. [Google Scholar]
- Lyth, D.H.; Riotto, A. Particle physics models of inflation and the cosmological density perturbation. Phys. Rept. 1999, 314, 1–146. [Google Scholar] [CrossRef]
- Linde, A.D. Initial Conditions For Inflation. Phys. Lett. 1985, 162B, 281. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Sasaki, M.; Stewart, E.D. A General analytic formula for the spectral index of the density perturbations produced during inflation. Prog. Theor. Phys. 1996, 95, 71–78. [Google Scholar] [CrossRef]
- Turok, N. A critical review of inflation. Class. Quant. Grav. 2002, 19, 3449. [Google Scholar] [CrossRef]
- Linde, A.D. Inflation and string cosmology. Prog. Theor. Phys. Suppl. 2006, 163, 295. [Google Scholar] [CrossRef]
- Kachru, S.; Kallosh, R.; Linde, A.D.; Maldacena, J.M.; McAllister, L.P.; Trivedi, S.P. Towards inflation in string theory. JCAP 2003, 0310, 013. [Google Scholar] [CrossRef]
- Brandenberger, R. Initial Conditions for Inflation—A Short Review. arXiv 2016, arXiv:1601.01918. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopaedia Inflationaris. Phys. Dark Univ. 2014, 5–6, 75–235. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Chatterjee, S.; Chen, S.; Cordes, J.M.; et al. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. Astrophys. J. Lett. 2020, 905, L34. [Google Scholar] [CrossRef]
- Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blecha, L.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; et al. The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background. Astrophys. J. Lett. 2023, 951, L8. [Google Scholar] [CrossRef]
- Hild, S.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity Studies for Third-Generation Gravitational Wave Observatories. Class. Quant. Grav. 2011, 28, 094013. [Google Scholar] [CrossRef]
- Baker, J.; Bellovary, J.; Bender, P.L.; Berti, E.; Caldwell, R.; Camp, J.; Conklin, J.W.; Cornish, N.; Cutler, C.; DeRosa, R.; et al. The Laser Interferometer Space Antenna: Unveiling the Millihertz Gravitational Wave Sky. arXiv 2019, arXiv:1907.06482. [Google Scholar]
- Smith, T.L.; Caldwell, R. LISA for Cosmologists: Calculating the Signal-to-Noise Ratio for Stochastic and Deterministic Sources. Phys. Rev. D 2019, 100, 104055. [Google Scholar] [CrossRef]
- Crowder, J.; Cornish, N.J. Beyond LISA: Exploring future gravitational wave missions. Phys. Rev. D 2005, 72, 083005. [Google Scholar] [CrossRef]
- Smith, T.L.; Caldwell, R. Sensitivity to a Frequency-Dependent Circular Polarization in an Isotropic Stochastic Gravitational Wave Background. Phys. Rev. D 2017, 95, 044036. [Google Scholar] [CrossRef]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. arXiv 2020, arXiv:2006.13545. [Google Scholar] [CrossRef]
- Weltman, A.; Bull, P.; Camera, S.; Kelley, K.; Padmanabhan, H.; Pritchard, J.; Raccanelli, A.; Riemer-Sørensen, S.; Shao, L.; Andrianomena, S.; et al. Fundamental physics with the Square Kilometre Array. Publ. Astron. Soc. Austral. 2020, 37, e002. [Google Scholar] [CrossRef]
- Auclair, P.; Bacon, D.; Baker, T.; Barreiro, T.; Bartolo, N.; Belgacem, E.; Bellomo, N.; Ben-Dayan, I.; Bertacca, D.; Besancon, M.; et al. Cosmology with the Laser Interferometer Space Antenna. arXiv 2023, arXiv:2204.05434. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Abitbol, M.H.; Adachi, S.; Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D.; Alvarez, M.A.; Arnold, K.; et al. The Simons Observatory: Astro2020 Decadal Project Whitepaper. Bull. Am. Astron. Soc. 2019, 51, 147. [Google Scholar]
- Nishizawa, A.; Kobayashi, T. Parity-violating gravity and GW170817. Phys. Rev. D 2018, 98, 124018. [Google Scholar] [CrossRef]
- Wagle, P.; Yunes, N.; Garfinkle, D.; Bieri, L. Hair loss in parity violating gravity. Class. Quant. Grav. 2019, 36, 115004. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N.; Tanaka, T. Gravitational Waves from Quasi-Circular Black Hole Binaries in Dynamical Chern–Simons Gravity. Phys. Rev. Lett. 2012, 109, 251105. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Chirality of gravitational waves in Chern–Simons f(R) gravity cosmology. Phys. Rev. D 2022, 105, 104054. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Kinetic axion F(R) gravity inflation. Phys. Rev. D 2022, 106, 044041. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rept. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Kinetic Axion Chern Simons Inflationary Dynamics. 2023; Unpublished work. [Google Scholar]
- Hwang, J.; Noh, H. Classical evolution and quantum generation in generalized gravity theories including string corrections and tachyons: Unified analyses. Phys. Rev. D 2005, 71, 063536. [Google Scholar] [CrossRef]
- Shah, P.; Samanta, G.C. Stability analysis for cosmological models in f(R) gravity using dynamical system analysis. Eur. Phys. J. C 2019, 79, 414. [Google Scholar] [CrossRef]
| Fixed Point | (x,z,u,v) | Eigenvalues | Stability | q | |
|---|---|---|---|---|---|
| (0,−4,5,0) | (−6,−5,4,0) | Non Hyperbolic | 1 | ||
| (0,0,−1,2) | (0,−6,−3,0) | Non Hyperbolic | −1 | −1 | |
| (,3,,) | (6,3,3,) | Saddle | 0 |
| Fixed Point | (x,y,z,u,v,p,q) | Eigenvalues | Stability | q | |
|---|---|---|---|---|---|
| (0,0,−4,5,0,0,0) | (−6,−5,−4,4,−3,0,0) | Non Hyperbolic | 1 | ||
| (0,0,0,−1,2,0,0) | (0,0,−6,−4,−3,−3,0) | Non Hyperbolic | −1 | −1 | |
| (,0,3,,,0,0) | (6,3,3,3,2,,6) | Saddle | 0 | ||
| (0,0,2,,1,,0) | (4,4,,,−2,2,1) | Saddle | 0 | ||
| (0,0,,,,0,) | (−3,3,3,,,,−1) | Saddle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oikonomou, V.K.; Fronimos, F.P.; Razina, O.; Tsyba, P. Kinetic Axion f(R) Gravity Phase Space. Symmetry 2023, 15, 1897. https://doi.org/10.3390/sym15101897
Oikonomou VK, Fronimos FP, Razina O, Tsyba P. Kinetic Axion f(R) Gravity Phase Space. Symmetry. 2023; 15(10):1897. https://doi.org/10.3390/sym15101897
Chicago/Turabian StyleOikonomou, Vasilis K., Fotis P. Fronimos, Olga Razina, and Pyotr Tsyba. 2023. "Kinetic Axion f(R) Gravity Phase Space" Symmetry 15, no. 10: 1897. https://doi.org/10.3390/sym15101897
APA StyleOikonomou, V. K., Fronimos, F. P., Razina, O., & Tsyba, P. (2023). Kinetic Axion f(R) Gravity Phase Space. Symmetry, 15(10), 1897. https://doi.org/10.3390/sym15101897








