Proposal for Mediative Fuzzy Control: From Type-1 to Type-3
Abstract
:1. Introduction
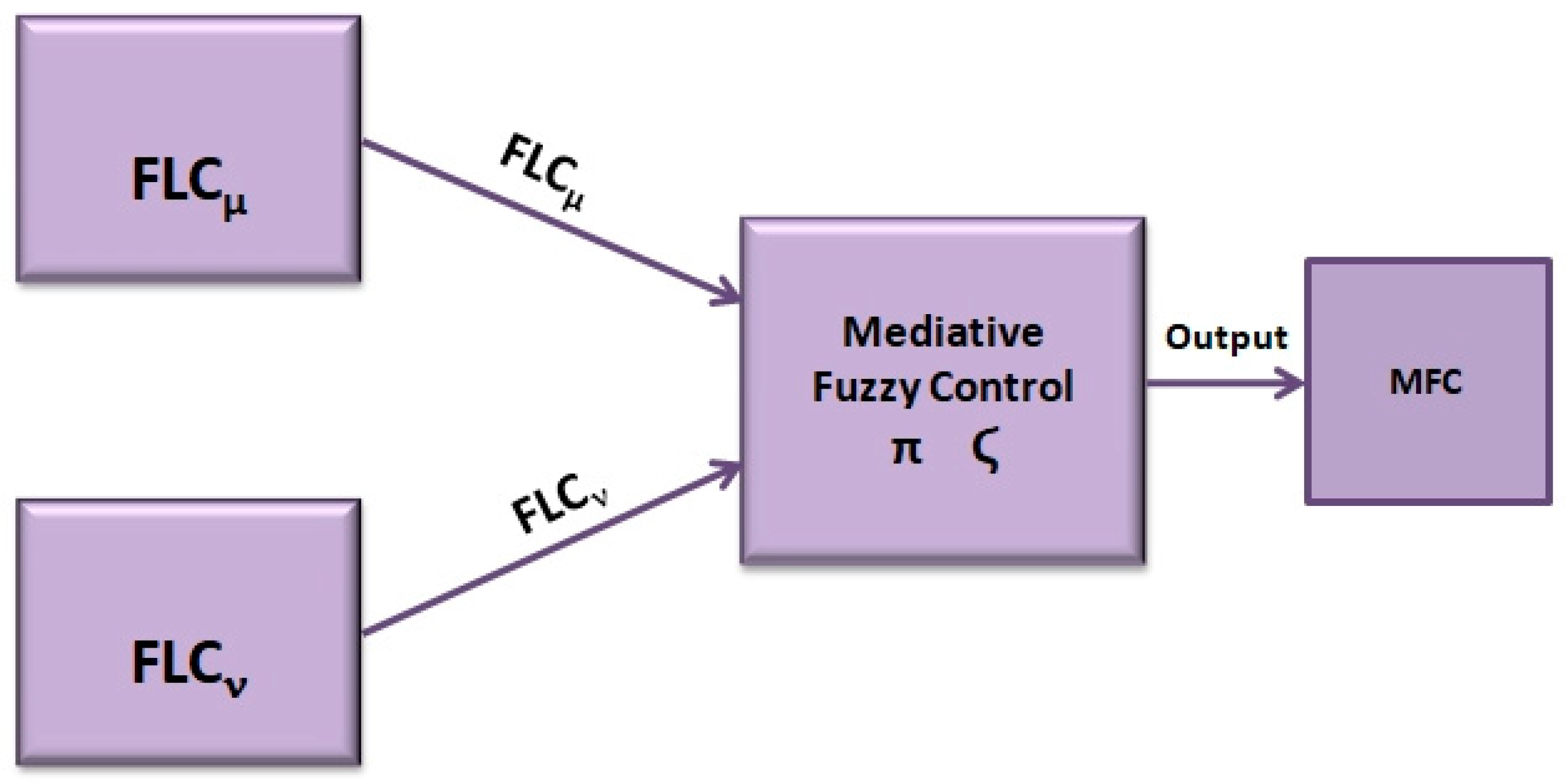
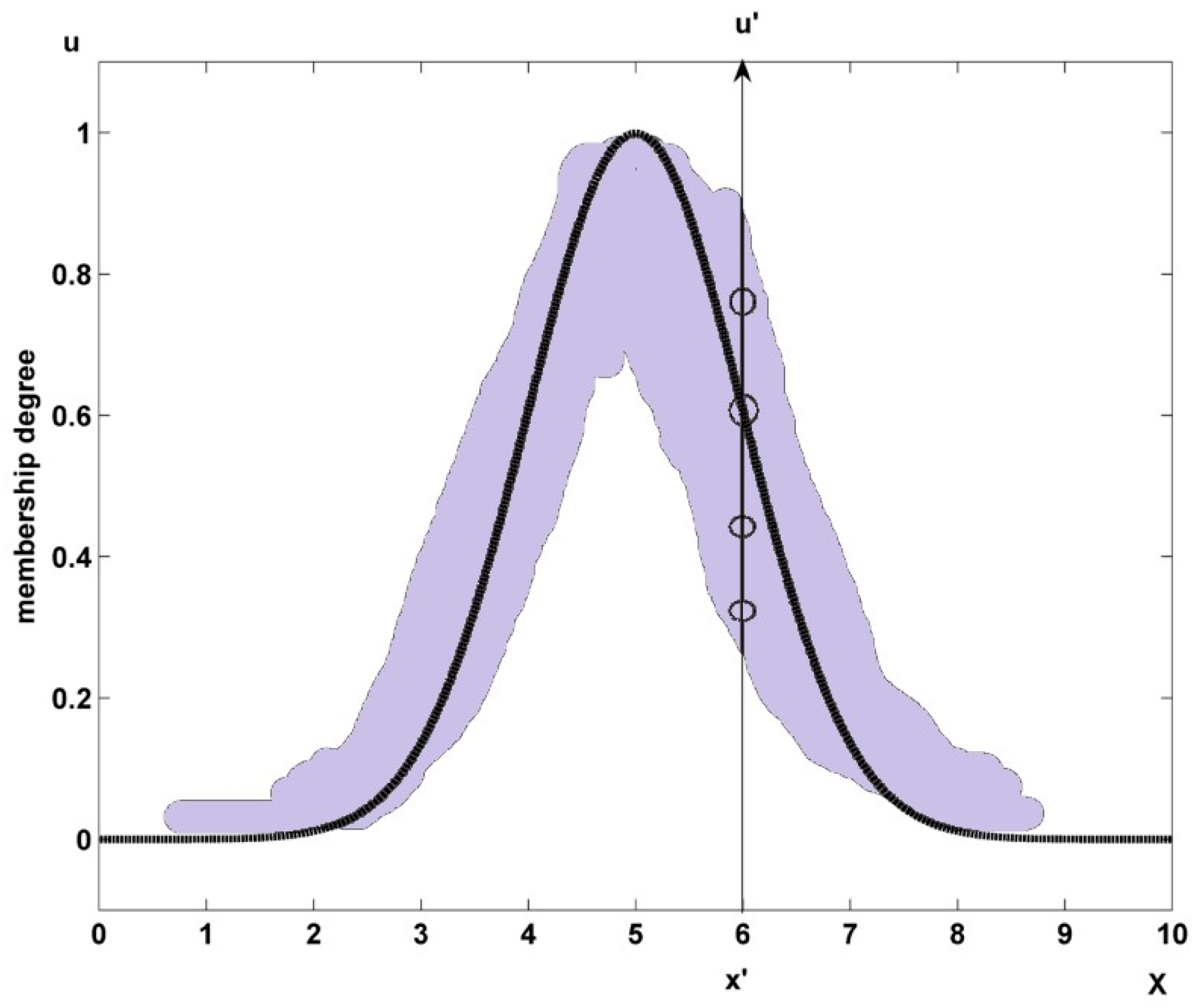
2. Mediative Fuzzy Logic for Type-1 Controller
3. Proposed Mediative Type-1 Fuzzy Controller
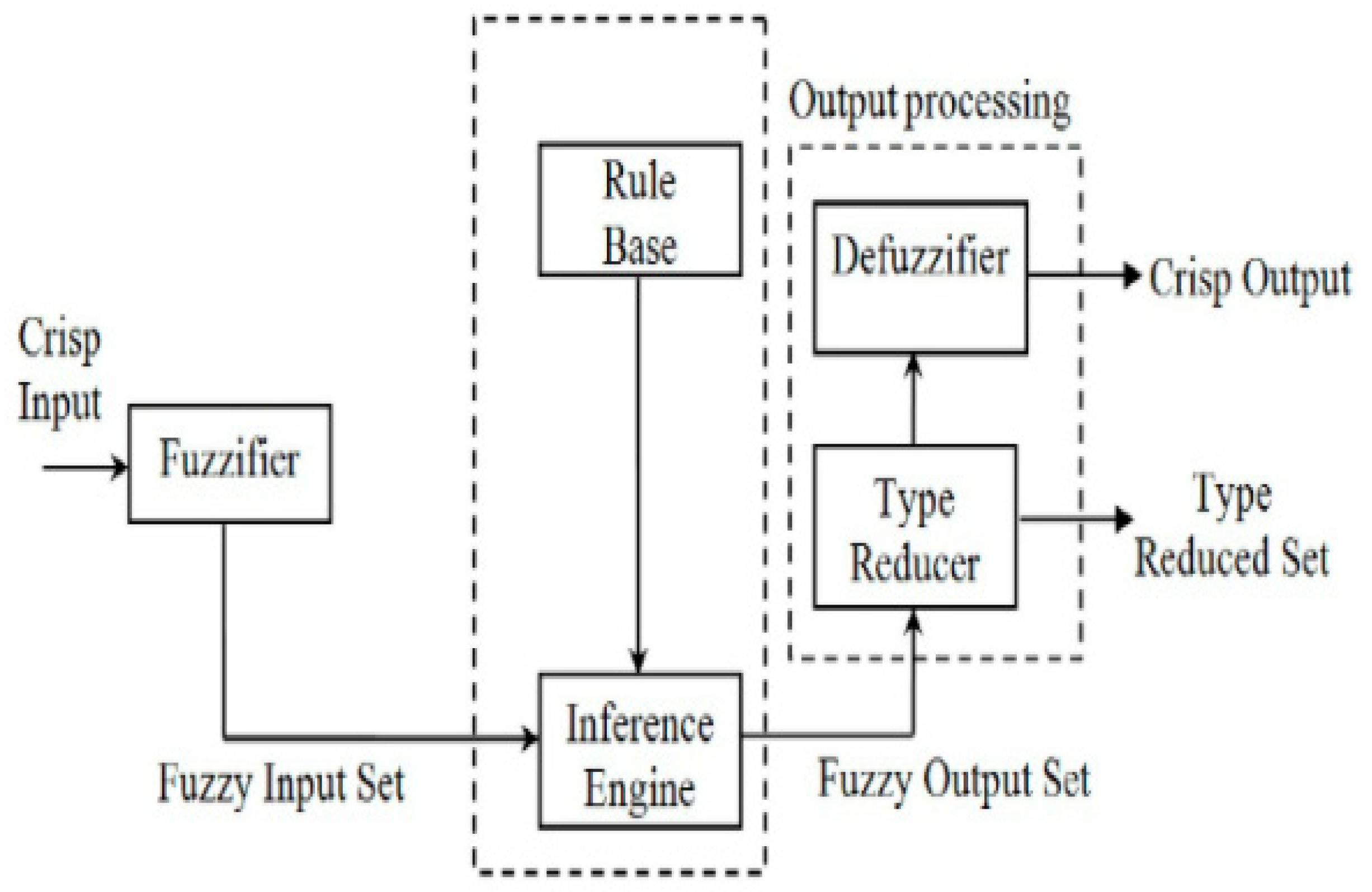
4. Mediative Type-2 Fuzzy Controller
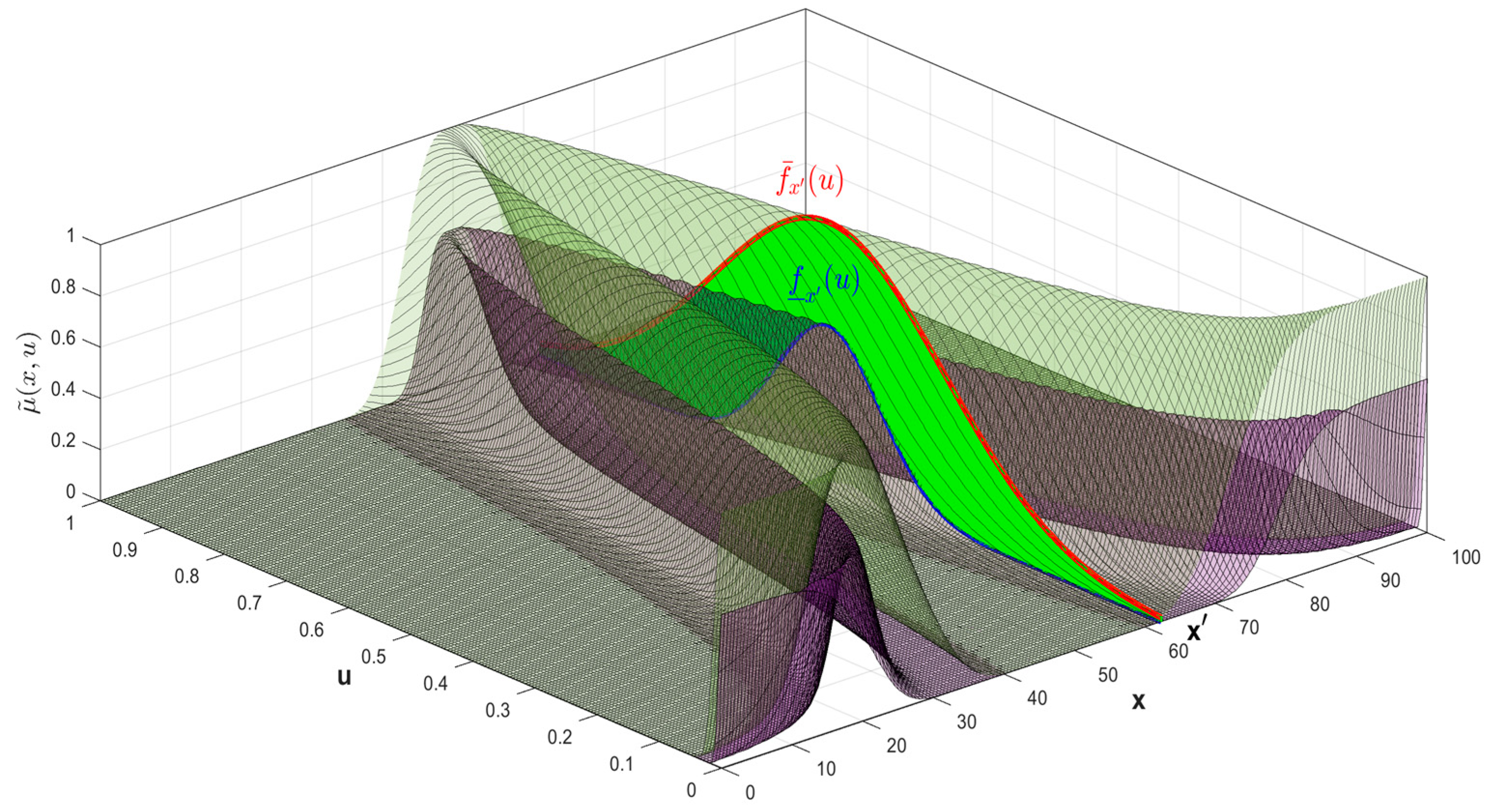
5. Mediative Type-3 Fuzzy Controller
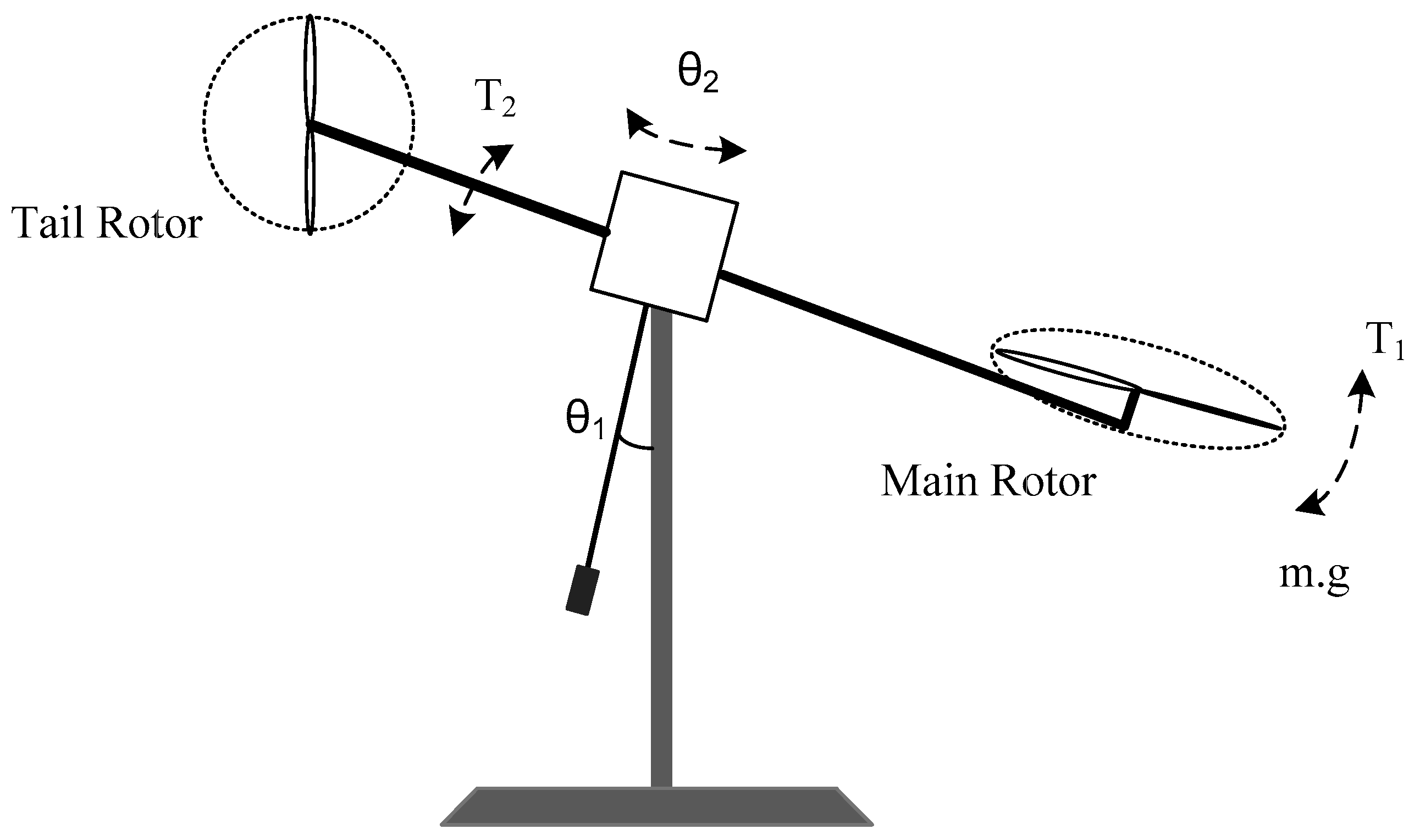
6. Illustrative Example
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Knowledge representation in Fuzzy Logic. In IEEE Transactions on Knowledge Data Engineering; Springer: Boston, MA, USA, 1989; Volume 1, p. 89. [Google Scholar]
- Montiel, O.; Castillo, O.; Melin, P.; Rodríguez Días, A.; Sepúlveda, R. Reducing the cycling problem in evolutionary algorithms. In Proceedings of the ICAI-2005, Las Vegas, NV, USA, 27–30 June 2005; pp. 426–432. [Google Scholar]
- Montiel, O.; Castillo, O.; Melin, P.; Sepulveda, R. Mediative fuzzy logic: A new approach for contradictory knowledge management. Soft Comput. 2008, 12, 251–256. [Google Scholar] [CrossRef]
- Iancu, I. Heart disease diagnosis based on mediative fuzzy logic. Artif. Intell. Med. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Dhiman, N.; Sharma, M.K. Mediative Sugeno’s-TSK Fuzzy Logic Based Screening Analysis to Diagnosis of Heart Disease. Appl. Math. 2019, 10, 448–467. [Google Scholar] [CrossRef]
- Sharma, M.K.; Dhiman, N.; Mishra, V.N. Mediative Fuzzy Logic of Sugeno-Tsk Model for the Diagnosis of Diabetes. J. Phys. Conf. Ser. 2021, 1724, 012028. [Google Scholar] [CrossRef]
- Sharma, M.K.; Dhiman, N.; Vandana Mishra, V.N. Mediative fuzzy logic mathematical model: A contradictory management prediction in COVID-19 pandemic. Appl. Soft Comput. 2021, 105, 107285. [Google Scholar] [CrossRef]
- Sharma, M.K.; Dhiman, N.; Mishra, L.N.; Mishra, V.N.; Sahani, S.K. Mediative Fuzzy Extension Technique and Its Consistent Measurement in the Decision Making of Medical Application. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Towards Interval Type-3 Intuitionistic Fuzzy Sets and Systems. Mathematics 2022, 10, 4091. [Google Scholar] [CrossRef]
- Qasem, S.N.; Ahmadian, A.; Mohammadzadeh, A.; Rathinasamy, S.; Pahlevanzadeh, B. A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inform. Sci. 2021, 572, 424–443. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Sabzalian, M.H.; Zhang, W. An interval type-3 fuzzy system and a new online fractional-order learning algorithm: Theory and practice. IEEE Trans. Fuzzy Syst. 2020, 28, 1940–1950. [Google Scholar] [CrossRef]
- Liu, Z.; Mohammadzadeh, A.; Turabieh, H.; Mafarja, M.; Band, S.S.; Mosavi, A. A New Online Learned Interval Type-3 Fuzzy Control System for Solar Energy Management Systems. IEEE Access 2021, 9, 10498–10508. [Google Scholar] [CrossRef]
- Singh, D.; Verma, N.K.; Ghosh, A.K.; Malagaudanavar, A.K. An Approach Towards the Design of Interval Type-3 TS Fuzzy System. IEEE Trans. Fuzzy Syst. 2021, 30, 3880–3893. [Google Scholar] [CrossRef]
- Wang, J.H.; Tavoosi, J.; Mohammadzadeh, A.; Mobayen, S.; Asad, J.H.; Assawinchaichote, W.; Skruch, P. Non-Singleton Type-3 Fuzzy Approach for Flowmeter Fault Detection: Experimental Study in a Gas Industry. Sensors 2021, 21, 7419. [Google Scholar] [CrossRef] [PubMed]
- Alattas, K.A.; Mohammadzadeh, A.; Mobayen, S.; Aly, A.A.; Felemban, B.F. A New Data-Driven Control System for MEMSs Gyroscopes: Dynamics Estimation by Type-3 Fuzzy Systems. Micromachines 2021, 12, 1390. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Raise, A.; Mohammadzadeh, A.; Rathinasamy, S.; Band, S.S.; Mosavi, A. Deep learned recurrent type-3 fuzzy system: Application for renewable energy modeling/prediction. Energy Rep. 2021, 7, 8115–8127. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, C.; Mohammadzadeh, A. Type-3 Fuzzy Control of Robotic Manipulators. Symmetry 2023, 15, 483. [Google Scholar] [CrossRef]
- Huang, H.; Xu, H.; Chen, F.; Zhang, C.; Mohammadzadeh, A. An Applied Type-3 Fuzzy Logic System: Practical Matlab Simulink and M-Files for Robotic, Control, and Modeling Applications. Symmetry 2023, 15, 475. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic Fuzzy Sets: Theory and Applications; Springer: Heidelberg, Germany, 1999. [Google Scholar]
- Mendel, J.M.; Bob John, R.I. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. A new method for fuzzy inference in intuitionistic fuzzy systems. In Proceedings of the International Conference NAFIPS 2003, Chicago, IL, USA, 24–26 July 2003; IEEE Press: Chicago, IL, USA; pp. 20–25. [Google Scholar]
- Melin, P.; Castillo, O. Adaptive intelligent control of aircraft systems with a hybrid approach combining neural networks, fuzzy logic and fractal theory. Appl. Soft Comput. 2003, 3, 353–362. [Google Scholar] [CrossRef]
- Mendel, J.M.; Hagras, H.; Tan, W.-W.; Melek, W.W.; Ying, H. Introduction to Type-2 Fuzzy Logic Control; Wiley and IEEE Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- JMoreno, J.E.; Sanchez, M.A.; Mendoza, O.; Rodríguez-Díaz, A.; Castillo, O.; Melin, P.; Castro, J.R. Design of an interval Type-2 fuzzy model with justifiable uncertainty. Inf. Sci. 2020, 513, 206–221. [Google Scholar] [CrossRef]
- Castillo, O.; Castro, J.R.; Melin, P. Interval Type-3 Fuzzy Systems: Theory and Design, 1st ed.; Springer: Cham, Switzerland, 2022; pp. 45–67. [Google Scholar]
- Mendez, G.M.; Lopez-Juarez, I.; Montes-Dorantes, P.N.; Garcia, M.A. A New Method for the Design of Interval Type-3 Fuzzy Logic Systems with Uncertain Type-2 Non-Singleton Inputs (IT3 NSFLS-2): A Case Study in a Hot Strip Mill. IEEE Access 2023, 11, 44065–44081. [Google Scholar] [CrossRef]
- Castillo, O.; Kutlu, F.; Atan, O. Intuitionistic fuzzy control of twin rotor multiple input multiple output systems. J. Intell. Fuzzy Syst. 2020, 38, 821–833. [Google Scholar] [CrossRef]
- Nabipour, N.; Qasem, S.N.; Jermsittiparsert, K. Type-3 fuzzy voltage management in PV/hydrogen fuel cell/battery hybrid systems. Int. J. Hydrog. Energy 2020, 45, 32478–33249. [Google Scholar] [CrossRef]
- Taghieh, A.; Aly, A.A.; Felemban, B.F.; Althobaiti, A.; Mohammadzadeh, A.; Bartoszewicz, A. A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems. Electronics 2022, 11, 63. [Google Scholar] [CrossRef]
- Vafaie, R.H.; Mohammadzadeh, A.; Piran, M. A new type-3 fuzzy predictive controller for MEMS gyroscopes. Nonlinear Dyn. 2021, 106, 381–403. [Google Scholar] [CrossRef]
- Tian, M.-W.; Yan, S.-R.; Mohammadzadeh, A.; Tavoosi, J.; Mobayen, S.; Safdar, R.; Assawinchaichote, W.; Vu, M.T.; Zhilenkov, A. Stability of Interval Type-3 Fuzzy Controllers for Autonomous Vehicles. Mathematics 2021, 9, 2742. [Google Scholar] [CrossRef]

| Main Rotor | |||||||
| MF | a | b | c | d | |||
| NB | −5 | −5 | −3.5 | −0.5 | 0.3 | 0.2 | 0.2 |
| N | −3.5 | −1.5 | 0 | 0.3 | 0.2 | 0.2 | |
| Z | −1.5 | 0 | 1.5 | - | 0.3 | 0.2 | 0.2 |
| P | 0 | 1.5 | 3 | 0.3 | 0.2 | 0.2 | |
| PB | 0.5 | 3 | 5 | 5 | 0.3 | 0.2 | 0.2 |
| Tail Rotor | |||||||
| MF | a | b | c | d | |||
| NB | −5 | −5 | −3 | −1 | 0.3 | 0.2 | 0.2 |
| N | −3 | −1 | −0.5 | 0.3 | 0.2 | 0.2 | |
| Z | −1 | −0.5 | 1 | - | 0.3 | 0.2 | 0.2 |
| P | −0.5 | 1 | 2.5 | 0.3 | 0.2 | 0.2 | |
| PB | 1 | 2.5 | 5 | 5 | 0.3 | 0.2 | 0.2 |
| Main Rotor | |||||||
| MF | a | b | c | d | |||
| NB | −5 | −5 | −2.5 | −1 | 0.3 | 0.2 | 0.2 |
| N | −2.5 | −1 | 0 | 0.3 | 0.2 | 0.2 | |
| Z | −1 | 0 | 1.5 | - | 0.3 | 0.2 | 0.2 |
| P | 0 | 1.5 | 3 | 0.3 | 0.2 | 0.2 | |
| PB | 1.5 | 3 | 5 | 5 | 0.3 | 0.2 | 0.2 |
| Tail Rotor | |||||||
| MF | a | b | c | d | |||
| NB | −5 | −5 | −3 | −1 | 0.3 | 0.2 | 0.2 |
| N | −3 | −1.5 | −0.5 | 0.3 | 0.2 | 0.2 | |
| Z | −1.5 | −0.5 | 1.5 | - | 0.3 | 0.2 | 0.2 |
| P | −0.5 | 1.5 | 2.5 | 0.3 | 0.2 | 0.2 | |
| PB | 1.5 | 2.5 | 5 | 5 | 0.3 | 0.2 | 0.2 |
| Main and Tail Rotors | |||||||
|---|---|---|---|---|---|---|---|
| MF | a | b | c | d | |||
| NB | −10 | −10 | −7.5 | −0.5 | 0.3 | 0.2 | 0.2 |
| N | −7.5 | −5 | 0 | 0.3 | 0.2 | 0.2 | |
| Z | −5 | 0 | 5 | - | 0.3 | 0.2 | 0.2 |
| P | 0 | 5 | 7.5 | 0.3 | 0.2 | 0.2 | |
| PB | 5 | 7.5 | 10 | 10 | 0.3 | 0.2 | 0.2 |
| Reference Signal | Rotor | PID [28] | Intuitionistic [28] | Mediative Type-1 (This Work) |
|---|---|---|---|---|
| Step | Main | 1.465 | 1.128 | 1.060 |
| Step | Tail | 3.963 | 2.713 | 2.355 |
| Saw | Main | 1.549 | 1.170 | 1.085 |
| Saw | Tail | 7.743 | 6.664 | 6.344 |
| Sinus | Main | 0.811 | 0.226 | 0.155 |
| Sinus | Tail | 8.380 | 6.486 | 6.222 |
| Reference Signal | Rotor | Mediative Type-1 | Mediative Type-2 | Mediative Type-3 |
|---|---|---|---|---|
| Step | Main | 1.060 | 1.031 | 0.871 |
| Step | Tail | 2.355 | 2.299 | 2.132 |
| Saw | Main | 1.085 | 1.037 | 0.925 |
| Saw | Tail | 6.344 | 6.289 | 6.021 |
| Sinus | Main | 0.155 | 0.127 | 0.094 |
| Sinus | Tail | 6.222 | 6.056 | 5.812 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo, O.; Melin, P. Proposal for Mediative Fuzzy Control: From Type-1 to Type-3. Symmetry 2023, 15, 1941. https://doi.org/10.3390/sym15101941
Castillo O, Melin P. Proposal for Mediative Fuzzy Control: From Type-1 to Type-3. Symmetry. 2023; 15(10):1941. https://doi.org/10.3390/sym15101941
Chicago/Turabian StyleCastillo, Oscar, and Patricia Melin. 2023. "Proposal for Mediative Fuzzy Control: From Type-1 to Type-3" Symmetry 15, no. 10: 1941. https://doi.org/10.3390/sym15101941
APA StyleCastillo, O., & Melin, P. (2023). Proposal for Mediative Fuzzy Control: From Type-1 to Type-3. Symmetry, 15(10), 1941. https://doi.org/10.3390/sym15101941







