Hadronic Isospin Helicity and the Consequent SU(4) Gauge Theory
Abstract
:1. Introduction
2. Spin and Casimir Operators of the LG, the Mass Squared and Pauli–Lubański Operator
2.1. Spin
2.2. The Role of Spin in Defining the Generators of the Lorentz Group
2.3. Casimir Operators of the LG and Dirac Equation
2.4. Spinor-Helicity Formalism
3. Physics of the Spin Helicity Operator
4. Hadronic Isospin and
4.1. The Hadronic Isospin
4.2. Hypercharge Operator and Helicity Operator
4.3. Electro-Strong Symmetry Breaking
4.4. Covariant Derivative after Symmetry Breaking
5. The Higgs Mechanism Applied to Hadronic Interactions
5.1. The Hadronic Higgs
5.2. Discussion of the Vector Boson Masses
6. Results and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
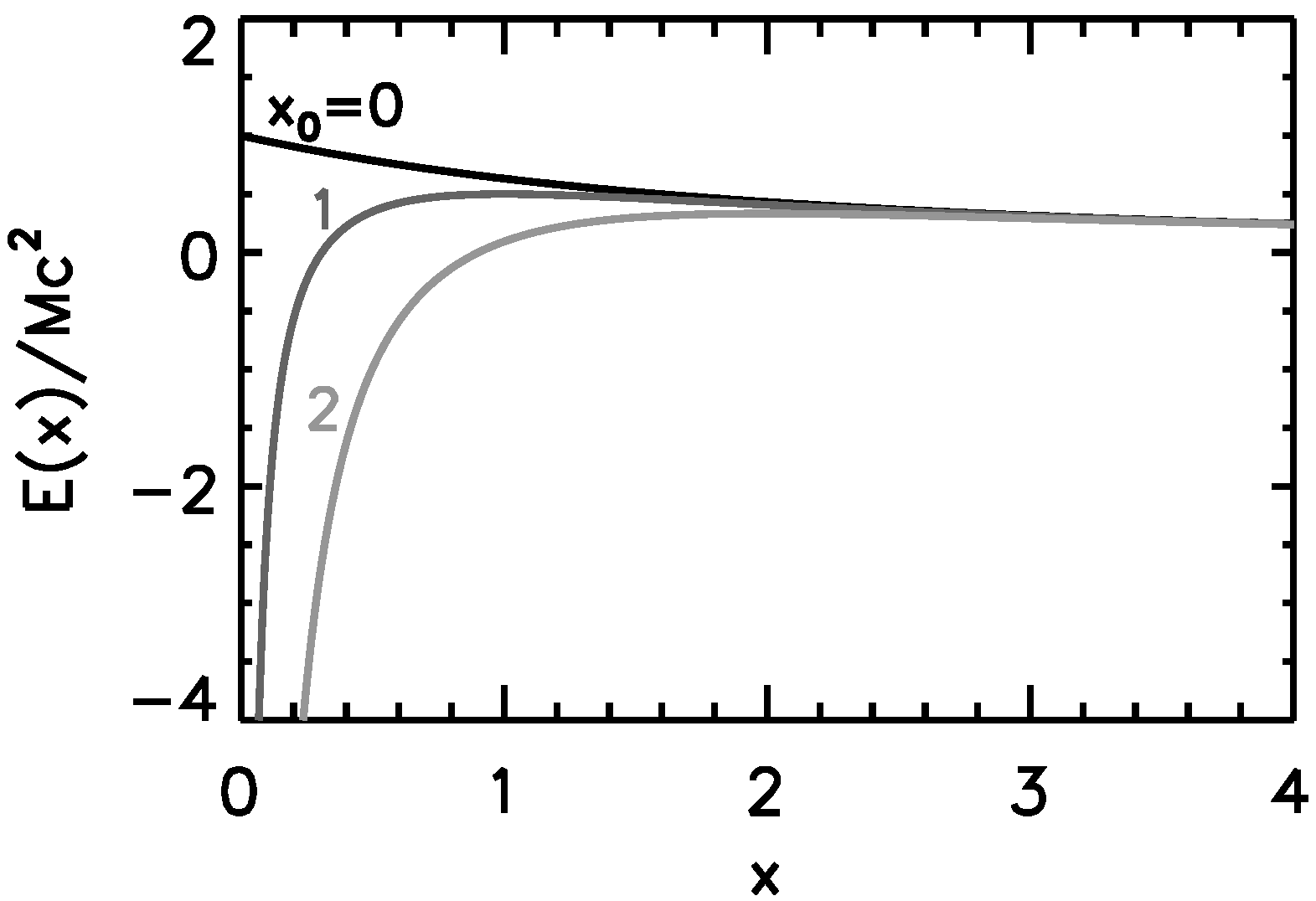
Appendix A. On the Strong Coupling Constant
References
- Kaku, M. Quantum Field Theory, a Modern Introduction; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley Publishing Company: Reading, MA, USA, 1995. [Google Scholar]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Yang, C.N.; Mills, R.L. Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 1954, 96, 191. [Google Scholar] [CrossRef]
- Weinberg, S. A model of leptons. Phys. Rev. Lett. 1967, 19, 1264. [Google Scholar] [CrossRef]
- Gell-Mann, M. A schematic model of baryons and mesons. Phys. Lett. 1964, 8, 214. [Google Scholar] [CrossRef]
- Zweig, G. An SU(3) Model for Strong Interaction Symmetry and Its Breaking, CERN Report, 1964, 8182/TH.401. Available online: https://cds.cern.ch/record/352337/files/CERN-TH-401.pdf (accessed on 31 July 2023).
- Heisenberg, W. Über den Bau der Atomkerne. I. Z. Physik 1932, 77, 1. [Google Scholar] [CrossRef]
- Pati, J.C.; Salam, A. Unified lepton-hadron symmetry and a gauge theory of the basic interactions. Phys. Rev. D 1973, 8, 1240. [Google Scholar] [CrossRef]
- Pati, J.C.; Salam, A. Lepton number as the fourth “color”. Phys. Rev. D 1974, 10, 275. [Google Scholar] [CrossRef]
- Blumhofer, A.; Lampe, B. A low-energy compatible SU(4)-type model for vector leptoquarks of mass 1 ≤ TeV. Eur. Phys. J. C 1999, 7, 141–148. [Google Scholar] [CrossRef]
- Rolli, S.; Tanabashi, M. Leptoquarks Review; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2016. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of particle physics: Particle Data Group. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Yukawa, H. On the Interaction of Elementary Particles, I. Proc. Phys. Math. Soc. Jpn. 1935, 17, 48–57. [Google Scholar] [CrossRef]
- Marsch, E.; Narita, Y. Fermion unification model based on the intrinsic SU(8) symmetry of a generalized Dirac equation. Front. Phys. 2015, 3, 82. [Google Scholar] [CrossRef]
- Marsch, E.; Narita, Y. Fundamental fermion interactions via vector bosons of unified SU(2) ⊗ SU(4) gauge fields. Front. Phys. 2016, 4, 5. [Google Scholar] [CrossRef]
- Marsch, E.; Narita, Y. Dirac equation based on the vector representation of the Lorentz group. Eur. Phys. J. Plus 2020, 135, 782. [Google Scholar] [CrossRef]
- Marsch, E.; Narita, Y. Connecting in the Dirac equation the Clifford algebra of Lorentz invariance with the Lie algebra of SU(N). Symmetry 2021, 13, 475. [Google Scholar] [CrossRef]
- Marsch, E.; Narita, Y. Lorentz invariance and the spinor helicity formalism yield the U(1) and SU(3) symmetry. Eur. Phys. J. Plus 2022, 137, 818. [Google Scholar] [CrossRef]
- Marsch, E.; Narita, Y. A new route to Symmetries through the extended Dirac equation. Symmetry 2023, 15, 492. [Google Scholar] [CrossRef]
- Glashow, S.L. Partial-symmetries of weak interactions. Nucl. Phys. 1961, 22, 579–588. [Google Scholar] [CrossRef]
- Weinberg, S. Lectures on Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Tomonaga, S.-I. The Story of Spin; The University of Chicago Press: Chicago, IL, USA, 1997. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley and Sons, Inc.: New York, NY, USA, 2015. [Google Scholar]
- Wigner, E. On unitary representations of the inhomogeneous Lorentz group. Ann. Math. Second. Ser. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Bargman, V.; Wigner, E. Group theoretical discussion of relativistic wave equations. Proc. Natl. Acad. Sci. USA 1948, 34, 211–223. [Google Scholar]
- Joos, H. Zur Darstellungstheorie der inhomogenen Lorentzgruppe als Grundlage quantenmechanischer Kinematik. Fortschritte Phys. 1962, 10, 65–146. [Google Scholar] [CrossRef]
- Lubański, J.K. Sur la theorie des particules elementaires de spin quelconque I. Physica 1942, 9, 310–324. [Google Scholar] [CrossRef]
- Lubański, J.K. Sur la theorie des particules elementaires de spin quelconque II. Physica 1941, 9, 325–338. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the electron. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1928, 117, 610–624. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Relativistic wave equations. Proc. R. Soc. Lond. 1936, 155, 447–459. [Google Scholar] [CrossRef]
- Coleman, S.; Mandula, J. All possible symmetries of the S matrix. Phys. Rev. 1967, 159, 1251. [Google Scholar] [CrossRef]
- Georgi, H.; Glashow, S.L. Unity of all elementary particle forces. Phys. Rev. Lett. 1974, 32, 438. [Google Scholar] [CrossRef]
- Fritzsch, H.; Minkowski, P. Unified interactions of leptons and hadrons. Ann. Phys. 1975, 93, 193–266. [Google Scholar] [CrossRef]
- Georgi, H.; Glashow, S.L. Unextended hypercolor and unification. Phys. Rev. Lett. 1981, 47, 1511. [Google Scholar] [CrossRef]
- Doršer, I.; Fajfer, S.; Greljo, S.A.; Kamenik, J.F.; Košnik, N. Physics of leptoquarks in precision experiments and at particle colliders. Phys. Rep. 2016, 641, 1–68. [Google Scholar] [CrossRef]
- Higgs, P. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 1964, 13, 508. [Google Scholar] [CrossRef]
- Machleidt, R. The meson theory of nuclear forces and nuclear structure. In Advances in Nuclear Physics; Negele, J.W., Vogt, E., Eds.; Springer: Boston, MA, USA, 1989; Volume 19, p. 189. [Google Scholar] [CrossRef]
- Machner, H. Einführung in die Kern- und Elementarteilchenphysik; Wiley-VCH Verlag: Weinheim, Germany, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marsch, E.; Narita, Y. Hadronic Isospin Helicity and the Consequent SU(4) Gauge Theory. Symmetry 2023, 15, 1953. https://doi.org/10.3390/sym15101953
Marsch E, Narita Y. Hadronic Isospin Helicity and the Consequent SU(4) Gauge Theory. Symmetry. 2023; 15(10):1953. https://doi.org/10.3390/sym15101953
Chicago/Turabian StyleMarsch, Eckart, and Yasuhito Narita. 2023. "Hadronic Isospin Helicity and the Consequent SU(4) Gauge Theory" Symmetry 15, no. 10: 1953. https://doi.org/10.3390/sym15101953




