Next Article in Journal
Exact Solutions to Some Nonlinear Time-Fractional Evolution Equations Using the Generalized Kudryashov Method in Mathematical Physics
Next Article in Special Issue
Relationship between Body Composition Asymmetry and Specific Performance in Taekwondo Athletes: A Cross-Sectional Study
Previous Article in Journal
UAV Dynamic Non-Terrestrial Transmission Channel Analysis Based on SSCM-RT Model
Previous Article in Special Issue
Contralateral Asymmetry in Cycling Power Is Reproducible and Independent of Exercise Intensity at Submaximal Power Outputs
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 15
Issue 10
10.3390/sym15101960
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Test–Retest Reliability of the Magnitude and Direction of Asymmetry in the Countermovement Jump, Drop Jump, and Countermovement Rebound Jump

by
Jiaqing Xu
1,
Matthew J. Jordan
2,
Shyam Chavda
1,
Anthony Turner
1 and
Chris Bishop
1,*
1
Faculty of Science and Technology, London Sport Institute, Middlesex University, StoneX Stadium, Greenlands Lane, London NW4 1RL, UK
2
Faculty of Kinesiology, Sport Medicine Centre, University of Calgary, KNB 2212, 2500 University Drive NW, Calgary, AB T2N 1N4, Canada
*
Author to whom correspondence should be addressed.
Symmetry 2023, 15(10), 1960; https://doi.org/10.3390/sym15101960
Submission received: 11 September 2023 / Revised: 16 October 2023 / Accepted: 22 October 2023 / Published: 23 October 2023
(This article belongs to the Special Issue Symmetry and Asymmetry in Sport Sciences)
Browse Figures
Versions Notes

Abstract

:
This study aimed to investigate the test–retest reliability of three bilateral jump tests to assess asymmetry and determine the consistency of both the magnitude and direction of asymmetry between two testing sessions. Thirty-three participants performed the countermovement jump (CMJ), drop jump (DJ), and countermovement rebound jump (CMRJ—jump 1: CMRJ1; jump 2: CMRJ2) over two sessions. Inter-limb asymmetry was calculated for kinetic metrics, including the mean propulsive force, net braking impulse, and net propulsive impulse. Test reliability was computed using intraclass correlation coefficients (ICC), coefficients of variation (CV), and standard error of measurement. Furthermore, analysis of variance was used to determine the systematic bias between jump types and sessions. Kappa coefficients were utilised to assess the consistency of asymmetry favouring the same limb. Results showed poor to excellent reliability for all jump tests between sessions (ICC range = 0.19–0.99, CV range = 2.80–11.09%). A significantly higher magnitude of asymmetry was revealed for the net braking impulse during the DJ compared to the CMRJ2 (p ≥ 0.014, g ≤ 0.53). When computing the direction of asymmetry between test sessions, Kappa coefficients revealed that levels of agreement were substantial (Kappa = 0.63–0.70) for the CMJ, moderate to almost perfect (Kappa = 0.59–0.94) for the CMRJ1, moderate to almost perfect (Kappa = 0.58–0.81) for the DJ, and slight to moderate for the CMRJ2 (Kappa = 0.19–0.57). These results underscore the variable nature of both the magnitude and direction of asymmetry during jump testing. Thus, practitioners should carefully choose evaluation methods and metrics characterised by low variability to ensure robust asymmetry assessments.

1. Introduction

The countermovement jump (CMJ) and drop jump (DJ) are widely employed assessments for evaluating slow and fast stretch-shortening cycle (SSC) mechanics, respectively [1]. Owing to the similarities of these two jump tests to sport-specific movement, such as sprinting, cutting, or kicking [2], the CMJ and DJ tests have also been used to quantify inter-limb asymmetries [2,3,4]. Inter-limb asymmetry pertains to the discrepancy in performance outcomes or neuromuscular function between limbs [5], where the side-to-side difference (often a kinetic measure) appears to be task-specific [4] and can negatively impact athletic performance measures such as linear and change of direction speed times [6]. Thus, measuring inter-limb asymmetries via force platforms (FP) coupled with the subsequent force-time analysis during bilateral and unilateral CMJ and DJ tests has become a prominent research avenue in recent years [7]. An additional development has arisen regarding the countermovement rebound jump (CMRJ), which has been shown to yield reliable metrics of jump performance, comparable to those from CMJ and DJ tests [8]. Given the inherent similarities between these three jump actions in terms of demands and movement characteristics, the magnitude and direction of asymmetry observed in the CMRJ may also resemble those found in the other two tests. However, to the authors’ knowledge, no empirical investigation has been conducted to corroborate this suggestion.
There has been a rise in empirical investigations exploring the reliability of asymmetry derived from metrics collected during unilateral and bilateral jump tests [2,3,4,6,9]. These selected metrics should be reliable in providing practitioners with meaningful information to support their decision-making in athletic evaluation [5]. For example, previous investigations have reported moderate to excellent within- and between-session reliabilities for peak force, concentric impulse, and jump height in the unilateral CMJ (intraclass correlation coefficient ([ICC] ≥ 0.78, coefficient of variation [CV] ≤ 6.3%) [2,3,4,7] and DJ tests (ICC ≥ 0.60, CV ≤ 11.2%) [2,4,7], and bilateral CMJ test (ICC ≥ 0.85, CV ≤ 9.23%) [3]. This body of literature substantiated the reliability of these kinetic metrics as robust measures of inter-limb asymmetry across various jump actions. Notably, Bishop et al. [7] have also recommended the inclusion of additional metrics, such as mean force and braking and propulsive impulse, in the forthcoming asymmetry studies. These metrics offer valuable insights into the underlying jump strategies utilised by participants, extending the assessment beyond performance measures (e.g., jump height). However, further information regarding the reliability of asymmetry metrics collected from the bilateral CMJ, DJ, and CMRJ tests across two testing sessions has yet to be determined.
The concept of the ‘direction of asymmetry’ has been explored by a number of researchers in recent years. When using healthy athletes, Impellizzeri et al. [10] outlined this concept as referring to the consistency of asymmetry favouring the same limb during a given movement task, such as jumping. Previous research has indicated that the direction of asymmetry might show just as much variability as the magnitude [2,3,4,5,11,12]. To comprehensively understand asymmetry, Bishop et al. [7] employed Kappa coefficients to determine consistency in the direction of asymmetry between two testing sessions, using the unilateral CMJ and DJ. Findings showed substantial levels of agreement for asymmetry in the CMJ (Kappa = 0.64–0.66) and fair to moderate levels of agreement in the DJ (Kappa = 0.36–0.56). More recently, Bishop et al. [2] examined the asymmetry for jump height and concentric impulse in the unilateral CMJ and jump height with reactive strength index in the unilateral DJ. Results showed poor to substantial levels of agreement for the direction of asymmetry during CMJ (Kappa = −0.06 to 0.77) and DJ (Kappa = −0.10 to 0.78) tests, when tested at multiple time points across a competitive soccer season. Furthermore, other investigations have also revealed poor to slight levels of agreement for the direction of asymmetry in the unilateral CMJ (Kappa = −0.10 to 0.15) and substantial levels in the bilateral CMJ (Kappa range = 0.65 to 0.74, excluding the peak force with a Kappa value of 0.49) [6]. While bilateral jump testing has been proposed to provide more interpretation regarding the compensatory strategies between limbs compared to unilateral jump testing [6], it is important to note that the consistency in the direction of asymmetry might not be directly comparable. This emphasises the fact that the asymmetry characteristics measured during unilateral tasks may not accurately represent the outcomes observed during bilateral tasks [3]. Therefore, further research is warranted to examine the inter-limb asymmetry during bilateral CMJ, DJ, and CMRJ tests, aiming to verify whether both the magnitude and direction remain consistent across two testing sessions.
From an asymmetry standpoint, the existing literature suggests that further research is required to examine a variety of metrics during bilateral jump tasks in particular, thereby providing practitioners with another option to gain reliable inter-limb asymmetry data between test sessions. Therefore, the aims of this study were threefold: (1) to examine the between-session reliability of bilateral CMJ, DJ, and CMRJ tests that can be used to quantify asymmetries, (2) to explore the presence of any significant differences in asymmetry between jump types and test sessions, and to (3) determine how consistently asymmetry favours the same limb across each jump test between sessions. It was hypothesised that (1) all three jump types were reliable enough to be used for quantifying asymmetries, (2) no significant differences in asymmetry were revealed between jump types and test sessions, and (3) similar levels of agreement in both the magnitude and direction of asymmetry would be evident across the three jump types.

2. Materials and Methods

2.1. Study Design

This study utilised a test–retest design, whereby the mean propulsive force, net braking impulse, and net propulsive impulse were determined during the CMJ, DJ, and CMRJ tests. Participants completed three trials of each jump in the first testing session on a pair of embedded force platforms (FP), with the second testing sessions designed identically and separated by 48–96 h. All metrics measured from each jump during the two test sessions were compared, to aid in interpreting the reliability and systematic bias between sessions. These values were also compared to quantify any statistical significance between the different types of jumps.

2.2. Participants

Thirty-three physically active sports science students (age: 27.2 ± 5.9 years, height: 1.78 ± 0.8 cm, body mass: 77.5 ± 11.5 kg) volunteered to participate in this study. This sample size was chosen because G power analysis (Version 3.1, University of Dusseldorf, Dusseldorf, Germany) showed that 26 participants were needed to have a statistical power of 0.8 and a type 1 alpha level of 0.05. Therefore, this study recruited 33 participants and showed a statistical power of 0.88. All participants had at least one year’s experience of strength training and were free of any injuries at the time of data collection, and none of them were professional athletes beyond college level at the time of participation. A written informed consent form was provided from all participants, and this study was approved by the London Sport Institute research and ethics committee at Middlesex University (Application No: 21808).

2.3. Materials and Procedures

Before data collection, all participants were given 10 min to perform a standard warm-up and dynamic stretching consisting of movements that facilitate the CMJ, DJ, and CMRJ performance, and the same content was applied to the second testing session. These stretches consisted of forward lunge rotations, the ‘world’s greatest stretch’, and forward and lateral hip swings [13]. Then, participants were provided with a demonstration of three jump actions and given five minutes to familiarise themselves with those three jump types [14]. Participants were required to jump with both feet, with their hands on their hips, to minimise the influence of arm-swing on the estimation of the centre of mass (COM) location [1]. To accurately estimate body mass, they were also required to keep standing still for at least one second before the movement initiation in CMJ and CMRJ and afterwards landing in the DJ [1]. Finally, an external verbal cue—‘jump as high as you can whilst spending the shortest time on the ground’—was used to promote the maximum jump performance and enable the self-preferred jump strategy to be achieved [1,15]. Test order was randomised to minimise the influence of potential fatigue on the jump outcomes, and the same order was retained in the second session for each participant [7]. Ninety seconds of rest were used to separate each trial to ensure adequate recovery and maintain maximum jump performance [13].
All variables were measured via twin-embedded FP (9281EA, Kistler Instruments Ltd., Hook, UK) that recorded the ground reaction force (GRF) at a sampling frequency of 1000 Hz. In the CMJ and CMRJ tests, participants completed each trial by take-off and landing on the same FP. One FP method was used during the DJ measures, participants stepped off from a box (i.e., 0.30 m), contacted the FP, and rebounded immediately into the vertical jump [16]. Custom analyses of the GRF data were conducted using MATLAB version 9.12 software (R2022a; MathWorks, Natick, MA, USA), and these GRF data were then used to calculate the vertical velocity and displacement acted on participants’ COM [17]. The braking and propulsive sub-phases of the CMJ and DJ tests were defined according to suggestions by previous investigations [16,17]. The method to define the braking and propulsive sub-phases in the CMRJ1 (i.e., the first jump of the CMRJ) was identical to CMJ, while the method to define these sub-phases in the CMRJ2 (i.e., the second jump of the CMRJ) was identical to the DJ [8]. The calculations of the mean propulsive force, net braking impulse, and net propulsive impulse were in line with previous literature [18,19].

2.4. Statistical Analysis

All data were initially recorded in Microsoft Excel as mean and standard deviation (SD) of the three jumps, and then transferred to SPSS (version 27; SPSS Inc., Chicago, IL, USA) for the subsequent statistical analysis. The normality of the data was assessed by the Shapiro–Wilk statistic, and homogeneity of variance was verified with Levene’s test. As suggested by Bishop et al. [12], the asymmetry score was assessed via the formula: (left value − right value)/total × 100. The between-session reliability for all measured variables was computed using a two-way random model intraclass correlation coefficient (ICC) with 95% confidence intervals (CI), coefficient of variation (CV) with 95% CI, and standard error of measurement (SEM) using formula: (SD × √ (1 − ICC)), where the SD was calculated by using the mean value from each participant [20]. The interpretation of ICC was in agreement with Koo and Li [21], where an ICC value > 0.90 = excellent, 0.75–0.90 = good, 0.50–0.74 = moderate, and <0.50 = poor. CV was calculated as (CV% = SD/mean × 100), with CV values considered good if <5%, moderate if between 5–10%, and poor if >10% [22].
A two-way repeated measures analysis of variance (ANOVA, session x jump type) was used to determine the differences in all measured variables from three jump types between sessions, with the statistical significance set at α < 0.05. The magnitude of differences for test measures and asymmetry values between jump types and testing sessions were quantified using Hedges’ g effect sizes (ES) with 95% CI via the formula: ((Mean1 − Mean2)/SD pooled) [7]. The ES values were interpreted in line with Rhea [23], as g < 0.35 = trivial; 0.35–0.80 = small; 0.81–1.50 = moderate; and >1.5 = large.
Kappa coefficients were computed to determine the levels of agreement for the direction of asymmetry (i.e., how asymmetry consistently favoured the same side of the lower limbs). This method was chosen to characterise the degree of agreement between the two methods after eliminating any agreement by chance [24]. According to the suggestion by Bishop et al. [2], these values were interpreted as Kappa ≤ 0 = poor; 0.01–0.20 = slight; 0.21–0.40 = fair; 0.41–0.60 = moderate; 0.61–0.80 = substantial; and 0.81–0.99 = almost perfect. Considering that the asymmetry values are ratio values derived as a percentage from left- and right-side scores, applying the Kappa coefficient presents itself as a substitute statistical technique in contrast to conventional reliability measures (i.e., ICC and CV). The Kappa analysis accounts for the consistency in the direction of asymmetry, which the conventional measures are unable to do when absolute percentage values are used [2].

3. Results

Between-session reliability for test measures is presented in Table 1. The relative reliability (ICC) ranged from poor to excellent for CMJ metrics (ICC = 0.38–0.99), DJ metrics (ICC = 0.19–0.97), and CMRJ metrics (ICC = 0.38–0.99). All test measures of kinetic metrics showed good to moderate CV (2.80–8.54%), but net braking impulse-L showed poor CV during the CMJ (10.10%) and CMRJ1 (10.23%). No significant differences in kinetic metrics were found between jump types (p ≥ 0.065) and testing sessions (p ≥ 0.212). The reliability and magnitude of asymmetry for each metric are presented in Table 2. All data showed moderate to good reliability (ICC = 0.73–0.86) and poor CV values (≤37.39%) in all three jump types, with the SEM also computed for mean asymmetry scores between two sessions: CMJ (0.76–6.75%), DJ (1.24–4.35%), and CMRJ (0.77–4.66%). The ANOVA revealed significantly higher mean asymmetry values for the net braking impulse in the DJ test than the CMRJ2 test for both sessions 1 (p = 0.019, g = 0.53) and 2 (p = 0.014, g = 0.35). No other significant differences in magnitude of asymmetry were present between jump types (p ≥ 0.212) and testing sessions (p ≥ 0.077).
Kappa coefficients and descriptive levels of agreement are presented in Table 3. The Kappa values ranged from slight to almost perfect during three jump tests (CMJ = 0.63–0.70; DJ = 0.58–0.81; CMRJ1 = 0.59–0.94; CMRJ2 = 0.19–0.57), highlighting the variable nature in the direction and magnitude of asymmetry across two testing sessions. Owing to the potential intra-subject variability, the individual asymmetry scores for each metric were presented for the CMJ (Figure 1), DJ (Figure 2), CMRJ1 (Figure 3), and CMRJ2 (Figure 4).

4. Discussion

The aims of this study were threefold: (1) to examine the between-session reliability of bilateral CMJ, DJ, and CMRJ tests that can be used to quantify asymmetries, (2) to explore the presence of any significant differences in asymmetry between jump types and test sessions, and (3) to determine how consistently asymmetry favours the same limb across each jump test for measured variables. Results showed poor to excellent reliability for all jump tests between sessions. A significantly higher magnitude of asymmetry was revealed for the net braking impulse during the DJ compared to the CMRJ2 (p ≥ 0.014, g ≤ 0.53). Kappa coefficients revealed slight to almost perfect levels of agreement for asymmetry between test sessions, with the strongest consistency shown for the CMRJ1.
The data in Table 1 show the between-session reliability for kinetic metrics from each jump test. Our results aligned with previous investigations [3,25], showcasing excellent reliability for the mean propulsive force (ICC ≥ 0.94, CV ≤ 5.45%, SEM ≤ 54.10 N) and net propulsive impulse (ICC ≥ 0.93, CV ≤ 5.64%, SEM ≤ 4.84 N.s) in both sides during three jump actions. However, our first hypothesis was partially confirmed, where the reliability for the net braking impulse was poor for the left side in the CMJ (ICC = 0.38, CV = 10.10%, SEM = 25.21 N.s) and CMRJ1 (ICC = 0.30, CV = 10.23%, SEM = 22.44 N.s) and for both sides in the DJ (L: ICC = 0.23, CV = 11.09%, SEM = 27.41 N.s; R: ICC = 0.19, CV = 6.40%, SEM = 17.03 N.s). This discrepancy could potentially be attributed to the absence of constraints on countermovement depth within this study. That said, participants were not directed through verbal cues to execute a rapid countermovement; instead, they initiated their countermovement towards a certain position with their self-preferred timings, so as to not cause unnecessary changes to their natural jump coordination patterns. Noting that the impulse is the product of net GRF and time, any changes in the jump strategies between testing sessions would alter the time spent in ground contact, contributing to poor reliability of the net braking impulse in two jump actions [4,26]. Thus, as Bishop et al. [3] suggested, practitioners should be cautious of monitoring braking impulse (or eccentric impulse) during the CMJ test (especially in unilateral testing), although this now appears to potentially hold true for bilateral jumping as well. Further to this, the poor reliability of the net braking impulse in the DJ could be attributed to the variability of the body weight estimation [27]. During the DJ test, participants kept standing still for at least 1 s (for weight estimation) upon landing from the rebound jump [16]. Even minor movement or postural adjustment during this weighing phase could introduce inaccuracies in the calculated body weight and the subsequent net GRF [6,17,27]. Compared to the CMRJ test where the weighing phase was before the movement initiation, the DJ may pose higher technical challenges to those participants [4]. This explanation is further supported by the excellent reliability demonstrated across all braking and propulsive impulses in the CMRJ2 (ICC ≥ 0.93, CV ≤ 5.59%). From a practical standpoint, practitioners may consider using the CMRJ over the DJ when computing metrics that necessitate accurate body weight estimation, particularly when working with participants who have limited jump testing experience.
The data in Table 2 display the inter-limb asymmetry values and between-session reliability. In line with previous findings [6], our results showed that the asymmetry values presented good reliability (ICC = 0.75–0.86), with net braking and propulsive impulse in the DJ showing moderate reliability (ICC = 0.73) and braking impulse in the CMRJ2 showing moderate reliability (ICC = 0.74) as well. However, this is not necessarily a positive finding, where the asymmetry for all metrics presented poor absolute reliability (CV ≥ 10%, SEM ≤ 4.66%). This might be explained by the fact that the asymmetry was calculated from left- and right-side impulses and ultimately presented as a ratio number [2]. Noting that, the ratio values can be easily influenced by changes in their constituent parts, particularly since impulse itself is a composite of net force and time [2,28]. Therefore, variations in the net force and time could affect the calculated asymmetry for impulse and practitioners should be mindful of its variable nature when utilising asymmetry for longitudinal monitoring [4,5,12]. For the magnitude of asymmetry, systematic bias was assessed between test sessions with no significant differences reported. However, when comparing between jump types, the asymmetry for the net braking impulse was significantly higher in the DJ than the CMRJ2 by approximately 4% in both test sessions (p ≥ 0.014, g ≤ 0.53). The reason behind these discrepancies could be attributed to the alternations of movement strategies from participants [29,30,31]. Specifically, participants in this study performed the DJ by ‘stepping off’ the drop box rather than ‘jumping off’, possibly indicating that the leading leg made initial contact with the FP before the contralateral limb did. In this instance, a variation in time required to generate the braking impulse would arise [7,26]. In contrast, participants completed the two jumps for the CMRJ in a continuous manner with both feet, and this approach likely facilitated simultaneous contact with the FP. Collectively, more familiarisation trials coupled with specific verbal cues (i.e., landing with both feet) are key considerations for practitioners when using the bilateral DJ test to quantify inter-limb asymmetry [3,7].
The data in Table 3 display the Kappa coefficients, showing how consistently asymmetry favoured the same limb for each kinetic metric between testing sessions. To the authors’ best knowledge, this is the first study to quantify the direction of asymmetry in three bilateral jump actions across two testing sessions. Results showed that when comparing between test sessions, levels of agreement were substantial (Kappa = 0.63–0.70) for the CMJ, moderate to almost perfect (Kappa = 0.59–0.94) for the CMRJ1, moderate to almost perfect (Kappa = 0.58–0.81) for the DJ, and slight to moderate for the CMRJ2 (Kappa = 0.19–0.57). These findings aligned with the observation of Pérez-Castilla et al. [6] who reported substantial (Kappa = 0.65–0.74) levels of agreement in the CMJ using variables like mean force, jump height and concentric impulse. Furthermore, it has been suggested that greater levels of agreement tend to be associated with heightened test reliability between sessions [7]. Similarly, in our study, the asymmetry for the net braking impulse in the CMRJ2 deemed only moderate relative reliability (ICC = 0.73) and notably displayed the highest CV (38.51%) amongst all asymmetry data within three jump actions. Thus, it is likely that the reduced levels of reliability are also associated with lower levels of agreement in asymmetry. In summary, given the variable nature in both magnitude and direction of asymmetry, it is recommended, as by Bishop et al. [9], that the measured asymmetry for kinetic metrics should be analysed individually.
Individual asymmetry values for kinetic metrics across jump tests are presented in Figure 1, Figure 2, Figure 3 and Figure 4. For example, in the middle plot of Figure 4 (CMRJ2 test), 11/33 (33%) participants showed asymmetry on difference sides for the net braking impulse between test sessions. Conversely, in the case of the DJ, only 3/33 (9%) participants showed asymmetry favouring different sides for the net braking impulse across two sessions. Despite both the DJ and CMRJ2 tests assessing inter-limb asymmetry during fast stretch-shortening cycle actions [1,7], more inconsistency in direction of asymmetry was evident during the CMRJ2 test. Therefore, the present study confirms that the direction of asymmetry appears to be task-dependent and variable, underscoring the need for future investigations to be cognisant of this aspect when selecting jumping-based assessments for asymmetry evaluation, and even reconsidering its relevance for sport performance in non-injured athletes in the first place [32].
Collectively, when aiming to evaluate the asymmetry of athletes or monitor the magnitude and direction of asymmetry longitudinally, practitioners are advised to select an evaluation method (i.e., the jump test) that sufficiently captures the movement patterns inherent in their respective sports [3,5,9]. It is equally vital to choose metrics that exhibit acceptable variability (CV < 10%) to ensure the robustness of the findings, as recommended in existing literature [3,9,26,32,33]. Furthermore, within the context of a long-term monitoring programme, it is recommended to incorporate asymmetry assessments at a more frequent interval among athletes [7,32]. This strategy enables practitioners to discern evolving trends in both the magnitude and direction of asymmetry, which serve as a useful tool for making informed decisions when planning target training interventions for athletes [7]. For example, in Figure 1, Figure 2, Figure 3 and Figure 4, participants 16, 23, and 28 are showing very different magnitudes in asymmetry for each metric across three jump actions, but do show consistency in right-limb dominance across three jump types. Nonetheless, it is essential to acknowledge certain limitations within this study. Firstly, the scope of the investigation exclusively encompassed the measurement of bilateral jump asymmetries, implying that the derived conclusions may be predominantly applicable to bilateral movements, such as weightlifting or rowing. Secondly, the present study only measured three metrics. Consequently, the results lack the depth to comprehensively explain the underlying rationale of varying shifts in the direction of asymmetry between sessions. Thus, future studies should also aim to compare both the magnitude and direction asymmetry for different metrics between comparable unilateral and bilateral jump actions, to provide a more holistic understanding of inter-limb differences.

5. Conclusions

In summary, all three jump actions have demonstrated their reliability in assessing inter-limb asymmetry between sessions. However, it is crucial to acknowledge that the net braking impulse exhibits poor reliability across CMJ, DJ, and CMRJ tests, prompting careful consideration when employing this metric to establish meaningful changes between sessions. Furthermore, it becomes evident that the direction of asymmetry is as variable as the magnitude, both of which cannot yield consistent values over time. Thus, the analysis of asymmetry for measured metrics at jump testing should be conducted individually. Finally, and although a relatively minor consideration, augmenting the number of familiarisation trials prior to data collection is recommended to bolster the reliability of measured asymmetry values.

Author Contributions

Conceptualisation, J.X., A.T. and C.B.; methodology, J.X., A.T. and C.B.; software, J.X., A.T. and C.B.; validation, J.X., A.T. and C.B.; formal analysis, J.X., C.B. and S.C.; investigation, J.X., C.B. and S.C.; resources, J.X., A.T. and C.B.; data curation, J.X. and C.B.; writing—original draft preparation, J.X. and C.B.; writing—review and editing, all authors; visualisation, J.X. and C.B.; supervision, A.T. and C.B.; project administration, A.T. and C.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted according to the guidelines of the Declaration of Helsinki, according to current national laws and regulations, and approved by the by the London Sport Institute research and ethics committee at Middlesex University (Application No: 21461).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Acknowledgments

The authors warmly thank the participants of this study.

Conflicts of Interest

The authors declare no conflict of interest.

Correction Statement

This article has been republished with a minor correction to resolve an error in Table 1. Specifically, the value [196.27 ± 134.62] listed in [Row 4/Column 3, i.e., Mean Propulsive Force-R (N) in session 1] is incorrect. The accurate value should be [796.27 ± 134.62]. This change does not affect the scientific content of the article.

References

  1. Xu, J.; Turner, A.; Comfort, P.; Harry, J.R.; McMahon, J.J.; Chavda, S.; Bishop, C. A Systematic Review of the Different Calculation Methods for Measuring Jump Height during the Countermovement and Drop Jump Tests. Sports Med. 2023, 53, 1055–1072. [Google Scholar] [CrossRef] [PubMed]
  2. Bishop, C.; Read, P.; Chavda, S.; Jarvis, P.; Brazier, J.; Bromley, T.; Turner, A. Magnitude Or Direction? Seasonal Variation of Interlimb Asymmetry in Elite Academy Soccer. J. Strength Cond. Res. 2022, 36, 1031–1037. [Google Scholar] [CrossRef] [PubMed]
  3. Bishop, C.; Abbott, W.; Brashill, C.; Turner, A.; Lake, J.; Read, P. Bilateral Vs. Unilateral Countermovement Jumps: Comparing the Magnitude and Direction of Asymmetry in Elite Academy Soccer Players. J. Strength Cond. Res. 2022, 36, 1660–1666. [Google Scholar] [CrossRef] [PubMed]
  4. Bishop, C.; Pereira, L.A.; Reis, V.P.; Read, P.; Turner, A.N.; Loturco, I. Comparing the Magnitude and Direction of Asymmetry during the Squat, Countermovement and Drop Jump Tests in Elite Youth Female Soccer Players. J. Sports Sci. 2020, 38, 1296–1303. [Google Scholar] [CrossRef] [PubMed]
  5. Bishop, C.; Brashill, C.; Abbott, W.; Read, P.; Lake, J.; Turner, A. Jumping asymmetries are associated with speed, change of direction speed, and jump performance in elite academy soccer players. J. Strength Cond. Res. 2021, 35, 1841–1847. [Google Scholar] [CrossRef] [PubMed]
  6. Pérez-Castilla, A.; García-Ramos, A.; Janicijevic, D.; Delgado-García, G.; De la Cruz, J.C.; Rojas, F.J.; Cepero, M. Between-Session Reliability of Performance and Asymmetry Variables obtained during Unilateral and Bilateral Countermovement Jumps in Basketball Players. PLoS ONE 2021, 16, e0255458. [Google Scholar] [CrossRef] [PubMed]
  7. Bishop, C.; Read, P.; Chavda, S.; Jarvis, P.; Turner, A. Using Unilateral Strength, Power and Reactive Strength Tests to Detect the Magnitude and Direction of Asymmetry: A Test-Retest Design. Sports 2019, 7, 58. [Google Scholar] [CrossRef] [PubMed]
  8. Bronze, S.H.; McMahon, J.J. Test-retest reliability of reactive strength index variants obtained from the countermovementrebound jump. In Proceedings of the UK Strength and Conditioning Association (UKSCA) Annual Conference, 3 September 2020; Available online: https://www.uksca.org.uk/uksca-iq/article/weekly-theme-poster-week/2035/test-retest-reliabilityof-reactive-strength-index-variants-obtained-from-the-countermovement-rebound-jump (accessed on 2 September 2023).
  9. Bishop, C.; Lake, J.; Loturco, I.; Papadopoulos, K.; Turner, A.; Read, P. Interlimb Asymmetries: The Need for an Individual Approach to Data Analysis. J. Strength Cond. Res. 2021, 35, 695–701. [Google Scholar] [CrossRef] [PubMed]
  10. Impellizzeri, F.M.; Rampinini, E.; Maffiuletti, N.; Marcora, S.M. A Vertical Jump Force Test for Assessing Bilateral Strength Asymmetry in Athletes. Med. Sci. Sports Exerc. 2007, 39, 2044. [Google Scholar] [CrossRef]
  11. Maloney, S.J. The Relationship between Asymmetry and Athletic Performance: A Critical Review. J. Strength Cond. Res. 2019, 33, 2579–2593. [Google Scholar] [CrossRef] [PubMed]
  12. Bishop, C.; Read, P.; Lake, J.; Chavda, S.; Turner, A. Interlimb Asymmetries: Understanding how to Calculate Differences from Bilateral and Unilateral Tests. Strength Cond. J. 2018, 40, 1–6. [Google Scholar] [CrossRef]
  13. Bishop, C.; Jarvis, P.; Turner, A.; Balsalobre-Fernandez, C. Validity and Reliability of Strategy Metrics to Assess Countermovement Jump Performance using the Newly Developed My Jump Lab Smartphone Application. J. Hum. Kinet. 2022, 83, 185–195. [Google Scholar] [CrossRef] [PubMed]
  14. Comyns, T.M.; Murphy, J.; O’Leary, D. Reliability, Usefulness, and Validity of Field-Based Vertical Jump Measuring Devices. J. Strength Cond. Res. 2022, 37, 1594–1599. [Google Scholar] [CrossRef] [PubMed]
  15. Comyns, T.M.; Brady, C.J.; Molloy, J. Effect of Attentional Focus Strategies on the Biomechanical Performance of the Drop Jump. J. Strength Cond. Res. 2019, 33, 626–632. [Google Scholar] [CrossRef]
  16. McMahon, J.J.; Lake, J.P.; Stratford, C.; Comfort, P. A Proposed Method for Evaluating Drop Jump Performance with One Force Platform. Biomechanics 2021, 1, 178–189. [Google Scholar] [CrossRef]
  17. McMahon, J.J.; Suchomel, T.J.; Lake, J.P.; Comfort, P. Understanding the Key Phases of the Countermovement Jump Force-Time Curve. Strength Cond. J. 2018, 40, 96–106. [Google Scholar] [CrossRef]
  18. Pedley, J.S.; Radnor, J.M.; Lloyd, R.S.; Oliver, J.L. Analyzing Drop Jump Ground Reaction Forces in Microsoft Excel. Strength Cond. J. 2023. [Google Scholar] [CrossRef]
  19. Chavda, S.; Bromley, T.; Jarvis, P.; Williams, S.; Bishop, C.; Turner, A.N.; Lake, J.P.; Mundy, P.D. Force-Time Characteristics of the Countermovement Jump: Analyzing the Curve in Excel. Strength Cond. J. 2018, 40, 67–77. [Google Scholar] [CrossRef]
  20. Weir, J.P. Quantifying Test-Retest Reliability using the Intraclass Correlation Coefficient and the SEM. J. Strength Cond. Res. 2005, 19, 231–240. [Google Scholar]
  21. Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
  22. Duthie, G.; Pyne, D.; Hooper, S. The Reliability of Video Based Time Motion Analysis. J. Hum. Mov. Stud. 2003, 44, 259–272. [Google Scholar]
  23. Rhea, M.R. Determining the Magnitude of Treatment Effects in Strength Training Research through the use of the Effect Size. J. Strength Cond. Res. 2004, 18, 918–920. [Google Scholar] [PubMed]
  24. Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
  25. Heishman, A.; Daub, B.; Miller, R.; Brown, B.; Freitas, E.; Bemben, M. Countermovement Jump Inter-Limb Asymmetries in Collegiate Basketball Players. Sports. 2019, 7, 103. [Google Scholar] [CrossRef] [PubMed]
  26. Chavda, S.; Turner, A.N.; Comfort, P.; Haff, G.G.; Williams, S.; Bishop, C.; Lake, J.P. A Practical Guide to Analyzing the Force-Time Curve of Isometric Tasks in Excel. Strength Cond. J. 2020, 42, 26–37. [Google Scholar] [CrossRef]
  27. Benjanuvatra, N.; Lay, B.S.; Alderson, J.A.; Blanksby, B.A. Comparison of Ground Reaction Force Asymmetry in One-and Two-Legged Countermovement Jumps. J. Strength Cond. Res. 2013, 27, 2700–2707. [Google Scholar] [CrossRef] [PubMed]
  28. Bishop, C.; Shrier, I.; Jordan, M. Ratio Data: Understanding Pitfalls and Knowing when to Standardise. Symmetry 2023, 15, 318. [Google Scholar] [CrossRef]
  29. Maloney, S.J.; Fletcher, I.M.; Richards, J. A Comparison of Methods to Determine Bilateral Asymmetries in Vertical Leg Stiffness. J. Sports Sci. 2016, 34, 829–835. [Google Scholar] [CrossRef] [PubMed]
  30. Arampatzis, A.; Schade, F.; Walsh, M.; Brüggemann, G. Influence of Leg Stiffness and its Effect on Myodynamic Jumping Performance. J. Electromyogr. Kinesiol. 2001, 11, 355–364. [Google Scholar] [CrossRef] [PubMed]
  31. Bishop, C.; Turner, A.; Jordan, M.; Harry, J.; Loturco, I.; Lake, J.; Comfort, P. A Framework to Guide Practitioners for Selecting Metrics during the Countermovement and Drop Jump Tests. J. Strength Cond. Res. 2022, 44, 95–103. [Google Scholar] [CrossRef]
  32. Bishop, C.; Turner, A.; Jarvis, P.; Chavda, S.; Read, P. Considerations for Selecting Field-Based Strength and Power Fitness Tests to Measure Asymmetries. J. Strength Cond. Res. 2017, 31, 2635–2644. [Google Scholar] [CrossRef] [PubMed]
  33. Bishop, C.; Turner, A.; Read, P. Effects of Inter-Limb Asymmetries on Physical and Sports Performance: A Systematic Review. J. Sports Sci. 2018, 36, 1135–1144. [Google Scholar] [CrossRef]
Symmetry 15 01960 g001
Figure 1. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the countermovement jump. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Figure 1. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the countermovement jump. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Symmetry 15 01960 g001
Symmetry 15 01960 g002
Figure 2. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the countermovement rebound jump 1. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Figure 2. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the countermovement rebound jump 1. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Symmetry 15 01960 g002
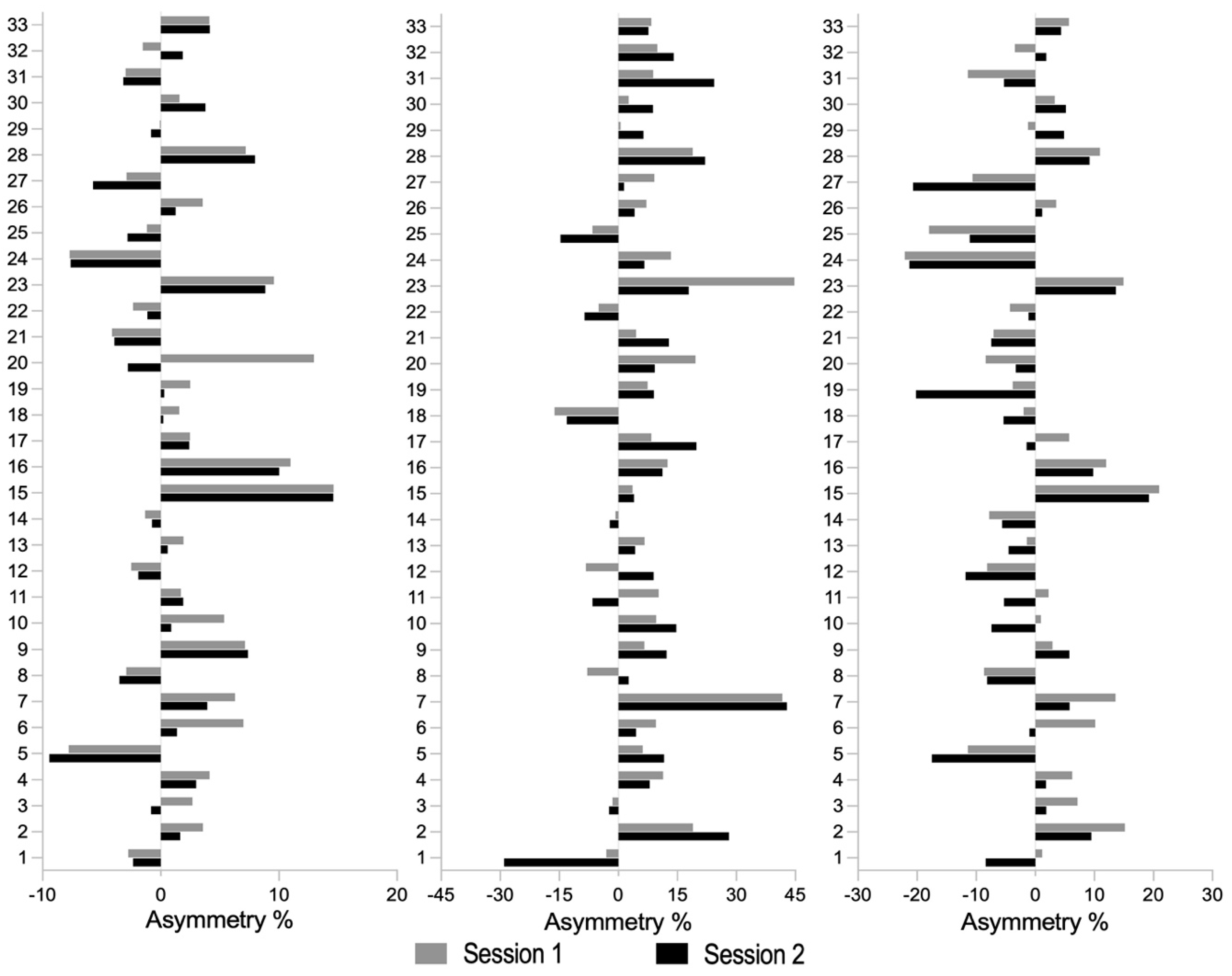
Symmetry 15 01960 g003
Figure 3. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the drop jump. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Figure 3. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the drop jump. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Symmetry 15 01960 g003
Symmetry 15 01960 g004
Figure 4. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the countermovement rebound jump 2. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Figure 4. Individual asymmetry data for mean propulsive force (left), net braking impulse (middle), and net propulsive impulse (right) during the countermovement rebound jump 2. Note: right side bar (above 0) means that the right leg scores higher asymmetry; left side bar (below 0) means that the left leg scores higher asymmetry.
Symmetry 15 01960 g004
Table 1. Mean within-session data (± SD) and between-session reliability for test measures of kinetic metrics reported from the average of all trials.
Table 1. Mean within-session data (± SD) and between-session reliability for test measures of kinetic metrics reported from the average of all trials.
Test/MetricTest Session 1Test Session 2Between-Session
Mean ± SDMean ± SDHedges’ g (95% CI)DescriptorICC (95% CI)CV (95% CI)SEM
CMJMean Propulsive Force-L (N)781.30 ± 129.18784.10 ± 134.34−0.02 (−0.10, 0.06)Trivial0.98 (0.95, 0.99)3.07 (2.33, 3.08)20.17
Mean Propulsive Force-R (N)796.27 ± 134.62791.06 ± 135.720.04 (−0.16, 0.23)Trivial0.98 (0.96, 0.99)2.84 (2.16, 3.53)19.38
Net Braking Impulse-L (N.s)44.15 ± 12.9043.40 ± 13.180.06 (−0.03, 0.16)Trivial0.38 (−0.25, 0.69)10.10 (7.44, 12.17)25.21
Net Braking Impulse-R (N.s)47.04 ± 14.1945.48 ± 15.010.10 (0.02, 0.19)Trivial0.91 (0.83, 0.96)8.54 (6.48, 10.60)4.11
Net Propulsive Impulse-L (N.s)95.45 ± 20.6695.56 ± 20.46−0.05 (−0.38, 0.28)Trivial0.97 (0.93, 0.98)3.85 (2.92, 4.78)3.67
Net Propulsive Impulse-R (N.s)94.07 ± 22.3393.77 ± 23.000.01 (−0.32, 0.34)Trivial0.99 (0.98, 0.99)2.80 (2.12, 3.47)2.36
CMRJ1Mean Propulsive Force-L (N)796.69 ± 140.14783.76 ± 129.780.09 (0.01, 0.18)Trivial0.95 (0.90, 0.97)3.13 (2.38, 3.89)30.04
Mean Propulsive Force-R (N)814.87 ± 138.86798.69 ± 132.900.12 (−0.08, 0.31)Trivial0.95 (0.89, 0.97)3.00 (2.27, 3.72)30.79
Net Braking Impulse-L (N.s)43.63 ± 11.8841.92 ± 17.880.11 (−0.09, 0.31)Trivial0.30 (−0.42, 0.65)10.23 (7.76, 12.70)22.44
Net Braking Impulse-R (N.s)47.14 ± 13.7146.50 ± 13.470.05 (−0.04, 0.13)Trivial0.95 (0.90, 0.98)6.33 (4.80, 7.85)2.99
Net Propulsive Impulse-L (N.s)91.24 ± 20.4789.67 ± 21.570.07 (−0.26, 0.40)Trivial0.98 (0.96, 0.99)3.37 (2.55, 4.18)3.02
Net Propulsive Impulse-R (N.s)90.38 ± 20.5388.27 ± 20.590.10 (−0.23, 0.43)Trivial0.98 (0.95, 0.99)3.59 (2.72, 4.46)3.01
DJMean Propulsive Force-L (N)929.05 ± 223.78924.62 ± 217.720.02 (−0.06, 0.10)Trivial0.94 (0.87, 0.97)5.07 (3.85, 6.30)54.10
Mean Propulsive Force-R (N)946.99 ± 229.29964.41 ± 219.02−0.08 (−0.27, 0.12)Trivial0.97 (0.95, 0.99)4.27 (3.24, 5.30)35.70
Net Braking Impulse-L (N.s)83.73 ± 22.0682.74 ± 13.350.05 (−0.24, 0.34)Trivial0.23 (−0.54, 0.62)11.09 (8.41, 13.76)27.41
Net Braking Impulse-R (N.s)95.85 ± 19.8796.01 ± 19.64−0.01 (−0.09, 0.07)Trivial0.19 (−0.99, 0.53)6.40 (4.85, 7.94)17.03
Net Propulsive Impulse-L (N.s)90.61 ± 20.2288.64 ± 21.510.09 (−0.24, 0.42)Trivial0.97 (0.95, 0.99)4.43 (3.36, 5.50)3.33
Net Propulsive Impulse-R (N.s)87.48 ± 21.6489.24 ± 21.63−0.08 (−0.41, 0.25)Trivial0.96 (0.92, 0.98)5.39 (4.09, 6.68)4.24
CMRJ2Mean Propulsive Force-L (N)882.17 ± 221.31892.21 ± 212.98−0.05 (−0.13, 0.04)Trivial0.95 (0.90, 0.98)5.45 (4.14, 6.77)46.45
Mean Propulsive Force-R (N)915.05 ± 222.91915.47 ± 215.130.00 (−0.20, 0.19)Trivial0.95 (0.91, 0.98)4.99 (3.79, 6.20)45.91
Net Braking Impulse-L (N.s)97.56 ± 22.3797.00 ± 24.680.02 (−0.27, 0.31)Trivial0.95 (0.91, 0.98)5.59 (4.24, 6.94)4.94
Net Braking Impulse-R (N.s)105.43 ± 24.70105.46 ± 25.280.00 (−0.08, 0.08)Trivial0.96 (0.92, 0.98)5.32 (4.04, 6.61)4.90
Net Propulsive Impulse-L (N.s)86.17 ± 18.2386.20 ± 17.250.00 (−0.33, 0.33)Trivial0.94 (0.89, 0.97)4.94 (3.75, 6.14)4.12
Net Propulsive Impulse-R (N.s)88.74 ± 19.9686.29 ± 18.920.12 (−0.21, 0.46)Trivial0.93 (0.87, 0.97)5.64 (4.28, 7.00)4.84
ICC = intraclass correlation coefficient; CI = confidence intervals; SEM = standard error of measurement; CMJ = countermovement jump; DJ = drop jump; CMRJ1 = first jump of countermovement rebound jump; CMRJ2 = second jump of countermovement rebound jump; L = left; R = right; N = Newton; N.s = Newton seconds; s = seconds.
Table 2. Mean asymmetry percentage (± SD) and between-session reliability reported from the average of all trials.
Table 2. Mean asymmetry percentage (± SD) and between-session reliability reported from the average of all trials.
Test/MetricTest Session 1Test Session 2Between-Session
Asymmetry %Asymmetry %Hedges’ g (95% CI)DescriptorICC (95% CI)CV (95% CI)SEM
CMJMean Propulsive Force2.59 ± 1.732.56 ± 1.680.02 (−0.07, 0.10)Trivial0.75 (0.49, 0.88)29.48 (22.37, 36.06)0.76
Net Braking Impulse10.93 ± 8.2414.43 ± 15.09−0.29 (−0.41, 0.18)Small0.76 (0.51, 0.89)28.88 (21.91, 35.85)6.75
Net Propulsive Impulse5.39 ± 5.135.80 ± 4.11−0.13 (−0.22, 0.04)Trivial0.78 (0.56, 0.89)36.11 (27.44, 42.82)1.97
CMRJ1Mean Propulsive Force2.53 ± 1.542.53 ± 2.040.00 (−0.08, 0.08)Trivial0.78 (0.55, 0.89)30.29 (22.99, 37.60)0.77
Net Braking Impulse12.70 ± 8.3014.34 ± 12.19−0.16 (−0.25, −0.06)Trivial0.75 (0.50, 0.88)20.74 (15.74, 25.75)4.66
Net Propulsive Impulse5.78 ± 3.366.16 ± 4.78−0.09 (−0.18, 0.00)Trivial0.78 (0.55, 0.89)30.96 (23.49, 38.43)1.75
DJMean Propulsive Force3.72 ± 3.424.57 ± 3.54−0.24 (−0.34, −0.13)Small0.86 (0.70, 0.93)28.16 (21.34, 34.95)1.24
Net Braking Impulse11.39 ± 9.14 *10.60 ± 9.74 *0.07 (−0.02, 0.15)Trivial0.73 (0.45, 0.87)30.64 (23.25, 38.04)4.35
Net Propulsive Impulse7.92 ± 6.058.08 ± 5.72−0.03 (−0.11, 0.06)Trivial0.73 (0.45, 0.87)35.46 (26.90, 44.01)2.71
CMRJ2Mean Propulsive Force3.50 ± 2.973.15 ± 3.050.11 (0.02, 0.20)Trivial0.76 (0.52, 0.88)33.82 (25.66, 41.97)1.32
Net Braking Impulse7.39 ± 5.58 *7.71 ± 6.20 *−0.05 (−0.14, 0.03)Trivial0.73 (0.44, 0.88)38.51 (27.62, 45.19)2.63
Net Propulsive Impulse6.39 ± 4.886.81 ± 4.55−0.09 (−0.17, 0.00)Trivial0.77 (0.54, 0.89)37.39 (28.37, 46.42)2.03
* Significant different asymmetry score for net braking impulse between DJ and CMRJ2 in both test sessions 1 (p = 0.019) and 2 (p = 0.014). ICC = intraclass correlation coefficient; CI = confidence intervals; SEM = standard error of measurement; CMJ = countermovement jump; DJ = drop jump; CMRJ1 = first jump of countermovement rebound jump; CMRJ2 = second jump of countermovement rebound jump.
Table 3. Kappa coefficients and accompanying descriptors for levels of agreement describing how consistently asymmetry favoured the same side across two testing sessions.
Table 3. Kappa coefficients and accompanying descriptors for levels of agreement describing how consistently asymmetry favoured the same side across two testing sessions.
Test/MetricSession 1 to Session 2 KappaDescriptor
CMJMean Propulsive Force0.70Substantial
Net Braking Impulse0.63Substantial
Net Propulsive Impulse0.70Substantial
CMRJ1Mean Propulsive Force0.59Moderate
Net Braking Impulse0.68Substantial
Net Propulsive Impulse0.94Almost perfect
DJMean Propulsive Force0.81Almost perfect
Net Braking Impulse0.67Substantial
Net Propulsive Impulse0.58Moderate
CMRJ2Mean Propulsive Force0.54Moderate
Net Braking Impulse0.19Slight
Net Propulsive Impulse0.57Moderate
CMJ = countermovement jump; DJ = drop jump; CMRJ1 = first jump of countermovement rebound jump; CMRJ2 = second jump of countermovement rebound jump.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xu, J.; Jordan, M.J.; Chavda, S.; Turner, A.; Bishop, C. Test–Retest Reliability of the Magnitude and Direction of Asymmetry in the Countermovement Jump, Drop Jump, and Countermovement Rebound Jump. Symmetry 2023, 15, 1960. https://doi.org/10.3390/sym15101960

AMA Style

Xu J, Jordan MJ, Chavda S, Turner A, Bishop C. Test–Retest Reliability of the Magnitude and Direction of Asymmetry in the Countermovement Jump, Drop Jump, and Countermovement Rebound Jump. Symmetry. 2023; 15(10):1960. https://doi.org/10.3390/sym15101960

Chicago/Turabian Style

Xu, Jiaqing, Matthew J. Jordan, Shyam Chavda, Anthony Turner, and Chris Bishop. 2023. "Test–Retest Reliability of the Magnitude and Direction of Asymmetry in the Countermovement Jump, Drop Jump, and Countermovement Rebound Jump" Symmetry 15, no. 10: 1960. https://doi.org/10.3390/sym15101960

APA Style

Xu, J., Jordan, M. J., Chavda, S., Turner, A., & Bishop, C. (2023). Test–Retest Reliability of the Magnitude and Direction of Asymmetry in the Countermovement Jump, Drop Jump, and Countermovement Rebound Jump. Symmetry, 15(10), 1960. https://doi.org/10.3390/sym15101960

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop