Performance Evaluation of Data Utility for a Differential Privacy Scheme Supporting Fault Tolerance

Abstract

The evolution of smart grids improves the sustainability, controllability, stability, and efficiency of traditional power grids. There is a challenging issue in smart grids with protecting users’ privacy while collecting and controlling individual fine-grained data. To ensure data integrity and address the privacy issue, differential privacy protection is an efficient method to resist differential attacks on aggregated data. However, due to differential noise and faulty smart meters, the problem of differential noise deviation has a great impact on the utility of aggregated data. In this paper, we further supplement the previous work by improving the prediction method, forming a relatively complete DP protection scheme (DPP-UFT) with fault tolerance, and providing a detailed performance evaluation process. The experimental results show that the proposed method of adding differential noise based on the estimated failure rate is related to the estimated failure rate and the noise factor. Compared with several other related literature, it has achieved a higher data utilization effect.

1. Introduction

The smart grid (SG) is an enhancement to the traditional grid with advanced metering infrastructure (AMI). AMI supports bidirectional electricity and information flow by automatically collecting grid operation and fine-grained state information so as to provide users with real-time power consumption information feedback and monitor the load dynamics of SG in real time [1]. However, advanced information technology increases the vulnerability of network attacks [2]. Complex system scale makes it difficult to predict network attacks and system failures [3].

In recent years, much literature has focused on homomorphic encryption algorithms [4,5,6,7,8,9]. Differential attack [6,7] is a main attack scenario in homomorphic aggregation. Differential privacy (DP) protection prevents differential attacks during homomorphic aggregation by adding differential noise. In addition, as a low-cost device running in an unknown environment, smart meters are prone to failures, so homomorphic encryption with fault tolerance has to consider the following issues:

(1)

The decryption aggregation value cannot be realized due to the lack of part of the key of the faulty meter.

(2)

The sum of differential noise added by non-faulty meters cannot meet the requirements of DP, which increases the probability of a DP attack.

Jia et al. [7] proposed the HDA differential aggregation scheme; however, no fault tolerance method was proposed. Oksuz et al. [8] proposed an efficient data aggregation and dynamic billing system with block-chain technology to aggregate user data. The scheme proposed by Cao et al. [10] can realize encryption based on the differential privacy noise working on the switching state of each electrical equipment. It also fails to provide an analysis of the utility and errors of the aggregated data. The additional redundant noise reduces the utility of the scheme to aggregate data in the schemes supporting encrypted and differential fault tolerance [11,12,13,14,15]. Bao et al. [16] proposed a secure data aggregation scheme that achieves data integrity and fault tolerance simultaneously. Wang et al. [17] added differential noise to the consumption data before the smart meters sent it to the utility provider to estimate the user’s demand.

Nevertheless, the above algorithms working on DP protection do not consider encrypted fault tolerance and differential fault tolerance simultaneously and do not focus on the impact of DP differential noise on data availability during differential aggregate encryption.

We have proposed a differential privacy protection scheme supporting high data utility and fault tolerance (Zhang et al. [2]), based on which we further make the following contributions in this paper:

(1)

We further supplement the previous work by improving the prediction method.

(2)

We form a more perfect privacy protection model (DPP-UFT) with fault tolerance based on the previous work (Zhang et al. [2]).

(3)

We compare the performance evaluation of our scheme and several other related literature in terms of the impact of faulty meters and differential noise on data utilization.

The remainder of this paper is structured as follows:

Section 2 describes in detail the privacy protection model. Section 3 proposes the predictive failure rate method based on the DPP-UFT model and the impact of differential noise added by fault tolerance on the utility of aggregated data. Section 4 gives the conclusion that the data utilization of our proposed method in support of fault tolerance is significantly improved compared with other related literature within a certain range of estimated failure rates.

2. The Scheme DPP-UFT

2.1. System Model

Figure 1 shows the system model of DPP-UFT from the perspective of smart meter communication. In the communication model in Figure 1, the smart grid can be divided into three levels, namely, NAN (neighborhood area network), BAN (building area network), and HAN (householding area network). Each substation is assumed to cover a NAN, has a control center (CC) responsible for coordinating the distribution of power and communication with the trusted authority (TA) and the SMs, and can receive the data collected by the SMs in the NAN through its gateway (GW).

2.2. Security Requirements

Security and privacy issues must be addressed during smart metering.

Security Requirement 1: The fine-grained power consumption data of individual users is private and secure. It should not be obtained by CC, gateways, and other users.

Security requirement 2: Individual power consumption data aggregated over time is private and secure. Only the CC with keys has the right to obtain the aggregated data.

Security requirement 3: The fine-grained data of target users cannot be obtained by calculating the difference between the aggregated consumption in any two ranges.

An attack could be by an unauthorized entity obtaining private data or tampering with data without detection (e.g., a network attack), which is not the focus of this chapter. In this work, it is assumed that the household meter is tamper-proof [18,19], and therefore individual data are always accurately measured.

2.3. Attack Scenario

(1)

External attack: An external attacker may obtain personal information by intercepting communications in the model to infer the personal data of the target user.

(2)

Internal attack: It is assumed that the information flow in this model is reliable and untampered. The internal attacker is a participant in the system model. It may be SMs, aggregators, or CCs. It is assumed that they are semi-trusted, that is, execute strictly the protocol, including sending and transmitting data, which are authentic and reliable without malicious tampering [20,21,22]. However, they are curious about the individual fine-grained power consumption. The following attack is possible:

• CC may attack the target user based on the information sent by the SMs to GW or the union of up to N−2 m.
• CC may infer the data of the target user based on the encrypted aggregate value sent to it by GW.
• GW may try to obtain the user information of the target user through decryption or other available information flow according to the encrypted message sent by the user.
• The internal meter node may combine with other nodes to infer the data of the target node by stealing the information flow between the nodes.

(3)

Differential attack: The attacker can obtain the data of the target user by interpolating the aggregated values of his presence and absence by attacking the servers in CC. Differential privacy protection must meet two conditions at the same time: protect individual privacy from disclosure and reduce noise error deviation, so as to improve the utility of aggregated value [23].

2.4. The DPP-UFT Scheme

2.4.1. Grouping and Key Initialization

(1)

Smart Metering

At each spatial aggregation timestamp t, the individual user meter $U_{\mathrm{i}}$ reads the power consumption value $m_{(\mathrm{i},\mathrm{t})}$ until the time aggregation period T. After accumulating the power consumption in the continuous time period $t\in \{0,1,\cdots ,T\}$ and summing them up to $C_{(\mathrm{i},\mathrm{t})}={\displaystyle {\sum }_{t=1}^T{m}_{(\mathrm{i},\mathrm{t})}}$, send it to the CC for grouping.

(2)

Grouping

Once CC receives the aggregated value $C_{(\mathrm{i},\mathrm{t})}$ of the group from the last time aggregation period, it will calculate the bill of a single user according to the specific charging standard and the resort power consumption of all users according to different power consumptions. The grouping process is shown in Algorithm 1.

Algorithm 1: Similar consumption-based grouping

Input: A real array C = [c1, c2, …, cN] representing the set of power consumption of N users in the NAN region, a character array U = [u1, u2, …, uN] representing the set of N users, a character empty array G is defined, and an integer constant p, n defined. n is the number of groups, and p is the number of SMs in the group.

Output: G

1. U’ = Sort (U with C)

2. n = N/p

3. for (i = 0; i < n; i++){

4. for (j = 1; j < = p; j++){

5. G[i + 1]+ = U’[i×p + j];

6. }

7. }

8. if N%p! = 0{

9. for (i = n×p + 1; i < = N; i++){

10. G[n + 1]+ = U’[i]

11. }

12. }

(3)

Key Generation

• For each user $U_{\mathrm{i}}\in U$, TA first chooses a random number $S_{\mathrm{i}}\in Z_{\mathrm{N}}$ as $U_{\mathrm{i}}$‘s key and sends it to $U_{\mathrm{i}}$ securely.
• TA computes $S_0\in Z_{}$ so that $S_0+{\displaystyle {\sum }_{i=1}^n{S}_{\mathrm{i}}}=0\mathrm{mod} n$
• TA securely sends $(\lambda ,\alpha ,S_0)$ to CC as the private key of CC (assuming that there is a secure communication method to pass the key).

2.4.2. The Encryption and Aggregation of Supporting Fault-Tolerance

On the basis of similar consumption-based grouping and reducing the overall differential noise, the scheme considered two cases of fault tolerance encryption and fault tolerance difference in the distributed encryption process so that the aggregate value could still be decrypted correctly when there was a fault meter. To reduce redundant noise, the UPP-UFT added the differential noise with the pre-estimated noise parameter $1-\alpha \prime /\alpha$ instead of 1 in a distributed manner.

2.4.3. Differential Privacy with a Pre-Estimated Failure Rate

Theorem 1.

If we assume that M out of N meters in a group will fail (with an estimated failure rate α), then the pre-estimated total added noise satisfies:

$${\displaystyle {\sum }_{i=1}^{N-M}\widehat{G}(N-M,\lambda )} = Lap(\lambda ),$$

(1)

and it satisfies different privacy protections.

where, $\widehat{G}(N-M,\lambda )=G_1(N-M,\lambda )-G_2(N-M,\lambda )$, $G_1(N-M,\lambda ),G_2(N-M,\lambda )$, is an independent and identically distributed random variable with a gamma distribution of probability density function $g(x,n,t)=\frac{{(1/\lambda )}^{1/n}}{\mathrm{\Gamma }(1/n)}·x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n^{-1}$}\right.}·e^{\raisebox{1ex}{$-x$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}(\mathrm{x}\ge 0)$.

Proof. 

According to the additive property of gamma distribution [15], the sum of independent and identically distributed random variables follows a gamma distribution, that is, ${\displaystyle {\sum }_{i=0}^{n}G(k_i,\lambda )}=G(1/{\displaystyle {\sum }_{i=1}^n\frac{1}{k_i},\lambda })$, and the sum of pre-estimated noise is:

$$\begin{array}{l}{\displaystyle {\sum }_{i=1}^{N-M}(G_1(N-M,\lambda )-G_2(N-M,\lambda ))}\\ =G_1\left(1/{\displaystyle {\sum }_{i=1}^{N-M}\frac{1}{(N-M)}},\lambda \right)-G_2\left(1/{\displaystyle {\sum }_{i=1}^{N-M}\frac{1}{(N-M)}},\lambda \right)\\ =G_1(1,\lambda )-G_2(1,\lambda )=Lap(\lambda )\end{array}$$

(2)

Equation (2) shows that the sum of Laplacian noise added by ($N-M$) non-faulty users is ${\displaystyle {\sum }_{i=1}^{N-M}(G_1(N-M,\lambda )-G_2(N-M,\lambda ))}$ (wherein the estimated failure rate is $\alpha$ and the number of users in the group is $N$), which satisfies differential privacy. Under this assumption, the data with differential noise submitted by each non-faulty meter to the GW inside the CC are of the form ${\mathrm{g}}^{m_{i,t}+\widehat{G}(N-M,\lambda )}$; however, if the actual failure rate is ${\alpha }^{\prime }\ne \alpha$, the sum of the actual distributed differential noise will also vary with it. □

Corollary 1.

When the actual failure rate is ${\alpha }^{\prime }\le \alpha$, the redundant noise generated satisfies:

$${\displaystyle {\sum }_{i=1}^{N-M^{\prime }}\widehat{G}(N-M,\lambda )}=Lap(\lambda )+{\displaystyle {\sum }_{i=1}^{M-M^{\prime }}\widehat{G}(N-M,\lambda )}$$

(3)

Proof. 

According to the preset distributed differential noise value and Equation (1), the sum of $(N-M^{\prime })$ non-faulty electricity meters $(M^{\prime }=N,{\alpha }^{\prime }\le \alpha )$ is ${\displaystyle {\sum }_{i=1}^{N-M^{\prime }}(\widehat{G}(N-M,\lambda )}$ which satisfies the following equation:

$$\begin{array}{l}{\displaystyle {\sum }_{i=1}^{N-M^{\prime }}\widehat{G}(N-M,\lambda )}\\ ={\displaystyle {\sum }_{i=1}^{N-M^{\prime }}(G_1(N-M,\lambda )-G_2(N-M,\lambda ))}\\ ={\displaystyle {\sum }_{i=1}^{N-M}\widehat{G}(N-M,\lambda )}+{\displaystyle {\sum }_{i=1}^{M-M\prime }\widehat{G}(N-M,\lambda )}\\ =Lap(\lambda )+{\displaystyle {\sum }_{i=1}^{M-M^{\prime }}\widehat{G}(N-M,\lambda )}\end{array}$$

(4)

in which the redundant noise is ${\displaystyle {\sum }_{i=1}^{M-M^{\prime }}(\widehat{G}(N-M,\lambda )}$. □

2.4.4. Encryption of the Power Consumption

Adding a part of differential noise to the individual data is not enough to protect the privacy of the individual data, so it is necessary to encrypt the individual data. The expression of the encrypted value after adding noise to the meter of an individual user is:

$$C_{i,t}=g^{m_{i,t}+\widehat{G}(N-M,\lambda )}·h_t^{Si}\mathrm{mod} n^2$$

(5)

where $t\in T$ and $h_t=H(t)$.

2.4.5. Aggregation and Decryption with Fault-Tolerance

According to Equation (5), CC homomorphically aggregates the ciphertext of all non-faulty nodes in the following form:

$$\begin{array}{l}{\tilde{C}}_{\mathrm{t}}={\displaystyle {\prod }_{i=1}^{N-M^{\prime }}{C}_{i,t}}\mathrm{mod}{n}^2\\ =g^{{\displaystyle {\sum }_{i=1}^{N-M^{\prime }}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}{h}_{\mathrm{t}}^{{\displaystyle {\sum }_{i=1}^{N-M^{\prime }}{S}_i}}\mathrm{mod}{n}^2\end{array}$$

(6)

Equation (6) can be further expressed as follows:

$${\tilde{C}}_{\mathrm{t}}=g^{{\displaystyle \sum _{U_i\in (U/\widehat{U})}{m}_{i,t}+(N-M^{\prime })\widehat{G}(N-M,\lambda ))}}{h}_{\mathrm{t}}^{{\displaystyle \sum _{U_i\in (U/\widehat{U})}{S}_i}}\mathrm{mod}{n}^2$$

(7)

where $\widehat{U}$ represents the faulty meters.

(1)

CC will send faulty users to TA. Once it has not received reports from the faulty meter $\widehat{U}\subset U$, TA will calculate the keys’ sum ${\overline{C}}_t$ of the faulty nodes and send them to CC, where

$${\overline{C}}_t={\displaystyle {\prod }_{U_i\in \widehat{U}}{h}_t^{S_i}=}{h}_t^{{\displaystyle {\sum }_{U_i\in \widehat{U}}{S}_i}}$$

(8)

(2)

GW computes ${\tilde{C}}_t·{\overline{C}}_t$ and sends it to CC according to Equation (8), where

$$\begin{array}{l}{\tilde{C}}_{\mathrm{t}}·{\overline{C}}_{\mathrm{t}}\\ =g^{{\displaystyle \sum _{U_i\in (U/\widehat{U})}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}{h}_{\mathrm{t}}^{{\displaystyle \sum _{U_i\in (U/\widehat{U})}{S}_i}}{h}_{\mathrm{t}}^{{\displaystyle \sum _{U_i\in \widehat{U}}{S}_i}}\mathrm{mod}{n}^2\\ =g^{{\displaystyle \sum _{U_i\in (U/\widehat{U})}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}{h}_{\mathrm{t}}^{{\displaystyle \sum _{U_i\in U}{S}_i}}\mathrm{mod}{n}^2\end{array}$$

(9)

(3)

According to Equation (9), CC computes the aggregated value with noise added by secret key S₀ as follows:

$$S(t)={\displaystyle \sum _{U_{\mathrm{i}}\in (U/\widehat{U})}{m}_{(\mathrm{i},\mathrm{t})}+Lap(\lambda )+(M-M^{\prime })\widehat{G}(N-M,\lambda )}$$

(10)

2.4.6. Correctness Analysis

CC decrypts the aggregate value (Equation (10)) received with the key as follows:

$$\begin{array}{l}{\tilde{C}}_t·{\overline{C}}_t·h_t{}^{S_0}\\ ={\displaystyle \prod _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}(g^{(m_{i,t}+\widehat{G}(N-M,\lambda ))}·h_t^{S_i})}{\overline{C}}_t·h_t{}^{S_0}\mathrm{mod}{n}^2\end{array}$$

(11)

According to the additive homomorphic property of Paillier encryption, Equation (11) can be transformed as follows:

$$\begin{array}{l}{g}^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}·h^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}{S}_i}}·{\overline{C}}_t{h}_t{}^{S_0}\mathrm{mod}{n}^2\\ =g^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}·h^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}{S}_i}}·h^{{\displaystyle \sum _{U_i\in (\widehat{\mathrm{U}})}{S}_i}}·h_t{}^{S_0}\mathrm{mod}{n}^2\end{array}$$

(12)

Equation (12) can be transformed as follows ${\displaystyle \sum _{i=1}^n{s}_i+}{s}_0=0\mathrm{mod}N\Rightarrow {\displaystyle \sum _{i=1}^n{s}_i+}{s}_0=\mu N$:

$$g^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}·h_t{}^{\mu N}\mathrm{mod}{n}^2$$

(13)

CC uses the key to decrypt the noise-added aggregate value obtained with Equation (13) as follows:

$$\begin{array}{l}D({\tilde{C}}_{\mathrm{t}}·{\overline{C}}_{\mathrm{t}}·h_{\mathrm{t}}^{S_0})\\ =L({({\tilde{C}}_{\mathrm{t}}·{\overline{C}}_{\mathrm{t}}·h_{\mathrm{t}}^{S_0})}^{\lambda }\mathrm{mod} N^2)·\alpha \mathrm{mod} n \\ ={\displaystyle {\sum }_{U_{\mathrm{i}}\in (U/\widehat{U})}(m_{\mathrm{i},\mathrm{t}}+\widehat{G}(N-M,\lambda ))}\\ ={\displaystyle {\sum }_{U_{\mathrm{i}}\in (U/\widehat{U})}{m}_{\mathrm{i},\mathrm{t}}+Lap(\lambda )+(M-M^{\prime })}\widehat{G}(N-M,\lambda )\end{array}$$

(14)

$D({\tilde{C}}_{\mathrm{t}}·{\overline{C}}_{\mathrm{t}}·h_{\mathrm{t}}^{S_0})$ is the sum of the power consumption of the differential privacy of $N-M^{\prime }$ users, which verifies the correctness of the encryption method.

2.5. Security Analysis

(1)

External attacks. The external attacker A overhears the data sent by individual users to the GW in the form of $g^{m_{(i,t)}+G_1(N-M,\lambda )-G_2(N-M,\lambda )}·h_t^{{}^{S_i}}$. According to the semantic security property of the Paillier cipher against plaintext attacks, any attacker A cannot decrypt the data without the individual meter key $s_i$ owned by TA and the individual meter. Therefore, the encrypted aggregate value $g^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}·h_t{}^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}{S}_i}}$ can be decrypted by the sum of keys to obtain the sum of noisy data from these nodes rather than the individual data $m_{i,t}$.

(2)

Internal attacks. The data $g^{(m_{i,t}+\widehat{G}(N-M,\lambda ))}·h_t^{{}^{S_i}}$ sent by SM to GW resists all semi-trusted internal attackers due to the key $s_i$ owned by TA and SM.

CC can send the fault information of one or some users to TA; however, it can only get the hash function ${\overline{C}}_t$ of the key sum of all faulty meters from TA, where $s_i$ or ${\displaystyle \sum s_i}$ cannot be obtained. CC and the user have different key authorities, $S_0$ is kept secret by CC, and the private key Si of the faulty meter is known only to TA and SM itself.

(3)

Fault-tolerant reliability. The scheme solves the problems of cryptographic and differential fault tolerance. When $\widehat{U}(\widehat{U}\subset U)$ fails, CC can still report to TA and receive ${\overline{C}}_{\mathrm{t}}$ and obtain the correct noise-added aggregation value ${}^{{\displaystyle \sum _{U_i\in (\mathrm{U}/\widehat{\mathrm{U}})}(m_{i,t}+\widehat{G}(N-M,\lambda ))}}$ of non-faulty users. Then, the distributed differential noise is set by predicting the failure rate so that the non-faulty nodes meet the requirements of overall differential privacy through the added differential noise.

(4)

Differential Privacy. This scheme considers the sum of distributed differential noise in the case of the pre-estimated failure rate as $Lap(\lambda )+(M-M^{\prime })G(N-M,\lambda )$. This method of adding distributed differential noise to the prior value of the previous failure rate ensures the overall differential privacy requirements and reduces the additional differential noise.

3. Utility Analysis and Performance Evaluation

The experiment uses an i5-2500 desktop computer running at 2.5 GHz with 4 GB of RAM and 1 MB of flash memory. The simulation environment uses the MIRACL library [24] and the Paillier library (libpaillier-0.8) [25] to evaluate the operation cost of the scheme. The Paillier cipher parameters with 1024 bits of modular sum are used for homomorphic encryption and decryption, the RSA key with 512 bits is used for asymmetric encryption and decryption, and the MD5 algorithm is used for hash calculation. The experimental power consumption simulation platform refers to the statistical data of UK household power consumption in 2017 [26], and on this basis, it is extended to generate the power consumption data of 2000 residential meters in a certain district every minute.

Table 1. Comparison between related schemes.

Scheme	DP	RN	RMSE	U	Data/State Privacy	Encryption Method	Encryption Overhead	FT
PPADF [16]	✖	✖	—	✖	Data	Pre-computed auxiliary information	O(N)	✔
FTA [20]	✔	✔	$O(\sqrt{1+M\prime })$	✔	Data	Modular addition	O(N×K×B)	✔
DPA-FT [27] †	✔	✖	O(1) †	✖	Data	Diffie–Hellman	O(N)	✔
DP-NILM [28]	✔	✖	—	✖	State	Markov, Laplace noise	O(N×A)	✖
DPP-UFT [ours]	✔	✔	O(1)	✔	Data	Paillier	O(N)	✔

N: the number of smart meters per aggregator DP: different privacy. M’: actual number of faulty meters. RN: reducing noise. K: the number of paired nodes in FTA. U: data utility. B: the time point of the future key in FTA. FT: fault tolerance. A: average number of appliances per household in DP-NILM. †: no supporting differential fault tolerance.

lists several of the most relevant literature and compares them in terms of implementation function, storage cost, computational cost, and practicality of aggregated data. PPADF represents the scheme proposed by Bao et al. [16], FTA [20] represents the scheme proposed by Won et al. [20], and DPA-FT represents the scheme proposed by Bao et al. [27]. DP-NILM represents the scheme proposed by Hui et al. [28].

3.1. Storage Overhead Comparison

DPP-UFT (ours), DPA-FT [27], and DP-NILM [28] have no special requirements on storage costs. In order to provide backup keys for faulty meters and differential noise to provide a fault-tolerant solution, FTA [20] sets a buffer in the memory of the aggregator to store B future passwords and solves the problem that homomorphic aggregation cannot decrypt correctly when there is a faulty meter or node communication failure, but the accompanying cost is also inevitable, mainly manifested in:

(1)

GW needs to set up a buffer to store standby passwords. Assuming that the number of meter users is 220, the modulo value in the modulo addition operation is, that is, the width of the random number in the future password is 64 bits, and the meter reading takes up 64 bits, so the total width of a future password is 128 bits. The value of B is set to the aggregated value for one month, and the number of cycles is 2880 (taking 15 min as an example). Without calculating the width of the added differential noise, the total storage capacity is approximately 45 GB. The storage cost will also increase with an increase in the number of meters or cycles.

(2)

If the number of time points in B is too low, the meter cannot be repaired for a long time. The fault-tolerant scheme is meaningless. If the number of time points in B is too high, the memory occupancy rate and processing time of the gateway will be seriously challenged, which will bring a higher delay to the whole system.

(3)

All meters within each GW send B alternate passwords simultaneously, and the communication bandwidth is also greatly affected because each user node sends (1 + B) encrypted data simultaneously, including one current encrypted data and B alternate encrypted data, the latter including $Lap(\lambda )+\widehat{G}(N,\lambda )$.

3.2. Computation Overhead Analysis

The encryption cost of N user nodes in DP-NILM [28] is O(N). In each spatial aggregation cycle, each user should select K user nodes and paired nodes, and some random numbers generated are added to the differential data as noise. The total sum of random numbers in this random perturbation encryption method is zero. However, in each billing cycle, the random key needs to be generated through the cooperation of K paired nodes and produces B future encrypted values. The computational cost of each node is O(K×B). Then, the total computational cost is O(N×K×B), and the scheme DPP-UFT [ours] does not include the storage and encryption calculation process of the backup password. Each node in the network considers the faulty meter and performs the Paillier encryption operation based on fault tolerance. Similar to the homomorphic aggregation of the scheme DPA-FT [27], the computation cost of a single node is O(1) for the homomorphic encryption with two exponential operations and one multiplication operation. In addition, the grouping and the process of estimating the failure rate used in the scheme are completed in the initialization phase, which does not affect the overall computation and communication costs.

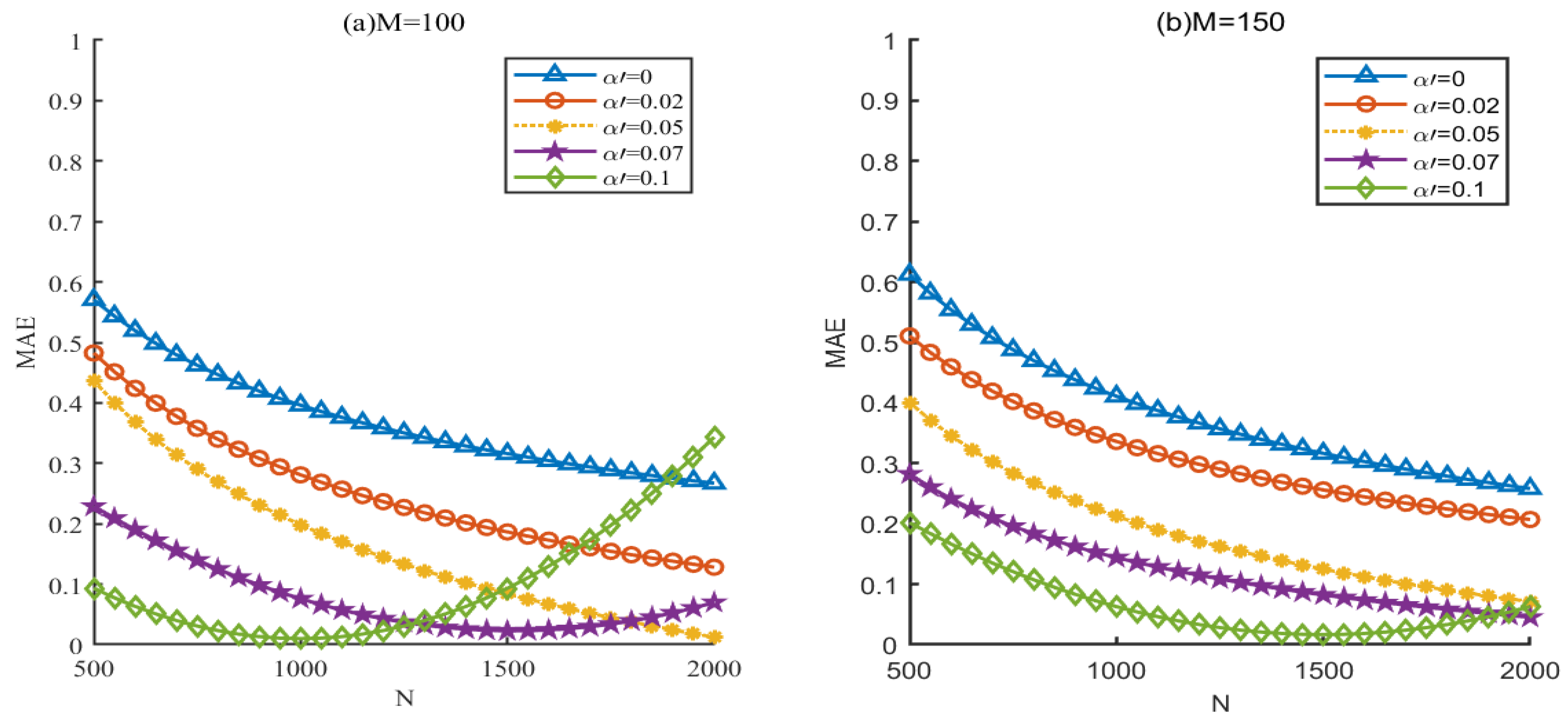
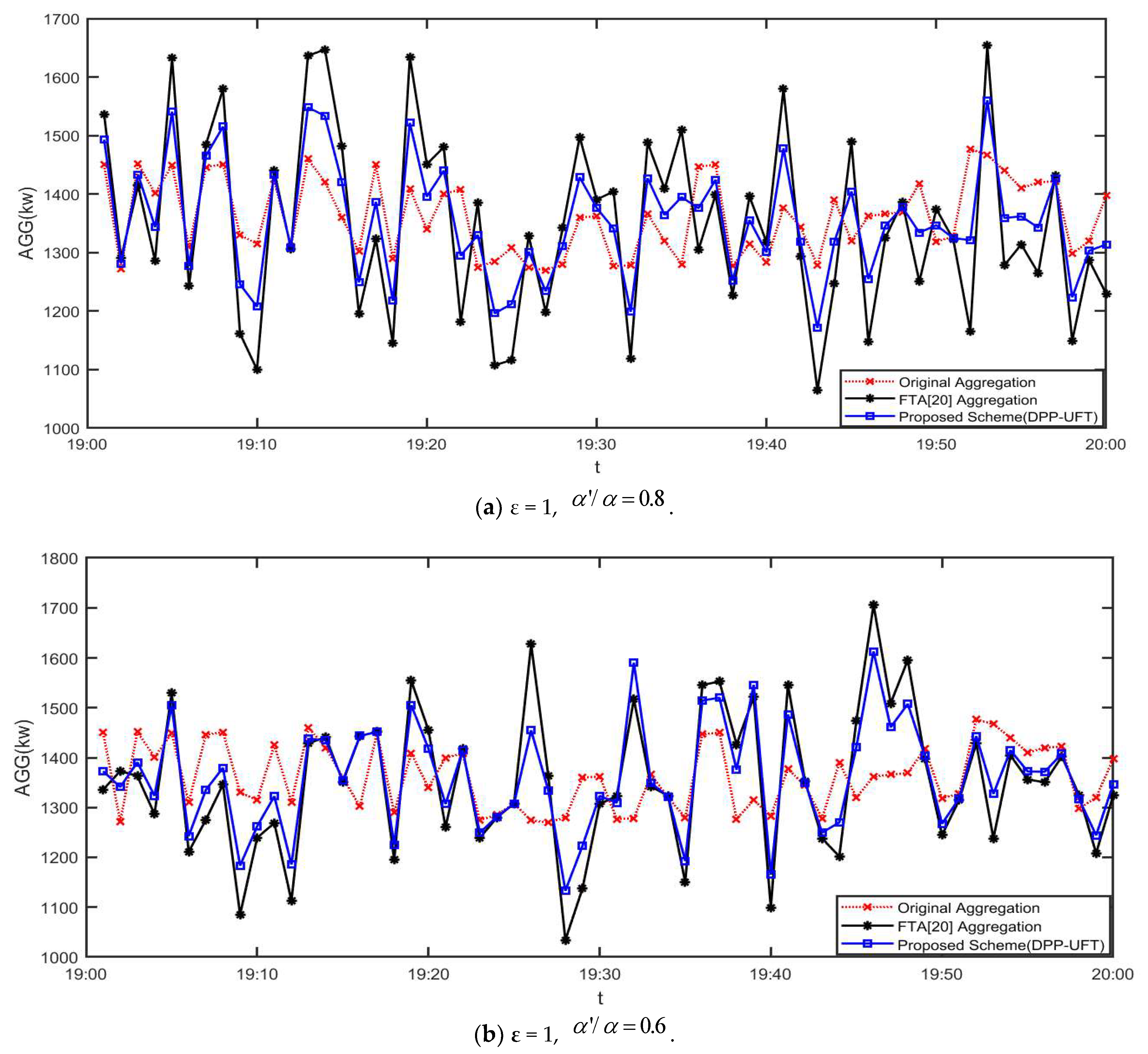
3.3. Aggregated Data Utility

DPP-UFT improves the availability of differential aggregated data in two aspects:

(1)

Similar Consumption-based Grouping

DPA-FT [27], DP-NILM [28], and FTA [20] schemes are all based on traditional neighborhood grouping. According to Theorem 1 (Equation (1)), we derive the data of the mean absolute error (MAE) of the power consumption value and the standard deviation (SD) and the mean absolute error within the group after grouping, and we compare the MAE and SD under the two grouping methods according to Equations (15) and (16) in

Table 2. Comparison between two groupings.

N	Grouping Based on Adjacent Region [20,27,28]		Grouping Based on Similar Consumption
	Mean	SD	Mean	SD
500	0.321	0.045	0.198	0.017
1000	0.274	0.037	0.133	0.011
1500	0.198	0.018	0.099	0.005
2000	0.178	0.011	0.074	0.0009

, where

$$\begin{array}{ll}MAE& =\frac{{\displaystyle {\sum }_{i=1}^N(m_{i,t}+\widehat{G}(N,\lambda )-m_{i,t})}}{N}\\ & =\frac{{\displaystyle {\sum }_{i=1}^N\widehat{\mathrm{G}}(N,\lambda )}}{N}\\ & =\frac{LAP(\lambda )}{N}\end{array}$$

(15)

$$SD=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^N{(m_{i,t}-\frac{Lap(\lambda )}{N})}^2}}{N}}$$

(16)

It can be seen from Table 2 that the MAE based on similar consumption-based grouping is significantly reduced compared with the grouping based on adjacent regions under the same N value, which indicates that the average differential noise of similar consumption-based grouping is decreasing, and it is obviously reduced with the increase in users in the group, especially the variance between the distributed differential noise and the mean noise, which is also significantly reduced. This indicates that the peaks and valleys of user power consumption in the group are more similar to the mean.

(2)

Distributed Differential Noise with a Pre-estimated Failure Rate

DPA-FT [27] also proposed a Diffie–Hellman-based differential privacy homomorphic aggregation scheme with fault tolerance but does not consider how to reduce differential noise, nor does it discuss the problem of insufficient overall differential noise caused by faulty meters. Assuming the users N in the group and the actual number of faulty users M’, according to Corollary 1, the added differential noise can be derived in the following form:

$$\begin{array}{l}{\displaystyle {\sum }_{U_i\in U/\widehat{U}}\widehat{G}(N,\lambda )}\\ =(N-M^{\prime })(G_1(N,\lambda )-G_2(N,\lambda ))\\ =N(G_1(N,\lambda )-G_2(N,\lambda ))-M^{\prime }\widehat{G}(N,\lambda )\\ =Lap(\lambda )-M^{\prime }\widehat{G}(N,\lambda )\end{array}$$

(17)

Obviously, the distributed differential noise added in DPA-FT [27] cannot meet the overall differential demand Lap(λ), especially when the error rate is high. The overall differential noise is obviously insufficient, and the probability of a differential attack will significantly increase. In order to compensate for this problem, FTA [20] appends B “future passwords” to each meter while sending encrypted measurements. The total noise $(1+M^{\prime })Lap(\lambda )$ meets the overall differential demand. The difference between the total noise value of the FTA scheme [20] and the proposed scheme is $M^{\prime }Lap(\lambda )+(M-M^{\prime })\widehat{G}(N-M,\lambda )$. The reasoning process is as follows:

$$\begin{array}{l}(1+M^{\prime })Lap(\lambda )-(N-M^{\prime })\widehat{G}(N-M,\lambda )\\ =M^{\prime }Lap(\lambda )-(M-M^{\prime })\widehat{G}(N-M,\lambda )\end{array}$$

(18)

Figure 2 shows the comparison of the mean absolute error MAE $MAE=\frac{{\displaystyle {\sum }_{i=1}^{\left|M-M^{\prime }\right|}\widehat{G}(N-M)}}{N}$ of the overall differential noise satisfying the predicted error rate with the number of user nodes in the group, the actual number, and the actual error rate. When the total number in the group is 2000 and the pre-estimated faulty meters are 100 and 150, respectively, the mean absolute error of the noise difference and the noise difference satisfying the overall differential privacy are the smallest when the actual number of faults is equal to the estimated number of faults, and the mean absolute error of the noise difference in the two cases ${\alpha }^{\prime }>\alpha$ and ${\alpha }^{\prime }<\alpha$ is symmetrically distributed by ${\alpha }^{\prime }<\alpha$. When the actual added differential noise at ${\prime }^{\alpha }>\alpha$ cannot meet the overall demand, the probability of a differential attack will be improved, which further verifies Equation (18).

(3)

Utility Comparison

DPP-UFT [ours] and FTA [20] both take measures in this aspect, but on the premise of ensuring the overall differential noise, it brings redundant noise. Therefore, the two schemes are compared in terms of reducing redundant noise and improving the utility of aggregation.

The experimental power consumption simulation platform on this basis generates power consumption data of 2000 residential meters per minute from 19:00 to 20:00 on the first Saturday of April. Different values of ε (0.5 and 1, respectively) are set in the experiment; the global sensitivity, which is the power demand of all applications and lights, is 33 KW, and each user holds the individual sensitivity, which is the sum of the power demand of the users. Both schemes use the aggregated value of noise added by CC decryption as the experimental data source. In order to compare the influence of the pre-estimated failure rate adopted in this scheme on the actual differential noise, the actual failure rate is set to 20, and the failure rate ratio corresponding to the two cases of the estimated failure rate of 25 and 33 is approximated ${\alpha }^{\prime }/\alpha =0.8$ and ${\alpha }^{\prime }/\alpha =0.6$, respectively. In this way, the difference between the two schemes with the same number of users, different failure rate ratios (actual failure rate and estimated failure rate ratio), and the difference between the noise-added aggregation value at different time points and the real aggregation value in the region is solved, which directly reflects the utility of the power supplier/power company for the aggregated data.

Comparing Figure 3a,c, under the premise of the same failure rate ($\alpha \prime /\alpha =0.8$) and the same number of users, when ε = 0.5, the noise of DPP-UFT and FTA schemes is about 12% higher than that of ε = 1. When the FTA scheme varies from 1100 to 1700 KW in Figure 3a (ε = 1), the differential aggregation value of the DPP-UFT scheme varies from 1250 to 1450 KW, while the DPP-UFT scheme varies from 1100 to 1600 KW in Figure 3c (ε = 0.5). The same noise difference can be seen in Figure 3b,d; when ε = 0.5, the noise of the DPP-UFT and FTA schemes is about 11% higher than that of ε = 1. When the FTA scheme varies from 1100 to 1700 KW in Figure 3b (ε = 1), the differential aggregation value of the DPP-UFT scheme varies from 1100 to 1600 KW, while the DPP-UFT scheme varies from 900 to 1800 KW in Figure 3d (ε = 0.5).

It can be seen that the differential noise increases with the decrease in ε because the total amount of differential noise added in the group is $\lambda =\raisebox{1ex}{$G{S}_f$}\!\left/ \!\raisebox{-1ex}{$\epsilon $}\right.=\raisebox{1ex}{${\max }_i{m}_{i,t}$}\!\left/ \!\raisebox{-1ex}{$\epsilon $}\right.$, and the differential privacy is inversely proportional to ε when the highest sensitivity GS_f in the group is equal. Equation (2) is verified.

The paper also compares the utilization rates under the same parameters ε and different estimated failure rates $\alpha \prime /\alpha$ (ε = 1 in Figure 3a,b and ε = 0.5 in Figure 3c,d). The utilization rates in Figure 3a,c are 12% and 9% higher than those in Figure 3b,d respectively.

In the DPP-UFT scheme, the noise value will increase slightly with the decrease in ${\alpha }^{\prime }/\alpha$, as shown in Figure 3a,b. Especially when the estimated failure rate is close to the actual failure rate, compared with the FTA scheme, which does not use the estimated failure rate to eliminate redundant differential noise, the noise-added aggregation value of the DPP-UFT scheme fluctuates closer to the actual aggregation value. It indicates that the added redundant noise is significantly reduced, which further verifies Equations (7) and (14) and verifies the effectiveness of the method of adding differential noise based on faulty meters adopted in this scheme in noise reduction.

To summarize the above experimental results, it is shown that the aggregation value of DPP-UFT is closer to the true aggregation value. This result depends on two factors. (1) The algorithm based on approximate power consumption grouping reduces the within-group mean absolute error (MAE) and the deviation from the mean error (see Table 2), which reduces Lap(λ). (2) From Equation (18), it can be concluded that when the actual error rate of the DPP-UFT scheme is closer to the estimated error rate, especially when ${\alpha }^{\prime }/\alpha =0.8$, the aggregation value of DPP-UFT is closer to the true aggregation value compared with FTA, and the deviation error of FTA aggregation noise is larger. Therefore, the scheme DPP-UFT optimizes the differential noise from the two parts of the equation. It is proven that UPP-UFT fundamentally reduces the overall differential noise value Lap(λ). The encryption method of adding differential noise based on the estimated failure rate and approximate power consumption group achieves the expected effect of improving the practicability of aggregated data.

4. Conclusions

The paper provides a differential privacy protection scheme supporting high data utility and fault tolerance (DPP-UFT) based on the predictive failure rate method. We focus on the performance evaluation of the proposed DPP-UFT in terms of the utility of aggregated data. From the information presented in the previous sections, the following conclusions are drawn:

(1)

The differential privacy is inversely proportional to ε when the highest sensitivity GS_f in the group is equal, which satisfies Equation (2).

(2)

In the DPP-UFT scheme, the noise value will increase slightly with the decrease in ${\alpha }^{\prime }/\alpha$, which satisfies Equations (7) and (14).

(3)

The performance evaluation further verifies the effectiveness of the method of adding differential noise based on faulty meters adopted in this scheme for noise reduction.

This paper evaluates and complements the performance of the infinite separability of Laplacian noise based on previous research to improve the data utilization rate based on fault tolerance. The specific improvement methods are as follows: Based on the infinite separability of differential Laplacian noise, an approximate power consumption grouping algorithm is proposed to reduce the mean absolute error (MAE) and the deviation from the mean error to reduce aggregate differential noise. This point can be concluded from the performance evaluation experiment in Figure 2. The improved method considered by the scheme based on the estimated failure rate makes the scheme more resilient in terms of aggregate differential noise. It can be concluded from Figure 3a–d for the performance evaluation experiment: The aggregate differential noise is directly related to parameter ε and the estimated failure rate, and it decreases with the increase in parameter ε. The higher the estimated failure rate, the lower the aggregate noise value and the higher the data utilization rate $\alpha \prime /\alpha$. The performance evaluation once again verified that, compared with the traditional partitioning method based on traditional neighborhood grouping, our proposed partitioning method based on approximate power consumption groups has a certain improvement in the utilization of aggregated data.