Novel Computations of the Time-Fractional Coupled Korteweg–de Vries Equations via Non-Singular Kernel Operators in Terms of the Natural Transform
Abstract
:1. Introduction
2. Important Notations
3. The Proposed Scheme
3.1. Case I
3.2. Case II
4. Numerical Results
5. Results Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Ullah, I.; Ali, A.; Saifullah, S. Analysis of time-fractional non-linear Kawahara Equations with power law kernel. Chaos Solitons Fractals 2022, 9, 100084. [Google Scholar] [CrossRef]
- Ikram, M.D.; Asjad, M.I.; Akgül, A.; Baleanu, D. Effects of hybrid nanofluid on novel fractional model of heat transfer flow between two parallel plates. Alex. Eng. J. 2021, 60, 3593–3604. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Jin, H.; Wang, Z. Boundedness, blowup and critical mass phenomenon in competing chemotaxis. J. Differ. Equ. 2016, 260, 162–196. [Google Scholar] [CrossRef]
- Guo, C.; Hu, J.; Wu, Y.; Celikovsky, S. Non-Singular Fixed-Time Tracking Control of Uncertain Nonlinear Pure-Feedback Systems With Practical State Constraints. IEEE Trans. Circuits Syst. Regul. Pap. 2023, 70, 3746–3758. [Google Scholar] [CrossRef]
- Guo, C.; Hu, J.; Hao, J.; Celikovsky, S.; Hu, X. Fixed-time safe tracking control of uncertain high-order nonlinear pure-feedback systems via unified transformation functions. Kybernetika 2023, 59, 342–364. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Wang, W.; Zhang, H. A Predictor-Corrector Compact Difference Scheme for a Nonlinear Fractional Differential Equation. Fractal Fract. 2023, 7, 521. [Google Scholar] [CrossRef]
- Wang, W.; Khan, M.A.; Kumam, P.; Thounthong, P. A comparison study of bank data in fractional calculus. Chaos Solitons Fractals 2019, 126, 369–384. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Partohaghighi, M.; Saifullah, S.; Akgül, A.; Jarad, F. Oscillatory and complex behaviour of Caputo-Fabrizio fractional order HIV-1 infection model. Aims Math 2021, 7, 4778–4792. [Google Scholar] [CrossRef]
- Khan, A.; Ali, A.; Ahmad, S.; Saifullah, S.; Nonlaopon, K.; Akgül, A. Nonlinear Schrödinger equation under non-singular fractional operators: A computational study. Results Phys. 2022, 43, 106062. [Google Scholar] [CrossRef]
- Rahman, F.; Ali, A.; Saifullah, S. Analysis of time-fractional ϕ4-equation with singular and non-singular kernels. Int. J. Appl. Comput. Math. 2021, 7, 192. [Google Scholar] [CrossRef]
- Khan, A.; Akram, T.; Khan, A.; Ahmad, S.; Nonlaopon, K. Investigation of time fractional nonlinear KdV-Burgers equation under fractional operators with nonsingular kernels. AIMS Math 2023, 8, 1251–1268. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. Extension of the resistance, inductance, capacitance electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1687814015591937. [Google Scholar] [CrossRef]
- Wang, K. Exact travelling wave solution for the local fractional Camassa-Holm-Kadomtsev-Petviashvili equation. Alex. Eng. J. 2023, 63, 371–376. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive control of time delay teleoperation system with uncertain dynamics. Front. Neurorobot. 2022, 16, 928863. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Alijani, Z.; Shiri, B.; Perfilieva, I.; Baleanu, D. Numerical solution of a new mathematical model for intravenous drug administration. Evol. Intell. 2023, 1–17. [Google Scholar] [CrossRef]
- Shiri, B.; Alijani, Z.; Karaca, Y. A Power Series Method for the Fuzzy Fractional Logistic Differential Equation. Fractals 2023. [Google Scholar] [CrossRef]
- Cheng, B.; Wang, M.; Zhao, S.; Zhai, Z.; Zhu, D.; Chen, J. Situation-Aware Dynamic Service Coordination in an IoT Environment. IEEE/ACM Trans. Netw. 2017, 25, 2082–2095. [Google Scholar] [CrossRef]
- Zheng, W.; Zhou, Y.; Liu, S.; Tian, J.; Yang, B.; Yin, L. A Deep Fusion Matching Network Semantic Reasoning Model. Appl. Sci. 2022, 12, 3416. [Google Scholar] [CrossRef]
- Zheng, W.; Yin, L. Characterization inference based on joint-optimization of multi-layer semantics and deep fusion matching network. PeerJ Comput. Sci. 2022, 8, e908. [Google Scholar] [CrossRef]
- Yan, L. Numerical solutions of fractional Fokker–Planck equations using iterative Laplace transform method. Abstr. Appl. Anal. 2013, 2013. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K. Local fractional Laplace variational iteration method for solving nonlinear partial differential equations on Cantor sets within local fractional operators. J. Zankoy-Sulaimani-Part A 2014, 16, 49–57. [Google Scholar]
- El-Ajou, A.; Arqub, O.A.; Momani, S. Approximate analytical solution of the nonlinear fractional KdV Burgers equation: A new iterative algorithm. J. Comput. Phys. 2015, 293, 81–95. [Google Scholar] [CrossRef]
- Hendi, F.A. Laplace Adomian decomposition method for solving the nonlinear Volterra integral equation with weakly kernels. Stud. Nonlinear Sci. 2011, 2, 129–134. [Google Scholar]
- Hashmi, M.S.; Khan, N.; Iqbal, S. Optimal homotopy asymptotic method for solving nonlinear Fredholm integral equations of second kind. Appl. Math. Comput. 2012, 218, 10982–10989. [Google Scholar] [CrossRef]
- Rawashdeh, M. Using the reduced differential transform method to solve nonlinear PDEs arises in biology and physics. World Appl. Sci. J. 2013, 23, 1037–1043. [Google Scholar]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial. Differ. Equ. Int. J. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Saad Alshehry, A.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional View Analysis of Kuramoto-Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Elhanbaly, A.; Abdou, M.A. Adomian decomposition method for solving fractional nonlinear differential equations. Appl. Math. Comput. 2006, 182, 313–324. [Google Scholar] [CrossRef]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving fractional-order diffusion equations in a plasma and fluids via a novel transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The analysis of fractional-order nonlinear systems of third order KdV and Burgers equations via a novel transform. Complexity 2022, 2022, 4935809. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of fractional-order regularized long-wave models via a novel transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Korteweg, D.J.; De Vries, G. XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Fung, M.K. KdV equation as an Euler–Poincaré equation. Chin. J. Phys. 1997, 35, 789–796. [Google Scholar]
- El-Wakil, S.A.; Abulwafa, E.M.; Zahran, M.A.; Mahmoud, A.A. Time-fractional KdV equation: Formulation and solution using variational methods. Nonlinear Dyn. 2011, 65, 55–63. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Zhou, M.X.; Kanth, A.R.; Aruna, K.; Raghavendar, K.; Rezazadeh, H.; Inc, M.; Aly, A.A. Numerical solutions of time fractional Zakharov-Kuznetsov equation via natural transform decomposition method with nonsingular kernel derivatives. J. Funct. Spaces 2021, 2021, 9884027. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. Aims Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Merdan, M.; Mohyud-Din, S.T. A new method for time-fractionel coupled-KDV equations with modified Riemann–Liouville derivative. Stud. Nonlinear Sci. 2011, 2, 77–86. [Google Scholar]
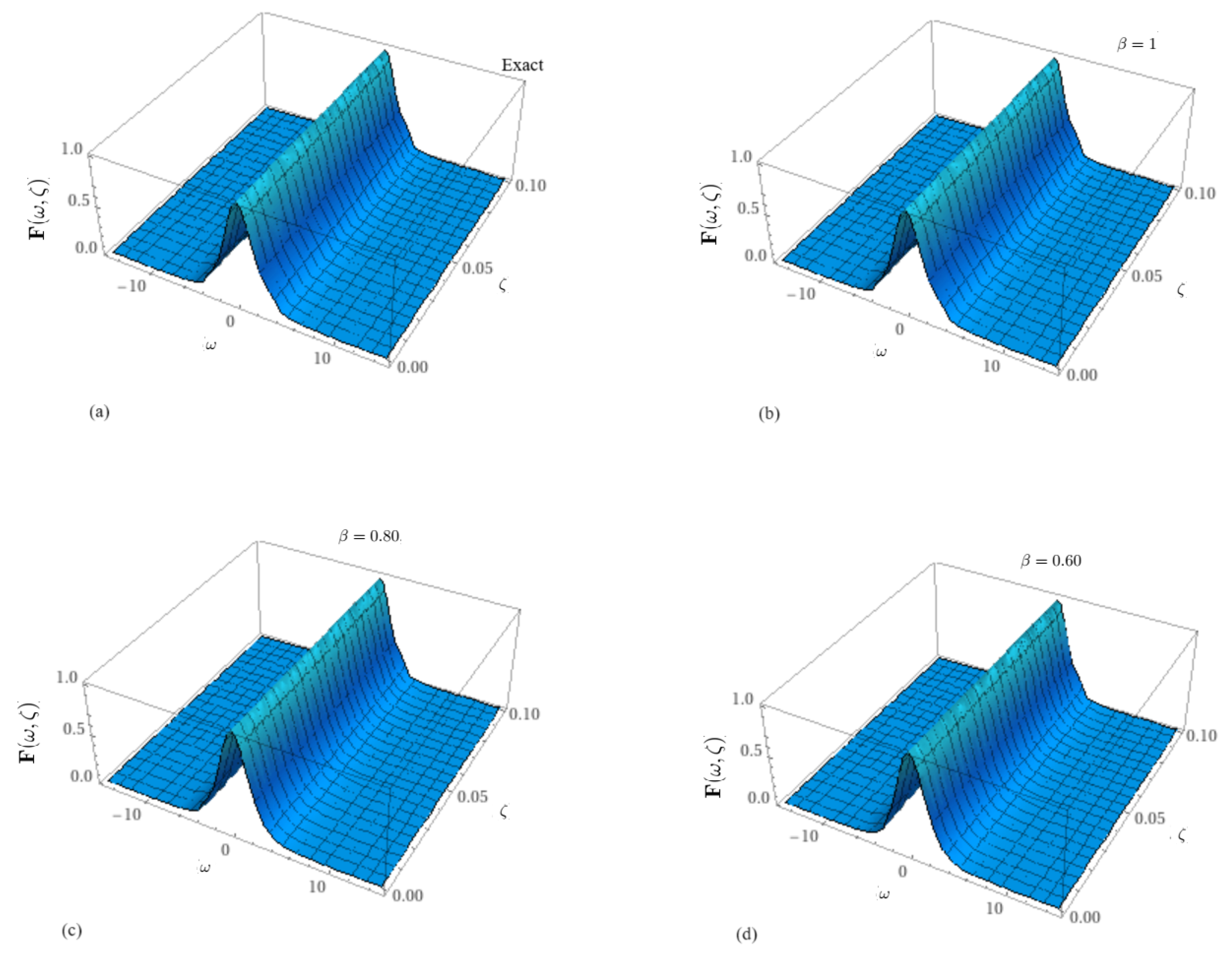
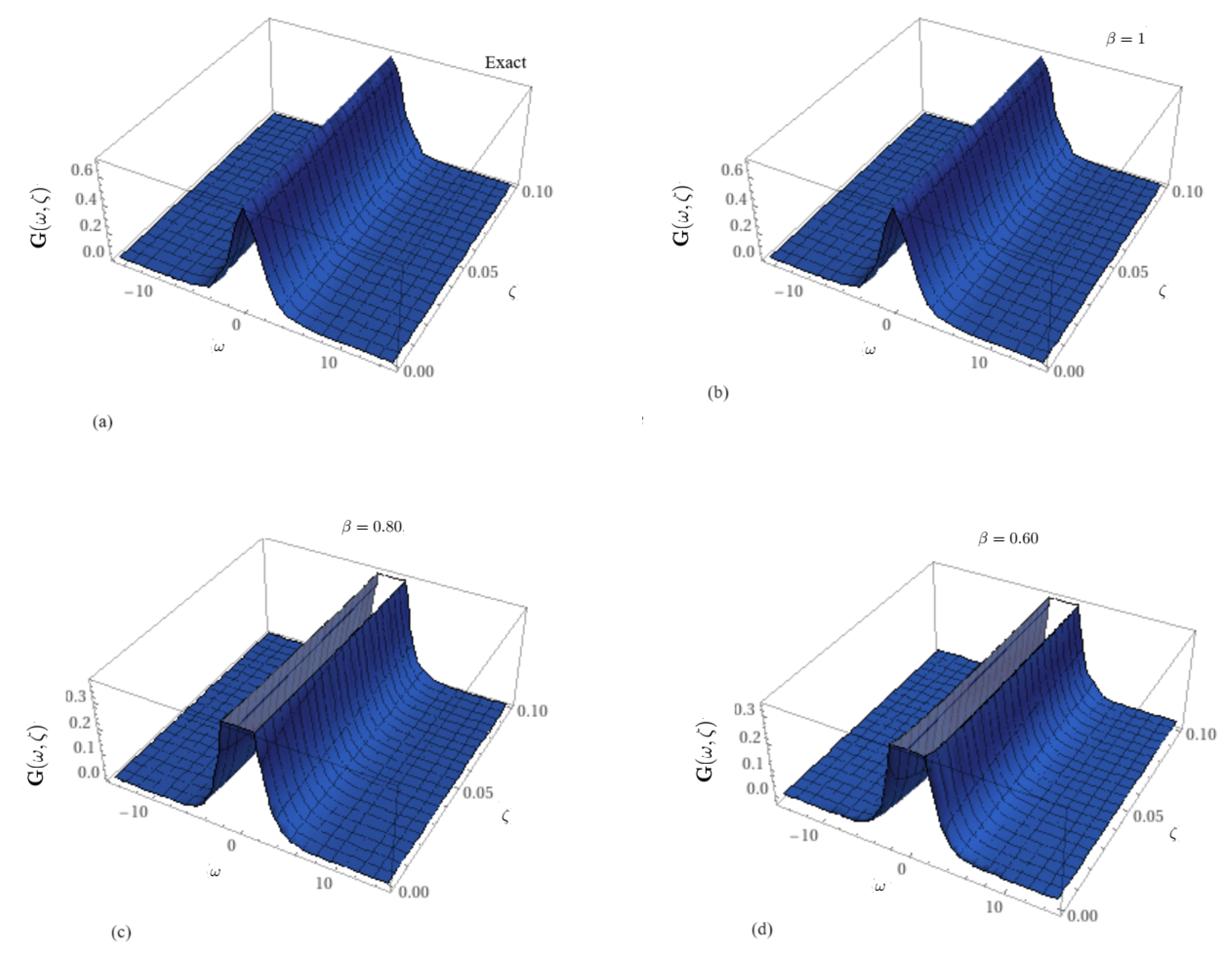
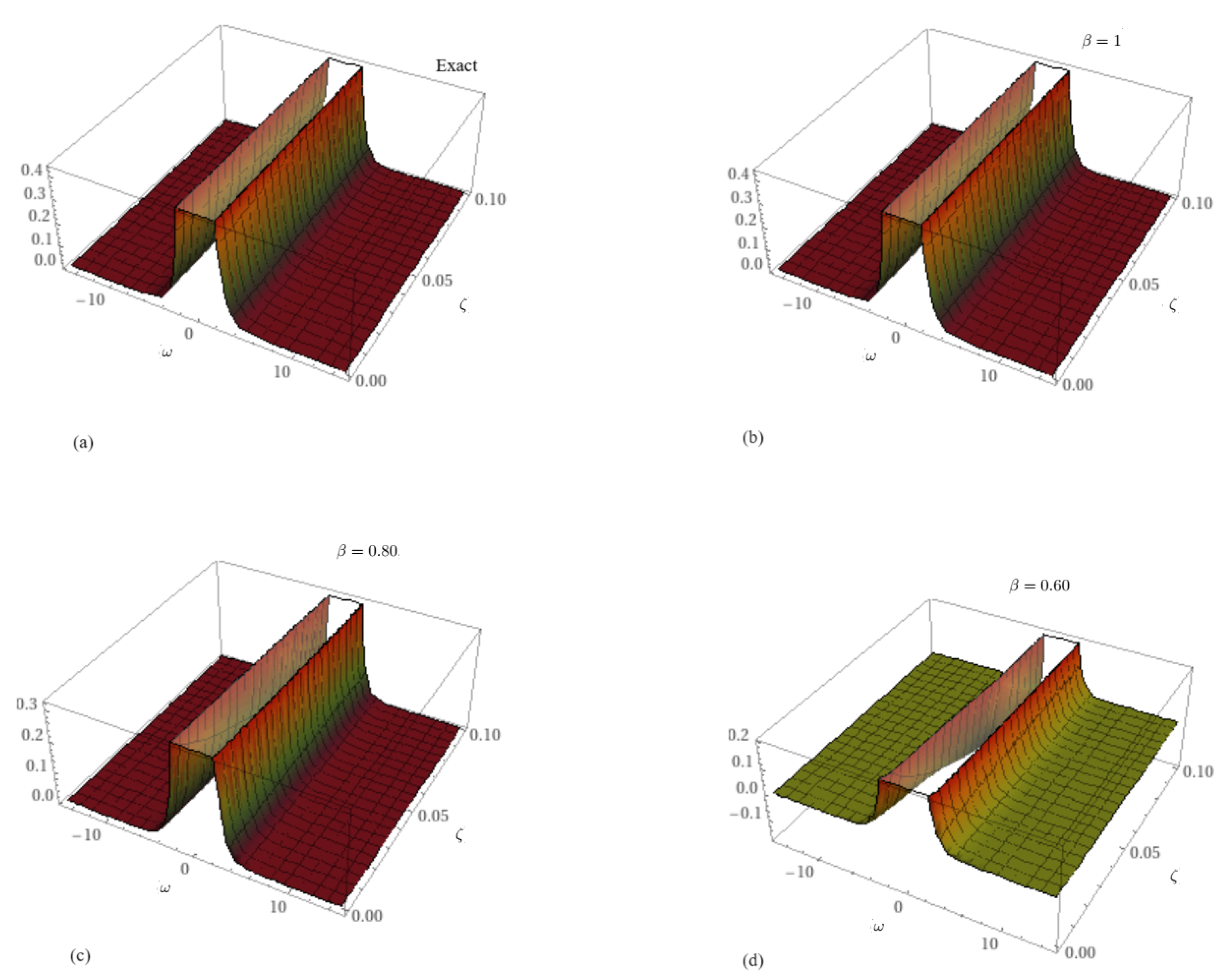
| Solution at 0.6 | Solution at 0.8 | at 1 | at 1 | Exact Solution | |
|---|---|---|---|---|---|
| (0.2, 0. 001) | 0.99027100 | 0.99020853 | 0.99016496 | 0.99016496 | 0.99016472 |
| (0.4, 0.001) | 0.96143650 | 0.96131642 | 0.96123266 | 0.96123266 | 0.96123245 |
| (0.6, 0.001) | 0.91569002 | 0.91552126 | 0.91540355 | 0.91540355 | 0.91540338 |
| (0.8, 0.001) | 0.85631323 | 0.85610742 | 0.85596388 | 0.85596388 | 0.85596376 |
| (0.2, 0.003) | 0.99061654 | 0.99047022 | 0.99036232 | 0.99036232 | 0.99036016 |
| (0.4, 0.003) | 0.96210071 | 0.96181945 | 0.96161204 | 0.96161204 | 0.96161013 |
| (0.6, 0.003) | 0.91662353 | 0.91622824 | 0.91593673 | 0.91593673 | 0.91593519 |
| (0.8, 0.003) | 0.85745160 | 0.85696957 | 0.85661408 | 0.85661408 | 0.85661298 |
| (0.2, 0.005) | 0.99093770 | 0.99072253 | 0.99055968 | 0.99055968 | 0.99055367 |
| (0.4, 0.005) | 0.96271807 | 0.96230447 | 0.96199141 | 0.96199141 | 0.96198610 |
| (0.6, 0.005) | 0.91749119 | 0.91690990 | 0.91646991 | 0.91646991 | 0.91646564 |
| (0.8, 0.005) | 0.85850969 | 0.85780082 | 0.85726428 | 0.85726428 | 0.85726123 |
| Solution at 0.6 | Solution at 0.8 | at 1 | at 1 | Exact Solution | |
|---|---|---|---|---|---|
| (0.2, 0.001) | 0.70051685 | 0.70038434 | 0.70029191 | 0.70029191 | 0.70015219 |
| (0.4, 0.001) | 0.68039479 | 0.68014006 | 0.67996239 | 0.67996239 | 0.67969398 |
| (0.6, 0.001) | 0.64827277 | 0.64791477 | 0.64766507 | 0.64766507 | 0.64728793 |
| (0.8, 0.001) | 0.60645870 | 0.60602213 | 0.60571762 | 0.60571762 | 0.60525778 |
| (0.2, 0.003) | 0.70124984 | 0.70093946 | 0.70071057 | 0.70071057 | 0.70029038 |
| (0.4, 0.003) | 0.68180379 | 0.68120716 | 0.68076716 | 0.68076716 | 0.67996104 |
| (0.6, 0.003) | 0.65025304 | 0.64941451 | 0.64879612 | 0.64879612 | 0.64766398 |
| (0.8, 0.003) | 0.60887356 | 0.60785100 | 0.60709690 | 0.60709690 | 0.60571685 |
| (0.2, 0.005) | 0.70193113 | 0.70147470 | 0.70112922 | 0.70112922 | 0.70042721 |
| (0.4, 0.005) | 0.68311342 | 0.68223603 | 0.68157193 | 0.68157193 | 0.68022689 |
| (0.6, 0.005) | 0.65209362 | 0.65086052 | 0.64992717 | 0.64992717 | 0.64803907 |
| (0.8, 0.005) | 0.61111810 | 0.60961437 | 0.60847618 | 0.60847618 | 0.60617523 |
| Error of [50] | Error | Error | ||
|---|---|---|---|---|
| −10 | 0.1 | 2.99039 | 1.6125789000 | 1.6125789000 |
| −10 | 0.2 | 2.33335 | 6.1317061000 | 6.1317061000 |
| −5 | 0.1 | 3.96592 | 4.3621745000 | 4.3621745000 |
| −5 | 0.2 | 0.0000338049 | 1.6588950200 | 1.6588950200 |
| 5 | 0.1 | 3.97592 | 4.8456311000 | 4.8456311000 |
| 5 | 0.2 | 0.0000378049 | 2.0470878500 | 2.0470878500 |
| 10 | 0.1 | 2.96039 | 1.7918592000 | 1.7918592000 |
| 10 | 0.2 | 2.37335 | 7.5713342000 | 7.5713342000 |
| Error of [50] | Error | Error | ||
|---|---|---|---|---|
| −10 | 0.1 | 2.18624 | 3.8791346860 | 3.8791346860 |
| −10 | 0.2 | 1.64872 | 7.8076524100 | 7.8076524100 |
| −5 | 0.1 | 2.88312 | 2.7814445650 | 2.7814445650 |
| −5 | 0.2 | 0.0000287824 | 5.5982968930 | 5.5982968930 |
| 5 | 0.1 | 2.98312 | 2.7371653580 | 2.7371653580 |
| 5 | 0.2 | 0.0000247824 | 5.4189576320 | 5.4189576320 |
| 10 | 0.1 | 2.09624 | 3.8173772900 | 3.8173772900 |
| 10 | 0.2 | 1.72872 | 7.5575220640 | 7.5575220640 |
| Solution at 0.6 | Solution at 0.8 | at 1 | at 1 | Exact Solution | |
|---|---|---|---|---|---|
| (0.2, 0.001) | 0.99027100 | 0.99020853 | 0.99016496 | 0.99016496 | 0.99016472 |
| (0.4, 0.001) | 0.96143650 | 0.96131642 | 0.96123266 | 0.96123266 | 0.96123245 |
| (0.6, 0.001) | 0.91569002 | 0.91552126 | 0.91540355 | 0.91540355 | 0.91540338 |
| (0.8, 0.001) | 0.85631323 | 0.85610742 | 0.85596388 | 0.85596388 | 0.85596376 |
| (0.2, 0.003) | 0.99061654 | 0.99047022 | 0.99036232 | 0.99036232 | 0.99036016 |
| (0.4, 0.003) | 0.96210071 | 0.96181945 | 0.96161204 | 0.96161204 | 0.96161013 |
| (0.6, 0.003) | 0.91662353 | 0.91622824 | 0.91593673 | 0.91593673 | 0.91593519 |
| (0.8, 0.003) | 0.85745160 | 0.85696957 | 0.85661408 | 0.85661408 | 0.85661298 |
| (0.2, 0.005) | 0.99093770 | 0.99072253 | 0.99055968 | 0.99055968 | 0.99055367 |
| (0.4, 0.005) | 0.96271807 | 0.96230447 | 0.96199141 | 0.96199141 | 0.96198610 |
| (0.6, 0.005) | 0.91749119 | 0.91690990 | 0.91646991 | 0.91646991 | 0.91646564 |
| (0.8, 0.005) | 0.85850969 | 0.85780082 | 0.85726428 | 0.85726428 | 0.85726123 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, A.B.M.; Alhawael, G. Novel Computations of the Time-Fractional Coupled Korteweg–de Vries Equations via Non-Singular Kernel Operators in Terms of the Natural Transform. Symmetry 2023, 15, 2010. https://doi.org/10.3390/sym15112010
Alzahrani ABM, Alhawael G. Novel Computations of the Time-Fractional Coupled Korteweg–de Vries Equations via Non-Singular Kernel Operators in Terms of the Natural Transform. Symmetry. 2023; 15(11):2010. https://doi.org/10.3390/sym15112010
Chicago/Turabian StyleAlzahrani, Abdulrahman B. M., and Ghadah Alhawael. 2023. "Novel Computations of the Time-Fractional Coupled Korteweg–de Vries Equations via Non-Singular Kernel Operators in Terms of the Natural Transform" Symmetry 15, no. 11: 2010. https://doi.org/10.3390/sym15112010




