Improved Gorilla Troops Optimizer-Based Fuzzy PD-(1+PI) Controller for Frequency Regulation of Smart Grid under Symmetry and Cyber Attacks
Abstract
:1. Introduction
- An improved adaptation of GTO, i.e., iGTO, was developed by changing some parameters of the GTO algorithm and introducing sine-cosine-based scaling factors to control the movement of gorillas during the search procedure.
- The effectiveness of iGTO is verified over GTO, GJO, GWO, GSA, PSO, TLBO and ALO techniques using numerous benchmark functions.
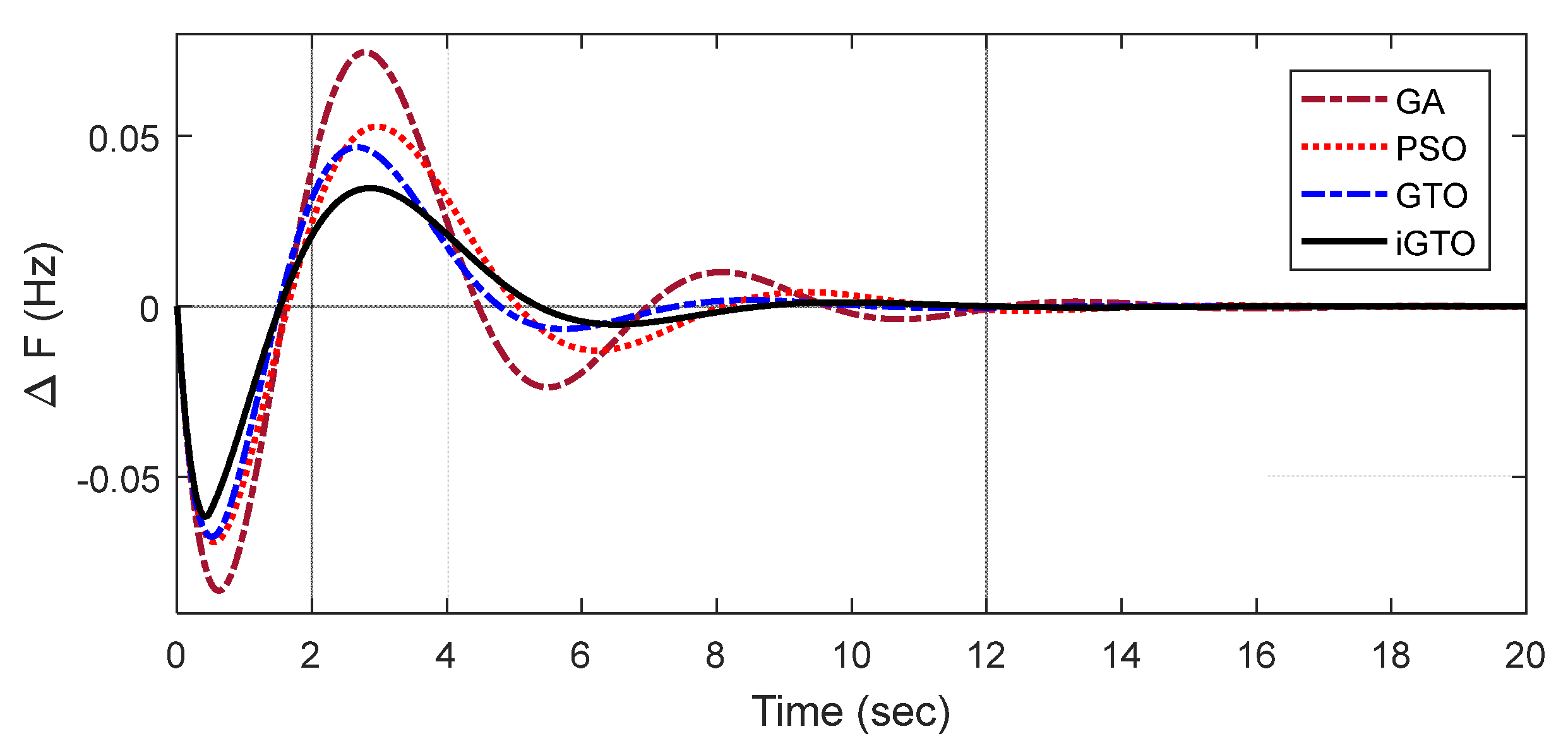
- The effectiveness of iGTO in engineering problems is also demonstrated over GTO, PSO and Genetic Algorithm (GA).
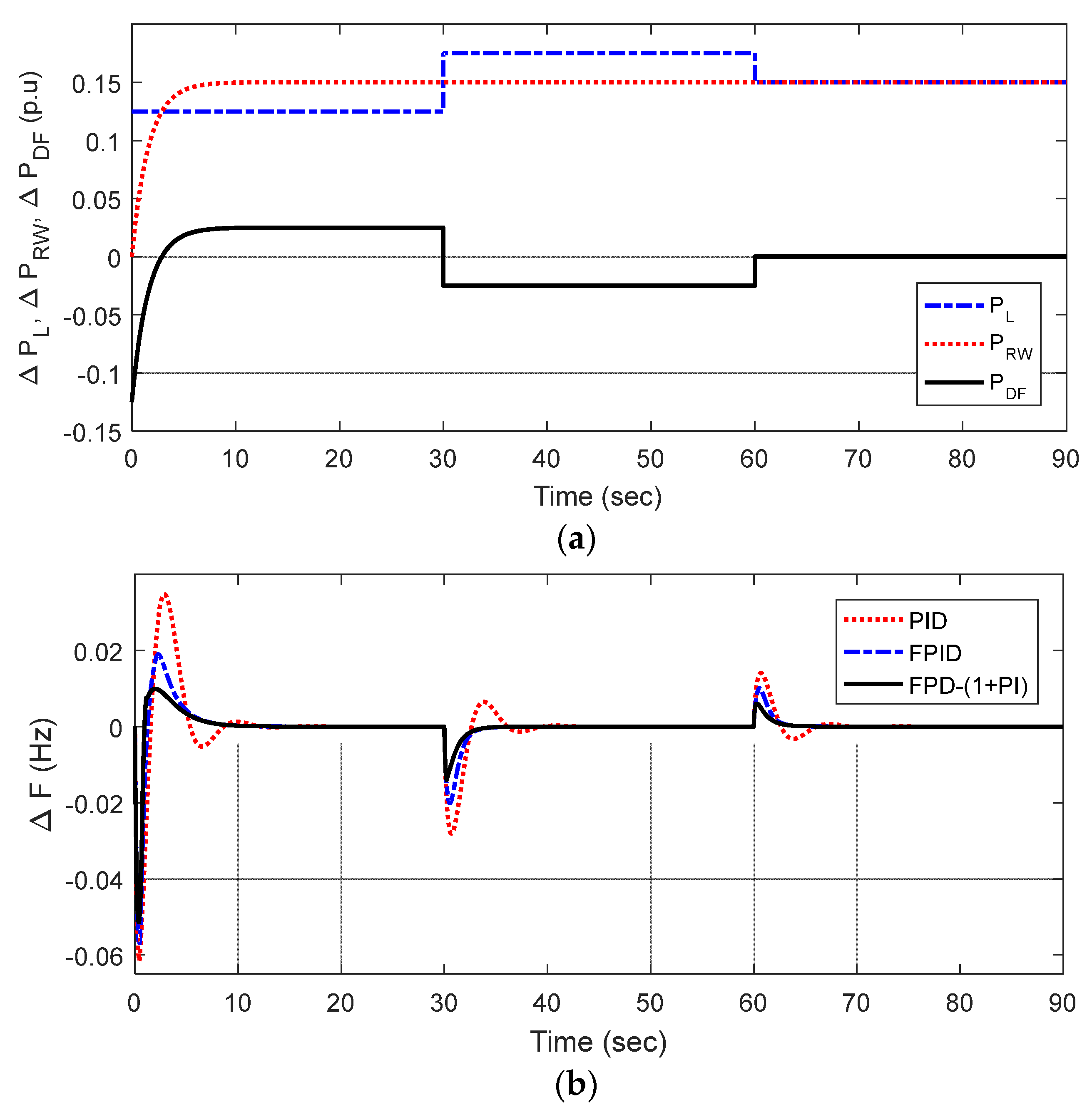
- Furthermore, the iGTO is used to design a fuzzy PD-(1+PI) i.e., FPD-(1+PI) structure for the frequency control of a smartgrid system and the superiority of FPD-(1+PI) over the FPID and PID structure is demonstrated.
- The effectiveness of the projected frequency control scheme under various cyberattacks, like denial of service (DoS) and data transmission delay, is investigated.
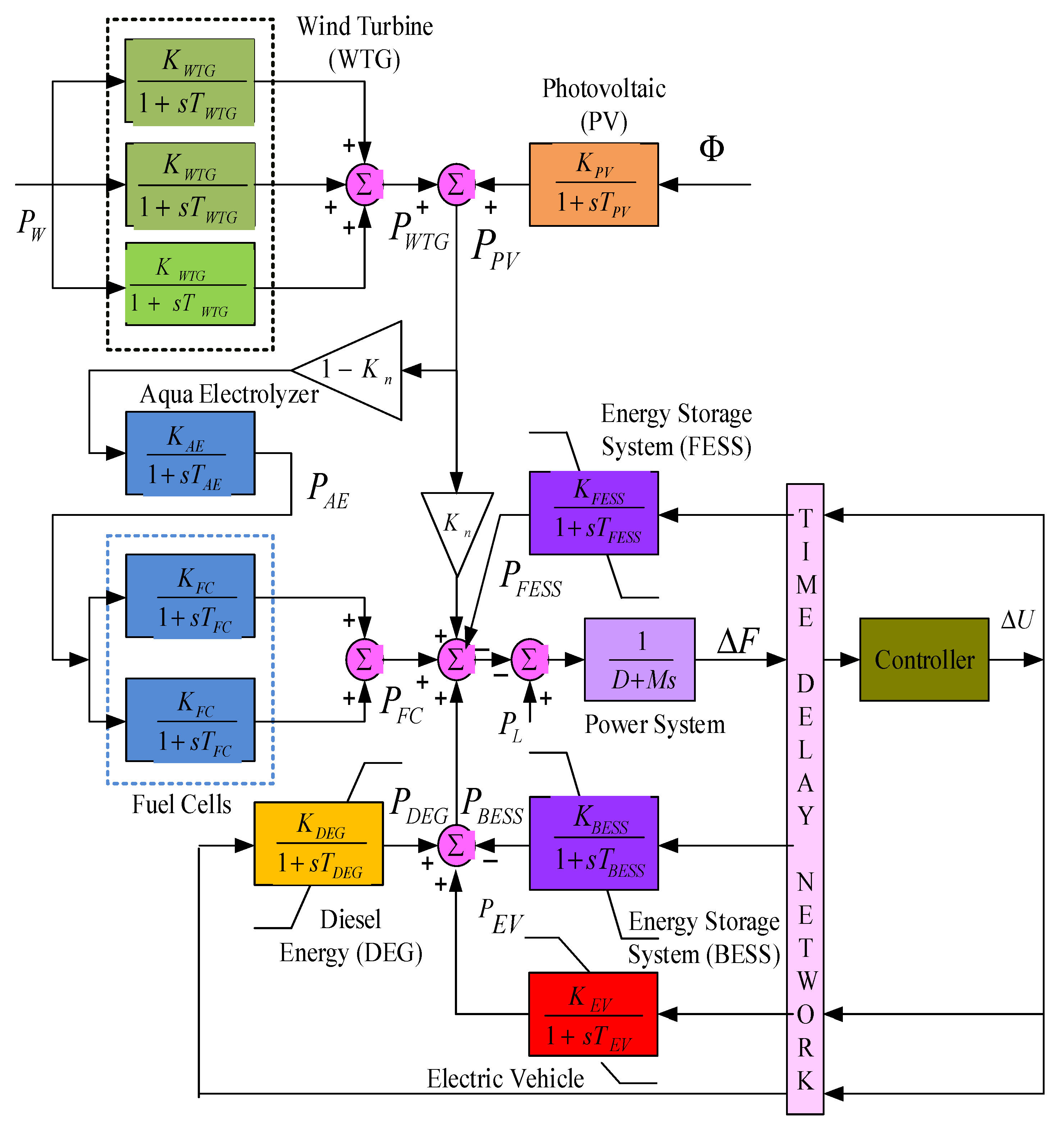
2. Test System
2.1. Modeling of Components
2.1.1. Wind Turbine
2.1.2. Photovoltaic Cell
2.1.3. Aquaelectrolyzer
2.1.4. Diesel Engine Generator
2.1.5. Energy Storage System Modelling
2.1.6. Electric Vehicle
2.1.7. Power System
3. Controller Structure and Objective Function
4. Improved Gorilla Troops Optimizer
4.1. Gorilla Troops Optimizer (GTO)
4.1.1. Initialization Phase
4.1.2. Exploration Phase
4.1.3. Exploitation Phase
4.2. Improved Gorilla Troops Optimizer (iGTO)
5. Results and Discussions
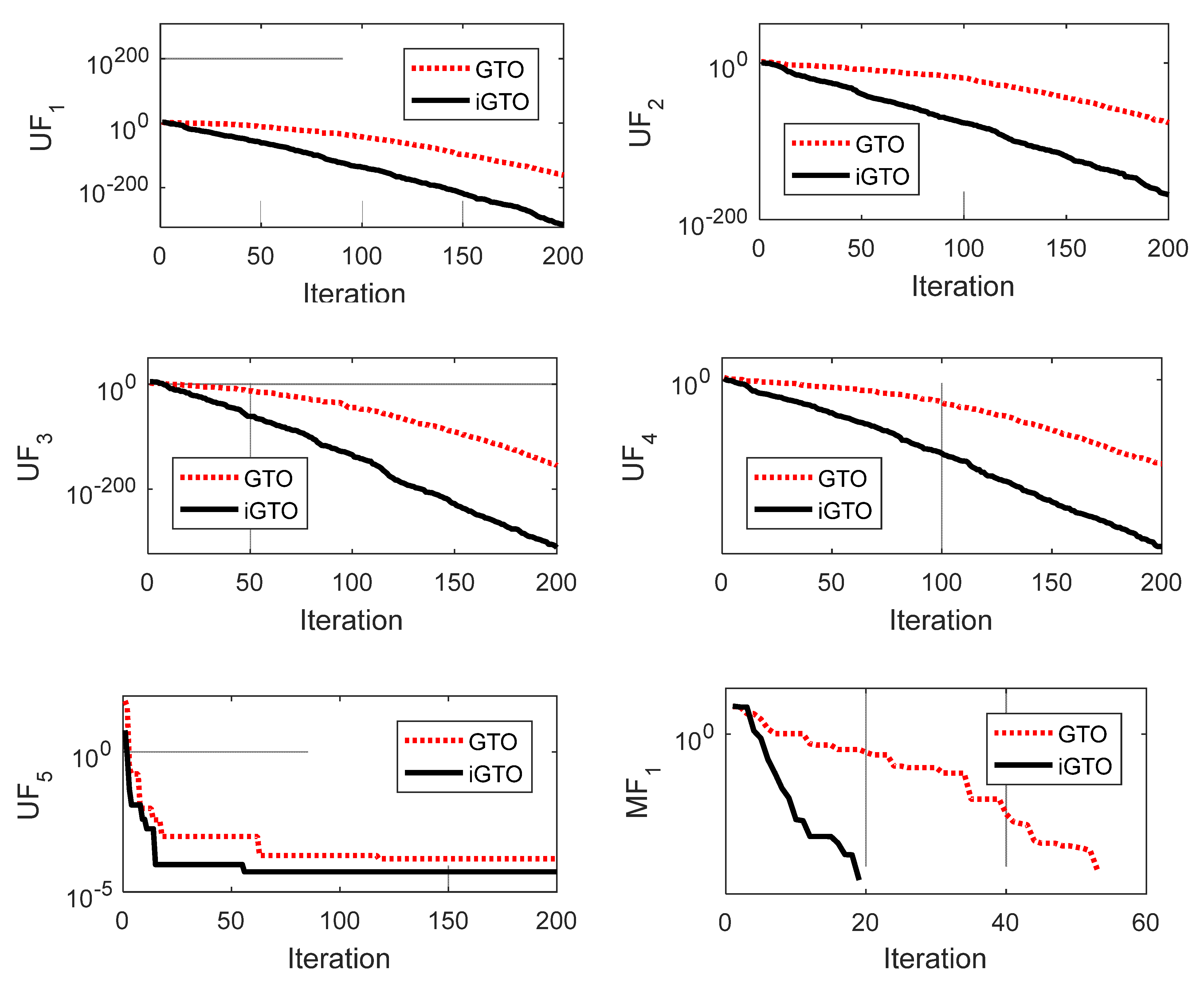
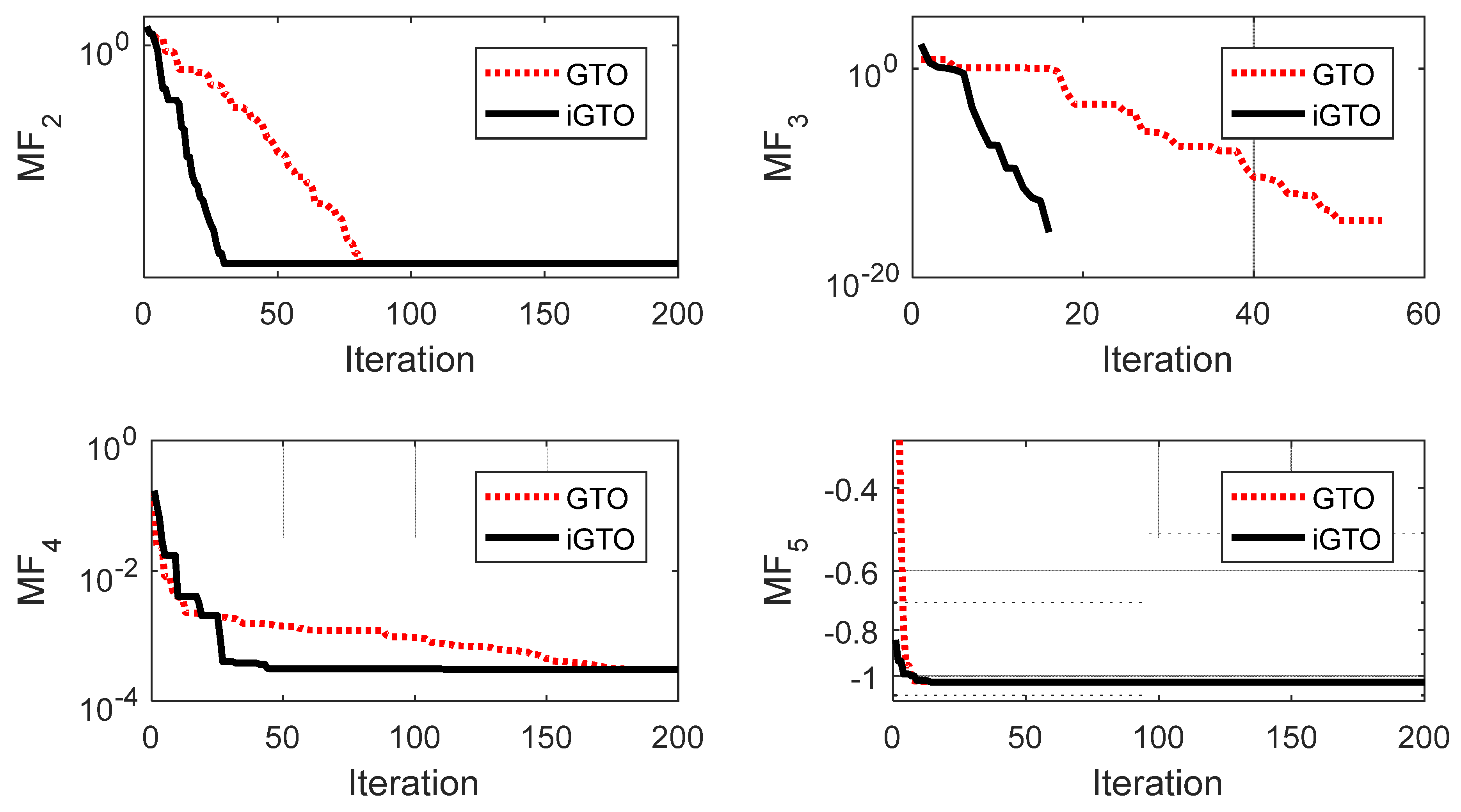
5.1. Assessment of iGTO
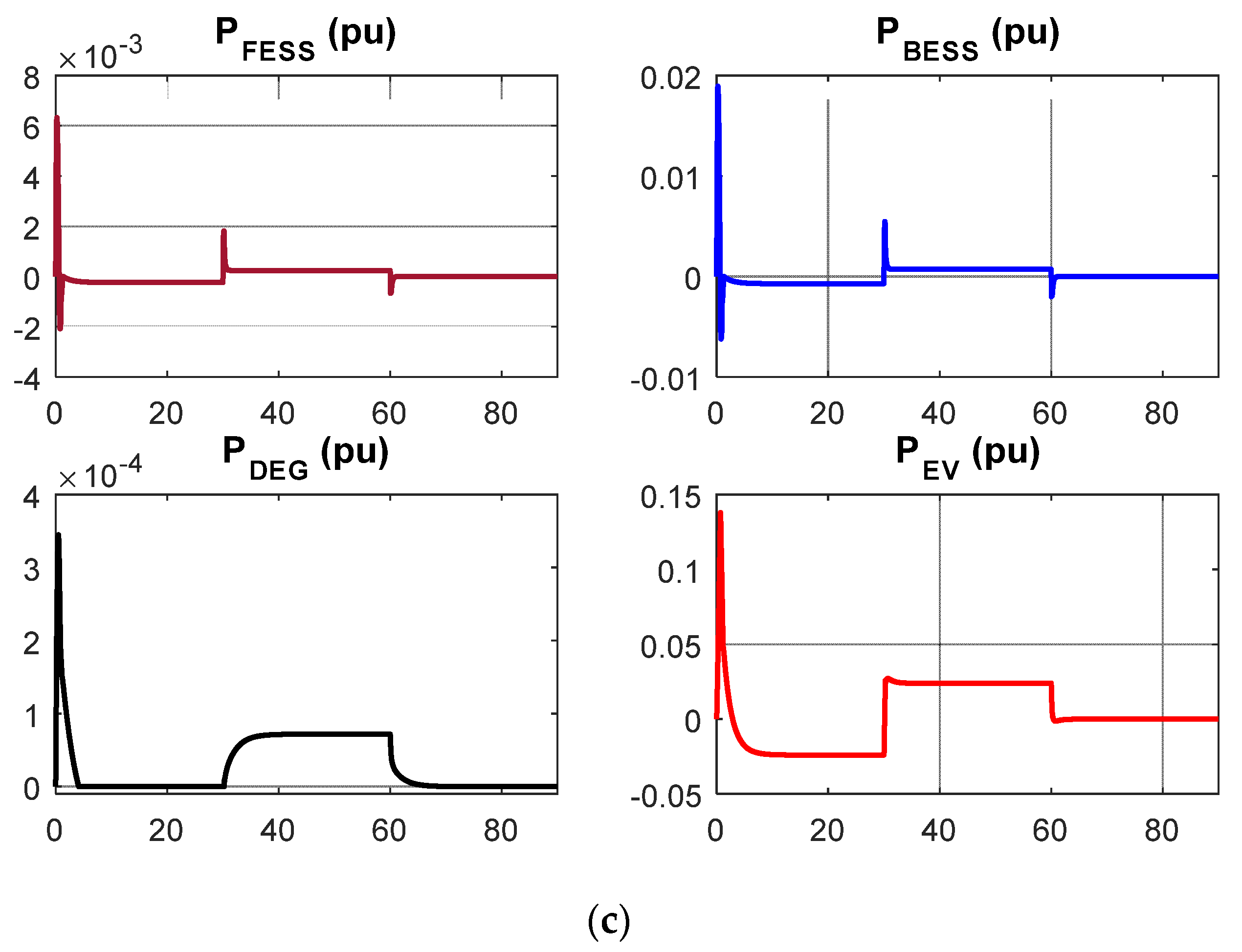
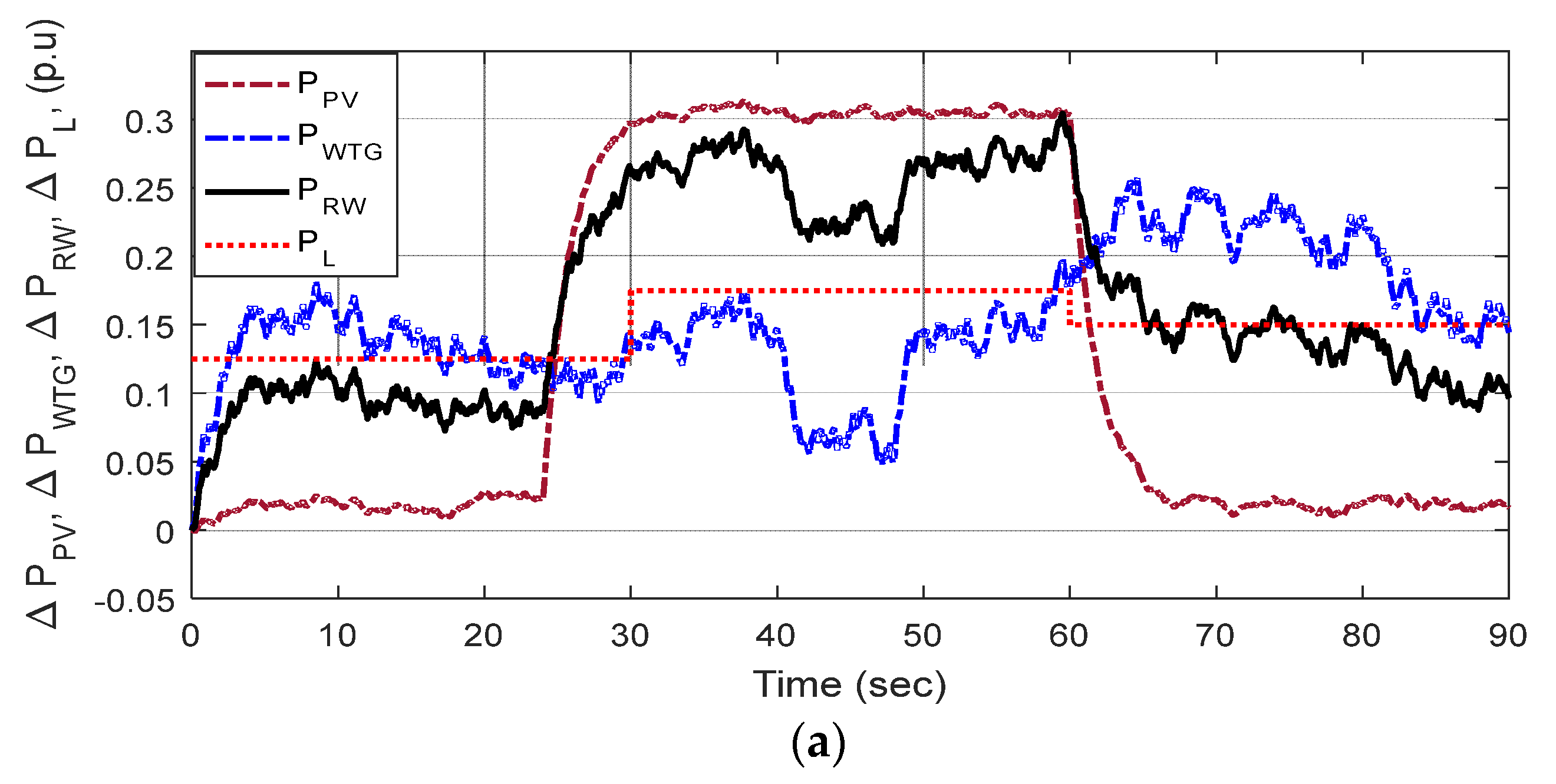
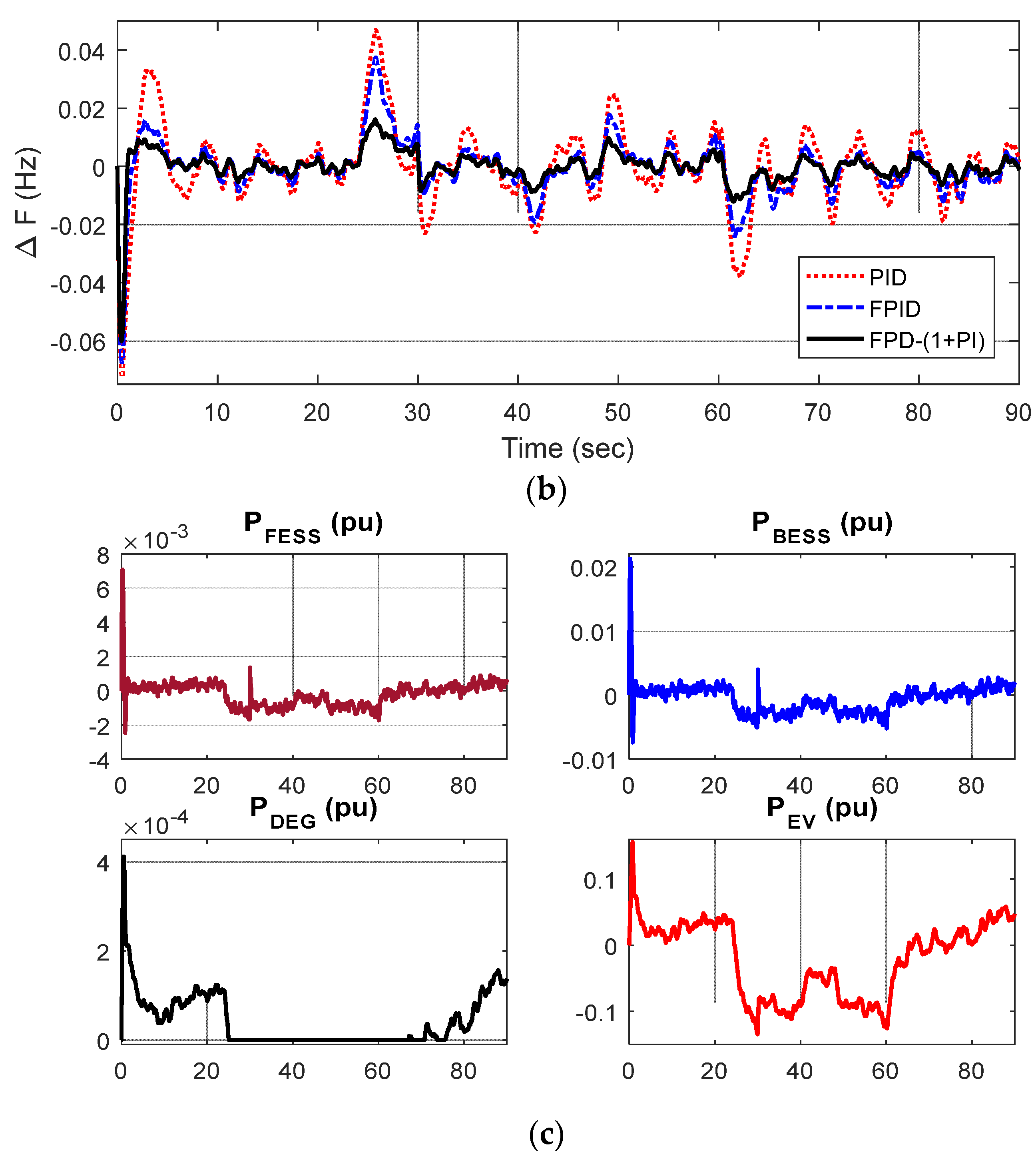
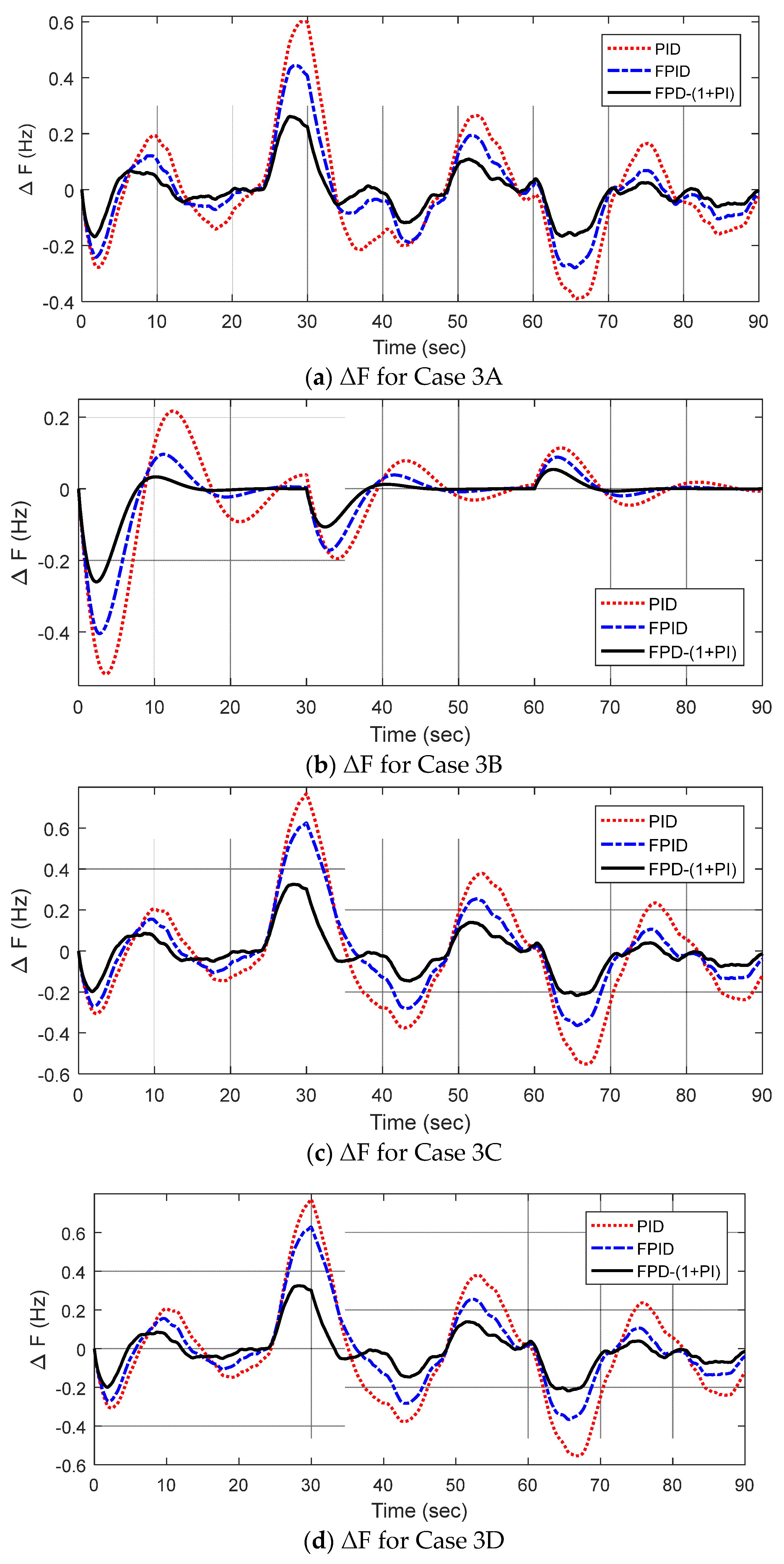
5.2. Application of iGTO for Controller Design
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- John, T.; Lam, S.P. Voltage and frequency control during microgrid islanding in a multi-area multi-microgrid system. IET Gener. Transm. Distrib. 2017, 11, 1502–1512. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Khooban, M.-H. Secondary Load Frequency Control of Time-Delay Stand-Alone Microgrids With Electric Vehicles. IEEE Trans. Ind. Electron. 2017, 65, 7416–7422. [Google Scholar] [CrossRef]
- Ahmed, M.; Meegahapola, L.; Vahidnia, A.; Datta, M. Stability and Control Aspects of Microgrid Architectures—A Comprehensive Review. IEEE Access 2020, 8, 144730–144766. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. Secondary load frequency control for multi-microgrids: HiL real-time. Soft Comput. 2019, 23, 5785–5798. [Google Scholar] [CrossRef]
- Nayak, P.C.; Prusty, U.C.; Prusty, R.C.; Panda, S. Imperialist competitive algorithm optimized cascade controller for load frequency control of multi-microgrid system. Energy Sour. Part A Recover. Util. Environ. Eff. 2021, 1–23. [Google Scholar] [CrossRef]
- Pannala, S.; Patari, N.; Srivastava, A.K.; Padhy, N.P. Effective Control and Management Scheme for Isolated and Grid Connected DC Microgrid. IEEE Trans. Ind. Appl. 2020, 56, 6767–6780. [Google Scholar] [CrossRef]
- Wu, X.; Xu, Y.; He, J.; Wang, X.; Vasquez, J.C.; Guerrero, J.M. Pinning-Based Hierarchical and Distributed Cooperative Control for AC Microgrid Clusters. IEEE Trans. Power Electron. 2020, 35, 9865–9885. [Google Scholar] [CrossRef]
- Pham, T.N.; Trinh, H.; Van Hien, L. Load Frequency Control of Power Systems With Electric Vehicles and Diverse Transmission Links Using Distributed Functional Observers. IEEE Trans. Smart Grid 2016, 7, 238–252. [Google Scholar] [CrossRef]
- Nayak, P.C.; Bisoi, S.; Prusty, R.C.; Panda, S. Performance Analysis of PDF+(1+PI) Controller for Load Frequency Control of the Multi Microgrid System Using Genetic Algorithm. In Proceedings of the International Conference on Information Technology (ICIT), Amman, Jordan, 9–11 April 2019; Volume 18, pp. 448–453. [Google Scholar]
- Khadanga, R.K.; Kumar, A.; Panda, S. Frequency control in hybrid distributed power systems via type-2 fuzzy PID controller. IET Renew. Power Gener. 2020, 15, 1–18. [Google Scholar] [CrossRef]
- Mu, C.; Zhang, Y.; Jia, H.; He, H. Energy-Storage-Based Intelligent Frequency Control of MicrogridWith Stochastic Model Uncertainties. IEEE Trans. Smart Grid 2020, 11, 1748–1758. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.; Yu, H.; Wang, Y.; Qi, C.; Yang, J.; Song, F. Optimal operation of microgrid with multi-energy complementary based on moth flame optimization algorithm. Energy Sour. Part A Recover. Util. Environ. Effects 2019, 42, 785–806. [Google Scholar] [CrossRef]
- Zhao, H.; Hong, M.; Lin, W.; Loparo, K.A. Voltage and Frequency Regulation of MicrogridWith Battery Energy Storage Systems. IEEE Trans. Smart Grid 2017, 10, 414–424. [Google Scholar] [CrossRef]
- Kumar, A.; Khadanga, R.K.; Panda, S. Reinforced modified equilibrium optimization technique-based MS-PID frequency regulator for a hybrid power system with renewable energy sources. Soft Comput. 2021, 26, 5437–5455. [Google Scholar] [CrossRef]
- Bevrani, H.; Daneshmand, P.R. Fuzzy Logic-Based Load-Frequency Control Concerning High Penetration of Wind Turbines. IEEE Syst. J. 2011, 6, 173–180. [Google Scholar] [CrossRef]
- Khadanga, R.K.; Kumar, A.; Panda, S. A novel sine augmented scaled sine cosine algorithm for frequency control issues of a hybrid distributed two-area power system. Neural Comput. Appl. 2021, 33, 12791–12804. [Google Scholar] [CrossRef]
- Nayak, P.; Prusty, R.; Panda, S. Grasshopper optimization algorithm optimized multistage controller for automatic generation control of a power system with FACTS devices. Prot. ControlModern Power Syst. 2021, 6, 1–15. [Google Scholar]
- Murugan, S.; Jaishankar, M.; Premkumar, K. Hybrid DC–AC Microgrid Energy Management System Using an Artificial Gorilla Troops Optimizer Optimized Neural Network. Energies 2022, 15, 8187. [Google Scholar] [CrossRef]
- Li, Z.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Bilevel Model for Analyzing Coordinated Cyber-Physical Attacks on Power Systems. IEEE Trans. Smart Grid 2015, 7, 2260–2272. [Google Scholar] [CrossRef]
- Sekar, K.; Arasan, E.; Chandrasekaran, K. Grey Wolf Optimization and Fed Fast Terminal Sliding Mode Controllers Based on Interleaved Boost Converters for Symmetric PV Systems under Asymmetric Partial Shading. Symmetry 2023, 15, 1339. [Google Scholar] [CrossRef]
- Govindaraju, S.K.; Sivalingam, R.; Panda, S.; Sahu, P.R.; Padmanaban, S. Frequency Control of Power System with Distributed Sources by Adaptive Type 2 Fuzzy PID Controller. Electr. Power Compon. Syst. 2023, 1–22. [Google Scholar] [CrossRef]
- Raghuraman, S.; Subramani, C.; Dash, S. A modified whale optimization algorithm-based adaptive fuzzy logic PID controller for load frequency control of autonomous power generation systems. Automatika 2017, 58, 410–421. [Google Scholar]
- Raghuraman, S.; Subramani, C.; Dash, S. A hybrid stochastic fractal search and local unimodal sampling based multistage PDF plus (1+PI) controller for automatic generation control of power systems. J. Franklin Inst. 2017, 354, 4762–4783. [Google Scholar]
- Khokhar, B.; Dahiya, S.; Parmar, K.S. Load frequency control of a microgrid employing a 2D Sine Logistic map based chaotic sine cosine algorithm. Appl. Soft Comput. 2021, 109, 107564. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Diab, A.E.G. Design of cascaded controller based on coyote optimizer for load frequency control in multi-area power systems with renewable sources. Control Eng. Pract. 2022, 121, 105058. [Google Scholar] [CrossRef]
- Shayeghi, H.; Rahnama, A.; Alhelou, H.H. Frequency control of fully-renewable interconnected microgrid using fuzzy cascade controller with demand response program considering. Energy Rep. 2021, 7, 6077–6094. [Google Scholar] [CrossRef]
- Irudayaraj, A.X.R.; Wahab, N.I.A.; Umamaheswari, M.G.; Radzi, M.A.M.; Sulaiman, N.B.; Veerasamy, V.; Prasanna, S.C.; Ramachandran, R. A Matignon’s Theorem Based Stability Analysis of Hybrid Power System for Automatic Load Frequency Control Using Atom Search Optimized FOPID Controller. IEEE Access 2020, 8, 168751–168772. [Google Scholar] [CrossRef]
- Padhy, S.; Panda, S. Application of a simplified Grey Wolf optimization technique for adaptive fuzzy PID controller design for frequency regulation of a distributed power generation system. Prot. Control Mod. Power Syst. 2021, 6, 1–6. [Google Scholar] [CrossRef]
- Sharma, M.; Dhundhara, S.; Arya, Y.; Prakash, S. Frequency stabilization in deregulated energy system using coordinated operation of fuzzy controller and redox flow battery. Int. J. Energy Res. 2020, 45, 7457–7475. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Fractional Order AGC for Distributed Energy Resources Using Robust Optimization. IEEE Trans. Smart Grid 2015, 7, 2175–2186. [Google Scholar] [CrossRef]

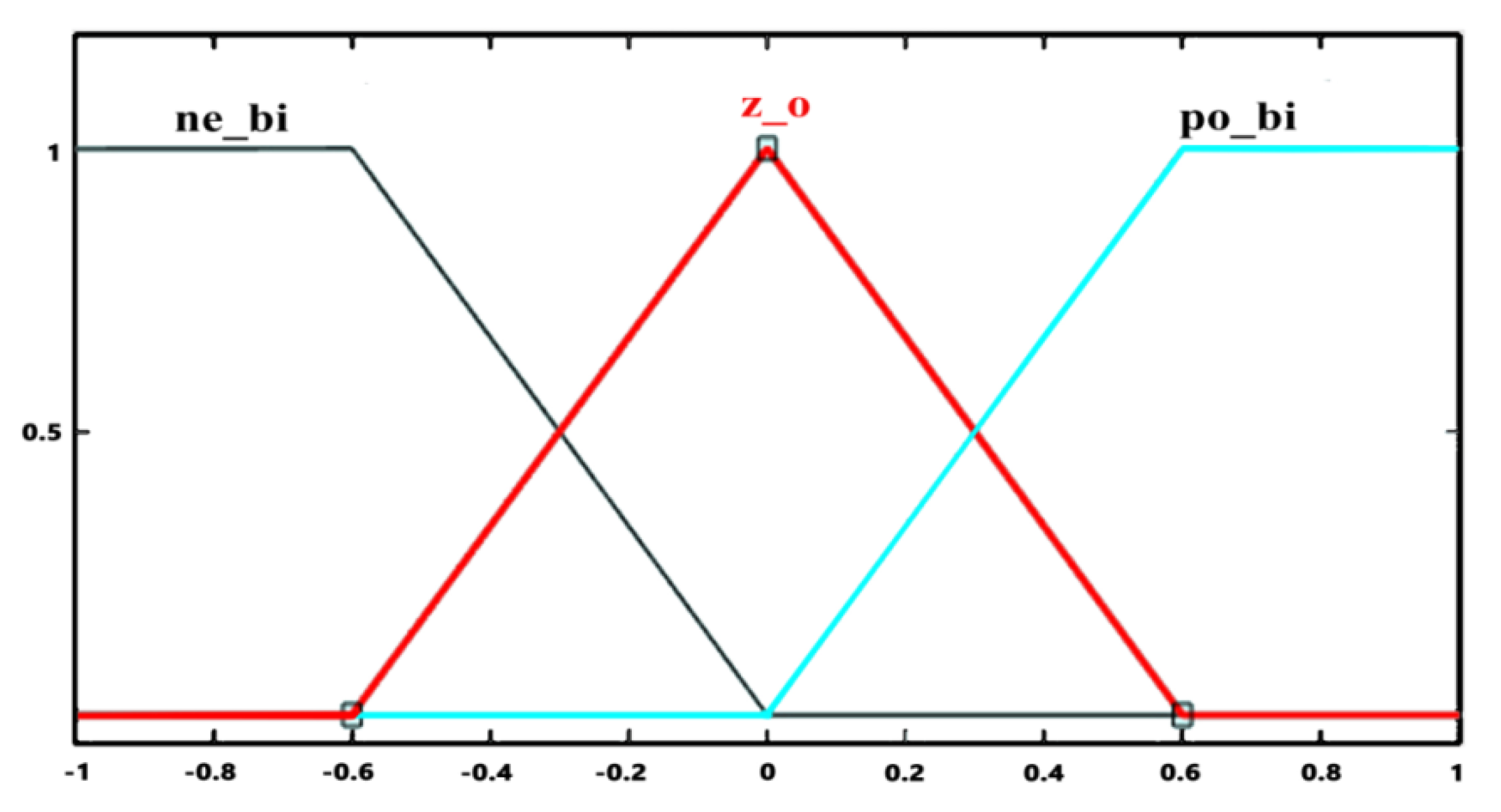

| e\e* | ne_bi | z_o | po_bi |
| ne_bi | ne_bi | ne_bi | z_o |
| z_o | ne_bi | z_o | po_bi |
| po_bi | z_o | po_bi | po_bi |
| Function Name | Expression | Range | D |
|---|---|---|---|
| Sphere F1 | [−100, 100] | 30 | |
| Schwefel-1 F2 | [−10, 10] | 30 | |
| Schwefel-2 F3 | [−100, 100] | 30 | |
| Schwefel-3 F4 | [−100, 100] | 30 | |
| Quartic F7 | [−1.28, 1.28] | 30 | |
| Generalized Rastrigin F9 | [−5.12, 5.12] | 30 | |
| Ackley F10 | [−32, 32] | 30 | |
| Generalized Griewank F11 | [−600, 600] | 30 | |
| Kowalik F15 | [−5, 5] | 4 | |
| Six-Hump Camel-Back F16 | [−5, 5] | 2 |
| Function | Indices | iGTO | GTO | GJO | GWO | GSA | PSO | TLBO | ALO |
|---|---|---|---|---|---|---|---|---|---|
(Min = 0) | Best | 0 | 1.94 × 10−170 | 2.83 × 10−46 | 1.22 × 10−23 | 1.57 × 10−09 | 1.63 × 10−10 | 2.59 × 10−43 | 1.23 × 10−6 |
| Worst | 2.16 × 10−300 | 2.07 × 10−147 | 6.4 × 10−40 | 2.97 × 10−20 | 1.53 × 10−06 | 2.09 × 10−07 | 5.1 × 10−41 | 2.72 × 10−5 | |
| Ave. | 7.23 × 10−302 | 6.91 × 10−149 | 6.3 × 10−41 | 3.37 × 10−21 | 7.21 × 10−09 | 3.42 × 10−08 | 1.03 × 10−41 | 9.09 × 10−6 | |
| SD | 0 | 3.77 × 10−148 | 1.51 × 10−40 | 6.45 × 10−21 | 3.78 × 10−09 | 5.35 × 10−08 | 1.47 × 10−41 | 7.74 × 10−6 | |
(Min = 0) | Best | 1.64 × 10−178 | 6.68 × 10−85 | 2.28 × 10−25 | 3.75 × 10−14 | 1.66 × 10−4 | 1.5 × 10−5 | 1.38 × 10−22 | 7.28 × 10−4 |
| Worst | 9.92 × 10−160 | 4.21 × 10−76 | 2.17 × 10−22 | 2.99 × 10−13 | 4.45 × 10−4 | 7.56 × 10−4 | 7.83 × 10−21 | 33.87 | |
| Ave. | 5.47 × 10−161 | 1.94 × 10−77 | 2.23 × 10−23 | 6.12 × 10−13 | 2.42 × 10−4 | 1.18 × 10−4 | 1.53 × 10−21 | 5.08 | |
| SD | 1.89 × 10−160 | 7.76 × 10−77 | 4.3 × 10−23 | 7.08 × 10−13 | 5.91 × 10−5 | 1.14 × 10−4 | 1.45 × 10−21 | 7.81 | |
(Min = 0) | Best | 0 | 1.74 × 10−165 | 3.69 × 10−26 | 8.64 × 10−11 | 1.85 × 10−2 | 2.66 × 10−3 | 2.13 × 10−19 | 0.701 |
| Worst | 6.44 × 10−294 | 3.27 × 10−144 | 1.6 × 10−19 | 3.38 × 10−7 | 37.29 | 1.41 × 10−1 | 1.94 × 10−16 | 1551.35 | |
| Ave. | 2.23 × 10−296 | 2.26 × 10−146 | 1.51 × 10−20 | 2.4 × 10−8 | 7.11 | 2.43 × 10−2 | 2.99 × 10−17 | 294.37 | |
| SD | 0 | 7.39 × 10−145 | 3.53 × 10−20 | 6.89 × 10−8 | 10.01 | 2.89 × 10−2 | 4.9 × 10−17 | 353.97 | |
(Min = 0) | Best | 2.42 × 10−170 | 2.62 × 10−83 | 4.93 × 10−18 | 5.52 × 10−8 | 2.93 × 10−5 | 7.06 × 10−4 | 1.77 × 10−18 | 9.39 × 10−3 |
| Worst | 6.62 × 10−150 | 5.89 × 10-75 | 4.66 × 10-15 | 8.25 × 10-6 | 8.95 × 10-5 | 3.74 × 10-2 | 3.51 × 10-17 | 14.68 | |
| Ave. | 2.21 × 10−151 | 2.24 × 10−76 | 1.28 × 10−15 | 1.08 × 10−6 | 6.25 × 10−5 | 1.01 × 10−2 | 7.68 × 10−18 | 3.26 | |
| SD | 1.21 × 10−150 | 1.07 × 10−75 | 1.27 × 10−15 | 1.64 × 10−6 | 1.56 × 10−5 | 8.42 × 10−3 | 7.04 × 10−18 | 3.62 | |
(Min = 0) | Best | 1.62 × 10−06 | 1.64 × 10−05 | 6.73 × 10−05 | 2.35 × 10−4 | 2.85 × 10−3 | 4.79 × 10−3 | 3.41 × 10−3 | 1.59 × 10−2 |
| Worst | 3.15 × 10−04 | 7.27 × 10−04 | 2.85 × 10−3 | 4.69 × 10−3 | 3.67 × 10−2 | 3.55 × 10−2 | 3.162 × 10−3 | 1.75 × 10−1 | |
| Ave. | 1.21 × 10−04 | 2.07 × 10−04 | 7.77 × 10−4 | 1.37 × 10−3 | 1.58 × 10−2 | 1.81 × 10−2 | 1.71 × 10−3 | 6.65 × 10−2 | |
| SD | 9.96 × 10−05 | 1.68 × 10−04 | 0.000657 | 1.06 × 10−3 | 7.91 × 10−3 | 7.87 × 10−3 | 7.19 × 10−4 | 3.68 × 10−2 | |
(Min = 0) | Best | 0 | 0 | 0 | 0 | 0.994961 | 2.992063 | 0.013259 | 7.95967 |
| Worst | 0 | 0 | 18.13774 | 9.140608 | 14.92438 | 16.24605 | 14.22896 | 49.74783 | |
| Ave. | 0 | 0 | 0.604591 | 2.653841 | 7.429027 | 8.659233 | 5.500317 | 23.74631 | |
| SD | 0 | 0 | 3.311483 | 2.834879 | 3.404116 | 3.173189 | 3.437944 | 11.01983 | |
(Min = 0) | Best | 8.88 × 10−16 | 8.88 × 10−16 | 4.44 × 10−15 | 2.08 × 10−12 | 8.09 × 10−5 | 1.07 × 10−5 | 4.44 × 10−15 | 5.57 × 10−4 |
| Worst | 8.88 × 10−16 | 8.88 × 10−16 | 7.99 × 10−15 | 1 × 10−10 | 1.88 × 10−4 | 4.44 × 10−4 | 7.54 × 10−15 | 5.191245 | |
| Ave. | 8.88 × 10−16 | 8.88 × 10−16 | 4.8 × 10−15 | 2 × 10−11 | 1.22 × 10−4 | 1.51 × 10−4 | 4.9 × 10−15 | 1.389097 | |
| SD | 0 | 0 | 1.08 × 10−15 | 2.13 × 10−11 | 2.7 × 10−5 | 1.15 × 10−4 | 1.9 × 10−15 | 1.345589 | |
(Min = 0) | Best | 0 | 0 | 0 | 0 | 2.16691 | 6.15 × 10−2 | 0 | 5.52 × 10−2 |
| Worst | 0 | 0 | 0.173643 | 0.101945 | 11.33721 | 3.00736 | 9.65 × 10−2 | 0.32496 | |
| Ave. | 0 | 0 | 1.32 × 10−2 | 2.98 × 10−2 | 5.60349 | 0.9394 | 1.65 × 10−2 | 0.179803 | |
| SD | 0 | 0 | 3.9472 × 10−2 | 0.026988 | 2.647036 | 0.760557 | 2.3714 × 10−2 | 7.5028 × 10−2 | |
(Min = 3 × 10−4) | Best | 3.074 × 10−04 | 3.075 × 10−04 | 3.13 × 10−4 | 3.38 × 10−4 | 9.23 × 10−4 | 3.43 × 10−4 | 3.07 × 10−4 | 6.27 × 10−4 |
| Worst | 5.84 × 10−04 | 1.51 × 10−3 | 2.04 × 10−2 | 2.10 × 10−2 | 1.40 × 10−2 | 1.35 × 10−3 | 2.04 × 10−2 | 2.11 × 10−2 | |
| Ave. | 3.24 × 10−04 | 3.68 × 10−04 | 1.40 × 10−3 | 2.65 × 10−3 | 3.42 × 10−3 | 8.74 × 10−4 | 1.76 × 10−3 | 2.66 × 10−3 | |
| SD | 5.14 × 10−05 | 2.32 × 10−04 | 1.47 × 10−4 | 6.08 × 10−3 | 3.24 × 10−3 | 1.91 × 10−4 | 5.06 × 10−3 | 3.67 × 10−3 | |
(Min = −1.0316) | Best | −1.0326 | −1.0326 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 |
| Worst | −1.0326 | −1.0326 | −1.03162 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | |
| Ave. | −1.0326 | −1.0326 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | |
| SD | 0 | 0 | 1.63 × 10−6 | 1.28 × 10−7 | 1.56 × 10−10 | 5.38 × 10−16 | 5.61 × 10−16 | 3.17 × 10−13 |
| Method/Controller | K1 | K2 | Kp | KI | KD | Kpp | J Value |
|---|---|---|---|---|---|---|---|
| GA:PID | - | - | 1.2919 | 1.1205 | 0.4004 | - | 4.3437 |
| PSO:PID | - | - | 1.1929 | 1.1781 | 0.8990 | - | 3.3486 |
| GTO:PID | - | - | 1.2845 | 0.9990 | 0.8657 | - | 3.2751 |
| iGTO:PID | - | - | 1.6751 | 1.4743 | 1.3569 | - | 2.2011 |
| iGTO:FPID | 1.5116 | 1.8655 | 1.1764 | 1.5499 | 0.0683 | - | 1.1935 |
| iGTO:FPD-(1+PI) | 1.3505 | 0.0898 | 1.6262 | 1.4180 | 2.1881 | 0.1843 | 0.9417 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pachaiyappan, R.; Arasan, E.; Chandrasekaran, K. Improved Gorilla Troops Optimizer-Based Fuzzy PD-(1+PI) Controller for Frequency Regulation of Smart Grid under Symmetry and Cyber Attacks. Symmetry 2023, 15, 2013. https://doi.org/10.3390/sym15112013
Pachaiyappan R, Arasan E, Chandrasekaran K. Improved Gorilla Troops Optimizer-Based Fuzzy PD-(1+PI) Controller for Frequency Regulation of Smart Grid under Symmetry and Cyber Attacks. Symmetry. 2023; 15(11):2013. https://doi.org/10.3390/sym15112013
Chicago/Turabian StylePachaiyappan, Rajivgandhi, Elankurisil Arasan, and Kannan Chandrasekaran. 2023. "Improved Gorilla Troops Optimizer-Based Fuzzy PD-(1+PI) Controller for Frequency Regulation of Smart Grid under Symmetry and Cyber Attacks" Symmetry 15, no. 11: 2013. https://doi.org/10.3390/sym15112013





