Weight Optimization Decision Algorithm in (p,q)-Rung Probabilistic Hesitant Orthopair Fuzzy Environments

Abstract

Aiming at the fuzzification of a decision environment and the challenge of determining the weights associated with the interaction among decision-makers, this study offers an original method for (p,q)-rung probabilistic hesitant orthopair fuzzy multi-objective group decision-making, which is founded on the weight optimization principle. Firstly, the notion of a probabilistic hesitant fuzzy set is expanded to a (p,q)-rung. Secondly, the determination of subjective and objective weights is accomplished through the utilization of the Analytic Network Process (ANP) and the Entropy Method. According to the degree of deviation and dispersion of each weight, an optimal objective function is constructed, and the neural network is used to iteratively solve for the best scheme of the comprehensive weight. Subsequently, the Elimination Et Choice Translating Reality (ELECTRE) approach was refined and applied to decision-making in the (p,q)-rung probabilistic hesitant orthopair fuzzy environment. Finally, comparative analysis was used to demonstrate the new method’s effectiveness and superiority.

1. Introduction

Since Zadeh [1] proposed a method based on fuzzy sets in 1965, it has been used more and more in practical applications. Atanassov [2] introduced the concept of an intuitionistic fuzzy set that takes a membership degree, non-membership degree, and hesitant degree into consideration. Torra [3] proposed the hesitant fuzzy set theory in order to more precisely define the membership function and resolve the issue of inconsistent preferences among decision-makers. As an illustration, there are interval-valued hesitant fuzzy sets [4], dual hesitant fuzzy sets [5], hesitant triangular fuzzy sets [6], and hesitant linguistic fuzzy sets [7]. Xu et al. [8] proposed the definition of a probabilistic hesitant fuzzy set in order to properly consider the probability of each membership degree. Yager [9] introduced the concept of q-rung orthopair fuzzy sets in 2017, taking into account the restricted value range of membership degrees and non-membership degrees in previous fuzzy sets. In 2022, Seikh and Mandal [10] proposed the concept of p,q-quasirung orthopair fuzzy sets to further expand the value range of a membership degree and non-membership degree. However, none of the above-mentioned fuzzy sets can truly encompass fuzzy information, and intuitionistic fuzzy sets do not account for the hesitation of actual decision-makers. p,q-quasirung orthopair fuzzy sets and probabilistic hesitant fuzzy sets restrict the preferences of decision makers for alternatives and the values of membership and non-membership degrees, respectively. Consequently, in order to evaluate the overall qualities of the alternatives specifically, the concept of (p,q)-rung probabilistic hesitant orthopair fuzzy sets is introduced.

When experts make decisions on some schemes, determining the weight is a crucial issue. Since it is challenging to precisely define the attribute weights in practical problems, academicians have proposed a variety of solutions. Universal techniques for calculating subjective weights include the Best-Worst Method (BWM), the Linear Barycentric Weighting Approach (LBWA), the Full Consistency Method (FUCOM), and the Analytic Network Process (ANP), among others. The BWM technique [11] is very simple to learn and apply, but it has the potential to oversimplify complicated choice scenarios by focusing only on the best and worst traits and ignoring other crucial considerations. The LBWA approach [12] is straightforward, intuitive, and simple to understand; yet, this method relies too heavily on the weight of the index and ignores the internal relationship and interactions between the indicators. The FUCOM technique [13] is a fuzzy trade-off approach that helps decision-makers weigh various decision criteria. However, the operation of this method is tedious and easily affected by various factors, and the conclusion is not intuitive enough. The ANP technique [14] is applied to complex decision situations in which the guidelines and plans are interdependent from feedback. It allows decision-makers to properly comprehend and analyze the interdependencies across criteria, making decision-making more realistic and detailed. To some extent, this also helps to address the uncertainty of the outcomes produced by changes in individual preferences. A typical objective weighting method is the entropy method [15]. It determines the relative weight of each criterion based on its entropy value, avoiding the problem of subjective weighting. This technique considers the amount of information contained in each criterion and allows for a more comprehensive assessment of each criterion’s value. Single subjective and objective procedures frequently have inconsistent subjective preferences or objective rules; however, the integrated weighing method can combine the benefits of the two methods while alleviating their drawbacks. As a result, in order to account for the interaction of decision-makers as well as the link between qualities, this research employs the ANP technique and the entropy method to get the subjective and objective weights, respectively. Furthermore, taking the degree of deviation and dispersion between subjective and objective weighting as the objective function, a weighted optimal mathematical model is constructed, and the neural network is used to iteratively solve for the optimal solution of the combination weight, taking into account the influence of subjective and objective weights on the combination weight. This method simulates the operation of the human brain nervous system by connecting and calculating many nodes to achieve the combination and output of the nonlinear model.

For multi-attribute group decision-making problems, scholars have proposed a variety of decision methods, such as the Vlse Kriterijumski Optimizacioni Racun (VIKOR), the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS), the Multi-Attributive Border Approximation Area Comparison (MABAC), the Elimination Et Choice Translating Reality (ELECTRE), etc. The VIKOR technique [16] is an easy-to-understand and applicable multi-standard decision-making method, which enables decision-makers to combine the priority of their choice with its weighting. However, it does not always make it plain how to find a compromised solution, which might make the decision-making process difficult to understand. The TOPSIS method [17] is an approach to the ideal solution developed by Hwang and Yoon. Its flexibility is manifested in the fact that it can use any indicator, any decision-maker opinion, and questions applicable to a variety of domains. However, it requires a high standardization of the data and needs to transform the indicator data into dimensionless relative indicators for comparison and ranking. This may make certain assumptions and transformations on the data, leading to an increased uncertainty and subjectivity of the results. The MABAC technique [18] is a multi-criteria decision-making method that assesses and ranks alternatives based on a variety of factors. This method uses a geometric representation method called “edge approximation domain”, which can visually compare the selection results and help to better understand and communicate when making decisions. However, for the selection of large-scale data sets, we must classify them and determine their scope, and the amount of calculations is very large. As a result, it is unsuitable for complex choice issues. Almeida [19] created the ELECTRE technique in 2005, which determines the ideal answer by establishing a series of preference relations and evaluating the alternative solutions. This method can uniformly analyze a variety of criteria, analyze a large amount of information, and use quantitative description or hierarchical comparison to describe the relationship between the criteria, thus giving a clear judgment conclusion. This assists decision-makers in understanding and interpreting the final decision. The theory and application of the ELECTRE approach have been investigated by academics. Chen [20] analyzed the multi-criteria selection process using the interval-valued intuitionistic fuzzy ELECTRE multi-criteria assessment and selection approach. To increase the accuracy and consistency of weight calculation, Jagtap [21] suggested an updated Simos and Analytic hierarchy process (AHP) weighting method. According to available research, the ELECTRE approach is an excellent strategy to handle the decision problem. As a result, in order to adapt to the new fuzzy environment, the ELECTRE method must be improved and extended.

In summary, intensive research on fuzzy sets and weights has yielded astonishing findings and made significant contributions to decision-making in many areas. However, in the current research, it is critical to broaden the desirable attribute value range. Furthermore, there is less research on the interaction between decision-makers and the link between qualities in the decision-making context. Exploring strategies to improve existing decision-making processes is also of interest. As a result, in the (p,q)-rung probabilistic hesitant orthopair fuzzy environment, the weighted optimal solution of multi-attribute group decision-making is given, and the modified ELECTRE method is given. The remainder of the paper is organized as follows: The requirements for the remainder of the paper are introduced in Section 2; Section 3 defines (p,q)-rung probabilistic hesitant orthopair fuzzy sets and their related concepts; Section 4 defines the weighted optimal mathematical model and presents an upgraded (p,q)-rung probabilistic hesitant orthopair fuzzy ELECTRE approach, taking into account the mutual effects of decision-makers and the link between characteristics. The algorithm’s efficacy and applicability are proven through a comparative study of similar studies, using logistics location as an example; The conclusion is offered in Section 5.

2. Preliminaries

This chapter mainly expounds some basic knowledge of fuzzy sets in order to help us better understand the relevant theories provided.

Definition 1

([2]). If $X$ is a non-empty universe, then the intuitionistic fuzzy set $B$ on  $X$ is defined as:

$$B=\left\{<x,\right.{\mu }_B(x),{\nu }_B(x)>\left|\left.x\in X\right\}\right.$$

where ${\mu }_B(x):|\to \left[0,1\right]$ is the membership function of $B$,${\nu }_B(x):|\to \left[0,1\right]$ is the non-membership function of $B$, and $\forall x\in X,0\le {\mu }_B(x)+{\nu }_B(x)\le 1$. For the above intuitionistic fuzzy set, refer to ${\pi }_B(x)=1-{\mu }_B(x)-{\nu }_B(x)$ as the hesitancy degree of $X$ to $B$, and $\forall x\in X,0\le {\pi }_B(x)\le 1$.

Definition 2

([3]). If $X$ is a non-empty universe, then the hesitant fuzzy set $B$ on $X$ is defined as:

$$B=\left\{<x,f_B(x)>|x\in \left.X\right\}\right.$$

where $f_B(x)$ is the set formed by different values in the interval [0,1], $x$ is the membership degree of the set $B$, and $f_B(x)$ is called the hesitant fuzzy element.

Definition 3

([8]). If $X$ is a non-empty universe, then the probabilistic hesitant fuzzy set $B$ on $X$is defined as:

$$B=\left\{<x,f_B(x)|p_B(x)|x\in \left.X\right\}\right.$$

where set $f_B(x)|p_B(x)=\{u_{B,s}(x)|p_{B,s}(x)|s=1,2,\dots l,{\displaystyle \sum _{s=1}^l{p}_{B,s}(x)\le 1}\}$ is called the probabilistic hesitant fuzzy number, and $u_{B,s}(x)\in [0,1]$ is the membership degree. The real number $p_{B,s}(x)\in \left[0,1\right]$ represents the probability value corresponding to the membership degree, and $l$ is the number of probabilistic hesitant fuzzy numbers.

Definition 4

([22]). If $X$ is a non-empty universe, then the probabilistic q-rung orthopair probabilistic hesitant fuzzy set $B$ on  $X$ is defined as:

$$B=\left\{<x,f_B(x)\right.|p_B(x)\left.>|x\in X\right\}$$

where: $f_B(x)|p_B(x)=\left\{<u_{B,s}(x)\right.,v_{B,s}(x)>|p_{B,s}(x)|u^q{}_{B,s}(x)+v^q{}_{B,s}(x)\le 1,p_{B,s}(x)\in [0,1],$ $q\in N_{+},$$u_{B,s}(x)\in [0,1],v_{B,s}(x)\in [0,1],|s=1,2\dots ,l,{\displaystyle \sum _{s=1}^l{p}_{B,s}(x)\le \left.1\right\}}$.

The hesitancy degree is ${\pi }_{B,p}(x)={\left({\displaystyle \sum _{s=1}^l{p}_{B,s}(x){\pi }_{B,s}(x)}\right)}^{\frac{1}{q}}$, q is a positive integer, and ${\pi }_{B,s}(x)={}^q\sqrt{1-{{\mu }^q}_{B,s}(x)-{{\nu }^q}_{B,s}(x)}$.

3. (p,q)-Rung Probabilistic Hesitant Orthopair Fuzzy Sets

{<0.81,0.82>|1} is a q-rung probability hesitant orthopair fuzzy number. According to definition (4), when q = 3,${0.81}^3+{0.82}^3>1$, and when q = 4, some of the original information is lost. As a result, in order to properly deal with decision circumstances, a more flexible fuzzy set is required.

Definition 5.

Let X be a non-empty universe, and the following is a (p,q)-rung probabilistic hesitant orthopair fuzzy set:

$$B=\left\{<x,f_B(x)\right.|p_B(x)\left.>|x\in X\right\}$$

where: $f_B(x)|p_B(x)=\left\{<u_{B,s}(x)\right.,v_{B,s}(x)>|p_{B,s}(x)|u^p{}_{B,s}(x)+v^q{}_{B,s}(x)\le 1,p_{B,s}(x)\in [0,1],$$p\in N_{+},q\in N_{+},$ $u_{B,s}(x)\in [0,1],v_{B,s}(x)\in [0,1],|s=1,2\dots ,l,{\displaystyle \sum _{s=1}^l{p}_{B,s}(x)\le \left.1\right\}}$.

$u_{B,s}(x),v_{B,s}(x)$ denote the possible membership and possible non-membership of $x\in B$, respectively, $p_{B,s}(x)$ is the corresponding probability of  $<u_{B,s}(x),v_{B,s}(x)>$, and $(p,q)$ is a positive integer pair. Each pair $\left\{<\right.u_{B,s}(x),v_{B,s}(x)>|p_{B,s}(x\left.)\right\}$ will be referred to in this paper as (p,q)-rung probabilistic hesitant orthopair fuzzy numbers, abbreviated as $\left\{<\right.u_{B,s},v_{B,s}>|\left.p_{B,s}\right\}$.

There are many kinds of pairs of positive integers satisfying (p,q), such as {0.7, 0.9|1}, whose (p,q) can take (4.3), (4.4), (5,3) and other positive integers. Therefore, in order to calculate and compare the fuzzy information of the index in a convenient manner, the value principle of (p,q) is prescribed in this paper.

The values of the s-th fuzzy numbers and of a (p,q)-rung probabilistic hesitant orthopair fuzzy set are as follows:

$$\left\{\begin{array}{l}0\le u^{p_s}{}_{B,s}(x)+v^{q_s}{}_{B,s}(x)\le 1\\ {\min \left[\right(\mathrm{p}}_s{+\mathrm{q}}_s{)+|\mathrm{p}}_s{-\mathrm{q}}_s|]\\ u_{B,s}(x)\le v_{B,s}(x),p_s\ge q_s\\ u_{B,s}(x)\ge v_{B,s}(x),p_s\le q_s\\ p_s\in N_{+},q_s\in N_{+}\end{array}\right.$$

The values of this fuzzy set (p,q) are as follows:

$$\begin{array}{l}p=\max \{p_s|s=1,\dots ,l\}\\ q=\max \{q_s|s=1,\dots ,l\}\end{array}$$

Definition 6.

If  $A=\left\{<u_{A,i}\right.,v_{A,i}>|\left.p_{A,i}\right\},B=\left\{<u_{B,s}\right.,v_{B,s}>|\left.p_{B,s}\right\}$ are two (p,q)-rung probabilistic hesitant orthopair fuzzy numbers and  $\lambda \ge 0$ , then the operation rules are as follows:

$$\begin{array}{l}1.A^C=\left\{<v_{A,i}\right.,u_{A,i}>|\left.p_{A,i}\right\}\\ 2.A^{\lambda }=\left\{<u^{\lambda }{}_{A,i}\right.,\sqrt[q]{1-{(1-v^q{}_{A,i})}^{\lambda }}>|\left.p_{A,i}\right\}\\ 3.\lambda A=\left\{<\sqrt[p]{1-{(1-u^p{}_{A,i})}^{\lambda }}\right.,v^{\lambda }{}_{A,i}>|\left.p_{A,i}\right\}\\ 4.A\oplus B=\left\{<\sqrt[p]{u^p{}_{A,i}+u^p{}_{B,s}-u^p{}_{A,i}{u}^p{}_{B,s}}\right.,v_{A,i}{v}_{B,s}>|\left.p_{A,i}{p}_{B,s}\right\}\\ 5.A\otimes B=\left\{<u_{A,i}{u}_{B,s}\right.,\sqrt[q]{v^q{}_{A,i}+v^q{}_{B,s}-v^q{}_{A,i}{v}^q{}_{B,s}}>|\left.p_{A,i}{p}_{B,s}\right\}\end{array}$$

Definition 7.

Let X be a non-empty universe.  $B=\left\{<x,f_B(x)\right.|p_B(x)\left.>|x\in X\right\}$ is a (p,q)-rung probabilistic hesitant orthopair fuzzy set, and  $B_b(p)=\left\{<u_{b,s}\right.,v_{b,s}>|p(s)|s=1,2,\dots ,\left.l\right\}$ is its (p,q)-rung probabilistic hesitant orthopair fuzzy number. The hesitance degree  ${\pi }_{B,s}(x)$ of its s-th element can be mathematically represented as follows:

$${\pi }_{B,s}(x)=\sqrt[k]{\frac{2-u^p{}_{B,s}(x)-v^q{}_{B,s}(x)-p_{B,s}(x)}{2}}$$

The overall hesitancy of B is as follows:

$$\stackrel{—}{{\pi }_{B,s}(x)}=\frac{1}{l}{\displaystyle \sum _{s=1}^l{\pi }_{B,s}(x)}$$

where$k$ is the least common multiple of p and q, and ${\pi }_{B,s}(x)\in [0,1],\stackrel{—}{{\pi }_{B,s}(x)}\in [0,1]$.

To demonstrate that Definition 5 can handle decision cases better than Definition 4, we apply the new fuzzy set theory to data at the beginning of this section.

Assume {<0.81,0.82>|1} is set on an element’s attribute values. We can get ${0.81}^4+{0.82}^3<1$ by using Definition 5. Furthermore, it preserves more original information and can cope with fuzzy information more successfully than ${0.81}^4+{0.82}^4<1$.

3.1. Ranking of (p,q)-Rung Probabilistic Hesitant Orthopair Fuzzy Sets

According to Li’s theory [23], decision-makers often aspire for a high degree of membership in the scheme, a low degree of non-membership, and minimal hesitancy during the decision-making process. Hence, the inclusion of hesitancy as a crucial factor must be taken into account while evaluating decision-related information. The score function presented in this work takes into account the element of individuals’ hesitancy comprehensively, hence enhancing its alignment with real-world circumstances. The precise functional form can be expressed as follows:

Definition 8.

Let  $B_b(p)=\left\{<u_{b,s}\right.,v_{b,s}>|p(s)|s=1,2,\dots ,\left.l\right\}$ be a (p,q)-rung probabilistic hesitant orthopair fuzzy number, denote (1) as the score function of  $B_b(p)$, and $S(B_b(p))\in [0,1]$.

$$S(B_b(p))=\frac{1}{4}\left(2+\frac{{\displaystyle \sum _{s=1}^l{p}_s(u^p{}_{b,s}-v^q{}_{b,s})}}{{\displaystyle \sum _{s=1}^l{p}_s}}+\frac{\frac{{\displaystyle \sum _{s=1}^l{p}_s(u^p{}_{b,s}-v^q{}_{b,s})}}{{\displaystyle \sum _{s=1}^l{p}_s}}}{1+\frac{1}{l}{\displaystyle \sum _{s=1}^l{\pi }_{b,s}^k}}\right)$$

(1)

Part $\frac{{\displaystyle \sum _{s=1}^l{p}_s(u^p{}_{b,s}-v^q{}_{b,s})}}{{\displaystyle \sum _{s=1}^l{p}_s}}$ represents the herd mentality of humanity. When support exceeds opposition, that is $u\succ v$. According to the value principle of (p,q) in this paper, $u^p\succ v^q$ can be obtained, thus $\frac{{\displaystyle \sum _{s=1}^l{p}_s(u^p{}_{b,s}-v^q{}_{b,s})}}{{\displaystyle \sum _{s=1}^l{p}_s}}\succ 0$, and hesitant individuals choose to support at this time; in the contrary situation, they began to oppose the attitude. $\frac{1}{1+\frac{1}{l}{\displaystyle \sum _{s=1}^l{\pi }_{b,s}^k}}$ implies that the decision-maker favors the occurrence with the lower degree of uncertainty, which is better in keeping with the actual decision circumstance.

Definition 9.

Let $B_b(p)=\left\{<u_{b,s}\right.,v_{b,s}>|p(s)|s=1,2,\dots ,\left.l\right\}$ be a (p,q)-rung probabilistic hesitant orthopair fuzzy number, denote (2) as the exact function of $B_b(p)$, and $H(B_b(p))\in [0,1]$.

$$H(B_b(p))=\frac{{\displaystyle \sum _{s=1}^l{p}_s(u^p{}_{b,s}+v^q{}_{b,s})}}{{\displaystyle \sum _{s=1}^l{p}_s}}$$

(2)

Definition 10.

If  $B_{b_1}(p_{b_1})$ and  $B_{b_2}(p_{b_2})$ are two (p,q)-rung probabilistic hesitant orthopair fuzzy sets,  $S(B_{b_1}(p_{b_1}))$,  $S(B_{b_2}(p_{b_2}))$ are their scoring functions, and  $H(B_{b_1}(p_{b_1})),H(B_{b_2}(p_{b_2}))$ are their exact functions, then the comparison principle of two (p,q)-rung probabilistic hesitant orthopair fuzzy numbers is as follows:

If  $S(B_{b_1}(p_{b_1}))\prec S(B_{b_2}(p_{b_2}))$, then  $B_{b_1}(p_{b_1})\prec B_{b_2}(p_{b_2})$

If  $S(B_{b_1}(p_{b_1}))\succ S(B_{b_2}(p_{b_2}))$, then  $B_{b_1}(p_{b_1})\succ B_{b_2}(p_{b_2})$

If  $S(B_{b_1}(p_{b_1}))=S(B_{b_2}(p_{b_2}))$, then when

$(1)$$H(B_{b_1}(p_{b_1}))\succ H(B_{b_2}(p_{b_2}))$, there are  $B_{b_1}(p_{b_1})\succ B_{b_2}(p_{b_2})$

$(2)$$H(B_{b_1}(p_{b_1}))\prec H(B_{b_2}(p_{b_2}))$, there are  $B_{b_1}(p_{b_1})\prec B_{b_2}(p_{b_2})$

$(3)$$H(B_{b_1}(p_{b_1}))=H(B_{b_2}(p_{b_2}))$, there are  $B_{b_1}(p_{b_1})=B_{b_2}(p_{b_2})$

3.2. Entropy Measure of (p,q)-Rung Probabilistic Hesitant Orthopair Fuzzy Sets

Definition 11.

If  $Z=\left\{<x,f_Z(x)\right.|p_Z(x)\left.>|x\in X\right\}$ is a (p,q)-rung probabilistic hesitant orthopair fuzzy set over a non-empty universe of  $X=\left\{x_1,x_2,\dots ,\left.x_n\right\}\right.$  , then the following entropy formula is derived:

$$E(Z)=\frac{1}{2nl}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{s=1}^l[2-|u_{\sigma (s)}^p(x_i)}-v_{\sigma (s)}^q(x_i)|\max \{(u_{\sigma (s)}^p(x_i),v_{\sigma (s)}^q(x_i)\}-|u_{\sigma (s)}^p(x_i)-v_{\sigma (s)}^q(x_i)|p_{\sigma (s)}(x_i)]}$$

(3)

Theorem 1.

This paper proposes an entropy formula with the following five properties:

$(p1):0\le E(Z)\le 1$

$(p2):E(Z)=0\iff Z=\left\{<0,1>|\left.1\right\}\right.or Z=\left\{<1,0>|\left.1\right\}\right.$

$(p3):E(Z)=1\iff Z=\left\{<a,a>|\left.b\right\}\right.$,$a\in [0,1]$,$b\in [0,1]$

$(p4):E(Z)=E(Z^C)$

$(p5):E(Z_1)\le E(Z_2)$, If  $Z_2$‘s information is more ambiguous than $Z_1$‘s information.

Proof of Theorem 1.

$(p1),(p2),(p3),p(4)$ clearly hold, and it follows to prove whether $p(5)$ holds.

Assuming $X=\{x\}$, consider the following equation:

$$f(x,y,z)=[2-|x^p-y^q|\max \{x^p,y^q\}-|x^p-y^q|z],x,y,z\in [0,1],x^p+y^q\le 1,p,q\in N_{+}$$

When $x\le y$, according to the value principle of (p,q) in this paper, $x^p\le y^q$ can be obtained.

Take the partial derivatives with respect to $x,y,z$ separately:

$$\frac{\partial f}{\partial x}=p{x}^{p-1}{y}^q+p{x}^{p-1}z\ge 0, \frac{\partial f}{\partial y}=q{y}^{q-1}(x^p-2y^q)-q{y}^{q-1}z\le 0, \frac{\partial f}{\partial z}\le 0$$

So, as $x\le y$, $f$ is increasing with $x$, decreasing with $y$, and decreasing with $z$.

When $x\ge y$, according to the value principle of (p,q) in this paper, $x^p\ge y^q$ can be obtained.

$$\frac{\partial f}{\partial x}=p{x}^{p-1}(y^q-2x^p)-p{x}^{p-1}z\le 0, \frac{\partial f}{\partial y}=q{y}^{q-1}{x}^p+q{y}^{q-1}z\ge 0, \frac{\partial f}{\partial z}\le 0$$

So, as $x\ge y$, $f$ is decreasing with $x$, increasing with $y$, and decreasing with $z$.

So, based on the preceding stages, we can obtain:

When $u_{\sigma (2)}(x_i)\le v_{\sigma (2)}(x_i),u_{\sigma (1)}(x_i)\le u_{\sigma (2)}(x_i),v_{\sigma (1)}(x_i)\ge v_{\sigma (2)}(x_i),p_{\sigma (1)}(x_i)\ge p_{\sigma (2)}(x_i)$ or $u_{\sigma (2)}(x_i)\ge v_{\sigma (2)}(x_i),u_{\sigma (1)}(x_i)\ge u_{\sigma (2)}(x_i),v_{\sigma (1)}(x_i)\le v_{\sigma (2)}(x_i),p_{\sigma (1)}(x_i)\ge p_{\sigma (2)}(x_i)$, we have $f(u_{\sigma (1)}(x_i),v_{\sigma (1)}(x_i),p_{\sigma (1)}(x_i))\le f(u_{\sigma (2)}(x_i),v_{\sigma (2)}(x_i),p_{\sigma (2)}(x_i))$.

Hence, $E(Z_1)=\frac{1}{2nl}{\displaystyle \sum _{i=1}^{n}f(u_{\sigma (1)}(x_i),v_{\sigma (1)}(x_i),p_{\sigma (1)}(x_i))}\le E(Z_2)=\frac{1}{2nl}{\displaystyle \sum _{i=1}^{n}f(u_{\sigma (2)}(x_i),v_{\sigma (2)}(x_i),p_{\sigma (2)}(x_i))}$.

That is, when the information of $Z_2$ is more ambiguous than the information of $Z_1$, there is $E(Z_1)\le E(Z_2)$. ☐

3.3. The Distance Measures of (p,q)-Rung Probabilistic Hesitant Orthopair Fuzzy Sets

Distance measurement is a perennially contentious issue in the decision-making process, and it is also a crucial component of fuzzy set theory. It has been utilized extensively in numerous disciplines, including that of pattern recognition, attribute decision-making, etc. A distance measure can quantify the spread between two alternatives in a decision analysis. The closer the distance between the alternative to be chosen and the ideal alternative, the more likely this alternative is to be chosen.

According to the concept of hesitant fuzzy sets, the cardinality of two hesitant fuzzy sets is not necessarily equal, which depends on the subjective will of decision-makers. As an extension of hesitant fuzzy sets, (p,q)-rung probability hesitant orthopair fuzzy sets also have this property. To enable a meaningful comparison, it is imperative to modify their respective structures. This adjustment serves the purpose of preserving the inherent fuzziness of the fuzzy set, while also simplifying the computation of the distance between the two sets. The proposed adjustment system is outlined as follows:

Normalization: The procedure is the same as that of reference [24] for the normalization of probabilistic hesitant fuzzy sets.

Ranking: The fuzzy numbers in the (p,q)-rung probabilistic hesitant orthopair fuzzy set are sorted according to the values of membership degree to the power of p—non-membership degree to the power of q. If the values are equal, the fuzzy numbers are sorted according to membership degree to the power of p + non-membership degree to the power of q.

Expansion: The expansion process is the same as the expansion process of probabilistic hesitant fuzzy sets in the literature [25].

Example 1.

Let   $A=\{<0.6,0.4>|0.54,<0.6,0.6>|0.36\}$  and  $B=\{<0.5,0.3>|0.32,<0.7,0.4>|0.32,<0.3,0.1>|0.16\}$  be two (p,q)-rung probabilistic hesitant orthopair fuzzy sets.

Since $0.54+0.36<1,0.32+0.32+0.16=0.8<1$, $A,B$ must be normalized first.

According to the value principle of (p,q) in this paper, $p=1,q=2$, in this case:

$$\begin{array}{l}\stackrel{-}{A}=\{<0.6,0.4>|0.6,<0.6,0.6>|0.4\}\\ \stackrel{-}{B}=\{<0.5,0.3>|0.4,<0.7,0.4>|0.4,<0.3,0.1>|0.2\}\end{array}$$

Second, sort it to get:

$$\begin{array}{l}\stackrel{--}{A}=\{<0.6,0.4>|0.6,<0.6,0.6>|0.4\}\\ \stackrel{--}{B}=\{<0.7,0.4>|0.4,<0.5,0.3>|0.4<0.3,0.1>|0.2\}\end{array}$$

Finally, it can be obtained through expansion:

$$\begin{array}{l}\stackrel{---}{A}=\{<0.6,0.4>|0.4,<0.6,0.4>|0.2,<0.6,0.6>|0.2,<0.6,0.6>|0.2\}\\ \stackrel{---}{B}=\{<0.7,0.4>|0.4,<0.5,0.3>|0.2,<0.5,0.3>|0.2,<0.3,0.1>|0.2\}\end{array}$$

It has been determined that the transformed fuzzy set still contains the original fuzzy data. The following section proposes the properties and formulations of distance measures for (p,q)-rung probabilistic hesitant orthopair fuzzy sets.

Theorem 2.

A distance measure in a (p,q)-rung probabilistic hesitant orthopair fuzzy environment must possess the following four properties:

$$\begin{array}{l}E1:0\le D(B_1,B_2)\le 1\\ E2:D(B_1,B_2)=D(B_2,B_1)\\ E3:D(B_1,B_2)=0\iff B_1=B_2\\ E4:D(B_1,B_2)+D(B_2,B_3)\ge D(B_1,B_3)\end{array}$$

Based on Theorem 1, we will now investigate the distance measures of (p,q)-rung probabilistic hesitant orthopair fuzzy sets.

Definition 12.

Let the domain of discourse be  $B=\left\{x_1,x_2,\dots ,x_n\right\}$  and two (p,q)-rung probabilistic hesitant orthopair fuzzy sets be  $B_1=\left\{x_i,<u_{B_1,j}(x_i),v_{B_1,j}(x_i)\right.>|p_{B_1,j}(x_i)|x_i\in B,j=1,\dots ,\left.l\right\}$, $B_2=$$\left\{x_i,<u_{B_2,j}(x_i),v_{B_2,j}(x_i)\right.$ $>|p_{B_2,j}(x_i)|x_i\in B,j=1,\dots ,\left.l\right\}$, respectively. Then the distance measure between $B_1,B_2$ can be defined as follows.

$$D(B_1,B_2)=\frac{1}{4|B|}{\displaystyle \sum _{i=1}^B{\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}(x_i)}{p}_{\sigma (s)}(x_i)\cdot (|b^u{}_{is}}}|+|b^v{}_{is}|+|b^{\pi }{}_{is}|+|b^u{}_{is}-b^v{}_{is}-b^{\pi }{}_{is}|)$$

(4)

where:

$$\begin{array}{l}{b}^u{}_{is}=u^p{}_{B_1,\sigma (s)}(x_i)-u^p{}_{B_2,\sigma (s)}(x_i)\\ b^v{}_{is}=v^q{}_{B_1,\sigma (s)}(x_i)-v^q{}_{B_2,\sigma (s)}(x_i)\\ b^{\pi }{}_{is}={\pi }^k{}_{B_1,\sigma (s)}(x_i)-{\pi }^k{}_{B_2,\sigma (s)}(x_i)\end{array}$$

$p_{\sigma (s)}$ is the probability value corresponding to the s-th element of the (p,q)-rung probabilistic hesitant orthopair fuzzy set corresponding to element  $x_i$  after normalization, sorting, and expansion;  $L_{B_1{ \mathrm{B}}_2}(x_i)$  is the number of elements of the (p,q)-rung probabilistic hesitant orthopair fuzzy set  $B_1,B_2$  after normalization, sorting, and expansion.

We now turn to show that the distance measure proposed by Equation (4) satisfies the requirements given in Theorem 2.

Let $B_1=\left\{x_i,<u_{B_1,j}(x_i),v_{B_1,j}(x_i)\right.>|p_{B_1,j}(x_i)|j=1,\dots ,\left.l\right\}$, $B_2=$$\left\{x_i,<u_{B_2,k}(x_i),v_{B_2,k}(x_i)\right.>|$ $p_{B_2,k}(x_i)$ $|k=1,\dots ,\left.s\right\}$, and $B_3=\left\{x_i,<u_{B_3,e}(x_i),v_{B_3,e}(x_i)\right.>|p_{B_3,e}(x_i)$$|e=1,\dots ,\left.h\right\}$ be (p,q)-rung probabilistic hesitant orthopair fuzzy sets defined on B, and $B=\{X\}$.

Normalize $B_1,B_2$, sort it, expand it, and then:

In order to achieve normalization, $B_1,B_2$ are subjected to a sorting process, followed by an expansion.

$$\begin{gathered} B_1=\left\{x_i,<u_{B_1,j}(x_i),v_{B_1,j}(x_i)\right.>|p_{B_1,j}(x_i)|j=1,\dots ,\left.l\right\}\Rightarrow \stackrel{-}{B_1}=\left\{x_i,<u_{B_1,\sigma (s)}(x_i),v_{B_1,\sigma (s)}(x_i)\right.>|p_{\sigma (s)}(x_i)|s=1,\dots ,\left.L_{B_1 B_2}\right\} \\ {B}_2=\left\{x_i,<u_{B_2,k}(x_i),v_{B_2,k}(x_i)\right.>|p_{B_2,k}(x_i)|k=1,\dots ,\left.s\right\}\Rightarrow \stackrel{-}{B_2}=\left\{x_i,<u_{B_2,\sigma (s)}(x_i),v_{B_2,\sigma (s)}(x_i)\right.>|p_{\sigma (s)}(x_i)|s=1,\dots ,\left.L_{B_1 B_2}\right\} \end{gathered}$$

For $E(1)$:

$D(B_1,B_2)\ge 0$ is clearly true.

Let’s prove $D(B_1,B_2)\le 1$.

$$\begin{array}{l}|b_s^u|+|b_s^v|+|b_s^{\pi }|=|u^p{}_{B_1,\sigma (s)}-u^p{}_{B_2,\sigma (s)}|+|v^p{}_{B_1,\sigma (s)}-v^p{}_{B_2,\sigma (s)}|+|{\pi }^k{}_{B_1,\sigma (s)}-{\pi }^k{}_{B_2,\sigma (s)}|\\ \le u^p{}_{B_1,\sigma (s)}+u^p{}_{B_2,\sigma (s)}+v^p{}_{B_1,\sigma (s)}+v^p{}_{B_2,\sigma (s)}+{\pi }^k{}_{B_1,\sigma (s)}+{\pi }^k{}_{B_2,\sigma (s)}\\ =u^p{}_{B_1,\sigma (s)}+v^p{}_{B_1,\sigma (s)}+{\pi }^k{}_{B_1,\sigma (s)}+u^p{}_{B_2,\sigma (s)}+v^p{}_{B_2,\sigma (s)}+{\pi }^k{}_{B_2,\sigma (s)}\\ \le 2\end{array}$$

Combining the above process, it can be obtained:

$$\begin{array}{l}|b_s^u-b_s^v-b_s^{\pi }|\le |b_s^u|+|b_s^v|+|b_s^{\pi }|\Rightarrow |b_s^u-b_s^v-b_s^{\pi }|\le 2\Rightarrow p_{\sigma (s)}(|b_s^u|+|b_s^v|+|b_s^{\pi }|+|b_s^u-b_s^v-\\ b_s^{\pi }|)\le 4p_{\sigma (s)}\Rightarrow |b_s^u-b_s^v-b_s^{\pi }|\le 2\Rightarrow p_{\sigma (s)}(|b_s^u|+|b_s^v|+|b_s^{\pi }|+|b_s^u-b_s^v-b_s^{\pi }|)\le 4p_{\sigma (s)}\Rightarrow \end{array}$$

$D(B_1,B_2)=\frac{1}{4}{\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}}{p}_{\sigma (s)}(|b^u{}_s}|+|b^v{}_s|+|b^{\pi }{}_s|+|b^u{}_s-b^v{}_s-b^{\pi }{}_s|)\le \frac{1}{4}{\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}}4p_{\sigma (s)}}={\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}}{p}_{\sigma (s)}}=1$

Therefore, $E(1)$ holds.

For $E(2)$:

$$\begin{array}{l}D(B_2,B_1)=\frac{1}{4}{\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}}{p}_{\sigma (s)}}(|u^p{}_{B_2,\sigma (s)}-u^p{}_{B_1,\sigma (s)}|+|v^p{}_{B_2,\sigma (s)}-v^p{}_{B_1,\sigma (s)}|+|{\pi }^k{}_{B_1,\sigma (s)}-{\pi }^k{}_{B_2,\sigma (s)}|\\ +|u^p{}_{B_2,\sigma (s)}-u^p{}_{B_1,\sigma (s)}-v^p{}_{B_2,\sigma (s)}+v^p{}_{B_1,\sigma (s)}-{\pi }^k{}_{B_1,\sigma (s)}+{\pi }^k{}_{B_2,\sigma (s)}|)\\ =\frac{1}{4}{\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}}{p}_{\sigma (s)}}(|u^p{}_{B_1,\sigma (s)}-u^p{}_{B_2,\sigma (s)}|+|v^p{}_{B_1,\sigma (s)}-v^p{}_{B_2,\sigma (s)}|+|{\pi }^k{}_{B_1,\sigma (s)}-{\pi }^k{}_{B_2,\sigma (s)}|\\ +|u^p{}_{B_1,\sigma (s)}-u^p{}_{B_2,\sigma (s)}-v^p{}_{B_1,\sigma (s)}+v^p{}_{B_2,\sigma (s)}-{\pi }^k{}_{B_1,\sigma (s)}+{\pi }^k{}_{B_2,\sigma (s)}|)\\ =D(B_1,B_2)\end{array}$$

Therefore, $E(2)$ holds.

For $E(3)$:

First, we demonstrate the sufficiency:

$$\begin{array}{l}D(B_1,B_2)=0\Rightarrow \frac{1}{4}{\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}}{p}_{\sigma (s)}(|b_s^u|+|b_s^v|+|b_s^{\pi }|+|b_s^u-b_s^v-b_s^{\pi }|)=0}\Rightarrow b_s^u=b_s^v=b_s^{\pi }=0\\ \Rightarrow u^p{}_{B_1,\sigma (s)}=u^p{}_{B_2,\sigma (s)},v^p{}_{B_1,\sigma (s)}=v^p{}_{B_2,\sigma (s)},{\pi }^k{}_{B_1,\sigma (s)}={\pi }^k{}_{B_2,\sigma (s)}\Rightarrow B_1=B_2\end{array}$$

Then demonstrate the necessity:

$$\begin{array}{l}{B}_1=B_2\Rightarrow u^p{}_{B_1,\sigma (s)}=u^p{}_{B_2,\sigma (s)},v^p{}_{B_1,\sigma (s)}=v^p{}_{B_2,\sigma (s)},{\pi }^k{}_{B_1,\sigma (s)}={\pi }^k{}_{B_2,\sigma (s)}\Rightarrow b_s^u=b_s^v=b_s^{\pi }=0\\ \frac{1}{4}{\displaystyle \sum _{s=1}^{L_{B_1{ \mathrm{B}}_2}}{p}_{\sigma (s)}(|b_s^u|+|b_s^v|+|b_s^{\pi }|+|b_s^u-b_s^v-b_s^{\pi }|)=0}\Rightarrow D(B_1,B_2)=0\end{array}$$

Therefore, $E(3)$ holds.

For $E(4)$:

Normalize $\stackrel{-}{B_1},\stackrel{-}{B_2}$ and $B_3$, sort it, expand it, and then:

$$\stackrel{-}{B_1}=\left\{x_i,<u_{B_1,\sigma (s)}(x_i),v_{B_1,\sigma (s)}(x_i)\right.>|p_{\sigma (s)}(x_i)|s=1,\dots ,\left.L_{B_1 B_2}\right\}\Rightarrow \stackrel{=}{B_1}=\left\{x_i,<u_{B_1,\sigma (j)}(x_i),v_{B_1,\sigma (j)}(x_i)\right.>|p_{\sigma (j)}(x_i)|j=1,\dots ,\left.L_{B_1 B_2{ \mathrm{B}}_3}\right\}$$

$$\stackrel{-}{B_2}=\left\{x_i,<u_{B_2,\sigma (s)}(x_i),v_{B_2,\sigma (s)}(x_i)\right.>|p_{\sigma (s)}(x_i)|s=1,\dots ,\left.L_{B_1 B_2}\right\}\Rightarrow \stackrel{=}{B_2}=\left\{x_i,<u_{B_2,\sigma (j)}(x_i),v_{B_2,\sigma (j)}(x_i)\right.>|p_{\sigma (j)}(x_i)|j=1,\dots ,\left.L_{B_1 B_2{ \mathrm{B}}_3}\right\}$$

$$B_3=\left\{x_i,<u_{B_3,e}(x_i),v_{B_3,e}(x_i)\right.>|p_{B_3,e}(x_i)|e=1,\dots ,\left.h\right\}\Rightarrow \stackrel{=}{B_3}=\left\{x_i,<u_{B_2,\sigma (j)}(x_i),v_{B_2,\sigma (j)}(x_i)\right.>|p_{\sigma (j)}(x_i)|j=1,\dots ,\left.L_{B_1 B_2{ \mathrm{B}}_3}\right\}$$

$$\begin{array}{l}D(B_1,B_2)+D(B_2,B_3)=\frac{1}{4}{\displaystyle \sum _{j=1}^{L_{B_1{ \mathrm{B}}_{2 }{B}_3}}{p}_{\sigma (j)}[}(|u^p{}_{B_1,\sigma (j)}-u^p{}_{B_2,\sigma (j)}|+|v^p{}_{B_1,\sigma (j)}-v^p{}_{B_2,\sigma (j)}|+|{\pi }^k{}_{B_1,\sigma (j)}-{\pi }^k{}_{B_2,\sigma (j)}|\\ +|u^p{}_{B_1,\sigma (j)}-u^p{}_{B_2,\sigma (j)}-v^p{}_{B_1,\sigma (j)}+v^p{}_{B_2,\sigma (j)}-{\pi }^k{}_{B_1,\sigma (j)}+{\pi }^k{}_{B_2,\sigma (j)}|)\\ +(|u^p{}_{B_2,\sigma (j)}-u^p{}_{B_3,\sigma (j)}|+|v^p{}_{B_2,\sigma (j)}-v^p{}_{B_3,\sigma (j)}|+|{\pi }^k{}_{B_2,\sigma (j)}-{\pi }^k{}_{B_3,\sigma (j)}|\\ +|u^p{}_{B_2,\sigma (j)}-u^p{}_{B_3,\sigma (j)}-v^p{}_{B_2,\sigma (j)}+v^p{}_{B_3,\sigma (j)}-{\pi }^k{}_{B_2,\sigma (j)}+{\pi }^k{}_{B_3,\sigma (j)}|)]\\ \ge \frac{1}{4}{\displaystyle \sum _{j=1}^{L_{B_1{ \mathrm{B}}_{2 }{B}_3}}{p}_{\sigma (j)}(}|u^p{}_{B_1,\sigma (j)}-u^p{}_{B_2,\sigma (j)}+u^p{}_{B_2,\sigma (j)}-u^p{}_{B_3,\sigma (j)}|\\ +|v^p{}_{B_1,\sigma (j)}-v^p{}_{B_2,\sigma (j)}+v^p{}_{B_2,\sigma (j)}-v^p{}_{B_3,\sigma (j)}|\\ +|{\pi }^k{}_{B_1,\sigma (j)}-{\pi }^k{}_{B_2,\sigma (j)}+{\pi }^k{}_{B_2,\sigma (j)}-{\pi }^k{}_{B_3,\sigma (j)}|\\ +|u^p{}_{B_1,\sigma (j)}-u^p{}_{B_2,\sigma (j)}-v^p{}_{B_1,\sigma (j)}+v^p{}_{B_2,\sigma (j)}-{\pi }^k{}_{B_1,\sigma (j)}+{\pi }^k{}_{B_2,\sigma (j)}\\ +u^p{}_{B_2,\sigma (j)}-u^p{}_{B_3,\sigma (j)}-v^p{}_{B_2,\sigma (j)}+v^p{}_{B_3,\sigma (j)}-{\pi }^k{}_{B_2,\sigma (j)}+{\pi }^k{}_{B_3,\sigma (j)}|)\\ =\frac{1}{4}{\displaystyle \sum _{j=1}^{L_{B_1{ \mathrm{B}}_{2 }{B}_3}}{p}_{\sigma (j)}[}(|u^p{}_{B_1,\sigma (j)}-u^p{}_{B_3,\sigma (j)}|+|v^p{}_{B_1,\sigma (j)}-v^p{}_{B_3,\sigma (j)}|+|{\pi }^k{}_{B_1,\sigma (j)}-{\pi }^k{}_{B_3,\sigma (j)}|\\ +|u^p{}_{B_1,\sigma (j)}-u^p{}_{B_3,\sigma (j)}-v^p{}_{B_1,\sigma (j)}+v^p{}_{B_3,\sigma (j)}-{\pi }^k{}_{B_1,\sigma (j)}+{\pi }^k{}_{B_3,\sigma (j)}|)\\ =D(B_1,B_3)\end{array}$$

Therefore, $E(4)$ holds.

Based on the previous proof, it can be concluded that the distance measure formula given in this paper fulfills the specified conditions.

4. Weight Optimization Algorithm in (p,q)-Rung Probabilistic Hesitant Orthopair Fuzzy Environments

4.1. Steps of the Algorithm

Due to the limitations of human cognitive ability and the unpredictability of objectivity, it is always challenging to acquire all attribute weighting information during multi-attribute decision-making. By using the ANP and entropy method to comprehensively evaluate the interaction among expert groups and the correlation degree of each index, a subjective evaluation index system based on ANP is established. On this basis, the weighted optimal mathematical model is constructed by taking the deviation and dispersion degree of the subjective and objective weighting as indicators, and the artificial neural network is used to calculate it iteratively. Then, the enhanced ELECTRE method is used to calculate the overall advantage value, overall disadvantage, value and comprehensive evaluation value of each alternative project. The procedure is as follows:

Step 1: Construct a (p,q)-rung probabilistic hesitant orthopair fuzzy decision matrix $T={(a_{ij})}_{m\times n}$ according to the decision information provided by the expert, where $a_{ij}=\left\{<f_{A_i}(C_j),\right.$ $g_{A_i}(C_j)\left.>|p_{A_i}(C_j)\right\}$ is the expert’s evaluation of alternative $A_i$ under attribute $C_j$.

Step 2: Subjective weights and objective weights are computed using the ANP and entropy weight method.

The ANP replaces the hierarchical structure of the Analytic Hierarchy Process (AHP) with a network structure in order to establish a more complex relationship of influence between decision-making elements. In view of the interdependence between the elements and levels, this method focuses on subjectivity, and its steps are:

(1)

The simulation network model is established. Through a literature review and expert interview, the factors influencing the ANP are systematically analyzed, the interaction relationship between the elements is determined, and the ANP network structure diagram is created.

(2)

Construct a network evaluation matrix, compile expert opinions using the Delphi method, and quantify the relative significance of each index in a matrix. Using the 1–9 scale criterion, the value of relevant importance is determined, and the priority vector is calculated.

(3)

Eigenvalues and eigenvectors are computed and their consistency is examined. The eigenvector is computed using the eigenvalue method and Equation (5), where ${\lambda }_{\max }$ is the largest eigenvalue of the eigenvector.

$$AW={\lambda }_{\max }W$$

(5)

Using Equation (6), ascertain if the matrix satisfies the condition.

$$CR=\frac{{\lambda }_{\max }-1/n-1}{RI}$$

(6)

Here, n is the order of the evaluation matrix, CI is the consistency index, CR is the consistency ratio, RI is the average random index, and it passes the consistency test if RI < 0.1.

(4)

Determine the super limit matrix $A^{\infty }$. The eigenvectors of each index that satisfy the consistency test are combined into a super matrix without weights. The unweighted supermatrix is normalized to produce the weighted supermatrix, which is then stabilized to produce the limited supermatrix. When $i\to \infty$, the limited super matrix is uniquely convergent, as shown by Equation (7), and the evaluation matrix weight ${\omega }_j\prime$ can be calculated.

$$A^{\infty }=\underset{i\to \infty }{\lim }{\left(A\right)}^i$$

(7)

The formula for the entropy weight method is:

$$w_j\prime \prime =\frac{1-E(C_j)}{n-{\displaystyle \sum _{j=1}^{n}E(C_j)}},j=1,2,\dots ,n$$

(8)

where $E(C_j)=\frac{1}{m}{\displaystyle \sum _{i=1}^{m}E(C_{ij}}),i=1,2,\dots ,m$.

Step 3: Due to the subjective limitations of the ANP, the entropy method cannot make subjective judgments that correspond to the actual situation. Consequently, a technique for combining the weights is required. Under the influence of both subjective and objective factors, the weighting coefficient ${\omega }_j$ is used as the comprehensive weighting to minimize the error and maximize the degree of dispersion. The weighted optimal mathematical model is as follows:

$$\begin{array}{c}\min T=\alpha {\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n\left[{\left(\left({\omega }_j-{\omega }_j{}^{\prime }\right)s_{ij}\right)}^2+{\left(\left({\omega }_j-{\omega }_j{}^{\prime \prime }\right)s_{ij}\right)}^2\right]}}-\beta {{\displaystyle \sum _{j=1}^n{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{h=1}^m\left[\left(s_{ij}-s_{hj}\right){\omega }_j\right]}}}}^2\\ s.t.{\displaystyle \sum _{j=1}^n{\omega }_j}=1\\ {\omega }_j>0,j=1,2,\dots ,n\end{array}$$

(9)

$\alpha$ and $\beta$ represent the importance degree, ${\omega }_j{}^{\prime }$ represents the subjective weight, ${\omega }_j{}^{\prime \prime }$ represents the objective weight, $s_{ij}$ is the j-th attribute value of the i-th evaluation object, and $m$ represents the total number of evaluation objects.

Given that Formula (9) represents a nonlinear model, it is worth noting that neural networks possess the capability to efficiently identify the optimal solution in a timely manner. The loss function is given by Formula (9), and the neural network is employed to maximize the weights in order to identify the most effective solution.

Step 4: Calculate the score function value.

Using Formula (1), the score $\phi ({\varphi }_{ij})$ of each element in the decision information matrix is obtained, and the score matrix $\Phi ={(\phi ({\varphi }_{ij}))}_{m\times n}$ is constructed. The scores of different types of planning are arranged by grade, the reference points whose intermediate values are odd planning are selected, and two points which are close to the intermediate values are selected as the reference points of even planning; the reference point is denoted by $A_{ij}{}^{+}$.

Step 5: Construct the weighted criteria decision matrix.

The distance $d({\varphi }_{ij},A_{ij}{}^{+})$ between each alternative and the reference point with the same property is obtained by using Formula (4), so as to obtain a standardized decision matrix $D={(d_{ij})}_{m\times n}$. Where:

$$d_{ij}=\left\{\begin{array}{l}d\left({\varphi }_{ij},A_{ij}{}^{+}\right),{\varphi }_{ij}\ge A_{ij}{}^{+}\\ -d\left({\varphi }_{ij},A_{ij}{}^{+}\right),{\varphi }_{ij}<A_{ij}{}^{+}\end{array}\right.$$

(10)

Multiplying the standardized decision matrix by the weights $\omega$ yields the weighted criteria decision matrix $L={(l_{ij})}_{m\times n}$.

Step 6: Compute the matrices of concordance and discordance.

Through the comparison of different alternative combinations, the concordance and discordance sets of each combination are found. The concordance sets for options $A_k$ and $A_l$ contain the condition that all $A_k$’s preferences are non-inferior to $A_l$, that is, $L_{kl}^{+}=\{j|l_{kj}\ge l_{lj}\}$, whereas the discordance sets contain the criterion that all $A_k$’s preferences are inferior to $A_l$, that is, $L_{kl}^{-}=\{j|l_{kj}<l_{lj}\}$. Equations (11) and (12) are then used to compute the consistency matrix $h={(h_{kl})}_{m\times n}$ and the inconsistency matrix $t={(t_{kl})}_{m\times n}$.

$$h_{kl}=\frac{{\displaystyle {\sum }_{j\in L_{kl}^{+}}{\omega }_j}}{{\displaystyle {\sum }_{j=1}^n{\omega }_j}}$$

(11)

$$t_{kl}=\frac{\underset{j\in L_{kl}^{-}}{\max }\left|d_{kj}-d_{lj}\right|}{\underset{j\in J}{\max }\left|d_{kj}-d_{lj}\right|}$$

(12)

Step 7: Compute the operation of the synthetic matrix.

The determination of the synthetic matrix $E={(e_{kl})}_{m\times m}$ is based on the concordance matrix and the discordance matrix, which allows for the reflection of the relative benefits of each alternative across several criteria. The matrix element $e_{kl}$ can be ascertained through the utilization of the subsequent equation:

$$e_{kl}=h_{kl}-t_{kl}$$

(13)

Step 8: Determine the advantage values, disadvantage values, and overall evaluation values.

To determine all the advantages and disadvantages of each option, add the values of each row and column in the exhaustive matrix.

$${\mu }_k={\displaystyle \sum _{l=1}^m{e}_{kl}},k=1,2,\dots ,m$$

(14)

$${\nu }_l={\displaystyle \sum _{k=1}^m{e}_{kl}},l=1,2,\dots ,m$$

(15)

The cumulative value of each option’s dominance is calculated as follows:

$${\sigma }_k={\mu }_k-{\nu }_l,k=l$$

(16)

Ultimately, the various alternatives are assessed and ordered based on their cumulative dominance value.

We use a flowchart to represent the above algorithm steps, and the content is shown in Figure 1.

4.2. Example

With the advancement of the economy, online purchasing has become the predominant method of shopping in modern society. A solid logistics address can reduce both transportation expenses and delivery time. A logistics company intends to select the most optimal address from several alternatives. After preliminary vetting, six addresses are available for selection, which are set as $A=\{A_1,A_2,A_3,A_4,A_5,A_6\}$, respectively, and $C=\{C_1,C_2,C_3,C_4,C_5,C_6\}$ are the six attributes considered for the logistics location to be selected, where $C_1$ stands for the “labor resource condition”, $C_2$ stands for the “regional policy”, $C_3$ stands for the “traffic condition”, $C_4$ stands for the “terrain condition”, $C_5$ stands for the “subject customer distribution”, and $C_6$ stands for the “surrounding environment”.

The evaluation of the alternatives by experts under each attribute constitutes a (p,q)-rung probability hesitant orthopair fuzzy matrix.

Step 1: The matrix is shown in

Table 1. (p,q)-rung probability hesitant orthopair fuzzy matrix.

	C1	C2	C3	C4	C5	C6
$A_1$	{<0.55,0.4>|0.3, <0.5,0.35>|0.7}	{<0.35,0.2>|1}	{<0.65,0.2>|0.6, <0.55,0.4>|0.4}	{<0.7,0.3>|0.4, <0.55,0.2>|0.6}	{<0.6,0.2>|0.7, <0.55,0.25>|0.3}	{<0.7,0.3>|1}
$A_2$	{<0.5,0.35>|1}	{<0.3,0.6>|0.3, <0.3,0.5>|0.7}	{<0.65,0.4>|1}	{<0.6,0.2>|0.7, <0.55,0.2>|0.3}	{<0.3,0.6>|1}	{<0.65,0.2>|1}
$A_3$	{<0.4,0.25>|0.4, <0.35,0.25>|0.6}	{<0.7,0.4>|1}	{<0.6,0.3>|1}	{<0.7,0.2>|1}	{<0.8,0.1>|1}	{<0.7,0.4>|0.4, <0.6,0.2>|0.2, <0.7,0.2>|0.4}
$A_4$	{<0.55,0.4>|0.7, <0.4,0.3>|0.3}	{<0.6,0.35>|0.6, <0.5,0.35>|0.4}	{<0.7,0.3>|1}	{<0.6,0.35>|1}	{<0.55,0.3>|0.4, <0.44,0.2>|0.6}	{<0.6,0.3>|1}
$A_5$	{<0.55,0.2>|1}	{<0.5,0.2>|1}	{<0.5,0.4>|0.5, <0.6,0.2>|0.5}	{<0.9,0.3>|0.4, <0.7,0.2>|0.6}	{<0.8,0.15>|0.6, <0.6,0.3>|0.4}	{<0.7,0.35>|1}
$A_6$	{<0.5,0.2>|0.7, <0.6,0.25>|0.3}	{<0.3,0.6>|0.1, <0.3,0.65>|0.9}	{<0.45,0.3>|1}	{<0.7,0.25>|1}	{<0.6,0.2>|1}	{<0.7,0.3>|1}

, set to $T$, and $p=1,q=2$ according to the value principle.

Step 2: The attribute entropy is computed using Equation (3), the entropy value of each attribute is displayed in

Table 2. Attribute entropy values.

E(C1)	E(C2)	E(C3)	E(C4)	E(C5)	E(C6)
0.76	0.784	0.647	0.572	0.649	0.544

, and the subjective and objective weights derived using the ANP and Equation (8) are displayed in

Table 3. Subjective and Objective weights.

	C1	C2	C3	C4	C5	C6
$\omega \prime$	0.22	0.2	0.08	0.12	0.1	0.28
$\omega \prime \prime$	0.118	0.105	0.173	0.21	0.171	0.223

.

Step 3: The neural network is employed to optimize the weights, the loss function is (9), and Adam is the optimization function. After 90 iterations, the loss value tends to stabilize, and

Table 4. Weights after optimization.

	C1	C2	C3	C4	C5	C6
$\omega$	0.1629	0.1632	0.1217	0.1611	0.1445	0.2465

displays the optimization results.

Step 4: The score function is computed using Equation (1), which is subsequently employed to sort the findings and determine the intermediate value that serves as the reference value. See

Table 5. Scoring matrix and reference values.

	C1	C2	C3	C4	C5	C6
$A_1$	0.6526	0.6274	0.7105	0.7215	0.7158	0.7677
$A_2$	0.6602	0.5068	0.7161	0.7183	0.4744	0.762
$A_3$	0.6214	0.7418	0.719	0.7863	0.8485	0.7363
$A_4$	0.6466	0.6760	0.7677	0.7064	0.6689	0.719
$A_5$	0.7153	0.6927	0.6806	0.7951	0.772	0.7556
$A_6$	0.6932	0.4529	0.6508	0.7779	0.7383	0.7677
Point of reference	$A_2$	$A_4$	$A_2$	$A_6$	$A_6$	$A_2$

.

Step 5: According to Formula (4), the distance is calculated, constructing the standardized decision matrix, and multiplying the weights yields the weighted criteria decision matrix as shown in

Table 6. The weighted criteria decision matrix.

	C1	C2	C3	C4	C5	C6
$A_1$	−0.0160	−0.0201	−0.0229	−0.0316	−0.0160	0.0200
$A_2$	0	−0.0214	0	−0.0319	−0.0448	0
$A_3$	−0.0340	0.0209	0.0253	0.0018	0.0250	−0.0247
$A_4$	−0.0192	0	0.0148	−0.0127	−0.0286	−0.0468
$A_5$	0.0108	0.0214	−0.0245	0.0187	0.0181	−0.0279
$A_6$	0.0174	−0.0335	−0.0226	0	0	0.0256

.

Step 6: Using Formulas (11) and (12), the concordance matrix and discordance matrix are calculated, respectively. The outcomes are shown in

Table 7. Concordance matrix.

	A1	A2	A3	A4	A5	A6
$A_1$	0	0.7153	0.4094	0.5539	0.3682	0.1632
$A_2$	0.2846	0	0.4094	0.4094	0.3682	0.2849
$A_3$	0.5905	0.5905	0	0.837	0.5127	0.5905
$A_4$	0.446	0.5905	0.1629	0	0.1217	0.2849
$A_5$	0.6317	0.6317	0.4872	0.8782	0	0.4688
$A_6$	0.8367	0.715	0.4094	0.715	0.5311	0

and

Table 8. Discordance matrix.

	A1	A2	A3	A4	A5	A6
$A_1$	0	0.9447	1	1	1	1
$A_2$	1	0	1	0.6895	1	1
$A_3$	0.4571	0.4327	0	0.2453	0.6724	0.802
$A_4$	0.8742	1	1	0	1	0.9545
$A_5$	0.6218	0.4621	1	1	0	0.6458
$A_6$	0.4	0.6	1	1	1	0

.

Step 7: The exhaustive matrix is calculated using Equation (13), as shown in

Table 9. Exhaustive matrix.

	A1	A2	A3	A4	A5	A6
$A_1$	0	−0.2294	−0.5906	−0.4461	−0.6318	−0.8368
$A_2$	−0.7154	0	−0.5906	−0.2801	−0.6318	−0.7151
$A_3$	0.1334	0.1578	0	0.5917	−0.1597	−0.2115
$A_4$	−0.4282	−0.4095	−0.8371	0	−0.8783	−0.6696
$A_5$	0.0099	0.1696	−0.5128	−0.1218	0	−0.177
$A_6$	0.4367	0.115	−0.5906	−0.285	−0.4689	0

.

Step 8: Using Equations (14)–(16), the overall advantage value, overall disadvantage value, and comprehensive evaluation value of each alternative are calculated. According to

Table 10. Results of the decision.

	A1	A2	A3	A4	A5	A6
$\mu$	−2.7347	−2.933	0.5117	−3.2227	−0.6321	0.7928
$\nu$	−0.5636	−0.1965	−3.1217	−0.5413	−2.7705	−2.61
$\sigma$	−2.1711	−2.7365	3.6334	−2.6814	2.1384	1.8172
Ranking	A3 > A5> A6 > A1> A4 > A2
Optimal solution	A3

, a greater total evaluation value denotes a superior option.

According to the above-mentioned algorithm, the six alternatives are ranked as $A_3>A_5>A_6>A_1>A_4>A_2$, with address $A_3$ being the finest option.

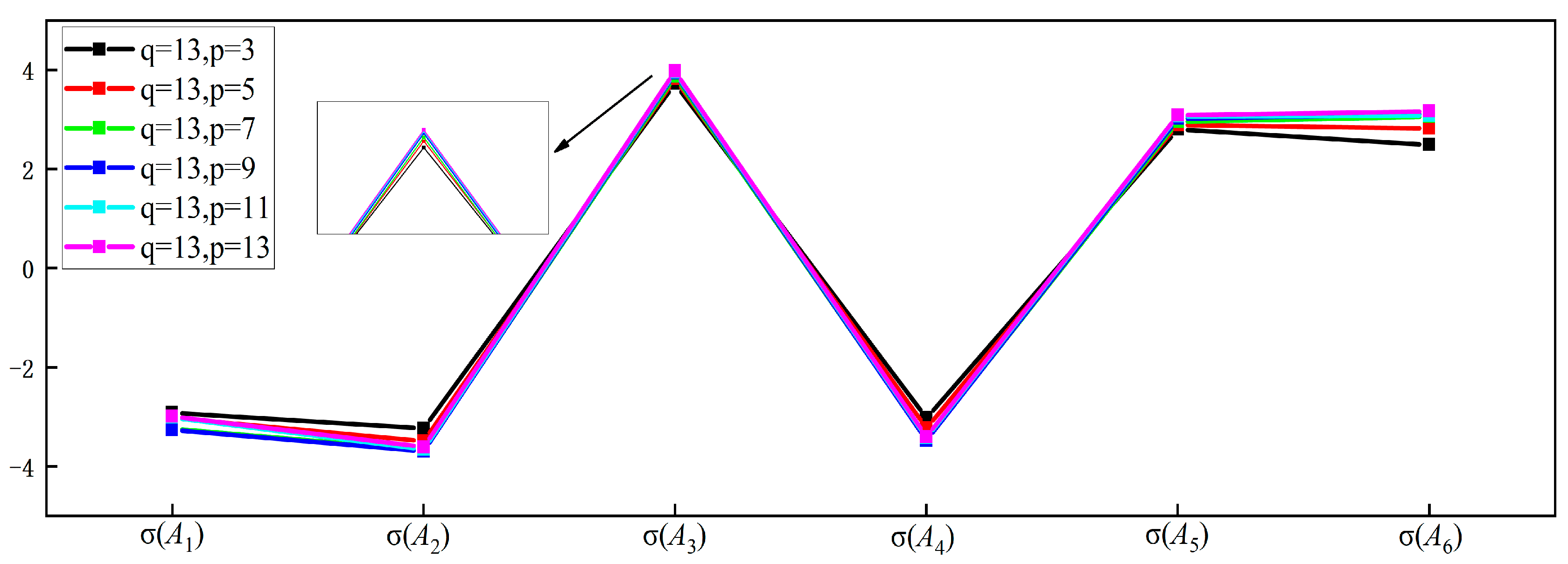
4.3. Parametric Analysis

In order to verify the stability of the study, we performed a sensitivity analysis on the parameters p and q in Section 4.3, and the results are presented in

Table 11. Different p values correspond to the ranking results of each program (q = 13).

Parametric p	σ(A1)	σ(A2)	σ(A3)	σ(A4)	σ(A5)	σ(A6)	Ranking
$p=3$	−2.9177	−3.2294	3.7254	−3.0214	2.8014	2.4881	A3> A5> A6> A1> A4> A2
$p=5$	−3.0193	−3.4914	3.8184	−3.2279	2.8927	2.8167	A3> A5> A6> A1> A4> A2
$p=7$	−3.2362	−3.6717	3.8717	−3.4575	2.9544	3.0544	A3> A6> A5> A1> A4> A2
$p=9$	−3.2589	−3.6924	3.9277	−3.4766	3.0154	3.1079	A3> A6> A5> A1> A4> A2
$p=11$	−3.0107	−3.6584	3.9548	−3.4281	3.0627	3.0793	A3> A6> A5> A1> A4> A2
$p=13$	−2.9875	−3.6069	3.9754	−3.4017	3.0849	3.1625	A3> A6> A5> A1> A4> A2

and

Table 12. Different q values correspond to the ranking results of each program (p = 3).

Parametric q	σ(A1)	σ(A2)	σ(A3)	σ(A4)	σ(A5)	σ(A6)	Ranking
$q=3$	−1.6793	−2.2344	2,8167	−2.1277	2.3883	2.0603	A3> A5> A6> A1> A4> A2
$q=5$	−1.4984	−2.0537	2.1033	−1.9463	2.1284	1.8794	A3> A5> A6> A1> A4> A2
$q=7$	−1.3372	−1.9197	1.9754	−1.8603	1.9509	1.5278	A3> A5> A6> A1> A4> A2
$q=9$	−1.3092	−1.8972	1.8793	−1.8355	1.8762	1.4572	A3> A5> A6> A1> A4> A2
$q=11$	−1. 2911	−1.8903	1.9742	−1.8287	1.7829	1.0164	A3> A5> A6> A1> A4> A2
$q=13$	−1.2896	−1.8864	1.9628	−1.8109	1.7728	0.7392	A3> A5> A6> A1> A4> A2

with concise analyses.

In order to more intuitively reflect the change in the comprehensive evaluation value of each scheme with the parameters p and q, Figure 2 and Figure 3 are given.

From Table 11 and Table 12 and Figure 2 and Figure 3, it can be seen that when one of the values of p and q is fixed, with the increase of the other parameter there is no change in the optimal scheme and the worst scheme, and the overall sorting result is relatively stable, which indicates that the method has good stability.

4.4. Comparative Analysis

The decision models from three references are used to compare and analyze the ranking results in order to demonstrate the efficacy of the author’s model. According to Ren’s method [22], the final decision scheme is determined by aggregating the evaluation information through the q-PHFPWMM. Shahzaib Ashra’s method [26] proposes and employs an entropy measure of probabilistic q-rung orthopair hesitant fuzzy sets in the ranking of three extended hybrid methods. In published works [27], Chen et al. rank alternatives using the GRA and TOPSIS methods. The parameter is set to 2, and Table 11 displays the results.

To describe the above results more clearly, we plotted the above data as a line chart. This is shown in Figure 4.

According to

Table 13. Calculation results of different methods.

Methods	Specific Data						Ranking
	A1	A2	A3	A4	A5	A6
Ren et al. [22] proposed method	0.478	0.3658	0.5759	0.461	0.5359	0.3733	A3> A5> A1> A4> A6> A2
Shahzaib Ashra et al. [26] proposed method	0.6919	0.498	0.8387	0.7203	0.8219	0.5432	A3> A5> A4> A1> A6> A2
Chen et al. [27] proposed method	0.521	0.3394	0.7603	0.4102	0.6672	0.4313	A3> A5> A1> A6> A4> A2
Our proposed paper	−2.1711	−2.7365	3.6334	−2.6814	2.1384	1.8172	A3> A5> A6> A1> A4> A2

, there are only minor differences in the ranking results of the four methods, and the optimal scheme and the worst scheme are the same, indicating that the results calculated by the proposed method are convincing and reflect the effectiveness of the proposed method. From Figure 4, we can see that the calculated value of the proposed method fluctuates obviously, while the differences of the other methods are small. When encountering some data with large ambiguity, the final scheme may not be judged. Therefore, the proposed method is superior to the other three methods.

In addition, Ren’s method [22] needs to construct the syntheses support matrix first, and then calculate the comprehensive evaluation value through the q-PHFPWMM to finally determine the score function value, which is too complex and has a huge amount of calculation. Shahzaib Ashra’s method [26] only regarded the difference in element values when calculating the weighted distance; it did not take into account the influence of hesitancy degree. Chen et al.’s [27] proposed method is unsuitable for data with a linear relationship between attributes.

In conclusion, despite the fact that each of the above decision-making methods has its own advantages and disadvantages and that the ranking sequence is not identical, the four methods yield the same final results. Experiments show that the proposed algorithm is feasible, not random. Thus, a new and credible method is proposed for solving multi-objective group decision-making problems.

5. Conclusions

A weight optimization group decision-making algorithm appropriate for (p,q)-rung probability hesitant orthopair fuzzy sets is proposed in this paper. The primary endeavor is demonstrated in the following ways:

(1)

In order to better solve the uncertain problems in life and make up for the limitations of q-rung orthopair probability hesitant fuzzy sets, the notion of (p,q)-rung probability hesitant orthopair fuzzy sets is proposed to expand the value range of elements, and its operation law and the value principle of (p,q) are given. Not only that, in order to be more consistent with the actual decision-making, and so decision-makers will turn to this scheme with higher support, we define a new hesitant degree, score function, accuracy function, entropy measure, and distance formula. Finally, we carry out a rigorous proof to ensure that the proposed formula is in line with the requirements.

(2)

A weight optimization model is established to determine the optimal weight. Firstly, the subjective and objective weights are obtained by using the ANP and entropy method to comprehensively evaluate the subject and object indexes. Then, after fully considering the influence of subjective and objective weighting on the comprehensive weight, the deviation and dispersion of subjective and objective weighting are used as optimization indicators to construct the weight optimization model. Finally, the weight optimization model is used as the loss function, and Adam is used as the optimization function to calculate the optimal weight through neural network iteration.

(3)

The ELECTRE method is improved and applied to the (p,q)-rung probability hesitant orthopair fuzzy environment. This method combines the optimal weights obtained by the weighted optimal mathematical model with the relevant definitions of (p,q)-rung probability hesitant orthopair fuzzy sets, and establishes a new multi-attribute decision-making model. In addition, this new multi-attribute decision-making model is applied to the practical application of logistics location. After calculating the optimal result, three different algorithms are selected to compare with the proposed algorithm to verify the superiority of the proposed model. Different p and q values are selected for sensitivity analysis to verify the stability of the algorithm.

Overall, the proposed algorithm not only solves the limitations of the existing methods, but also introduces concepts of a new fuzzy set, which can calculate a wider range of attribute values and enhance the convincing degree of the actual decision-making process. The final results verify the effectiveness and applicability of the proposed algorithm, which provides a valuable tool for decision-makers facing complex and uncertain decision scenarios.

6. Discussions

Many of the above research contents have many benefits, which not only make up for the shortcomings of q-rung orthopair probability hesitant fuzzy sets, but also assist decision-makers in better evaluations of indicators. It can be applied to control systems, emergency decisions, pattern recognitions, information retrievals, and other practical problems. However, there are also some shortcomings, such as the use of neural network for weight optimization and easy-to-appear local extreme values, so that the calculation results have a certain degree of change. Therefore, future research will investigate how to further enhance the algorithm’s precision. In addition, in the subsequent research, we will focus on the design of (p,q)-rung probability hesitant orthopair fuzzy aggregation operators to deal with the possible correlations between attributes, and apply the concept of (p,q)-rung probability hesitant orthopair fuzzy sets and rough sets to the application of three-way decisions.