Scheduling Scientific Workflow in Multi-Cloud: A Multi-Objective Minimum Weight Optimization Decision-Making Approach
Abstract
:1. Introduction
- Reducing workflow time (makespan);
- Reducing cost;
- Maximizing resource utilization;
- Increasing the workflow reliability for the customer;
- Reducing the risk probability of the workflow.
- By designing a fitness function to reduce makespan, cost, and risk probability and maximize resource utilization and reliability, service providers and users’ interests are taken into account simultaneously.
- A feasible solution is chosen and demonstrated through using the Pareto front’s optimal set utilizing a novel decision-making technique called minimum weight optimization (MWO), which takes into account user preferences.
- The performance of the MWO-based multi-objective algorithm is contrasted to that of five other conventional workflow scheduling decision-making techniques, such as Pareto optimum and WASPAS.
2. Related Work
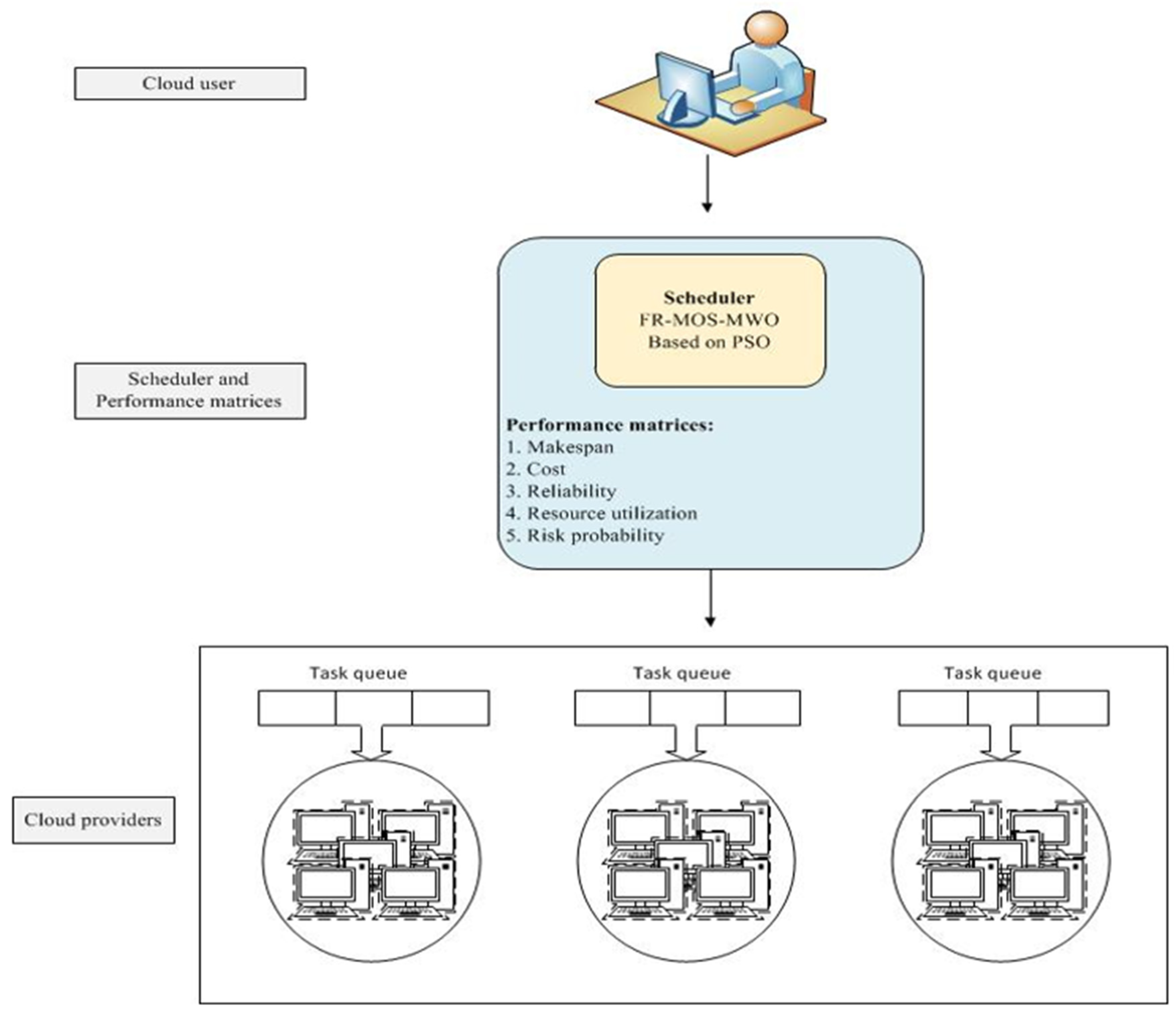
3. Scheduling Scenario
3.1. Workflow Model
3.2. Multi-Cloud Architecture
3.3. Makespan Computation
3.4. Cost Computation
3.5. Resource Utilization Computation
3.6. Reliability Computation
3.7. Workflow Risk Probability
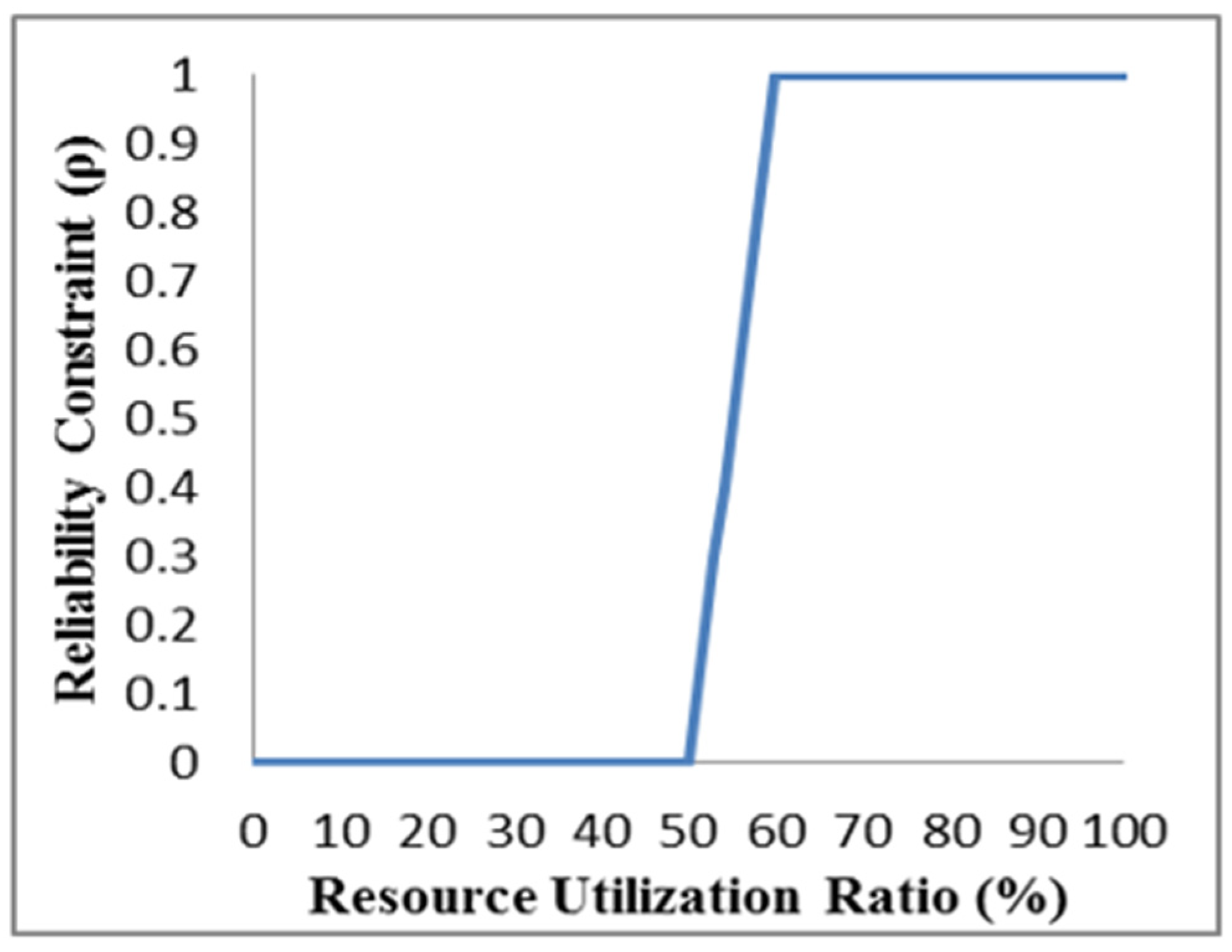
3.8. Fuzzy Logic
3.9. Problem Description
4. Multi-Objective Optimization Methods
4.1. Particle Swarm Optimization (PSO)
4.2. Multi-Objective Pareto Optimal Approach
- In all objectives, solution X is not worse than solution Y.
- X is simply superior to Y in at least one objective.
Pareto Optimality Method
4.3. Weighted Sum Function
4.3.1. Minimum Weight Optimization (MWO) Method
4.3.2. Weighted Aggregated Sum Product Assessment (WASPAS) Method
- Decision-Making and Selecting a Definitive Solution
4.3.3. Multi-Criteria Decision-Making (MCDM) Method
4.3.4. Linear Normalization
5. The Proposed Algorithms
5.1. The Five-Objective Case Study
5.2. Determining Attributes and Alternatives
5.3. FR-MOS-MWO Algorithm
| Algorithm 1: FR-MOS-MWO |
|
5.4. FR-MOS-PARETO Algorithm
| Algorithm 2: FR-MOS-PARETO |
|
5.5. Coding Strategy
| Algorithm 3: Order tasks |
|
6. Experimental Setup and Simulation Results
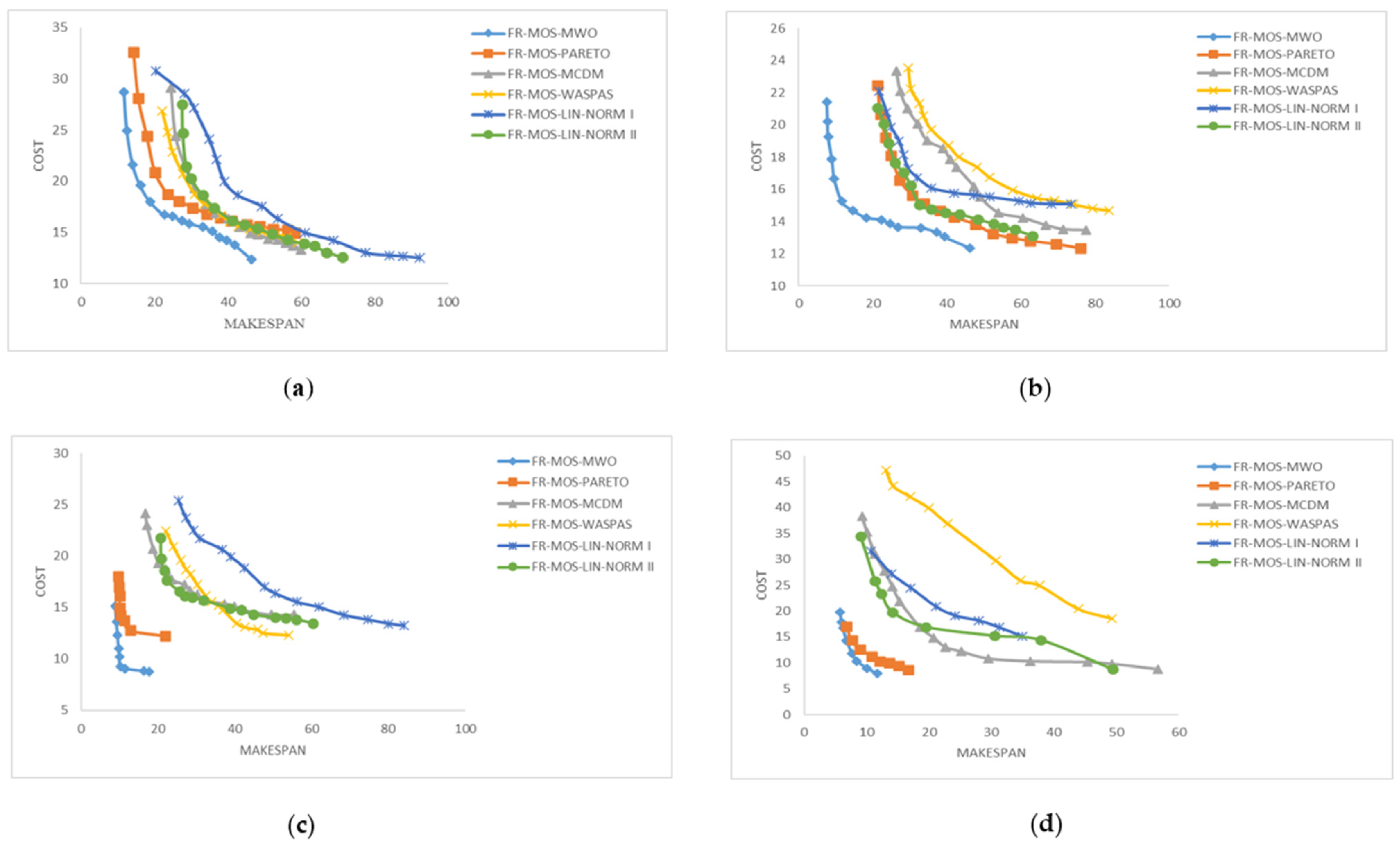
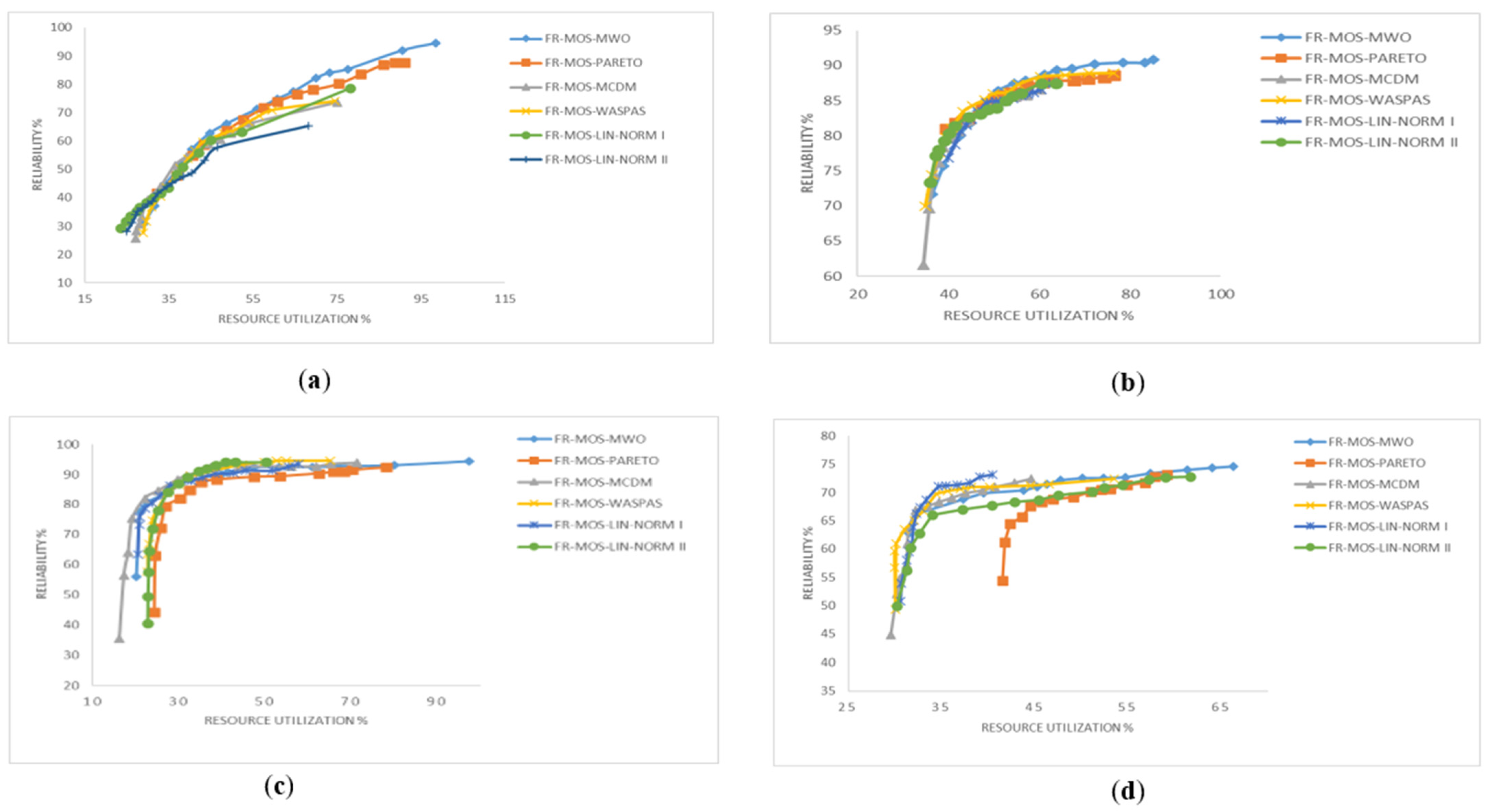
6.1. Simulation Results
6.2. Performance Measurement
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ebadifard, F. Dynamic task scheduling in cloud computing based on Naïve Bayesian classifier. In Proceedings of the International Conference for Young Researchers in Informatics, Mathematics, and Engineering, Kaunas, Lithuania, 28 April 2017; Volume 1852. [Google Scholar]
- Lin, B.; Guo, W.; Chen, G.; Xiong, N.; Li, R. Cost-Driven Scheduling for Deadline-Constrained Workflow on Multi-clouds. In Proceedings of the 2015 IEEE International Parallel and Distributed Processing Symposium Workshop (IPDPSW), Hyderabad, India, 25–29 May 2015; pp. 1191–1198. [Google Scholar] [CrossRef]
- Sooezi, N.; Abrishami, S.; Lotfian, M. Scheduling data-driven workflows in multi-cloud environment. In Proceedings of the 2015 IEEE 7th International Conference on Cloud Computing Technology and Science (CloudCom), Vancouver, BC, Canada, 30 November–3 December 2015; pp. 163–167. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, M. Multi-objective optimization model with AHP decision-making for cloud service composition. KSII Trans. Internet Inf. Syst. 2015, 9, 3293–3311. [Google Scholar] [CrossRef]
- Ebadifard, F.; Babamir, S.M. A Multi-Objective Approach With WASPAS Decision-Making for Workflow Scheduling in Cloud Environment. Int. J. Web Res. 2018, 1, 1–10. [Google Scholar]
- Li, J.; Su, S.; Cheng, X.; Huang, Q.; Zhang, Z. Cost-conscious scheduling for large graph processing in the cloud. In Proceedings of the 2011 IEEE International Conference on High Performance Computing and Communications, Banff, AB, Canada, 2–4 September 2011; pp. 808–813. [Google Scholar] [CrossRef]
- Jeannot, E.; Saule, E.; Trystram, D. Optimizing performance and reliability on heterogeneous parallel systems: Approximation algorithms and heuristics. J. Parallel Distrib. Comput. 2012, 72, 268–280. [Google Scholar] [CrossRef]
- Sih, G.C.; Lee, E.A. A Compile-Time Scheduling Heuristic for Interconnection-Constrained Heterogeneous Processor Architectures. IEEE Trans. Parallel Distrib. Syst. 1993, 4, 175–187. [Google Scholar] [CrossRef]
- Doǧan, A.; Özgüner, F. Biobjective scheduling algorithms for execution time-reliability trade-off in heterogeneous computing systems. Comput. J. 2005, 48, 300–314. [Google Scholar] [CrossRef]
- Bilgaiyan, S.; Sagnika, S.; Das, M. A Multi-objective Cat Swarm Optimization Algorithm for Workflow Scheduling in Cloud Computing Environment. Fortune 2015, 167, 62–66. [Google Scholar] [CrossRef]
- Udomkasemsub, O.; Xiaorong, L.; Achalakul, T. A multiple-objective workflow scheduling framework for cloud data analytics. In Proceedings of the 9th International Joint Conference on Computer Science and Software Engineering, Bangkok Thailand, 30 May–1 June 2012; pp. 391–398. [Google Scholar] [CrossRef]
- Wu, Z.; Ni, Z.; Gu, L.; Liu, X. A revised discrete particle swarm optimization for cloud workflow scheduling. In Proceedings of the 2010 International Conference on Computational Intelligence and Security, Nanning, China, 11–14 December 2010; pp. 184–188. [Google Scholar] [CrossRef]
- Khalili, A.; Babamir, S.M. Optimal scheduling workflows in cloud computing environment using Pareto-based Grey Wolf Optimizer. Concurr. Comput. 2017, 29, 1–11. [Google Scholar] [CrossRef]
- Yassa, S.; Chelouah, R.; Kadima, H.; Granado, B. Multi-objective approach for energy-aware workflow scheduling in cloud computing environments. Sci. World J. 2013, 2013, 350934. [Google Scholar] [CrossRef]
- Ebadifard, F.; Babamir, S.M. Scheduling scientific workflows on virtual machines using a Pareto and hypervolume based black hole optimization algorithm. J. Supercomput. 2020, 76, 7635–7688. [Google Scholar] [CrossRef]
- Kaur, P.; Mehta, S. Resource provisioning and work flow scheduling in clouds using augmented Shuffled Frog Leaping Algorithm. J. Parallel Distrib. Comput. 2017, 101, 41–50. [Google Scholar] [CrossRef]
- Zhang, M.; Li, H.; Liu, L.; Buyya, R. An adaptive multi-objective evolutionary algorithm for constrained workflow scheduling in Clouds. Distrib. Parallel Databases 2018, 36, 339–368. [Google Scholar] [CrossRef]
- Singh, V.; Gupta, I.; Jana, P.K. An Energy Efficient Algorithm for Workflow Scheduling in IaaS Cloud. J. Grid Comput. 2019, 18, 357–376. [Google Scholar] [CrossRef]
- Verma, A.; Kaushal, S. A hybrid multi-objective Particle Swarm Optimization for scientific workflow scheduling. Parallel Comput. 2017, 62, 1–19. [Google Scholar] [CrossRef]
- Dharwadkar, N.V.; Poojara, S.R.; Kadam, P.M. Fault Tolerant and Optimal Task Clustering for Scientific Workflow in Cloud. Int. J. Cloud Appl. Comput. 2018, 8, 1–19. [Google Scholar] [CrossRef]
- Xu, H.; Yang, B.; Qi, W.; Ahene, E. A multi-objective optimization approach to workflow scheduling in clouds considering fault recovery. KSII Trans. Internet Inf. Syst. 2016, 10, 976–995. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, G.; Sun, J.; Zhou, J.; Wei, T.; Hu, S. Minimizing cost and makespan for workflow scheduling in cloud using fuzzy dominance sort based HEFT. Futur. Gener. Comput. Syst. 2019, 93, 278–289. [Google Scholar] [CrossRef]
- Ajeena Beegom, A.S.; Rajasree, M.S. Non-dominated sorting based PSO algorithm for workflow task scheduling in cloud computing systems. J. Intell. Fuzzy Syst. 2019, 37, 6801–6813. [Google Scholar] [CrossRef]
- Alazzam, H.; Alhenawi, E.; Al-Sayyed, R. A hybrid job scheduling algorithm based on Tabu and Harmony search algorithms. J. Supercomput. 2019, 75, 7994–8011. [Google Scholar] [CrossRef]
- Durillo, J.J.; Fard, H.M.; Prodan, R. MOHEFT: A multi-objective list-based method for workflow scheduling. In Proceedings of the 4th IEEE International Conference on Cloud Computing Technology and Science Proceedings (CloudCom 2012), Taipei, Taiwan, 3–6 December 2012; pp. 185–192. [Google Scholar] [CrossRef]
- Durillo, J.J.; Prodan, R. Multi-objective workflow scheduling in Amazon EC2. Cluster Comput. 2014, 17, 169–189. [Google Scholar] [CrossRef]
- Durillo, J.J.; Prodan, R.; Barbosa, J.G. Pareto tradeoff scheduling of workflows on federated commercial Clouds. Simul. Model. Pract. Theory 2015, 58, 95–111. [Google Scholar] [CrossRef]
- Talukder, A.K.M.K.A.; Kirley, M.; Buyya, R. Multiobjective differential evolution for scheduling workflow applications on global Grids. Concurr. Comput. Pract. Exp. 2009, 21, 1742–1756. [Google Scholar] [CrossRef]
- Tsai, J.T.; Fang, J.C.; Chou, J.H. Optimized Task Scheduling and Resource Allocation on Cloud Computing Environment Using Improved Differential Evolution Algorithm; Elsevier: Amsterdam, The Netherlands, 2013; Volume 40, ISBN 8868721503. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, G.; Li, M.; Liu, X. Evolutionary Multi-Objective Workflow Scheduling in Cloud. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 1344–1357. [Google Scholar] [CrossRef]
- Yu, J.; Buyya, R.; Ramamohanarao, K. Workflow scheduling algorithms for grid computing. Stud. Comput. Intell. 2008, 146, 173–214. [Google Scholar] [CrossRef]
- Kalra, M.; Singh, S. Multi-criteria workflow scheduling on clouds under deadline and budget constraints. Concurr. Comput. 2019, 31, e5193. [Google Scholar] [CrossRef]
- Yao, G.; Ding, Y.; Hao, K. Multi-objective workflow scheduling in cloud system based on cooperative multi-swarm optimization algorithm. J. Cent. South Univ. 2017, 24, 1050–1062. [Google Scholar] [CrossRef]
- Farid, M.; Latip, R.; Hussin, M.; Asilah Wati Abdul Hamid, N. Weighted-adaptive Inertia Strategy for Multi-objective Scheduling in Multi-clouds. Comput. Mater. Contin. 2022, 72, 1529–1560. [Google Scholar] [CrossRef]
- Casas, I.; Taheri, J.; Ranjan, R.; Zomaya, A.Y. PSO-DS: A scheduling engine for scientific workflow managers. J. Supercomput. 2017, 73, 3924–3947. [Google Scholar] [CrossRef]
- Farid, M.; Latip, R.; Hussin, M.; Abdul Hamid, N.A.W. Scheduling scientific workflow using multi-objective algorithm with fuzzy resource utilization in multi-cloud environment. IEEE Access 2020, 8, 24309–24322. [Google Scholar] [CrossRef]
- Rodriguez, M.A.; Buyya, R. Deadline Based Resource Provisioning and Scheduling Algorithm for Scientific Workflows on Clouds. IEEE Trans. Cloud Comput. 2014, 2, 222–235. [Google Scholar] [CrossRef]
- Li, Z.; Ge, J.; Hu, H.H.; Song, W.; Hu, H.H.; Luo, B. Cost and Energy Aware Scheduling Algorithm for Scientific Workflows with Deadline Constraint in Clouds. IEEE Trans. Serv. Comput. 2015, 11, 713–726. [Google Scholar] [CrossRef]
- Zhang, C.; Green, R.; Alam, M. Reliability and utilization evaluation of a cloud computing system allowing partial failures. In Proceedings of the 2014 IEEE 7th International Conference on Cloud Computing, Anchorage, AK, USA, 27 June–2 July 2014; pp. 936–937. [Google Scholar] [CrossRef]
- Kianpisheh, S.; Charkari, N.M.; Kargahi, M. Reliability-driven scheduling of time/cost-constrained grid workflows. Futur. Gener. Comput. Syst. 2016, 55, 1–16. [Google Scholar] [CrossRef]
- Poola, D.; Ramamohanarao, K.; Buyya, R. Enhancing reliability of workflow execution using task replication and spot instances. ACM Trans. Auton. Adapt. Syst. 2016, 10, 1–21. [Google Scholar] [CrossRef]
- Li, Z.; Ge, J.; Yang, H.; Huang, L.; Hu, H.; Hu, H.; Luo, B. A security and cost aware scheduling algorithm for heterogeneous tasks of scientific workflow in clouds. Futur. Gener. Comput. Syst. 2016, 65, 140–152. [Google Scholar] [CrossRef]
- Zeng, L.; Veeravalli, B.; Li, X. SABA: A security-aware and budget-aware workflow scheduling strategy in clouds. J. Parallel Distrib. Comput. 2015, 75, 141–151. [Google Scholar] [CrossRef]
- Fard, H.M.; Prodan, R.; Fahringer, T. Multi-objective list scheduling of workflow applications in distributed computing infrastructures. J. Parallel Distrib. Comput. 2014, 74, 2152–2165. [Google Scholar] [CrossRef]
- Zhang, L.; Li, K.K.; Li, C.; Li, K.K. Bi-objective workflow scheduling of the energy consumption and reliability in heterogeneous computing systems. Inf. Sci. 2017, 379, 241–256. [Google Scholar] [CrossRef]
- Tang, X.; Li, K.; Zeng, Z.; Veeravalli, B. A novel security-driven scheduling algorithm for precedence-constrained tasks in heterogeneous distributed systems. IEEE Trans. Comput. 2011, 60, 1017–1029. [Google Scholar] [CrossRef]
- Xie, T.; Qin, X. Performance evaluation of a new scheduling algorithm for distributed systems with security heterogeneity. J. Parallel Distrib. Comput. 2007, 67, 1067–1081. [Google Scholar] [CrossRef]
- Xie, T.; Qin, X. Scheduling security-critical real-time applications on clusters. IEEE Trans. Comput. 2006, 55, 864–879. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y.; Guo, Z.; Liu, W.; Yang, C. Securing the Intermediate Data of Scientific Workflows in Clouds with ACISO. IEEE Access 2019, 7, 126603–126617. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mendel, J.M. Fuzzy Logic Systems for Engineering: A Tutorial. Proc. IEEE 1995, 83, 345–377. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Alvarez-Benitez, J.E.; Everson, R.M.; Fieldsend, J.E. A MOPSO Algorithm Based Exclusively on Pareto Dominance Concepts. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 459–473. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, M. A memetic particle swarm optimization for constrained multi-objective optimization problems. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC 2011, New Orleans, LA, USA, 5–8 June 2011; pp. 1636–1643. [Google Scholar] [CrossRef]
- Leong, W.F.; Yen, G.G. PSO-based multiobjective optimization with dynamic population size and adaptive local archives. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 2008, 38, 1270–1293. [Google Scholar] [CrossRef]
- Masdari, M.; Salehi, F.; Jalali, M.; Bidaki, M. A Survey of PSO-Based Scheduling Algorithms in Cloud Computing. J. Netw. Syst. Manag. 2017, 25, 122–158. [Google Scholar] [CrossRef]
- Farid, M.; Latip, R.; Hussin, M.; Abdul Hamid, N.A.W. A Survey on QoS Requirements Based on Particle Swarm Optimization Scheduling Techniques for Workflow Scheduling in Cloud Computing. Symmetry 2020, 12, 551. [Google Scholar] [CrossRef]
- Dai, H.P.; Chen, D.D.; Zheng, Z.S. Effects of random values for particle swarm optimization algorithm. Algorithms 2018, 11, 23. [Google Scholar] [CrossRef]
- del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.-C.; Harley, R.G. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Comput. 2008, 12, 171–192. [Google Scholar] [CrossRef]
- Cappelletti, F.; Penna, P.; Prada, A.; Gasparella, A. Development of algorithms for building retrofit. In Start-Up Creation Smart Eco-Efficient Built Environ; Woodhead Publishing: Sawston, UK, 2016; pp. 349–373. [Google Scholar] [CrossRef]
- Cafaro, M.; Aloisio, G.; Juve, G.; Deelman, E. Grids, Clouds and Virtualization; Springer: Berlin/Heidelberg, Germany, 2011; pp. 71–91. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems With Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Shift-based density estimation for pareto-based algorithms in many-objective optimization. IEEE Trans. Evol. Comput. 2014, 18, 348–365. [Google Scholar] [CrossRef]
- Zhang, Z.; Cherkasova, L.; Loo, B.T. Optimizing cost and performance trade-offs for MapReduce job processing in the cloud. In Proceedings of the 2014 IEEE Network Operations and Management Symposium (NOMS), Krakow, Poland, 5–9 May 2014. [Google Scholar] [CrossRef]
- Park, J.; Jeong, H.Y. The QoS-based MCDM system for SaaS ERP applications with Social Network. J. Supercomput. 2013, 66, 614–632. [Google Scholar] [CrossRef]
- Liu, D.; Stewart, T.J. Integrated object-oriented framework for MCDM and DSS modelling. Decis. Support Syst. 2004, 38, 421–434. [Google Scholar] [CrossRef]
- Qin, X.S.; Huang, G.H.; Chakma, A.; Nie, X.H.; Lin, Q.G. A MCDM-based expert system for climate-change impact assessment and adaptation planning—A case study for the Georgia Basin, Canada. Expert Syst. Appl. 2008, 34, 2164–2179. [Google Scholar] [CrossRef]
- Kraujalienė, L. Comparative Analysis of Multicriteria Decision-Making Methods Evaluating the Efficiency of Technology Transfer. Bus. Manag. Educ. 2019, 17, 72–93. [Google Scholar] [CrossRef]
- Rauf, M.; Guan, Z.; Sarfraz, S.; Mumtaz, J.; Shehab, E.; Jahanzaib, M.; Hanif, M. A smart algorithm for multi-criteria optimization of model sequencing problem in assembly lines. Robot. Comput. Integr. Manuf. 2020, 61, 101844. [Google Scholar] [CrossRef]
- Chakravarthi, K.K.; Shyamala, L.; Vaidehi, V. TOPSIS inspired cost-efficient concurrent workflow scheduling algorithm in cloud. J. King Saud Univ. Comput. Inf. Sci. 2020, 34, 2359–2369. [Google Scholar] [CrossRef]
- Fard, H.M.; Prodan, R.; Barrionuevo, J.J.D.; Fahringer, T. A multi-objective approach for workflow scheduling in heterogeneous environments. In Proceedings of the 2012 12th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGrid 2012), Ottawa, ON, Canada, 13–16 May 2012; pp. 300–309. [Google Scholar] [CrossRef]
- Ambursa, F.U.; Latip, R.; Abdullah, A.; Subramaniam, S. A particle swarm optimization and min–max-based workflow scheduling algorithm with QoS satisfaction for service-oriented grids. J. Supercomput. 2017, 73, 2018–2051. [Google Scholar] [CrossRef]
- Hu, H.; Li, Z.; Hu, H.; Chen, J.; Ge, J.; Li, C.; Chang, V. Multi-objective scheduling for scientific workflow in multicloud environment. J. Netw. Comput. Appl. 2018, 114, 108–122. [Google Scholar] [CrossRef]
- Shayeghi, H.; Jalili, A.; Shayanfar, H.A. Multi-stage fuzzy load frequency control using PSO. Energy Convers. Manag. 2008, 49, 2570–2580. [Google Scholar] [CrossRef]
- Jing, W.; Yongsheng, Z.; Haoxiong, Y.; Hao, Z. A Trade-off Pareto Solution Algorithm for Multi-objective Optimization. In Proceedings of the 2012 Fifth International Joint Conference on Computational Sciences and Optimization, Harbin, China, 23–26 June 2012; pp. 123–126. [Google Scholar] [CrossRef]
- Hartmanis, J.; Van Leeuwen, J. Advances in Natural Computation. In Proceedings of the First International Conference, ICNC 2005, Changsha, China, 27–29 August 2005; Volume 3. [Google Scholar] [CrossRef]
- Garg, R.; Singh, A.K. Multi-objective workflow grid scheduling using ε -fuzzy dominance sort based discrete particle swarm optimization. J. Supercomput. 2014, 68, 709–732. [Google Scholar] [CrossRef]


| Objective | Aggregation | Direction |
|---|---|---|
| Makespan | Additive | Min |
| Cost | Additive | Min |
| Resource Utilization | Additive | Max |
| Reliability | Multiplicative | Max |
| Risk Probability | Multiplicative | Min |
| Workflow | Methods | Makespan (H) | Cost ($) | Resource Utilization % | Reliability % | Risk Probability % |
|---|---|---|---|---|---|---|
| Montage | MWO | 20.10096 | 18.16248 | 98.41 | 94.39949675 | 0 |
| MCDM | 25.28155 | 19.07311 | 74.958 | 73.40873522 | 3.68121 × 10−18 | |
| NORMALIZATION1 | 24.53447 | 17.74348 | 77.902 | 78.49092802 | 1.2674 × 10−128 | |
| NORMALIZATION2 | 28.57465 | 20.19869 | 67.804 | 64.99937426 | 3.67288 × 10−48 | |
| WASPAS | 36.61334 | 18.17652 | 74.189 | 73.70053177 | 6.27629 × 10−60 | |
| PARETO | 27.20506 | 18.12757 | 89.439 | 86.92925785 | 0 | |
| CyberShake | MWO | 13.41054064 | 18.15663683 | 97.50642857 | 94.0787519 | 0 |
| MCDM | 42.10671 | 20.40252 | 71.40428571 | 94.3438238 | 0.005376047 | |
| NORMALIZATION1 | 25.03879 | 25.24809 | 57.87071429 | 93.0850308 | 0 | |
| NORMALIZATION2 | 20.89159132 | 18.427447 | 50.08142857 | 90.5211898 | 3.3656 × 10−229 | |
| WASPAS | 45.4625 | 19.15031 | 64.28714286 | 95.869359 | 0.117599759 | |
| PARETO | 22.14941565 | 20.74585587 | 77.915 | 93.7694293 | 2.4616 × 10−167 | |
| LIGO | MWO | 18.62719 | 19.31839 | 88.51 | 90.98273739 | 0 |
| MCDM | 34.33421 | 22.35154 | 79.558 | 83.59184932 | 4.21224 × 10−79 | |
| NORMALIZATION1 | 51.65373 | 21.31771 | 56.254 | 85.39737027 | 0 | |
| NORMALIZATION2 | 70.20769 | 14.59921 | 63.872 | 87.23663633 | 8.716 × 10−238 | |
| WASPAS | 33.1888 | 21.82187 | 68.448 | 86.43662257 | 1.72212 × 10−11 | |
| PARETO | 45.40331 | 25.88293 | 79.322 | 86.90678744 | 0 | |
| SIPHT | MWO | 5.602056079 | 6.79905612 | 66.675 | 73.9875787 | 0 |
| MCDM | 11.24748374 | 11.45402866 | 44.59333333 | 71.3080864 | 0.471667852 | |
| NORMALIZATION1 | 19.30668 | 36.79846 | 40.76166667 | 73.4901905 | 8.3689 × 10−130 | |
| NORMALIZATION2 | 16.32143348 | 11.75497218 | 61.68916667 | 71.3719201 | 6.6051 × 10−126 | |
| WASPAS | 30.47000992 | 12.64217567 | 52.97416667 | 71.7378019 | 6.4918 × 10−240 | |
| PARETO | 16.05690635 | 13.80430791 | 58.17333333 | 73.5531058 | 7.61767 × 10−46 |
| Workflow | Q-Metric | FR-MOS-MWO | FR-MOS-PARETO | FR-MOS-MCDM | FR-MOS-WASPAS | FR-MOS-LIN-NORM I | FR-MOS-LIN-NORM II |
|---|---|---|---|---|---|---|---|
| Montage | FR-MOS-MWO | - | True | True | True | True | True |
| FS-metric | 1.38 | 0.3 | 0.4 | 0.6 | 0.2 | 0.5 | |
| S-metric | 0.08 | 0.23 | 0.17 | 0.074 | 0.26 | 0.13 | |
| LIGO | FR-MOS-MWO | - | True | True | True | True | True |
| FS-metric | 0.69 | 0.26 | 0.064 | 0.127 | 0.003 | 0.38 | |
| S-metric | 0.022 | 0.107 | 0.153 | 0.119 | 0.121 | 0.038 | |
| SIPHT | FR-MOS-MWO | - | True | True | True | True | True |
| FS-metric | 1.01 | 0.839 | 1.0 | 1.84 | 1.72 | 2.59 | |
| S-metric | 0.07 | 0.16 | 0.24 | 0.32 | 0.11 | 0.84 | |
| CyberShake | FR-MOS-MWO | - | True | True | True | True | True |
| FS-metric | 0.244 | 0.063 | 0.0001 | 0.2 | 0.19 | 0.385 | |
| S-metric | 0.073 | 0.214 | 0.170 | 0.22 | 0.16 | 0.084 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farid, M.; Lim, H.S.; Lee, C.P.; Latip, R. Scheduling Scientific Workflow in Multi-Cloud: A Multi-Objective Minimum Weight Optimization Decision-Making Approach. Symmetry 2023, 15, 2047. https://doi.org/10.3390/sym15112047
Farid M, Lim HS, Lee CP, Latip R. Scheduling Scientific Workflow in Multi-Cloud: A Multi-Objective Minimum Weight Optimization Decision-Making Approach. Symmetry. 2023; 15(11):2047. https://doi.org/10.3390/sym15112047
Chicago/Turabian StyleFarid, Mazen, Heng Siong Lim, Chin Poo Lee, and Rohaya Latip. 2023. "Scheduling Scientific Workflow in Multi-Cloud: A Multi-Objective Minimum Weight Optimization Decision-Making Approach" Symmetry 15, no. 11: 2047. https://doi.org/10.3390/sym15112047
APA StyleFarid, M., Lim, H. S., Lee, C. P., & Latip, R. (2023). Scheduling Scientific Workflow in Multi-Cloud: A Multi-Objective Minimum Weight Optimization Decision-Making Approach. Symmetry, 15(11), 2047. https://doi.org/10.3390/sym15112047






