Analysis of Novel Energy-Efficient Converters to Ensure the Required Quality of Electrical Energy
Abstract
:1. Introduction
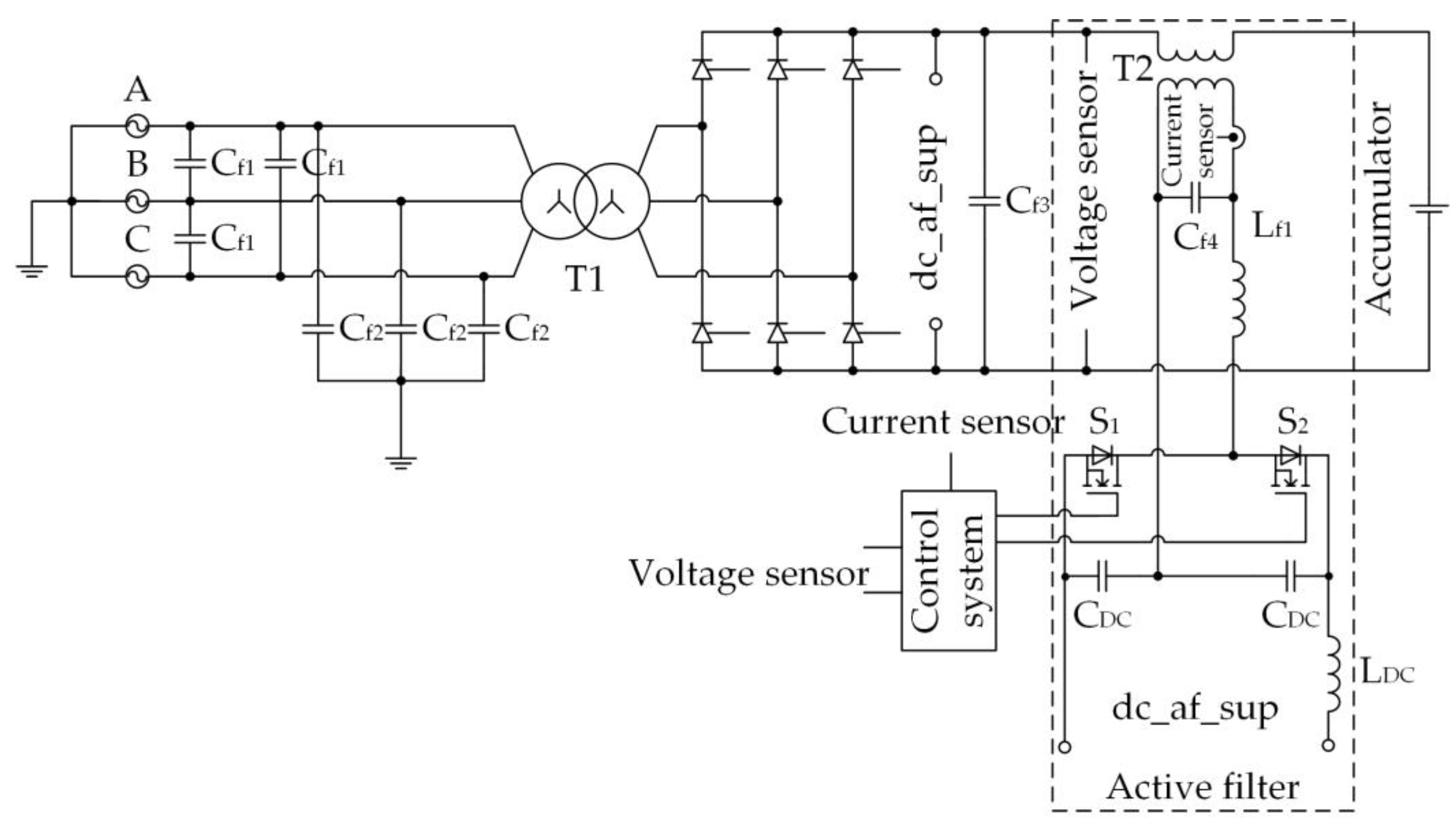
2. Active Filter Based on a Half-Bridge Circuit of a Single-Phase Voltage Inverter
- -
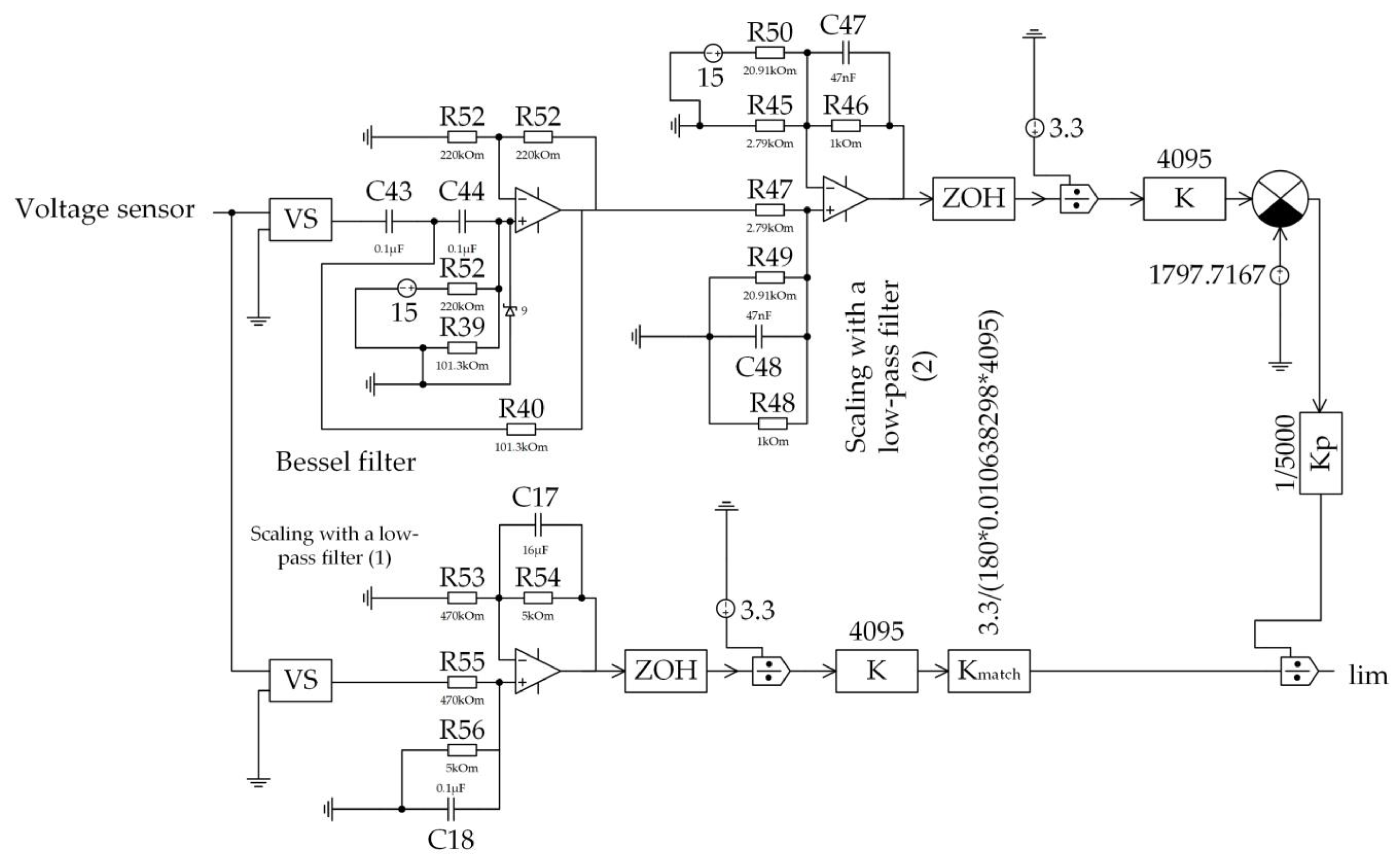
- Determination of the resistor and capacitor values for the selected cutoff frequency, 2 Hz in our case:
- -
- Determination of the resistor and capacitor values for the required gain, selected based on the calculation that Uin is the input voltage equal to the maximum according to the technical specification (270 V), and Uout_op is the output voltage of the operational amplifier (≈3 V):
3. Active Filter Based on an AC Voltage Regulator
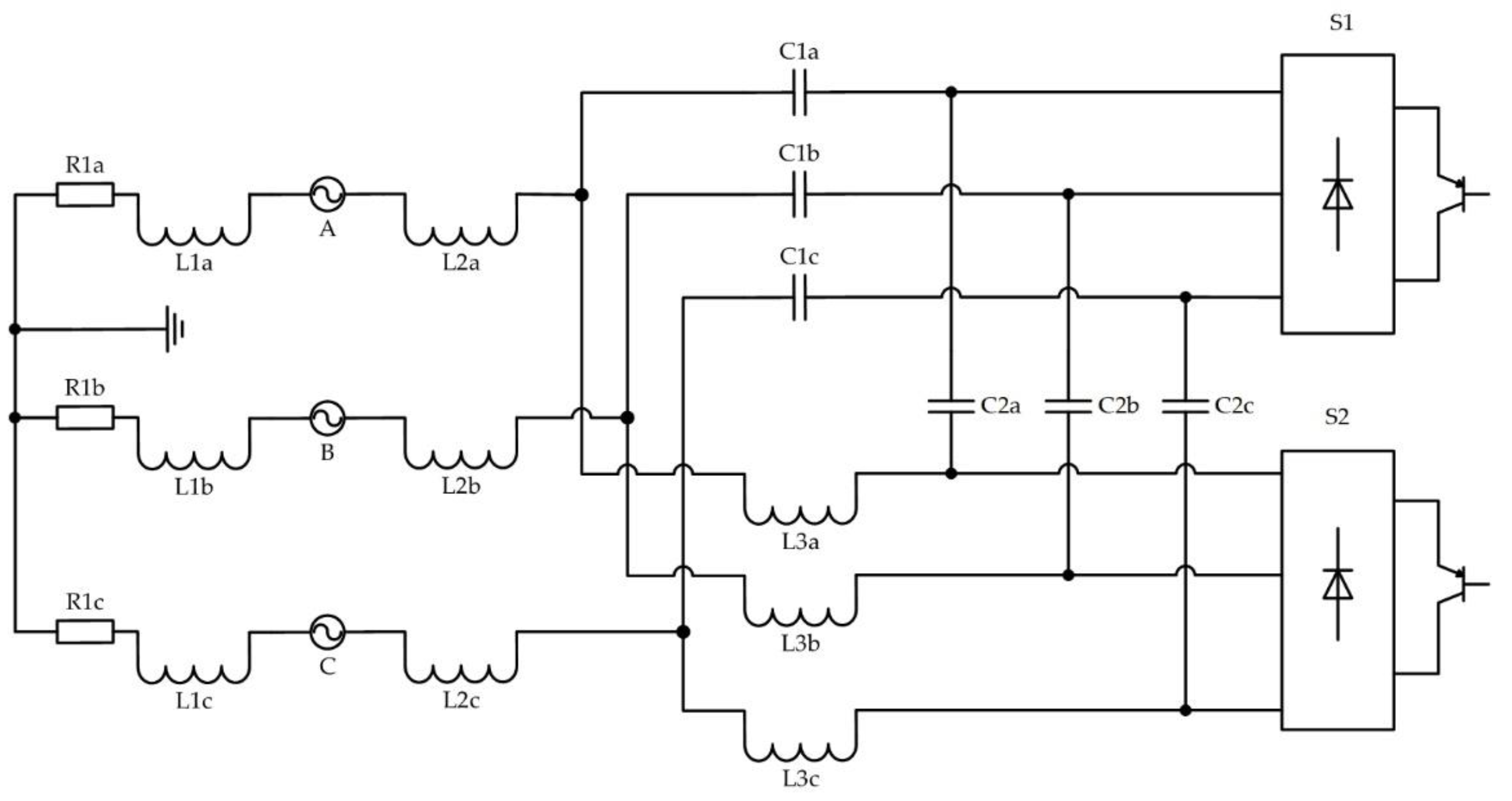
4. Reactive Power Compensator Based on an AC Voltage Regulator
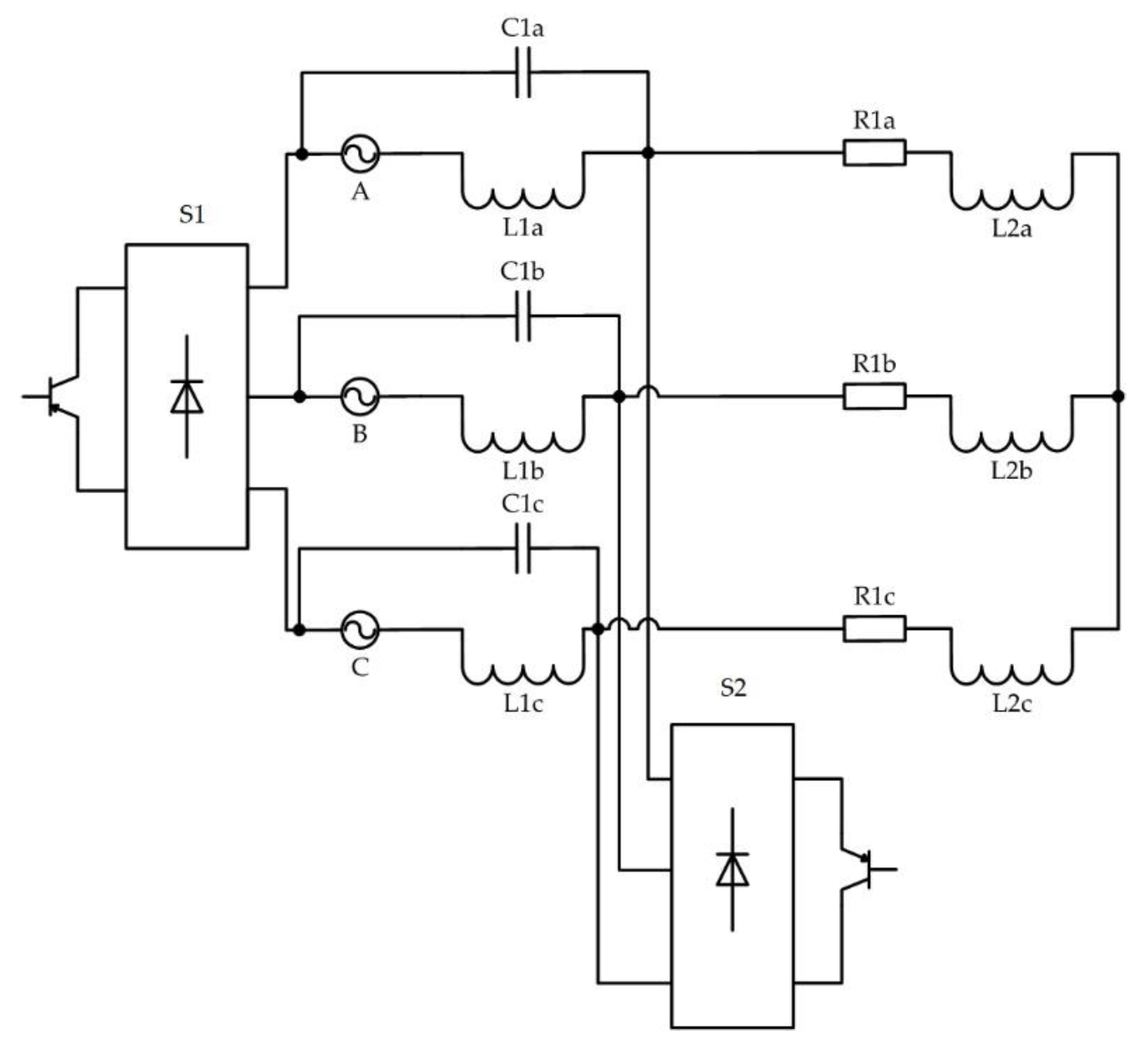
5. Voltage Drop Compensator Based on an AC Voltage Regulator
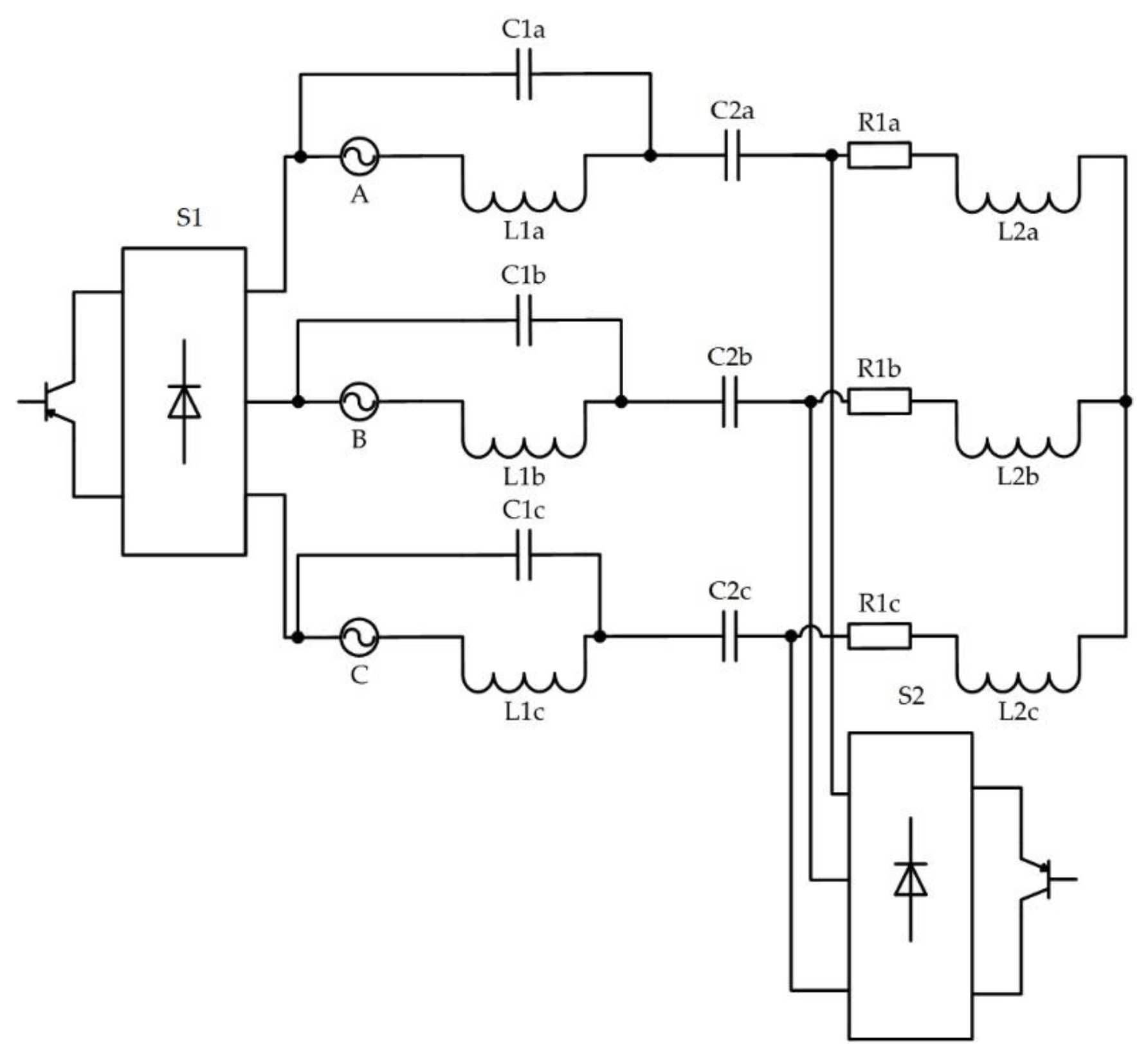
6. An Asymmetry Compensator Based on an AC Voltage Regulator
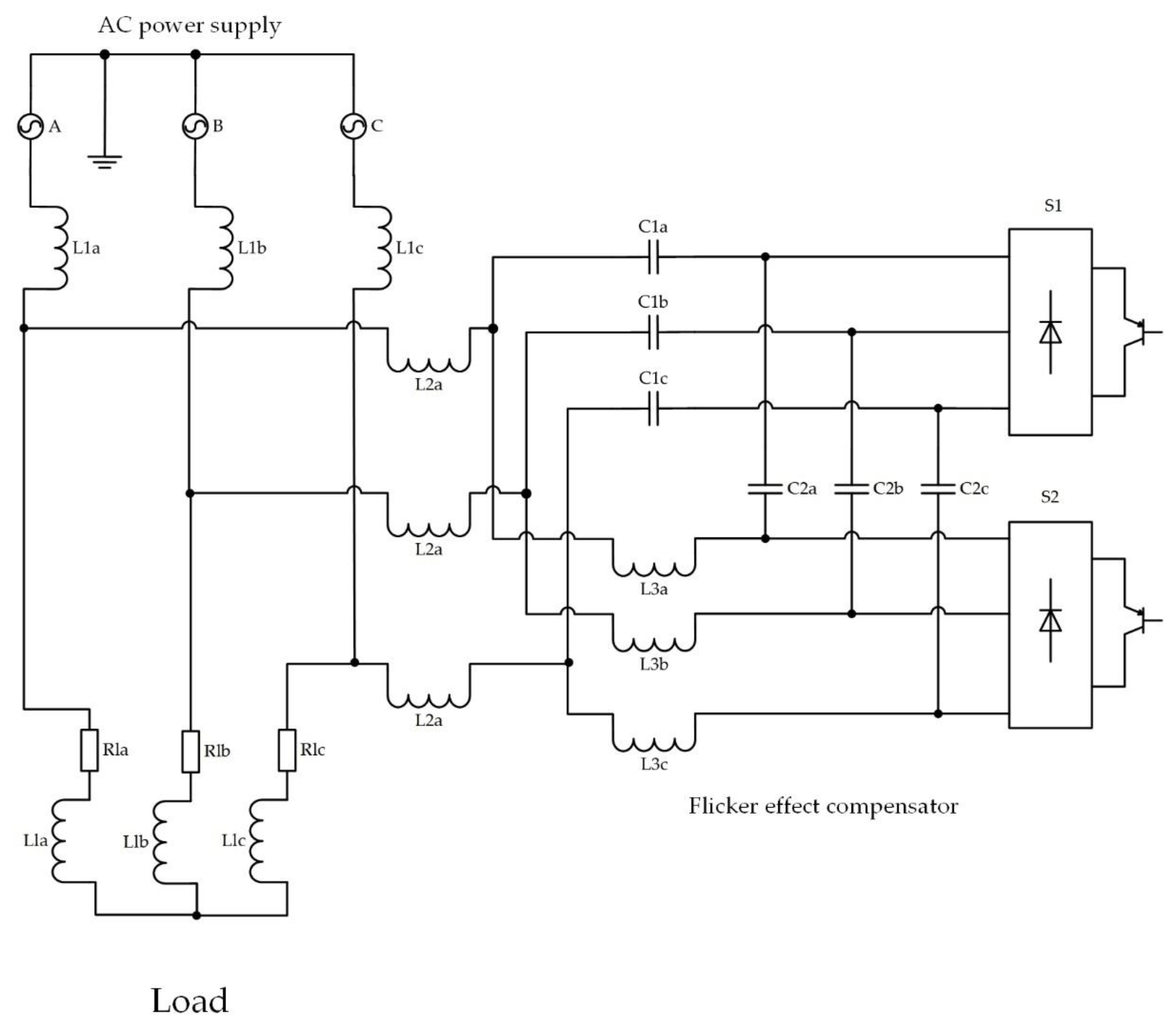
7. A Flicker Effect Compensator Based on an AC Voltage Regulator
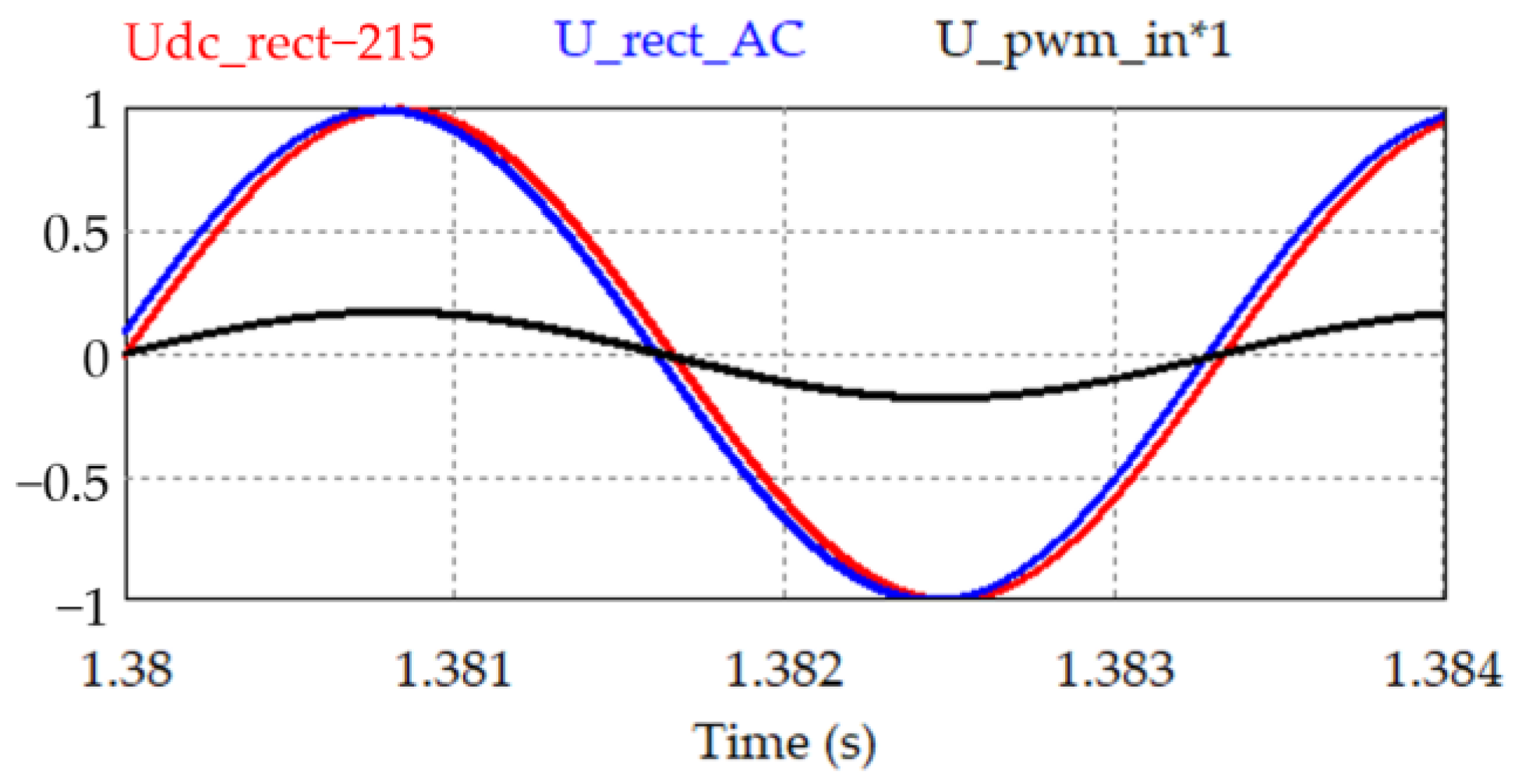
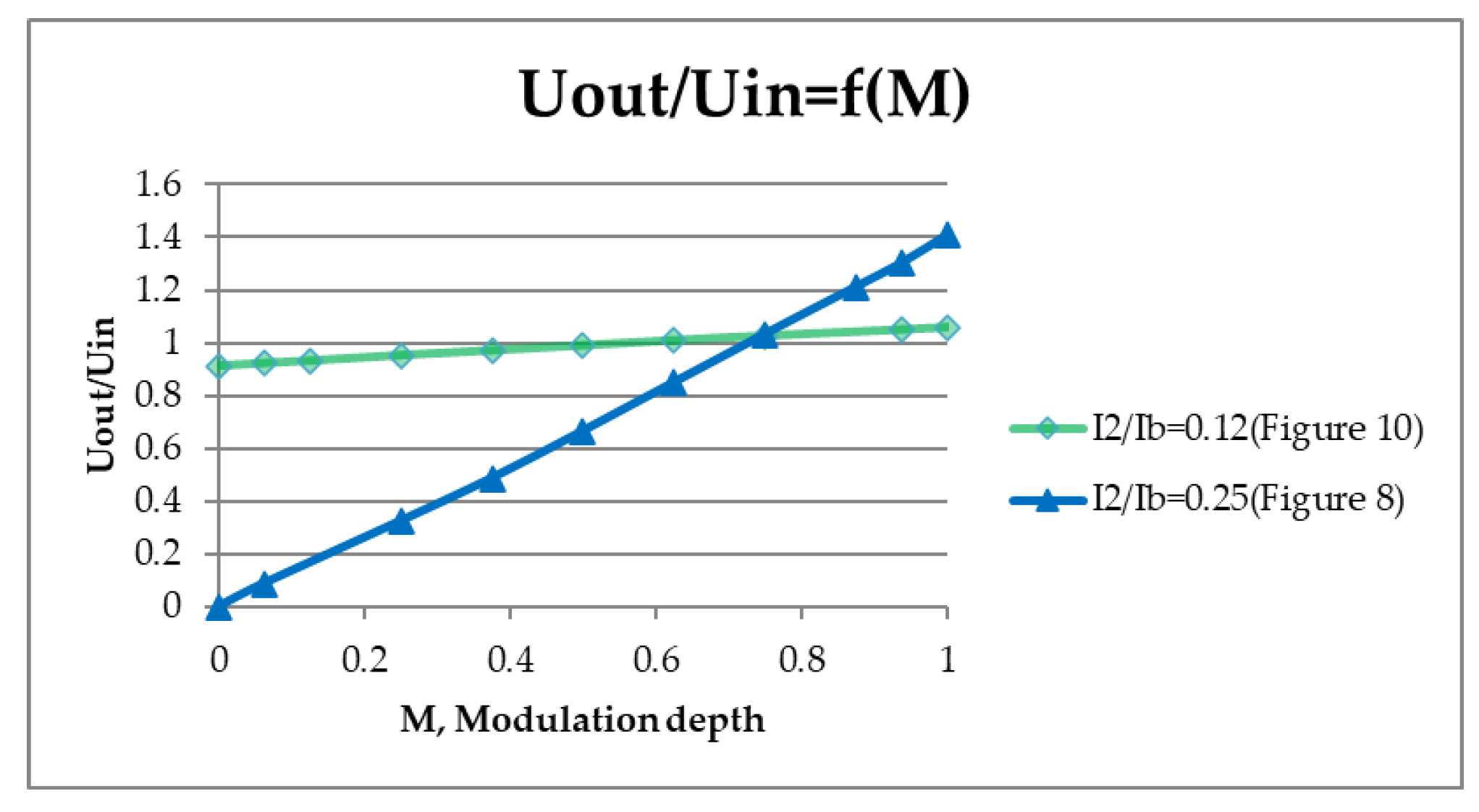
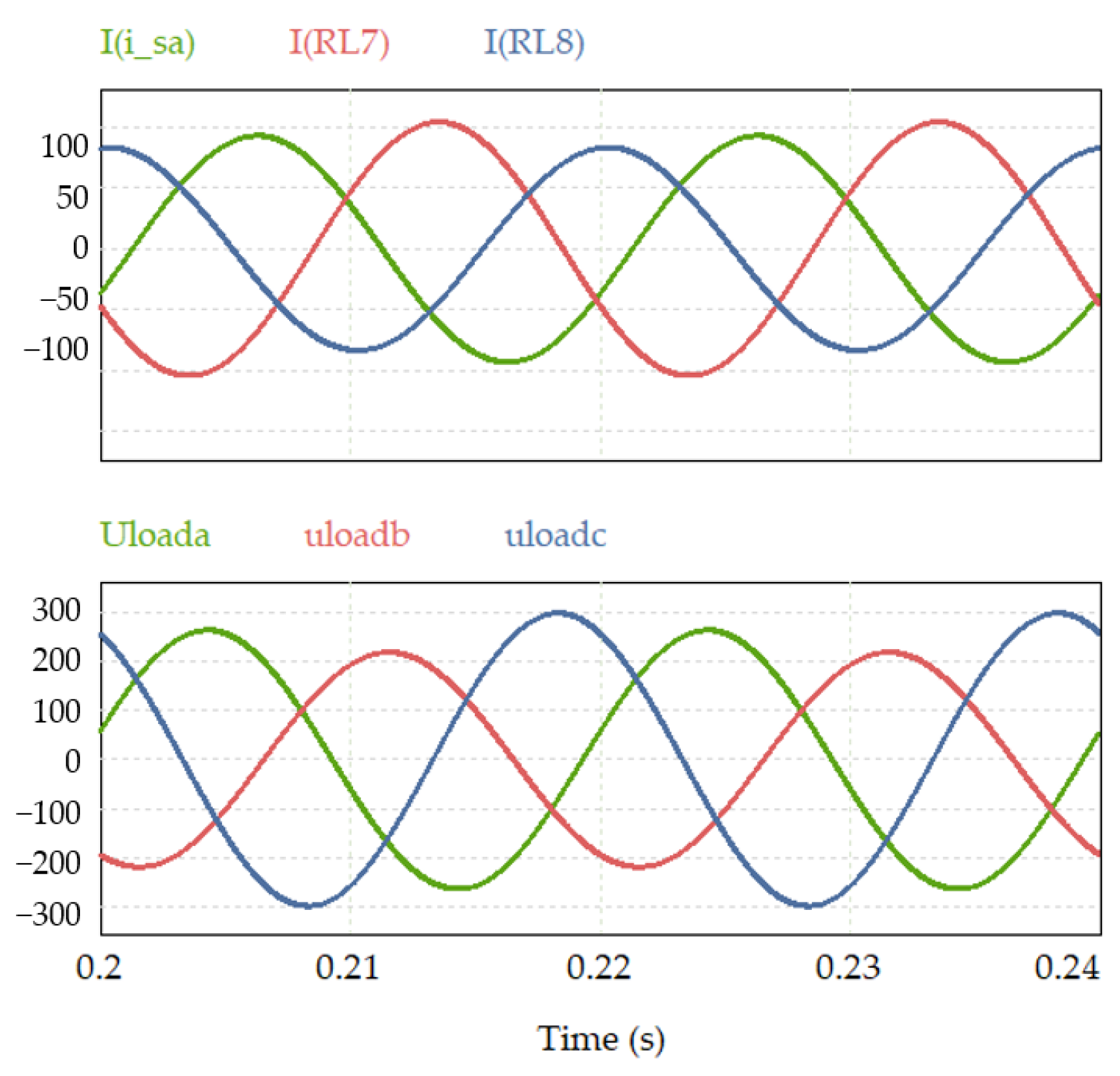
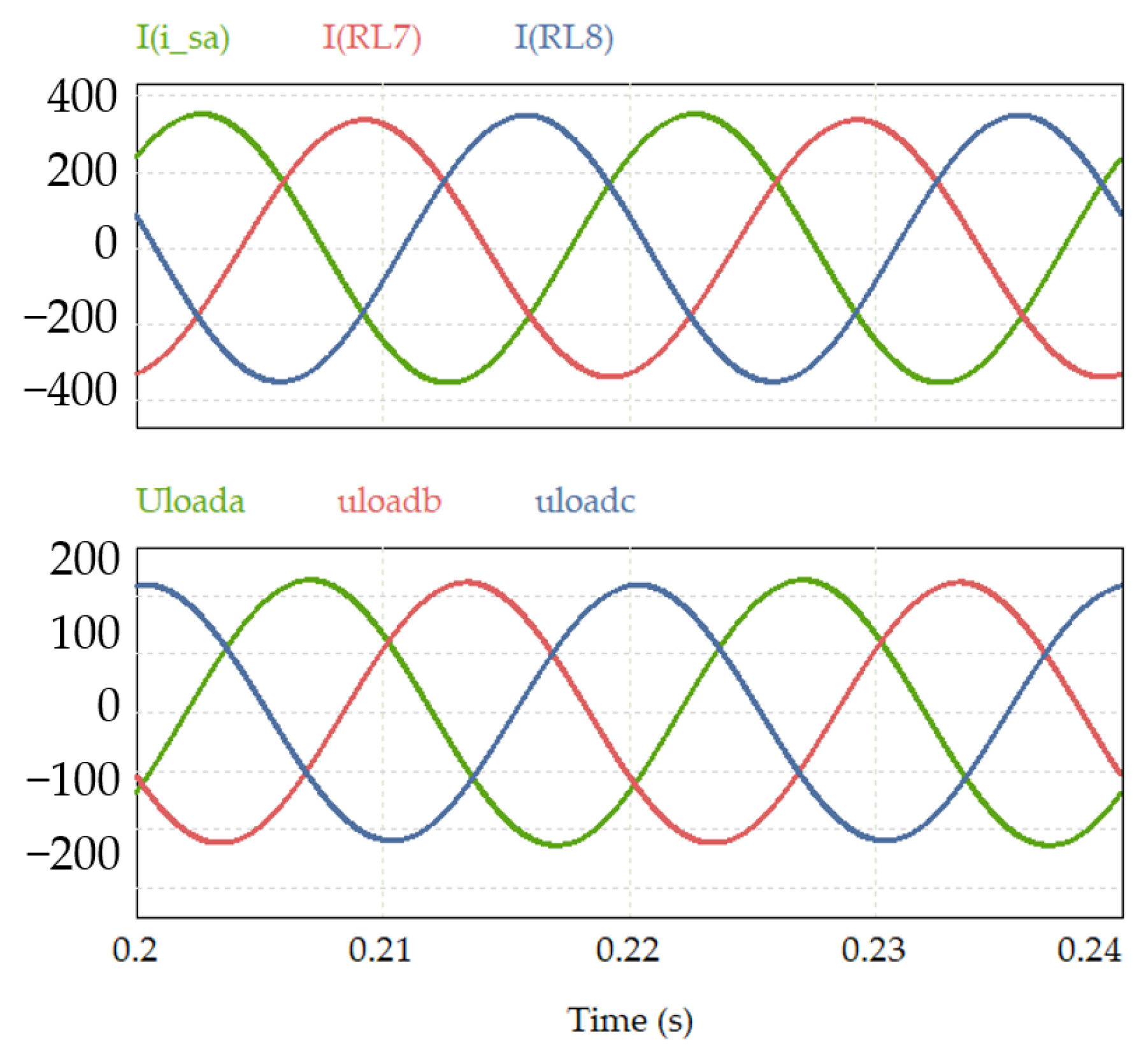
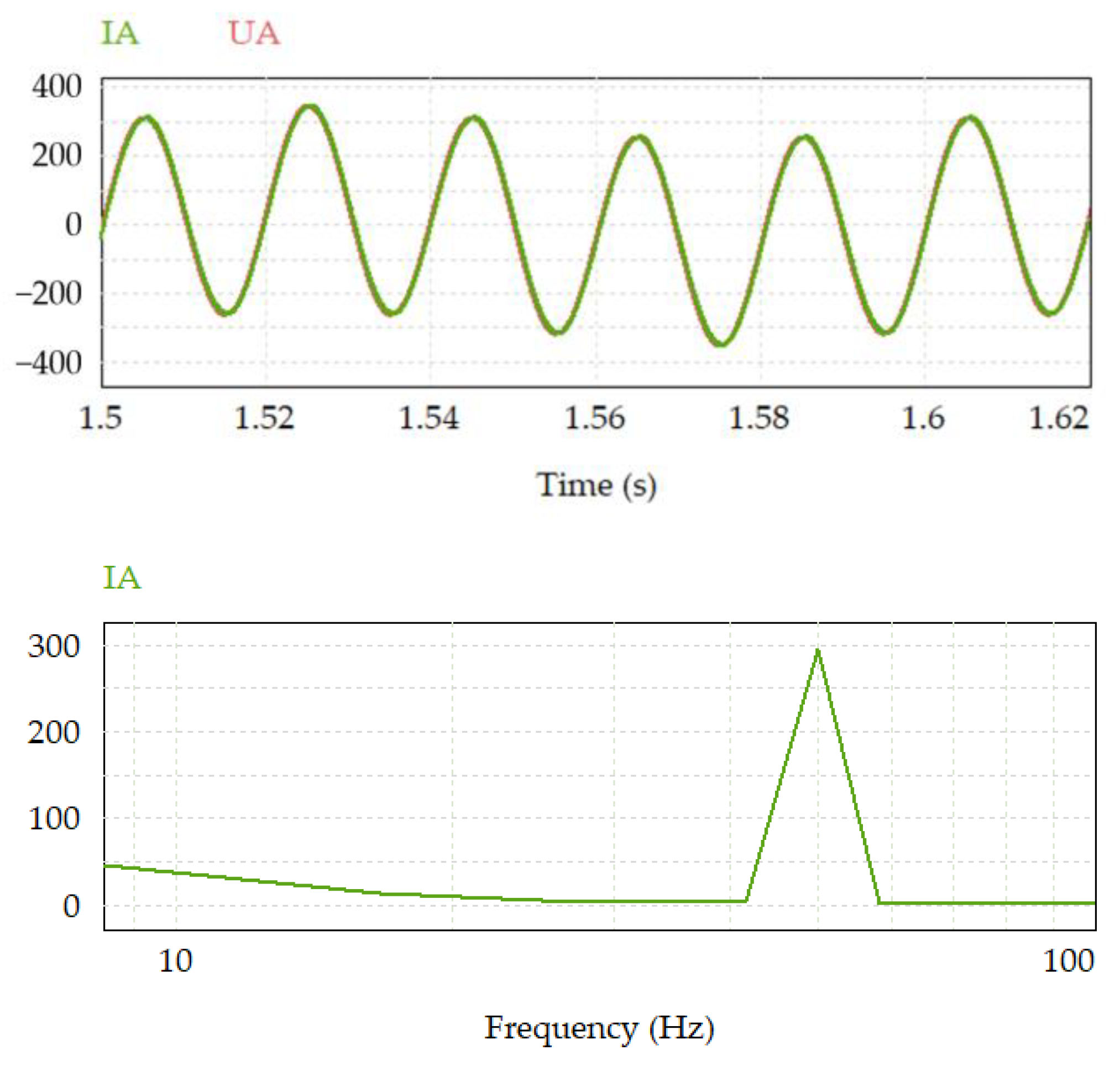
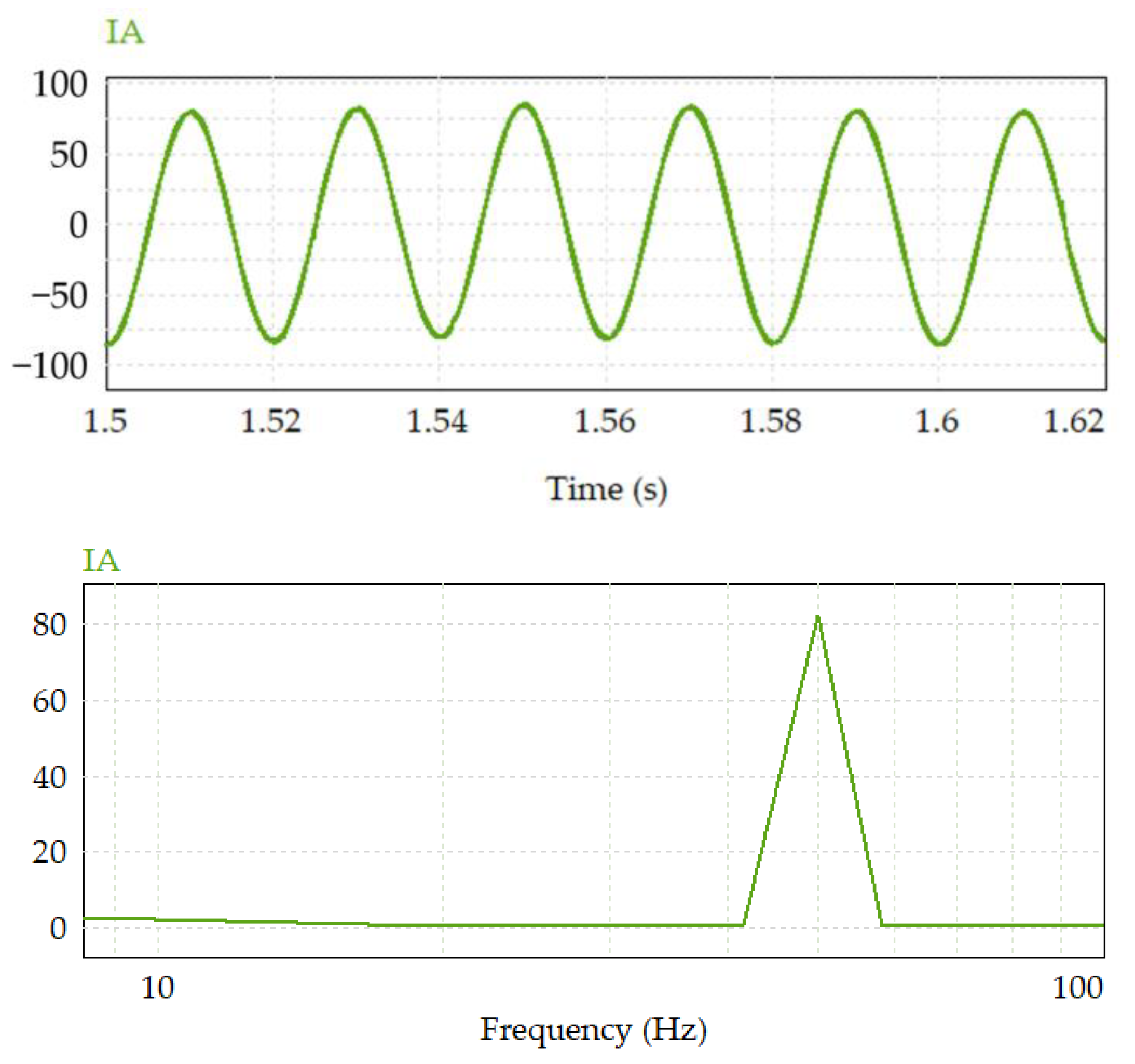
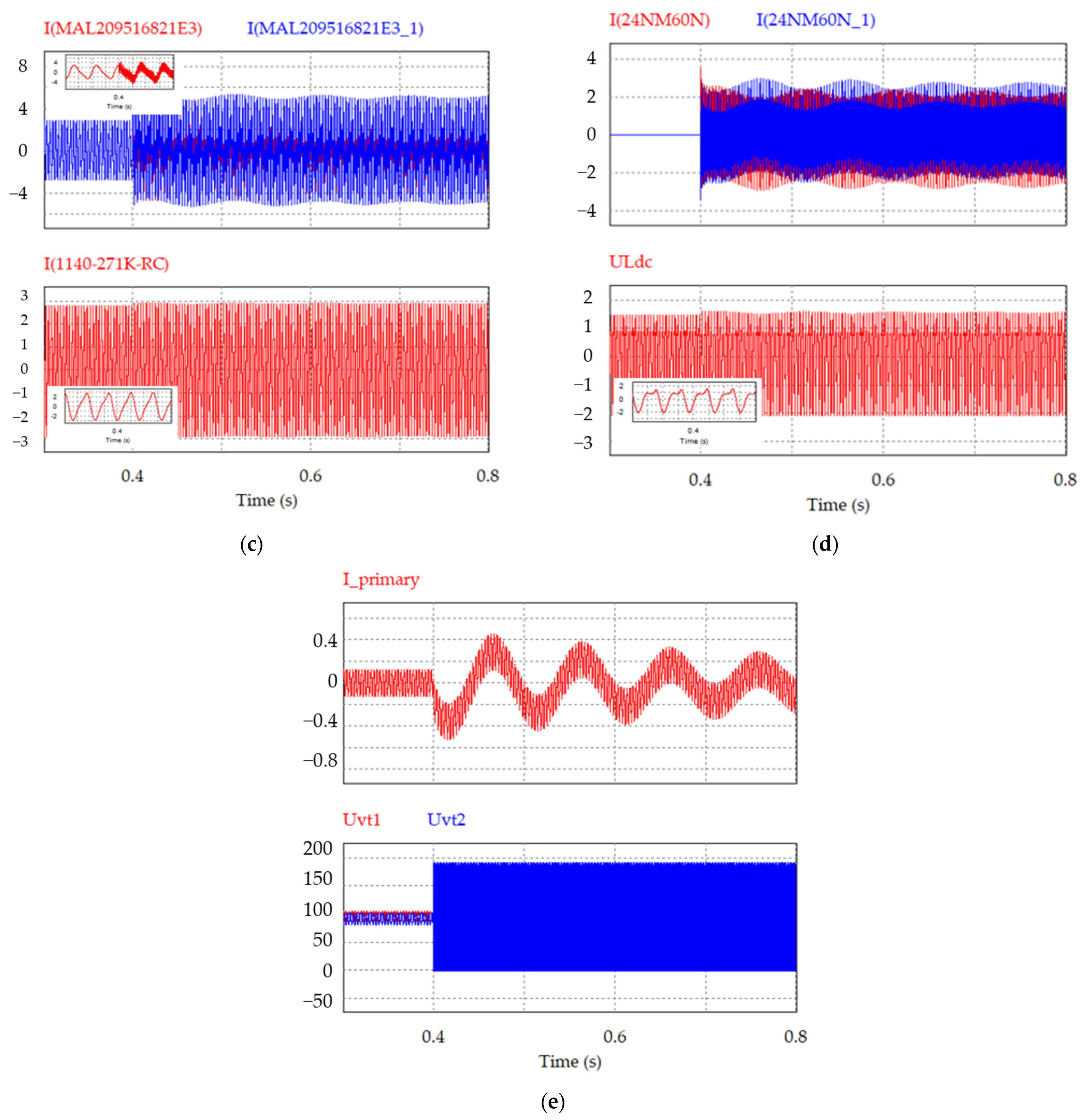
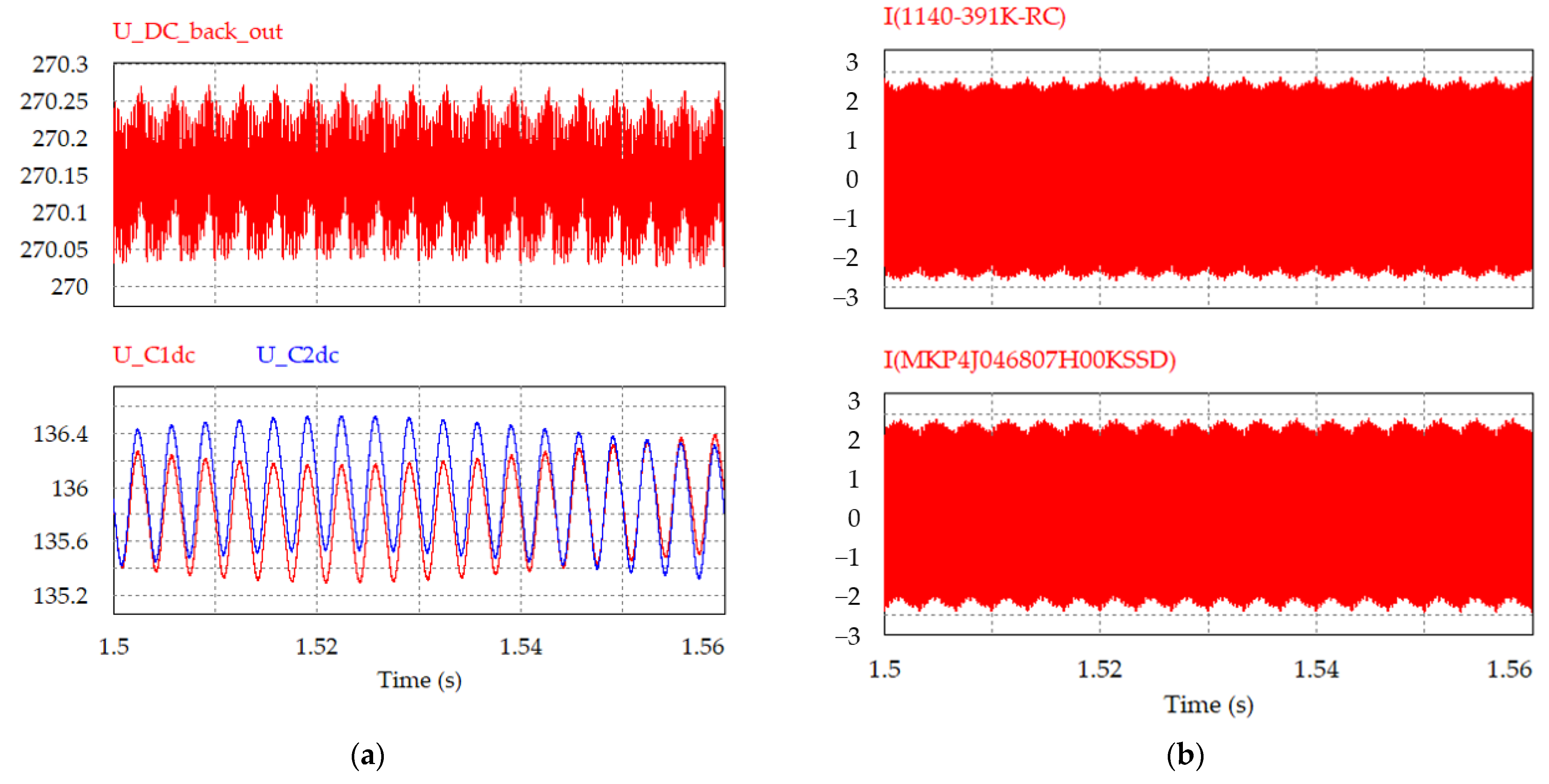
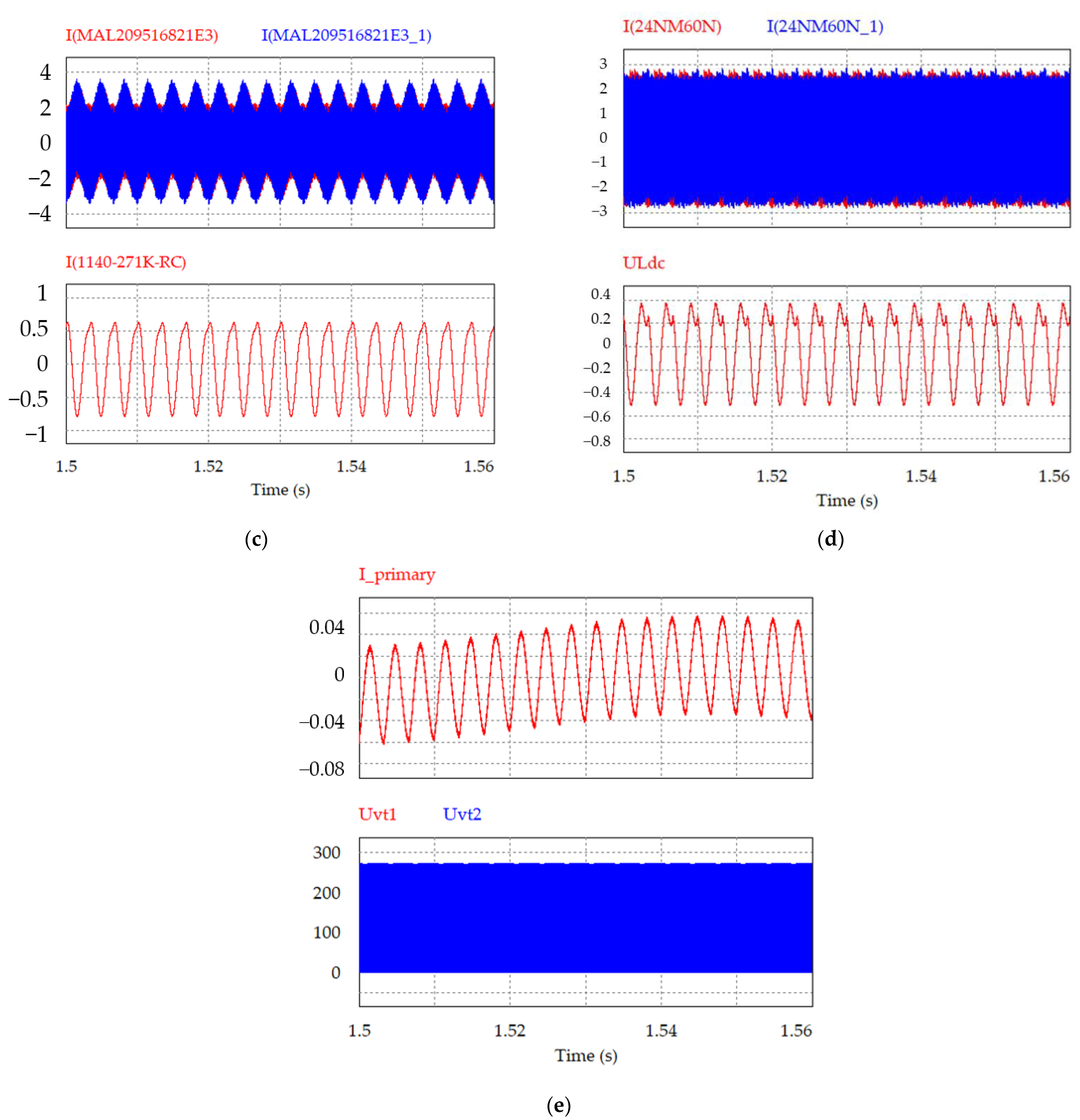
8. Experiment Results
- Uin = 253 V, Uout = 187 V, M = 4.89, Rl = 1.113 Om, switching of the filter, with a choke in the DC link, reset surge of the main voltage 253–126.5–253 V;
- Uin = 253 V, Uout = 187 V, M = 4.89, Rl = 1.113 Om, switching of the filter, two capacitors in parallel in the DC link, reset surge of the main voltage 253–126.5–253 V;
- Uin = 253 V, Uout = 187 V, M = 4.89, Rl = 1.113 Om, switching of the filter, without a choke in the DC link, reset surge of the main voltage 253–126.5–253 V;
- Uin = 253 V, Uout = 187 V, M = 4.89, Rl = 1.113 Om, switching of the filter, two capacitors in parallel and without a choke in the DC link, reset surge of the main voltage 126.5–253–126.5 V;
- Uin = 253 V, Uout = 187 V, M = 4.89, Rl = 1.113 Om, the active filter does not work, the transistors are closed;
- Uin = 253 V, Uout = 187 V, M = 4.89, Rl = 1.113 Om, the transition process;
- Uin = 187 V, Uout = 270 V, M = 9.76, Rl = 1.715 Om, the maximum voltage of the charging and rectifying device;
- Operate on counter-EMF;
- Uin = 253 V, Uout = 187 V, M = 4.89, Rl = 1.113 Om, without filter capacitor at the output of the charging and rectifying device, ripple 3.188 V, THDI = 0.233%.
9. Conclusions
- The required ripple level did not exceed 0.2%.
- The possibility of compensation of the pulsation component is achieved both at a small output voltage value of the rectifier of the charging and rectifying device and at a maximum equal to 270 V, where the pulsation was 0.2 V.
- The presence of only two transistors indicates a low level of energy loss on semiconductors—25 W, which will reduce the size of the radiator.
- The disadvantages include a non-standard type of matching transformer; this will affect the cost of the entire power supply system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Global Voltage Stabilizer System Industry (2020 to 2027)—Market Trends and Drivers. Available online: https://finance.yahoo.com/news/global-voltage-stabilizer-system-industry-093300514.html (accessed on 27 October 2023).
- Tokarev, V.G.; Brovanov, S.V. An Investigation of the Performance of Single-and Double-Converter Parallel Active Power Filters under Various Modulation Modes. In Proceedings of the 2021 XV International Scientific-Technical Conference on Actual Problems Of Electronic Instrument Engineering (APEIE), Novosibirsk, Russia, 19–21 November 2021; pp. 111–114. [Google Scholar] [CrossRef]
- Banerji, A.; Biswas, S.K.; Singh, B. Review of Static Compensation of Autonomous Systems. Int. J. Power Electron. Drive Syst. 2012, 2, 51. [Google Scholar] [CrossRef]
- Ruman, S.; Hameed, S. A Novel Approach for Design and Analysis of Voltage-Controlled DSTATCOM for Power Quality Enhancement. TELKOMNIKA Indones. J. Electr. Eng. 2015, 15, 486–496. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Agrawal, A.; Agarwal, P.; Jena, P. Compensation of voltage flicker using unified power quality conditioner (UPQC). In Proceedings of the 2014 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Mumbai, India, 16–19 December 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Bezborodov, S.P.; Zinoviev, G.S. Analysis of the operating mode of the “inverted” voltage inverter. In Conversion Technology; NETI: Novosibirsk, Russia, 1975. (In Russian) [Google Scholar]
- Zinoviev, G.S. Analysis of voltage inverters as a reactive power compensator. In Conversion Technology; NETI: Novosibirsk, Russia, 1978. (In Russian) [Google Scholar]
- Zinoviev, G.S. Valve compensators of reactive power, distortion power and asymmetry power based on a voltage inverter. In Modern Tasks of Transformative Technology; Naukova dumka: Kiev, Ukraine, 1975; pp. 247–252. (In Russian) [Google Scholar]
- Muneshima, M.; Nishida, Y. A multilevel AC-AC conversion system and control method using Y-connected H-bridge circuits and bidirectional switches. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 4008–4013. [Google Scholar] [CrossRef]
- Alaei, R.; Khajehoddin, S.A.; Xu, W. A bidirectional ac/ac multilevel converter. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2610–2615. [Google Scholar] [CrossRef]
- Keyhani, H.; Toliyat, H.A. A soft-switched three-phase AC–AC converter with a high-frequency AC link. IEEE Trans. Ind. Appl. 2013, 50, 2637–2647. [Google Scholar] [CrossRef]
- Petry, C.A.; Fagundes, J.C.; Barbi, I. New direct ac-ac converters using switching modules solving the commutation problem. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; Volume 2, pp. 864–869. [Google Scholar] [CrossRef]
- Khan, M.M.; Rana, A.; Dong, F. Improved ac/ac choppers-based voltage regulator designs. IET Power Electron. 2014, 7, 1989–2000. [Google Scholar] [CrossRef]
- Petry, C.A.; Fagundes, J.C.S.; Barbi, I. New AC-AC converter topologies. In Proceedings of the 2003 IEEE International Symposium on Industrial Electronics (Cat. No. 03TH8692), Rio de Janeiro, Brazil, 9–11 June 2003; Volume 1, pp. 427–431. [Google Scholar] [CrossRef]
- Ahmed, N.A.; Miyatake, M.; Lee, H.W.; Nakaoka, M. A novel circuit topology of three-phase direct AC-AC PWM voltage regulator. In Proceedings of the Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; Volmue 4, pp. 2076–2081. [Google Scholar] [CrossRef]
- Fedyczak, Z.; Szcześniak, P.; Kaniewski, J.; Korbicz, J. Direct PWM AC choppers and frequency converters. In Measurements Models Systems and Design; Transport and Communication Publishers: Warsaw, Poland, 2007; pp. 393–424. [Google Scholar]
- Kartashev, I.I.; Chekhov, V.I. Static Reactive Power Compensators in Power Systems; Ryzhov, Y.P., Ed.; Publishing House of the MEI: Moscow, Russia, 1990; 68p. (In Russian) [Google Scholar]
- Tikhomirov, A.A.; Cherepanov, D.A.; Tikhonov, E.A.; Sysun, V.I. Transverse reactive power compensation scheme based on the electromechanical effect. Int. Res. J. 2014, 11 Pt 2, 71–72. (In Russian) [Google Scholar]
- Tarabin, I.V.; Skokov, R.B.; Terekhin, I.A.; Gorbachev, S.A. Reactive power compensation as a method of improving the quality of electrical energy and reducing losses on the example of IDGC of SIBERIA data. Fundam. Res. 2015, 2, 4876–4879. (In Russian) [Google Scholar]
- Magonov, S.V.; Shibeko, R.V. Reactive power compensation. In Youth and Science: Actual Problems of Fundamental and Applied Research; Federal State Budgetary Educational Institution of Higher Education Komsomolsk-on-Amur State University: Komsomolsk-on-Amur, Russia, 2019; pp. 346–349. (In Russian) [Google Scholar]
- Braslavsky, I.Y. Induction Semiconductor Electric Drive with Parametric Control; Energoatomizdat: Moscow, Russia, 1988. (In Russian) [Google Scholar]
- Strzelecki, R.M. (Ed.) Power Electronics in Smart Electrical Energy Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Zinoviev, G. Power Electronics; Novosibirsk State Technical University: Novosibirsk, Russia, 2014. (In Russian) [Google Scholar]
- Hofmeester, N.H.M.; Van den Bosch, P.P.J.; Klaassens, J.B. Modelling and control of an AC/AC boost-buck converter. In Proceedings of the 1993 Fifth European Conference on Power Electronics and Applications, Brighton, UK, 13–16 September 1993; pp. 85–90. [Google Scholar]
- Srinivasan, S.; Venkataramanan, G. Comparative evaluation of PWM AC-AC converters. In Proceedings of the PESC’95-Power Electronics Specialist Conference, Atlanta, GA, USA, 18–22 June 1995; Volume 1, pp. 529–535. [Google Scholar] [CrossRef]
- Zinoviev, G.S. Valve Converter. Russian Federation RF 2124263, 27 December 1998. (In Russian). [Google Scholar]
- Zinoviev, G.S.; Obukhov, A.E. Increasing pulse-width regulators of alternating voltage. Sci. Bull. Novosib. State Tech. Univ. 1997, 3, 111–120. (In Russian) [Google Scholar]
- Obuhov, A.; Otchenash, V.; Zinoviev, G. Buck-boost AC-AC voltage controllers. In Proceedings of the 9th International Conference on Power Electronics and Motion Control (EPE-PEMC 2000), Košice, Slovakia, 5–7 September 2000; pp. 194–197. [Google Scholar]
- Montero-Hernadez, O.C.; Enjeti, P.N. Application of a boost AC-AC converter to compensate for voltage sags in electric power distribution systems. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference, Conference Proceedings (Cat. No. 00CH37018), Galway, Ireland, 23 June 2000; Volume 1, pp. 470–475. [Google Scholar] [CrossRef]
- Fedyczak, Z.; Klytta, M.; Strzelecki, R. Three-phase AC-AC semiconductor transformer topologies and applications. In Proceedings of the PEDC 2001: 2nd Conference, Zielona Góra, Polska, 3–5 September 2001; pp. 25–38. [Google Scholar]
- Peng, F.Z.; Chen, L.; Zhang, F. Simple topologies of PWM AC-AC converters. IEEE Power Electron. Lett. 2003, 1, 10–13. [Google Scholar] [CrossRef]
- Floricău, D.; Dumitrescu, M.; Popa, I.; Ivanov, S. Basic Topologies of Direct PWM AC Choppers; Annals of the University of Craiova, Electrical Engineering Series; Craiova University: Craiova, Romania, 2006; Volume 30. [Google Scholar]
- Prasai, A.; Divan, D. Dynamic capacitor—VAR and harmonic compensation without inverters. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Liu, Q.; Deng, Y.; He, X. A novel AC-AC shunt active power filter without large energy storage elements. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]
- Brescia, E.; Massenio, P.R.; Di Nardo, M.; Cascella, G.L.; Gerada, C.; Cupertino, F. Nonintrusive Parameter Identification of IoT-Embedded Isotropic PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5195–5207. [Google Scholar] [CrossRef]
- Brescia, E.; Massenio, P.R.; Di Nardo, M.; Cascella, G.L.; Gerada, C.; Cupertino, F. Parameter Estimation of Isotropic PMSMs Based on Multiple Steady-State Measurements Collected During Regular Operations. IEEE Trans. Energy Convers. 2023, 1–16. [Google Scholar] [CrossRef]
- Dudin, A.; Ellinger, T.; Petzoldt, J.; Nos, O.V. State of charge control of the mixed-type battery energy storage system based on the modular multilevel converter. In Proceedings of the 2016 17th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Altai, Russia, 30 June–4 July 2016; pp. 395–400. [Google Scholar] [CrossRef]
- Reithmaier, S. DC-DC High Frequency Boost Converter. U.S. Patent 7 180 275, B2, 20 February 2007. [Google Scholar]
- Brown, A.E. DC-DC Converter Operable in an Asyncronous or Syncronous or Linear Mode. U.S. Patent 5 414 341, 9 May 1995. [Google Scholar]
- BU-907: Testing Lithium-Based Batteries. Available online: https://batteryuniversity.com/index.php/learn/article/testing_lithium_based_batteries (accessed on 27 October 2023).
- SKiiP 603 GD123-3DUL V3. Available online: https://www.semikron-danfoss.com/products/product-classes/ipm.html#view/table/items/20/filters/icnom-in-a=600 (accessed on 27 October 2023).
- Agunov, A.V. Smoothing device of DC traction substations based on a power active filter. News St. Petersburg Univ. Railw. Transp. 2013, 2, 96–99. (In Russian) [Google Scholar]
- Zhang, H.; Lu, R.; Zhu, C.; Zhao, Y. On-line measurement of internal resistance of lithium ion battery for EV and its application research. Int. J. u-e-Serv. Sci. Technol. 2014, 7, 301–310. [Google Scholar] [CrossRef]
- Hato, Y.; Chen, C.H.; Hirota, T.; Kamiya, Y.; Daisho, Y.; Inami, S. Degradation predictions of lithium iron phosphate battery. World Electr. Veh. J. 2015, 7, 25–31. [Google Scholar] [CrossRef]
- Ruddell, A.J.; Dutton, A.G.; Wenzl, H.; Ropeter, C.; Sauer, D.U.; Merten, J.; Orfanogiannis, C.; Twidell, J.W.; Vezin, P. Analysis of battery current microcycles in autonomous renewable energy systems. J. Power Source 2002, 112, 531–546. [Google Scholar] [CrossRef]
- Charging LiFeP04 Batteries Summary of Manufacturer Recommendations. Available online: http://www.hoffmanengineering.com/Power-Management-from-Hoffman-Engineering (accessed on 27 October 2023).
- Park, J.H.; Jeong, H.G.; Lee, K.B. Output current ripple reduction algorithms for home energy storage systems. Energies 2013, 6, 5552–5569. [Google Scholar] [CrossRef]
- Kaneko, G.; Inoue, S.; Taniguchi, K.; Hirota, T.; Kamiya, Y.; Daisho, Y.; Inami, S. Analysis of degradation mechanism of lithium iron phosphate battery. World Electr. Veh. J. 2013, 6, 555–561. [Google Scholar] [CrossRef]
- From 1 Hour to Just 10 Seconds: Using the Low-Frequency AC-IR Method as a Quicker and More Stable Alternative to DC-IR Testing of Lithium Ion Batteries. Available online: https://www.hioki.com/en/ (accessed on 27 October 2023).
- Keil, P.; Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—An experimental study with different 18650 high-power cells. J. Energy Storage 2016, 6, 125–141. [Google Scholar] [CrossRef]
- Krieger, E.M. Effects of Variability and Rate on Battery Charge Storage and Lifespan. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2013. [Google Scholar]
- Ahmad, A.A.; Abrishamifar, A.; Samadi, S. Low-frequency current ripple reduction in front-end boost converter with single-phase inverter load. IET Power Electron. 2012, 5, 1676–1683. [Google Scholar] [CrossRef]
- Sritharan, T. Impact of Current Waveforms on Battery Behaviour; University of Toronto: Toronto, ON, Canada, 2012. [Google Scholar]
- Mirzaee, H.; Dutta, S.; Bhattacharya, S. A medium-voltage DC (MVDC) with series active injection for shipboard power system applications. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 2865–2870. [Google Scholar] [CrossRef]
- Hayes, T.C.; Horowitz, P. The art of Electronics; Cambridge University Press: Cambridge, UK, 1999; Volume 3. [Google Scholar]
- Ahmed, H.F.; Cha, H.; Khan, A.A. Design of dynamic voltage restorer for voltage sag and swell compensation using high-frequency-isolated direct AC-AC converter without commutation problem. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Wen, B.; Zhang, X.; Wang, Q.; Burgos, R.; Mattavelli, P.; Boroyevich, D. Comparison of three-phase ac-ac matrix converter and voltage dc-link back-to-back converter topologies based on EMI filter. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 2698–2706. [Google Scholar] [CrossRef]
- Qin, H.; Kimball, J.W. Ac-ac dual active bridge converter for solid state transformer. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3039–3044. [Google Scholar] [CrossRef]
- Keyhani, H.; Toliyat, H.A. Isolated ZVS high-frequency-link AC-AC converter with a reduced switch count. IEEE Trans. Power Electron. 2013, 29, 4156–4166. [Google Scholar] [CrossRef]
- Yu, X.; She, X.; Ni, X.; Huang, A.Q. System integration and hierarchical power management strategy for a solid-state transformer interfaced microgrid system. IEEE Trans. Power Electron. 2013, 29, 4414–4425. [Google Scholar] [CrossRef]
- Besselmann, T.; Mester, A.; Dujic, D. Power electronic traction transformer: Efficiency improvements under light-load conditions. IEEE Trans. Power Electron. 2013, 29, 3971–3981. [Google Scholar] [CrossRef]
- Zinoviev, G.S.; Konovalov, A.I.; Krasikov, N.A. Adjustable Converter of Alternating Voltage to Alternating. Certificate of Authorship No. 1128350; Bul. No. 45, 1984. (In Russian). [Google Scholar]
- Zinoviev, G.S.; Ulanov, E.I. Voltage Inverter Control Method. Certificate of Authorship No. 576651; Bul. No. 38, 1979. (In Russian). [Google Scholar]
- Zinoviev, G.S.; Manusov, V.Z. Direct Methods for Calculating the Energy Parameters of Valve Converters; Publishing House of Novosibirsk University: Novosibirsk, Russia, 1990. (In Russian) [Google Scholar]
- Zinoviev, G.S. Structures of valve converters with an arbitrary voltage conversion coefficient. Sci. Bull. NSTU 1997, 3, 71. (In Russian) [Google Scholar]
- Zinoviev, G.S.; Levin, E.Y.; Obukhov, A.E.; Popov, V.I. Step-up and step-down regulators of alternating voltage and direct frequency converters. Electr. Eng. 2000, 11, 16–20. (In Russian) [Google Scholar]
- Zinoviev, G.S.; Popov, A.V. Direct Frequency Converter. RF Patent No. 2215359, 27 October 2003. Bul. No. 30. (In Russian). [Google Scholar]
- Zinoviev, G.S.; Zotov, L.G. An Up-and-Down Direct Frequency Converter. RF Patent No. 2408968, 10 January 2011. Byul. 13. (In Russian). [Google Scholar]
- Zinoviev, G.S.; Sidorov, A.V.; Kharitonov, S.A. Three-Phase AC Voltage Stabilizer. RF Patent 2529887, 10 October 2014. Bul. No. 28. (In Russian). [Google Scholar]
- Zotov, L.G.; Zinoviev, G.S. Electronic transformers based on high-frequency resonant structures with switchable capacitors. Rep. Tomsk. State Univ. Control Syst. Radioelectron. 2013, 2, 64–69. (In Russian) [Google Scholar]
- Zinoviev, G.S.; Udovichenko, A.V. AC Voltage Regulator. Patent 2479102, 10 April 2013. Bul. No. 10. (In Russian). [Google Scholar]
- Zinoviev, G.S.; Udovichenko, A.V. Transformerless buck-boost AC voltage regulators with sinusoidal input and output currents. Tech. Elektrodynamika 2012, 3, 69–70. (In Russian) [Google Scholar]
- Zinoviev, G.S.; Udovichenko, A.V. Transformerless buck-boost AC voltage regulators with sinusoidal currents for soft–start devices of induction motors. In Proceedings of the Electric Drives of Alternating Current—EPT-2012, Ekaterinburg, Russia, 12–16 March 2012; pp. 55–58. (In Russian). [Google Scholar]
- Tekin, H.; Bulut, K.; Ertekin, D. A novel switched-capacitor and fuzzy logic-based quadratic boost converter with mitigated voltage stress, applicable for DC micro-grid. Electr. Eng. 2022, 104, 4391–4413. [Google Scholar] [CrossRef]
- Qi, Q.; Ghaderi, D.; Guerrero, J.M. Sliding mode controller-based switched-capacitor-based high DC gain and low voltage stress DC-DC boost converter for photovoltaic applications. Int. J. Electr. Power Energy Syst. 2021, 125, 106496. [Google Scholar] [CrossRef]
- Zabolev, R.Y. Dynamic Modes in Controlled Valve Converters; NSTU: Novosibirsk, Russia, 1997; 32p. (In Russian) [Google Scholar]
- Kosykh, E.; Udovichenko, A.; Lopatkin, N.; Zinoviev, G.; Grishanov, E.; Sarakhanova, R. Analysis of the Control System for a Soft Starter of an Induction Motor Based on a Multi-Zone AC Voltage Converter. Electronics 2022, 12, 56. [Google Scholar] [CrossRef]
- Construction of a Digital Filter with a Finite Impulse Response. Available online: http://habrahabr.ru/post/128140/ (accessed on 27 October 2023). (In Russian).

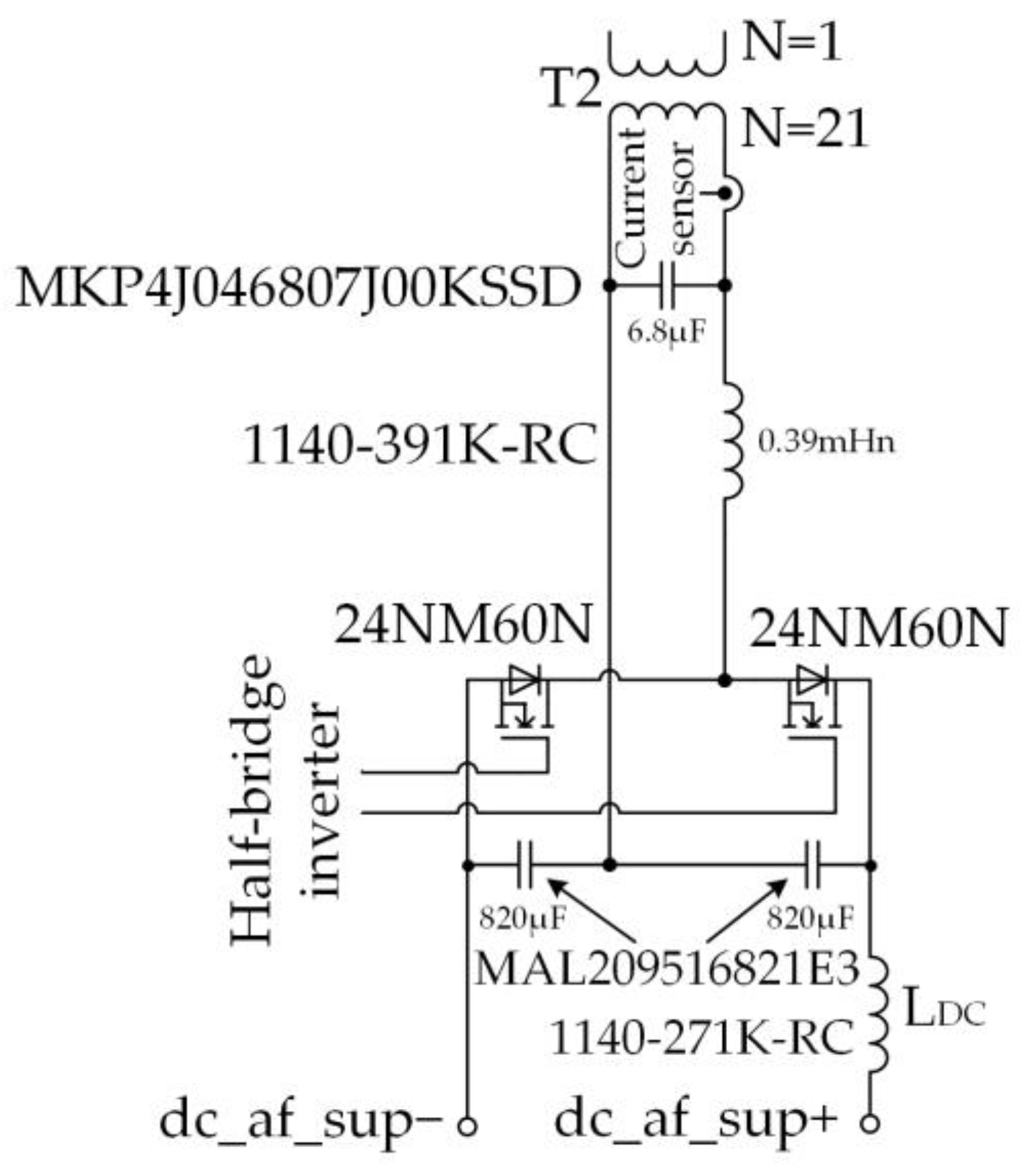



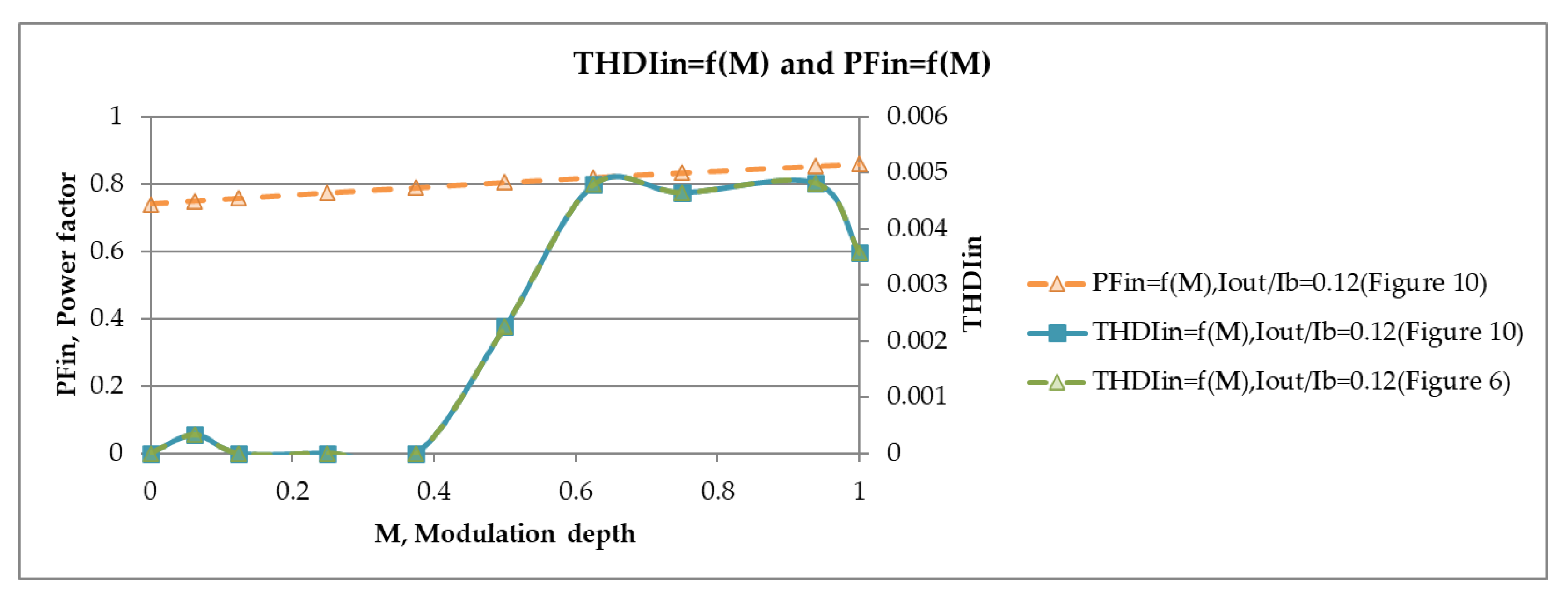
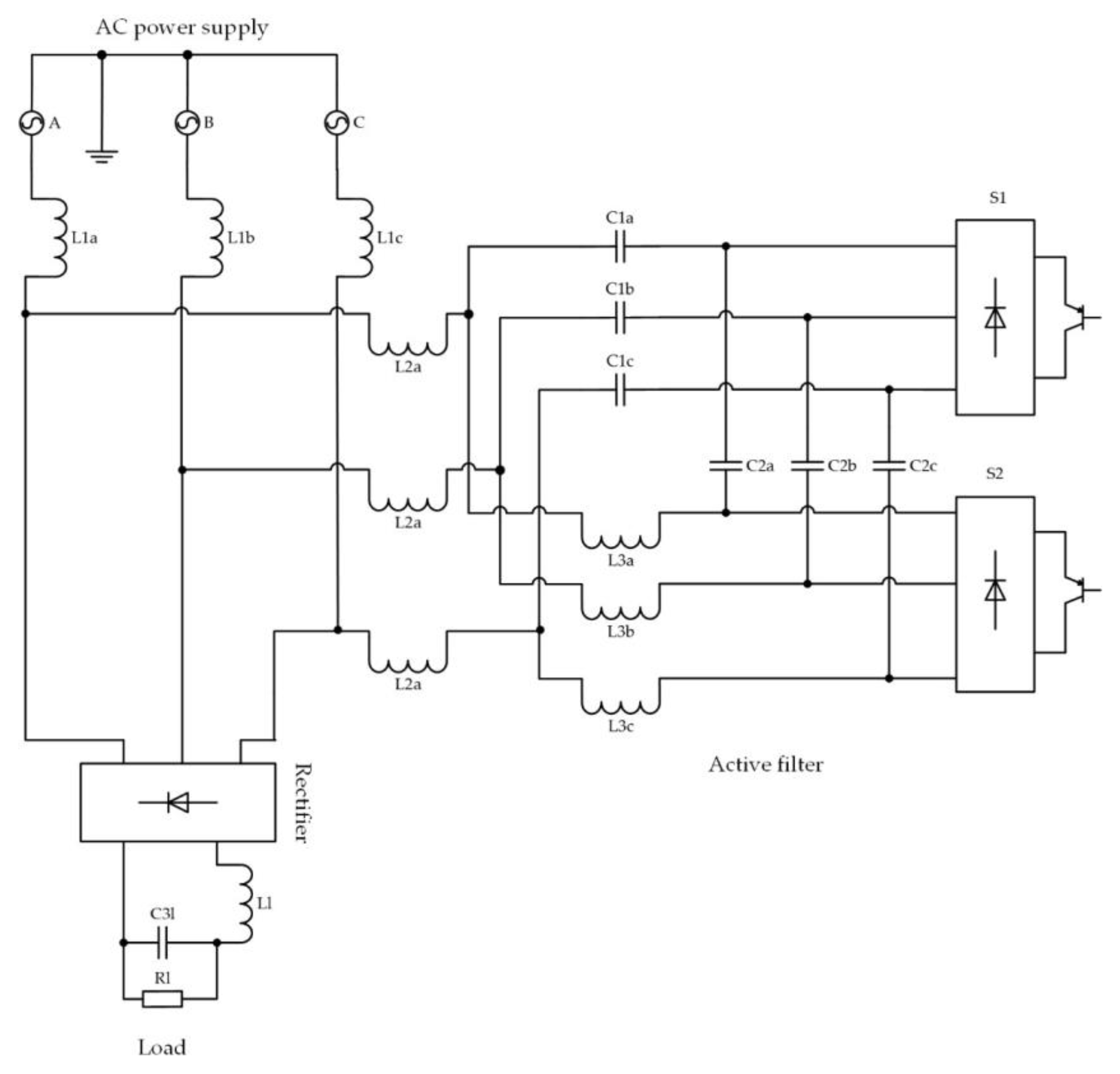

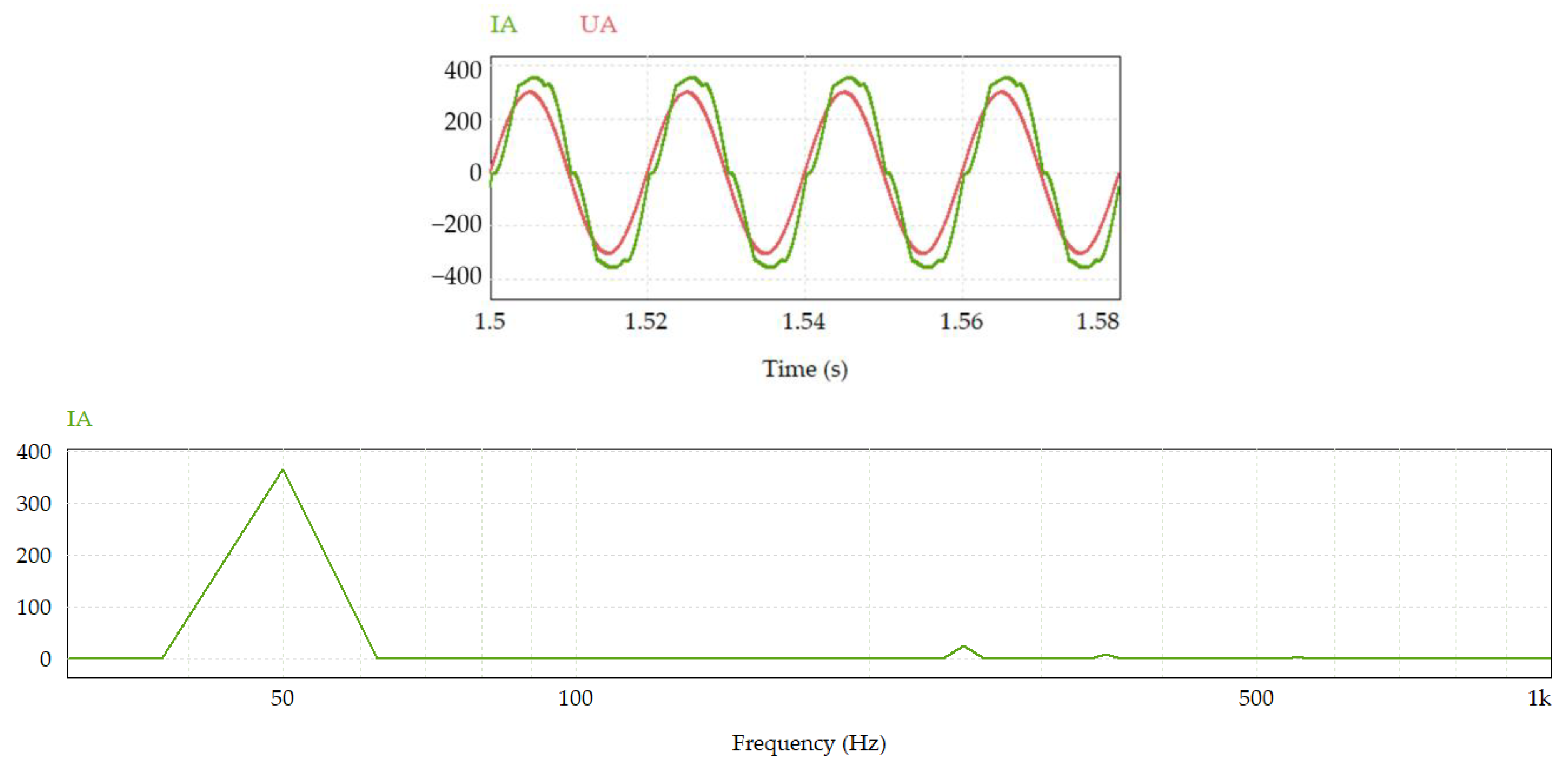
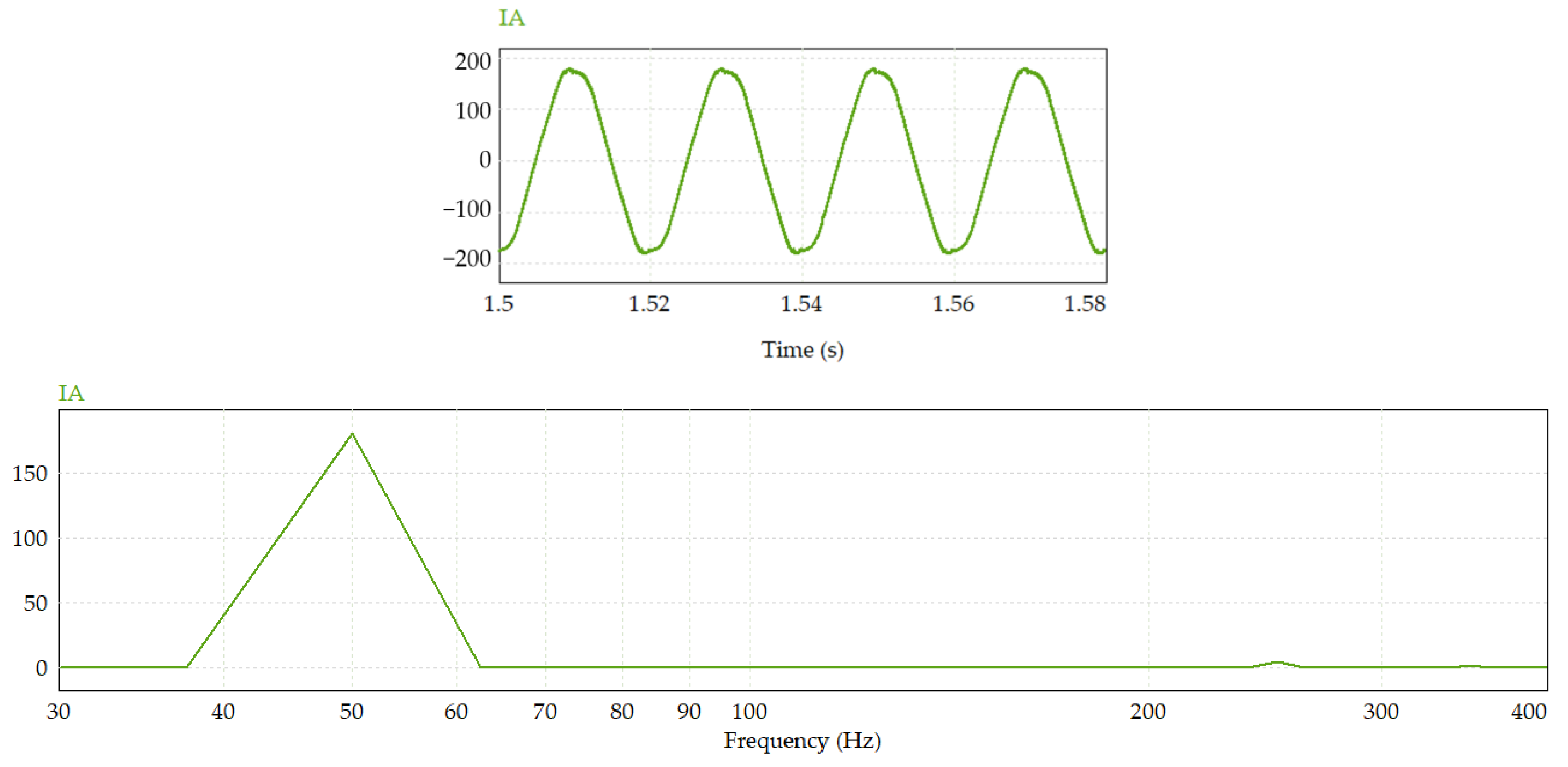


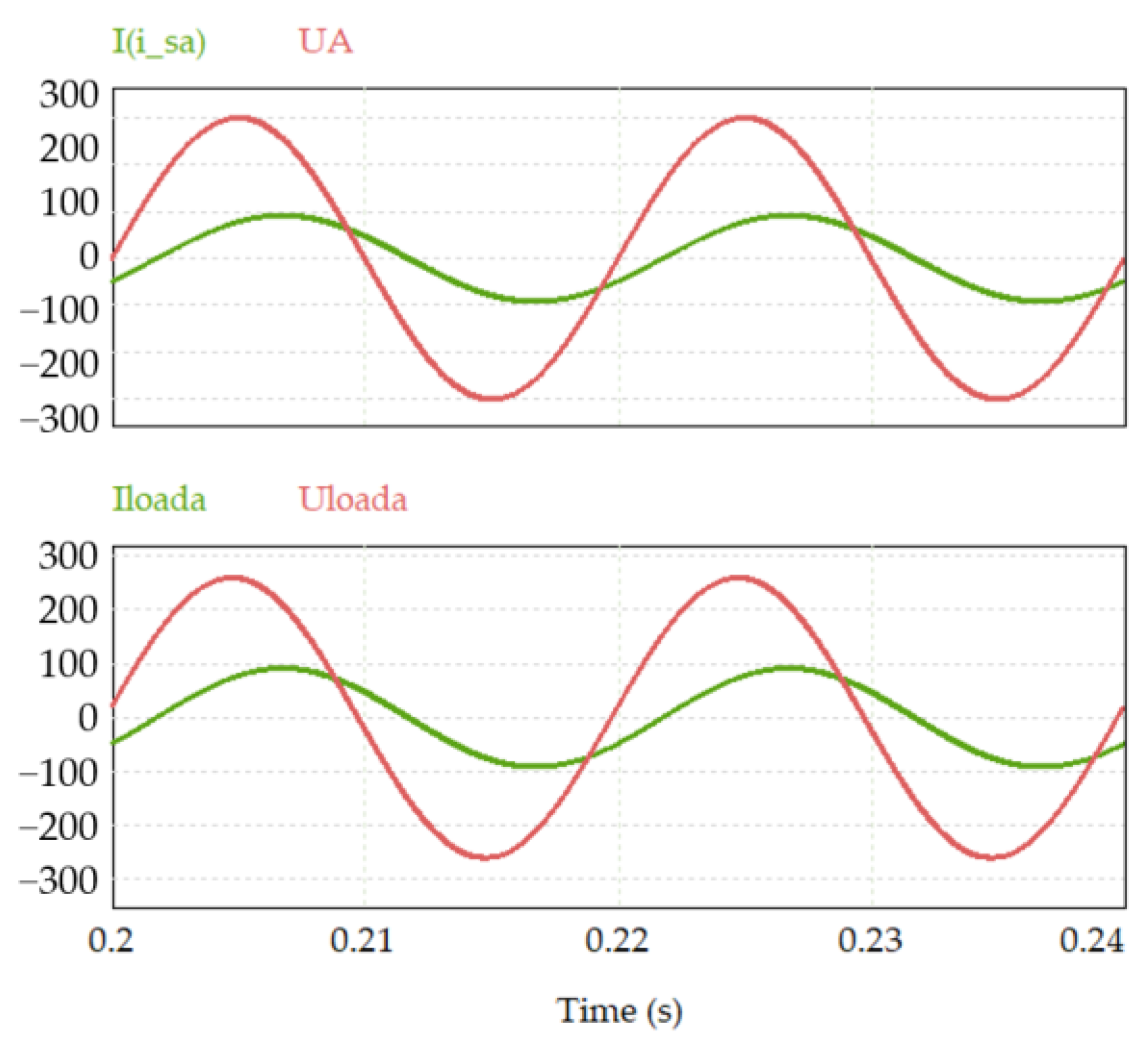
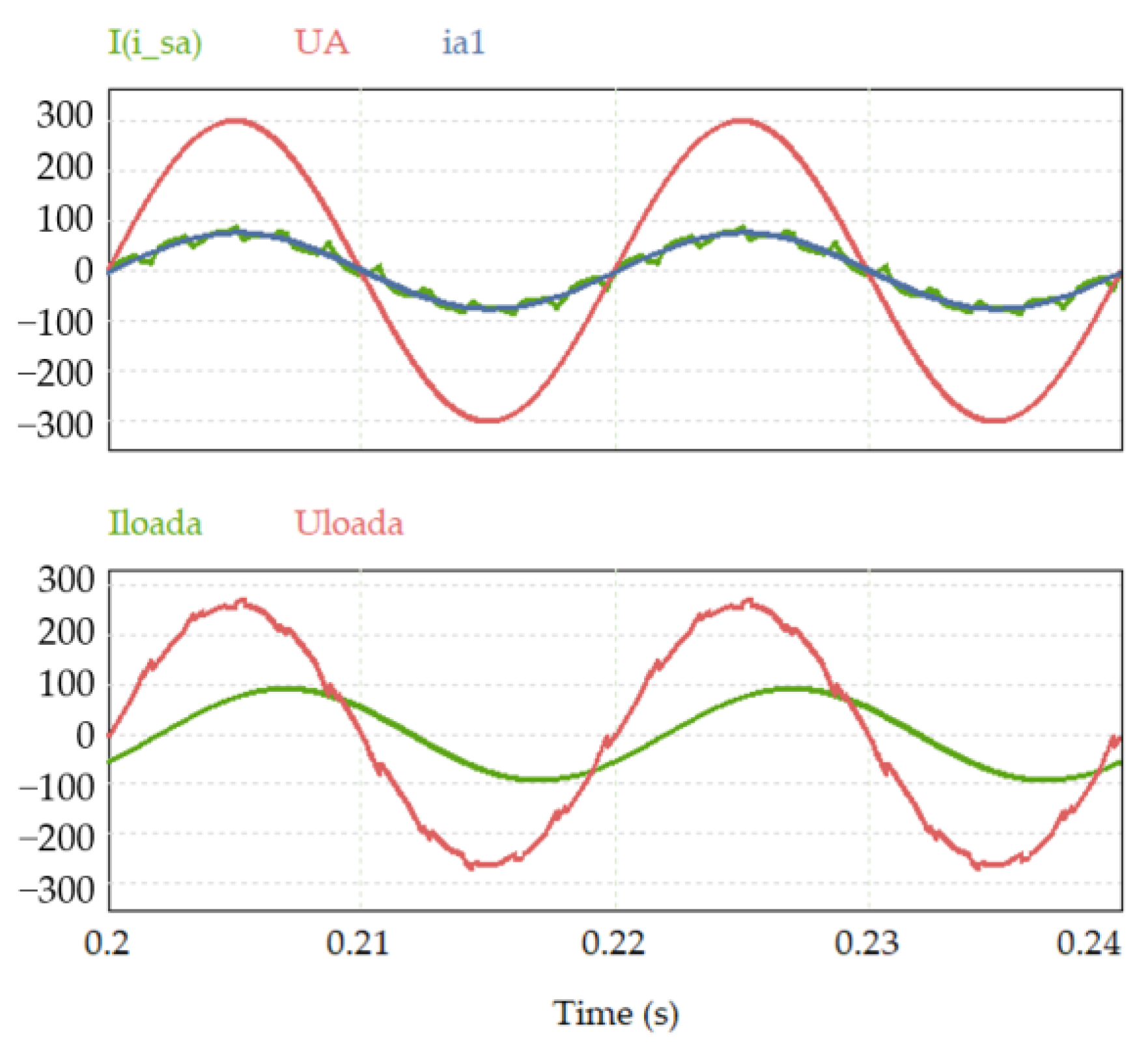
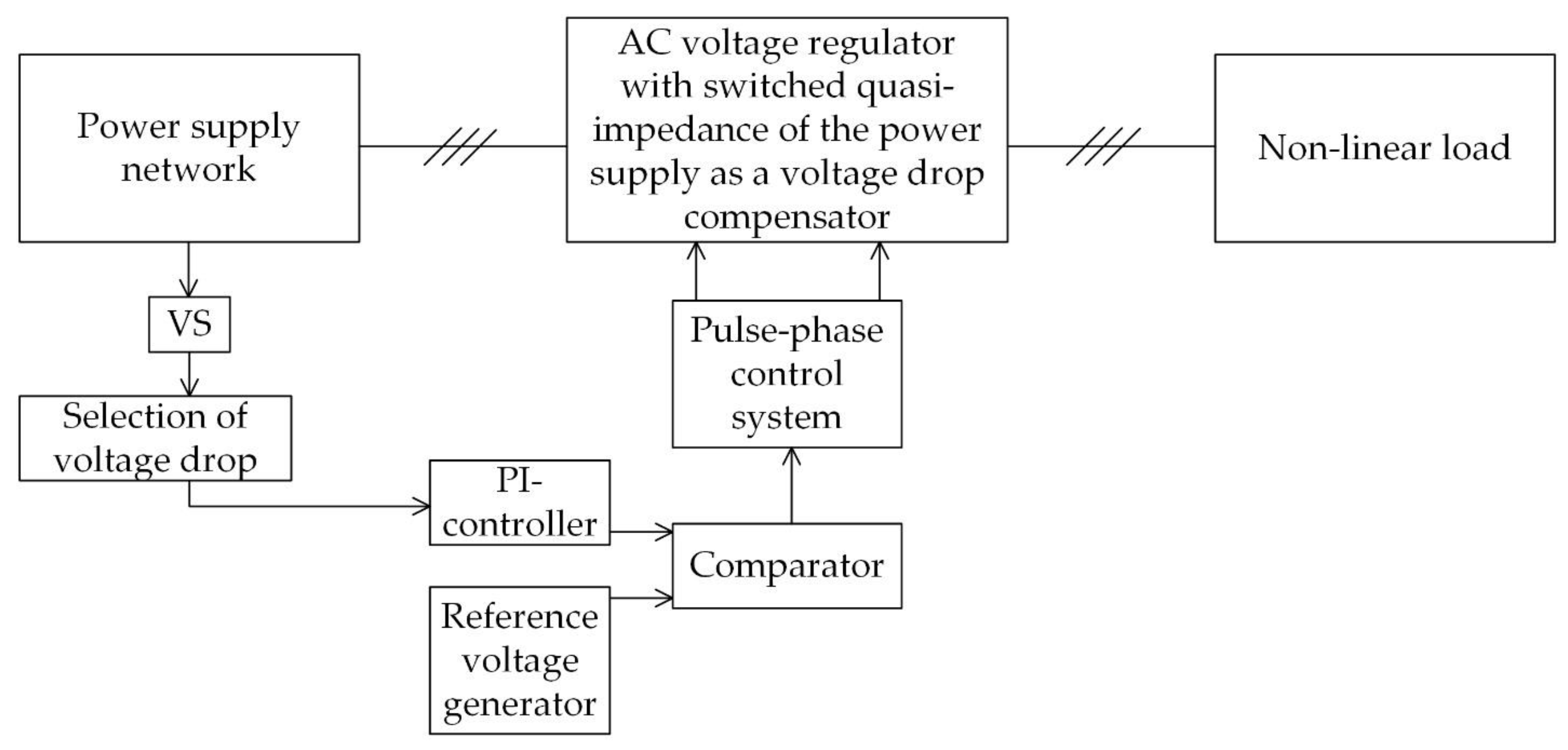
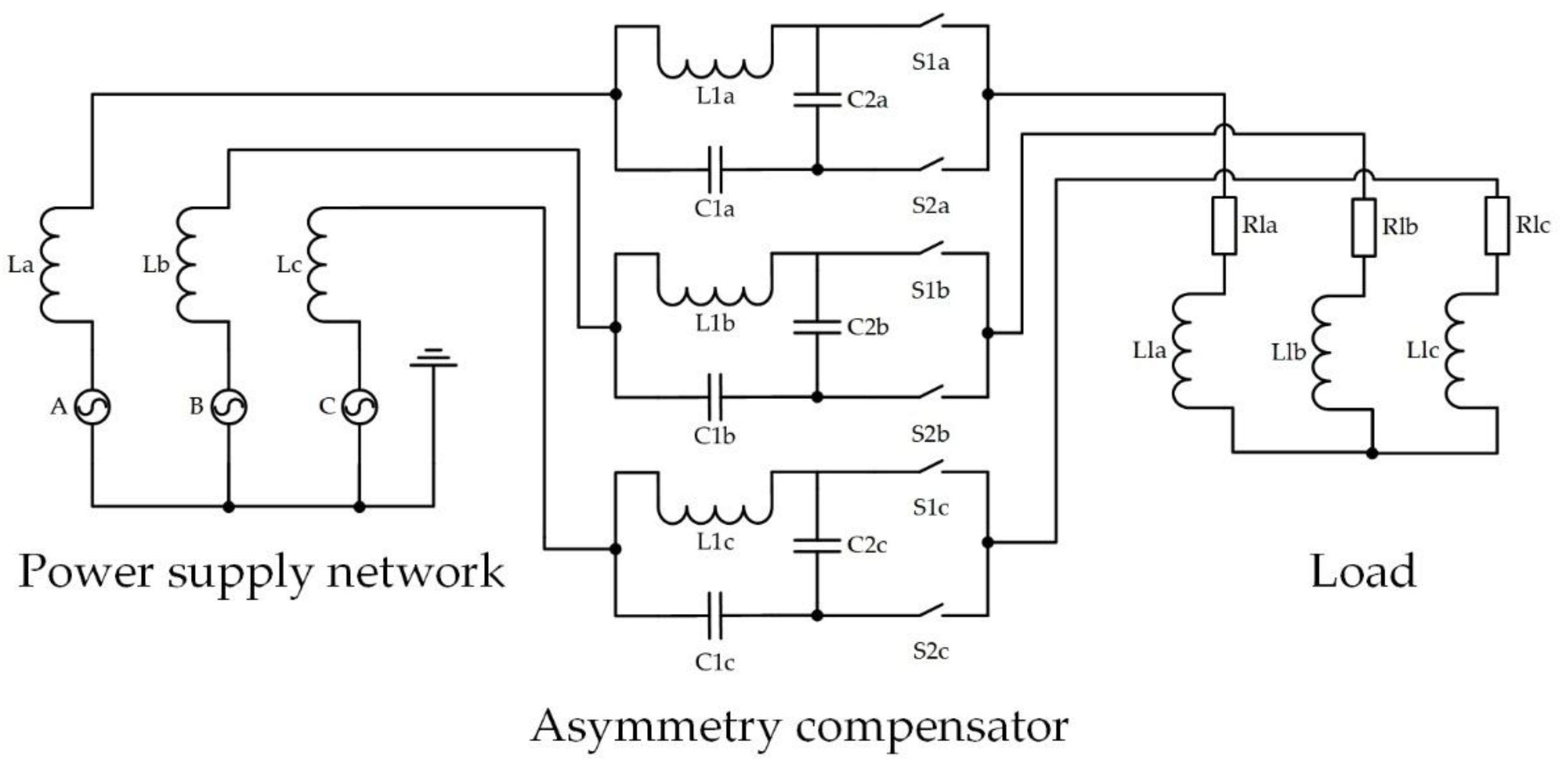




| Requirements for an Active Filter | |
|---|---|
| Transformer T2 | |
| Output voltage range, V | 72.1–135 |
| Ripple amplitude range, V | 3.2–5.9 |
| The current of the secondary winding of the matching transformer, A | 168 |
| Pulsation frequency, Hz | 300 |
| Power, W | 188.5 |
| Transformer efficiency, % | 98 |
| Inverter | |
| Transistors S1, S2 | 24NM60N |
| Transistor current, A | 3.696 |
| The maximum voltage applied to the transistor, V | 270 |
| Inductance of the choke on the AC side, Lf1, μH | 390 |
| Capacitance of the capacitor on the AC side, Cf4, μF | 6.8 |
| Inductance of the choke on the DC side, Ldc, μH | 270 |
| Capacitance of the capacitor on the DC side, CDC, μF | 820 |
| Type of Converter | Number of Transistors per Phase | Number of Reactive Elements per Phase | The Possibility of Increasing the Voltage |
|---|---|---|---|
| AC voltage regulator with switchable cells and reactors | 6 | 8 | Yes |
| A converter operating as a unidirectional buck regulator of alternating voltage, as well as a bidirectional boost regulator | 8 | 5 | Yes |
| Matrix converter | 6 | 3 | No |
| H-bridge scheme | 16 | 2 | No |
| AC-AC resonant converter with high-frequency link | 4 | 3 | Yes |
| AC-AC regulator with soft switching | 16 | 7 | No |
| Three-phase AC-AC regulator with soft switching | 4 | 6 | No |
| Matrix converter with a reactive voltage source | 10 | 4 | Yes |
| Matrix converter with modification of the control method | 6 | 3 | Yes |
| Matrix converter with a combination of pulse-width modulation and pulse-width regulation in the control system | 6 | 3 | Yes |
| A circuit with a combined matrix converter and a boost AC voltage regulator | 4 | 4 | Yes |
| A circuit with a combined bridge matrix converter and an AC voltage Ćuk regulator | 7 | 6 | Yes |
| Combination of an AC voltage Ćuk regulator according to a classical zero matrix converter | 3 | 2 | Yes |
| An AC voltage regulator based on the concept of introducing a volt-additive using a high-frequency conversion | 3 | 1 | Yes |
| An AC voltage regulator based on the Arkadiev–Marx concept | 8 | 4 | Yes |
| A simple circuit of a buck–boost AC voltage regulator with a switched quasi-impedance of the power supply | 1 | 4 | Yes |
| AC voltage regulator with a switched quasi-impedance of the power supply | 1 | 2 | Yes |
| AC voltage regulator with a switched quasi-impedance of the power supply and a capacitor in the load | 1 | 3 | Yes |
| Type of Converter | Modulation Depth | THDI(ADE), % | THDI(PSIM), % | Efficiency, % |
|---|---|---|---|---|
| AC voltage regulator with a switched quasi-impedance of the power supply and a capacitor in the load | 0.75 | 3.2 | 3.1 | 98 |
| A simple circuit of a buck–boost AC voltage regulator with a switched quasi-impedance of the power supply | 0.7 | 4 | 3.94 | 96 |
| Uin, V | 253 | 253 | 220 | 220 | 220 | 187 |
| Uout, V | 187 | 232 | 220 | 220 | 232 | 270 |
| Udcmax, V | 187.348 | 232.299 | 220.424 | 218.941 | 232.313 | 270.269 |
| Udcmin, V | 187.003 | 231.964 | 220.11 | 218.614 | 231.971 | 270.029 |
| Udcave, V | 187.174 | 232.129 | 220.265 | 218.777 | 232.144 | 270.148 |
| KpU, % | 0.18432 | 0.144316 | 0.142556 | 0.149467 | 0.147322 | 0.08884 |
| KpU/KpU(without an active filter) | 6.600593 | 6.286236 | 5.371182 | 5.215144 | 4.8261 | 2.662608 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Udovichenko, A.; Grishanov, E.; Kosykh, E.; Mekhtiyev, A. Analysis of Novel Energy-Efficient Converters to Ensure the Required Quality of Electrical Energy. Symmetry 2023, 15, 2092. https://doi.org/10.3390/sym15112092
Udovichenko A, Grishanov E, Kosykh E, Mekhtiyev A. Analysis of Novel Energy-Efficient Converters to Ensure the Required Quality of Electrical Energy. Symmetry. 2023; 15(11):2092. https://doi.org/10.3390/sym15112092
Chicago/Turabian StyleUdovichenko, Aleksey, Evgeniy Grishanov, Evgeniy Kosykh, and Ali Mekhtiyev. 2023. "Analysis of Novel Energy-Efficient Converters to Ensure the Required Quality of Electrical Energy" Symmetry 15, no. 11: 2092. https://doi.org/10.3390/sym15112092
APA StyleUdovichenko, A., Grishanov, E., Kosykh, E., & Mekhtiyev, A. (2023). Analysis of Novel Energy-Efficient Converters to Ensure the Required Quality of Electrical Energy. Symmetry, 15(11), 2092. https://doi.org/10.3390/sym15112092







