Exact Solutions of Nonlinear Partial Differential Equations Using the Extended Kudryashov Method and Some Properties

Abstract

In this paper, we consider how to find new exact solutions for nonlinear partial differential equations using the extended Kudryashov method. This method mainly uses the Riccati equation and the Bernoulli equation where there are some underdetermined constant parameters. And we also use the concept of symmetry to study its reduction equation, Lie transformation group, self-adjointness, and conservation laws. This paper mainly studies the Boussinesq class and the shallow water wave equation in (1 + 1) dimensions and tries to find new exact solutions and symmetry properties of them.

1. Introduction

As a matter of common knowledge, many methods for finding the exact solutions of nonlinear partial differential equations have been derived in recent years. In addition, the research in this area is of great significance to the isolation theory, which describes natural selection as a mechanism for ensuring the adaptation of organisms to their environment, their morphological diversity, and partial differential equations. For example, the methods for finding exact solutions include the F-expansion method [1,2], the truncated expansion method [3,4], the sine-cosine function method [5], and so on [6,7]. The idea of this paper is to use an efficient and direct method, that is, the extended Kudryashov method [8,9,10,11,12], to find the exact solution of nonlinear partial differential equations. This method presupposes the general solution form of the equation, takes the simple form of the Riccati equation and Bernoulli equation, and simultaneously obtains the exact solution of the objective equation using the reduction of the coefficient equation.

In the second part of this work, we consider how to explore other properties of the classical Boussinesq equations [13] and the shallow water wave equation [14], and use the Lie method to obtain their symmetric infinitesimal generators, Lie transformation groups, and corresponding invariant solutions [15,16,17,18,19,20,21]. Wu and Zhang [22] derived the (1 + 1)-dimensional classical Boussinesq equation, which is used to simulate nonlinear dispersive long gravity waves propagating along two horizontal directions in shallow water of a uniform depth. In recent years, many scholars have studied the equation [23,24,25]. In the third part, we calculate the self-adjoint properties and their conservation laws [26,27,28,29,30,31,32,33].

2. Simple Description of the Method

In this section, we first briefly introduce how to use the extended Kudryashov method to obtain the exact solutions of the objective equation. The idea of this method is to substitute the form of the presupposed exact solution into the objective equation to determine the form of the solution according to the determining equation of the coefficient. The principle of the earliest proposed Kudryashov method [8,9,10] is to use the polynomial form of the solution of the Riccati equation to find the exact solution of the target equation. The modified Kudryashov method [11] proposed by Kabir et al. used a similar principle, but used the polynomial of the $exp\left(\eta \right)$ form solution. However, the extended Kudryashov method [12] combines the above two methods to obtain a more general formal solution, and the fractional form of the solution of the Riccati equation is added. On this basis, we improve the extended Kudryashov method and add the derivative term of the Bernoulli solution to further obtain some new exact solutions of the equation.

First, we consider the nonlinear equations

$$F_1(u,v,u_t,v_t,u_x,v_x,\dots )=0,$$

$$F_2(u,v,u_t,v_t,u_x,v_x,\dots )=0.$$

Step 1. Firstly, we give the general form of the preset exact solution

$$u(x,t)=A_0+{\displaystyle \sum _{K=1}^N}{\displaystyle \sum _{i+j=K}}{A}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+{\displaystyle \sum _{K=1}^N}{B}_K{\psi }^{-K}\left(\eta \right)+{\displaystyle \sum _{j=1}^N}{C}_j{\varphi }^{-j}\left(\xi \right),$$

(1)

$$v(x,t)=a_0+{\displaystyle \sum _{K=1}^N}{\displaystyle \sum _{i+j=K}}{a}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+{\displaystyle \sum _{K=1}^N}{b}_K{\psi }^{-K}\left(\eta \right)+{\displaystyle \sum _{j=1}^N}{c}_j{\varphi }^{-j}\left(\xi \right),$$

(2)

where $A_0,A_{ij}(i,j=0,1,2,3,\dots ,N),a_0,a_{ij}(i,j=0,1,2,3,\dots ,M),B_K,b_K,C_k,c_k$ are constants to be determined; $\xi ={\kappa }_{1}x+{\omega }_{1}t$,$\eta ={\kappa }_{2}x+{\omega }_{2}t,$ where ${\kappa }_1,{\kappa }_2,{\omega }_1,{\omega }_2$ are also underdetermined constants; and $\varphi \left(\xi \right)$ and $\psi \left(\eta \right)$ are the solutions of the Bernoulli and Riccati equations

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=R_2{\varphi }^2\left(\xi \right)-R_1\varphi \left(\xi \right),R_2\ne 0,\hfill \end{array}$$

(3)

$$\begin{array}{cc}& \frac{\mathrm{d}\psi }{\mathrm{d}\eta }=S_2{\psi }^2\left(\eta \right)+S_1\psi \left(\eta \right)+S_0,S_2\ne 0.\hfill \end{array}$$

(4)

Each derivative of $\varphi \left(\xi \right),\psi \left(\eta \right)$ can be expressed by the power of $\varphi ,\psi$, for example,

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^2\varphi }{\mathrm{d}{\xi }^2}=& 2R_2\varphi {\varphi }^{{}^{\prime }}-R_1{\varphi }^{{}^{\prime }}\hfill \\ \hfill =& 2R_2\varphi (R_2{\varphi }^2-R_1\varphi )-R_1(R_2{\varphi }^2-R_1\varphi )\hfill \\ \hfill =& 2R_2{\varphi }^3-3R_1{R}_2{\varphi }^2+R_1^2\varphi ,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^3\varphi }{\mathrm{d}{\xi }^3}=& 6R_2^2{\varphi }^2{\varphi }^{{}^{\prime }}-6R_1{R}_2\varphi {\varphi }^{{}^{\prime }}+R_1^2{\varphi }^{{}^{\prime }}\hfill \\ \hfill =& 6R_2^3{\varphi }^4-6R_1{R}_2^2-R_1{\varphi }^3-6R_1{R}_2^2{\varphi }^3+6R_1^2{R}_2+R_1^2{R}_2{\varphi }^2-R_1^3\varphi \hfill \\ \hfill =& 6R_2^3{\varphi }^4-12R_1{R}_2^2{\varphi }^3+7R_1^2{R}_2{\varphi }^2-R_1^3\varphi ,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^2\psi }{\mathrm{d}{\eta }^2}=& 2S_2\psi {\psi }^{{}^{\prime }}+S_1{\psi }^{{}^{\prime }}\hfill \\ \hfill =& 2S_2^2{\psi }^3+2S_1{S}_2{\psi }^2+2S_0{S}_2\psi +S_1{S}_2{\psi }^2+S_1^2\psi +S_0{S}_1\hfill \\ \hfill =& 2S_2^2{\psi }^3+3S_1{S}_2{\psi }^2+2S_0{S}_2\psi +S_1^2\psi +S_0{S}_1,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^3\psi }{\mathrm{d}{\eta }^3}=& 6S_2^2{\psi }^2{\psi }^{{}^{\prime }}=6S_1{S}_2\psi {\psi }^{{}^{\prime }}+2S_0{S}_2{\psi }^{{}^{\prime }}+S_1^2{\psi }^{{}^{\prime }}\hfill \\ \hfill =& 6S_2^3{\psi }^4+6S_1{S}_2^2{\psi }^3+6S_0{S}_2^2|{\psi }^2+6S_1{S}_2^2{\psi }^3+6S_1^2{S}_2{\psi }^2\hfill \\ \hfill & +6S_0{S}_1{S}_2\psi +2S_0{S}_1{S}_2\psi +2S_0^2{S}_2+S_1^2{S}_2{\psi }^2+S_1^3\psi +S_0{S}_1^2\hfill \\ \hfill =& 6S_2^3{\psi }^4+12S_1{S}_2^2{\psi }^3+8S_0{S}_2^2{\psi }^2+7S_1^2{S}_2{\psi }^2+8S_0{S}_1{S}_2\psi +S_1^3\psi +S_0{S}_1^2,\hfill \end{array}$$

(8)

where $R_1,R_2,S_0,S_1,S_2$ are constants to be determined. As a matter of common knowledge, the solution of Equation (3) has the following form:

$$\varphi \left(\xi \right)=\left\{\begin{array}{c}\frac{R_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)},R_1\ne 0,\hfill \\ \frac{-1}{R_2\xi +{\xi }_0},R_1=0,\hfill \end{array}\right.$$

where ${\xi }_0$ is a constant of integration. Similar to the above, we know that the solutions of Equation (4) have the following forms:

$$\psi \left(\eta \right)=\left\{\begin{array}{c}\frac{-S_1}{2S_2}-\frac{\sqrt{\mu }}{2S_2}tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0),\mu >0,\hfill \\ \frac{-S_1}{2S_2}-\frac{\sqrt{\mu }}{2S_2}coth(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0),\mu >0,\hfill \end{array}\right.$$

$$\psi \left(\eta \right)=\left\{\begin{array}{c}\frac{-S_1}{2S_2}+\frac{\sqrt{-\mu }}{2S_2}tan(\frac{\sqrt{-\mu }}{2}\eta +{\eta }_0),\mu <0,\hfill \\ \frac{-S_1}{2S_2}-\frac{\sqrt{-\mu }}{2S_2}cot(\frac{\sqrt{-\mu }}{2}\eta +{\eta }_0),\mu <0,\hfill \end{array}\right.$$

where $\mu =S_1^2-4S_0{S}_2$ and ${\eta }_0$ is an integration constant. And the solution has a special form

$$\psi \left(\eta \right)=\frac{-1}{S_2\eta +{\eta }_0},S_0=S_1=0.$$

Step 2. Secondly, we need to use the homogeneous balance method to balance the nonlinear term with the highest derivative term in the equation, so as to determine the value of M and N and determine the form of the exact solution.

Step 3. After obtaining the general form of the solutions, we substitute them into Equations (1) and (2), and the derivative terms of $\varphi$ and $\psi$ are replaced by the polynomial forms of $\varphi$ and $\psi$ using the above differential equation. Then, the obtained polynomial is used to separate the power coefficients of $\varphi$ and $\psi$, and a series of determining equations concerning parameters $A_0,A_{ij}(i,j=0,1,2,3,\dots ,N),a_0,a_{ij}(i,j=0,1,2,3,\dots ,M),B_K,b_K,{\kappa }_1,{\kappa }_2,$

${\omega }_1,{\omega }_2$ are obtained.

Step 4. After proposing the coefficient equation of $\varphi$ and $\psi$, we can obtain the relationship between the parameters ${\kappa }_1,{\kappa }_2,{\omega }_1,{\omega }_2,A_0,A_{ij}(i,j=0,1,2,3,\dots ,N),B_K,b_K,a_0,a_{ij}(i,j=0,1,2,3,\dots ,M)$ by solving the equation simultaneously; thus, we can obtain the general expression of the solution $u,v$.

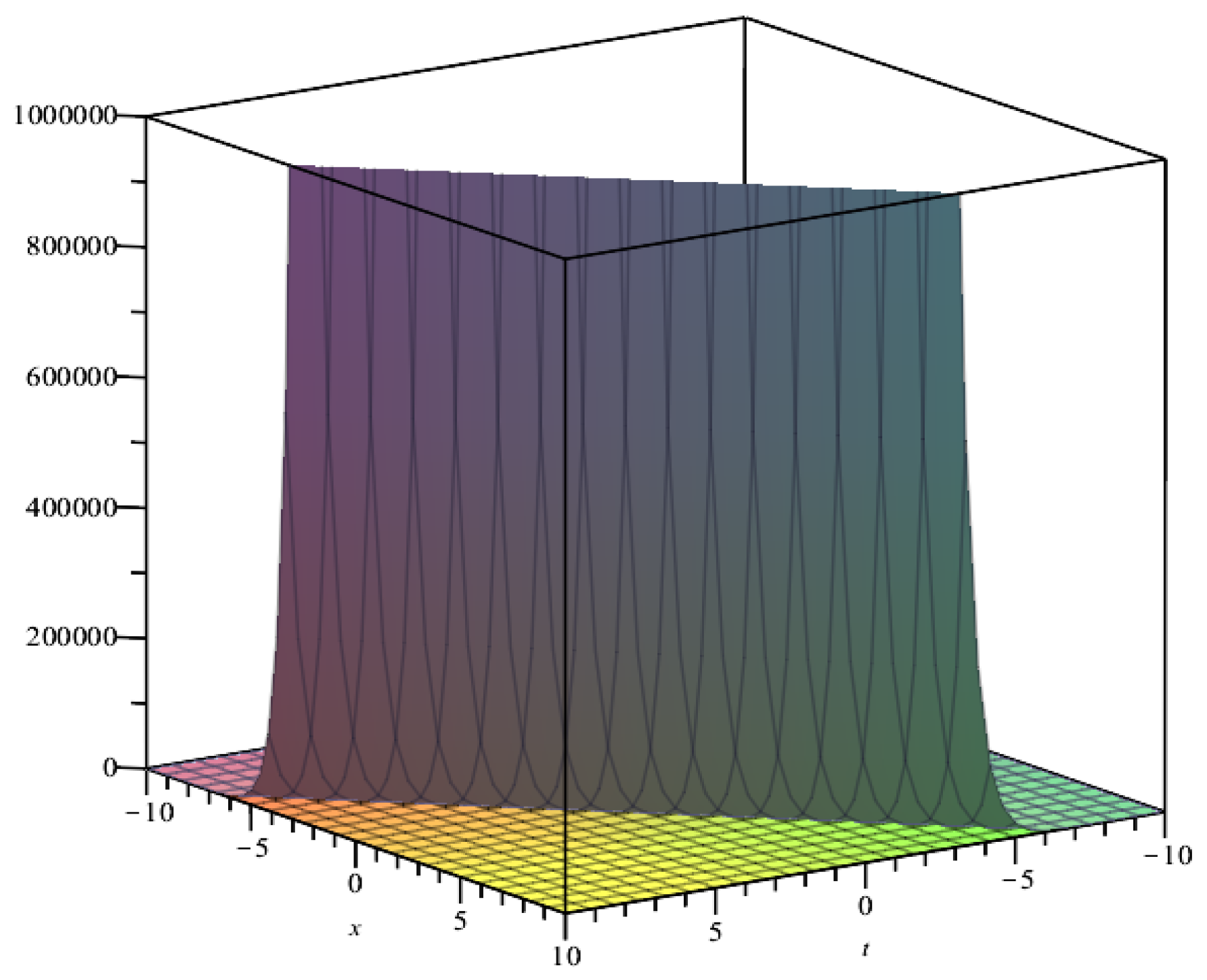
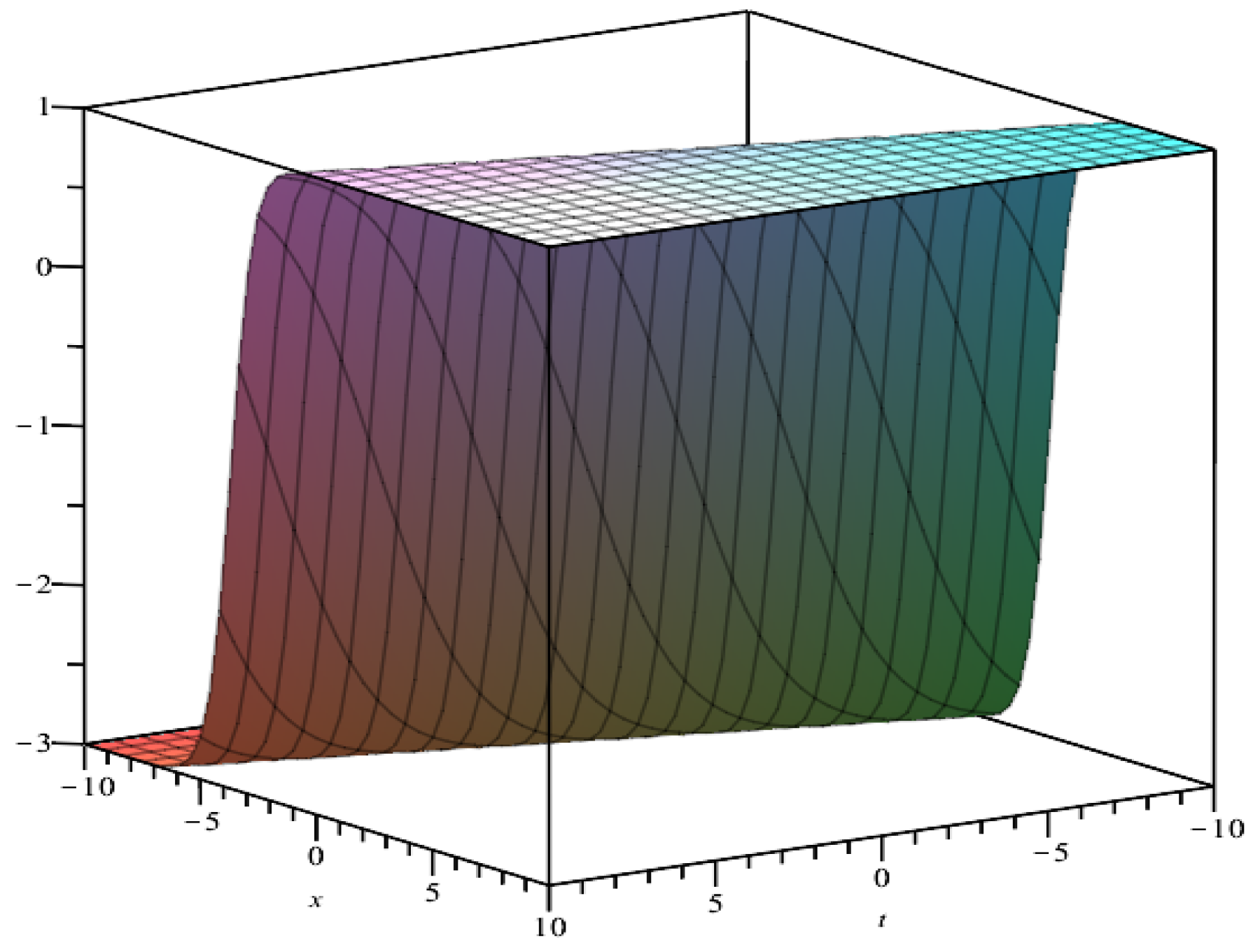
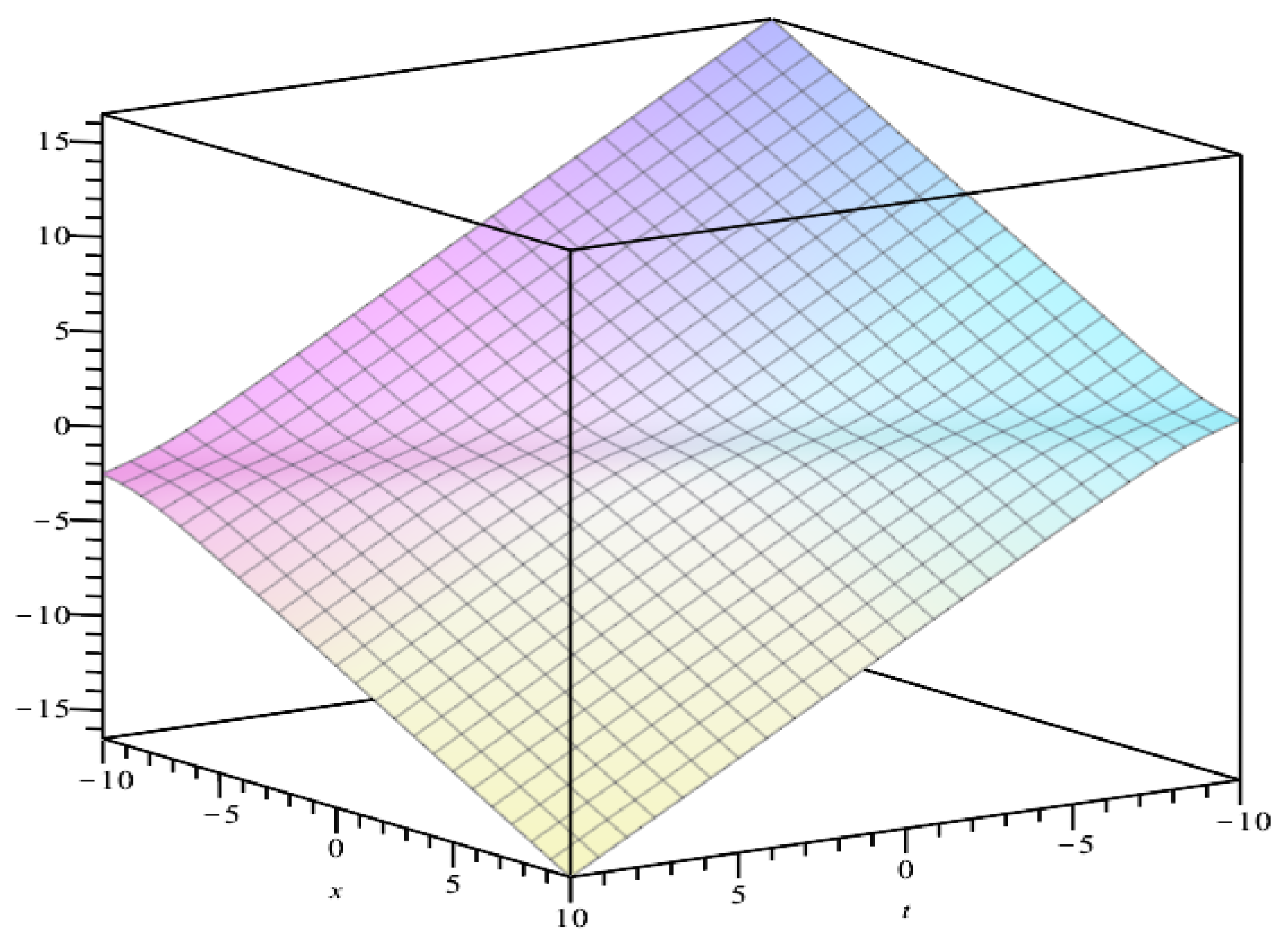
3. Exact Solutions of the Boussinesq Class

In the following sections, we will use the extended Kudryashov method to deal with some different partial differential equations and obtain their exact solutions. We first study the (1 + 1)-dimensional Boussinesq class for the evolution of two horizontal nonlinear dispersive long gravity waves propagating in shallow water of uniform depth:

$$\left\{\begin{array}{c}{v}_t+{\left[(1+v)u\right]}_x+\frac{1}{3}{u}_{xxx}=0,\hfill \\ u_t+u{u}_x+v_x=0.\hfill \end{array}\right.$$

(9)

In order to obtain the exact solutions of the (1 + 1)-dimensional Boussinesq class, we can set

$$\left\{\begin{array}{c}u(x,t)=A_0+{\displaystyle \sum _{K=1}^N}{\displaystyle \sum _{i+j=K}}{A}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+{\displaystyle \sum _{K=1}^N}{B}_K{\psi }^{-K}\left(\eta \right)+{\displaystyle \sum _{j=1}^N}{C}_j{\psi }^{-j}\left(\eta \right),\hfill \\ v(x,t)=a_0+{\displaystyle \sum _{K=1}^M}{\displaystyle \sum _{i+j=K}}{a}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+{\displaystyle \sum _{K=1}^M}{b}_K{\psi }^{-K}\left(\eta \right)+{\displaystyle \sum _{j=1}^M}{c}_j{\psi }^{-j}\left(\eta \right).\hfill \end{array}\right.$$

(10)

Firstly, we need to apply the homogeneous balance method to the target equation to determine the values of M and N. Then, by calculation, we can conclude that $N=1,M=2$. Therefore, we can determine the exact solution of the following general form:

$$\left\{\begin{array}{cc}u(x,t)=\hfill & A_0+A_{10}\varphi \left(\xi \right)+A_{01}\psi \left(\eta \right)+\frac{B_1}{\psi \left(\eta \right)}+\frac{C_1}{\varphi \left(\xi \right)},\hfill \\ v(x,t)=\hfill & a_0+a_{10}\varphi \left(\xi \right)+a_{01}\psi \left(\eta \right)+a_{20}{\varphi }^2\left(\xi \right)+a_{02}{\psi }^2\left(\eta \right)+a_{11}\varphi \left(\xi \right)\psi \left(\eta \right)\hfill \\ & +\frac{b_1}{\psi \left(\eta \right)}+\frac{b_2}{{\psi }^2\left(\eta \right)}+\frac{c_1}{\varphi \left(\xi \right)}+\frac{c_2}{{\varphi }^2\left(\xi \right)},\hfill \end{array}\right.$$

(11)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t$,$\eta ={\kappa }_{2}x+{\omega }_{2}t$, and the coefficients encountered in the calculation process ${\kappa }_1$, ${\kappa }_2$, ${\omega }_1,$${\omega }_2$, $A_0$$,A_{10}$, $A_{01}$, $B_1,$$a_0,$$a_{01}$, $a_{02},$$a_{10},$$a_{11},$$a_{20}$, $b_1,$$b_2$ are underdetermined constants. And $\varphi \left(\xi \right)$ and $\psi \left(\eta \right)$ are the solution of the Bernoulli and the Riccati equations, respectively. After bringing the preset exact solution form (11) into the target equation, i.e., Equation (9), we obtain a series of algebraic equations by extracting the coefficients. By solving these algebraic equations, we can obtain a series of exact solutions of Equation (9). We list some results as follows:

$$\begin{array}{cc}\hfill & u_1(x,t)=A_0,\hfill \\ & v_1(x,t)=a_0+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}+\frac{c_2{(R_2+R_{1}exp(R_1\xi +{\xi }_0))}^2}{R_1^2},\hfill \end{array}$$

(12)

where $\xi ={\kappa }_{1}x-{\kappa }_1{A}_{0}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$\begin{array}{cc}\hfill u_2(x,t)=& A_0,\hfill \\ \hfill v_2(x,t)=& -b_1(S_2\eta +{\eta }_0)+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}+\frac{c_2{\left(R_{1}exp(R_1\xi +{\xi }_0)\right)}^2}{R_1^2}\hfill \\ & +\frac{c_2{R}_2}{R_1^2},\hfill \end{array}$$

(13)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x-\frac{c_1{\kappa }_1{R}_2{A}_0+b_1{\kappa }_2{s}_2{A}_0+c_1{\omega }_1{R}_2}{b_1{s}_2}t,$

$$\begin{array}{cc}\hfill u_3(x,t)=& A_0+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},\hfill \\ \hfill v_3(x,t)=& -\frac{c_1{\kappa }_1{A}_0+C_1{\kappa }_1+c_1{\omega }_1}{C_1{\kappa }_1}+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}\hfill \\ & +\frac{c_2{(R_2+R_{1}exp(R_1\xi +{\xi }_0))}^2}{R_1^2},\hfill \end{array}$$

(14)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,{\kappa }_{2}x+{\omega }_{2}t,$

$$\begin{array}{cc}\hfill & u_4(x,t)=-\frac{c_1{\omega }_1{R}_2+b_1{\omega }_2{s}_2}{b_1{\kappa }_2{s}_2}++\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},\hfill \\ & v_4(x,t)=a_0+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}+\frac{c_2{(R_2+R_{1}exp(R_1\xi +{\xi }_0))}^2}{R_1^2},\hfill \end{array}$$

(15)

where $\xi ={\omega }_{1}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$\begin{array}{cc}\hfill u_5(x,t)=& A_0+\frac{C_1\left(R_{1}exp(R_1\xi +{\xi }_0)\right)}{R_1},\hfill \\ \hfill v_5(x,t)=& a_0-\frac{2S_2{b}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}\hfill \\ & +\frac{c_2{(R_2+R_{1}exp(R_1\xi +{\xi }_0))}^2}{R_1^2},\hfill \end{array}$$

(16)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\omega }_{2}t,S_2=-\frac{R_2(c_1{\kappa }_1{A}_0+a_0{C}_1{\kappa }_1+C_1{\kappa }_1+c_1{\omega }_1)}{b_1{\omega }_2},$

$$\begin{array}{cc}\hfill u_6(x,t)=& A_0+\frac{C_1\left(R_{1}exp(R_1\xi +{\xi }_0)\right)}{R_1},\hfill \\ \hfill v_6(x,t)=& -\frac{4c_1{\kappa }_1{A}_0{b}_2-b_1^2{C}_1{\kappa }_1+4c_1{\omega }_1{b}_2}{4C_1{b}_2{\kappa }_1}-\frac{2S_2{b}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}\hfill \\ & +\frac{4S_2^2{b}_2}{{(S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0))}^2}+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}\hfill \\ & +\frac{c_2{(R_2+R_{1}exp(R_1\xi +{\xi }_0))}^2}{R_1^2},\hfill \end{array}$$

(17)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,S_2=-\frac{C_1{R}_2{b}_1{\kappa }_1}{4b_2{\omega }_2}.$

Figure 1 and Figure 2 show the geometries of the solutions $u_1(x,t),v_1(x,t)$ and $u_2(x,t),v_2(x,t)$ as determined by (12) and (13), respectively. Figure 3 and Figure 4 show the geometries of the solutions $u_5(x,t),v_5(x,t)$ and $u_6(x,t),v_6(x,t)$ as determined by (16) and (17), respectively. As shown in Figure 1, Figure 2, Figure 3 and Figure 4, the single lumps are localized in the $(x,t)$ plane and they are permanent lumps.

4. Exact Solutions of the Shallow Water Wave Equation

In this section, we study the shallow water wave equation:

$$v_t+v_x-v_{xxt}-4v{v}_t-2v_x{\partial }_x^{-1}{v}_t=0.$$

(18)

We will make a potential transformation on it first, i.e.,

$$v(x,t)=u_x(x,t).$$

Equation (18) can be transformed into

$$u_{xt}+u_{xx}-u_{xxxt}-4u_x{u}_{xt}-2u_{xx}{u}_t=0.$$

(19)

We study Equation (19) next. The shallow water wave equation plays a significant role in the field around the soliton. Then, we obtain some new general solutions of Equation (19) using the extended Kudryashov method. First let

$$u(x,t)=A_0+{\displaystyle \sum _{K=1}^N}{\displaystyle \sum _{i+j=K}}{A}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+{\displaystyle \sum _{K=1}^N}{B}_K{\psi }^{-K}\left(\eta \right)+{\displaystyle \sum _{j=1}^N}{C}_j{\psi }^{-j}\left(\eta \right).$$

(20)

Then, we also determine the value of N using the homogeneous balance method. If $N=1$, we can obtain the following general solution of Equation (19):

$$u(x,t)=A_0+A_{10}\varphi \left(\xi \right)+A_{01}\psi \left(\eta \right)+\frac{B_1}{\psi \left(\eta \right)}+\frac{C_1}{\varphi \left(\xi \right)}.$$

(21)

After substituting Equation (21) into (19), we can obtain a series of coefficient equations concerning the constant coefficients ${\kappa }_1,{\kappa }_2,{\omega }_1,$ ${\omega }_2,A_0,A_{10},A_{01},B_1.$ Then, these equations are solved simultaneously, and the exact solution expression of u can be obtained. We list some results as follows:

$$u_1(x,t)=A_0+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(22)

where $\xi ={\kappa }_{1}x+\frac{1}{4R_1^2{\kappa }_1}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,C_1=\frac{5R_1^2{\kappa }_1^2-1}{6R_2{\kappa }_1},$

$$u_2(x,t)=A_0-2R_2{\omega }_1\frac{1}{R_2\xi +{\xi }_0},$$

(23)

where $\xi =-{\omega }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$u_3(x,t)=A_0-2R_2{\kappa }_1\frac{R_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)},$$

(24)

where $\xi ={\kappa }_{1}x+\frac{{\kappa }_1}{(R_1{\kappa }_1-1)(R_1{\kappa }_1+1)}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$u_4(x,t)=A_0-\frac{2S_2{B}_1}{S_1+\sqrt{2}tanh\left({\eta }_0\right)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(25)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,C_1=\frac{5R_1^2{\kappa }_1^2-1}{6R_2{\kappa }_1},$

$$u_5(x,t)=A_0-B_1(S_2\eta +{\eta }_0)+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(26)

where $\xi ={\kappa }_{1}x+\frac{1}{4R_1^2{\kappa }_1}t,\eta ={\omega }_{2}t,C_1=-\frac{8{\kappa }_1^2{B}_1{S}_2{\omega }_2{R}_1^2-5R_1^2{\kappa }_1^2+1}{6R_2{\kappa }_1},$

$$u_6(x,t)=A_0-B_1(S_2\eta +{\eta }_0)+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(27)

where $\xi ={\kappa }_{1}x+\frac{1}{4R_1^2{\kappa }_1}t,\eta ={\kappa }_{2}x,B_1=-\frac{-5R_1^2{\kappa }_1^2+6C_1{R}_2{\kappa }_1+1}{4S_2{\kappa }_2},$

$$u_7(x,t)=A_0-\frac{2S_2{B}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(28)

where $\xi ={\kappa }_{1}x+\frac{1}{4R_1^2{\kappa }_1}t,\eta ={\kappa }_{2}x,C_1=\frac{5R_1^2{\kappa }_1^2-1}{6R_2{\kappa }_1},$

$$u_8(x,t)=A_0-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)},$$

(29)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$u_9(x,t)=A_0-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}-C_1(R_2\xi +{\xi }_0),$$

(30)

where $\xi ={\kappa }_{1}x-\frac{4S_2{\kappa }_2^2{S}_0{\omega }_2+{\kappa }_2+{\omega }_2}{2C_1{R}_2{\kappa }_2}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$u_{10}(x,t)=A_0-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(31)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$u_{11}(x,t)=A_0-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(32)

where $\xi =-\frac{2S_2{B}_1{\kappa }_2{\omega }_2+{\kappa }_2+{\omega }_2}{2C_1{R}_2{\kappa }_2}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$u_{12}(x,t)=A_0-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(33)

where $\xi ={\kappa }_{1}x+\frac{1}{4R_1^2{\kappa }_1}t,\eta =-2R_1^2{\kappa }_1^2{\omega }_{2}x+{\omega }_{2}t,$

$$u_{13}(x,t)=A_0-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(34)

where $\xi =-\frac{1}{2C_1{R}_2}t,\eta ={\kappa }_{2}x,$

$$\begin{array}{cc}\hfill u_{14}(x,t)=& A_0-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}\hfill \\ & -\frac{2S_2{B}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)},\hfill \end{array}$$

(35)

where $\xi ={\kappa }_{1}x+\frac{1}{4R_1^2{\kappa }_1}t,\eta =-2R_1^2{\kappa }_1^2{\omega }_{2}x+{\omega }_{2}t,$

$$\begin{array}{cc}\hfill B_1=& -4RootOf(-1568{\omega }_2^4{\kappa }_1^8{R}_1^8{S}_1^4-588{\omega }_2^2{\kappa }_1^6{R}_1^6{S}_1^2+588{\omega }_2^2{R}_1^4{\kappa }_1^4{S}_1^2+98R_1^4{\kappa }_1^4\hfill \\ & +49R_1^2{\kappa }_1^2-49+(18,816R_1^5{\kappa }_1^5{S}_1^3{\omega }_2^3-896{\omega }_2^2{R}_1^4{\kappa }_1^4{S}_1^2-168R_1^2{\kappa }_1^2+168)z^2\hfill \\ & +(768R_1{\kappa }_1{S}_1{\omega }_2-128)z^4),\hfill \\ \hfill C_1=& \frac{1}{21R_2{\kappa }_1}\left(8RootOf\right(-1568{\omega }_2^4{\kappa }_1^8{R}_1^8{S}_1^4-588{\omega }_2^2{\kappa }_1^6{R}_1^6{S}_1^2+588{\omega }_2^2{R}_1^4{\kappa }_1^4{S}_1^2\hfill \\ \hfill & +49R_1^2{\kappa }_1^2-49+(18,816R_1^5{\kappa }_1^5{S}_1^3{\omega }_2^3-896{\omega }_2^2{R}_1^4{\kappa }_1^4{S}_1^2-168R_1^2{\kappa }_1^2+168)z^2\hfill \\ \hfill & +(768R_1{\kappa }_1{S}_1{\omega }_2-128)z^4{)}^2+28{\omega }_2^2{R}_1^4{\kappa }_1^4{S}_1^2+14R_1^2{\kappa }_1^2-7)+98R_1^4{\kappa }_1^4,\hfill \\ \hfill S_2& =-\frac{1}{14{\omega }_2{\kappa }_1^2{R}_1^2}\left(RootOf\right(-1568{\omega }_2^4{\kappa }_1^8{R}_1^8{S}_1^4-588{\omega }_2^2{\kappa }_1^6{R}_1^6{S}_1^2+588{\omega }_2^2{\kappa }_1^4{R}_1^4{S}_1^2\hfill \\ \hfill & +98R_1^4{\kappa }_1^4+49R_1^2{\kappa }_1^2-49+(18,816R_1^5{\kappa }_1^5{S}_1^3{\omega }_2^3-896{\omega }_2^2{R}_1^4{\kappa }_1^4{S}_1^2-168R_1^2{\kappa }_1^2\hfill \\ \hfill & +168)z^2+(768R_1{\kappa }_1{S}_1{\omega }_2-128)z^4\left)\right),\hfill \end{array}$$

(36)

where $RootOf$ denotes the solutions of the polynomial $f\left(z\right)=0$.

$$u_{15}(x,t)=A_0-\frac{\pm 14\sqrt{2}i{S}_2{S}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(37)

where $\xi =\pm \frac{\sqrt{2}i{S}_1}{4}t,\eta ={\kappa }_{2}x+{\omega }_{2}t,$

$$u_{16}(x,t)=A_0-\frac{\pm 14S_2\sqrt{2}i{S}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)},$$

(38)

where $\eta ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x-\frac{{\kappa }_2}{6{\kappa }_2^2{S}_1^2+1},S_2=\pm \frac{\sqrt{2}i}{4},$

$$u_{17}(x,t)=A_0-\frac{\pm 14\sqrt{2}i{S}_2{S}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu \eta }}{2}+{\eta }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(39)

where $\eta ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x-\frac{{\kappa }_2}{6{\kappa }_2^2{S}_1^2+1},S_2=\pm \frac{\sqrt{2}i{S}_1}{4},$

$$u_{18}(x,t)=A_0-2R_2{\kappa }_1\frac{R_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)}-\frac{2S_2{B}_1}{S_1+\sqrt{2}tanh\left({\eta }_0\right)},$$

(40)

where $\xi ={\kappa }_{1}x+\frac{{\kappa }_1}{(R_1{\kappa }_1-1)(R_1{\kappa }_1+1)}t,$

$$u_{19}(x,t)=A_0-A_{10}\frac{1}{{\xi }_0}-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu }\eta }{2}+{\eta }_0)}-C_1\left({\xi }_0\right),$$

(41)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x+\frac{{\kappa }_2}{48{\kappa }_2{S}_2^2-1}t,$

$$u_{20}(x,t)=A_0-A_{10}\frac{1}{{\xi }_0}-\frac{\pm 14\sqrt{2}i{S}_2{\kappa }_2{S}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu }\eta }{2}+{\eta }_0)}-C_1\left({\xi }_0\right),$$

(42)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta ={\kappa }_{2}x-\frac{{\kappa }_2}{6{\kappa }_2^2{S}_1^2+1}t,S_2=\pm \frac{\sqrt{2}i{S}_1}{4},$

$$\begin{array}{cc}\hfill u_{21}(x,t)=& A_0+A_{10}\frac{R_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)}+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}\hfill \\ & -B_1(S_2\eta +{\eta }_0),\hfill \end{array}$$

(43)

where $\xi ={\kappa }_{1}x,\eta ={\kappa }_{2}x+{\omega }_{2}t,S_2=-\frac{1}{2B_1{\omega }_2},$

$$u_{22}(x,t)=A_0-2R_2{\kappa }_1\frac{R_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)}-B_1(S_2\eta +{\eta }_0),$$

(44)

where $\xi ={\kappa }_{1}x+{\omega }_{1}t,\eta =-\frac{-{\kappa }_1^2{R}_1^2{\omega }_1+2{\kappa }_1{B}_1{S}_2{\omega }_2+{\kappa }_1+{\omega }_1}{4B_1{S}_2{\omega }_1}x+{\omega }_{2}t,$

$$\begin{array}{cc}\hfill u_{23}(x,t)=& A_0+A_{10}\frac{R_1}{R_2+R_{1}exp\left({\xi }_0\right)}-\frac{4S_2{\kappa }_2{S}_0}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu }\eta }{2}+{\eta }_0)}\hfill \\ & +\frac{C_1(R_2+R_{1}exp\left({\xi }_0\right))}{R_1},\hfill \end{array}$$

(45)

where $\eta ={\kappa }_{2}x+{\omega }_{2}t,S_2=-\frac{{\kappa }_2+{\omega }_2}{4{\kappa }_2^2{S}_0{\omega }_2},$

$$\begin{array}{cc}\hfill u_{24}(x,t)=& A_0+A_{10}\frac{R_1}{R_2+R_{1}exp\left({\xi }_0\right)}-\frac{\pm 14\sqrt{2}i{S}_2{\kappa }_2{S}_1}{S_1+\sqrt{2}tanh(\frac{\sqrt{\mu }\eta }{2}+{\eta }_0)}\hfill \\ & +\frac{C_1(R_2+R_{1}exp\left({\xi }_0\right))}{R_1},\hfill \end{array}$$

(46)

where $\eta ={\kappa }_{2}x-\frac{{\kappa }_2}{6{\kappa }_2^2{S}_1^2+1}t,S_2=\pm \frac{\sqrt{2}i{S}_1}{4},$

$$u_{25}(x,t)=A_0-A_{01}(\frac{S_1}{2S_2}+\frac{\sqrt{\mu }}{2S_2}tanh\left({\eta }_0\right))+\frac{C_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},$$

(47)

where $\xi ={\kappa }_{1}x+\frac{1}{4R_1^2{\kappa }_1}t,C_1=\frac{5R_1^2{\kappa }_1^2-1}{6R_2{\kappa }_1}.$

Figure 5 and Figure 6 show the geometries of the solutions $u_3(x,t)$ and $u_{22}(x,t)$ as determined by (24) and (44), respectively. As shown in Figure 5, the single lump is localized in the $(x,t)$ plane and it is a permanent lump. And as shown in Figure 6, we observe that the breather in the $(x,t)$ plane is intermittent along the t direction and localized in the x direction.

5. Lie Symmetry Analysis

5.1. Lie Symmetry and Lie Group

In this part, we will analyze the Lie symmetry and the invariant solutions of the shallow water wave equation and the Boussinesq class. In this section, Lie symmetry analysis is performed and we consider one Lie group of the transformation parameter

$$\begin{array}{cc}\hfill & t\to t+ϵ{\xi }^1(x,t,u,v),x\to x+ϵ{\xi }^2(x,t,u,v),\hfill \\ \hfill & u\to u+ϵ{\xi }^3(x,t,u,v),v\to v+ϵ{\eta }^1(x,t,u,v),\hfill \end{array}$$

with a tiny parameter $ϵ\le 1$. In addition, we consider the corresponding infinitesimal generator of the Lie group transformation of the form

$$X={\xi }^1(t,x,u,v)\frac{\partial }{\partial t}+{\xi }^2(t,x,u,v)\frac{\partial }{\partial x}+{\eta }^1(t,x,u,v)\frac{\partial }{\partial u}+{\eta }^2(t,x,u,v)\frac{\partial }{\partial v}.$$

(48)

and the corresponding Lie–Bäcklund symmetry

$$X={\eta }^1(t,x,u,v,u_i,v_i)\frac{\partial }{\partial u}+{\eta }^2(t,x,u,v,u_i,v_i)\frac{\partial }{\partial v},$$

(49)

where $u_i,v_i$ denotes any order derivative of u, v with respect to the independent variables x, t. Note that $Xx={\xi }^2(t,x,u,v)$ (see [25,26,27,28]). Using Maple, we obtain the infinitesimal generators of Equation (9):

$$\begin{array}{cc}\hfill & X_1=\frac{\partial }{\partial t},X_2=\frac{\partial }{\partial x},\hfill \\ & X_3=t\frac{\partial }{\partial x}+\frac{\partial }{\partial u},\hfill \\ \hfill & X_4=\frac{x}{2}\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}-\frac{u}{2}\frac{\partial }{\partial u}-(1+v)\frac{\partial }{\partial v},\hfill \end{array}$$

(50)

and the Lie–Bäcklund symmetries

$$\begin{array}{cc}\hfill & X_5=-u_t\frac{\partial }{\partial u},X_6=-u_x\frac{\partial }{\partial u},\hfill \\ & X_6=(1-t{u}_x)\frac{\partial }{\partial u},\hfill \\ \hfill & X_7=(-\frac{u}{2}-\frac{x}{2}{u}_x-t{u}_t)\frac{\partial }{\partial u}+(-1-v-\frac{x}{2}{v}_x-t{v}_t)\frac{\partial }{\partial v}.\hfill \end{array}$$

(51)

In addition, we obtain the infinitesimal generators of Equation (19)

$$\begin{array}{cc}\hfill & Z_1=\frac{\partial }{\partial x}+f_1\left(t\right)\frac{\partial }{\partial t}+\frac{f_1\left(t\right)}{2}\frac{\partial }{\partial u},\hfill \\ & Z_2=f_2\left(t\right)\frac{\partial }{\partial t}+(\frac{f_2\left(t\right)}{2}+1)\frac{\partial }{\partial u},\hfill \\ \hfill & Z_3=x\frac{\partial }{\partial x}+f_3\left(t\right)\frac{\partial }{\partial t}+(f_3\left(t\right)+\frac{t}{2}+\frac{x}{2}-u)\frac{\partial }{\partial u},\hfill \end{array}$$

where $f_i\left(t\right)$ is an arbitrary function related to t and the Lie–Bäcklund symmetries

$$\begin{array}{cc}\hfill & Z_4=u\frac{\partial }{\partial u},Z_5=u_t\frac{\partial }{\partial u},\hfill \\ & Z_6=u_x\frac{\partial }{\partial u},Z_7=(-2t{u}_t+t)\frac{\partial }{\partial u},\hfill \\ \hfill & Z_8=(3u_x^2+u_{xxx})\frac{\partial }{\partial u},Z_9=(-t{u}_t+x{u}_x-\frac{1}{2}x+u).\hfill \end{array}$$

(52)

The Lie transformation groups corresponding to the infinitesimal generator of Equation (19) are shown in the following, where $Z_1$ corresponds to the group

$$\left\{\begin{array}{c}\frac{d{x}^{\ast }}{dϵ}=1,\hfill \\ \frac{d{t}^{\ast }}{dϵ}=t,\hfill \\ \frac{d{u}^{\ast }}{dϵ}=\frac{t}{2},\hfill \end{array}\right.$$

(53)

where $x^{\ast }=x,t^{\ast }=t,u^{\ast }=u$, at $ϵ=0$. Then, we can obtain

$$\left\{\begin{array}{c}{x}^{\ast }=x+ϵ,\hfill \\ t^{\ast }=t{e}^{ϵ},\hfill \\ u^{\ast }=\frac{t{e}^{ϵ}}{2}+u-\frac{t}{2},\hfill \end{array}\right.$$

(54)

when $f_1\left(t\right)=t$. The transformation group calculation method corresponding to the remaining infinitesimal generators is similar. For example, when $f_2\left(t\right)=t$, $Z_2$ corresponds to the group

$$\left\{\begin{array}{c}{x}^{\ast }=x,\hfill \\ t^{\ast }=t{e}^{ϵ},\hfill \\ u^{\ast }=\frac{t{e}^{ϵ}}{2}+ϵ-\frac{t}{2}+u.\hfill \end{array}\right.$$

(55)

When $f_3\left(t\right)=t$, $Z_3$ corresponds to the group

$$\left\{\begin{array}{c}{x}^{\ast }=x{e}^{ϵ},\hfill \\ t^{\ast }=t{e}^{ϵ},\hfill \\ u^{\ast }=\frac{(-2t-x+4u)e^{ϵ}}{4}+\frac{(t+\frac{x}{2})e^{ϵ}}{2}.\hfill \end{array}\right.$$

(56)

And the calculation method for Equation (9) is similar. For example, $X_4$ corresponding to

$$\left\{\begin{array}{c}{x}^{\ast }=x{e}^{\frac{ϵ}{2}},\hfill \\ t^{\ast }=t{e}^{ϵ},\hfill \\ u^{\ast }=u{e}^{\frac{-ϵ}{2}},\hfill \\ v^{\ast }=(1+v)e^{-ϵ}-1.\hfill \end{array}\right.$$

(57)

5.2. Canonical Coordinates and Invariant Solution

Definition 1. 

The change of coordinates $y=Y\left(x\right)=(y_1\left(x\right),y_2\left(x\right),\dots ,y_n\left(x\right))$ defines a set of canonical coordinates for the one-parameter Lie group of transformations $x^{\ast }=X(x;ϵ)$. According to such coordinates, the group becomes

$$\left\{\begin{array}{c}{y}_i^{\ast }=y_i,i=1,2,\dots ,n-1,\hfill \\ y_n^{\ast }=y_n+ϵ.\hfill \end{array}\right.$$

(58)

Thus, we know that every symmetric infinitesimal generator can derive the corresponding canonical coordinates by computing

$$Xr=0,Xs=0,Xv=1,$$

where X denotes the symmetric infinitesimal generator of the target equation. Next, we apply it to Equation (19). For the infinitesimal generator $Z_1$, when $f_1\left(t\right)=t$, the corresponding canonical coordinate is

$$\begin{array}{cc}\hfill Z_{1}r& =\frac{\partial r}{\partial x}+t\frac{\partial r}{\partial t}=0,\hfill \\ \hfill Z_{1}s& =t\frac{\partial s}{\partial t}+\frac{\partial s}{\partial u}=0,\hfill \\ \hfill Z_{1}v& =t\frac{\partial v}{\partial t}=1.\hfill \end{array}$$

(59)

We can obtain one canonical coordinate corresponding to $Z_1$, i.e.,

$$r=-lnt+x,s=u-\frac{t}{2},v=lnt.$$

(60)

Similarly, the canonical coordinate corresponding to $Z_2$ is

$$r=x,s=u-\frac{t}{2}-lnt,v=lnt.$$

(61)

And when $f_3\left(t\right)=1$, the canonical coordinate corresponding to $Z_3$ is

$$r=-lnx+t,s=-\frac{x(2t+x-4u)}{4},v=lnx.$$

(62)

Then, we consider a k-order differential equation. Its form is as follows:

$$F(x,u,u_{\left(1\right)},\dots ,u_{\left(k\right)})=0,$$

(63)

where u represents the dependent variable, $x=(x_1,x_2,\dots ,x_n)$ represents n independent variables, and $u_{\left(j\right)}$ represents all j-order derivatives of u with respect to x. Thus, Equation (58) gives the infinitesimal generator

$$X={\xi }_i(x,u)\frac{\partial }{\partial x_i}+\eta (x,u)\frac{\partial }{\partial u}.$$

(64)

Definition 2. 

$u=\theta \left(x\right)$ is an invariant solution of Equation (63) corresponding to (64) as given by Equation (63) if, and only if,

(i) 

$u=\theta \left(x\right)$ is an invariant surface of Equation (63);

(ii) 

$u=\theta \left(x\right)$ solves (63). It follows that $u=\theta \left(x\right)$ is an invariant solution of (63) under (64) if, and only if, $u=\theta \left(x\right)$ satisfies $X(u-\theta (x\left)\right)=0$ when $u=\theta \left(x\right)$, i.e.,

$${\xi }_i(x,\theta \left(x\right))\frac{\partial \theta }{\partial x_i}=\eta (x,\theta \left(x\right));$$

(65)

(iii) 

$F(x,u,u_{\left(1\right)},\dots ,u_{\left(k\right)})=0$, where $u_{i_1{i}_2,\dots ,i_j}=\frac{{\partial }^j\theta \left(x\right)}{\partial x_{i_1}\dots \partial x_{i_j}}$, $i_j=1,2,\dots ,n$ for $j=1,2,\dots ,k$.

Then, Equation (65) is an invariant surface of the invariant solution of (63).

Then, we will consider some invariants and invariant solutions of the equations using the above method. First, we learn that Equation (9) has the following form of symmetry

$$\begin{array}{c}\hfill X_4=\frac{x}{2}\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}-\frac{u}{2}\frac{\partial }{\partial u}-(1+v)\frac{\partial }{\partial v}.\end{array}$$

(66)

Then, the corresponding characteristic equations are

$$\frac{dx}{\frac{x}{2}}=\frac{dt}{t}=\frac{du}{-\frac{u}{2}}=\frac{dv}{-(1+v)}.$$

We obtain the similarity variables and the similarity forms as follows:

$$s=\frac{x}{\sqrt{t}},u=\frac{U\left(s\right)}{\sqrt{t}},v=\frac{Q\left(s\right)}{t}-1.$$

(67)

After substituting (67) into Equation (9), we can obtain an ordinary differential equation as follows:

$$\begin{array}{cc}\hfill & -\frac{Q_{s}s}{2}-Q+Q\left(U_s\right)+\frac{U_{sss}}{3}=0,\hfill \\ \hfill & -\frac{U_{s}s}{2}-\frac{U}{2}+U{U}_s+Q_s=0.\hfill \end{array}$$

(68)

Then, it can be derived by calculation that Equation (68) has the following general solution:

$$\begin{array}{cc}\hfill U=& s,Q=C_1,\hfill \\ \hfill U=& g\left(f\right),\frac{3g^4}{8}-\frac{3g^{3}f}{2}+(\frac{15f^2}{8}-\frac{C-1}{2})g^2\left(f\right)+(-g_{ff}-\frac{3f^3}{4}+C_{1}f)g+g_{ff}f\hfill \\ & -\frac{C_1{f}^2}{2}+\frac{g_f^2}{2}-g_f+C_2=0,\hfill \\ \hfill Q=& \frac{-6U_{s}Us+3U_s{s}^2+3Us-4U_{sss}}{12U_s-12}.\hfill \end{array}$$

(69)

We choose the first solution for convenience. Bringing U and Q back to Equation (68), we can obtain

$$u=\frac{x}{t},v=\frac{C_1}{t}-1.$$

(70)

Then, Formula (70) is an invariant solution of Equation (9).

Next, we use the same method to deal with Equation (19). We choose the infinitesimal generator $Z_2$ as an example. When $f_2\left(t\right)=1,$

$$Z_2=\frac{\partial }{\partial t}+\frac{3}{2}\frac{\partial }{\partial u}.$$

The characteristic equation corresponding to this symmetry is as follows:

$$\frac{dx}{0}=\frac{dt}{1}=\frac{du}{\frac{3}{2}}.$$

(71)

Its similarity variables are

$$x=r,u-\frac{3t}{2}=Q\left(r\right).$$

(72)

Coming back to Equation (19), we can obtain

$$-2Q_{xx}=0.$$

(73)

After solving (73), we have an invariant solution of Equation (19)

$$Q\left(r\right)=Q\left(x\right)=C_{2}x+C_3,$$

(74)

i.e.,

$$u=\frac{3t}{2}+C_{2}x+C_3,$$

(75)

where $C_i(i=1,2,3)$ denotes the arbitrary constants.

In addition, we find that the concept of symmetry can be used to reduce the order. First, we use transformation

$$v\left(z\right)=u(x,t),z=x-kt,$$

where k is an arbitrary constant. Then, Equation (19) can be transformed into the following ordinary differential equation form:

$$-k{v}^{{}^{\prime }}+v^{{}^{″}}+k{v}^{{}^{″″}}+6k{v}^{{}^{\prime }}{v}^{{}^{″}}=0.$$

(76)

It has symmetries

$$\begin{array}{cc}\hfill & Y_1=\frac{\partial }{\partial z},Y_2=\frac{\partial }{\partial v},\hfill \\ & Y_3=-z\frac{\partial }{\partial z}+\frac{3kv-kz+z}{3k}\frac{\partial }{\partial v},\hfill \\ \hfill & Y_4=\frac{\partial }{\partial z}+\frac{\partial }{\partial v}.\hfill \end{array}$$

(77)

If we select $Y_3$ as the symmetry used to reduce the order, then we can obtain the reduced equation

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill b_{aaa}=& (\frac{10b_a}{b}+10b)b_{aa}-\frac{15b_a^3}{b^2}-30b_a^2+[(6a-35)b^2-6b]b_a+(-12a^2+24a)b^5\hfill \\ & +(30a-50)b^4-18b^3,\hfill \end{array}\end{array}$$

(78)

where $a=\frac{(6kv-kz+z)z}{6k},b\left(a\right)=\frac{3k}{z(3z{v}^{{}^{\prime }}k+3kv-kz+z)}$, $z=e^{\int bda+C_1}$,

$v=\frac{6e^{-\int bda-C_1}ak+k{e}^{\int bda+C_1}-e^{\int bda+C_1}}{6k}.$ If we select $Y_4$ as the symmetry used to reduce the order, then we can obtain the reduced equation

$$b_{aaa}=\frac{10b_a{b}_{aa}}{b}-\frac{15b_a^3}{b^2}+(-\frac{(5k+1)b^2}{k}-6b)b_a,$$

(79)

where $a=v-z,b\left(a\right)=\frac{1}{-a+v^{{}^{\prime }}},z=\int bda+C_1,v=a+\int bda+C_1.$

Figure 7 and Figure 8 show the geometries of the invariant solutions (70) and (75) for Equation (9) and Equation (19), respectively. From Figure 7, we observe that the invariant solution $u,v$ is symmetrical about a point in space. And from Figure 8, we observe that the invariant solution (75) is a plane solution.

6. Self-Adjointness and Conservation Laws

In this section, we will calculate the self-adjoint properties and conservation laws of the objective equations using the Ibragimov method [29,30,31,32,33]. First, let us introduce some notations and definitions

$$\begin{array}{cc}\hfill & x=(x^1,x^2,\dots ,x^n),\hfill \\ \hfill & u_i^{\alpha }=D_i\left(u_{\alpha }\right),u_{ij}^{\alpha }=D_i{D}_j\left(u^{\alpha }\right)\cdots ,v_i^{\alpha }=D_i\left(v_{\alpha }\right),v_{ij}^{\alpha }=D_i{D}_j\left(v^{\alpha }\right)\cdots ,\hfill \end{array}$$

where $D_i$ represents the total derivative operator concerning the independent variable and $x_k(k=1,2,\dots )$ represents the independent variables, i.e.,

$$D_i=\frac{\partial }{\partial x^i}+u_i^{\alpha }\frac{\partial }{\partial u^{\alpha }}+v_i^{\alpha }\frac{\partial }{\partial v^{\alpha }}+u_{ij}^{\alpha }\frac{\partial }{\partial u_j^{\alpha }}+v_{ij}^{\alpha }\frac{\partial }{\partial v_j^{\alpha }}+\cdots .$$

Next, we deal with a system of m differential equations. It has the following form:

$$F_{\alpha }(x,u,u_{\left(1\right)},\dots ,u_{\left(s\right)})=0,\alpha =1,2,\dots ,m,$$

(80)

which has the form of an adjoint equation

$$F_{\alpha }^{\ast }(x,u^1,u^2,u_{\left(1\right)}^1,u_{\left(1\right)}^2,\dots ,u_{\left(s\right)}^1,u_{\left(s\right)}^2)=0,\alpha =1,2,\dots ,m,$$

(81)

where

$$\begin{array}{cc}\hfill & F_{\alpha }^{\ast }(x,u^1,u^2,u_{\left(1\right)}^1,u_{\left(1\right)}^2,\dots ,u_{\left(s\right)}^1,u_{\left(s\right)}^2)=\frac{\delta \mathcal{L}}{\delta u^{\alpha }},\hfill \\ \hfill & u_{\left(1\right)}^1=u_i^{\alpha },u_{\left(s\right)}^1=u_{i_1\dots i_s}^{\alpha },\hfill \\ \hfill & u_{\left(1\right)}^2=v_i^{\alpha },u_{\left(s\right)}^2=v_{i_1\dots i_s}^{\alpha },\hfill \end{array}$$

(82)

where $\mathcal{L}$ denotes the formal Lagrangian for Equation (80), i.e.,

$$\mathcal{L}={\displaystyle \sum _{i=1}^m}{v}^i{F}_i(x,u,u_{\left(1\right)},\dots ,u_{\left(s\right)}),$$

(83)

and $\frac{\delta }{\delta u^{\alpha }}$ denotes the variational derivative. It has the following form

$$\frac{\delta }{\delta u^{\alpha }}=\frac{\partial }{\partial u^{\alpha }}+{\displaystyle \sum _{s=1}^{\infty }}{(-1)}^s{D}_{i_i}\cdots D_{i_s}\frac{\partial }{\partial u_{i_1\cdots i_s}^{\alpha }}.$$

Definition 3. 

We can state that Equation (80) is strictly self-adjoint if the adjoint from Equation (81) is equivalent to Equation (82) upon the transformation

$$v^{\alpha }=u^{\alpha },\alpha =1,2,\dots ,m.$$

This shows that the equation

$$F_{\alpha }^{\ast }(x,u,v,u_{\left(1\right)},v_{\left(1\right)},\dots ,u_{\left(s\right)},v_{\left(s\right)})=F_{\alpha }(x,u,v,u_{\left(1\right)},v_{\left(1\right)},\dots ,u_{\left(s\right)},v_{\left(s\right)}).$$

(84)

Definition 4. 

Equation (80) is said to be quasi self-adjoint if the adjoint equations from Equation (81) are satisfied for all solutions u of the original equation, i.e., Equation (80) upon the substitution

$$v^{\alpha }={\varphi }^{\alpha }\left(u\right),\alpha =1,\dots ,m,$$

(85)

such that

$$\varphi \left(u\right)\ne 0.$$

In other words, Equation (81) holds after the substitution (85), where not all ${\varphi }^{\alpha }\left(u\right)$ vanish simultaneously.

Definition 5. 

Equation (80) will be called nonlinearly self-adjoint if the adjoint from Equation (81) is satisfied for all solutions u of Equation (80) upon the substitution

$$v^{\alpha }={\varphi }^{\alpha }(x,u),\alpha =1,2,\dots ,m,$$

such that

$${\varphi }^{\alpha }(x,u)\ne 0.$$

This shows that

$$F_{\alpha }^{\ast }(x,u,\varphi (x.u),\dots ,u_{\left(s\right)},{\varphi }_{\left(s\right)})={\lambda }_{\alpha }^{\beta }{F}_{\beta }(x,u,u_{\left(1\right)},\dots ,u_{\left(s\right)}),$$

(86)

where

$$\varphi ={\varphi }^{\alpha }(x,u),{\varphi }_k=D_i\dots D_k\left({\varphi }^{\alpha }(x,u)\right).k=1,\dots ,s.$$

Next, we use the above method to prove that

$$\left\{\begin{array}{c}{v}_t+{\left[(1+v)u\right]}_x+\frac{1}{3}{u}_{xxx}=0,\hfill \\ u_t+u{u}_x+v_x=0,\hfill \end{array}\right.$$

is strictly self-adjoint.

The formal Lagrangian equation of the (1 + 1)-dimensional classical Boussinesq reads

$$\begin{array}{cc}\hfill \mathcal{L}& ={\omega }^1{F}^1+{\omega }_2{F}^2\hfill \\ \hfill & ={\omega }_1(v_t+{\left[(1+v)u\right]}_x+\frac{1}{3}{u}_{xxx})+{\omega }_2(u_t+u{u}_x+v_x).\hfill \end{array}$$

(87)

Then, $F_{\alpha }^{\ast }=\frac{\delta \mathcal{L}}{\delta u},$ i.e.,

$$\begin{array}{cc}\hfill F_1^{\ast }& =\frac{\delta \mathcal{L}}{\delta u}={\omega }^1{v}_x-{\omega }_x^1(1+v)-v_x{\omega }^1-\frac{1}{3}{\omega }_{xxx}^1-{\omega }_t^2+{\omega }^2{u}_x-{\omega }^2{u}_x-{\omega }_x^{2}u,\hfill \\ \hfill F_2^{\ast }& =\frac{\delta \mathcal{L}}{\delta v}=-{\omega }_t^1-u_x{\omega }^1-u_x-{\omega }_x^{1}u+{\omega }^1{u}_x-{\omega }_x^2.\hfill \end{array}$$

(88)

Let

$${\omega }^1=-u,{\omega }^2=-v,$$

then

$$\begin{array}{cc}\hfill & F_1^{\ast }=v_t+{\left[(1+v)u\right]}_x+\frac{1}{3}{u}_{xxx}=F_1,\hfill \\ \hfill & F_2^{\ast }=u_t+u{u}_x+v_x=F_2.\hfill \end{array}$$

According to Definition 3, the (1 + 1)-dimensional Boussinesq class is strictly self-adjoint.

Similarly, we can prove that

$$u_{xt}+u_{xx}-u_{xxxt}-4u_x{u}_{xt}-2u_{xx}{u}_t=0,$$

is nonlinearly self-adjoint.

It is not difficult to verify that the (1 + 1)-dimensional shallow water wave equation does not satisfy the strictly self-adjoint condition, so we will not show this in this section. But, if we change the shallow water wave equations into the following equivalent form, we can verify its self-adjointness:

$$\frac{1}{u}(u_{xt}+u_{xx}-u_{xxxt}-4u_x{u}_{xt}-2u_{xx}{u}_t)=0,$$

(89)

where $\mu (x,u)=\frac{1}{u}$. Then, the its Lagrangian has the following forms:

$$\mathcal{L}=\frac{v}{u}(u_{xt}+u_{xx}-u_{xxxt}-4u_x{u}_{xt}-2u_{xx}{u}_t).$$

(90)

Then, we calculate its variational derivative and find

$$\begin{array}{cc}\hfill \frac{\delta \mathcal{L}}{\delta u}=& \frac{v_{xxx}{u}_t}{u^2}+\frac{3v_{xx}{u}_{tx}}{u^2}+\frac{3v_x{u}_{txx}}{u^2}+\frac{2v{u}_x^2}{u^3}-\frac{v_{txxx}}{u}+\frac{4v_t{u}_x^2}{u^2}-\frac{v_t{u}_x}{u^2}-\frac{2v_t{u}_{xx}}{u}\hfill \\ \hfill & -\frac{6v_{tx}{u}_x^2}{u^3}+\frac{6v_t{u}_x^3}{u^4}+\frac{3v_{txx}{u}_x}{u^2}+\frac{3v_{tx}{u}_{xx}}{u^2}+\frac{v_t{u}_{xxx}}{u^2}-\frac{4v_{tx}{u}_x}{u}-\frac{4v_x{u}_{tx}}{u}\hfill \\ \hfill & +\frac{v{u}_{txxx}}{u^2}+\frac{v_{xx}}{u^2}+\frac{2v{u}_t{u}_x}{u^2}-\frac{2v_{xx}{u}_t}{u}-\frac{6v{u}_{txx}{u}_x}{u^3}-\frac{6v{u}_{tx}{u}_{xx}}{u^3}-\frac{2v{u}_t{u}_{xxx}}{u^3}\hfill \\ \hfill & -\frac{24v{u}_t{u}_x^3}{u^5}+\frac{8v_x{u}_x{u}_t}{u^2}-\frac{12v{u}_x^2{u}_t}{u^3}+\frac{8v{u}_x{u}_{tx}}{u^2}+\frac{4v{u}_{xx}{u}_t}{u^2}-\frac{6v_t{u}_x{u}_{xx}}{u^3}\hfill \\ \hfill & -\frac{6v_x{u}_t{u}_{xx}}{u^3}+\frac{18v{u}_{tx}{u}_x^2}{u^4}+\frac{v_{tx}}{u}-\frac{v{u}_{tx}}{u^2}-\frac{v_x{u}_t}{u^2}-\frac{v{u}_{xx}}{u^2}+\frac{18v{u}_x{u}_t{u}_{xx}}{u^4}\hfill \\ & -\frac{v(u_{tx}+u_{xx}-u_{txxx}-4u_x{u}_{tx}-2u_{xx}{u}_t)}{u^2}-\frac{12v_x{u}_{tx}{u}_x}{u^3}-\frac{2v_x{u}_x}{u^2}\hfill \\ & +\frac{18v_x{u}_t{u}_x^2}{u^4}-\frac{6v_{xx}{u}_t{u}_x}{u^3}.\hfill \end{array}$$

(91)

Let $v=-u,$ we obtain

$$F^{\ast }=\frac{\delta \mathcal{L}}{\delta u}=\frac{1}{u}(u_{xt}+u_{xx}-u_{xxxt}-4u_x{u}_{xt}-2u_{xx}{u}_t)=F.$$

(92)

Then, Equation (89) is nonlinearly self-adjoint according to Defination 5.

Theorem 1. 

Any Lie point, Lie–Bäcklund, and nonlocal symmetry

$$X={\xi }^i(x,u,u_{\left(1\right)},\dots )\frac{\partial }{\partial x^i}+{\eta }^{\alpha }(x,u,u_{\left(1\right)},\dots )\frac{\partial }{\partial u^{\alpha }},$$

of Equation (80) derives to the conservation law $D_i\left(C^i\right)=0$, i.e.,

$$\begin{array}{cc}\hfill C^i=& {\xi }^i\mathcal{L}+W^{\alpha }[\frac{\partial \mathcal{L}}{\partial u_i^{\alpha }}-D_j\left(\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }}\right)+D_j{D}_j\left(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }}\right)-\cdots ]\hfill \\ \hfill & +D_j\left(W^{\alpha }\right)[\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }}-D_k\left(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }}\right)+\cdots ]+D_j{D}_k\left(W^{\alpha }\right)[\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }}-\cdots ]+\cdots ,\hfill \end{array}$$

(93)

with Lie–Bäcklund symmetry $W^{\alpha }={\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha },\alpha =1,\dots ,m.$

According to the above content, we know that the (1 + 1)-dimensional Boussinesq class has a symmetry as follows:

$$X_1=\frac{x}{2}\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}-\frac{u}{2}\frac{\partial }{\partial u}+(-1-v)\frac{\partial }{\partial v}.$$

Thus, we can discuss the symmetry $X_1$. According to the calculation, it can be known that

$$W^1=-\frac{u}{2}-\frac{x{u}_x}{2}-t{u}_t,W^2=-1-v-\frac{x{v}_x}{2}-t{v}_t.$$

Then,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill C^1=& \frac{x}{2}\mathcal{L}+W^1[(1+v){\omega }^1+\frac{1}{3}{\omega }_{xx}^1)+u{\omega }^2]+W^2[u{\omega }^1+{\omega }_2]+W_x^1(-\frac{1}{3}{\omega }_x^1)\hfill \\ & +W_{xx}^1(\frac{1}{3}{\omega }^1)\hfill \\ \hfill =& \frac{x[w(v_t+v_{x}u+(1+v)u_x+\frac{u_{xxx}}{3})+{\omega }^2(u_t+u{u}_x+v_x)]}{2}+(-\frac{u}{2}-\frac{x{u}_x}{2}\hfill \\ \hfill & -t{u}_t)[(1+v){\omega }^1+\frac{{\omega }_{xx}^1}{3}+{\omega }^{2}u]+(-1-v-\frac{x{v}_x}{2}-t{v}_t)(u{\omega }_1+{\omega }_2)\hfill \\ \hfill & +(-\frac{3u_{xx}}{2}-\frac{x{u}_{xxx}}{2}-t{u}_{xxx})\frac{{\omega }^1}{3}+(-u_x-\frac{x{u}_{xx}}{2}-t{u}_{tx})(-\frac{{\omega }_x^1}{3})\hfill \\ \hfill =& \frac{{\omega }_x^1{u}_x}{3}+\frac{{\omega }_x^{1}x{u}_{xx}}{6}+\frac{3{\omega }_x^{1}t{u}_{tx}}{3}-\frac{{\omega }_x^1{u}_{xx}}{2}-\frac{{\omega }^{1}t{u}_{txx}}{3}-\frac{3u{\omega }^1}{2}-\frac{3{\omega }^{1}vu}{2}\hfill \\ \hfill & -u{\omega }^{1}t{v}_t-{\omega }^2-{\omega }^{2}v-{\omega }^{2}t{v}_t-{\omega }^{1}t{u}_t-{\omega }^{1}vt{u}_t-\frac{{\omega }_{xx}^{1}u}{6}-\frac{{\omega }_{xx}^{1}x{u}_x}{6}\hfill \\ \hfill & -\frac{{\omega }^2{u}^2}{2}-{\omega }^{2}ut{u}_t+\frac{u_t{\omega }^{2}x}{2}+\frac{v_t{\omega }^{1}x}{2},\hfill \end{array}\end{array}$$

(94)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill C^2=& t\mathcal{L}+W^2{\omega }^1+W^1{\omega }^2\hfill \\ \hfill =& t[{\omega }_1(v_t+{[(1+v)u]}_x+\frac{1}{3}{u}_{xxx})+{\omega }_2(u_t+u{u}_x+v_x)]+(-1-v-\frac{x{v}_x}{2}\hfill \\ \hfill & -t{v}_t){\omega }^1+(-\frac{2}{u}-\frac{x{u}_x}{2}-t{u}_t)-{\omega }^2\hfill \\ \hfill =& -{\omega }^1-{\omega }^{1}v-\frac{{\omega }^{1}x{v}_x}{2}+u_t{\omega }^{2}t+u{u}_x{\omega }^{2}t+v_x{\omega }^{2}t+u_{x}v{\omega }^{1}t+u_x{\omega }^{1}t\hfill \\ \hfill & +\frac{u_{xxx}{\omega }^{1}t}{3}+v_{x}u-{\omega }^{1}t-\frac{-{\omega }^{2}u}{2}-\frac{{\omega }^{2}x{u}_x}{2}-u_t{\omega }^{2}t.\hfill \end{array}\end{array}$$

(95)

After eliminating ${\omega }^1$ and ${\omega }^2$ of $C^1$ via the substitution

$${\omega }^1=-u,{\omega }^2=-v,$$

we have

$$\begin{array}{cc}\hfill C^1=& -\frac{u_x^2}{3}-\frac{u_{x}t{u}_{tx}}{3}+\frac{2u{u}_{xx}}{3}+\frac{ut{u}_{txx}}{3}+\frac{3u^2}{2}+2u^{2}v+u^{2}t{v}_t+v+v^2+vt{v}_t+ut{u}_t\hfill \\ \hfill & +2uvt{u}_t+\frac{u_{xx}t{u}_t}{3}-\frac{u_{t}vx}{2}-\frac{v_{t}ux}{2},\hfill \\ \hfill C^2=& u+\frac{3uv}{2}+\frac{ux{v}_x}{2}-2u{u}_{x}vt-v_{x}vt-v_x{u}^{2}t-u_{x}ut-\frac{u_{xxx}ut}{3}+\frac{vx{u}_x}{2}.\hfill \end{array}$$

We thus obtain the conservation law of the (1 + 1)-dimensional shallow water wave equations

$$[D_x{C}^1+D_t{C}^2]=0,$$

and we can simply verify it as follows:

$$\begin{array}{cc}\hfill D_x{C}^1+D_t{C}^2& =\frac{u_{xxx}}{3}+2uv{u}_x+v_x+u_t+2u{u}_x+u^2{v}_x+v_{t}u+v{v}_x+u_{t}v\hfill \\ \hfill & =u(v_t+u_x+u{v}_x+v{u}_x+\frac{u_{xxx}}{3})+v(u_t+u{u}_x+v_x)+(u_t+u{u}_x+v_x)\hfill \\ \hfill & =0.\hfill \end{array}$$

Then, the (1 + 1)-dimensional Boussinesq class has the following symmetry:

$$X=\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}+\frac{t}{2}\frac{\partial }{\partial u};$$

therefore, we can calculate

$$W=\frac{t}{2}-u_x-t{u}_t.$$

Then, we discuss the symmetry X. According to the calculation, it can be known that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill C^1=& \mathcal{L}+W[-4v{u}_{xt}-{(v-4v{u}_x)}_t-{(v-2u_t)}_x-{(-v)}_{xxt}]+W_t[v-4u_{x}v+{(-v)}_{xx}]\hfill \\ \hfill & +W_x[v-2u_{t}v+{(-v)}_{xt}]+W_{xx}\left[{(-v)}_t\right]+W_{xt}\left[{(-v)}_x\right]+W_{xxt}[-v]\hfill \\ \hfill =& v_{x}t{u}_t-\frac{v_{x}t}{2}-2u_x{u}_{tx}-vt{u}_{tt}-v_{txx}t{u}_t+v_{xx}t{u}_{tt}+v_{tx}t{u}_{tx}+v_{t}t{u}_{txx}+vt{u}_{ttxx}\hfill \\ \hfill & +2u_{t}vt{u}_{tx}+t{u}_{tx}+v_{x}t{u}_{ttx}+\frac{v}{2}-\frac{v_{xx}}{2}-2v{u}_{tx}t{u}_t+v_t{u}_x+v{u}_{txx}+2v_t{u}_{x}t\hfill \\ \hfill & -4v_t{u}_x^2+\frac{t{v}_{txx}}{2}-v_{txx}{u}_x+v_{xx}{u}_{xt}+v_{xx}{u}_t+v_{tx}{u}_{xx}+v_t{u}_{xxx}+v_x{u}_{txx}\hfill \\ \hfill & +v_{t}t{u}_t+v_x{u}_x+4v{u}_x{u}_t-\frac{v_{t}t}{2}-4v_t{u}_{x}t{u}_t+4v{u}_{x}t{u}_{tt}-vt{u}_{tx}+v_x{u}_{tx},\hfill \\ \hfill C^2=& t\mathcal{L}+W[-2u_{xx}v-v-4{\left(u_{x}v\right)}_x-{(-v)}_{xxx}]+W_x[v-4u_{x}v+{(-v)}_{xx}]\hfill \\ \hfill & +W_{xxx}[-v]+W_{xx}[-{(-v)}_x]\hfill \\ \hfill =& v{u}_{xxx}-v_x{u}_{xxx}-v_{x}t{u}_{txx}-v{u}_{xx}+2v{u}_{xx}{u}_x+v_{xx}{u}_{xx}+v_{xx}t{u}_{tx}+2u_{xx}tv\hfill \\ \hfill & -\frac{v_{x}t}{2}+v_{x}t{u}_t+2v_x{u}_{x}t-4v_x{u}_x^2-4v_x{u}_{x}t{u}_t+\frac{v_{xxx}t}{2}-v_{xxx}{u}_x-v_{xxx}t{u}_t\hfill \\ & -4u_{xx}{u}_{t}tv+v_x{u}_x.\hfill \end{array}\end{array}$$

(96)

7. Conclusions

In this paper, we mainly apply the improved extended Kudryashov method to the shallow water wave equations and the Boussinesq class to find some new exact solutions by presetting the general solution form of the objective equation. This method is convenient to apply to various nonlinear partial differential equations. This method uses the new exact solutions of the objective equation obtained when the Riccati equation and the Bernoullli equation are the simplest forms of solutions. We improve the form of the preset solution on the basis of the original method and add the $C_j$ term to make the form more general so as to obtain more exact solutions of the target equation.

In other parts of this paper, we can map one solution to another using the point symmetry and Lie–Bäcklund symmetry of the shallow water wave equations and the Boussinesq class solved using the Lie method. In addition, the invariant solution of the equation can be obtained using the infinitesimal generator. In the last part, we use the idea of symmetry to determine the self-adjointness of two equations and use infinitesimal generators to calculate the conservation laws of the two groups of equations.