Dynamics and Soliton Propagation in a Modified Oskolkov Equation: Phase Plot Insights
Abstract
:1. Introduction
- Phase portraits;
- Time series;
- Poincaré maps;
- Multistability.
2. Lie Group Analysis and Symmetry Reductions
- Step 1:
- Identify classical Lie point symmetries, specifically translational symmetries in our case, for the suggested model.
- Step 2:
- Construct an algebra (in our case, an Abelian algebra) based on the identified symmetries.
- Step 3:
- Determine the similarity variables corresponding to each symmetry.
- Step 4:
- Utilize the identified symmetries to reduce the PDE to an ODE.
- Step 5:
- Derive solutions in the form of traveling waves from the resulting ODE.
2.1. Lie Symmetries
2.2. Symmetry Reductions
- Reduction using the symmetry
- Reduction using the symmetry
- Reduction using the symmetry +
3. Analytical Solutions
- Type 1: For and , we have
- Type 2: For and , we have
- Type 3: For , and , we have
- Type 4: For , and , we have
- Type 5: For and , we have
- Type 6: For = and , we have
- Type 7: For , , and , we have
- Type 8: For , , we have
- Type 9: For , , we have
- Type 10: For , we have
- Type 11: For , we have
- Type 12: For , we have
- Type 13: For , we have
- Type 14: For and , we have
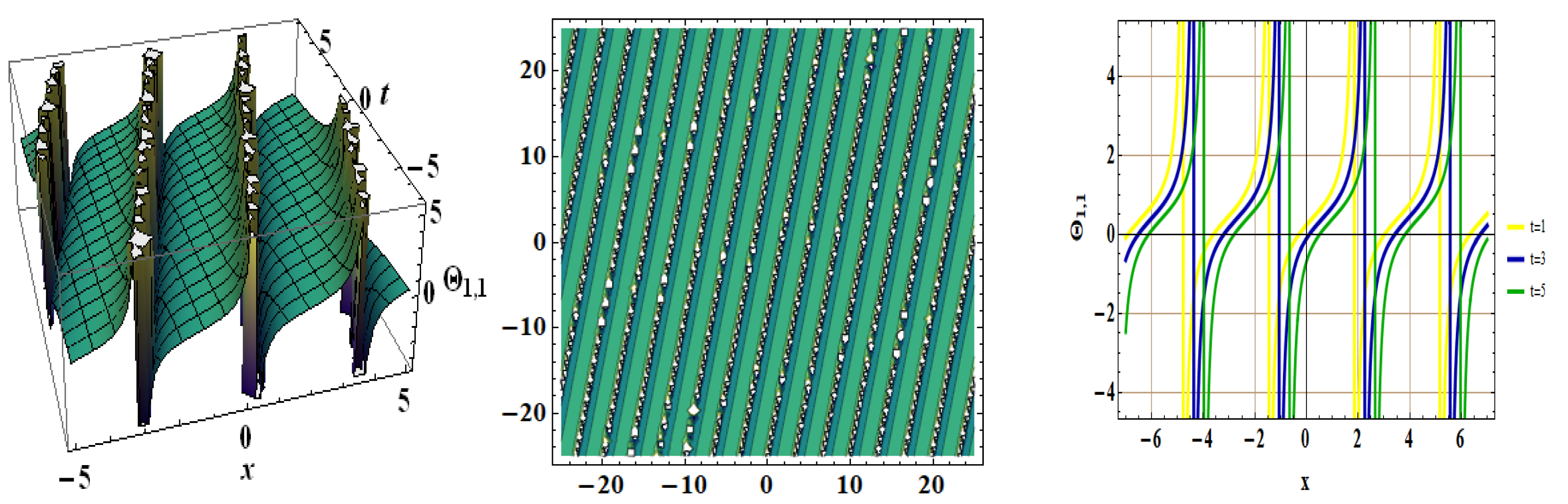
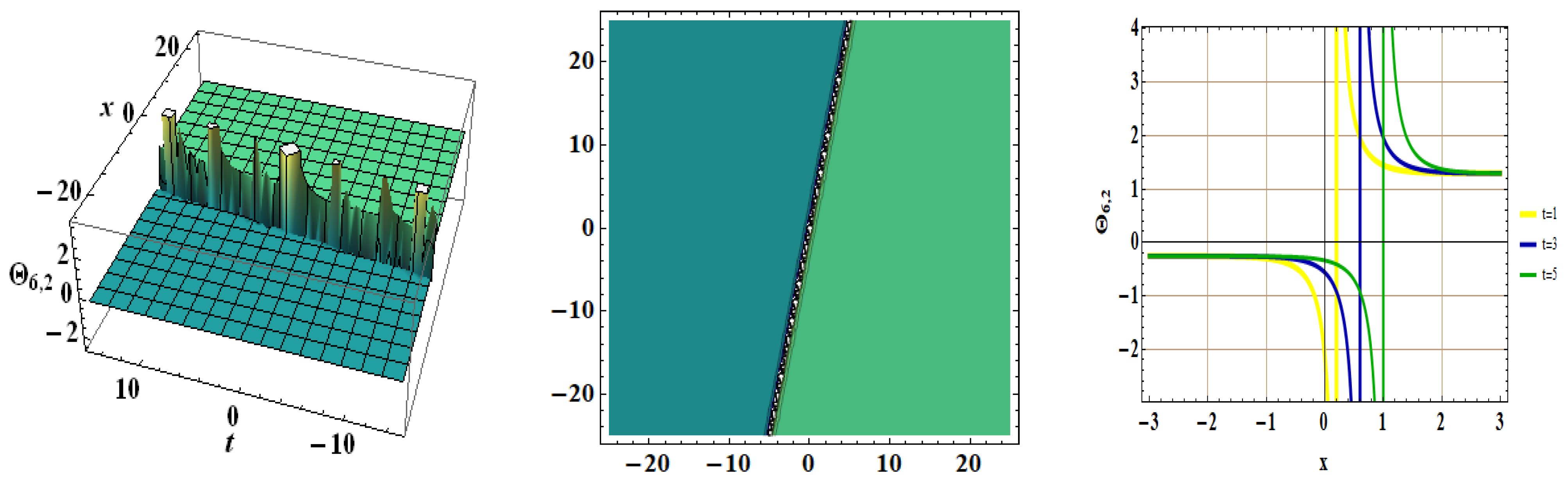
4. Graphical Illustration
5. Dynamics of the Investigating Model
5.1. Bifurcation Analysis
- Case 1: Let and .
- Case 2: Let and .
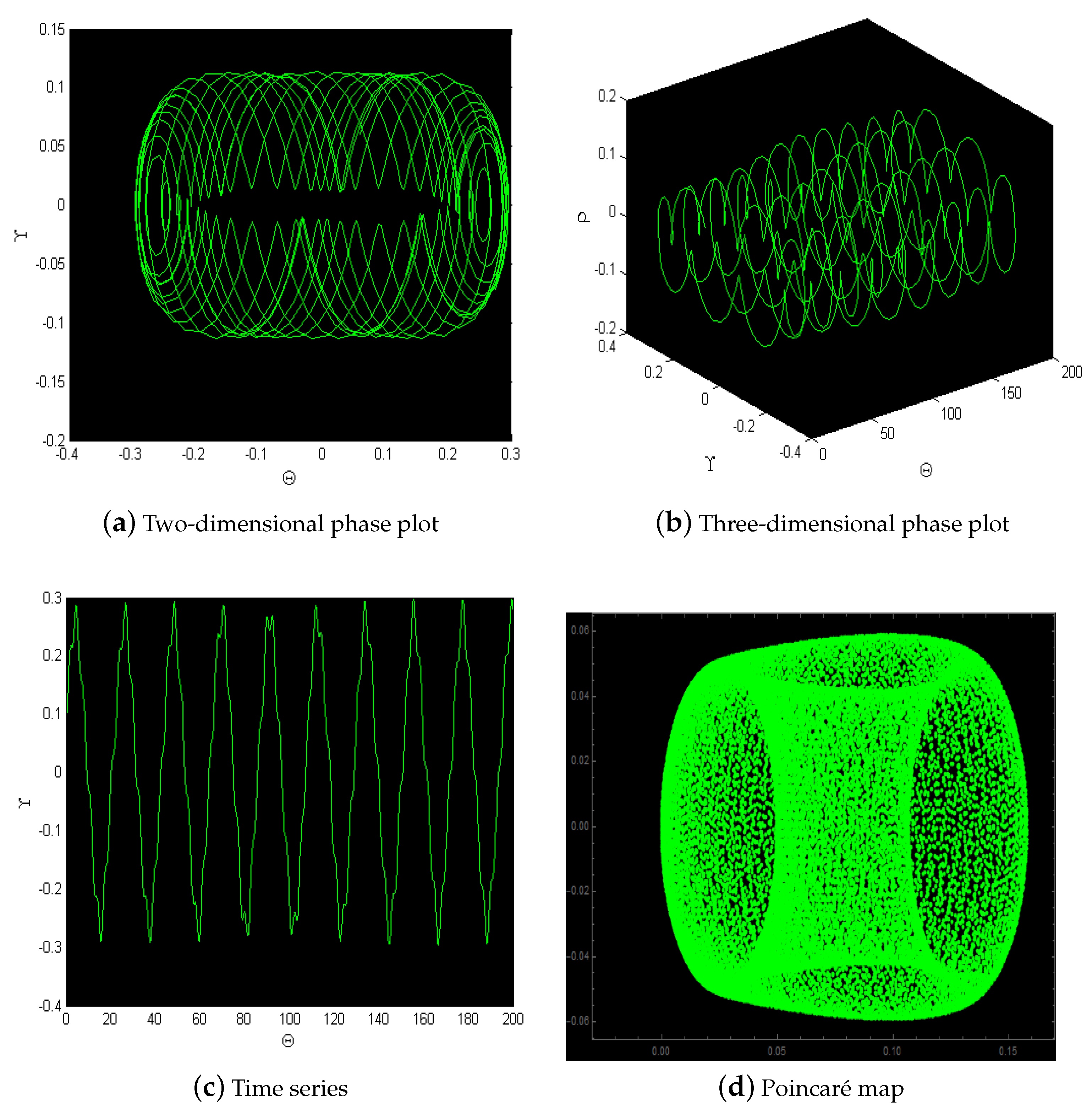
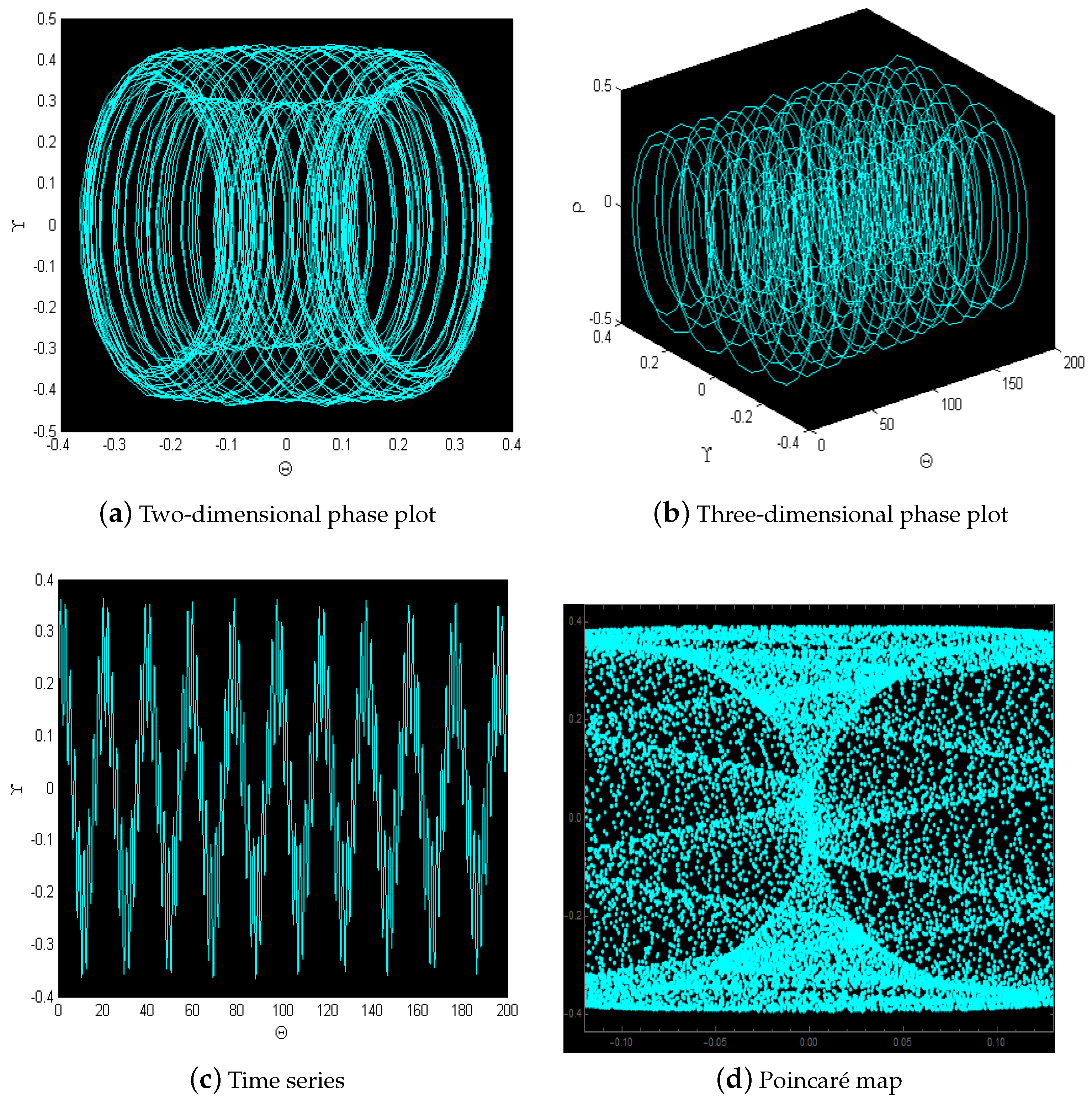
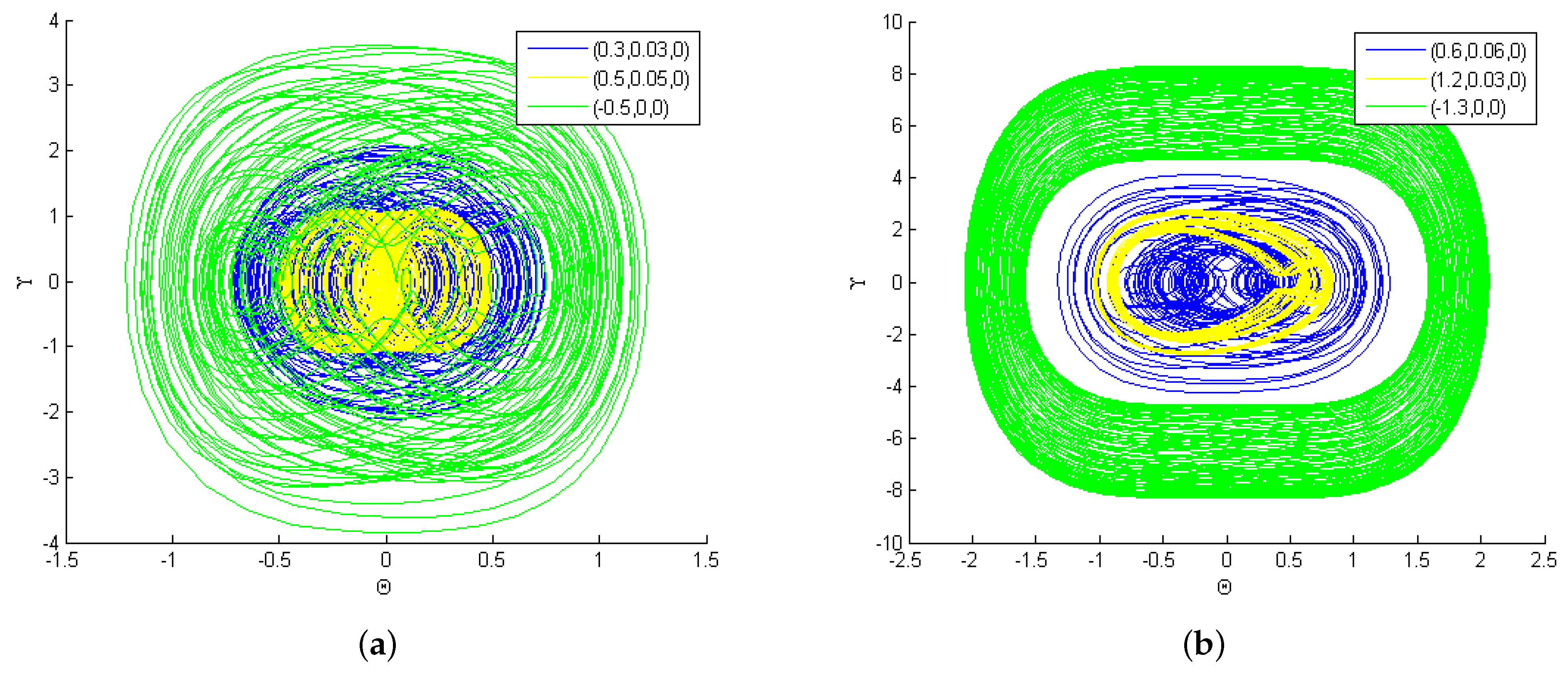
5.2. Behavior of Chaotic Motion
5.3. Multistability Analysis
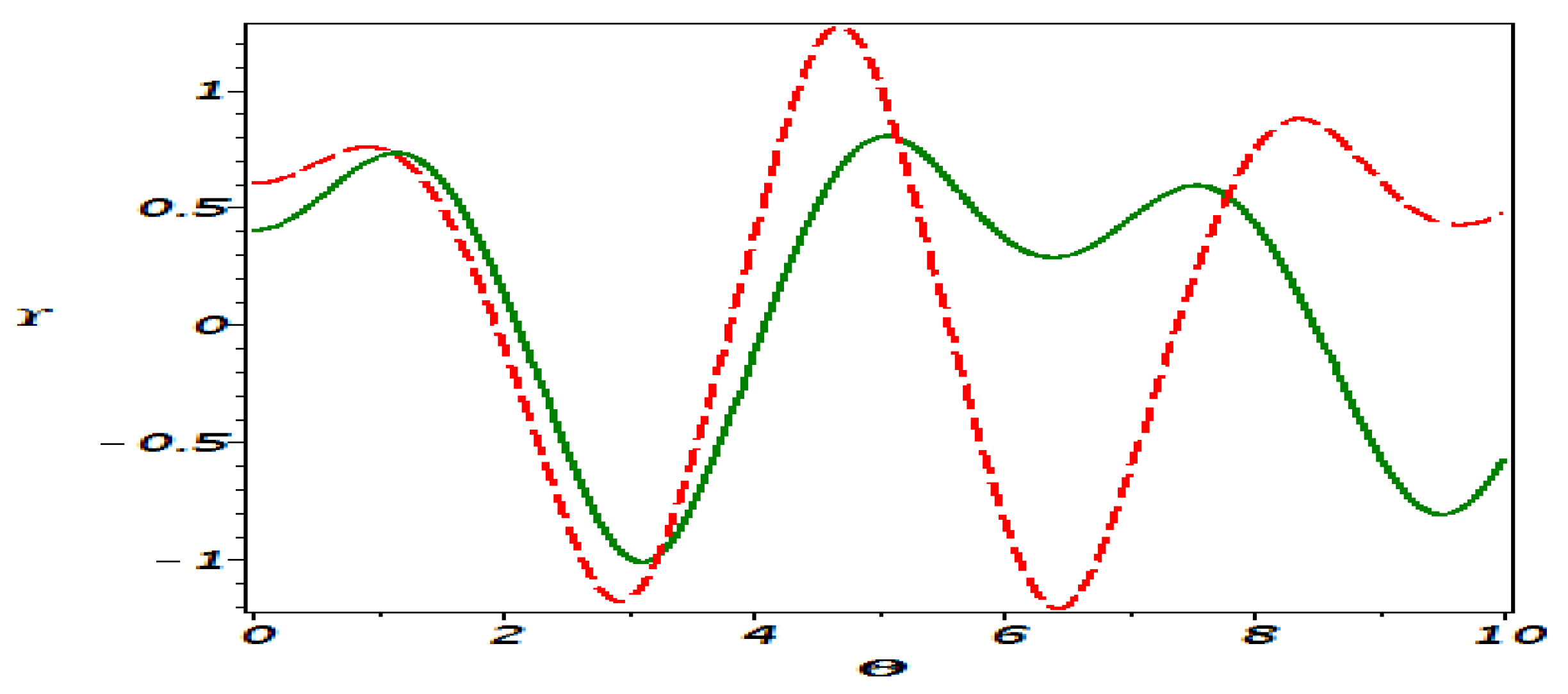
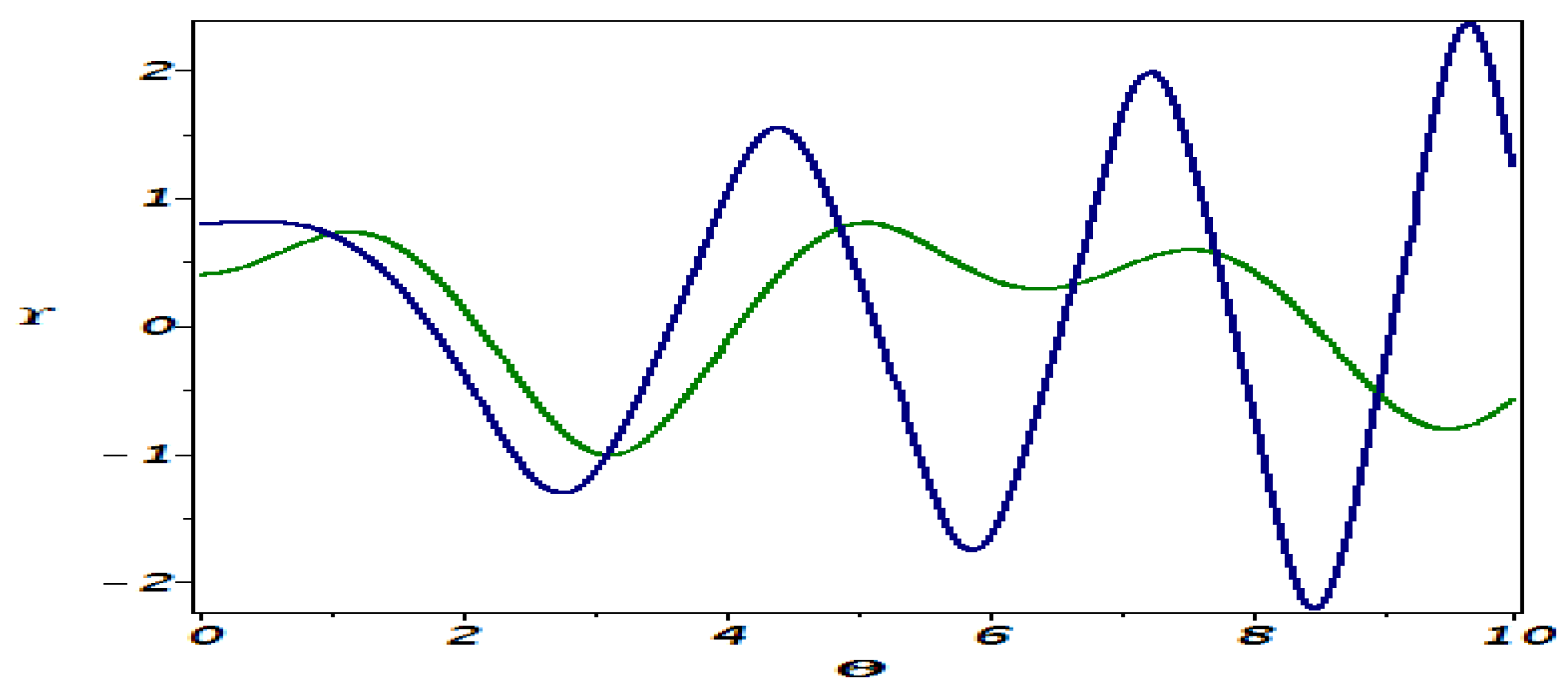
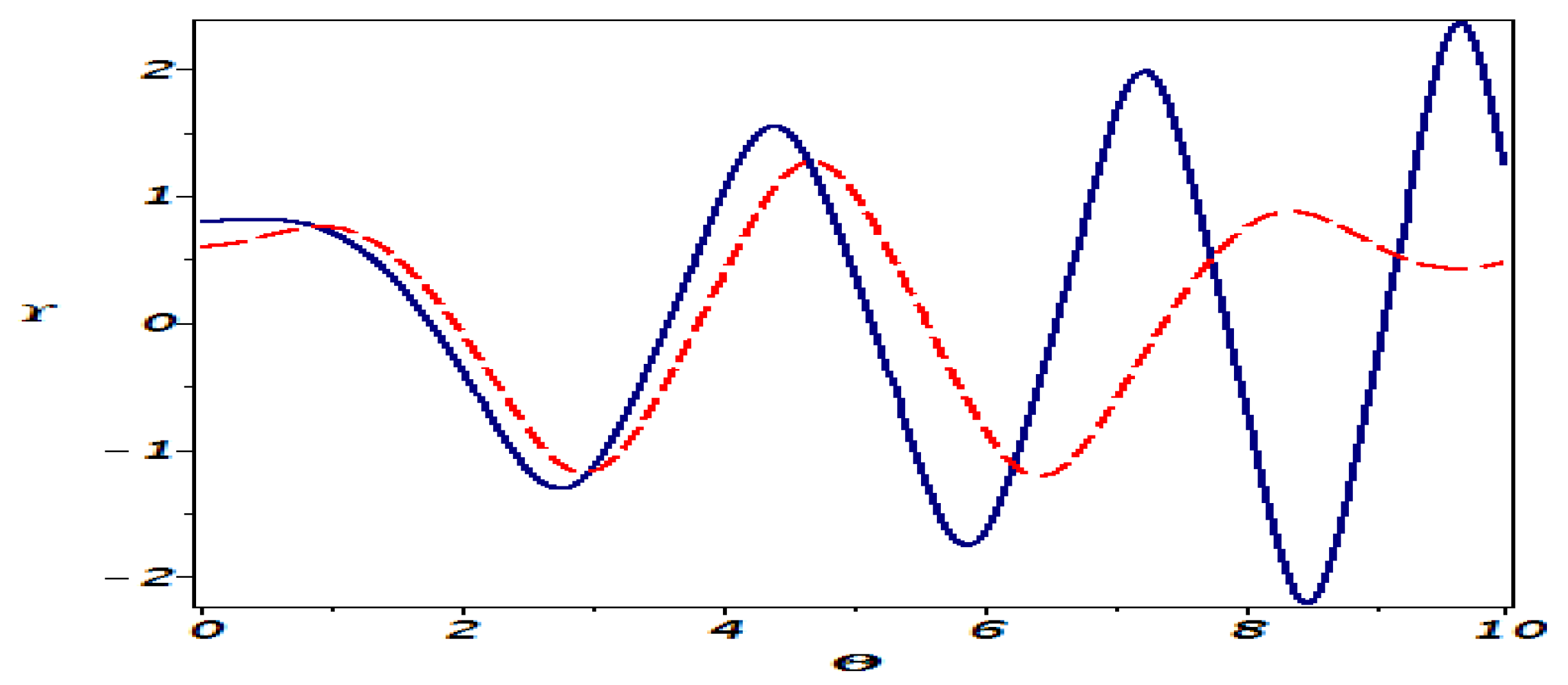
6. Sensitivity Analysis
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zobeiry, N.; Humfeld, K.D. A physics-informed machine learning approach for solving heat transfer equation in advanced manufacturing and engineering applications. Eng. Appl. Artif. Intell. 2021, 101, 104232. [Google Scholar] [CrossRef]
- Bruzzone, O.A.; Perri, D.V.; Easdale, M.H. Vegetation responses to variations in climate: A combined ordinary differential equation and sequential Monte Carlo estimation approach. Ecol. Inform. 2023, 73, 101913. [Google Scholar] [CrossRef]
- Raza, N.; Ullah, M.A. A comparative study of heat transfer analysis of fractional Maxwell fluid by using Caputo and Caputo–Fabrizio derivatives. Can. J. Phys. 2020, 98, 89–101. [Google Scholar] [CrossRef]
- Jornet, M. Modeling of Allee effect in biofilm formation via the stochastic bistable Allen–Cahn partial differential equation. Stoch. Anal. Appl. 2021, 39, 22–32. [Google Scholar] [CrossRef]
- Sgura, I.; Lawless, A.S.; Bozzini, B. Parameter estimation for a morphochemical reaction-diffusion model of electrochemical pattern formation. Inverse Probl. Sci. Eng. 2019, 27, 618–647. [Google Scholar] [CrossRef]
- Zhang, R.F.; Li, M.C. Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations. Nonlinear Dyn. 2022, 108, 521–531. [Google Scholar] [CrossRef]
- Pandir, Y.; Ekin, A. New solitary wave solutions of the Korteweg-de Vries (KdV) equation by new version of the trial equation method. Electron. J. Appl. Math. 2023, 1, 101–113. [Google Scholar] [CrossRef]
- Cherniha, R. Comments on the paper “Exact solutions of nonlinear diffusion-convection-reaction equation: A Lie symmetry approach”. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105922. [Google Scholar] [CrossRef]
- Yin, Y.H.; Lü, X.; Ma, W.X. Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3 + 1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 2022, 108, 4181–4194. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Albalahi, A.M.; Albadrani, S.; Aly, E.S.; Sidaoui, R.; Matouk, A.E. The analytical solutions of the stochastic fractional Kuramoto–Sivashinsky equation by using the Riccati equation method. Math. Probl. Eng. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- Shah, R.; Alkhezi, Y.; Alhamad, K. An Analytical Approach to Solve the Fractional Benney Equation Using the q-Homotopy Analysis Transform Method. Symmetry 2023, 15, 669. [Google Scholar] [CrossRef]
- Kazmi, S.S.; Jhangeer, A.; Raza, N.; Alrebdi, H.I.; Abdel-Aty, A.H.; Eleuch, H. The Analysis of Bifurcation, Quasi-Periodic and Solitons Patterns to the New Form of the Generalized q-Deformed Sinh-Gordon Equation. Symmetry 2023, 15, 1324. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, L. Some novel physical structures of a (2 + 1)-dimensional variable-coefficient Korteweg–de Vries system. Chaos Solitons Fractals 2023, 171, 113430. [Google Scholar] [CrossRef]
- Ma, Y.L.; Wazwaz, A.M.; Li, B.Q. Novel bifurcation solitons for an extended Kadomtsev–Petviashvili equation in fluids. Phys. Lett. A 2021, 413, 127585. [Google Scholar] [CrossRef]
- Zhang, W.X.; Liu, Y. Integrability and multisoliton solutions of the reverse space and/or time nonlocal Fokas–Lenells equation. Nonlinear Dyn. 2022, 108, 2531–2549. [Google Scholar] [CrossRef]
- Gözükizil, Ö.F.; Akçagil, S. The tanh-coth method for some nonlinear pseudoparabolic equations with exact solutions. Adv. Differ. Equations 2013, 2013, 1–18. [Google Scholar] [CrossRef]
- Roshid, M.M.; Roshid, H.O. Exact and explicit traveling wave solutions to two nonlinear evolution equations which describe incompressible viscoelastic Kelvin-Voigt fluid. Heliyon 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Karakoc, S.B.G.; Bhowmik, S.K.; Sucu, D.Y. A Novel Scheme Based on Collocation Finite Element Method to Generalised Oskolkov Equation. J. Sci. Arts 2021, 21, 895–908. [Google Scholar] [CrossRef]
- Ghanbari, B. New analytical solutions for the oskolkov-type equations in fluid dynamics via a modified methodology. Results Phys. 2021, 28, 104610. [Google Scholar] [CrossRef]
- Kaplan, M.; Butt, A.R.; Thabet, H.; Akbulut, A.; Raza, N.; Kumar, D. An effective computational approach and sensitivity analysis to pseudo-parabolic-type equations. Waves Random Complex Media 2021, 1–15. [Google Scholar] [CrossRef]
- Uddin, S.; Karim, S.; Alshammari, F.S.; Roshid, H.O.; Noor, N.F.M.; Hoque, F.; Nadeem, M.; Akgül, A. Bifurcation analysis of travelling waves and multi-rogue wave solutions for a nonlinear pseudo-parabolic model of visco-elastic Kelvin-Voigt fluid. Math. Probl. Eng. 2022, 2022, 8227124. [Google Scholar] [CrossRef]
- Roshid, M.M.; Bairagi, T.; Rahman, M.M. Lump, interaction of lump and kink and solitonic solution of nonlinear evolution equation which describe incompressible viscoelastic Kelvin–Voigt fluid. Partial. Differ. Equations Appl. Math. 2022, 5, 100354. [Google Scholar] [CrossRef]
- Akinfe, K.T. A reliable analytic technique for the modified prototypical Kelvin–Voigt viscoelastic fluid model by means of the hyperbolic tangent function. Partial. Differ. Equations Appl. Math. 2023, 7, 100523. [Google Scholar] [CrossRef]
- Hussain, A.; Usman, M.; Al-Sinan, B.R.; Osman, W.M.; Ibrahim, T.F. Symmetry analysis and closed-form invariant solutions of the nonlinear wave equations in elasticity using optimal system of Lie subalgebra. Chin. J. Phys. 2023, 83, 1–13. [Google Scholar] [CrossRef]
- Almusawa, H.; Jhangeer, A. Nonlinear self-adjointness, conserved quantities and Lie symmetry of dust size distribution on a shock wave in quantum dusty plasma. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106660. [Google Scholar] [CrossRef]
- Rahman, R.U.; Al-Maaitah, A.F.; Qousini, M.; Az-Zo’bi, E.A.; Eldin, S.M.; Abuzar, M. New soliton solutions and modulation instability analysis of fractional Huxley equation. Results Phys. 2023, 44, 106163. [Google Scholar] [CrossRef]
- Alrebdi, H.I.; Rafiq, M.H.; Fatima, N.; Raza, N.; Rafiq, M.N.; Alshahrani, B.; Abdel-Aty, A.H. Soliton structures and dynamical behaviors for the integrable system of Drinfel’d–Sokolov–Wilson equations in dispersive media. Results Phys. 2023, 46, 106269. [Google Scholar] [CrossRef]
- Raza, N.; Kazmi, S.S. Qualitative analysis and stationary optical patterns of nonlinear Schrödinger equation including nonlinear chromatic dispersion. Opt. Quantum Electron. 2023, 55, 718. [Google Scholar] [CrossRef]
- Talafha, A.M.; Jhangeer, A.; Kazmi, S.S. Dynamical analysis of (4 + 1)-dimensional Davey Srewartson Kadomtsev Petviashvili equation by employing Lie symmetry approach. Ain Shams Eng. J. 2023, 14, 102537. [Google Scholar] [CrossRef]
- Matouk, A.E.; Lahcene, B. Chaotic dynamics in some fractional predator–prey models via a new Caputo operator based on the generalised Gamma function. Chaos Solitons Fractals 2023, 166, 112946. [Google Scholar] [CrossRef]
- Rafiq, M.H.; Jannat, N.; Rafiq, M.N. Sensitivity analysis and analytical study of the three-component coupled NLS-type equations in fiber optics. Opt. Quantum Electron. 2023, 55, 637. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1993; Volume 107. [Google Scholar]
- Liu, H.; Lie, J.L. symmetry analysis and exact solutions for the short pulse equation. Nonlinear Anal. Theory Methods Appl. 2009, 71, 2126–2133. [Google Scholar] [CrossRef]
- Crawford, J.D. Introduction to bifurcation theory. Rev. Mod. Phys. 1991, 63, 991. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.B.; Jhangeer, A.; Martinovic, J.; Kazmi, S.S. Dynamics and Soliton Propagation in a Modified Oskolkov Equation: Phase Plot Insights. Symmetry 2023, 15, 2171. https://doi.org/10.3390/sym15122171
Riaz MB, Jhangeer A, Martinovic J, Kazmi SS. Dynamics and Soliton Propagation in a Modified Oskolkov Equation: Phase Plot Insights. Symmetry. 2023; 15(12):2171. https://doi.org/10.3390/sym15122171
Chicago/Turabian StyleRiaz, Muhammad Bilal, Adil Jhangeer, Jan Martinovic, and Syeda Sarwat Kazmi. 2023. "Dynamics and Soliton Propagation in a Modified Oskolkov Equation: Phase Plot Insights" Symmetry 15, no. 12: 2171. https://doi.org/10.3390/sym15122171
APA StyleRiaz, M. B., Jhangeer, A., Martinovic, J., & Kazmi, S. S. (2023). Dynamics and Soliton Propagation in a Modified Oskolkov Equation: Phase Plot Insights. Symmetry, 15(12), 2171. https://doi.org/10.3390/sym15122171






