A New Iterative Method for Investigating Modified Camassa–Holm and Modified Degasperis–Procesi Equations within Caputo Operator

Abstract

In this paper, we employ the new iterative method to investigate two prominent nonlinear partial differential equations, namely the modified Camassa–Holm (mCH) equation and the modified Degasperis–Procesi (mDP) equation, both within the framework of the Caputo operator. The mCH and mDP equations are fundamental in studying wave propagation and soliton dynamics, exhibiting complex behavior and intriguing mathematical structures. The new iterative method (NIM), a powerful numerical technique, is utilized to obtain analytical and numerical solutions for these equations, offering insights into their dynamic properties and behavior. Through systematic analysis and computation, we unveil the unique features of the mCH and the mDP equations, shedding light on their applicability in various scientific and engineering domains. This research contributes to the ongoing exploration of nonlinear wave equations and their solutions, emphasizing the versatility of the new iterative method in tackling complex mathematical problems. Numerical results and comparative analyses are presented to validate the effectiveness of the new iterative method in solving these equations, highlighting its potential for broader applications in mathematical modeling and analysis.

1. Introduction

Fractional calculus (FC) is a straightforward and practical tool for precisely solving a wide range of equations. This dynamic field of mathematics produces the main important fractional differential equations (FDEs), which generalizes the integer order to its fractional order and gives rise to a diverse class of mathematical frameworks [1,2,3]. Recent years have seen an extensive study of many physical processes described by fractional differential equations, with important implications in many branches of science and engineering [4,5,6,7]. Different basic ideas of fractional derivatives were proposed by people like Hadamard, Liouville–Caputo, Riemann–Liouville, Caputo–Fabrizio, Atangana–Baleanu operators [8,9,10,11]. In order to derive the Caputo fractional derivative in the correct sequence, an ordinary derivative is first calculated, followed by a fractional integral. On the contrary, the Riemann–Liouville derivative is calculated in reverse when a fractional denominator is utilized. In contrast to the fractional Caputo derivative, which permits more intricate initial and boundary conditions, the Riemann–Liouville derivative restricts itself to the former. Numerous studies have provided descriptions of the Caputo fractional derivative, which is extensively employed in mathematical modeling and analysis to provide insightful information regarding the dynamics of fractional-order systems. The investigation and practical implementation of the fractional derivative remain subjects of ongoing fascination and scholarly inquiry across multiple disciplines, such as mathematical biology and the analysis of memory phenomena [12]. Astrophysics, hydrology, nuclear engineering, meteorology, and astrobiology are just some of the many scientific and commercial fields that have benefited from nonlinear models [13,14].

Fractional partial differential equations (FPDEs) have attracted considerable interest from mathematicians in recent times on account of their wide-ranging applications in numerous disciplines, such as the fields of engineering, theoretical physics, biology, neuroscience, a solid-state materials science, plasma physics, and geophysical sciences, among others. FPDEs have also found applications in physiological scaling laws, electricity, dielectric behavior, chemical physics, financial mathematics, quantum mechanics, electromagnetism fractional dynamics, and quantum computing. Furthermore, viscoplastic and viscous flows, continuum mechanics, sphere flames, propagation of waves, processing of images, anomaly diffusion, the entropy turbulence, and subsurface containment transport are all uses of FPDEs [15,16,17,18,19,20,21,22,23]. These applications demonstrate FPDEs’ broad applicability and significance in addressing complicated phenomena across different fields [24,25,26].

The above-mentioned practical uses of FC in actual problems captured the interest of individuals. Researchers in mathematics recognized the need to look into numerical or analytical solutions to FPDEs and related systems [27,28,29]. Numerous substantial mathematical problems that reflect few of the physical processes in nature are frequently investigated using analytical and numerical approaches [30,31,32]. Li et al. (2020) delve into consensus problems in dynamically changing multiagent supply chain systems [33], while Li and Kai (2023) explore chaotic wave dynamics in nonlinear Schrodinger equations [34]. Peng et al. (2023) investigate opinion dynamics considering community structures, Gu, Li [35], and Liao (2024) propose an evolutionary multitasking approach for solving nonlinear equations [36], and Xuemin et al. (2023) introduce a socially aware incentive algorithm for resource-constrained networks [37]. These contributions span diverse fields, encompassing supply chain dynamics, nonlinear wave behavior, opinion formation, evolutionary computation, and socially aware network incentives. Mathematicians have developed different methods to solve FPDEs and related systems. Since the solutions to these problems help sustain the ongoing dynamics of natural systems [38,39,40], this is a well-established area of study. Researchers have worked tirelessly on this topic, and new, helpful ways have been produced regularly. The Elzaki transform decomposition [41], Sine-Gordon expansion [42], finite element [43], variational iteration [44,45], first integral [46], natural transform decomposition [47], generalized Kudryashov [48], finite volume [49], and many other procedures have been developed to address FPDEs and associated systems.

This paper focuses on the modified beta-equation family [50], which includes many important physical equations.

$${\mathfrak{D}}_{\rho }^p\zeta (\sigma ,\rho )-\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial \rho {\partial }^2\sigma }+({\beta }_{*}+1){\beta }^2(\sigma ,\rho )\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }-{\beta }_{*}\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }\frac{{\partial }^2\beta (\sigma ,\rho )}{\partial {\sigma }^2}+\beta (\sigma ,\rho )\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial {\sigma }^3}=0,0<p\le 1,$$

(1)

substituting ${\beta }_{*}=3$ gives mDP model

$${\mathfrak{D}}_{\rho }^p\beta (\sigma ,\rho )-\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial \rho {\partial }^2\sigma }+4{\beta }^2(\sigma ,\rho )\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }-3\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }\frac{{\partial }^2\beta (\sigma ,\rho )}{\partial {\sigma }^2}+\beta (\sigma ,\rho )\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial {\sigma }^3}=0,0<p\le 1,$$

(2)

substituting ${\beta }_{*}=2$ gives mCH model

$${\mathfrak{D}}_{\rho }^p\beta (\sigma ,\rho )-\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial \rho {\partial }^2\sigma }+3{\beta }^2(\sigma ,\rho )\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }-2\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }\frac{{\partial }^2\beta (\sigma ,\rho )}{\partial {\sigma }^2}+\beta (\sigma ,\rho )\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial {\sigma }^3}=0,0<p\le 1,$$

(3)

The horizontal component of the fluid velocity is denoted by $\beta$, while the spatial and temporal components are denoted by $\sigma$ and $\rho$, respectively. Similar to the mDP and mCH scenarios, the incompressible Euler equation was totally integrable using a Lax pair and emerges in shallow water [51]. Liu and Ouyang developed new solitary wave results for this problem [52] using numerical simulations. The fractional mDP and mCH equations are studied by Dubey et al. [53], who present a q-homotopy analysis method combine with a new method to obtain approximate solutions of the mDP and mCH equations; Behera and Mehra developed a wavelet-optimized finite difference technique [54]. Using a Lie symmetry approach, Kader and Latif [55] several bright and dark solitons solution for the mDP and mCH equations as Weierstrass and Jacobi elliptic functions, respectively.

NIM is a high-level numerical technique for solving difficult differential equations, notably ones with fractional derivatives. NIM’s versatility and efficiency in solving various mathematical problems set it distinct. It starts with an initial estimate and improves it through a succession of well-planned steps. Due to its usefulness in various scientific and technical fields, NIM is widely used by researchers and professionals seeking a dependable and adaptable approach to getting approximate solutions to complex mathematical models [56,57,58,59]. Through numerical analysis, its use has considerably improved our knowledge of and response to complicated real-world occurrences.

This study is organized as follows: In Section 2, we list a few basic definitions. In Section 3, we propose a basic idea of a new iterative method using a fractional partial differential equation problem. In Section 4, we perform a numerical test of the new method. Finally, in Section 5, we give the conclusions.

2. Basic Definitions

Definition 1. 

The Riemann–Liouville fractional integral operator for the p real-valued function $\beta (\sigma ,\rho )$ is represented as ${\mathcal{J}}_{\rho }^p$ and defined for $p\in {\mathbb{R}}^{+}$ [60]:

$${\mathcal{J}}_{\rho }^p\beta (\sigma ,\rho )=\left\{\begin{array}{cc}\frac{1}{\Gamma \left(p\right)}{\int }_0^{\rho }\frac{\beta (\sigma ,\eta )}{{(\rho -\eta )}^{1-p}}d\eta ,\hfill & 0\le \eta <\rho ,p>0\hfill \\ \beta (\sigma ,\rho ),\hfill & p=0.\hfill \end{array}\right.$$

Definition 2. 

The fractional derivative of order $p>0$, for the function $\beta (\sigma ,\rho )$ in the Caputo scenario is represented by $D_{\rho }^p$, and identified as [60]:

$$D_{\rho }^p\beta (\sigma ,\rho )=\left\{\begin{array}{cc}{\mathfrak{J}}_{\rho }^{n-p}\left(D_{\rho }^n\beta (\sigma ,\rho )\right),\hfill & 0<n-1<p\le n,\hfill \\ D_{\rho }^n\beta (\sigma ,\rho )),\hfill & p=n,\hfill \end{array}\right.$$

where $D_{\rho }^n=\frac{{\partial }^n}{\partial {\rho }^n}$, and $n\in \mathbb{N}$.

Consequently, for $\rho \ge 0$, and $n-1<p\le n,\varpi >-1$ the operators $D_{\rho }^p$ and ${\mathfrak{J}}_{\rho }^p$ satisfied the obeying properties:

1. $D_{\rho }^{p}c=0,c\in \mathbb{R}$.

2. $D_{\rho }^p{\rho }^{\beta }=\frac{\Gamma (\varpi +1)}{\Gamma (\varpi +1-p)}{\rho }^{\varpi -p}$.

3. $D_{\rho }^p{\mathfrak{J}}_{\rho }^p\beta (\sigma ,\rho )=\beta (\sigma ,\rho )$.

4. ${\mathfrak{J}}_{\rho }^p{D}_{\rho }^p\beta (\sigma ,\rho )=\beta (\sigma ,\rho )-{\sum }_{j=0}^{n-1}{D}_{\rho }^j\left(\sigma ,0^{+}\right)\frac{{\rho }^j}{j!}$, for $\beta \in C^n[a,b],n-1<p\le n$, $n\in \mathbb{N}$ and $a,b\in \mathbb{R}$.

3. Basic Idea of New Iterative Method (NIM)

Below are outlined fundamental steps in developing the new iterative method [61]. Let us consider the nonlinear equation:

$$\beta (\sigma ,\rho )=f(\sigma ,\rho )+M\beta (\sigma ,\rho )+N\kappa (\sigma ,\rho ),$$

(4)

where f is a sources term, M represents the linear and N represents the nonlinear terms operators. In accordance with the NIM approach, Equation (4)’s result can be expressed as:

$$\beta (\sigma ,\rho )=\sum _{m=0}^{\infty }{\beta }_m(\sigma ,\rho ),$$

(5)

where the linear function M is defined as

$$M\left(\sum _{m=0}^{\infty }{\beta }_m(\sigma ,\rho )\right)=\sum _{m=0}^{\infty }M\left({\beta }_m(\sigma ,\rho )\right),$$

(6)

where N is non-linear and can be represented as

$$N\left(\sum _{m=0}^{\infty }{\beta }_m(\sigma ,\rho )\right)=N\left({\beta }_0(\sigma ,\rho )\right)+\sum _{m=1}^{\infty }\left\{N\left(\sum _{j=0}^m{\beta }_j(\sigma ,\rho )\right)-N\left(\sum _{j=0}^{m-1}{\beta }_j(\sigma ,\rho )\right)\right\},$$

(7)

and by the use of Equations (5)–(7), the general Equation (4) takes the form

$$\sum _{m=1}^{\infty }{\beta }_i=f+\sum _{m=0}^{\infty }M\left({\beta }_m\right)+N\left({\beta }_0\right)+\sum _{m=1}^{\infty }\left[N\left(\sum _{j=0}^m{\beta }_j\right)-N\left(\sum _{j=0}^{m-1}{\beta }_j\right)\right].$$

(8)

To derive the terms of the result, we can establish the recursive relation as follows:

$$\left\{\begin{array}{c}{\beta }_0(\sigma ,\rho )=f\hfill \\ {\beta }_1(\sigma ,\rho )=M\left({\beta }_0\right)+N\left({\beta }_0\right)\hfill \\ {\beta }_2(\sigma ,\rho )=M\left({\beta }_1\right)+N\left({\beta }_0+{\beta }_1\right)-N\left({\beta }_0\right)\hfill \\ ⋮\hfill \\ {\beta }_m(\sigma ,\rho )=M\left({\beta }_{m-1}\right)+N\left({\beta }_0+{\beta }_1+\dots +{\beta }_{m-1}\right)-N\left({\beta }_0+{\beta }_1+\dots +{\beta }_{m-2}\right),\hfill \end{array}\right.$$

The Kth-order approximation is

$${\beta }_m(\sigma ,\rho )=\sum _{j=0}^{m-1}{\beta }_{m,j}(\sigma ,\rho )$$

(9)

4. Convergence Analysis of NIM

If N is analytical in a neighborhood of ${\beta }_0$ and

$$∥N^{\prime \prime \prime }\left({\beta }_0\right)∥=sup\left\{N^m\left({\beta }_0\right)\left(b_1,b_2,\dots ,b_n\right)/∥b_k∥\le 1,1\le k\le m\right\}\le l,$$

for any given number m and for certain real numbers $l>0$ and $\left|\beta k\right|\le M<\frac{1}{e}$, where $k=1,2,\dots$, then the series ${\sum }_{m=0}^{\infty }{G}_m$ exhibits absolute convergence. Furthermore,

$$∥G_m∥\le l{M}^m{e}^{m-1}(e-1),m=1,2,\cdots .$$

To establish the boundedness of $\left|{\beta }_k\right|$ for every k, we provide conditions on $N^{\left(j\right)}\left({\beta }_0\right)$ for which convergence of the series is assured. The subsequent theorem provides the conditions that are adequate for ensuring the convergence of the technique.

Theorem 1. 

If N is $C^{\infty }$ and $∥N^m\left({\beta }_0\right)∥\le M\le e^{-1}$ for all m, then the series ${\sum }_{m=0}^{\infty }{G}_m$ is absolutely convergent. These are the conditions of convergence of the series ${\sum }_{j=0}^{\infty }{\beta }_j$. The proofs of the theorem can be seen in [62].

5. Applications

Example 1. 

Consider the time-fractional mDP model:

$$\begin{array}{cc}\hfill & {\mathfrak{D}}_{\rho }^p\beta (\sigma ,\rho )=\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial \rho {\partial }^2\sigma }-4{\beta }^2(\sigma ,\rho )\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }+3\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }\frac{{\partial }^2\beta (\sigma ,\rho )}{\partial {\sigma }^2}+\beta (\sigma ,\rho )\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial {\sigma }^3},\sigma \in R,\hfill \\ & where0<p\le 1.\hfill \end{array}$$

(10)

with the initial condition

$$\begin{array}{c}\hfill \beta (\sigma ,0)=-\frac{15}{8}{sech}^2\left(\frac{\sigma }{2}\right).\end{array}$$

(11)

The exact solution is:

$$\begin{array}{c}\hfill \beta (\sigma ,\rho )=-\frac{15}{8}{sech}^2\left(\frac{\sigma }{2}-\frac{5\rho }{4}\right).\end{array}$$

(12)

Applying the RL integral to Equation (10), we arrive at an equivalent expression:

$$\begin{array}{cc}\hfill & \beta (\sigma ,\rho )=-\frac{15}{8}{sech}^2\left(\frac{\sigma }{2}\right)-{\mathcal{R}}_{\rho }^p\left[\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial \rho {\partial }^2\sigma }-4{\beta }^2(\sigma ,\rho )\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }+3\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }\frac{{\partial }^2\beta (\sigma ,\rho )}{\partial {\sigma }^2}+\beta (\sigma ,\rho )\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial {\sigma }^3}\right].\hfill \end{array}$$

(13)

Following the procedure outlined in NIM, we obtain the subsequent terms:

$$\begin{array}{cc}\hfill & {\beta }_0(\sigma ,\rho )=-\frac{15}{8}{sech}^2\left(\frac{\sigma }{2}\right),\hfill \\ \hfill & {\beta }_1(\sigma ,\rho )=-\frac{450{\rho }^p{sinh}^6\left(\frac{\sigma }{2}\right){csch}^5\left(\sigma \right)}{\Gamma (p+1)},\hfill \\ \hfill & {\beta }_2(\sigma ,\rho )=\frac{3375{\rho }^{2p}{sech}^{10}\left(\frac{\sigma }{2}\right)}{2048}\times \hfill \\ & (\frac{15{\rho }^{p}tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{\Gamma {(p+1)}^3\Gamma (3p+1)}\left(-\frac{225{\rho }^p\Gamma {(3p+1)}^2(2cosh\left(\sigma \right)-3)tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{\Gamma (4p+1)}\right)\hfill \\ & -\left(\frac{60\Gamma (p+1)\Gamma (2p+1){\rho }^{p}tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{\Gamma {(p+1)}^3\Gamma (3p+1)}(-38cosh\left(\sigma \right)+8cosh\left(2\sigma \right)+29)\right)\hfill \\ & -\frac{2(-122cosh(\sigma )+27cosh(2\sigma )+85)}{\Gamma (2p+1)}).\hfill \end{array}$$

(14)

The final solution, as determined by the NIM algorithm, is as follows:

$$\begin{array}{c}\hfill \beta (\sigma ,\rho )={\beta }_0(\sigma ,\rho )+{\beta }_1(\sigma ,\rho )+{\beta }_2(\sigma ,\rho )+\cdots ,\end{array}$$

(15)

$$\begin{array}{cc}\hfill \beta (\sigma ,\rho )=& -\frac{15}{8}{sech}^2\left(\frac{\sigma }{2}\right)-\frac{450{\rho }^p{sinh}^6\left(\frac{\sigma }{2}\right){csch}^5\left(\sigma \right)}{\Gamma (p+1)}+\frac{3375{\rho }^{2p}{sech}^{10}\left(\frac{\sigma }{2}\right)}{2048}\times \hfill \\ & (\frac{15{\rho }^{p}tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{\Gamma {(p+1)}^3\Gamma (3p+1)}\left(-\frac{225{\rho }^p\Gamma {(3p+1)}^2(2cosh\left(\sigma \right)-3)tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{\Gamma (4p+1)}\right)\hfill \\ & -\left(\frac{60\Gamma (p+1)\Gamma (2p+1){\rho }^{p}tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{\Gamma {(p+1)}^3\Gamma (3p+1)}(-38cosh\left(\sigma \right)+8cosh\left(2\sigma \right)+29)\right)\hfill \\ & -\frac{2(-122cosh(\sigma )+27cosh(2\sigma )+85)}{\Gamma (2p+1)})+\cdots .\hfill \end{array}$$

(16)

The above equation with fractional order $p=1$ is given as

$$\begin{array}{cc}\hfill \beta (\sigma ,\rho )=& -\frac{15}{8}{sech}^2\left(\frac{\sigma }{2}\right)-\frac{450\rho {sinh}^6\left(\frac{\sigma }{2}\right){csch}^5\left(\sigma \right)}{2}+\frac{3375{\rho }^2{\sec \mathrm{h}}^{10}\left(\frac{\sigma }{2}\right)}{2048}\times \hfill \\ & (\frac{15\rho tanh\left(\frac{\sigma }{2}\right){\sec \mathrm{h}}^2\left(\frac{\sigma }{2}\right)}{48}\left(-\frac{225\rho 36(2cosh\left(\sigma \right)-3)tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{24}\right)\hfill \\ & -\left(\frac{120\rho tanh\left(\frac{\sigma }{2}\right){sech}^2\left(\frac{\sigma }{2}\right)}{6}(-38cosh\left(\sigma \right)+8cosh\left(2\sigma \right)+29)\right)\hfill \\ & -\frac{2(-122cosh(\sigma )+27cosh(2\sigma )+85)}{2})+\cdots .\hfill \end{array}$$

(17)

Figure 1 depicts the exact result of Example 1 at $\rho =0.01$. The plot provides a reference to evaluate the accuracy of the numerical methods used to approximate the solution. Figure 2a–d showcase the solutions obtain applying the numerical iterative method for different fractional-order ($0.3$, $0.5$, $0.7$, and $1.0$) at $\eta =0.01$. These graphs offer insight into how the solution varies with changing fractional orders, aiding in understanding the impact of fractional differentiation on the system’s behavior. Figure 3, Figure 4 and Figure 5 present the absolute errors for Example 1 with varying p values ($0.5$, $0.7$, and $1.0$) at $\rho =0.01$. These figures highlight how the absolute error changes concerning different values of p, indicating the accuracy of the numerical approximations for distinct scenarios. Figure 6 illustrates a comparative analysis of the absolute errors corresponding to various fractional orders used in Example 1. This comparison offers a comprehensive understanding of how different fractional orders impact the accuracy of the numerical method employed.

Table 1. Comparisons of various fractional order of the new iterative method of Example 1 for $\rho =0.01$.

$\mathit{\sigma }$	${\mathit{NIM}}_{\mathit{P}=0.5}$	${\mathit{NIM}}_{\mathit{p}=0.7}$	${\mathit{NIM}}_{\mathit{P}=1}$	$\mathit{Exact}$	${\mathit{Error}}_{\mathit{p}=0.5}$	${\mathit{Error}}_{\mathit{p}=0.7}$	${\mathit{Error}}_{\mathit{p}=1}$
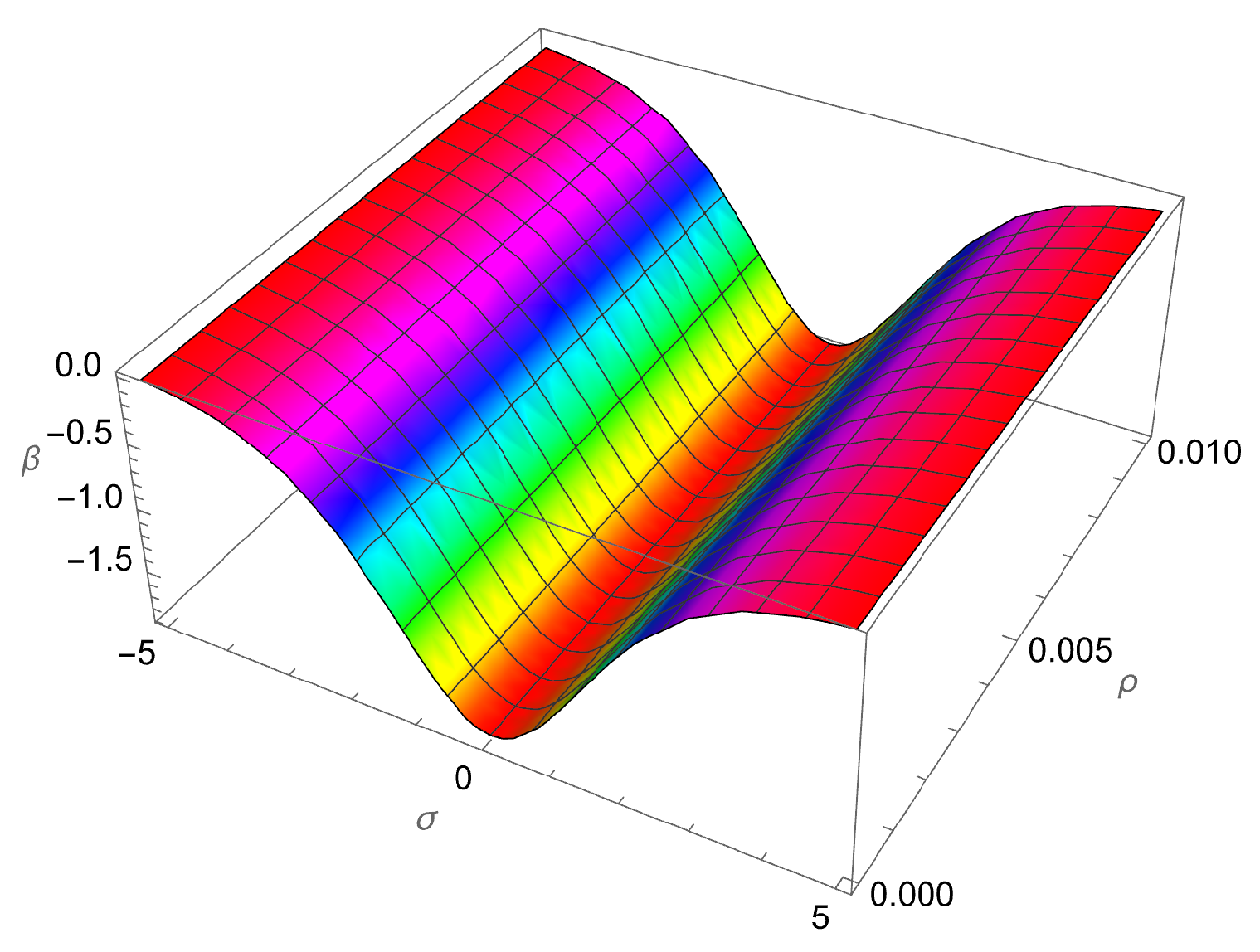
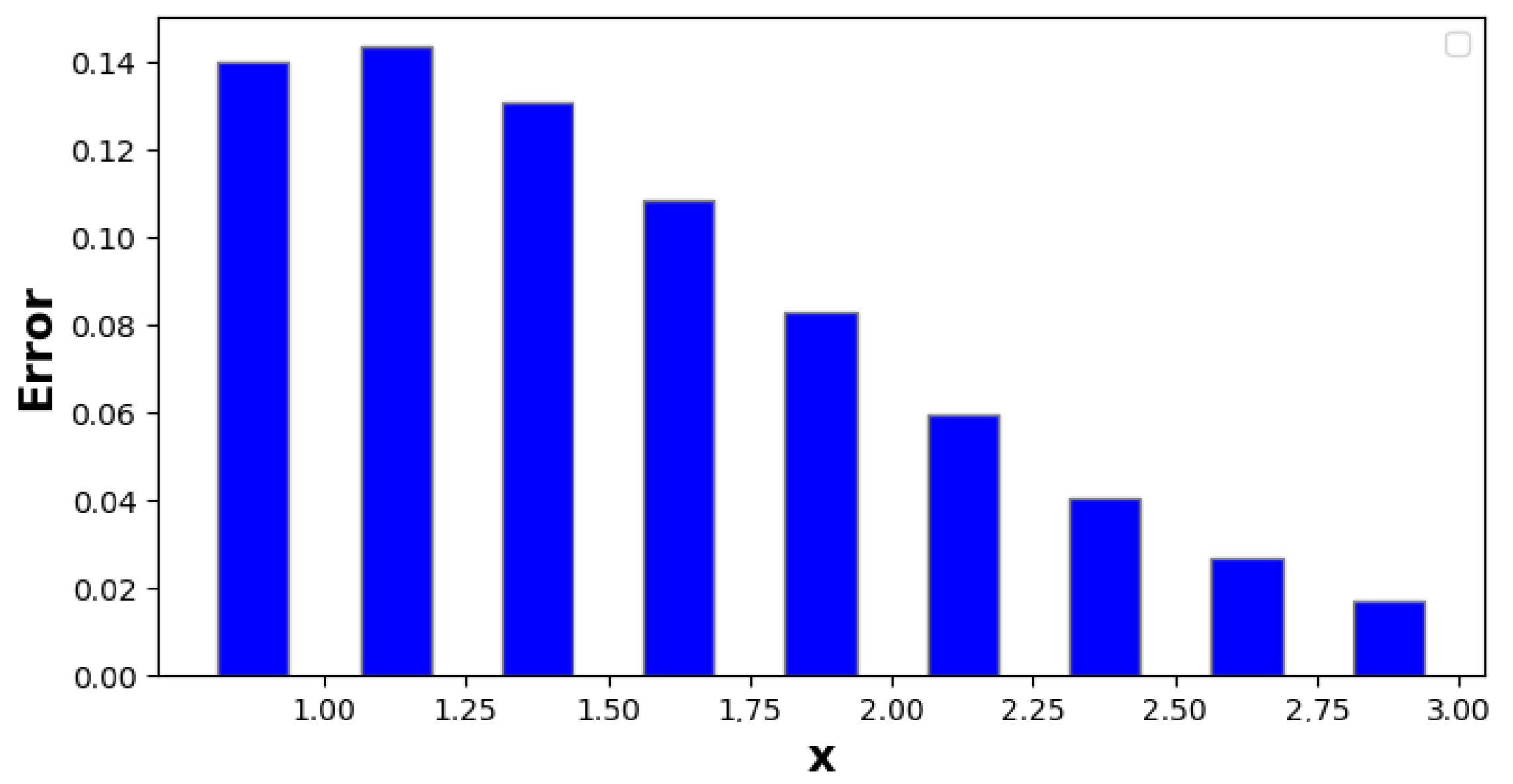
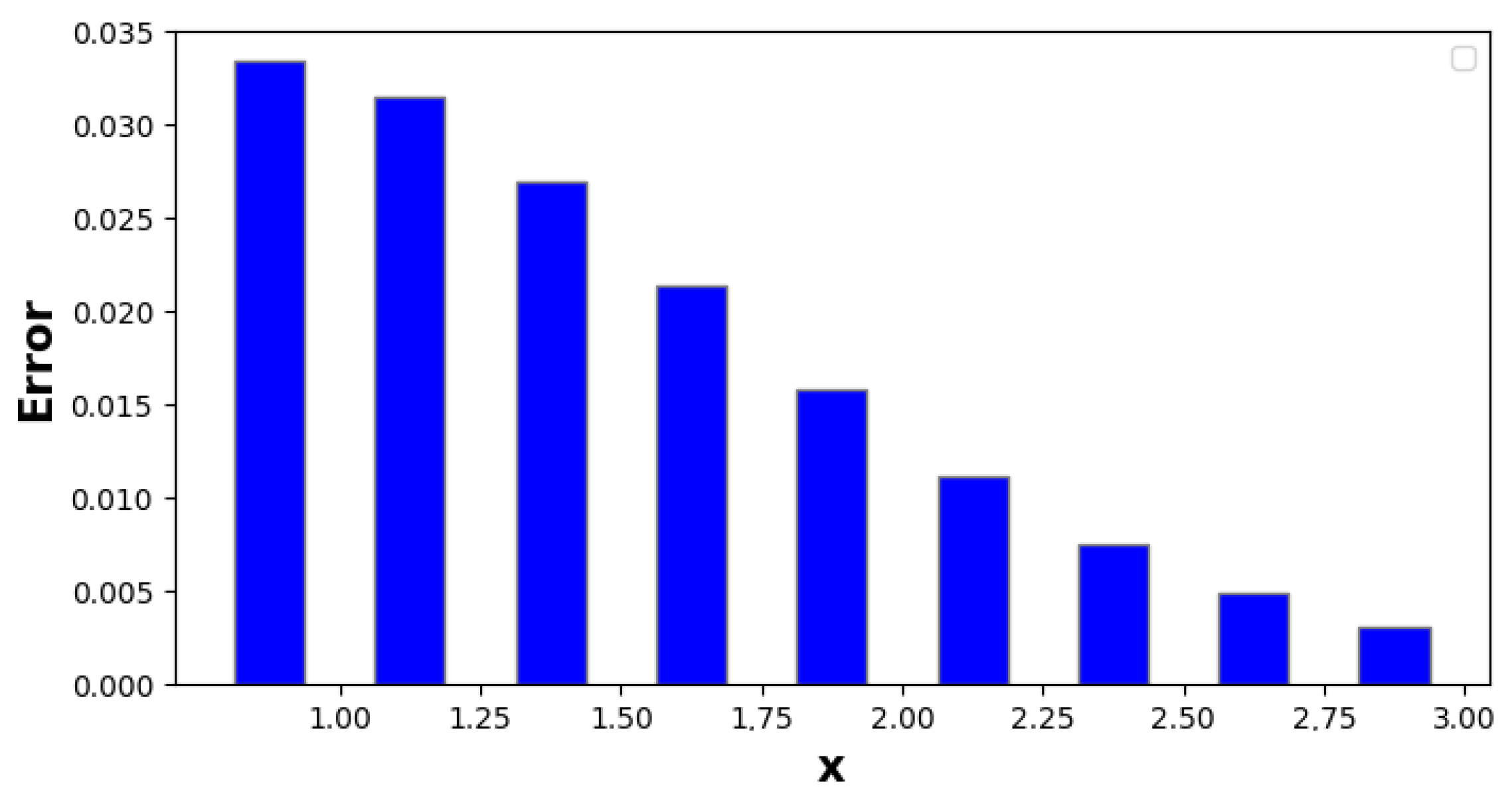
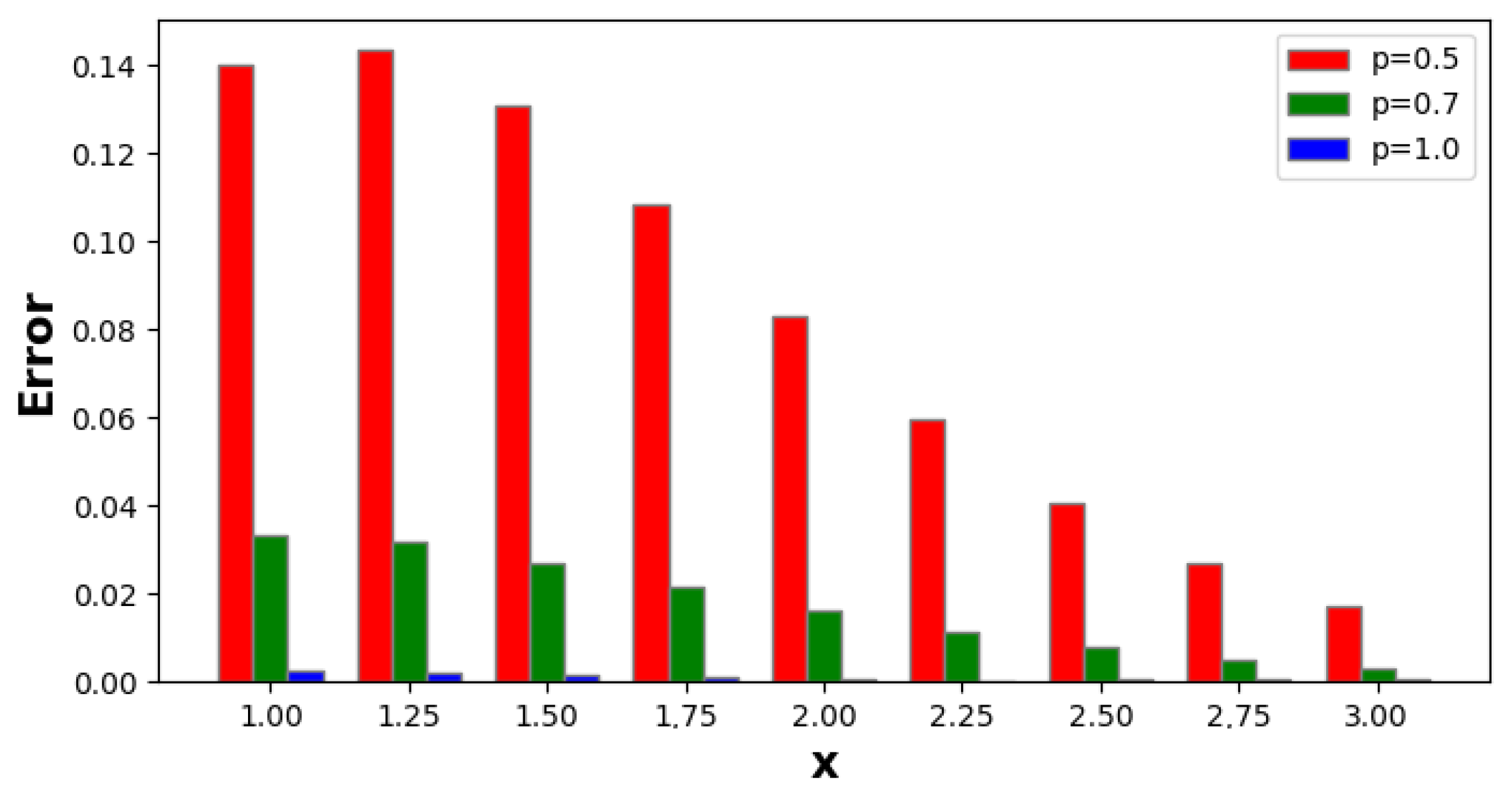
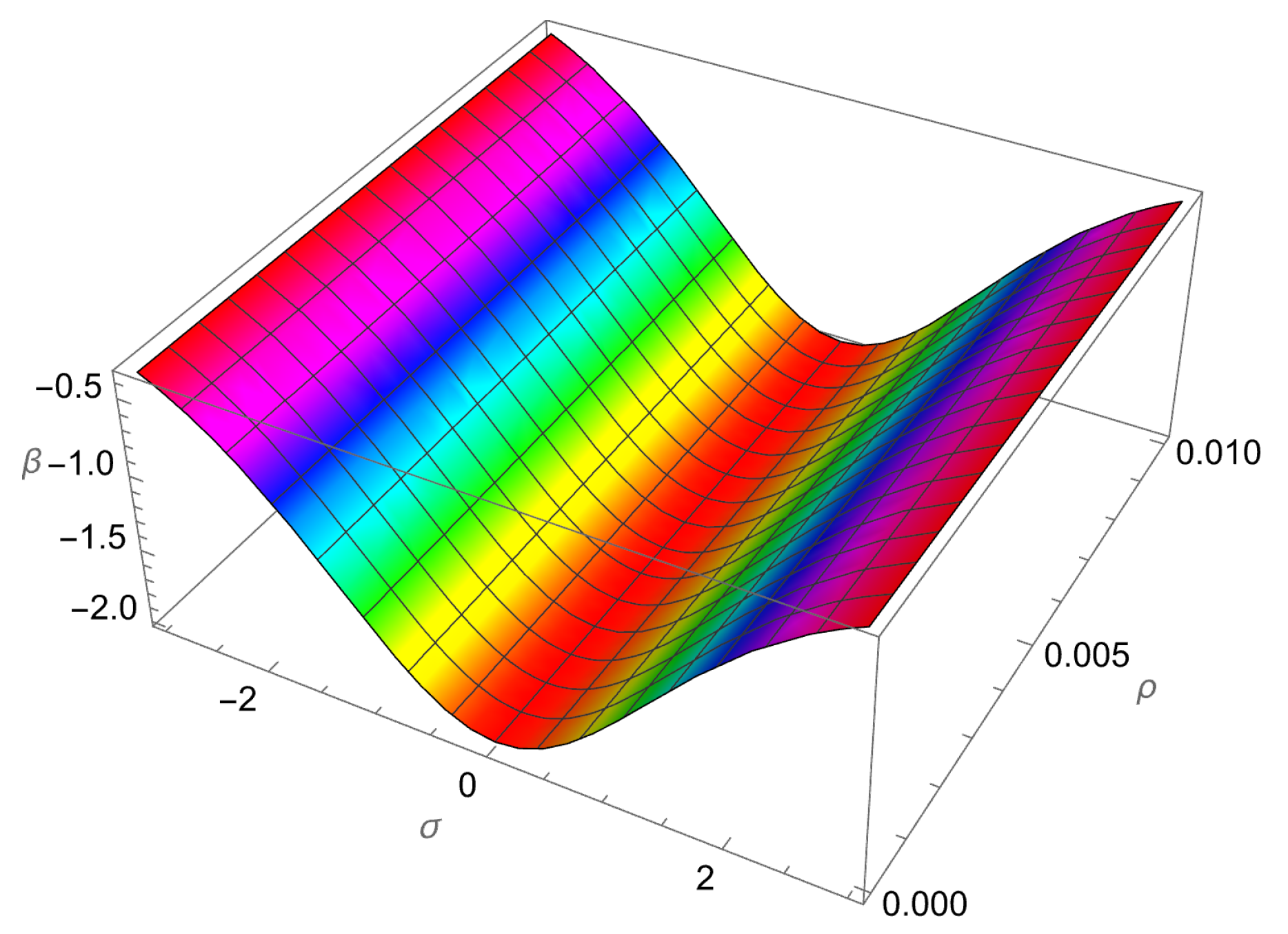
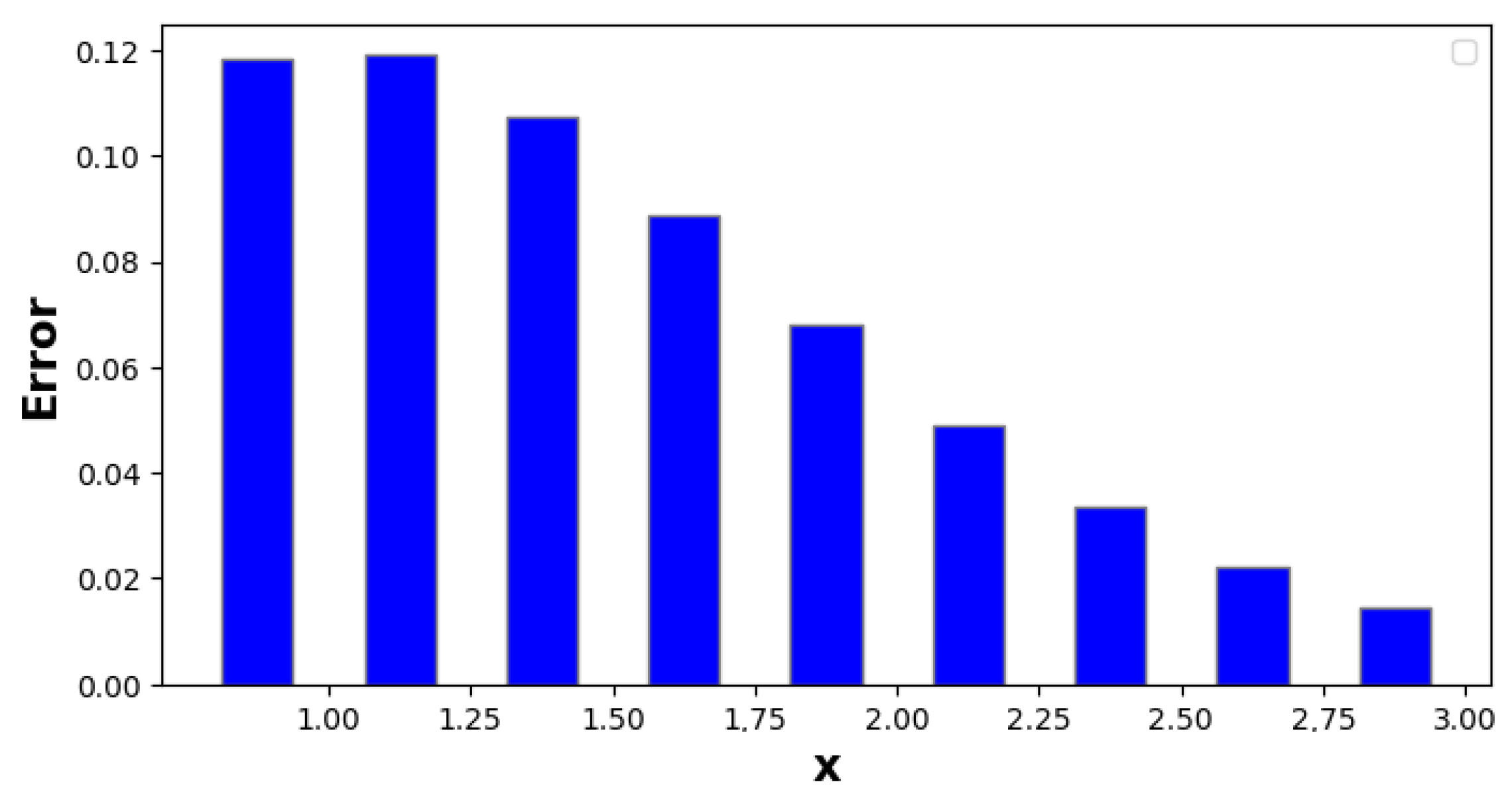
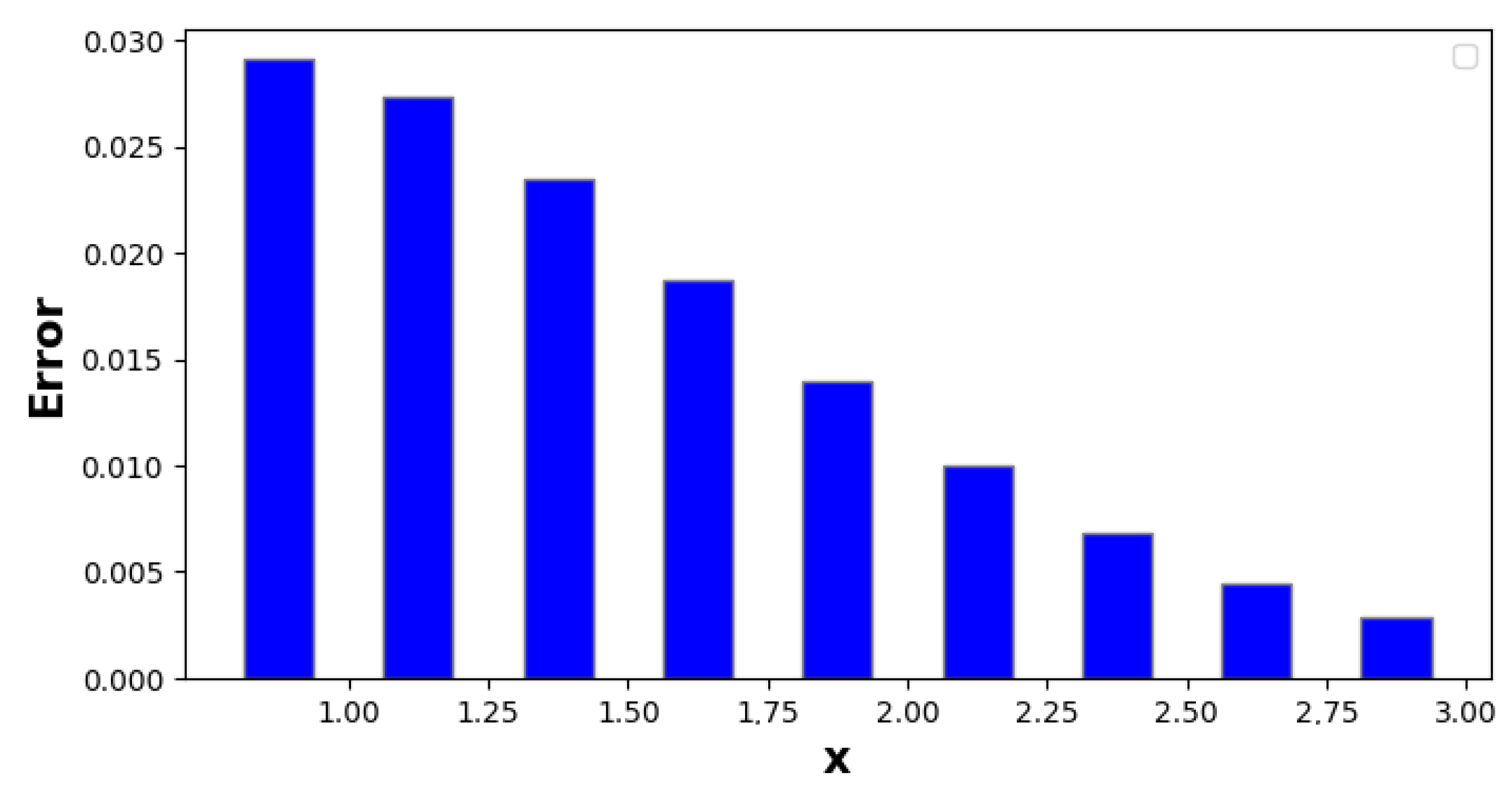
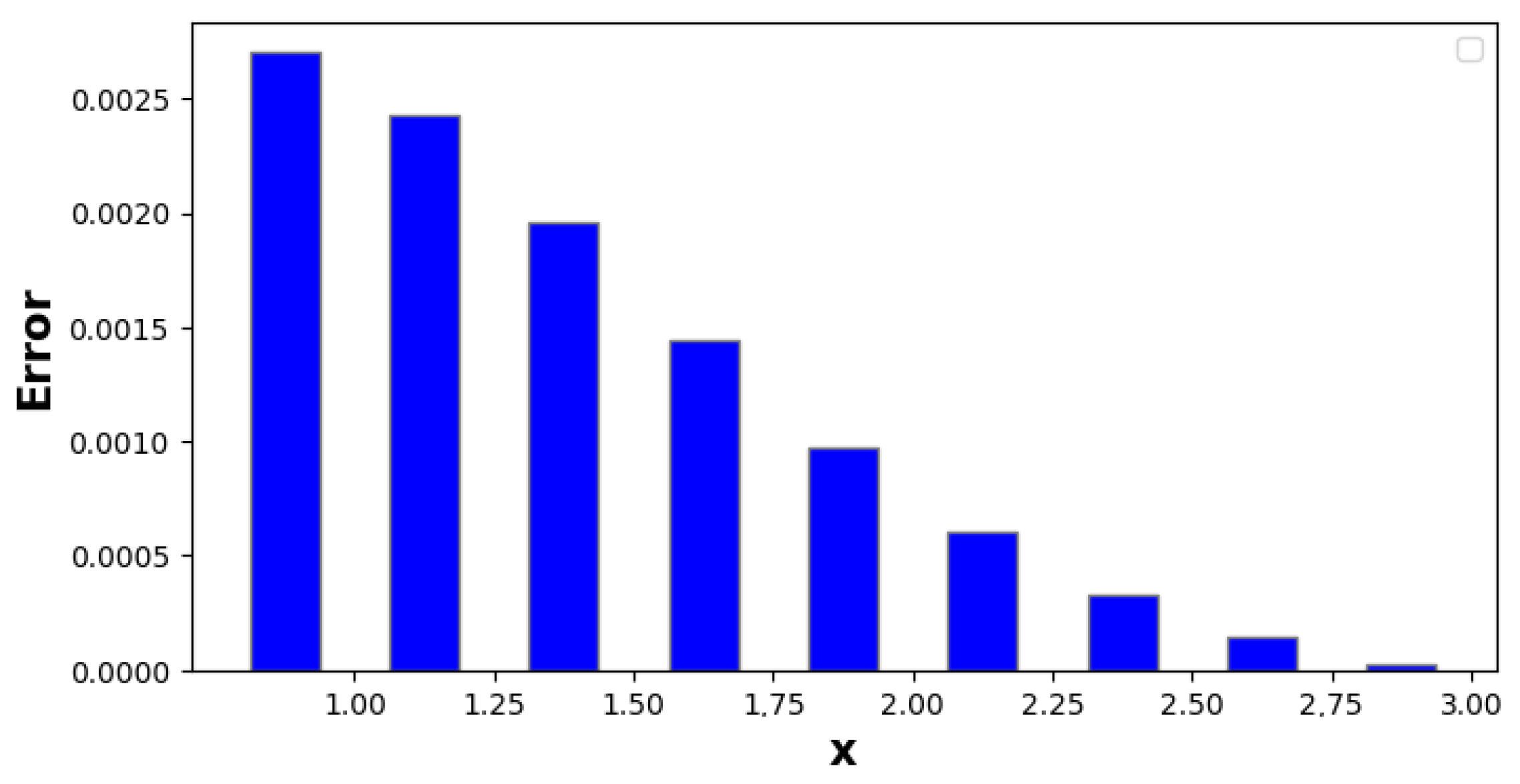
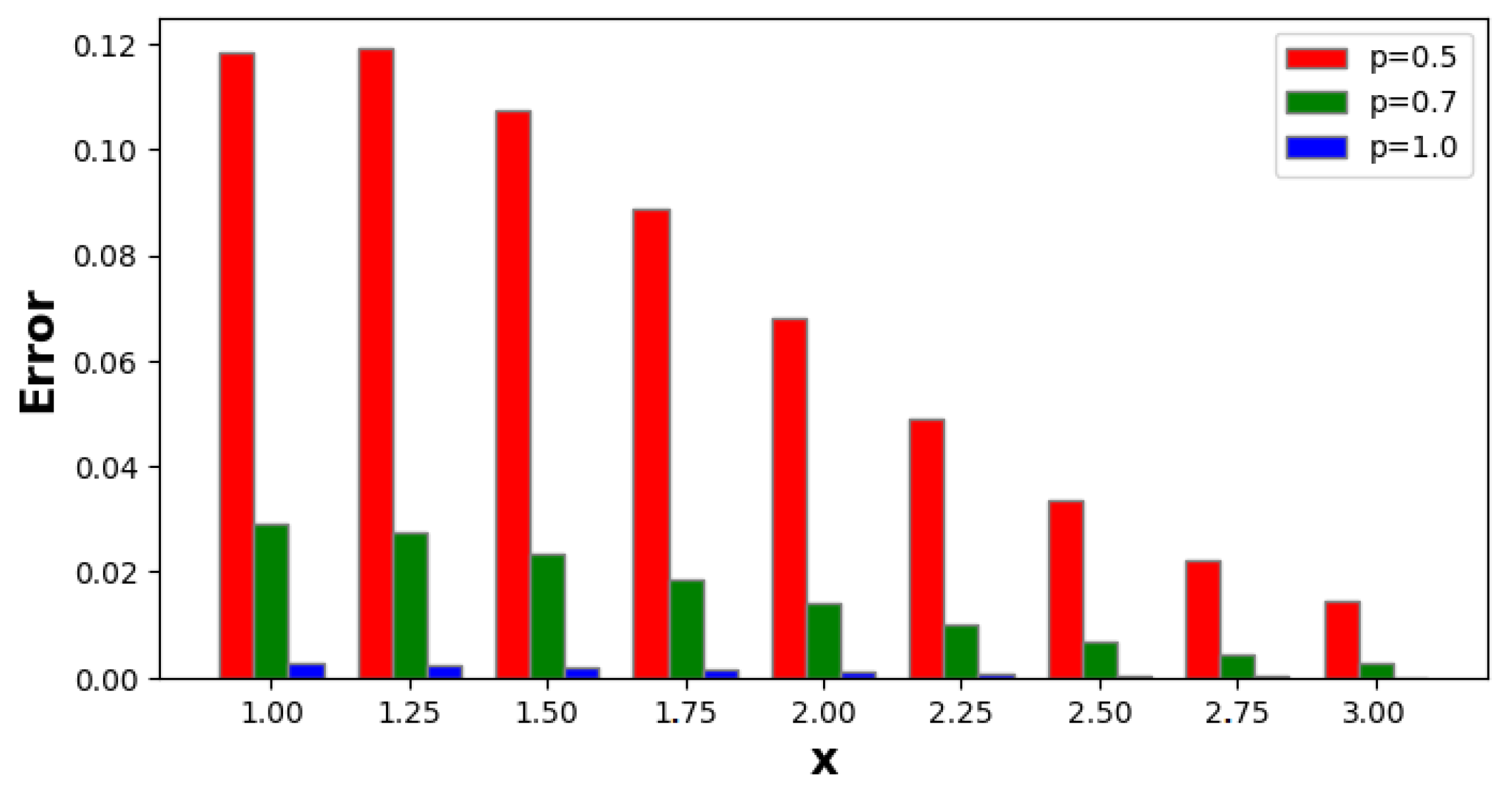
1.00	−1.61652	−1.50964	−1.47861	−1.47629	0.140224	0.0333514	2.31575 × 10${}^{-3}$
1.25	−1.44355	−1.33153	−1.30203	−1.30009	0.143463	0.0314393	1.94461 × 10${}^{-3}$
1.50	−1.25125	−1.14729	−1.12179	−1.12037	0.130877	0.0269171	1.41111 × 10${}^{-3}$
1.75	−1.05604	−0.96895	−0.948498	−0.947635	0.10841	0.021315	8.63402 × 10${}^{-4}$
2.00	−0.871842	−0.804775	−0.789349	−0.788952	0.0828896	0.015823	3.96629 × 10${}^{-4}$
2.25	−0.707665	−0.659374	−0.648295	−0.648244	0.0594201	0.0111292	5.07339 × 10${}^{-5}$
2.50	−0.567395	−0.534372	−0.52672	−0.526894	0.040501	0.00747861	1.74132 × 10${}^{-4}$
2.75	−0.451065	−0.429334	−0.424206	−0.424504	0.0265603	0.0048294	2.98781 × 10${}^{-4}$
3.00	−0.356509	−0.342599	−0.339242	−0.339592	0.0169163	0.00300629	3.50469 × 10${}^{-4}$

presents a quantitative comparison of the results obtained from the Numerical Inversion Method (NIM) for different fractional orders at $\rho =0.01$. It provides a tabulated summary, enabling a direct comparison of the solution accuracy across various fractional differentiation orders.

Table 2. Comparison of absolute error of ETDM [63] and NIM of Example 1 for $\rho =0.01$.

$\mathit{\sigma }$	$\mathit{EXACT}$	${\mathit{ETDM}}_{\mathit{P}=1.0}$	${\mathit{NIM}}_{\mathit{p}=1.0}$ [63]	$\mathit{ETDMError}$	$\mathit{NIMError}$
1	−1.49154	−1.5147	−1.50142	2.31613 × 10${}^{-2}$	2.324274 × 10${}^{-3}$
2	−0.802536	−0.807139	−0.80532	4.60314 × 10${}^{-3}$	3.806376 × 10${}^{-4}$
3	−0.34657	−0.343119	−0.34432	3.45024 × 10${}^{-3}$	3.588191 × 10${}^{-4}$
4	−0.1357	−0.133158	−0.13432	2.54244 × 10${}^{-3}$	2.55321 × 10${}^{-4}$
5	−0.0511053	−0.0499592	−0.05070	1.14616 × 10${}^{-3}$	1.14679 × 10${}^{-4}$
6	−0.0189647	−0.0185125	−0.01872	4.52272 × 10${}^{-4}$	4.52305 × 10${}^{-5}$
7	−0.00699915	−0.00682852	−0.00690	1.70632 × 10${}^{-4}$	1.70634 × 10${}^{-5}$
8	−0.00257789	−0.00251454	−0.00255	6.33528 × 10${}^{-5}$	6.33529 × 10${}^{-6}$
9	−0.000948764	−0.000925379	−0.00089	2.3385 × 10${}^{-5}$	2.33851 × 10${}^{-6}$
10	−0.000349087	−0.000340473	−0.00034	8.613563 × 10${}^{-6}$	8.613563 × 10${}^{-7}$

contrasts the absolute errors between the Numerical Inversion Method (NIM) and another method (ETDM, referenced as [63]) for Example 1 at $\rho =0.01$. This table facilitates a direct comparison of the accuracies achieved by these two distinct numerical techniques. Overall, the graphical figures and tables collectively offer a comprehensive analysis of the accuracy, precision, and comparative performance of different fractional orders and numerical methods employed in approximating the solution of Example 1 at $\rho =0.01$. These visual and tabulated representations are crucial for understanding the behavior of the system and assessing the reliability of the numerical techniques used.

Example 2. 

Consider the time-fractional mCH model is given as

$$\begin{array}{cc}\hfill & {\mathfrak{D}}_{\rho }^p\beta (\sigma ,\rho )=\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial \rho {\partial }^2\sigma }-3{\beta }^2(\sigma ,\rho )\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }+2\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }\frac{{\partial }^2\beta (\sigma ,\rho )}{\partial {\sigma }^2}+\beta (\sigma ,\rho )\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial {\sigma }^3},\sigma \in R,\hfill \\ & where0<p\le 1.\hfill \end{array}$$

(18)

with the initial condition

$$\begin{array}{cc}\hfill & \beta (\sigma ,0)=-2{sech}^2\left(\frac{\sigma }{2}\right),\hfill \end{array}$$

(19)

The exact solution is:

$$\begin{array}{cc}\hfill & \beta (\sigma ,\rho )=-2{sech}^2\left(\frac{\sigma -\rho }{2}\right).\hfill \end{array}$$

(20)

Applying the RL integral on Equation (18), we arrive at an equivalent expression:

$$\begin{array}{cc}\hfill & \beta (\sigma ,\rho )=-\frac{8k}{3}{cos}^2\left(\frac{\sigma }{4}\right)-{\mathcal{R}}_{\rho }^p\left[\beta (\sigma ,\rho )\frac{{\partial }^3\beta (\sigma ,\rho )}{\partial {\sigma }^3}+\beta (\sigma ,\rho )\frac{\partial \beta (\sigma ,\rho )}{\partial \sigma }+3\beta (\sigma ,\rho )\frac{{\partial }^2\beta (\sigma ,\rho )}{\partial {\sigma }^2}\right].\hfill \end{array}$$

(21)

Following the NIM procedure, we obtain the subsequent terms:

$$\begin{array}{cc}\hfill & {\beta }_0(\sigma ,\rho )=-2{sech}^2\left(\frac{\sigma }{2}\right),\hfill \\ \hfill & {\beta }_1(\sigma ,\rho )=-\frac{384{\rho }^p{sinh}^6\left(\frac{\sigma }{2}\right){csch}^5\left(\sigma \right)}{\Gamma (p+1)},\hfill \\ \hfill & {\beta }_2(\sigma ,\rho )=9{\rho }^{2p}{sech}^{10}\left(\frac{\sigma }{2}\right)\times \hfill \\ & (\frac{\left(6{\rho }^p{sech}^3\left(\frac{\sigma }{2}\right)\right)\left(\Gamma (p+1)\Gamma (2p+1)\left(-47sinh\left(\frac{\sigma }{2}\right)+23sinh\left(\frac{3\sigma }{2}\right)-4sinh\left(\frac{5\sigma }{2}\right)\right)\right)}{\Gamma {(p+1)}^3\Gamma (3p+1)}\hfill \\ & -\frac{\left(6{\rho }^p{sech}^3\left(\frac{\sigma }{2}\right)\right)\left(48{\rho }^p\Gamma {(3p+1)}^2(2cosh\left(\sigma \right)-3){tanh}^2\left(\frac{\sigma }{2}\right)sech\left(\frac{\sigma }{2}\right)\right)}{\left(\Gamma {(p+1)}^3\Gamma (3p+1)\right)\Gamma (4p+1)}\hfill \\ & +\frac{34cosh\left(\sigma \right)-7cosh\left(2\sigma \right)-25}{\Gamma (2p+1)}).\hfill \end{array}$$

(22)

The NIM algorithm yields the ultimate solution as follows:

$$\begin{array}{c}\hfill \beta (\sigma ,\rho )={\beta }_0(\sigma ,\rho )+{\beta }_1(\sigma ,\rho )+{\beta }_2(\sigma ,\rho )+\cdots .\end{array}$$

(23)

$$\begin{array}{cc}\hfill \beta (\sigma ,\rho )=& -2{sech}^2\left(\frac{\sigma }{2}\right)-\frac{384{\rho }^p{sinh}^6\left(\frac{\sigma }{2}\right){csch}^5\left(\sigma \right)}{\Gamma (p+1)}+9{\rho }^{2p}{sech}^{10}\left(\frac{\sigma }{2}\right)\times \hfill \\ & (\frac{\left(6{\rho }^p{sech}^3\left(\frac{\sigma }{2}\right)\right)\left(\Gamma (p+1)\Gamma (2p+1)\left(-47sinh\left(\frac{\sigma }{2}\right)+23sinh\left(\frac{3\sigma }{2}\right)-4sinh\left(\frac{5\sigma }{2}\right)\right)\right)}{\Gamma {(p+1)}^3\Gamma (3p+1)}\hfill \\ & -\frac{\left(6{\rho }^p{sech}^3\left(\frac{\sigma }{2}\right)\right)\left(48{\rho }^p\Gamma {(3p+1)}^2(2cosh\left(\sigma \right)-3){tanh}^2\left(\frac{\sigma }{2}\right)sech\left(\frac{\sigma }{2}\right)\right)}{\left(\Gamma {(p+1)}^3\Gamma (3p+1)\right)\Gamma (4p+1)}\hfill \\ & +\frac{34cosh\left(\sigma \right)-7cosh\left(2\sigma \right)-25}{\Gamma (2p+1)})+\cdots .\hfill \end{array}$$

(24)

The above equation put fractional order $p=1$ is given as

$$\begin{array}{cc}\hfill \beta (\sigma ,\rho )=& -2{sech}^2\left(\frac{\sigma }{2}\right)-384\rho {sinh}^6\left(\frac{\sigma }{2}\right){\csc \mathrm{h}}^5\left(\sigma \right)+9{\rho }^2{sech}^{10}\left(\frac{\sigma }{2}\right)\times \hfill \\ & (\frac{\left(6\rho {sech}^3\left(\frac{\sigma }{2}\right)\right)\left(2\left(-47sinh\left(\frac{\sigma }{2}\right)+23sinh\left(\frac{3\sigma }{2}\right)-4sinh\left(\frac{5\sigma }{2}\right)\right)\right)}{6}\hfill \\ & -\frac{\left(6\rho {sech}^3\left(\frac{\sigma }{2}\right)\right)\left(48\rho 36(2cosh\left(\sigma \right)-3){tanh}^2\left(\frac{\sigma }{2}\right)sech\left(\frac{\sigma }{2}\right)\right)}{\left(6\right)24}\hfill \\ & +\frac{34cosh\left(\sigma \right)-7cosh\left(2\sigma \right)-25}{2})+\cdots .\hfill \end{array}$$

(25)

Figure 7 illustrates the exact result of Example 2 concerning a parameter $\rho =0.01$. This figure serves as a benchmark against which numerical methods can be compared for accuracy and convergence. In Figure 8, panels (a) through (d) display the behavior of the new iterative method (NIM) for Example 2 under varying fractional orders ($0.3$, $0.5$, $0.7$, and $1.0$) while holding $\eta =0.01$. Figure 9, Figure 10 and Figure 11 present the absolute error analysis for Example 1, considering different values of parameter p ($0.5$, $0.7$, and $1.0$, respectively) with a fixed $\rho =0.01$. These figures provide a comparison of error trends under varying p values, elucidating the accuracy of the numerical method employed. Figure 12 compares the absolute errors associated with different fractional orders for Example 1. This plot aims to showcase the impact of fractional order variation on the accuracy of the method, aiding in the selection of an optimal fractional order for improved accuracy.

Table 3. Comparisons of fractional various order of new iterative method of Example 2 for $\rho =0.01$.

$\mathit{\sigma }$	${\mathit{NIM}}_{\mathit{P}=0.5}$	${\mathit{NIM}}_{\mathit{p}=0.7}$	${\mathit{NIM}}_{\mathit{P}=1}$	$\mathit{Exact}$	${\mathit{Error}}_{\mathit{p}=0.5}$	${\mathit{Error}}_{\mathit{p}=0.7}$	${\mathit{Error}}_{\mathit{p}=1}$
1.00	−1.69213	−1.60272	−1.57632	−1.57362	0.118512	0.0291003	2.70158 × 10${}^{-3}$
1.25	−1.5046	−1.41301	−1.38803	−1.38561	0.118991	0.0274026	2.42546 × 10${}^{-3}$
1.50	−1.30145	−1.21743	−1.19589	−1.19393	0.107518	0.0235019	1.96008 × 10${}^{-3}$
1.75	−1.09853	−1.02844	−1.01119	−1.00974	0.0887829	0.0186967	1.44558 × 10${}^{-3}$
2.00	−0.908565	−0.854575	−0.841566	−0.840589	0.0679769	0.0139868	9.77286 × 10${}^{-4}$
2.25	−0.739574	−0.700571	−0.691224	−0.690622	0.0489514	0.0099492	6.01402 × 10${}^{-4}$
2.50	−0.594898	−0.568096	−0.561633	−0.561306	0.0335926	0.00679071	3.27151 × 10${}^{-4}$
2.75	−0.474425	−0.456687	−0.45235	−0.452208	0.0222178	0.00447932	1.42767 × 10${}^{-4}$
3.00	−0.376033	−0.364611	−0.361769	−0.361741	0.0142926	0.00287059	2.83758 × 10${}^{-5}$

offers a tabulated comparison between different fractional orders utilized in the Numerical Inversion Method (NIM) for Example 1, considering a fixed value of $\rho =0.01$. This table likely includes metrics such as error values or convergence measures for each fractional order.

Table 4. Comparison of absolute error of ETDM [63] and NIM of Example 2 for $\rho =0.01$.

$\mathit{\sigma }$	$\mathit{EXACT}$	${\mathit{ETDM}}_{\mathit{P}=1.0}$	${\mathit{NIM}}_{\mathit{p}=1.0}$ [63]	$\mathit{ETDMError}$	$\mathit{NIMError}$
1	−1.58015	−1.60704	−1.59532	2.68901 × 10${}^{-2}$	2.7044 × 10${}^{-3}$
2	−0.846361	−0.856595	−0.85142	1.02336 × 10${}^{-2}$	9.720903 × 10${}^{-4}$
3	−0.364698	−0.365056	−0.36484	3.58019 × 10${}^{-4}$	2.62379 × 10${}^{-6}$
4	−0.14267	−0.141887	−0.14192	7.83511 × 10${}^{-4}$	7.853812 × 10${}^{-6}$
5	−0.0537117	−0.0532686	−0.05351	4.43118 × 10${}^{-4}$	4.412590 × 10${}^{-6}$
6	−0.0199294	−0.0197437	−0.01982	1.85674 × 10${}^{-4}$	1.848193 × 10${}^{-6}$
7	−0.00735482	−0.00728336	−0.00730	7.14593 × 10${}^{-5}$	7.11334 × 10${}^{-7}$
8	−0.00270884	−0.00268212	−0.00269	2.67196 × 10${}^{-5}$	2.659878 × 10${}^{-7}$
9	−0.000996952	−0.000987064	−0.00099	9.888168 × 10${}^{-6}$	9.843626 × 10${}^{-7}$
10	−0.000366816	−0.00036317	−0.00036	3.645592 × 10${}^{-6}$	3.629193 × 10${}^{-7}$

presents a comparative analysis between the absolute errors obtained from the Numerical Inversion Method (NIM) and another method, possibly the ETDM referenced from a prior study [63], for Example 1 with $\rho =0.01$. This table aids in assessing the performance and accuracy of the NIM concerning an alternative method.

6. Conclusions

In this research, the new iterative method has been effectively applied to investigate the modified Camassa–Holm and modified Degasperis–Procesi equations within the framework of the Caputo operator. Through this investigation, we have gained valuable insights into the dynamics of these nonlinear partial differential equations. The method has proven to be a versatile and powerful tool for obtaining both analytical and numerical solutions, shedding light on the complex behavior and soliton structures inherent in the modified Camassa–Holm and modified Degasperis–Procesi equations. These findings not only deepen our understanding of wave propagation and mathematical physics, but also highlight the broader applicability of the new iterative method in addressing intricate mathematical models. The successful application of the new iterative method in this study underscores its potential for further advancements in mathematical modeling, analysis, and computational science, with implications for a broad spectrum of science and engineering areas.