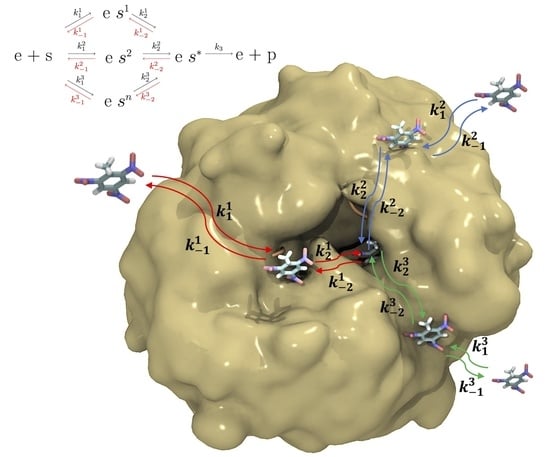
Steady State Kinetics for Enzymes with Multiple Binding Sites Upstream of the Catalytic Site

Abstract

The Michaelis–Menten mechanism, which describes the binding of a substrate to an enzyme, is a simplification of the process on a molecular scale. A more detailed model should include the binding of the substrate to precatalytic binding sites (PCBSs) prior to the transition to the catalytic site. Our work shows that the incorporation of PCBSs, in steady-state conditions, generates a Michaelis–Menten-type expression, in which the kinetic parameters KM and Vmax adopt more complex expressions than in the model without PCBSs. The equations governing reaction kinetics can be seen as generalized symmetries, relative to time translation actions over the state space of the underlying chemical system. The study of their structure and defining parameters can be interpreted as looking for invariants associated with these time evolution actions. The expression of $K_M$ decreases as the number of PCBSs increases, while $V_{max}$ reaches a minimum when the first PCBSs are incorporated into the model. To evaluate the trend of the dynamic behavior of the system, numerical simulations were performed based on schemes with different numbers of PCBSs and six conditions of kinetic constants. From these simulations, with equal kinetic constants for the formation of the Substrate/PCBS complex, it is observed that $K_M$ and $V_{max}$ are lower than those obtained with the Michaelis–Menten model. For the model with PCBSs, the $V_{max}$ reaches a minimum at one PCBS and that value is maintained for all of the systems evaluated. Since $K_M$ decreases with the number of PCBSs, the catalytic efficiency increases for enzymes fitting this model. All of these observations are consistent with the general equation obtained. This study allows us to explain, on the basis of the PCBS to $K_M$ and $V_{max}$ ratios, the effect on enzyme parameters due to mutations far from the catalytic site, at sites involved in the first enzyme/substrate interaction. In addition, it incorporates a new mechanism of enzyme activity regulation that could be fundamental to search for new activity-modulating sites or for the design of mutants with modified enzyme parameters.

1. Introduction

Enzymes are macromolecules, polymers of amino acids, that accelerate chemical reactions by several orders of magnitude, allowing them to occur at a rate capable of sustaining life [1]. This process occurs in a small region of the enzyme called the catalytic site, which is usually located in a groove or gap with controlled access to the solvent [2]. To access the catalytic site, the substrate must be transferred from the solvent, traveling a path that can span 20 Å, depending on the distance from the first contact [3]. As observed in simulations of the binding of 1,2,3-trichloropropane substrate to the enzyme haloalkane dehalogenase A and haloalkane dehalogenase A31, the substrate travels a 20 Å path from the solution to the catalytic site [4]. In this pathway, as shown by simulations of enzyme/ligand complex formation, in the first stage, the substrate interacts with the enzyme surface, decreasing its mobility and the number of water molecules in its hydration layer [5]. There may be different initial binding sites for the substrate on the surface of the protein, which determines its trajectory. This behavior has been observed in the binding path of the phosphate anion to the catalytic site of the phosphate-binding protein [6]. For this particular case, it is proposed that the regions near the catalytic site show charged residues that are distributed so that the substrate is directed to the catalytic site. In the same way, molecular dynamics simulations have identified previous binding sites for the enzyme Cephalosporin Acylase, an enzyme that can be used to synthesize the synthetic antibiotic Cephalosporin [7]. A similar process is observed during molecular dynamics simulations of the binding of the inhibitor Benzamidine to Trypsin, identifying sites of increased binding probability [8]. The mathematical models obtained considering steady-state kinetics have focused on multisubstrate models, for different inhibitors or systems with cooperativity, but the approach of precatalytic sites (PCBSs) has not been addressed [9,10]. The mathematical models obtained, considering steady-state kinetics, have focused on multisubstrate models for different inhibitors or systems with cooperativity, but the approach for precatalytic sites (PCBS) has not been addressed. The mathematical models obtained, considering steady-state kinetics, have focused on multisubstrate models for different inhibitors or systems with cooperativity, but the approach for precatalytic sites (PCBS) has not been addressed. Models used for enzymes with mutidomains that are cooperative, such as hemoglobin, employ the Hill equation, which has a sigmoid form but uses the same PCBS scheme [11]. To describe enzyme inhibition, the same scheme is used without PCBSs in which reversible steps representing inhibitor binding are added. If the enzyme processes several substrates, a model for several kinetic schemes is available using the same MM scheme as above. For the inhibition and multisubstrate models, the steady-state kinetics generate a rectangular hyperbole plot indistinguishable from the single-substrate case without an inhibitor, with kinetic parameters that include the factors associated with the inhibitors and the different substrates. However, all of the above models use the Michaelis–Menten scheme formulated in 1913, to which major contributions have been made, including those made by Briggs and Haldane in 1925 through those made by Schnell and Maini in 2003; the contributions are described in detail in the 2019 paper [12]. It is interesting to note that several mathematical papers have dealt with reaction networks using graph and category theory (see for example [13]) and were aimed at general theoretical aspects of reaction dynamics [14]. However, in the previous references the study of the influence of kinetic constants and the application to enzymatic dynamics, remain at a more theoretical/qualitative level than the present work. It is therefore unknown how the presence of PCBSs affects the catalytic capabilities of enzymes or whether this phenomenon could be associated with any enzyme function. To address this question we moved from the simple general scheme without PCBSs or Michaelis–Menten (MM), to one with PCBSs and evaluated how the kinetic parameters are affected by the presence of an increasing number of PCBSs. The kinetic scheme that was used in general (Figure 1a) and from which, considering steady state, the MM equation ($v=\frac{V_{\max }·\left[S\right]}{K_m+\left[S\right]}$) is obtained, includes the concentration of substrate (s), enzyme (e), product (p) and enzyme/substrate complex (es) (a simplified notation for concentration was used). From this model, we obtain an expression for the affinity of the enzyme for the substrate or Michaelis constant ($K_M=\frac{k_2+k_{-1}}{k_1}$) and the maximum possible activity at a given enzyme concentration ($V_{max}=k_2\ast E_{Total}$). From these kinetic parameters, it is possible to calculate the catalytic efficiency $Catalytic efficiency=\frac{V_{\max }}{K_M}$, which is an index of the selectivity of an enzyme towards a specific substrate. Thus, as $V_{m}ax$ increases and $K_M$ decreases for a given substrate, the catalytic efficiency of the enzyme increases with respect to that substrate, resulting in increased selectivity for that substrate. Since this is a relevant index to evaluate the activity of an enzyme, this is a widely used index to evaluate the activity of an enzyme. To evaluate the relationship between the number of PCBSs and the parameters $K_M$ and $V_{max}$, we worked with a kinetic model including i-PCBSs converging at the catalytic site (Figure 1b), and, under steady-state conditions, a mathematical expression for the Michaelis–Menten-type enzyme activity was derived. This dependence was evaluated by numerical simulation, using a program written in Python, which uses the Kinetics library [15,16,17].

2. Materials and Methods

We develop in detail the mathematical framework corresponding to the reaction network from (1b) in Section 3.1, with the main simplifying hypothesis being that the system is at equilibrium, which is justified under the assumption that the substrate concentration is much larger than the enzyme concentration. To simulate kinetic systems with various PCBSs we employed the Python package Kinetics [16], which has been previously successfully used for reactions with various substrates, inhibitors and metabolic pathways for flux control analysis. In our study, we used the “generic reactions” tool of this package to obtain the kinetic parameters of systems with different numbers of PCBSs. An enzyme concentration of 0.0002 mM was used in all simulations, and initial velocities were obtained from the first 10 iterations of the simulation. Kinetic parameters were obtained for substrate concentrations of 0.1, 0.2, 0.5, 5, 10, 100 mM. All units used are referential. However, if the ratio is maintained, they can be scaled to the units used experimentally; therefore, all concentration values will be considered as mM. Equivalent PCBSs with equal binding kinetic constants $k_j^i$ (j can take the values 1 and 2) and equal dissociation constants $k_{-j}^i$ (j can take the values 1 and 2) were considered in the simulations. Different conditions were evaluated for the kinetic constants, but the value of the dissociation constants was kept lower than the complex formation kinetic constants $k_{-1}^i=k_{-2}^i=0.01$, and the condition without PCBSs was simulated as a control. For all conditions evaluated, the simulation generates the parameters $V_{max}$ and $K_M$, which are obtained by calculation with the constants used. For

Table 1. Numerical simulation of enzyme kinetics for ${k_2^i=k}_1^i>k_{cat}$. For the simulations, the kinetic constants of substrate binding $k_1^i=10$, dissociation constants $k_{-1}^i=0.01$ and the catalytic constant with $k_{cat}=2$ at an enzyme concentration of 0.0002 mM and substrate concentration of 0.1, 0.2, 0.5, 5, 10, 100 mM were used. For the analysis of kinetics, the slope of the first 10 points for each substrate concentration was taken to obtain the kinetic parameters from the reciprocal doublings.

Kinetic Parameters	Michaelis–Menten *	$\mathit{i}=1$	$\mathit{i}=2$	$\mathit{i}=3$	$\mathit{i}=4$	$\mathit{i}=5$
$V_{max}$	$4\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.330\times {10}^{-4}$	$3.30\times {10}^{-4}$
$K_M$	$20.1\times {10}^{-2}$	$17.1\times {10}^{-2}$	$8.64\times {10}^{-2}$	$5.76\times {10}^{-2}$	$4.32\times {10}^{-2}$	$3.45\times {10}^{-2}$
Catalytic efficiency	$19.2\times {10}^{-4}$	$19.2\times {10}^{-4}$	$38.3\times {10}^{-4}$	$57.4\times {10}^{-4}$	$76.5\times {10}^{-4}$	$95.6\times {10}^{-4}$

* Numerical simulation without PCBS.

, the condition (a) $k_1^i=k_2^i>k_{cat}$ (with values of 10,10 and 2, respectively) was considered. For

Table 2. Numerical simulation of enzyme kinetics for ${k_{cat}>k}_1^i=k_2^i$. For the simulations, the kinetic constants of substrate binding $k_1^i=k_2^i=2$, dissociation constants $k_{-1}^i=0.01$ and the catalytic constant with $k_{cat}=10$ at an enzyme concentration of 0.0002 mM and substrate concentration of 0.1, 0.2, 0.5, 5, 10, 100 mM are used. For the analysis of kinetics, the slope of the first 10 points for each substrate concentration was taken to obtain the kinetic parameters from the reciprocal doublings.

Kinetic Parameters	Michaelis–Menten *	$\mathit{i}=1$	$\mathit{i}=2$	$\mathit{i}=3$	$\mathit{i}=4$	$\mathit{i}=5$
$V_{max}$	$2.00\times {10}^{-3}$	$3.32\times {10}^{-4}$	$3.32\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.31\times {10}^{-4}$
$K_M$	$505\times {10}^{-2}$	$86.6\times {10}^{-2}$	$43.3\times {10}^{-2}$	$28.8\times {10}^{-2}$	$21.6\times {10}^{-2}$	$17.3\times {10}^{-2}$
Catalytic efficiency	$3.97\times {10}^{-4}$	$3.83\times {10}^{-4}$	$7.67\times {10}^{-4}$	$11.5\times {10}^{-4}$	$15.3\times {10}^{-4}$	$19.1\times {10}^{-4}$

* Numerical simulation without PCBS.

, the condition (b) $k_{cat}>k_1^i=k_2^i$ (with values of 10, 2 and 2, respectively) was considered, and, for

Table 3. Numerical simulation of enzyme kinetics for ${k_{cat}>k}_1^i>k_2^i$. For the simulations, the kinetic constants of substrate binding $k_1^i=6$, $k_2^i=2$, dissociation constants $k_{-1}^i=0.01$ and the catalytic constant with $k_{cat}^i=10$ at an enzyme concentration of 0.0002 mM and substrate concentration of 0.1, 0.2, 0.5, 5, 10, 100 mM were used. For the analysis of kinetics, the slope of the first 10 points for each substrate concentration was taken to obtain the kinetic parameters from the reciprocal doublings.

Kinetic Parameters	Michaelis–Menten *	$\mathit{i}=1$	$\mathit{i}=2$	$\mathit{i}=3$	$\mathit{i}=4$	$\mathit{i}=5$
$V_{max}$	$20.0\times {10}^{-4}$	$3.32\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.31\times {10}^{-4}$	$3.31\times {10}^{-4}$
$K_M$	$505\times {10}^{-2}$	$28.9\times {10}^{-2}$	$14.4\times {10}^{-2}$	$9.63\times {10}^{-2}$	$7.22\times {10}^{-2}$	$3.46\times {10}^{-2}$
Catalytic efficiency	$3.97\times {10}^{-4}$	$11.5\times {10}^{-4}$	$23.0\times {10}^{-4}$	$34.0\times {10}^{-4}$	$46.0\times {10}^{-4}$	$96.6\times {10}^{-4}$

* Numerical simulation without PCBS.

, (c) $k_{cat}>k_1^i>k_2^i$ (with values of 10, 6 and 2, respectively) was considered. For Figure 2, in addition to the conditions evaluated in the tables, three extra conditions were tested: (d) $k_{cat}>k_2^i>k_1^i$, (e) $k_1^i>k_2^i>k_{cat}$ and (f) $k_2^i>k_1^i>k_{cat}$. The Python program to simulate each condition is accessible at [16].

3. Results

3.1. Steady-State Kinetics for an Enzyme with Several PCBSs

From scheme (1b), the species notation was changed to differentiate the free enzyme and substrate (e + s) from the enzyme–substrate complex (es). Thus, the complex c formed by the ligand bound to the i-sth PCBS is $c^i$, and the complex formed by the ligand bound to the catalytic site is called $c^{*}$. This change in notation was not incorporated in the schematic in (1b) to show similarity to the MM model. Based on the schematic in Figure 1b and according to the rate law, the change in the concentration of each species can be expressed as:

$$\frac{ds}{dt}=\sum _i{k}_{-1}^i{c}^i-\sum _i{k}_1^{i}e·s,$$

(1)

$$\frac{d{c}^i}{dt}=k_1^{i}e·s-k_{-1}^i{c}^i-k_2^i{c}^i+k_2^i{c}^{*},$$

(2)

$$\frac{d{c}^{*}}{dt}=\sum _i{k}_2^i{c}^i-\sum _i{k}_2^i{c}^{*}-k_3{c}^{*},$$

(3)

$$\frac{dp}{dt}=k_3{·c}^{*}.$$

(4)

Under the assumption that substrate concentration is much larger than enzyme concentration ($s\gg e$), we can work with the steady-state regime approximation of our reaction. In this case, we can then work assuming constant velocities, and we have that the concentrations of the enzyme substrate complex at each PCBS ($c^i$) and at the catalytic site ($c^{*}$) do not change. This is expressed as follows:

$$\frac{d{c}^i}{dt}\cong 0,\frac{d{c}^{*}}{dt}\cong 0.$$

(5)

Furthermore, we have the following equation, representing the mass balance for the enzyme:

$$e+\sum _i{c}^i+c^{*}=E_T,$$

(6)

where $E_T$ is the total molar concentration of the enzyme. The following Michaelis–Menten type equation is obtained by solving the system of Equations (2), (3) and (6) after expressing each equation as a function of $c^{*}$ to replace it in Equation (4).

$$\frac{dp}{dt}=\frac{k_3\frac{Q}{{\sum }_i{Q}_i+Q}{E}_{T}s}{\frac{1}{{\sum }_i{Q}_i+Q}+s}$$

(7)

where Q and $Q_i$ are:

$$Q=\frac{{\sum }_i\frac{k_1^i{k}_2^i}{k_{-1}^i+k_2^i}}{{\sum }_i\frac{k_{-2}^i{k}_1^i}{k_1^i+k_2^i}+k_3}$$

(8)

$$Q_i=\frac{k_1^i}{k_{-1}^i+k_2^i}+\left(\frac{k_{-2}^i}{k_{-1}^i+k_2^i}\right)\left(\frac{{\sum }_i\frac{k_1^i{k}_2^i}{k_{-1}^i+k_2^i}}{{\sum }_i\frac{k_{-2}^i{k}_1^i}{k_1^i+k_2^i}+k_3}\right)$$

(9)

Under these considerations, with a total of i PCBSs (Figure 1b), the enzyme kinetic parameters $K_M$ (11) and $V_{max}$ (10) adopt more complex forms than for the kinetic scheme without PCBSs (Figure 1a). This is analogous to the equation obtained (Appendix A.2) for two PCBSs.

$$V_{max}=k_3\frac{Q}{{\sum }_i{Q}_i+Q}{E}_T$$

(10)

$$K_M=\frac{1}{{\sum }_i{Q}_i+Q}$$

(11)

If we consider the kinetic constants $k_j^i>0$ to be fixed, the factors Q and $Q_i$ increase with the number of PCBSs. According to (10) and (11), both $V_{max}$ and $K_M$ decrease asymptotically with the number of PCBSs, to a minimum value that is determined by the values of the kinetic constants. However, the decrease in $K_M$ is sharper than the decrease in $V_{max}$ because the latter is smoothed by the Q factor at the numerator in (10). It is also interesting to note that for this model the substrate specificity, which is determined by the ratio $V_{max}/K_M=k_3{E}_{T}Q$ (using (10) and (11)) increases as a function of Q, which increases with the number of PCBSs. As it is proportional to Q, then again we find that, for enzymes with several PCBSs, the experimental determination would give kinetic parameters lower than predicted by the simple model without PCBSs.

For an enzyme with $i=3$ PCBSs, the kinetic parameters of the enzyme are determined by the following expressions:

$$v_{max}=k_3\frac{Q}{Q+Q_1+Q_2+Q_3}{E}_T$$

(12)

$$K_M=\frac{1}{Q+Q_1+Q_2+Q_3}$$

(13)

where:

$$Q=\frac{\frac{k_1^1{k}_2^1}{k_{-1}^1+k_2^1}+\frac{k_1^2{k}_2^2}{k_{-1}^2+k_2^1}+\frac{k_1^3{k}_2^3}{k_{-1}^3+k_2^3}}{k_3+\frac{k_{-2}^1{k}_{-1}^1}{k_{-1}^1+k_2^1}+\frac{k_{-2}^2{k}_{-1}^2}{k_{-1}^2+k_2^2}+\frac{k_{-2}^3{k}_{-1}^3}{k_{-1}^3+k_2^3}}$$

(14)

and:

$$Q_1=\frac{k_1^1}{k_{-1}^1+k_2^1}+\frac{k_{-2}^1}{k_{-1}^1+k_2^1}Q$$

(15)

$$Q_2=\frac{k_1^2}{k_{-1}^2+k_2^2}+\frac{k_{-2}^2}{k_{-1}^2+k_2^2}Q$$

(16)

$$Q_3=\frac{k_1^3}{k_{-1}^3+k_2^3}+\frac{k_{-2}^3}{k_{-1}^3+k_2^3}Q$$

(17)

Due to the complexity of the system of equations, a numerical simulation was used to evaluate the relationship between the number of PCBSs and the kinetic parameters.

3.2. Numerical System Simulation with PCBS

To simulate kinetic systems with various PCBSs, we used a Python package that has been used to simulate reactions with various substrates, inhibitors and metabolic pathways for flux control analysis [15]. In our study, we used the “generic reactions” tool of this package to obtain the kinetic parameters of systems with different numbers of PCBSs [16] if equivalent PCBSs with equal binding kinetic constants $k_1^i$ and equal dissociation constants $k_2^i$ are considered. For Table 1, we considered equal PCBSs much more affine than the catalytic site ($k_1^i=k_2^i>k_{cat}^i\gg k_{-1}^i=k_{-2}^i$) to the substrate; on the other hand, for Table 2, we considered PCBSs less affine than the catalytic site ($k_{cat}^i>k_1^i=k_2^i\gg k_{-1}^i=k_{-2}^i$). As we observed when comparing the blue and green curve (Figure 2), for a $k_{cat}$ lower than $k_1$ and $k_2$ (blue line), the system reaches a maximum for four PCBSs, unlike the one with a $k_{cat}$ higher than $k_1$ and $k_2$ (green line), which does not reach saturation for the number of PCBSs studied. On the kinetic constants $k_1$ and $k_2$, for equal $k_{cat}$ ($k_{cat}=10$), curves b, c and d (the orange, green and red lines), only the system with $k_1>k_2$ shows an increase in the catalytic efficiency, mainly for PCBSs=5, overlapping the curves for the other conditions (orange and red line). On the other hand, for a lower $k_{cat}$ ($k_{cat}$=1) than $k_1$ and $k_2$ (the purple and brown lines), $k_1>k_2$ or $k_2>k_1$ generates similar curves, overlapping in the graph, which shows that for these values of kinetic constants the studied condition ($k_1>k_2$ or $k_2>k_1$) is not relevant.

3.3. Dependence of Catalytic Efficiency on PCBS Number

Numerical simulation was used to obtain the product concentration of generic enzyme-catalyzed reactions with and without PCBSs. The values of $V_{max}$, $K_M$ and the catalytic efficiency were obtained under different values of kinetic constants. As shown in Table 1, Table 2 and Table 3, under the tested conditions, $V_{max}$ decreases rapidly to a minimum value with an increasing number of PCBSs. For $K_M$, the same trend is observed but with a sharper decrease with respect to $V_{max}$. Since the catalytic efficiency is the ratio between $K_{cat}$ and $K_M$, this parameter is a determinant of substrate selectivity and for comparing enzymes. Our results indicate that this parameter increases with the number of PCBSs for all of the systems studied (Figure 2). As observed in the conditions studied, the values of $k_1,k_2\ge k_{cat}$ generate a greater increase in catalytic efficiency. If $k_{cat}\ge k_1,k_2$ (b, c and d), the greatest increase in efficiency is obtained with $k_1>k_2$ (c); furthermore, if $k_1>k_2$, the system shows the same behavior (b and d).

4. Discussion

Enzymes are amino acid polymers that accelerate chemical reactions by several orders of magnitude under mild environmental conditions. The expression of MM models this ability well with an equation that is derived from a simple scheme that considers two stages: the first is binding to the catalytic site, and the second is catalysis (Figure 1a). To solve these kinetic equations, we work in a stationary regime and with initial velocities such that the second stage is irreversible. From this expression, the parameters $K_M$ and $V_{max}$ are obtained, which allow for characterizing the properties of an enzyme. However, the MM equation simplifies the first stage by not considering the substrate path from the initial binding site to the catalytic site. According to molecular simulation studies with different systems, the substrate could access the catalytic site by different pathways from several possible PCBSs. The number of PCBSs or their affinity could determine the enzyme activity, which would explain, for example, the effect on enzyme activity of some mutations far from the catalytic site. Some researchers have already adopted this approach and consider that residues far from the catalytic site may be of interest for designing enzymes with improved properties [17]. Considering this theoretical approach, on the basis of the diagram in Figure 1b, an expression under a steady-state regime of the MM type was obtained for monosubstrate enzymes with different numbers of PCBSs. The model establishes a number i of routes of a PCBS leading to the catalytic site with reversible steps, which are determined by their kinetic constants. After solving Equations (1)–(4), an undistinguishable expression of the MM equation was obtained, in which the kinetic parameters $K_M$ and $V_{max}$ are determined in complex form by the ratios of kinetic constants Q and $Q_i$ in (8) and (9). Considering the complexity of these expressions, a kinetic parameter neighborhood restricted to $k_1^i=k_2^i$ was explored (Appendix A). Under these restrictions, the catalytic efficiency was increasing with the number of PCBSs. If the behavior holds for a larger neighborhood, within the parameters accessible to the model, the overall expression could behave in the same way. For i PCBSs, the kinetic parameters decrease as a function of the factors Q and $Q_i$ in (8) and (9), as the number of PCBSs increases. According to the obtained equations, the experimental $K_M$ and $V_{max}$ parameters obtained for monosubstrate enzymes with several PCBSs correspond to the apparent parameters. This aspect, although real, cannot be appreciated from the experimental data because the model produces the same rectangular hyperbole shape. When analyzing the ratio between $k_{cat}$ and $K_M$ (catalytic efficiency) as a function of the number of PCBSs, it is observed that it increases with the number of PCBSs; the higher the number of PCBSs, the higher the catalytic efficiency. The absence of experimentally measured kinetic constants for the enzymatic reaction steps prevents us from corroborating some of our predictions. However, the $K_M$ and $V_{max}$ parameters are known for mutants in different regions far from the catalytic site and that do not affect the three-dimensional structure [18]. It has been observed that mutations in solvent contact regions of the enzyme $\beta$-lactamase, an enzyme that degrades $\beta$-lactam antibiotics, do not affect its activity as measured in relation to the sensitivity of the organism to the antibiotic [19]. However, some mutations in the region near the catalytic site can affect activity by making the organism more sensitive to the antibiotic. This effect is evident for some mutants distant to the catalytic site of the $\beta$-glycosidase enzyme with altered $k_{cat}$ and $K_M$ parameters [20]. In general, for this enzyme, 10 mutations distant to the catalytic site modify $K_M$ and $k_{cat}$, thereby decreasing the catalytic efficiency. According to our model, mutations in PCB that decrease or reduce the affinity of these sites for the substrate decrease catalytic efficiency. To explore some neighborhoods of the parameter space, numerical simulations of the kinetic steps were performed, allowing us to obtain the state of the system at each simulated step and the kinetic parameters with the pCBS Kinetics program [16]. As a control for each condition, the kinetic parameters were calculated in the systems with the MM scheme (Figure 1a), obtaining the same value for the simulation and the calculated one. Six conditions of kinetic constants were evaluated, considering different relationships between the constants that determine the formation of the substrate/PCBSs complex ($k_1^i$), constants that determine the passage of the substrate from the PCB to the catalytic site, and the one that directly determines the formation of product ($k_{cat}$ or $K_3$). For all systems, it is observed that KM and $V_{max}$ decrease with an increasing number of PCBSs (Table 1, Table 2 and Table 3), and the catalytic efficiency increases. For some conditions, such as a $k_{cat}$ lower than $k_1^i$ and $k_2^i$, the increase in the catalytic efficiency is relevant, which could explain the effect of mutations not directly connected to the catalytic site and which can determine the catalytic efficiency.

5. Conclusions

From the studies carried out, an MM-type expression was obtained for a kinetic scheme with several PCBSs, in which the kinetic parameters depend in a complex way on the kinetic constants. By including several PBCSs, the factors Q and $Q_i$ are obtained, which do not exist in the MM model and that make the KM and $V_{max}$ decrease as the number of PCBSs increases. Catalytic efficiency is determined by structural factors that define the (non-stochastic) pathways that the substrate must follow to reach the catalytic site. This is evident by observing that the catalytic efficiency increases linearly with the number of PCBSs up to four PCBSs. Due to the complex expression of Q and $Q_i$, the dynamic process could determine that some conditions studied are equivalent in spite of the different ratios of the constants. According to the model, it would be interesting to have in vitro studies or simulations to evaluate the predictions and to introduce kinetic constants consistent with an in vitro model.

6. Patents

This section is not mandatory but may be added if there are patents resulting from the work reported in this manuscript.