A General Single-Node Second-Order Dirichlet Boundary Condition for the Convection–Diffusion Equation Based on the Lattice Boltzmann Method

Abstract

A general single-node second-order Dirichlet boundary condition for curved boundaries for the convection–diffusion equation based on the lattice Boltzmann method has been developed. The boundary condition simply utilizes the bounce back rule for the temperature distribution and linear interpolation. The developed boundary condition is quite general and stable. The asymptotic analysis indicates that the proposed boundary scheme is of second-order accuracy. The comparison in terms of $L_2$-norm between the simulation results and the analytical solutions confirms that it is indeed second-order accurate for 2D and 3D symmetric flows comprising straight and curved boundaries. Moreover, the Nusselt numbers for a spherical particle in uniform flow obtained by current simulations agree very well with the predictions of empirical correlations and the data of previous direct numerical simulations with a maximal relative deviation within 8%.

1. Introduction

Particulate multiphase flows are ubiquitous in nature and industrial applications, e.g., volcanic eruption [1,2], biomass gasification [3,4] and nanotechnology [5,6]. To model these flows at the most detailed level with the so-called direct numerical simulations (DNSs), appropriate boundary conditions are required to account for the interactions between particles and a fluid, for example, Dirichlet boundary conditions for velocity and temperature. Thus, numerically stable and accurate boundary conditions are of great importance for the DNS methods.

Among all the DNS methods available, the lattice Boltzmann method (LBM) provides an alternative approach to solve the Navier–Stokes and convection–diffusion equations. The widely used second-order Dirichlet boundary schemes are interpolation-based boundary methods [7,8,9] and immersed boundary methods [10,11]. However, these boundary schemes are not purely local since they require at least two fluid nodes to achieve second-order accuracy. For dense suspensions, the number of fluid nodes between particles may not be sufficient for the interpolation-based boundary schemes when the gap between particles is small. In this case, the boundary schemes only have first-order accuracy. Therefore, a single-node Dirichlet boundary condition which still has second-order accuracy is essential for the application of the lattice Boltzmann method. To this end, Guo et al. [12] developed a non-equilibrium extrapolation method for the LBM. The comparison between the simulation results and the analytical solution for the porous plate problem with a temperature gradient indicates that the boundary condition is second-order accurate. Tang et al. [13] extended the boundary method of Guo et al. [12] for the internal-energy-based double population model. The simulation results for the thermal channel flow are in good agreement with the simulation results using the finite volume method. However, the sharp interface of the boundaries cannot be preserved since the boundary scheme developed by Guo et al. [12] is independent of the exact location of the boundaries. Huang and Yong [14] proposed a single-node second-order Dirichlet boundary condition for straight boundaries by employing an asymptotic analysis technique. However, the boundary method is only first-order accurate for curved boundaries. Zhang et al. [15] developed a single-node Dirichlet boundary condition for the convection–diffusion equation based on the lattice Boltzmann method. They modified the equilibrium temperature distribution by introducing a first-order spatial derivative of the fluid temperature. The boundary scheme is shown to be second-order accurate for straight and circular walls. Ginzburg and Silva [16], on the other hand, proposed a boundary approach called A-LSOB to enhance the locality and accuracy of single-node Dirichlet boundary condition. However, these two boundary conditions are very complicated due to the calculation of spatial derivative of the fluid temperature. Zhang et al. [17] developed a general single-node second-order Dirichlet boundary condition for curved boundaries for the MRT-LBM. A free parameter is introduced which is in the range [0, $\min \left(1,2\Delta \right)$], where $\Delta$ is the scaled distance between the wall node and the nearest fluid node. However, the choice of the free parameter has to be more careful for inclined and curved boundaries since $\Delta$ ranges from 0 to 1 in these cases. The free parameter may be valid for one boundary node but invalid for another.

In this work, we extend the range of validity of Zhang et al.’s [17] single-node second-order Dirichlet boundary condition to [0, $2\Delta$] for the regular lattice Boltzmann method. Therefore, the free parameter can be arbitrarily chosen within this range. The bounce back rule and linear interpolation are used to construct the second-order boundary scheme. The Dirichlet boundary condition is independent of the lattice model and collision operator. Moreover, the boundary condition proposed here is quite general, stable and suitable for inclined and curved boundaries.

2. Numerical Methods

2.1. The Convection–Diffusion Equation

The convection–diffusion equation is given as [18]:

$$\frac{\partial \varphi }{\partial t}+\frac{\partial }{\partial x_{\beta }}\left(v_{\beta }\varphi \right)=\frac{\partial }{\partial x_{\alpha }}\left(D_{\alpha \beta }\frac{\partial \varphi }{\partial x_{\beta }}\right)$$

(1)

where $\varphi$ is a scalar variable which represents the temperature or mass concentration. $v_{\beta }$ and $D_{\alpha \beta }$ are the fluid velocity component in the $x_{\beta }$ direction and diffusion coefficient, respectively. The Dirichlet boundary condition is expressed as

$$\varphi ={\varphi }_s$$

(2)

where ${\varphi }_s$ is the temperature or mass concentration at the boundary.

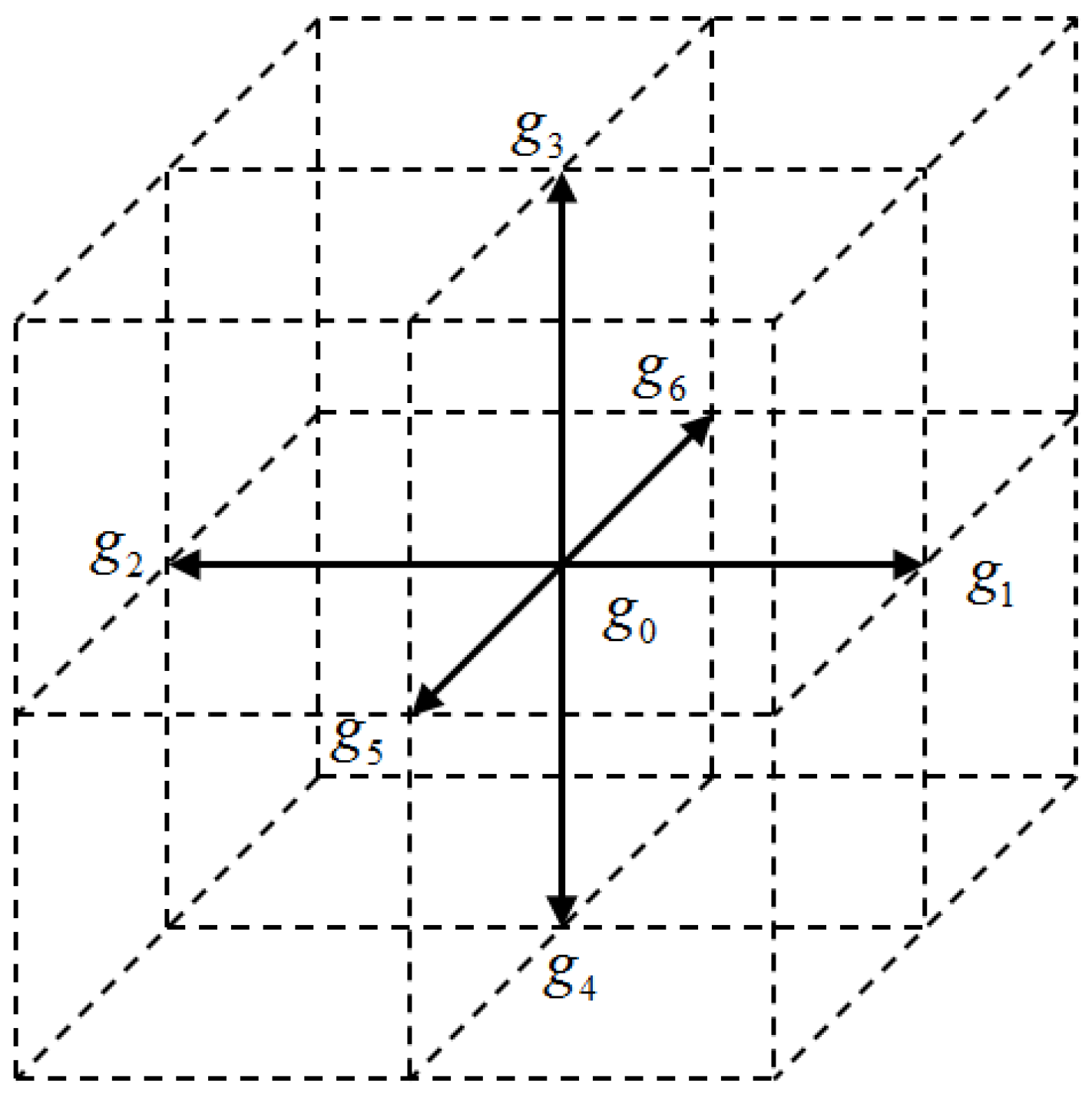
2.2. The Lattice Boltzmann Model

The lattice Boltzmann equation for the convection–diffusion equation with a Bhatnagar–Gross–Krook (BGK) [19] collision model is as follows:

$$g_i\left(\overrightarrow{x}+{\overrightarrow{c}}_i\Delta t,t+\Delta t\right)=g_i\left(\overrightarrow{x},t\right)-\frac{1}{{\tau }_c}\left[g_i\left(\overrightarrow{x},t\right)-g_i^{eq}\left(\overrightarrow{x},t\right)\right]$$

(3)

where $g_i$ and $g_i^{eq}$ are the temperature distribution function and equilibrium temperature distribution function, respectively. ${\overrightarrow{c}}_i$ is the lattice speed, where ${\overrightarrow{c}}_i={\overrightarrow{e}}_{i}c$ ($c=\Delta x/\Delta t$). ${\tau }_c$ is the single relaxation time. The D3Q7 lattice (Figure 1) is given by

$${\overrightarrow{e}}_i=\left\{\begin{array}{l}\left(0,0,0\right), i=0\\ \left(\pm 1,0,0\right),\left(0,\pm 1,0\right),\left(0,0,\pm 1\right), i=1\dots 6\end{array}\right.$$

(4)

The equilibrium temperature distribution is defined as:

$$g_i^{eq}=w_{i,c}\left(1+\frac{{\overrightarrow{e}}_i\cdot \overrightarrow{u}}{{\eta }_{D}c}\right)\varphi$$

(5)

$$w_{i,c}=\left\{\begin{array}{l}\frac{1}{4}, i=0\\ \frac{1}{8}, i=1\dots 6\end{array}\right.$$

(6)

where ${\eta }_D$ is equal to $\frac{1}{4}$. In the multiple-relaxation-time (MRT) model proposed by [18], the evolution equation for the temperature distribution becomes

$$g_i\left(\overrightarrow{x}+{\overrightarrow{c}}_i\Delta t,t+\Delta t\right)-g_i\left(\overrightarrow{x},t\right)=-{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{ij}\left[g_j\left(\overrightarrow{x},t\right)-g_j^{eq}\left(\overrightarrow{x},t\right)\right]}$$

(7)

where $N$ denotes the total number of discrete velocities. $M$ is the transformation matrix and given by

$$M=\left(\begin{array}{lllllll}1& 1& 1& 1& 1& 1& 1\\ 0& 1& -1& 0& 0& 0& 0\\ 0& 0& 0& 1& -1& 0& 0\\ 0& 0& 0& 0& 0& 1& -1\\ 6& -1& -1& -1& -1& -1& -1\\ 0& 2& 2& -1& -1& -1& -1\\ 0& 0& 0& 1& 1& -1& -1\end{array}\right)$$

(8)

The relaxation time matrix $S$ is defined as

$$S^{-1}=\left(\begin{array}{lllllll}{\tau }_0& 0& 0& 0& 0& 0& 0\\ 0& {\tau }_{\alpha \alpha }& {\tau }_{\alpha \beta }& {\tau }_{\alpha \lambda }& 0& 0& 0\\ 0& {\tau }_{\alpha \beta }& {\tau }_{\beta \beta }& {\tau }_{\beta \lambda }& 0& 0& 0\\ 0& {\tau }_{\alpha \lambda }& {\tau }_{\beta \lambda }& {\tau }_{\lambda \lambda }& 0& 0& 0\\ 0& 0& 0& 0& {\tau }_4& 0& 0\\ 0& 0& 0& 0& 0& {\tau }_5& 0\\ 0& 0& 0& 0& 0& 0& {\tau }_6\end{array}\right)$$

(9)

where $\alpha$, $\beta$, $\lambda$ are the components of the Cartesian coordinates. The non-zero value of the off-diagonal components in the relaxation matrix accounts for anisotropic diffusion. The relaxation coefficients can be calculated using the diffusion coefficient

$${\tau }_{\alpha \beta }=\frac{1}{2}{\delta }_{\alpha \beta }+\frac{\Delta t}{{\eta }_D\Delta x^2}{D}_{\alpha \beta }$$

(10)

where ${\delta }_{\alpha \beta }$ is the Kronecker’s delta. The macroscopic fluid temperature can be obtained via

$$\varphi ={\displaystyle {\sum }_i{g}_i}$$

(11)

The LBE can be split into two steps, namely, the collision and streaming operations.

$${\tilde{g}}_i\left(\overrightarrow{x},t\right)=g_i\left(\overrightarrow{x},t\right)-{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{ij}\left[g_j\left(\overrightarrow{x},t\right)-g_j^{eq}\left(\overrightarrow{x},t\right)\right]}$$

(12)

$$g_i\left(\overrightarrow{x}+{\overrightarrow{c}}_i\Delta t,t+\Delta t\right)={\tilde{g}}_i\left(\overrightarrow{x},t\right)$$

(13)

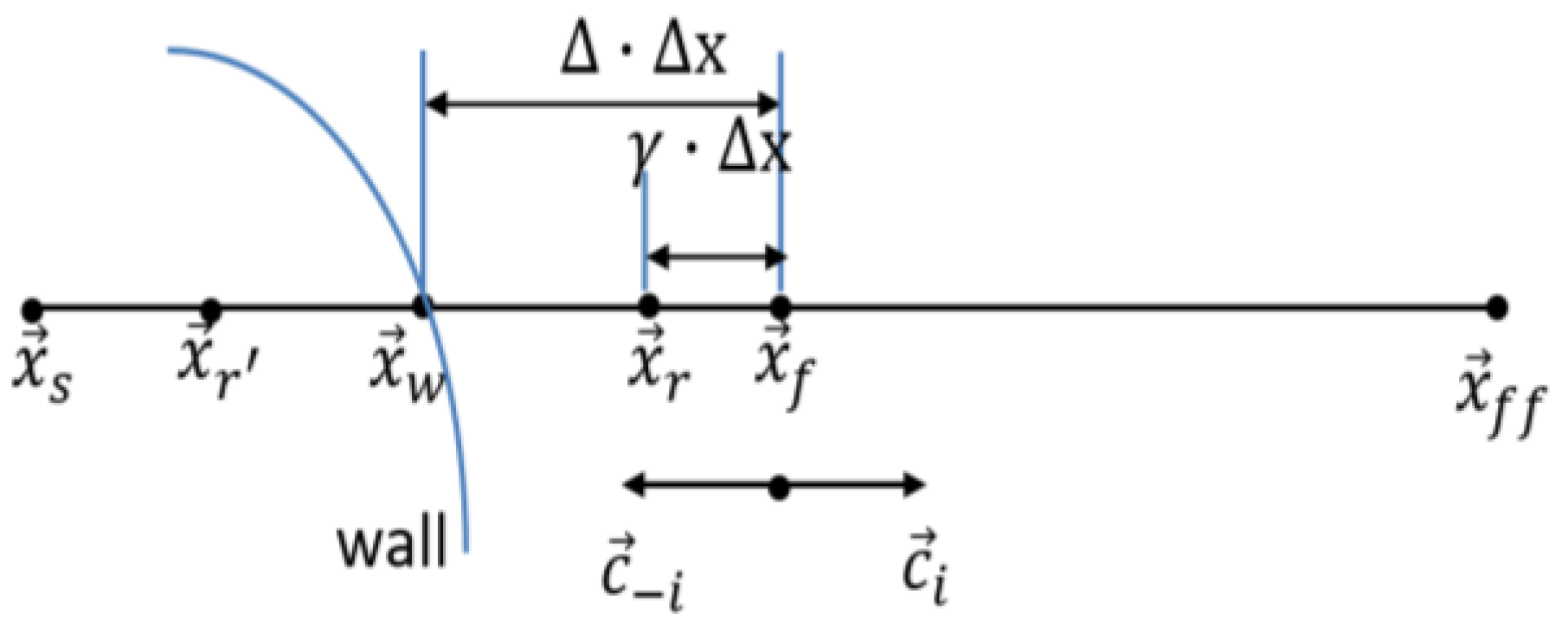
3. Dirichlet Boundary Condition

Figure 2 illustrates a wall located between two lattice nodes. To describe the relative position of the wall node, a coefficient is defined as

$$\Delta =\frac{\left|{\overrightarrow{x}}_f-{\overrightarrow{x}}_w\right|}{\left|{\overrightarrow{x}}_s-{\overrightarrow{x}}_f\right|}$$

(14)

In addition, the points ${\overrightarrow{x}}_r$ and ${\overrightarrow{x}}_{r^{\prime }}$ are defined, and can be calculated as

$${\overrightarrow{x}}_r={\overrightarrow{x}}_f-\gamma \Delta x{\overrightarrow{e}}_i$$

(15)

$$2{\overrightarrow{x}}_w={\overrightarrow{x}}_{r^{\prime }}+{\overrightarrow{x}}_r$$

(16)

where $\gamma \ge 0$. Therefore, the two points (${\overrightarrow{x}}_r$ and ${\overrightarrow{x}}_{r^{\prime }}$) are symmetric with respect to the boundary point. Based on Equations (14)–(16), we have

$$\left|{\overrightarrow{x}}_{r^{\prime }}-{\overrightarrow{x}}_f\right|=\left(2\Delta -\gamma \right)\Delta x$$

(17)

$$\left|{\overrightarrow{x}}_r-{\overrightarrow{x}}_f\right|=\gamma \Delta x$$

(18)

After the streaming step, the temperature distribution functions at the fluid node nearest to the wall are unknown. To calculate the unknown distributions, an interpolation scheme is used:

$$g_i({\overrightarrow{x}}_f,t+\Delta t)=\frac{1}{1+2\Delta -\gamma }{g}_i({\overrightarrow{x}}_{r^{\prime }},t+\Delta t)+\frac{2\Delta -\gamma }{1+2\Delta -\gamma }{g}_i({\overrightarrow{x}}_{ff},t+\Delta t)$$

(19)

Using Equation (13), we have

$$g_i\left({\overrightarrow{x}}_{ff},t+\Delta t\right)={\tilde{g}}_i\left({\overrightarrow{x}}_f,t\right)$$

(20)

To calculate $g_i\left({\overrightarrow{x}}_{r^{\prime }},t+\Delta t\right)$, the bounce back rule is adopted:

$$g_i^{neq}\left({\overrightarrow{x}}_{r^{\prime }},t+\Delta t\right)=-g_{-i}^{neq}\left({\overrightarrow{x}}_r,t+\Delta t\right)$$

(21)

The equilibrium temperature distributions at ${\overrightarrow{x}}_{r^{\prime }}$ and ${\overrightarrow{x}}_r$ are constructed using the wall temperature and velocity, where

$$g_i^{eq}\left({\overrightarrow{x}}_{r^{\prime }},t\right)=g_i^{eq}\left({\varphi }_s,{\overrightarrow{u}}_w\right),$$

(22)

$$g_{-i}^{eq}\left({\overrightarrow{x}}_r,t\right)=g_{-i}^{eq}\left({\varphi }_s,{\overrightarrow{u}}_w\right).$$

(23)

Thus,

$$g_i\left({\overrightarrow{x}}_{r^{\prime }},t+\Delta t\right)=-g_{-i}\left({\overrightarrow{x}}_r,t+\Delta t\right)+{\eta }_D{\varphi }_s$$

(24)

In Equation (24), $g_{-i}\left({\overrightarrow{x}}_r,t+\Delta t\right)$ is obtained by interpolation:

$$g_{-i}\left({\overrightarrow{x}}_r,t+\Delta t\right)=\gamma g_{-i}\left({\overrightarrow{x}}_s,t+\Delta t\right)+\left(1-\gamma \right)g_{-i}\left({\overrightarrow{x}}_f,t+\Delta t\right)$$

(25)

To calculate $g_{-i}\left({\overrightarrow{x}}_f,t+\Delta t\right)$ in Equation (25), the temporal approximation is applied, where

$$g_{-i}\left({\overrightarrow{x}}_f,t+\Delta t\right)\approx g_{-i}\left({\overrightarrow{x}}_f,t\right)$$

(26)

Recalling Equation (13) and inserting Equations (24)–(26) into Equation (19), we obtain

$$\begin{array}{ll}{g}_i({\overrightarrow{x}}_f,t+\Delta t)& =\frac{1}{1+2\Delta -\gamma }\left(-\left(1-\gamma \right)g_{-i}({\overrightarrow{x}}_f,t)-\gamma {\tilde{g}}_{-i}\left({\overrightarrow{x}}_f,t\right)+{\eta }_D{\varphi }_s\right)\\ & +\frac{2\Delta -\gamma }{1+2\Delta -\gamma }{\tilde{g}}_i({\overrightarrow{x}}_f,t)\end{array}$$

(27)

To ensure the numerical stability, $2\mathsf{\Delta }-\gamma$ and $1-\gamma$ have to be non-negative. Therefore, the constraint for $\gamma$ is [0, $\min \left(1,2\Delta \right)$]. Note that, if we set $l=2\Delta -\gamma$, Equation (27) becomes the boundary condition proposed by Zhang et al. [17] with $l\in \left[\max \left(0,2\Delta -1\right),2\Delta \right]$, which implies that Equation (27) is equivalent to the boundary condition proposed by Zhang et al. [17]. To overcome the shortcoming of Equation (27), we set

$$\gamma =\left\{\begin{array}{l}\gamma , \mathrm{if} 0\le \gamma \le \min (1,2\Delta )\\ 2\Delta -\gamma , \mathrm{if} 1<\gamma \le 2\Delta \end{array}\right.$$

(28)

Equation (28) ensures that the proposed boundary condition (Equation (27)) is always a convex combination of the temperature distributions for γ within the range [0, 2Δ]. Thus, the range of validity of the boundary condition proposed by Zhang et al. [17] is extended which is more suitable for the inclined and curved boundaries. Moreover, the proposed boundary condition is simple and purely local since it only involves one fluid node.

The implementation of the lattice Boltzmann method with the proposed Dirichlet boundary method involves the following steps:

(1)

Calculate the equilibrium temperature distribution function $g_i^{eq}\left(\overrightarrow{x},t\right)$.

(2)

Perform the collision step to calculate ${\tilde{g}}_i\left(\overrightarrow{x},t\right)$.

(3)

Apply domain boundary conditions for the temperature distribution functions and Dirichlet boundary condition for immersed objects and external walls.

(4)

Perform the streaming step $g_i\left(\overrightarrow{x}+{\overrightarrow{c}}_i\mathsf{\Delta }t,t+\mathsf{\Delta }t\right)={\tilde{g}}_i\left(\overrightarrow{x},t\right)$.

(5)

Calculate the fluid temperature $\varphi$.

(6)

Go to step (1) until the calculation is converged.

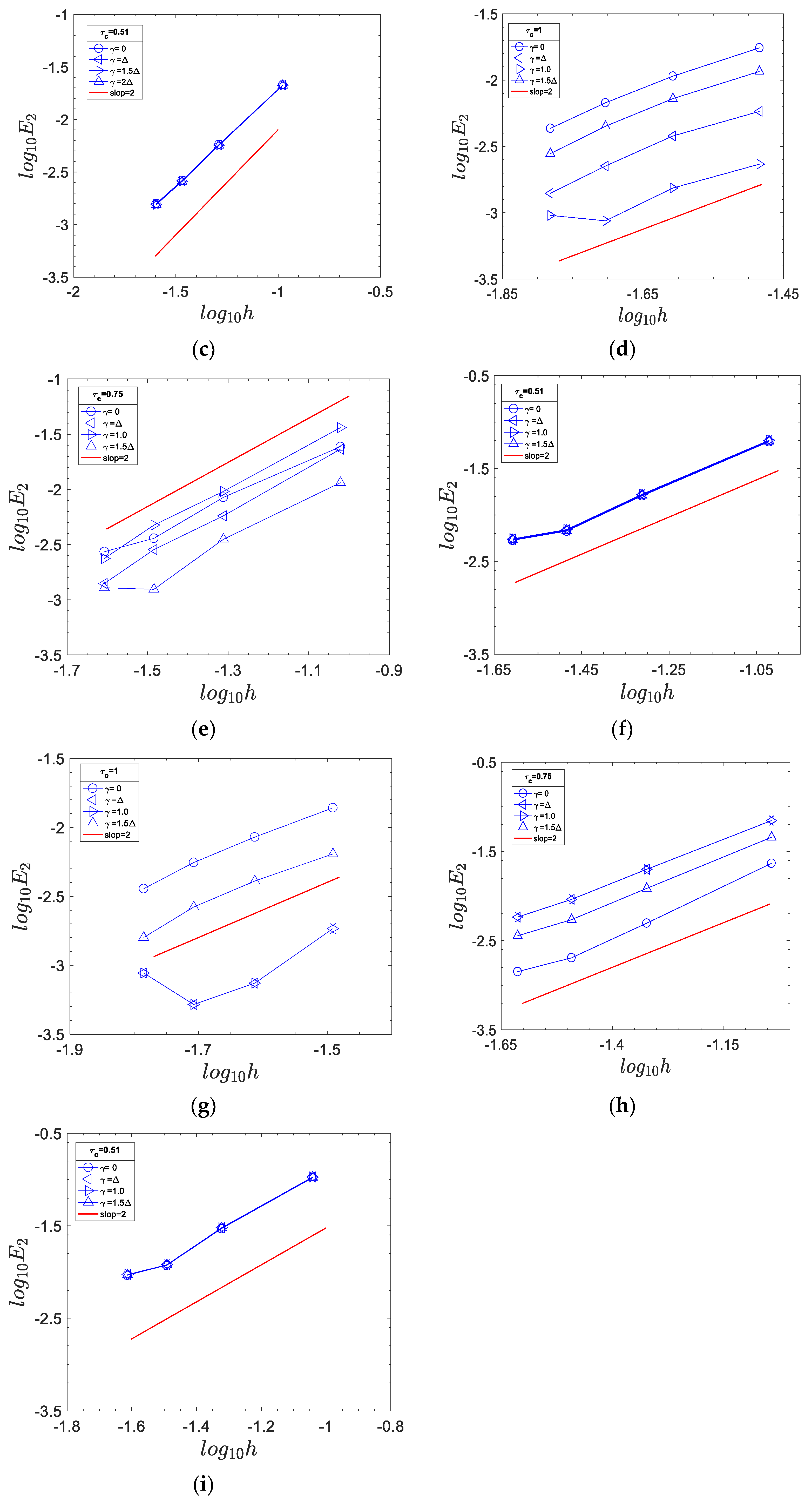
4. Asymptotic Analysis

With the diffusive scaling ($\Delta x\to \epsilon$ and $\Delta t\to {\epsilon }^2$) [20], the evolution equation and equilibrium distribution become

$$g_i(\overrightarrow{x}+{\overrightarrow{e}}_i\epsilon ,t+{\epsilon }^2)-g_i(t,\overrightarrow{x})=-{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{ij}\left[g_j(\overrightarrow{x},t)-g_j^{eq}(\overrightarrow{x},t)\right]}$$

(29)

$$g_i^{eq}(\overrightarrow{x},t)=w_{i,c}\varphi \left(1+\frac{\epsilon \cdot {\overrightarrow{e}}_i\cdot \overrightarrow{u}}{{\eta }_D}\right)$$

(30)

Expanding the temperature distribution function and the fluid temperature $\varphi$ in series of $\epsilon$ up to first order yields:

$$g_i=g_i^{(0)}+g_i^{(1)}\epsilon +\mathrm{O}\left({\epsilon }^2\right)$$

(31)

$$\varphi ={\varphi }^{(0)}+{\varphi }^{(1)}\epsilon +\mathrm{O}\left({\epsilon }^2\right)$$

(32)

According to Equation (11), we have

$${\varphi }^{(m)}={\displaystyle {\sum }_i{g}_i^{(m)}}$$

(33)

Expanding Equation (29) as a series of $\epsilon$ yields:

$$\begin{array}{l}{e}_{i\alpha }\frac{\partial g_i^{\left(0\right)}}{\partial x_{\alpha }}\epsilon +\mathrm{O}\left({\epsilon }^2\right)=\\ -{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{ij}\left[g_j^{\left(0\right)}-w_{j,c}{\varphi }^{\left(0\right)}+\left(g_j^{\left(1\right)}-w_{j,c}{\varphi }^{\left(1\right)}-\frac{w_{j,c}{\varphi }^{\left(0\right)}{\overrightarrow{e}}_j\cdot \overrightarrow{u}}{{\eta }_D}\right)\epsilon \right]}+\mathrm{O}\left({\epsilon }^2\right)\end{array}$$

(34)

Rearranging the terms having the same power of $\epsilon$ for Equation (34), we have

$$g_j^{\left(0\right)}-w_{j,c}{\varphi }^{\left(0\right)}=0$$

(35)

$$e_{i\alpha }\frac{\partial g_i^{\left(0\right)}}{\partial x_{\alpha }}=-{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{ij}\left[g_j^{\left(1\right)}-w_{j,c}{\varphi }^{\left(1\right)}-\frac{w_{j,c}{\varphi }^{\left(0\right)}{\overrightarrow{e}}_j\cdot \overrightarrow{u}}{{\eta }_D}\right]}$$

(36)

With Equations (35) and (36), we can derive the following relationships:

$$g_i^{\left(0\right)}+g_{-i}^{\left(0\right)}={\eta }_D{\varphi }^{\left(0\right)}$$

(37)

$$g_i^{\left(1\right)}+g_{-i}^{\left(1\right)}={\eta }_D{\varphi }^{\left(1\right)}$$

(38)

Assuming that the boundary is located between $\overrightarrow{x}$ and $\overrightarrow{x}+{\overrightarrow{e}}_i\epsilon$, we have

$${\overrightarrow{x}}_f={\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_i\epsilon ={\overrightarrow{x}}_w-\Delta {\overrightarrow{e}}_{-i}\epsilon$$

(39)

Inserting Equation (39) into Equation (27) and applying the Taylor expansion up to first order, we obtain

$$g_i\left({\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_i\epsilon ,t+{\epsilon }^2\right)=g_i^{\left(0\right)}+\epsilon g_i^{(1)}+\Delta \epsilon e_{i\alpha }\frac{\partial g_i^{(0)}}{\partial x_{\alpha }}+\mathrm{O}\left({\epsilon }^2\right)$$

(40)

Moreover, we have

$$\begin{array}{l}{\tilde{g}}_i\left({\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_i\epsilon ,t\right)=g_i\left({\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_i\epsilon ,t\right)-{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{ij}\left[g_j\left({\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_j\epsilon ,t\right)-g_j^{eq}\left({\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_j\epsilon ,t\right)\right]}\\ =g_i^{\left(0\right)}+\epsilon g_i^{(1)}+\Delta \epsilon e_{i\alpha }\frac{\partial g_i^{(0)}}{\partial x_{\alpha }}\\ -{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{ij}\left[g_j^{\left(0\right)}+\epsilon g_j^{(1)}+\Delta \epsilon e_{j\alpha }\frac{\partial g_j^{(0)}}{\partial x_{\alpha }}-w_{j,c}{\varphi }^{\left(0\right)}-\left(w_{j,c}{\varphi }^{\left(1\right)}+\frac{w_{j,c}{\varphi }^{\left(0\right)}{\overrightarrow{e}}_j\cdot \overrightarrow{u}}{{\eta }_D}+\Delta e_{j\alpha }\frac{\partial g_j^{\left(0\right)}}{\partial x_{\alpha }}\right)\epsilon \right]}+\mathrm{O}\left({\epsilon }^2\right)\\ =g_i^{\left(0\right)}+\epsilon g_i^{(1)}+\left(1+\Delta \right)\epsilon e_{i\alpha }\frac{\partial g_i^{(0)}}{\partial x_{\alpha }}+\mathrm{O}\left({\epsilon }^2\right)\end{array}$$

(41)

$$g_{-i}\left({\overrightarrow{x}}_w-\Delta {\overrightarrow{e}}_{-i}\epsilon ,t\right)=g_{-i}^{\left(0\right)}+\epsilon g_{-i}^{(1)}-\Delta \epsilon e_{-i\alpha }\frac{\partial g_{-i}^{(0)}}{\partial x_{\alpha }}+\mathrm{O}\left({\epsilon }^2\right)$$

(42)

$$\begin{array}{l}{\tilde{g}}_{-i}\left({\overrightarrow{x}}_w-\Delta {\overrightarrow{e}}_{-i}\epsilon ,t\right)=g_{-i}\left({\overrightarrow{x}}_w-\Delta {\overrightarrow{e}}_{-i}\epsilon ,t\right)-{\displaystyle \sum _{j=0}^{N-1}{\left(M^{-1}SM\right)}_{-ij}\left[g_j\left({\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_j\epsilon ,t\right)-g_j^{eq}\left({\overrightarrow{x}}_w+\Delta {\overrightarrow{e}}_j\epsilon ,t\right)\right]}\\ =g_{-i}^{\left(0\right)}+\epsilon g_{-i}^{(1)}-\Delta \epsilon e_{-i\alpha }\frac{\partial g_{-i}^{(0)}}{\partial x_{\alpha }}\\ -{\displaystyle \sum _{j=0}^{N-1}}{\left(M^{-1}SM\right)}_{-ij}\left[g_j^{\left(0\right)}+\epsilon g_j^{(1)}+\Delta \epsilon e_{j\alpha }\frac{\partial g_j^{(0)}}{\partial x_{\alpha }}-w_{j,c}{\varphi }^{\left(0\right)}-\left(w_{j,c}{\varphi }^{\left(1\right)}+\frac{w_{j,c}{\varphi }^{\left(0\right)}{\overrightarrow{e}}_j\cdot \overrightarrow{u}}{{\eta }_D}+\Delta e_{j\alpha }\frac{\partial g_j^{\left(0\right)}}{\partial x_{\alpha }}\right)\epsilon \right]+\mathrm{O}\left({\epsilon }^2\right)\\ =g_{-i}^{\left(0\right)}+\epsilon g_{-i}^{(1)}+\left(1-\Delta \right)\epsilon e_{-i\alpha }\frac{\partial g_{-i}^{(0)}}{\partial x_{\alpha }}+\mathrm{O}\left({\epsilon }^2\right)\end{array}$$

(43)

Equation (27) expressed in zeroth order with regard to $\epsilon$ yields

$$g_i^{\left(0\right)}=\frac{2\Delta -\gamma }{1+2\Delta -\gamma }{g}_i^{\left(0\right)}+\frac{1}{1+2\Delta -\gamma }\left(-\left(1-\gamma \right)g_{-i}^{\left(0\right)}-\gamma g_{-i}^{\left(0\right)}+{\eta }_D{\varphi }_s\right)$$

(44)

Using Equation (35), we obtain

$${\varphi }^{\left(0\right)}={\varphi }_s$$

(45)

Therefore, the Dirichlet boundary condition is satisfied by the zeroth-order solution. Considering the terms in ${\epsilon }^1$, we have

$$\begin{array}{l}{g}_i^{\left(1\right)}+\Delta e_{i\alpha }\frac{\partial g_i^{(0)}}{\partial x_{\alpha }}=\frac{2\Delta -\gamma }{1+2\Delta -\gamma }\left(g_i^{(1)}+\left(1+\Delta \right)e_{i\alpha }\frac{\partial g_i^{(0)}}{\partial x_{\alpha }}\right)\\ +\frac{1}{1+2\Delta -\gamma }\left(-\left(1-\gamma \right)g_{-i}^{(1)}+\left(1-\gamma \right)\Delta e_{-i\alpha }\frac{\partial g_{-i}^{(0)}}{\partial x_{\alpha }}-\gamma g_{-i}^{(1)}-\gamma \left(1-\Delta \right)e_{-i\alpha }\frac{\partial g_{-i}^{(0)}}{\partial x_{\alpha }}\right)\end{array}$$

(46)

Using Equations (35) and (36) yields

$$\frac{1}{1+2\Delta -\gamma }\left(g_i^{\left(1\right)}+g_{-i}^{(1)}\right)=\frac{\Delta -\gamma }{1+2\Delta -\gamma }\left(e_{i\alpha }\frac{\partial g_i^{(0)}}{\partial x_{\alpha }}+e_{-i\alpha }\frac{\partial g_{-i}^{(0)}}{\partial x_{\alpha }}\right)$$

(47)

Due to Equations (35) and (38), we obtain

$${\varphi }^{\left(1\right)}=0$$

(48)

Hence, at the boundary Equation (27) recovers the following boundary condition:

$$\varphi ={\varphi }_s+\mathrm{O}\left({\epsilon }^2\right),$$

(49)

which demonstrates that the proposed Dirichlet boundary condition is second-order accurate.

5. Numerical Simulations

In the following, the newly proposed Dirichlet boundary condition is used to simulate 2D channel flow, 2D cylindrical Couette flow, 3D circular pipe flow and a fluid flowing over a sphere to assess the accuracy of the boundary scheme. In the present work, only isotropic diffusion is considered. In addition, ${\tau }_0=0$ and ${\tau }_l=1$ ($l$ = 3, 4 in 2D and 4, 5, 6 in 3D) are used in all the simulations.

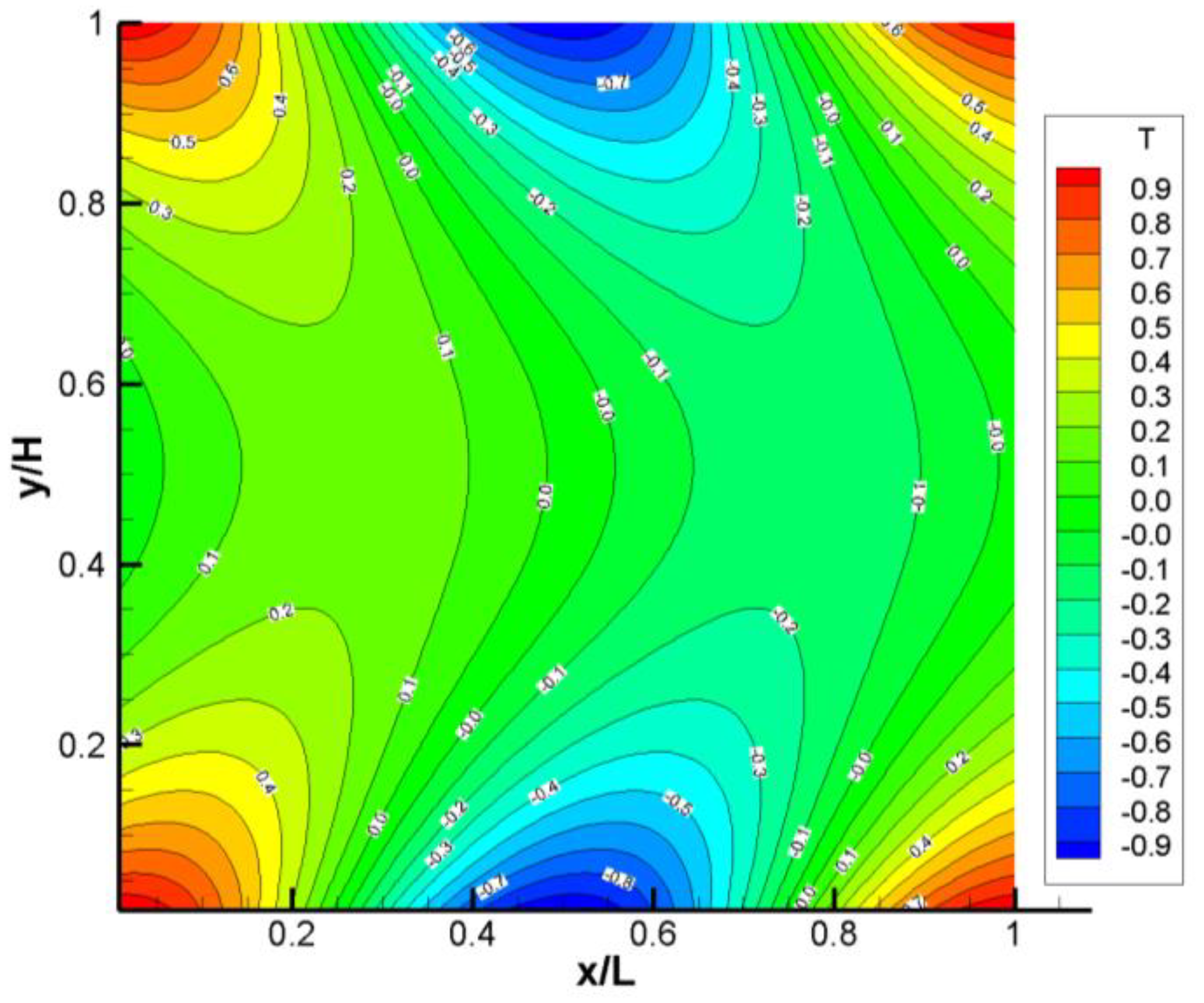
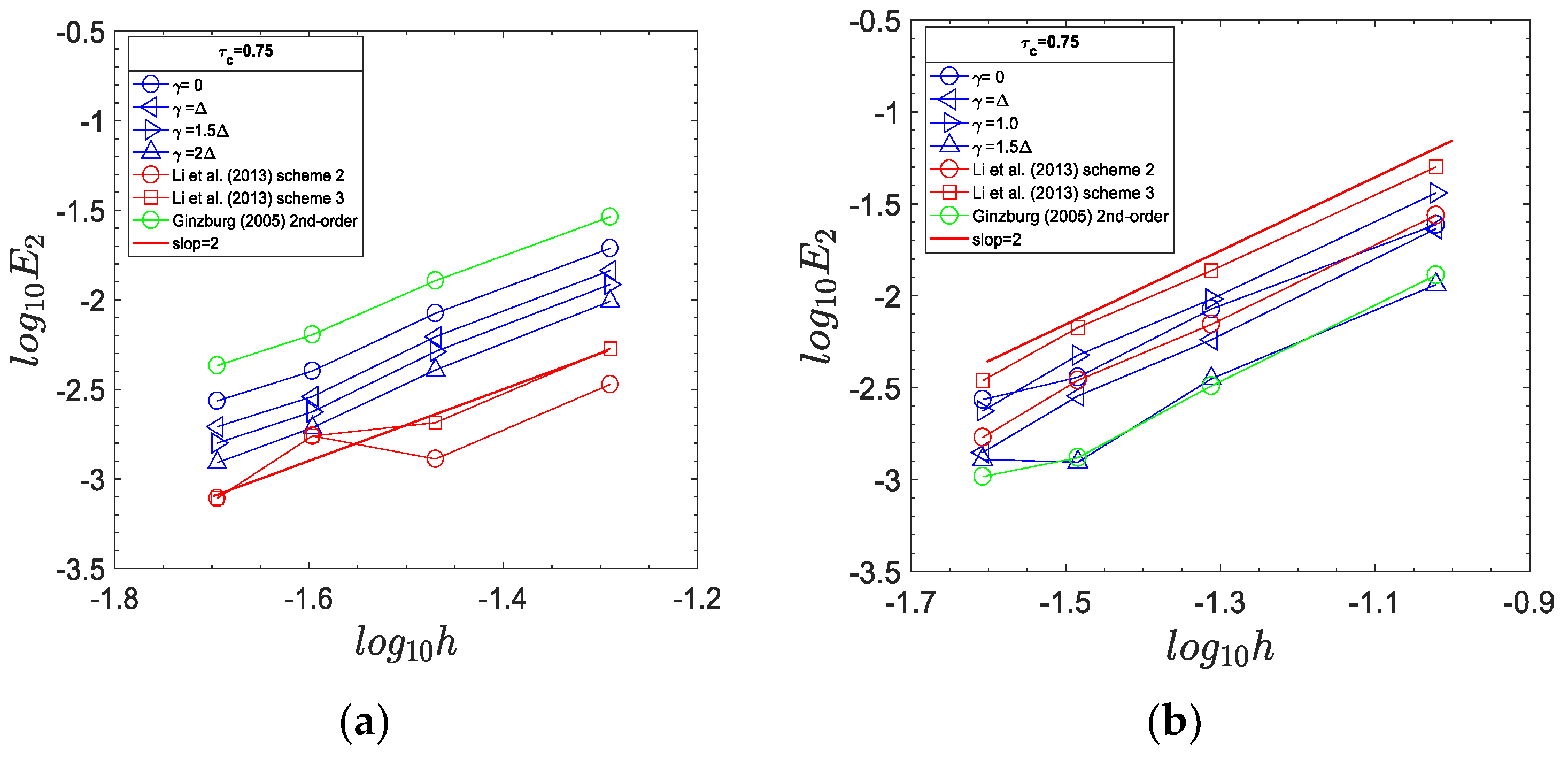
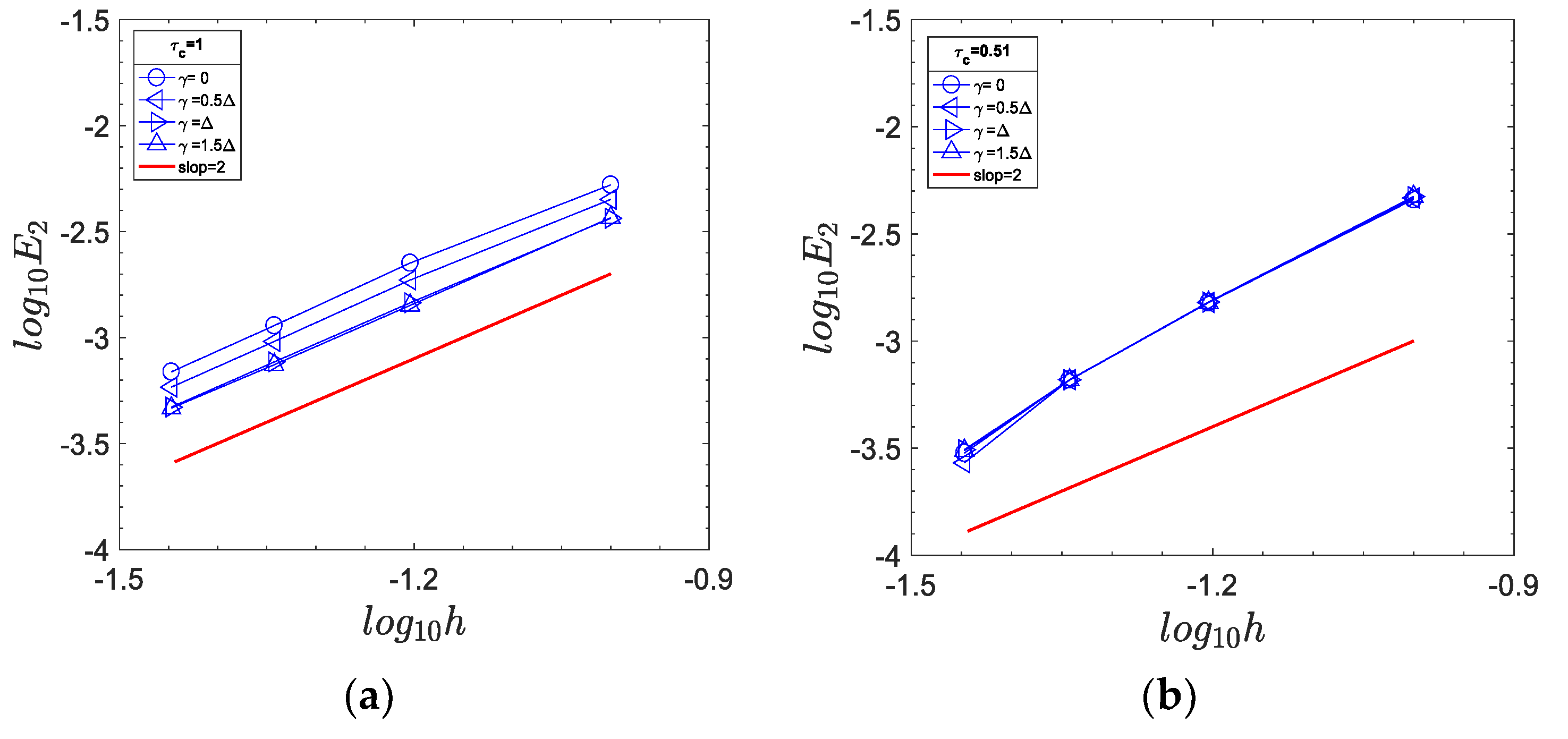
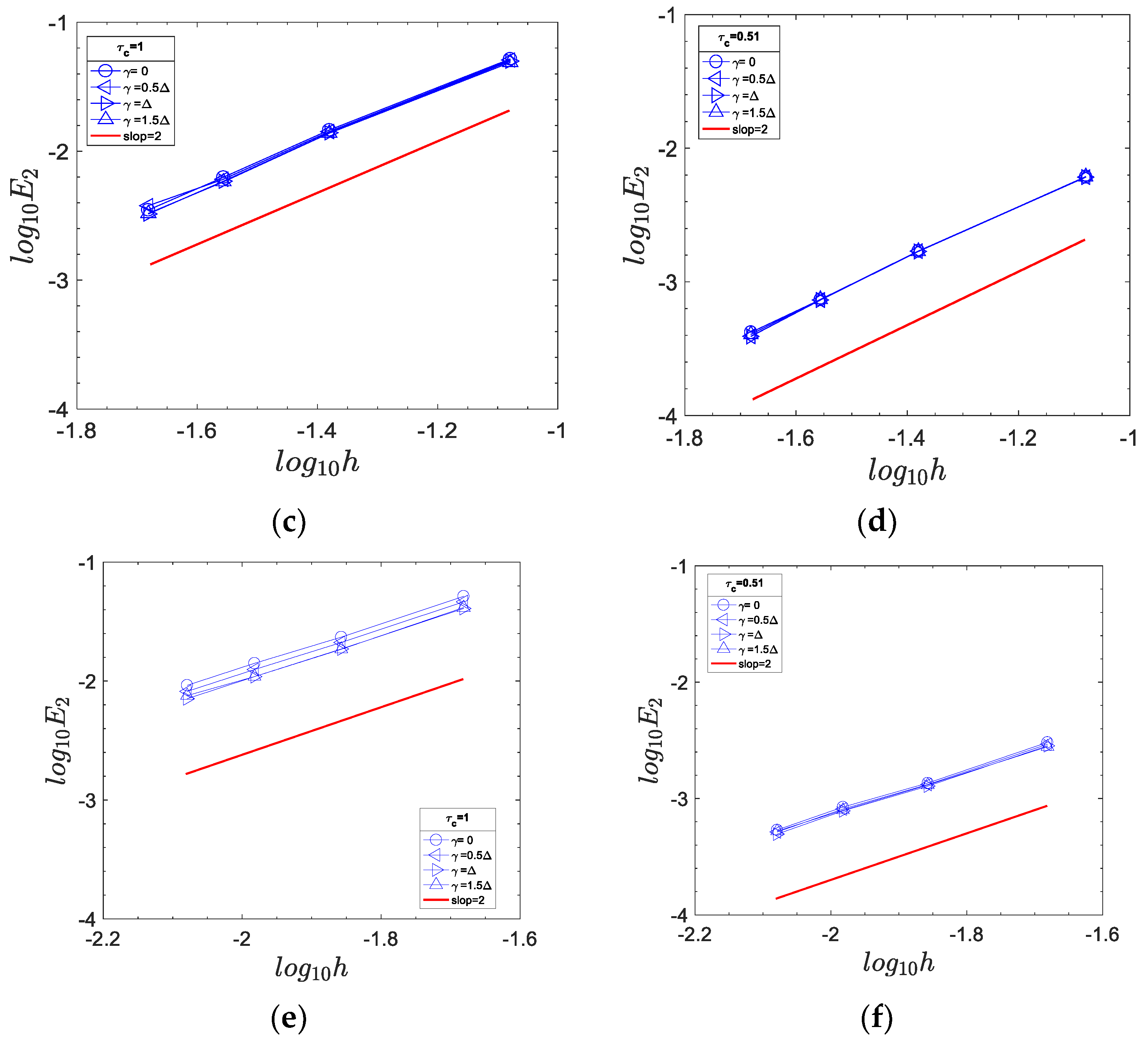
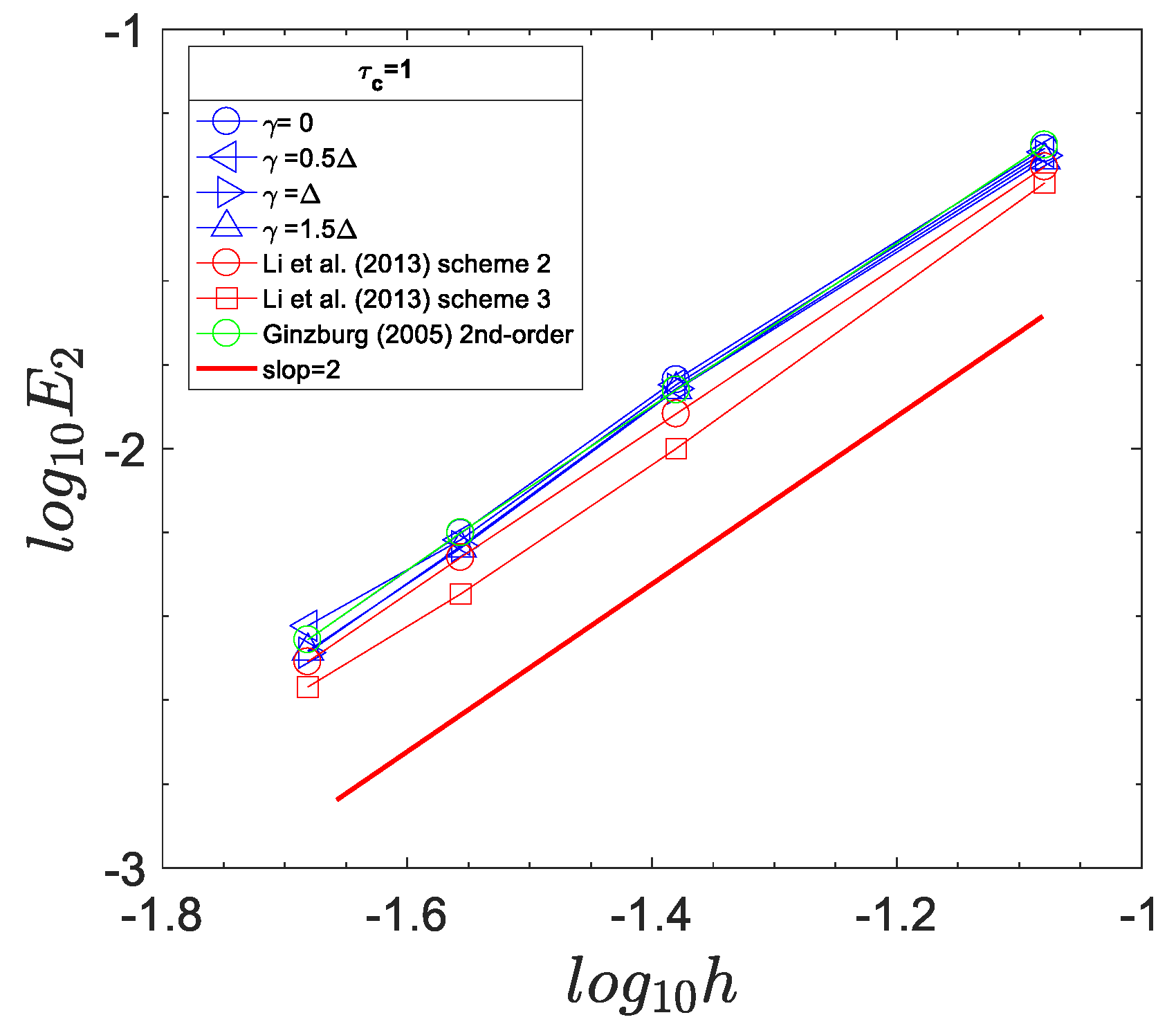
5.1. 2D Steady-State Symmetric Channel Flow

The first numerical case is the steady-state channel flow with heat transfer (Figure 3). The height of the channel is $H$. The numbers of lattices in $y$ and $x$ directions are $N_y$ and $2N_y$, respectively. Therefore, the lattice size $h$ is $1/(N_y-1+2\Delta )$. On the walls at $y=0$ and $y=H$, the temperature is given as

$$T\left(x,y=0\right)=T\left(x,y=H\right)=\cos \left(\frac{2\pi }{L}x\right)$$

(50)

The analytical solution expressed in complex form for the fluid temperature is as follows:

$$T(x,y)=real\left[e^{i\frac{2\pi }{L}x}\left(\frac{1-e^{-\lambda H}}{e^{\lambda H}-e^{-\lambda H}}{e}^{\lambda y}-\frac{1-e^{-\lambda H}}{e^{\lambda H}-e^{-\lambda H}}{e}^{-\lambda y}\right)\right],$$

(51)

where $\lambda =\frac{2\pi }{L}\sqrt{1+\frac{iUL}{2\pi D_t}}$, $U$ is the fluid velocity. The heat transfer for the channel flow is characterized by the Peclect number, where $Pe=HU/D_t$. In all the simulations, $Pe$ is fixed at 10. A periodic boundary condition for the fluid temperature is applied to the $x$ direction. The newly proposed thermal Dirichlet boundary condition is imposed at top and bottom walls. ${\tau }_c$ is set to 1, 0.75 and 0.51, respectively. Figure 4 shows the temperature contour for $H=59.5$, $\Delta =0.25$ and $\gamma =2\Delta$ as an illustration. It is clear that the temperature distribution is symmetric. The accuracy of the thermal boundary condition is evaluated in terms of the $L_2$-norm, $E_2$:

$$E_2=\frac{\sqrt{{\displaystyle \sum _i{\displaystyle \sum _j{\left(T_{LBM}(i,j)-T\left(i,j\right)\right)}^2}}}}{\sqrt{{\displaystyle \sum _i{\displaystyle \sum _j{\left(T(i,j)\right)}^2}}}},$$

(52)

where $T\left(i,j\right)$ is the analytical solution for the fluid temperature (Equation (51)). If $2\Delta \le 1$, $\gamma$ is equal to 0, $\Delta$, $1.5\Delta$ and $2\Delta$, whereas it is set to 0, $\Delta$, 1 and $1.5\Delta$ if $2\Delta >1$. Figure 5 plots the convergence order of the thermal boundary condition for different ${\tau }_c$ and $\gamma$. At ${\tau }_c=0.51$, the errors for different $\gamma$ are almost the same as shown in Figure 5c,f,i. As ${\tau }_c$ increases, a noticeable difference between different $\gamma$ is observed. For $\gamma \le 1$, the error decreases with increasing $\gamma$, whereas it increases with increasing $\gamma$ for $\gamma >1$. The comparison between different boundary schemes is shown in Figure 6. It demonstrates that the two-point boundary schemes proposed by Li et al. [8] and Ginzburg [7] are all second-order accurate. Moreover, it also implies that the current boundary condition only requires one fluid node to achieve the same accuracy as the boundary schemes proposed by Li et al. [8] and Ginzburg [7]. Figure 5 indicates that the Dirichlet boundary condition is numerically stable and second-order accurate over a wide range of ${\tau }_c$ and $\gamma$.

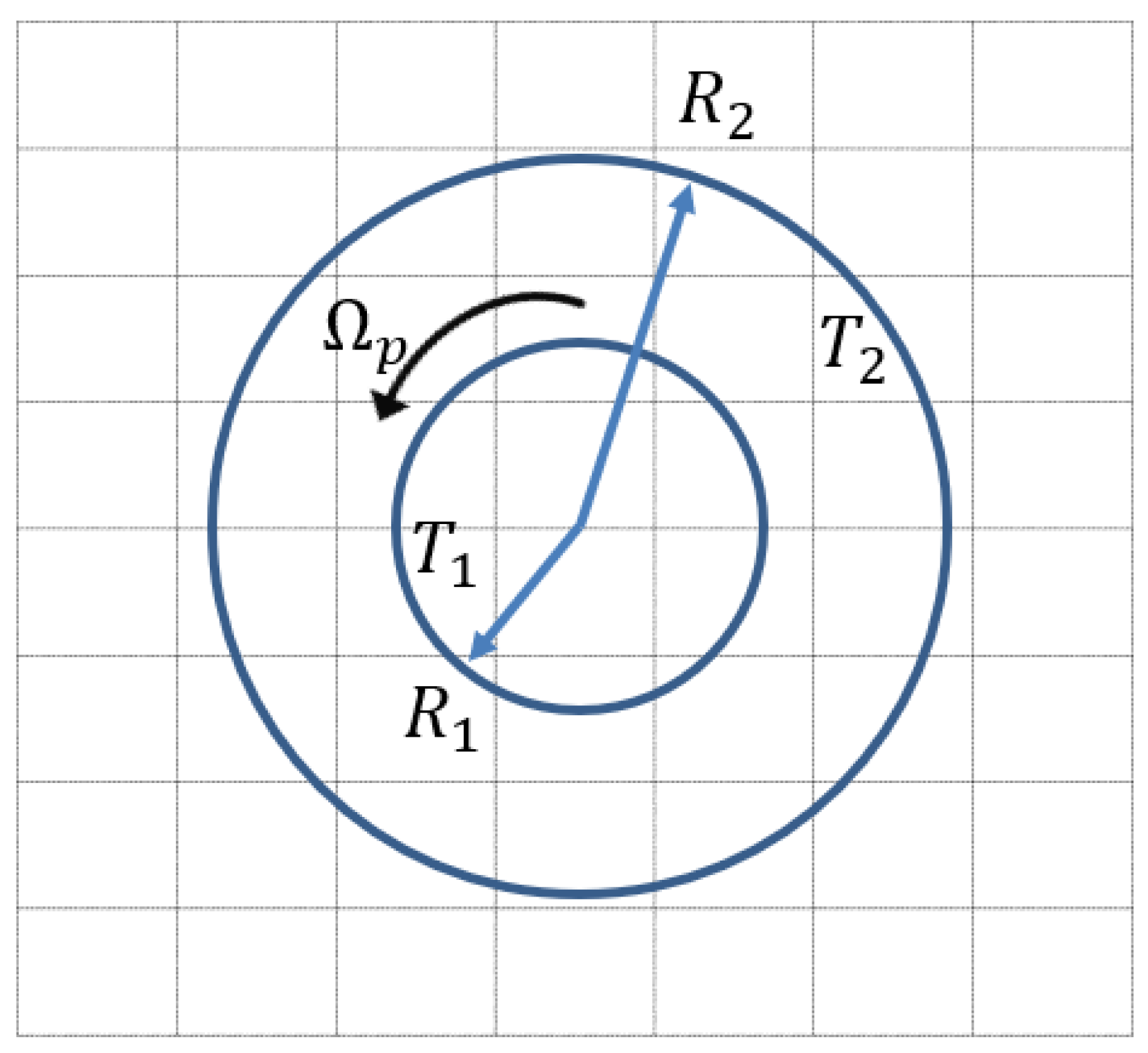
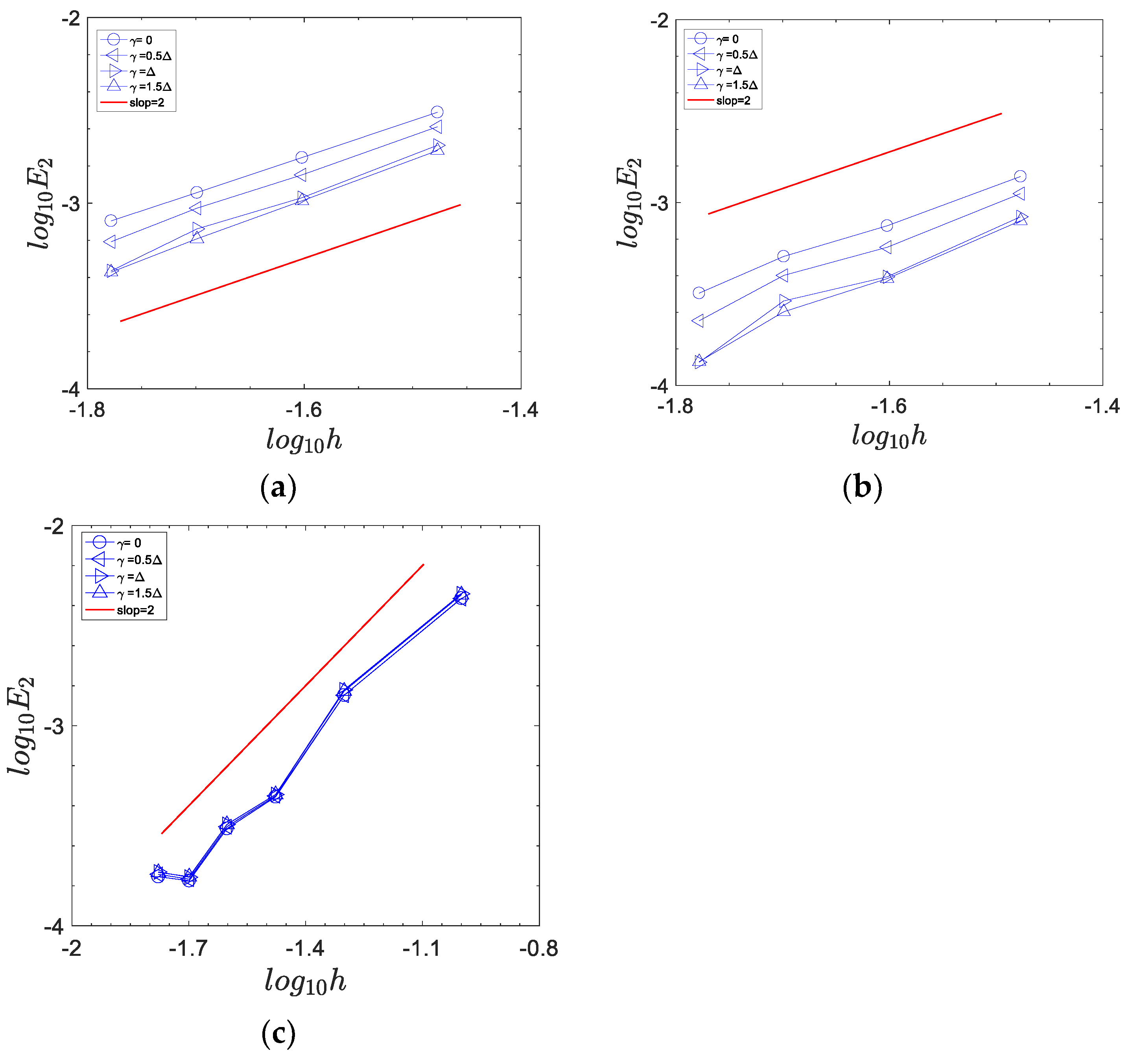
5.2. Couette Flow between Two Circular Cylinders

The analytical solution for the fluid temperature for the Couette flow between two circular cylinders (Figure 7) is given as

$$T\left(r\right)=\frac{\mathrm{Pr}{C}^2{R}_2^2}{r^2}+\frac{\mathrm{Pr}{C}^2\left(1/{\beta }^2-1\right)+\left(T_1-T_2\right)}{\ln \beta }\ln \left(\frac{r}{R_2}\right)+T_2+\mathrm{Pr}{C}^2$$

(53)

$$C=\frac{{\Omega }_p{R}_1\beta }{1-{\beta }^2}$$

(54)

where $\mathrm{Pr}$ and ${\mathsf{\Omega }}_p$ are the Prandtl number and the rotational velocity of the inner cylinder, where $\mathrm{Pr}=\upsilon /D_t$. $R_1$ and $R_2$ are the radii of inner and outer cylinders, respectively. $\beta$ is the ratio of $R_1$ to $R_2$. The Reynolds number is defined as $Re=\left(R_2-R_1\right){\mathsf{\Omega }}_p{R}_1/\upsilon$. The Reynolds number and Prandtl number are fixed at 10 and 1 for all the simulations. In these cases, $\beta =0.1, 0.4, 0.8$, ${\tau }_c=1, 0.51$ and $\gamma =0, 0.5\mathsf{\Delta }, \mathsf{\Delta }, 1.5\mathsf{\Delta }$. The temperatures of the inner cylinder ($T_1$) and outer cylinder ($T_2$) are set to 1 and 0, respectively. The non-slip hydrodynamic boundary condition proposed by Chen et al. [21] and the thermal Dirichlet boundary condition proposed in this work are applied to the inner and outer cylinders. The normalized temperature profiles for different $\beta$ are plotted in Figure 8 at $\gamma =1.5\mathsf{\Delta }$, $R_2=40$ and ${\tau }_c=0.53$. It is clear that the simulation results are in good agreement with the analytical solutions. The convergence order of the boundary condition described by Equation (52) is shown in Figure 9. Unlike 2D channel flow, a small difference between different $\gamma$ is observed. In Figure 10, we can see that the errors for the boundary schemes developed by Li et al. [8] are slightly smaller compared to the boundary schemes proposed by Ginzburg [7] and in the current work. All schemes have second-order accuracy for $\beta =0.4$ and ${\tau }_c=1$. Figure 9 demonstrates that the Dirichlet boundary condition is numerically stable and second-order accurate over a wide range of ${\tau }_c$ and $\gamma$ within the range [0, $2\Delta$] for 2D curved boundaries.

5.3. 3D Steady-State Symmetric Circular Pipe Flow

The third validation case is the 3D steady-state circular pipe flow with heat conduction. The temperature boundary conditions for the wall, inlet and outlet are as follows, respectively:

$$T\left(r=R,x\right)=\cos \left(\frac{2\pi }{L}x\right) \mathrm{and} T\left(r,x=L\right)=T\left(r,x=0\right)$$

(55)

The analytical solution for the fluid temperature at steady state in terms of complex form is solved to be

$$T\left(r,x\right)=real\left(e^{\frac{2\pi x}{L}i}\frac{I_0\left(\frac{2\pi }{L}r\right)}{I_0\left(\frac{2\pi }{L}R\right)}\right)$$

(56)

where $I_0$ is the modified Bessel’s function of the first kind of order 0. $L$ is the pipe length. Equation (56) indicates that the temperature distribution in the radial direction is symmetric. Figure 11 shows the $L_2$-norm $E_2$ for the fluid temperature with respect to the grid resolution. The difference between different $\gamma$ is very small at ${\tau }_c=0.51$ as already observed for 2D channel flow. As ${\tau }_c$ increases, the error decreases with increasing $\gamma$. In general, Figure 11 indicates that the Dirichlet boundary condition converges quadratically with increasing grid refinement.

5.4. Forced Convection of a Hot Sphere in Uniform Flow

In the past several decades, various empirical [22,23] and numerically [24] derived Nusselt number correlations have been proposed. In the last validation case, the heat transfer between a sphere and surrounding fluid in unform flow has been studied for $\mathrm{Pr}=1$. The diameter of the sphere is $d_p=$ 20 in lattice units. The sphere is placed in the middle of the computational domain with a domain size $20d_p\times 10d_p\times 10d_p$. The Dirichlet boundary condition for the fluid velocity and temperature were imposed onto the fluid at the inlet, whereas the Neumann boundary condition for the fluid velocity and temperature (the derivative in the flow direction is zero) were assigned at the outlet. The inlet fluid velocity was 0.05 for all the simulations. Symmetrical boundary conditions for the velocity and temperature were applied to the other boundaries. The fluid temperature around the hot sphere is symmetric and is shown in Figure 12 for $Re=60$ as an illustration. The simulation results together with the predictions of [22,23,24,25,26] are plotted in Figure 13. The maximal relative deviation is within 8% between current simulation results and the predictions of [22,23,24,25,26]. Our simulation results are in good agreement with the predictions of [24,26] with a maximal relative deviation within 2%. The comparison indicates that the thermal Dirichlet boundary condition can accurately calculate the heat transfer for forced convection involving curved boundaries.

6. Conclusions

A general single-node second-order Dirichlet boundary condition for curved boundaries for the lattice Boltzmann method has been developed. The numerical simulations of 2D and 3D symmetric flows with heat transfer indicate that the boundary condition is numerically stable over a wide range of ${\tau }_c$ and γ within the range [0, 2∆]. In addition, we show that the newly proposed boundary condition only needs one fluid node to achieve the same convergence order as the two-point boundary schemes for straight and curved boundaries. Comparisons with the analytical solution for 2D channel flow, cylindrical Couette flow and 3D pipe flow indicate that the boundary condition has second-order accuracy for 2D and 3D straight and curved boundaries, which is consistent with the asymptotic analysis. Further comparison of the Nusselt number for a spherical particle between present simulation results and the predictions of previous studies demonstrates that the boundary condition can accurately capture the convective heat transfer for curved boundaries since the maximal relative deviation is within 8%. In the future, the lattice Boltzmann method with proposed Dirichlet boundary condition will be used to study a gas–solid fluidized bed with heat transfer comprising spherical and non-spherical particles.