Observational and Energetic Properties of Astrophysical and Galactic Black Holes
Abstract
:1. Introduction
2. Analysis of Observational Properties of Accretion Disks to Extract Information about Black Hole Parameters
2.1. Novikov-Thorne Thin Accretion Disk Model
2.2. Methods to Extract Information about Parameters of Central Black Hole
2.2.1. Continuum-Fitting Method
2.2.2. X-ray Reflection Spectroscopy
2.2.3. Quasi-Periodic Oscillations
- The detected QPOs frequency is within the expected range for the matter orbiting nearly at the ISCO radius around the central source.
- The frequency of the QPOs is relatively insensitive to the properties of the accretion flow and is primarily determined by the spacetime properties. However, there is a slight dependence on the observed X-ray flux.
- The frequency of the QPOs can be measured with a high degree of accuracy.
3. Imaging, Optical and Observational Properties of Black Holes
3.1. Black Hole Shadow
3.2. Gravitational Lensing by Black Holes
3.3. Quasinormal Modes of Regular Black Holes
4. Black Hole Energetics
4.1. High Energetic Activity from Rapidly Rotating BHs
4.2. Black Hole as Unipolar Inductor
4.3. Black Hole in External Magnetic Field
4.4. Extracting Energy from Rapidly Rotating Black Holes: Blandford-Znajek Process
4.5. The Most Efficient Mechanism for the Energy Extraction from the Black Hole: Magnetic Penrose Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; Blackburn, L.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.; Ball, D.; Baloković, M.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Narzilloev, B.; Malafarina, D.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Particle motion around a static axially symmetric wormhole. Phys. Rev. D 2021, 104, 064016. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Narzilloev, B.; Abdujabbarov, A.; Ahmedov, B. Dynamics of Magnetized and Magnetically Charged Particles around Regular Nonminimal Magnetic Black Holes. Galaxies 2021, 9, 71. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B. Regular Bardeen Black Holes in Anti-de Sitter Spacetime versus Kerr Black Holes through Particle Dynamics. Galaxies 2021, 9, 63. [Google Scholar] [CrossRef]
- Narzilloev, B.; Shaymatov, S.; Hussain, I.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Motion of Particles and Gravitational Lensing Around (2+1)-dimensional BTZ black holes in Gauss-Bonnet Gravity. Eur. Phys. J. C 2021, 81, 849. [Google Scholar] [CrossRef]
- Narzilloev, B.; Hussain, I.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Dynamics and fundamental frequencies of test particles orbiting Kerr–Newman–NUT–Kiselev black hole in Rastall gravity. Eur. Phys. J. Plus 2021, 136, 1032. [Google Scholar] [CrossRef]
- Narzilloev, B.; Hussain, I.; Abdujabbarov, A.; Ahmedov, B. Optical properties of an axially symmetric black hole in the Rastall gravity. Eur. Phys. J. Plus 2022, 137, 645. [Google Scholar] [CrossRef]
- Narzilloev, B.; Ahmedov, B. Radiation Properties of the Accretion Disk around a Black Hole Surrounded by PFDM. Symmetry 2022, 14, 1765. [Google Scholar] [CrossRef]
- Narzilloev, B.; Ahmedov, B. Regular black hole solution in PFDM environment to explain the radiative efficiency of black hole candidates. New Astron. 2023, 98, 101922. [Google Scholar] [CrossRef]
- Narzilloev, B.; Abdujabbarov, A.; Hakimov, A. Redshift of photons emitted from the accretion disk of a regular black hole surrounded by dark matter. Int. J. Mod. Phys. A 2022, 37, 2250144. [Google Scholar] [CrossRef]
- Juraeva, N.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Palvanov, S. Distinguishing magnetically and electrically charged Reissner–Nordström black holes by magnetized particle motion. Eur. Phys. J. C 2021, 81, 70. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Rayimbaev, J.; Ahmedov, B. Test particles dynamics around deformed Reissner-Nordström black hole. Phys. Rev. D 2021, 102, 124078. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Shaymatov, S.; Jamil, M. Dynamics and epicyclic motions of particles around the Schwarzschild–de Sitter black hole in perfect fluid dark matter. Eur. Phys. J. C 2021, 81, 699. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Tadjimuratov, P. Can modified gravity silence radio-loud pulsars? Phys. Rev. D 2020, 102, 024019. [Google Scholar] [CrossRef]
- Fishbone, L.G.; Moncrief, V. Relativistic fluid disks in orbit around Kerr black holes. Astrophys. J. 1976, 207, 962–976. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics and black holes. In Les Houches Summer School of Theoretical Physics: Black Holes, Proceedings of the Ecole d’Eté de Physique Théorique, Les Astres Occlus, Les Houches, France, August, 1973; Gordon and Breach: New York, NY, USA, 1973; pp. 343–550. [Google Scholar]
- Page, D.N.; Thorne, K.S. Disk-Accretion onto a Black Hole. Time-Averaged Structure of Accretion Disk. Astrophys. J. 1974, 191, 499–506. [Google Scholar] [CrossRef]
- Banerjee, I.; Chakraborty, S.; SenGupta, S. Decoding signatures of extra dimensions and estimating spin of quasars from the continuum spectrum. Phys. Rev. D 2019, 100, 044045. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.N.; Cui, W.; Chen, W. Black Hole Spin in X-Ray Binaries: Observational Consequences. Astrophys. J. 1997, 482, L155–L158. [Google Scholar] [CrossRef] [Green Version]
- Bambi, C. A Code to Compute the Emission of Thin Accretion Disks in Non-Kerr Spacetimes and Test the Nature of Black Hole Candidates. Astrophys. J. 2012, 761, 174. [Google Scholar] [CrossRef]
- Kong, L.; Li, Z.; Bambi, C. Constraints on the Spacetime Geometry around 10 Stellar-Mass Black Hole Candidates from the Disk’s Thermal Spectrum. Astrophys. J. 2014, 797, 78. [Google Scholar] [CrossRef] [Green Version]
- McClintock, J.E.; Narayan, R.; Steiner, J.F. Black Hole Spin via Continuum Fitting and the Role of Spin in Powering Transient Jets. Space Sci. Rev. 2014, 183, 295–322. [Google Scholar] [CrossRef] [Green Version]
- McClintock, J.E.; Narayan, R.; Davis, S.W.; Gou, L.; Kulkarni, A.; Orosz, J.A.; Penna, R.F.; Remillard, R.A.; Steiner, J.F. Measuring the spins of accreting black holes. Class. Quantum Gravity 2011, 28, 114009. [Google Scholar] [CrossRef] [Green Version]
- Czerny, B.; Hryniewicz, K.; Nikolajuk, M.; Sadowski, A. Constraints on the black hole spin in the quasar SDSS J094533.99+100950.1. Mon. Not. R. Astron. Soc. 2011, 415, 2942. [Google Scholar] [CrossRef] [Green Version]
- Done, C.; Jin, C.; Middleton, M.; Ward, M. A new way to measure supermassive black hole spin in accretion disc-dominated active galaxies. Mon. Not. R. Astron. Soc. 2013, 434, 1955–1963. [Google Scholar] [CrossRef]
- Nampalliwar, S.; Bambi, C. Accreting Black Holes. In Tutorial Guide to X-ray and Gamma-ray Astronomy: Data Reduction and Analysis; Bambi, C., Ed.; Springer: Singapore, 2020; pp. 15–54. [Google Scholar] [CrossRef]
- Risaliti, G.; Harrison, F.; Madsen, K.; Walton, D.; Boggs, S.; Christensen, F.; Craig, W.; Grefenstette, B.; Hailey, C.; Nardini, E.; et al. A rapidly spinning supermassive black hole at the centre of NGC 1365. Nature 2013, 494, 449–451. [Google Scholar] [CrossRef] [Green Version]
- Remillard, R.A.; McClintock, J.E. X-ray Properties of Black-Hole Binaries. Ann. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef] [Green Version]
- van der Klis, M. A Review of Rapid X-ray Variability in X-ray Binaries. arXiv 2004, arXiv:astro-ph/0410551. [Google Scholar]
- Stella, L.; Vietri, M. Lense-Thirring precession and QPOs in low mass X-ray binaries. Nucl. Phys. B Proc. Suppl. 1999, 69, 135–140. [Google Scholar] [CrossRef] [Green Version]
- Stella, L.; Vietri, M. kHz Quasiperiodic Oscillations in Low-Mass X-Ray Binaries as Probes of General Relativity in the Strong-Field Regime. Phys. Rev. Lett. 1999, 82, 17–20. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M.; Morsink, S.M. Correlations in the Quasi-periodic Oscillation Frequencies of Low-Mass X-Ray Binaries and the Relativistic Precession Model. Astrophys. J. 1999, 524, L63–L66. [Google Scholar] [CrossRef] [Green Version]
- Abramowicz, M.A.; Karas, V.; Kluzniak, W.; Lee, W.H.; Rebusco, P. Nonlinear resonance in nearly geodesic motion in low mass x-ray binaries. Publ. Astron. Soc. Jap. 2003, 55, 466–467. [Google Scholar] [CrossRef] [Green Version]
- Abramowicz, M.A.; Kluzniak, W. A Precise determination of angular momentum in the black hole candidate GRO J1655-40. Astron. Astrophys. 2001, 374, L19. [Google Scholar] [CrossRef] [Green Version]
- Kluzniak, W.; Abramowicz, M.A. The physics of kHz QPOs—Strong gravity’s coupled anharmonic oscillators. arXiv 2001, arXiv:astro-ph/0105057. [Google Scholar] [CrossRef]
- Perez, C.A.; Silbergleit, A.S.; Wagoner, R.V.; Lehr, D.E. Relativistic diskoseismology. 1. Analytical results for ‘gravity modes’. Astrophys. J. 1997, 476, 589–604. [Google Scholar] [CrossRef]
- Silbergleit, A.S.; Wagoner, R.V.; Ortega-Rodríguez, M. Relativistic Diskoseismology. II. Analytical Results for c-modes. Astrophys. J. 2001, 548, 335–347. [Google Scholar]
- Wagoner, R.V.; Silbergleit, A.S.; Ortega-Rodríguez, M. “Stable” Quasi-periodic Oscillations and Black Hole Properties from Diskoseismology. Astrophys. J. 2001, 559, L25–L28. [Google Scholar] [CrossRef]
- Bambi, C. Quasi-periodic Oscillations. In Black Holes: A Laboratory for Testing Strong Gravity; Springer: Singapore, 2017; pp. 181–192. [Google Scholar] [CrossRef]
- Motta, S.E.; Belloni, T.M.; Stella, L.; Muñoz-Darias, T.; Fender, R. Precise mass and spin measurements for a stellar-mass black hole through X-ray timing: The case of GRO J1655-40. Mon. Not. R. Astron. Soc. 2013, 437, 2554–2565. [Google Scholar] [CrossRef] [Green Version]
- Kato, S. A Resonantly Excited Disk-Oscillation Model of High-Frequency QPOs of Microquasars. Publ. Astron. Soc. Jpn. 2012, 64, 139. [Google Scholar] [CrossRef] [Green Version]
- Abramowicz, M.A.; Kluzniak, W.; Stuchlik, Z.; Torok, G. The Orbital resonance model for twin peak kHz QPOs: Measuring the black hole spins in microquasars. arXiv 2004, arXiv:aastro-ph/0401464. [Google Scholar]
- Rayimbaev, J.; Abdujabbarov, A.; Abdulkhamidov, F.; Khamidov, V.; Djumanov, S.; Toshov, J.; Inoyatov, S. Quasiperiodic oscillation around charged black holes in Einstein–Maxwell-scalar theory. Eur. Phys. J. C 2022, 82, 1110. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Pantig, R.C.; Övgün, A.; Abdujabbarov, A.; Demir, D. Quasiperiodic oscillations, weak field lensing and shadow cast around black holes in Symmergent gravity. arXiv 2022, arXiv:gr-qc/2206.06599. [Google Scholar]
- Rayimbaev, J.; Bokhari, A.H.; Ahmedov, B. Quasiperiodic oscillations from noncommutative inspired black holes. Class. Quant. Grav. 2022, 39, 075021. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Majeed, B.; Jamil, M.; Jusufi, K.; Wang, A. Quasiperiodic oscillations, quasinormal modes and shadows of Bardeen–Kiselev Black Holes. Phys. Dark Univ. 2022, 35, 100930. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Bardiev, D.; Abdujabbarov, A.; Turaev, Y.; Stuchlík, Z. Quasi-periodic oscillation around regular Bardeen black holes in 4D Einstein–Gauss–Bonnet gravity. Int. J. Mod. Phys. D 2022, 31, 2250004. [Google Scholar] [CrossRef]
- Bardeen, J. Non-singular general-relativistic gravitational collapse. In Proceedings of the International Conference GR5, New York, NY, USA, 9–13 September 1968; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach: Tbilisi, Georgia, 1968; p. 174. [Google Scholar]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- Falcke, H.; Melia, F.; Agol, E. Viewing the Shadow of the Black Hole at the Galactic Center. Astrophys. J. 2000, 528, L13–L16. [Google Scholar] [CrossRef] [Green Version]
- Chan, C.k.; Psaltis, D.; Özel, F. GRay: A Massively Parallel GPU-based Code for Ray Tracing in Relativistic Spacetimes. Astrophys. J. 2013, 777, 13. [Google Scholar] [CrossRef]
- Bambi, C. Imaging Black Holes. In Black Holes: A Laboratory for Testing Strong Gravity; Springer: Singapore, 2017; pp. 193–205. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Rezzolla, L.; Ahmedov, B.J. A coordinate-independent characterization of a black hole shadow. Mon. Not. R. Astron. Soc. 2015, 454, 2423–2435. [Google Scholar] [CrossRef] [Green Version]
- Ahmedov, B. Development and perspectives of relativistic astrophysics in Uzbekistan. Arab. J. Math. 2022, 11, 141–153. [Google Scholar] [CrossRef]
- Ahmedov, B. Relativistic Astrophysics in Uzbekistan. In Under One Sky: The IAU Centenary Symposium; Sterken, C., Hearnshaw, J., Valls-Gabaud, D., Eds.; Cambridge University Press: Cambridge, UK, 2019; Volume 349, pp. 276–282. [Google Scholar] [CrossRef]
- Merritt, D. Dynamics and Evolution of Galactic Nuclei; Princton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Turimov, B.; Ahmedov, B.; Abdujabbarov, A.; Bambi, C. Gravitational lensing by a magnetized compact object in the presence of plasma. Int. J. Mod. Phys. D 2019, 28, 2040013. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlík, Z.; Schee, J.; Ahmedov, B. Electromagnetic perturbations of black holes in general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2018, 97, 084058. [Google Scholar] [CrossRef] [Green Version]
- Salpeter, E.E. Accretion of Interstellar Matter by Massive Objects. Astrophys. J. 1964, 140, 796–800. [Google Scholar] [CrossRef]
- Zeldovich, Y.; Novikov, I. Doklady Akademii Nauk. SSSR 1964, 158, 811. [Google Scholar]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Aliev, A.N.; Özdemir, N. Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 2002, 336, 241–248. [Google Scholar] [CrossRef] [Green Version]
- Aliev, A.N.; Frolov, V.P. Five-dimensional rotating black hole in a uniform magnetic field: The gyromagnetic ratio. Phys. Rev. D 2004, 69, 084022. [Google Scholar] [CrossRef] [Green Version]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Tursunov, A.; Stuchlík, Z.; Kološ, M.; Dadhich, N.; Ahmedov, B. Supermassive Black Holes as Possible Sources of Ultrahigh-energy Cosmic Rays. Astrophys. J. 2020, 895, 14. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Tursunov, A. Penrose Process: Its Variants and Astrophysical Applications. Universe 2021, 7, 416. [Google Scholar] [CrossRef]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. Mon. Not. R. Astron. Soc. 2018, 478, L89–L94. [Google Scholar] [CrossRef] [Green Version]
- Tursunov, A.; Dadhich, N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe 2019, 5, 125. [Google Scholar] [CrossRef]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Radiative Penrose process: Energy gain by a single radiating charged particle in the ergosphere of rotating black hole. Phys. Rev. D 2021, 103, 024021. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
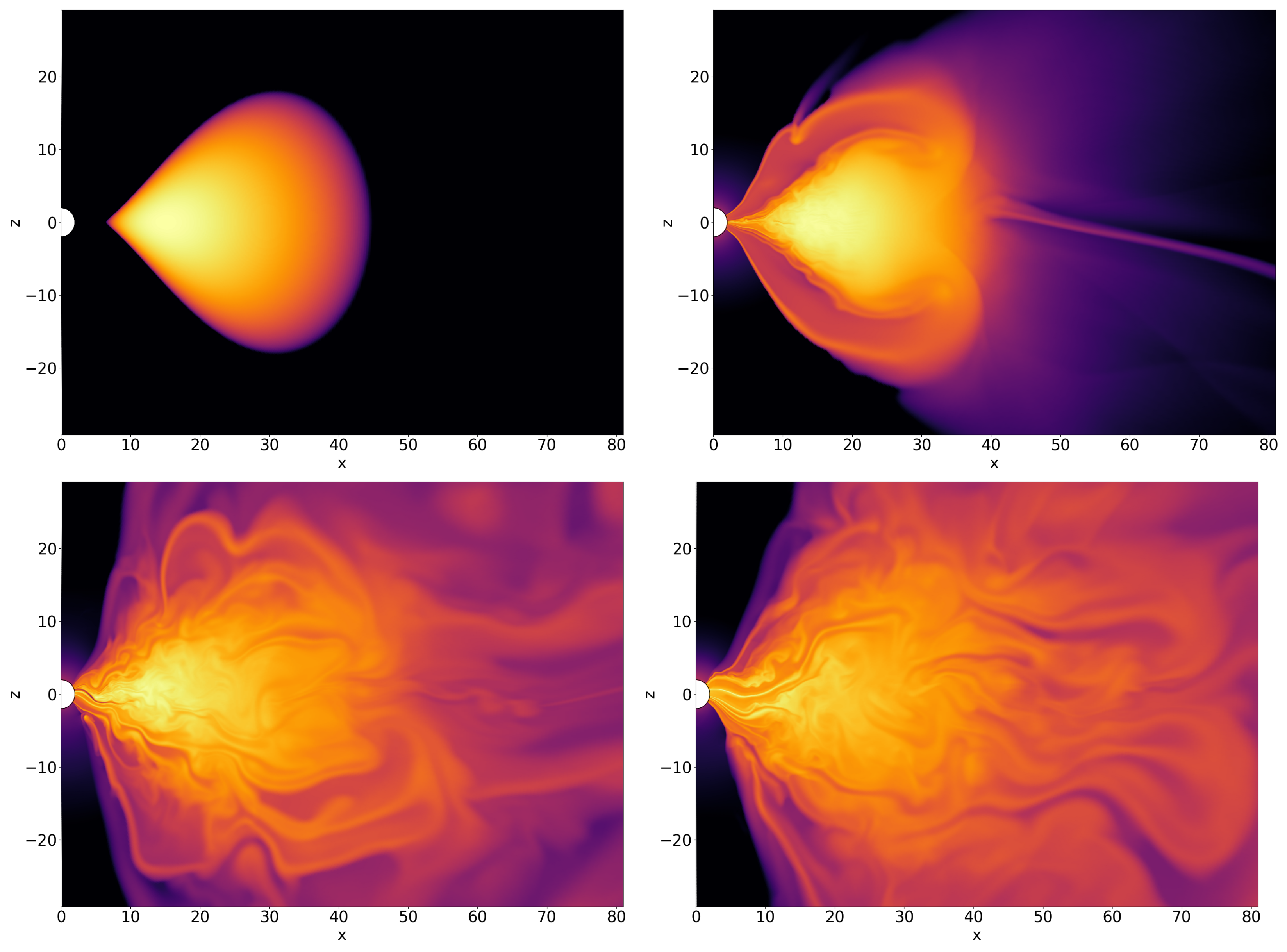
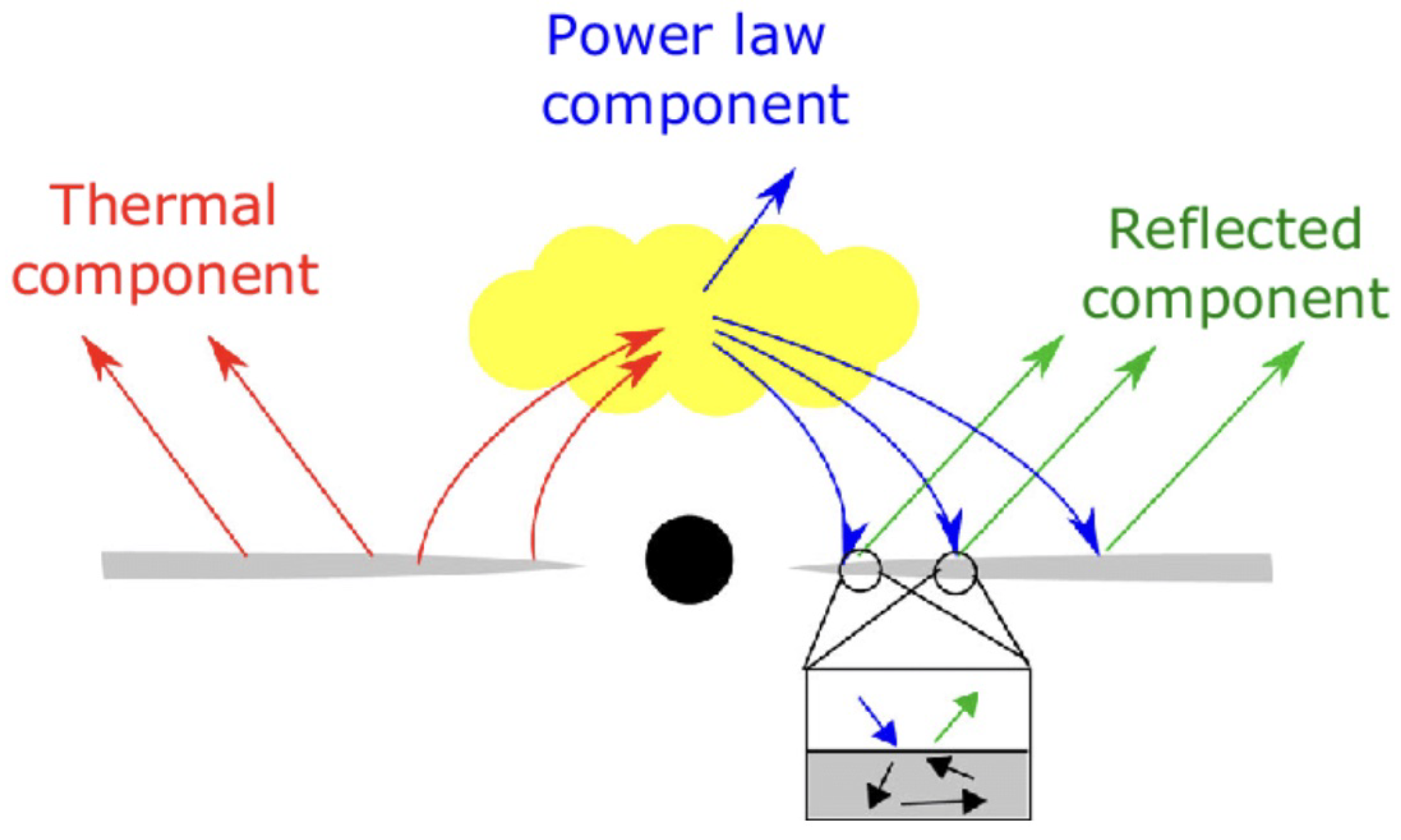




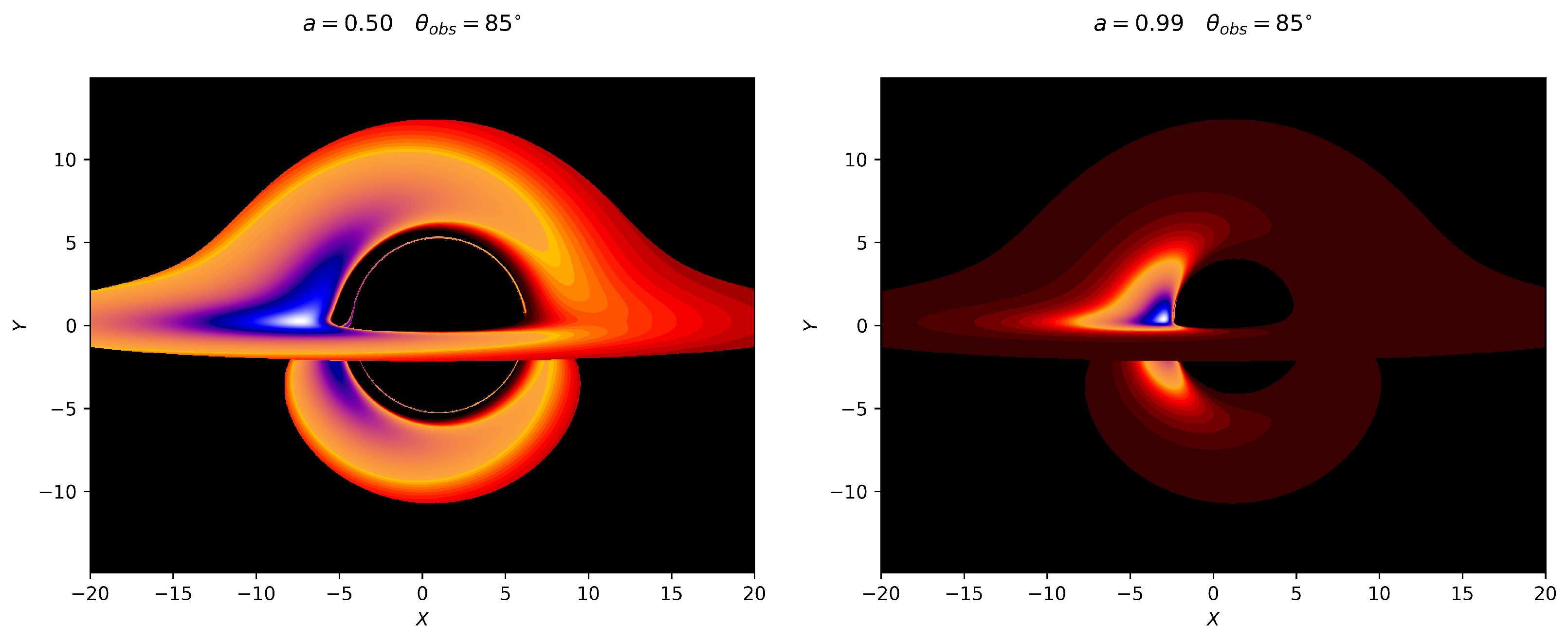




| Model | Assumed Mass () | References | |
|---|---|---|---|
| Relativistic precession model | 0.290 ± 0.003 | – | [41] |
| Diskoseismology model | 0.917 ± 0.024 | – | [39] |
| Warp resonance model | 0.9–0.99 | 5.1–5.7 | [42] |
| 3:2 Parametric resonance model | 0.96–0.99 | 6.0–6.6 | [43] |
| 2:1 Forced resonance model | 0.31–0.42 | 6.0–6.6 | [43] |
| 3:1 Forced resonance model | 0.50–0.59 | 6.0–6.6 | [43] |
| 2:1 Keplerian resonance model | 0.31–0.42 | 6.0–6.6 | [43] |
| 3:1 Keplerian resonance model | 0.45–0.53 | 6.0–6.6 | [43] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narzilloev, B.; Ahmedov, B. Observational and Energetic Properties of Astrophysical and Galactic Black Holes. Symmetry 2023, 15, 293. https://doi.org/10.3390/sym15020293
Narzilloev B, Ahmedov B. Observational and Energetic Properties of Astrophysical and Galactic Black Holes. Symmetry. 2023; 15(2):293. https://doi.org/10.3390/sym15020293
Chicago/Turabian StyleNarzilloev, Bakhtiyor, and Bobomurat Ahmedov. 2023. "Observational and Energetic Properties of Astrophysical and Galactic Black Holes" Symmetry 15, no. 2: 293. https://doi.org/10.3390/sym15020293
APA StyleNarzilloev, B., & Ahmedov, B. (2023). Observational and Energetic Properties of Astrophysical and Galactic Black Holes. Symmetry, 15(2), 293. https://doi.org/10.3390/sym15020293







