Symmetries of Scan Patterns of Laser Scanners with Rotational Risley Prisms
Abstract
:1. Introduction
- (i)
- Dual axis galvanometer scanners (GS) [20,21,22,23], which are the most precise optomechanical scanning system regarding beam positioning, as well as the most compact and cost-effective [1,2]. Regarding scanning modalities, GSs can work in raster [23,24,25], spiral [26,27], Lissajous [28,29], or (lately in) adaptive scanning [30].
- (ii)
- (iii)
- The increasingly utilized Micro-Electro-Mechanical Systems (MEMS) with oscillatory mirrors [35,36,37], which function similarly to 2D GSs, with the advantage of the focusing of the beam on the single mirror, which is oscillating on two perpendicular axes. However, their field-of-view (FOV) is (still) much smaller than for GSs.
- -
- The approximate method, which considers the first order/paraxial approximation for optical wedges (i.e., small angle prisms) [15], is simple and fast, but it only provides approximate scan patterns.
- -
- -
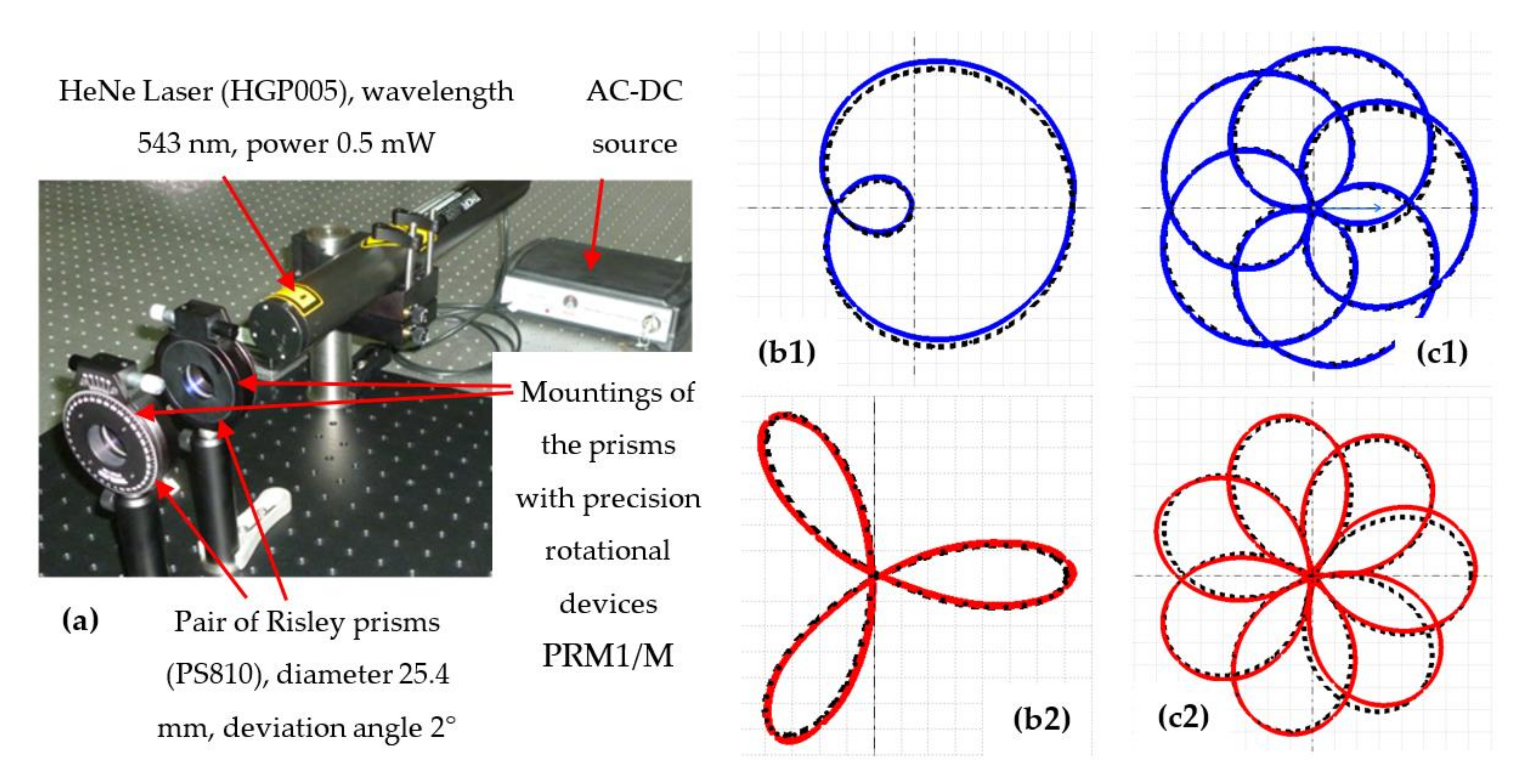
- The graphical method that we have introduced [40] and developed [41], for which ray-tracing is performed using a mechanical design program, in our case CATIA V5R20 (Dassault Systems, Paris, France). In this way, the simulation of exact scan patterns of Risley prisms can be achieved, in an intuitive, time-effective, and easy way.
- To explore the symmetries that can be obtained for scan patterns generated by a pair of rotational Risley prisms. Such symmetries are definitely present, as these patterns are, from a mathematical point of view, a type of rhodonea curve [42]. This can be seen from their shapes, which have been approached both by early works employing approximate methods [15] and by our (exact) graphical method studies [40,41].
- To perform a multi-parameter analysis that is necessary for such systems, by considering the different characteristic parameters of the scanner, to determine their impact on the symmetries of the patterns.
- To extract rules-of-thumb regarding the shape of scan patterns. Thus, existing symmetries can be helpful in simplifying the way such patterns are generated. Eventual symmetries could be applied in using only a portion of a pattern (that is precisely obtained) and then multiply it in a repetitive way to draw the entire pattern.
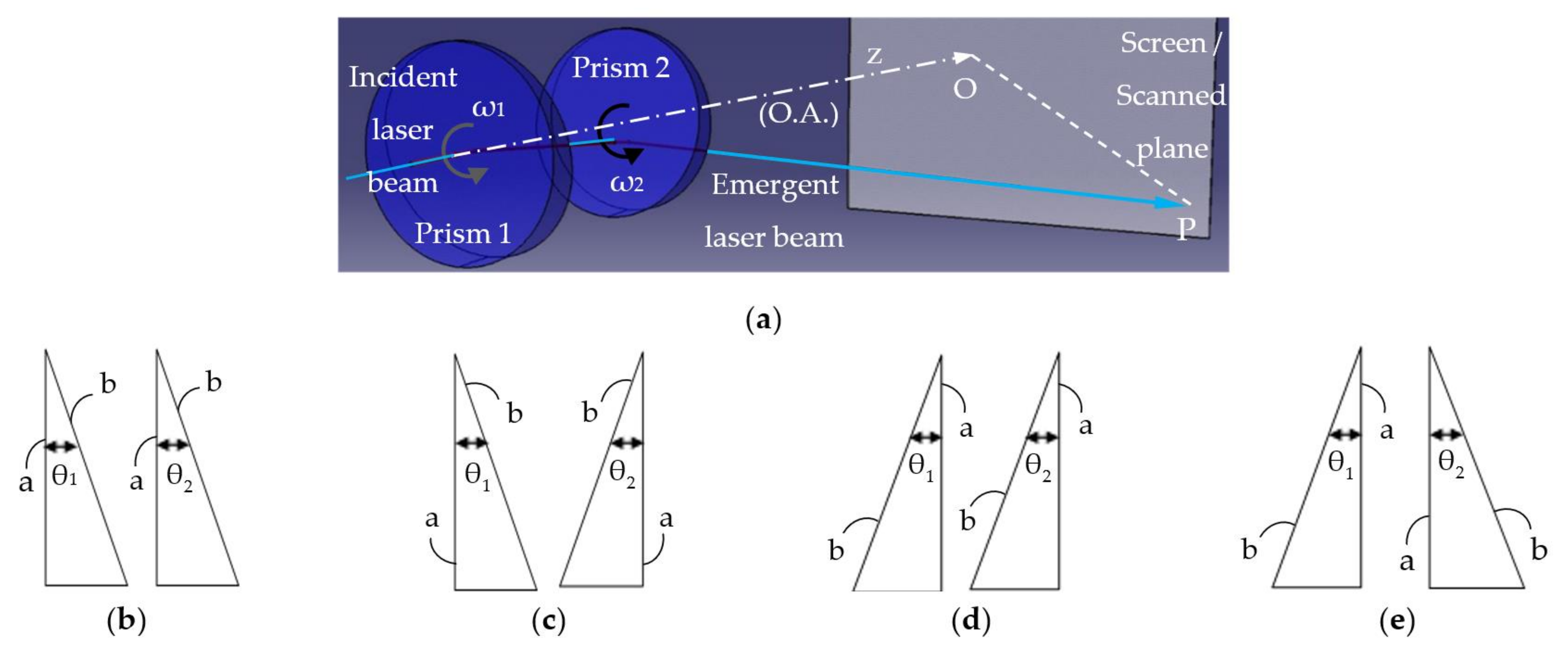
2. Laser Scanners with a Pair of Rotational Risley Prisms
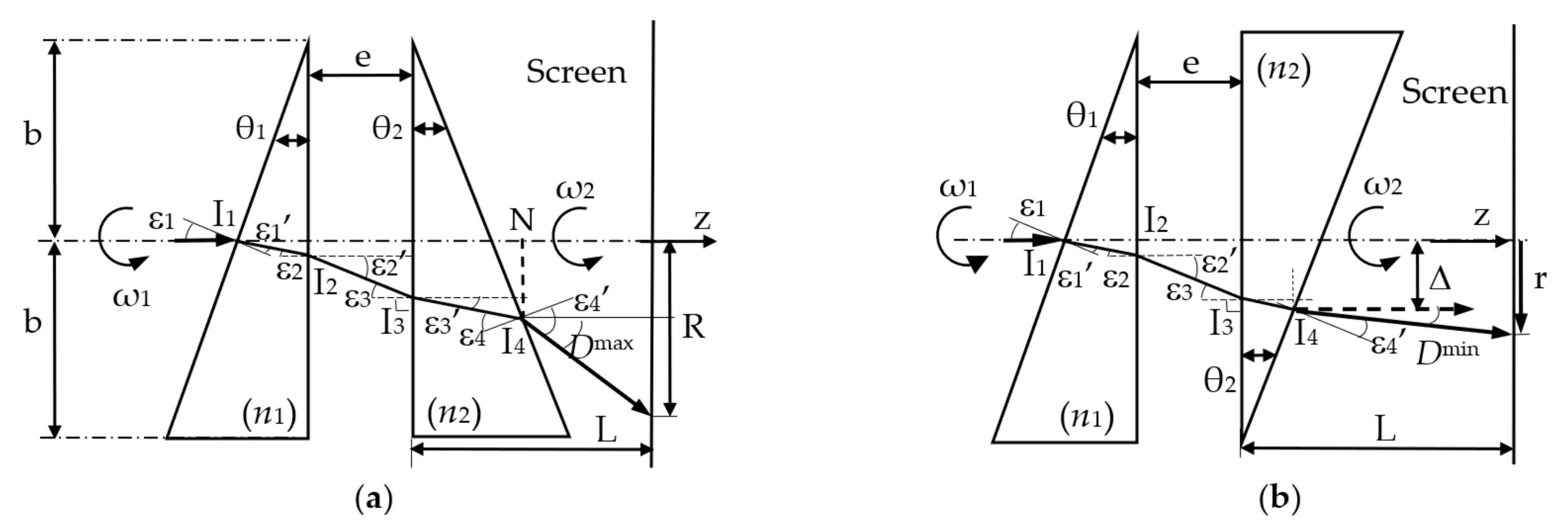
3. Graphical Method to Study the Symmetry of Scan Patterns
4. Results: Simulated Scan Patterns for the Different Scanner Parameters
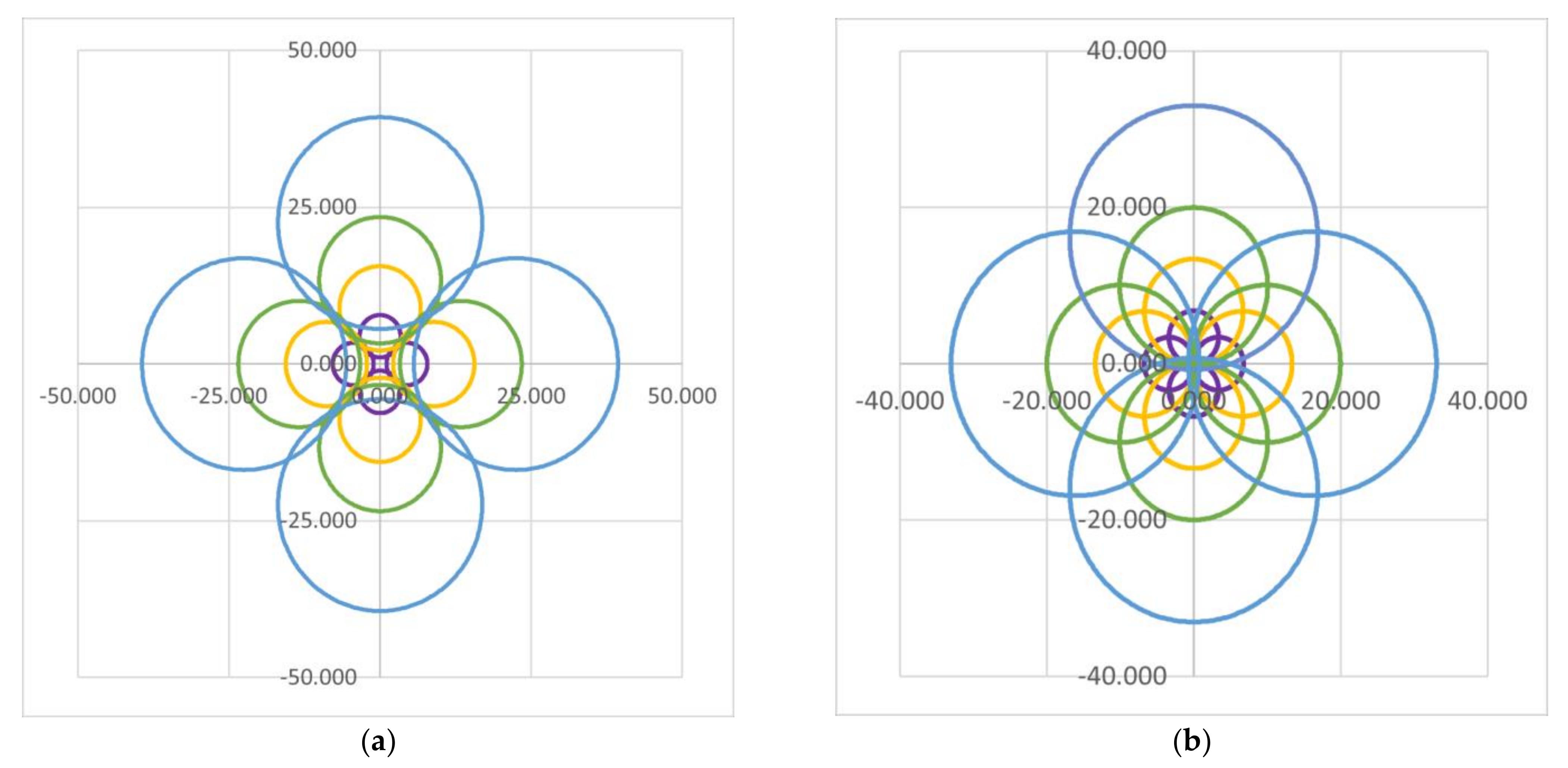
4.1. Scan Patterns Generated for Integer Values of M
4.2. Scan Patterns for Fractional Values of M
4.3. Scan Patterns for Two Particular Cases of M
- (a)
- Prism 1 is fixed in four successive positions, equally spaced with an angle Δφ1 = 90° regarding one another, while Prism 2 is mobile. Therefore, from Equation (2), M = ω2/0 = ∞ (where the notations in Figure 1 were utilized).
- (b)
- Prism 1 is mobile, and Prism 2 is fixed, with the latter positioned in four positions, each with an angle Δφ2 = 90° regarding one another. Therefore, in this case M = 0/ω1 = 0.
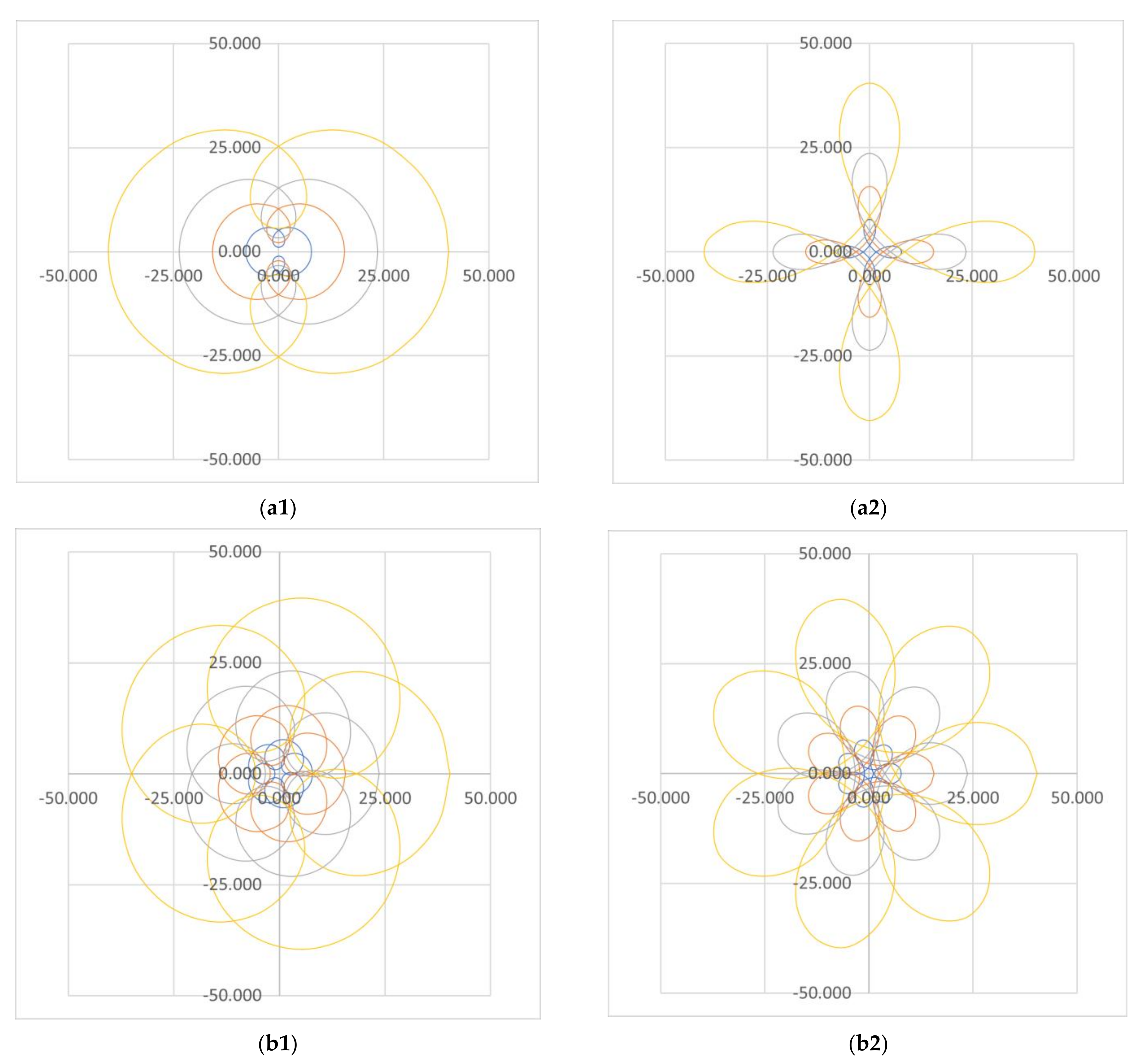
4.4. Scan Patterns Generated for Different Values of k
4.5. Scan Patterns Generated for Different Values of the Prism Angle θ = θ1 = θ2
4.6. Scan Patterns Generated for Different Values of the Refractive Index n = n1 = n2
5. Multi-Parameter Analysis of the Scan Patterns
5.1. Analysis Regarding Integer Values of M
- The symmetries of the patterns are identical for the same M, but with a different number of axes of symmetry about the sign of M—from all the simulations, i.e., from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.
- Inner loops are obtained for M > 0, while outer loops (or petals) are obtained for M < 0, the latter with a reference to rhodonea curves [42]. This aspect can be observed from all the performed simulations, but it has been pointed out in different studies, starting with seminal ones [15]. It does not influence symmetry, but it can be utilized to control the width of the generated loops, as well as their overlap (as pointed out in the following section), to eventually adjust the fill factor (FF) of the patterns.
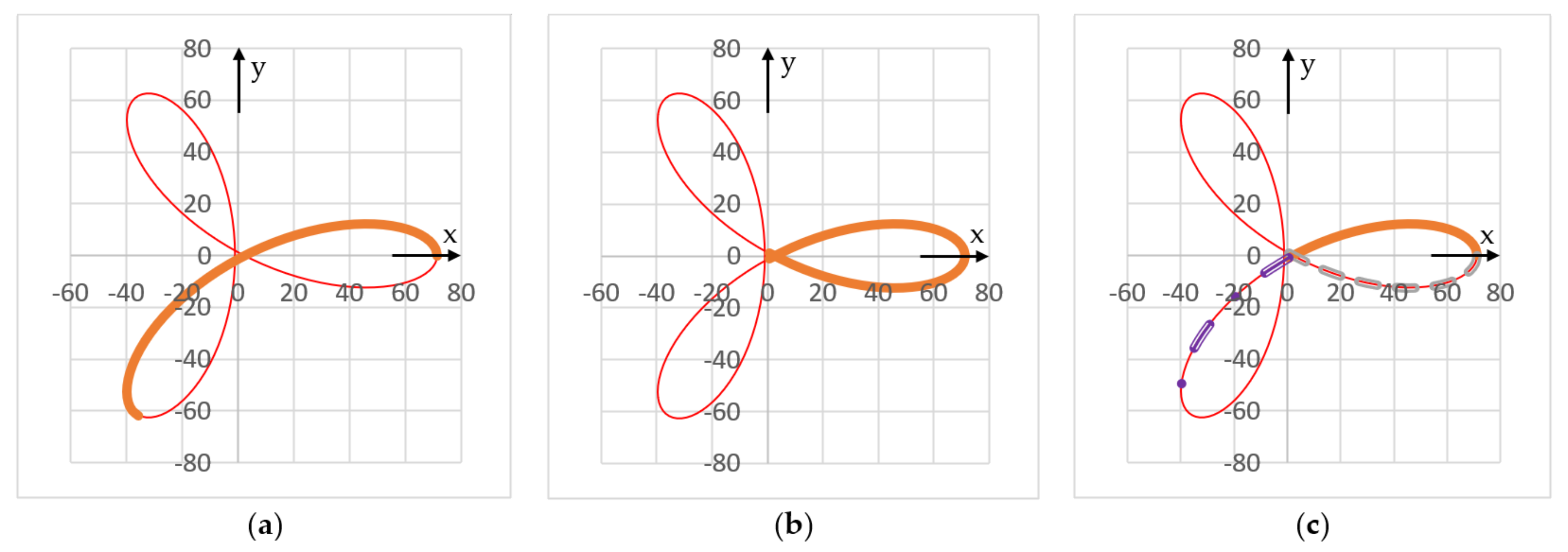
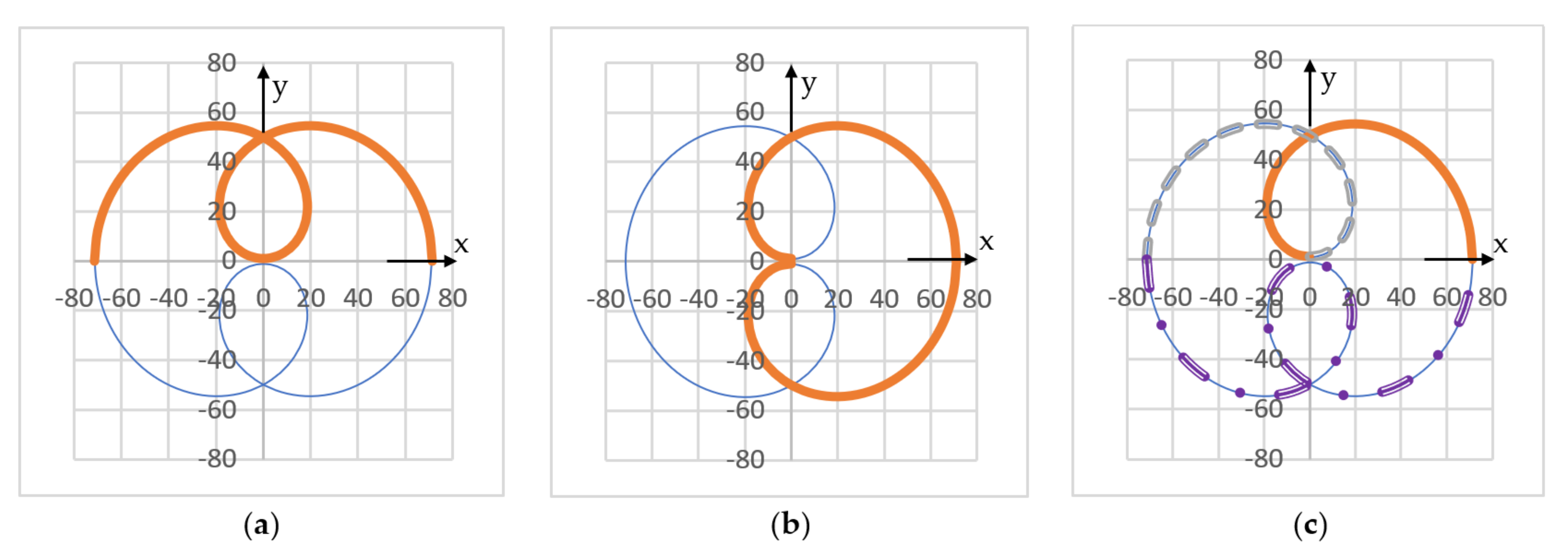
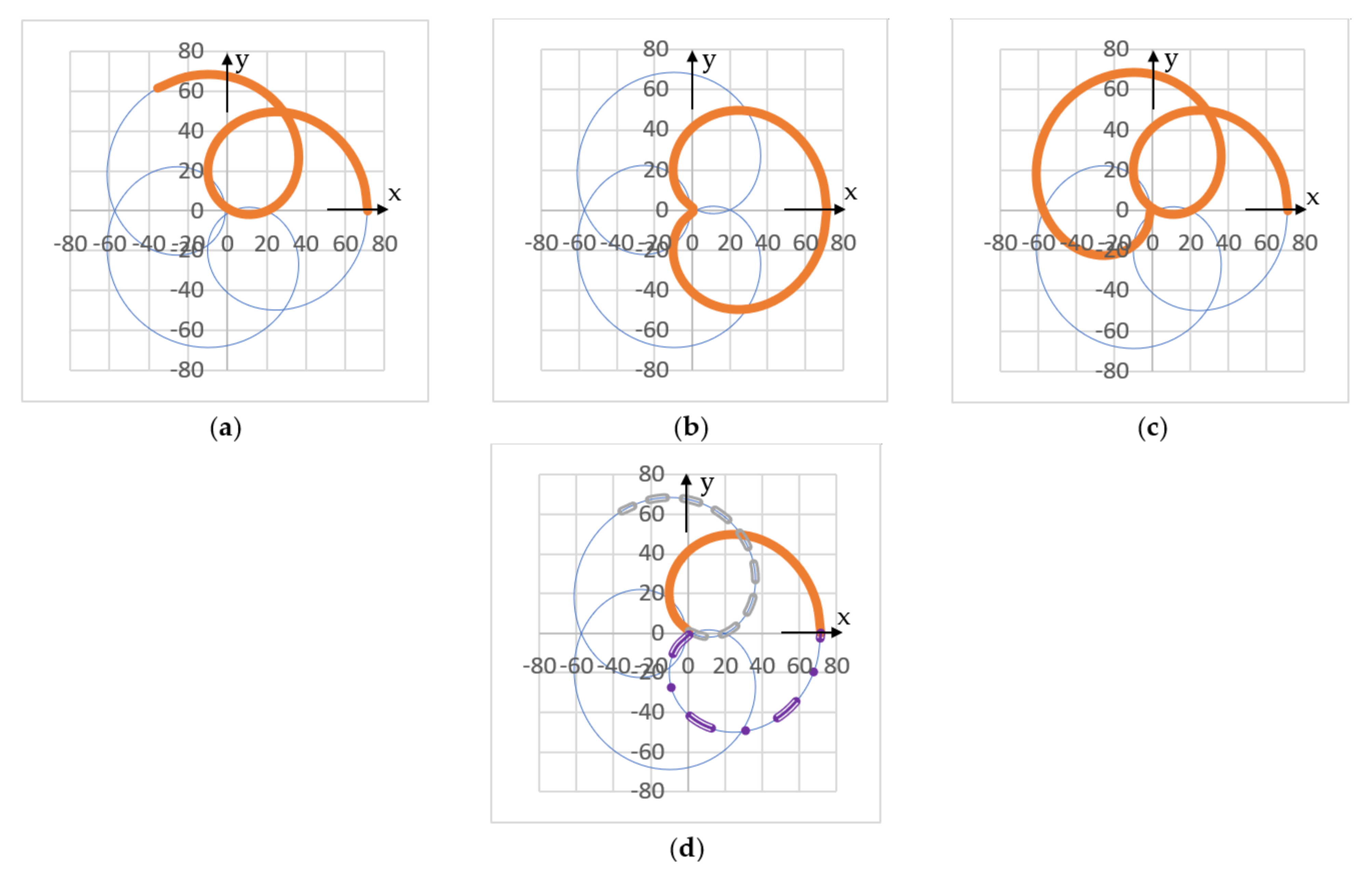
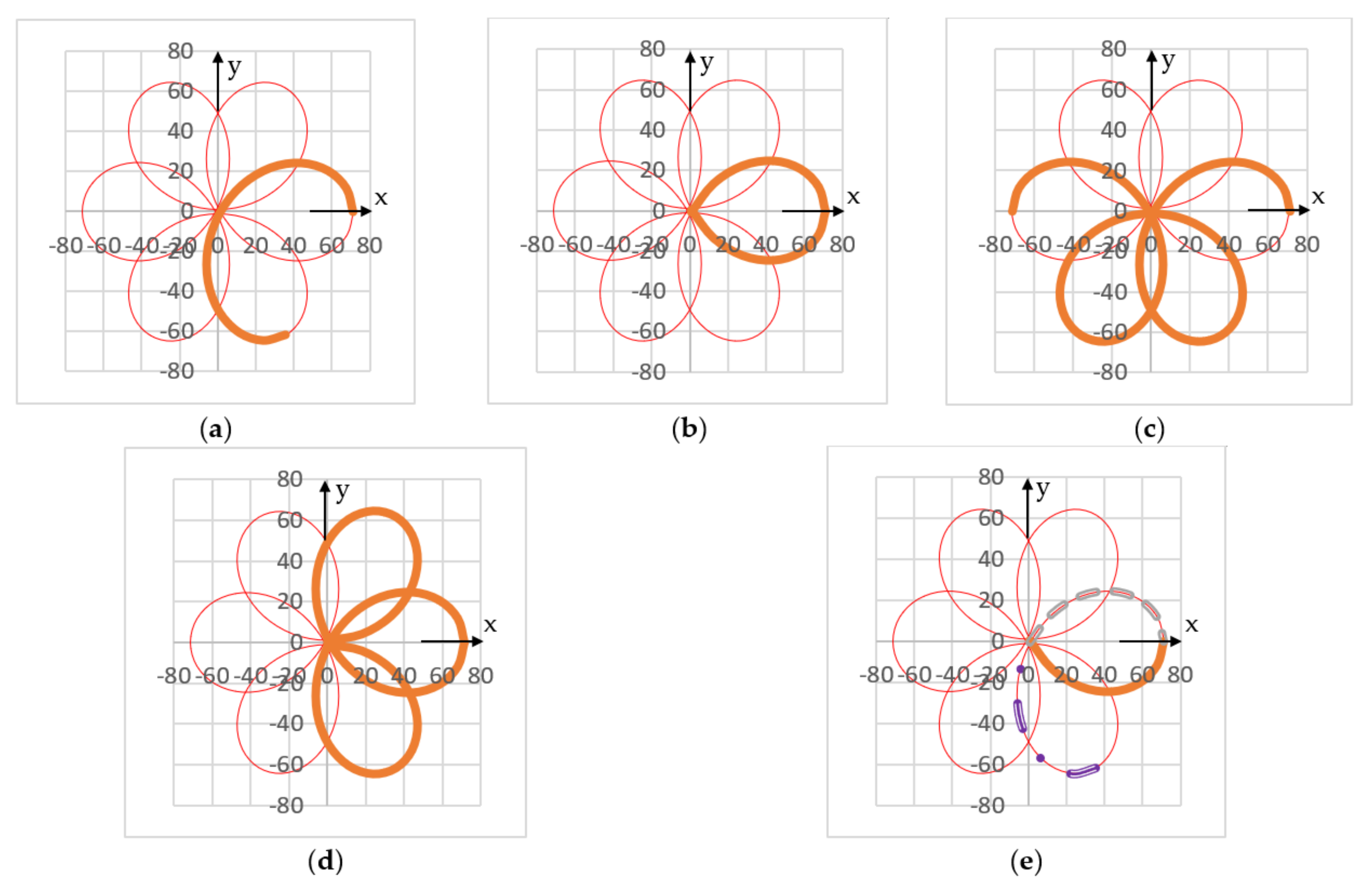
- The number of the axes of symmetry of a scan pattern is equal to its number of loops μ, because from [15,40,41], but also from all the simulations performed for M equal to ±2, ±3, ±4, ±5, and ±6 (i.e., from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 15 and Figure 16), one hasWe can conclude that the M ratio is the parameter that essentially determines the symmetries of the patterns. This rule can be verified from each simulation above. For example, for M = 2, there is only one symmetry axis, while for M = −2, there are three such axes (as noticed in Figure 4 and Figure 5, respectively). This rule is valid for all values of M, except for the particular cases of ±1, 0, and ∞, as presented in Table 1.
- The angle between two consecutive symmetry axes is (as the axes are equally spaced)
- From Equation (8) and observing the results of the performed simulations, a relationship between the number of loops (therefore, between the number of axes of symmetry) can be obtained [41]:
- A higher number of loops is important when a specific application requires to maximize the FF—as most applications do. In such cases, using negative values of M is a method of optimization.
- The number A of axes of symmetry can be observed from the performed simulations, from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 (Table 1). One may notice from the obtained patterns that for an odd value of μ, A = μ, while for an even value of μ, A = 2μ/2. Therefore, in all situationsi.e., except for the particular case of M = 1, for which the pattern becomes a circle centered in O, therefore it has an infinity of symmetry axis.
- From the analysis in Table 1, another form of Equation (10) can be obtained, regarding the number of symmetry axes:
- Structures of symmetry can be defined using (or extracted from) the patterns. We define such a structure of symmetry as a continuous part of the scan pattern that starts from a symmetry axis and can generate the entire pattern by being replicated with certain angles of rotation for an integer number of times.
- In applications, in order to be able to precisely predict the positioning of the (laser) spot at every moment and thus, to have repeatability, integer values of |M| > 1 are of the highest interest, because such values have the fundamental property of generating closed patterns, identical at every full rotation of the slow-moving prism (which is always Prism 1—Figure 1, Figure 2 and Figure 3). Moreover, such closed patterns simplify the control of the scanning process, which is always an issue—regarding both sensors and control structures for scanners of all types, both with oscillatory and with rotational elements [49,50,51].
5.2. Analysis Regarding Fractional Values of M
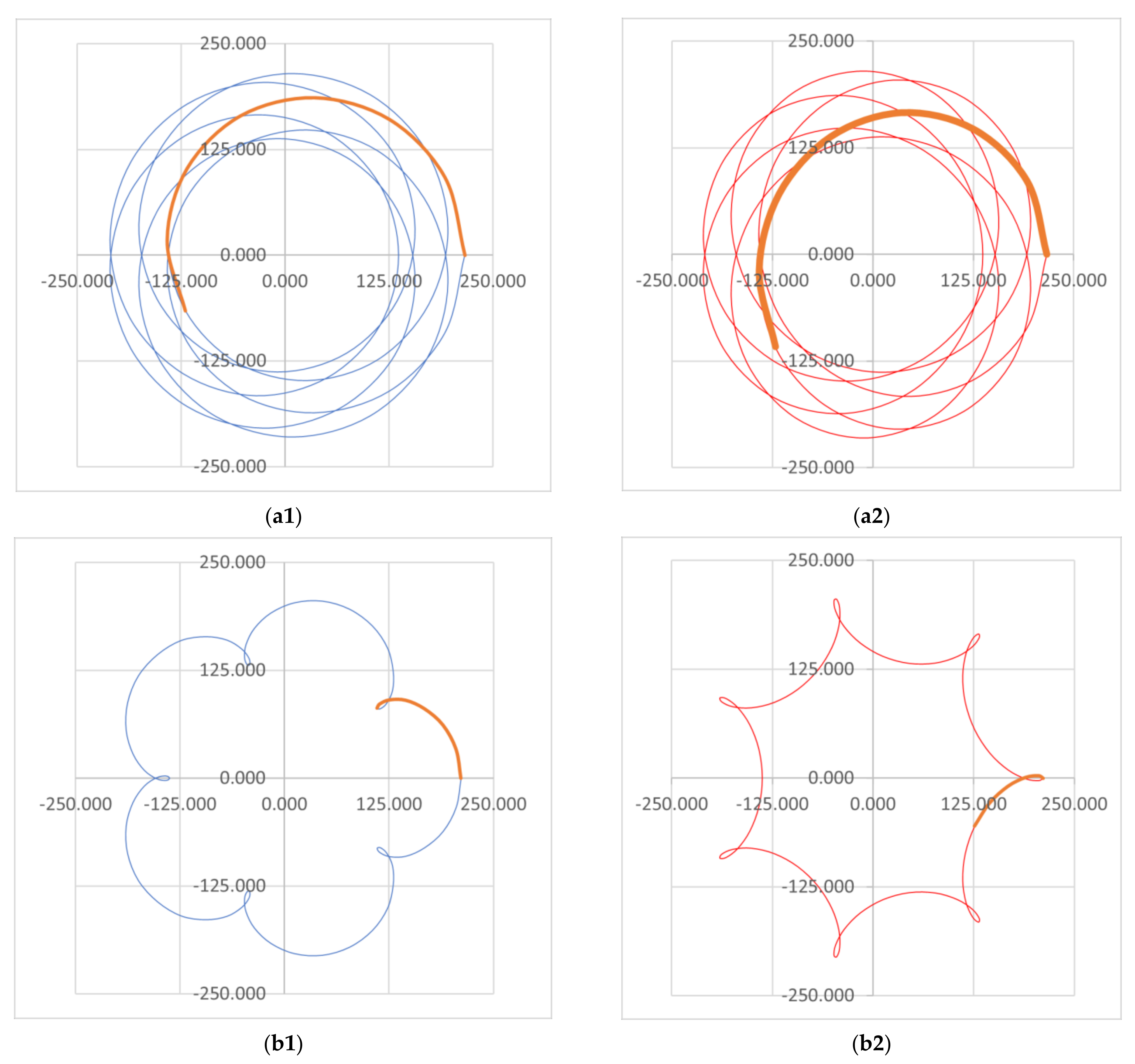
- Fractional values of M were only briefly considered in the present study because, as shown in Figure 12, such M ratios produce multiple spiral-like curves. Such patterns are closed if M is a rational fraction, and in that case, there is a certain symmetry; however, such patterns may be utilized only in part, i.e., for one of the spiral-like patterns. From the point of view of the scanning process, such cases are not of particular interest, as from Equation (1) they are obtained for ω1 > ω2. Therefore, the scan time is the same as in the M > 1 cases, equal to the rotation period of the slow-moving prism (which is, in the M > 1 case, Prism 2—Figure 1, Figure 2 and Figure 3), while the FF is not necessarily higher (as the latter only depends on |M| and the sign of M).
- If M is an irrational fraction, then the generated pattern is not closed, and symmetries cannot be extracted for such specific shapes; however, this latter case can be of interest when a high density (i.e., FF) of the patterns is the scope, in which case symmetries (as well as repeatability and eventually control) of the process might become less important.
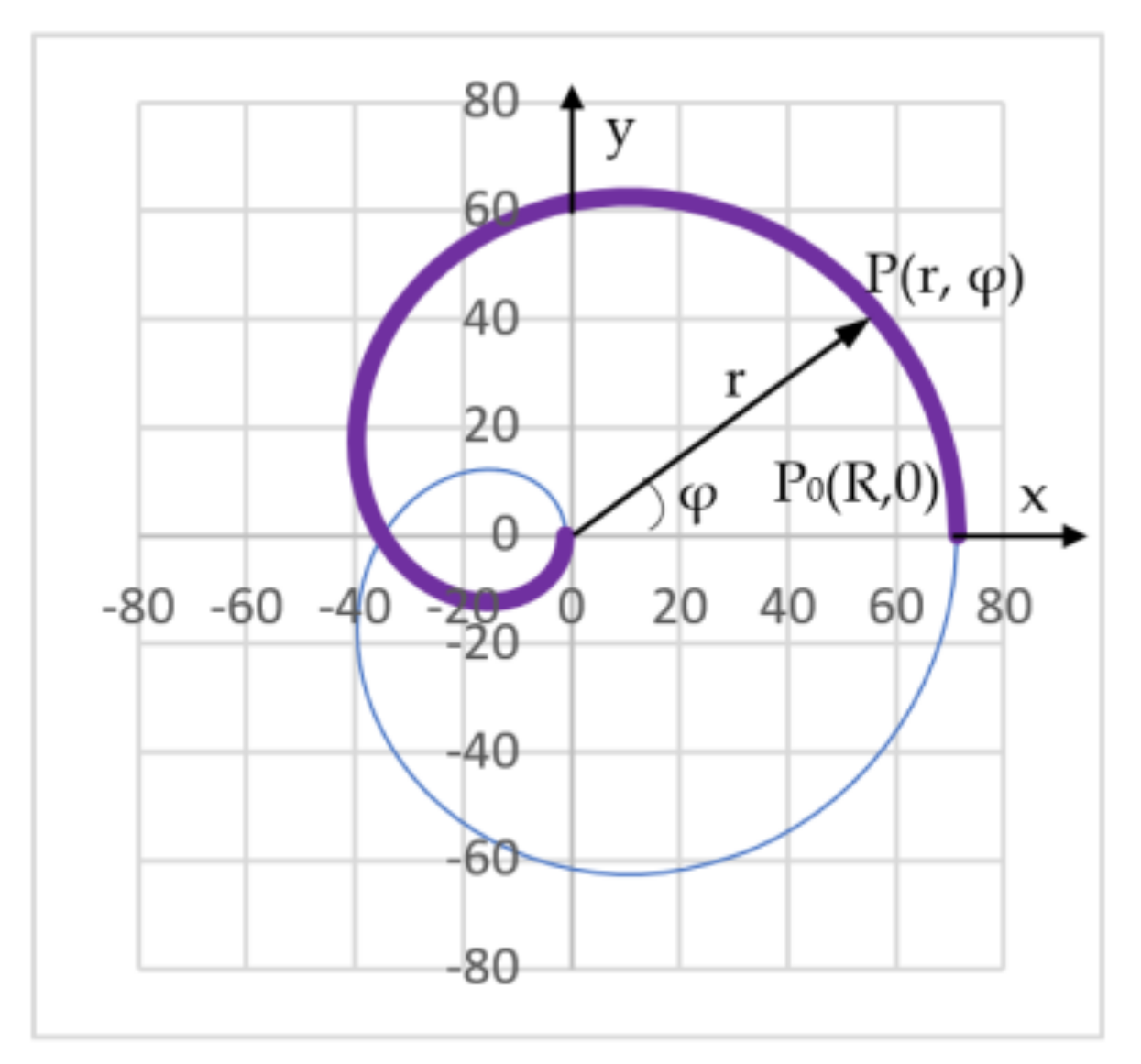
- For the particular cases of M = 0 or M = ∞ (i.e., when the second prism or the first one is fix, respectively, and only the other one is mobile), the produced scan pattern is a circle that is eccentric to the point O. Such a circle has as axis of symmetry the line OP0 = Ox—Figure 13. These circles can be placed in different positions, by modifying the initial phase of the movement, i.e., by shifting the position of the fixed prism.
5.3. Analysis Regarding Other Parameters of the Scanner
- The parameter k determines only the shape of the loops, as shown for example in Figure 14. One may observe that regardless of the value of k, the symmetries given by the parameter M are observed, as well.
- Scan patterns generated for different refractive indexes n of the two (identical) prisms have the same symmetries that are obtained according to the M parameter. However, different dimensions of the scan pattern are obtained (as shown in the examples in Figure 16), according to the minimum and maximum angles, respectively. These angles Dmin, max are provided by Equation (4). They produce the linear deviations (thus, the FOV) deduced and validated experimentally in [41] for all the four possible configurations of such scanners. Such dimensional characteristics are also briefly pointed out in Section 6.
- Similar to the case of the index n, the angle θ of the (identical) prisms produces only a scaling of the scan patterns (Figure 15). These patterns respect the symmetries achieved for the parameter M, as well, with dimensions according to Equation (4).
- The distance e between the two prisms and the distance L from the “a” diopter of the second prism and the scanned plane have no effect on symmetries. As studied in [41], these parameters determine only the dimensions and not the shape of the patterns.
6. Symmetry-Related Geometrical Aspects of the Scan Patterns
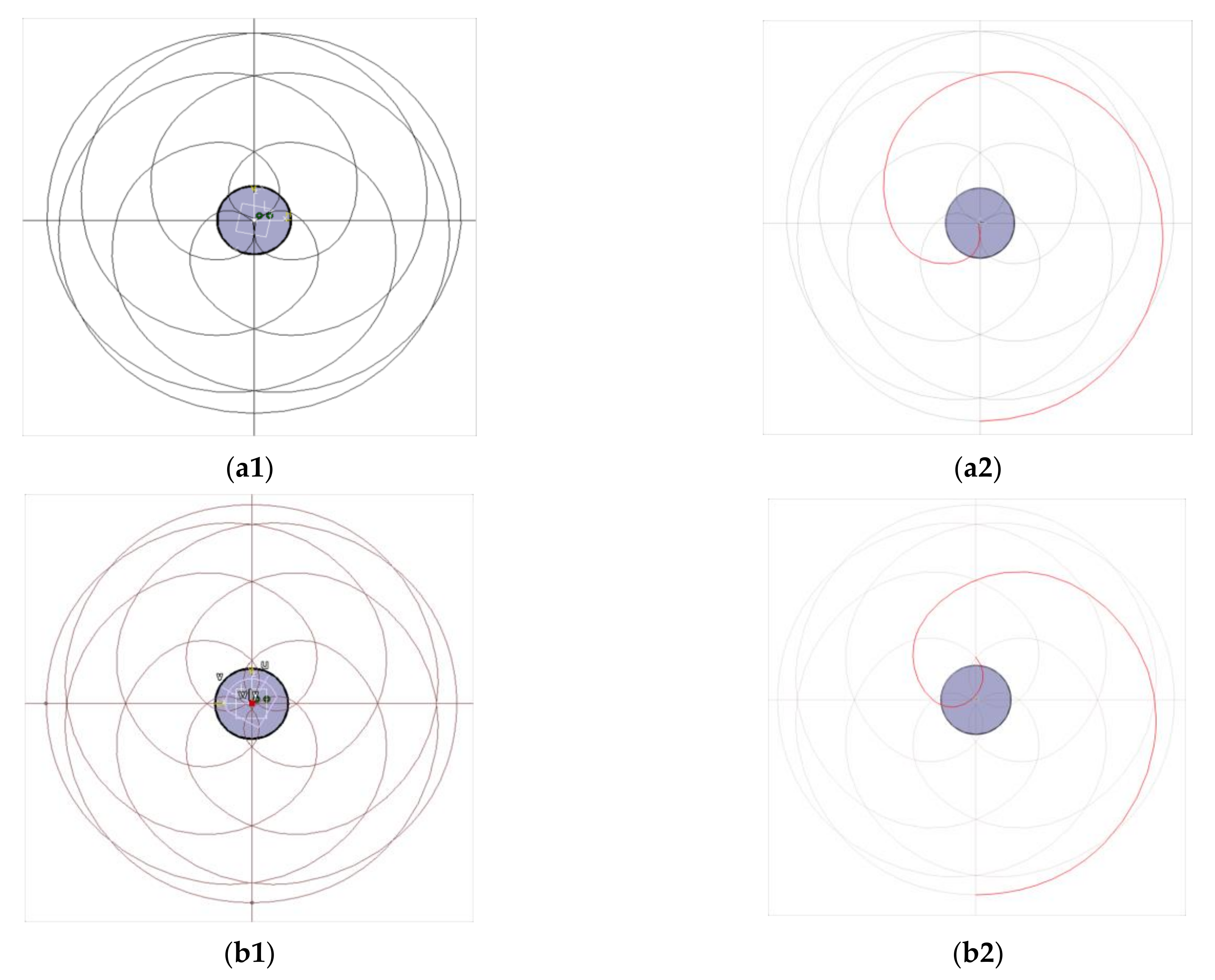
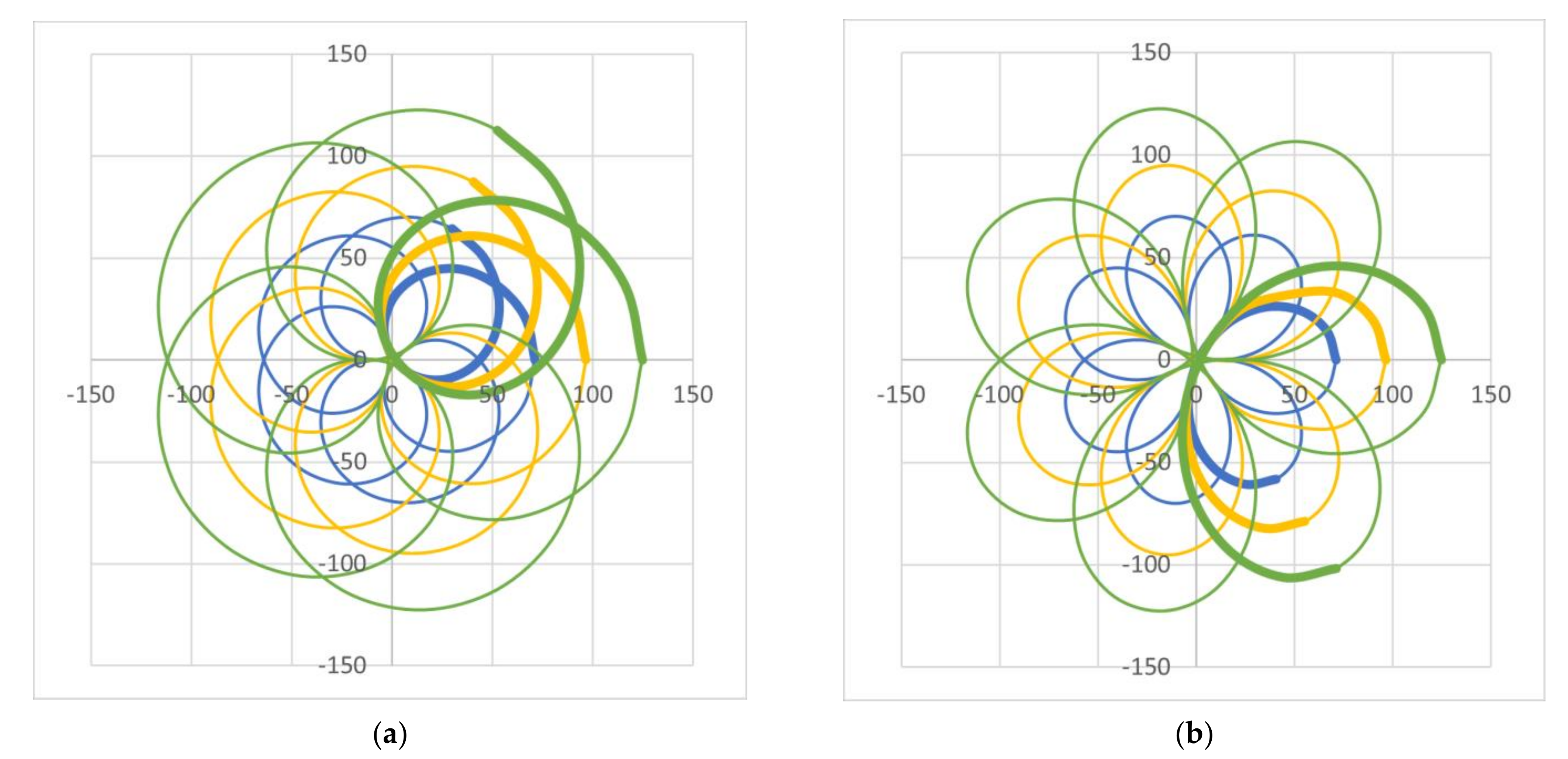
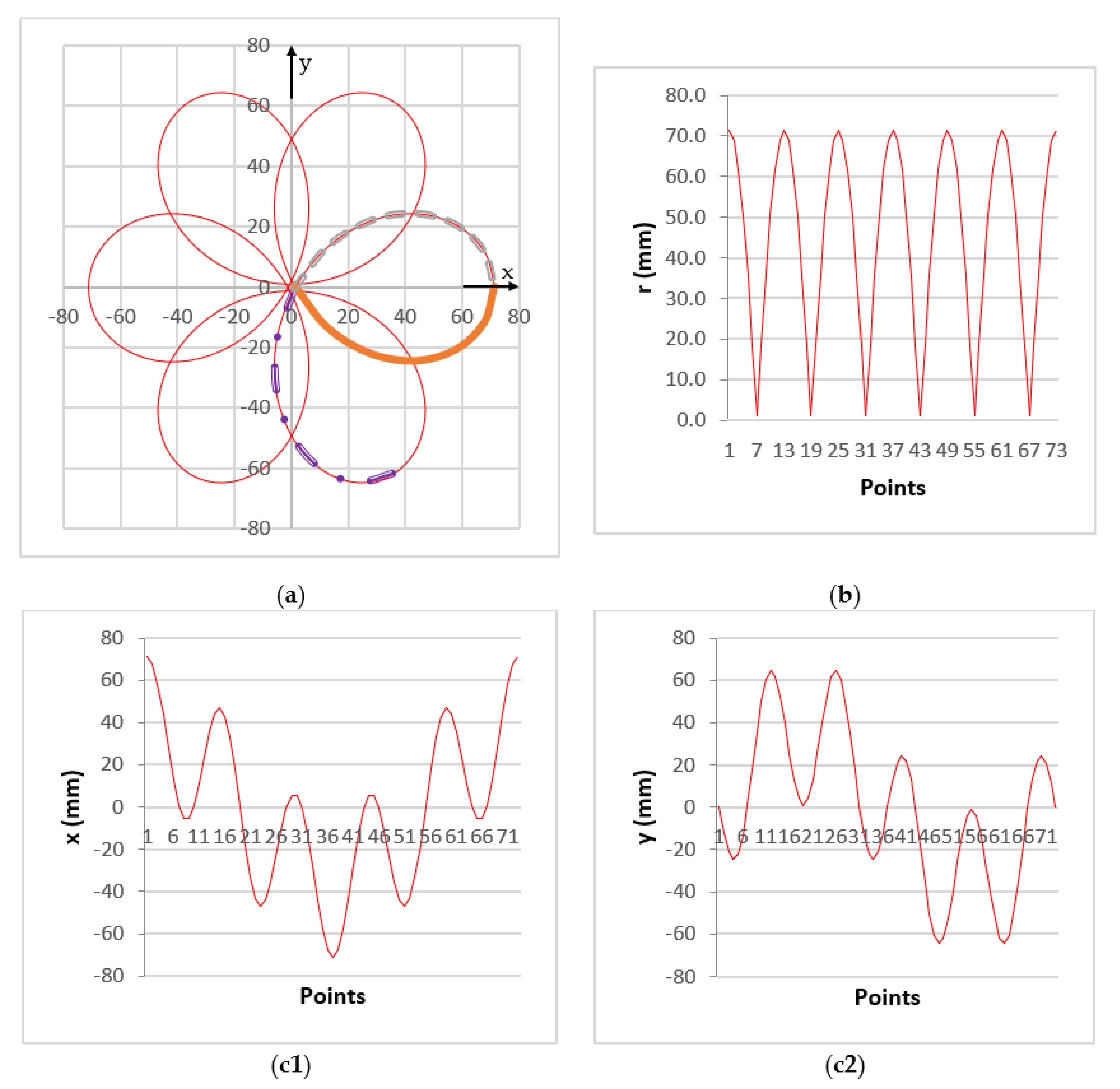
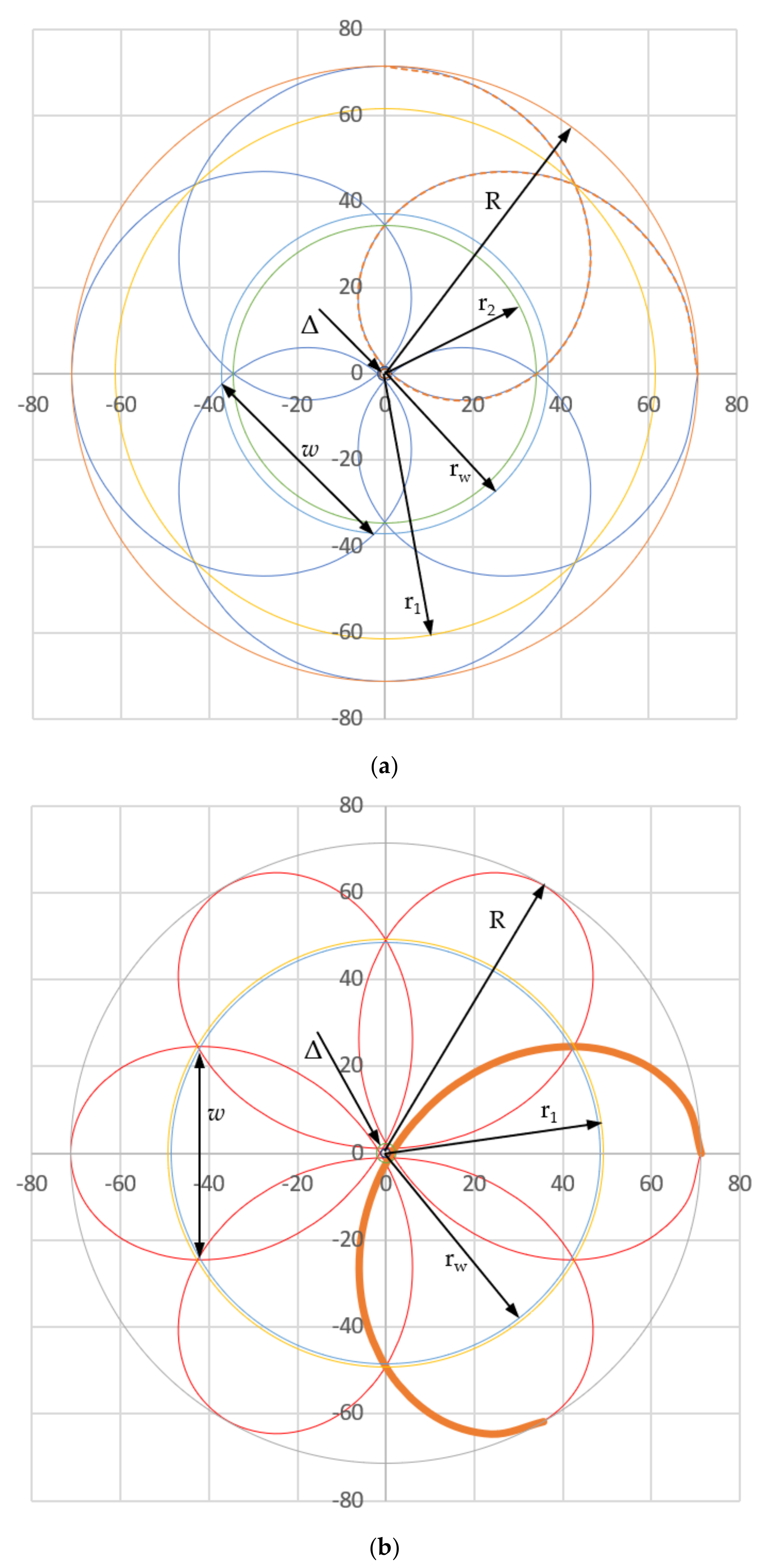
- The FOV of the scanner corresponds to the circle circumscribed to the scan pattern and is characterized by the radius R (Figure 2a). The value of R can be obtained graphically using the simulated pattern in Figure 19 (Table 2). Analytically it has the expressionobtained using the linear deviation through the two prisms (determined analytically in [41]) and the maximum deviation angle expressed in Equation (4) (Figure 2a).
- The radius Δ of the inner circle, inscribed in the scan pattern can be obtained (Table 2), in accordance with the value provided by Equation (7)—identical for M = 5 and M = −5.
7. Experiments
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bass, M. Handbook of Optics, 3rd ed.; Mc. Graw-Hill Inc.: New York, NY, USA, 2009; pp. 30.1–30.68. [Google Scholar]
- Marshall, G.F.; Stutz, G.E. (Eds.) Handbook of Optical and Laser Scanning, 2nd ed.; CRC Press: London, UK, 2011. [Google Scholar]
- Kiyokura, T.; Ito, T.; Sawada, R. Small Fourier transform spectroscope using an integrated prism-scanning interferometer. Appl. Spectrosc. 2001, 55, 1628–1633. [Google Scholar] [CrossRef]
- Garcia-Torales, G.; Strojnik, M.; Paez, G. Risley prisms to control wave-front tilt and displacement in a vectorial shearing interferometer. Appl. Opt. 2002, 41, 1380–1384. [Google Scholar] [CrossRef]
- Oka, K.; Kaneko, T. Compact complete imaging polarimeter using birefringent wedge prisms. Opt. Express 2003, 11, 1510–1519. [Google Scholar] [CrossRef]
- Tao, X.; Cho, H.; Janabi-Sharifi, F. Optical design of a variable view imaging system with the combination of a telecentric scanner and double wedge prisms. Appl. Opt. 2010, 49, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Cao, J.; Hao, Q.; Zhang, F.; Cheng, Y.; Kong, X. Superresolution imaging and field of view extension using a single camera with Risley prisms. Rev. Sci. Instrum. 2019, 90, 33701. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Liu, X.; Gong, W.; Sun, W.; Sun, J. Prelocation image stitching method based on flexible and precise boresight adjustment using Risley prisms. JOSA A 2019, 36, 305–311. [Google Scholar] [CrossRef]
- Li, A.; Yi, W.; Zuo, Q.; Sun, W. Performance characterization of scanning beam steered by tilting double prisms. Opt. Express 2016, 24, 23543–23556. [Google Scholar] [CrossRef]
- Li, A.; Jiang, X.; Sun, J.; Wang, L.; Li, Z.; Liu, L. Laser coarse-fine coupling scanning method by steering double prisms. Appl. Opt. 2012, 51, 356–364. [Google Scholar] [CrossRef]
- Florea, C.; Sanghera, J.; Aggarwal, I. Broadband beam steering using chalcogenide-based Risley prisms. Opt. Eng. 2011, 50, 033001. [Google Scholar]
- Zhou, Y.; Fan, D.; Fan, S.; Chen, Y.; Liu, G. Laser scanning by rotating polarization gratings. Appl. Opt. 2016, 55, 5149–5157. [Google Scholar] [CrossRef]
- Roy, G.; Cao, X.; Bernier, R.; Roy, S. Enhanced scanning agility using a double pair of Risley prisms. Appl. Opt. 2015, 54, 10213–10226. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Gong, W.; Zhang, Y.; Liu, X. Investigation of scan errors in the three-element Risley prism pair. Opt. Express 2018, 26, 25322–25335. [Google Scholar]
- Marshall, G.F. Risley Prism Scan Patterns. Proc. SPIE 1999, 3787, 74–86. [Google Scholar]
- Yang, Y. Analytic solution of free space optical beam steering using Risley prisms. J. Light. Technol. 2008, 26, 3576–3583. [Google Scholar] [CrossRef]
- Li, Y. Third-order theory of the Risley-prism-based beam steering system. Appl. Opt. 2011, 50, 679–686. [Google Scholar] [CrossRef]
- Li, Y. Closed form analytical inverse solutions for Risley-prism-based beam steering systems in different configurations. Appl. Opt. 2011, 50, 4302–4309. [Google Scholar] [CrossRef]
- Lai, S.-F.; Lee, C.-C. Analytic inverse solutions for Risley prisms in four different configurations for positing and tracking systems. Appl. Opt. 2018, 57, 10172–10182. [Google Scholar] [CrossRef]
- Montagu, J. Scanners-galvanometric and resonant. In Encyclopedia of Optical and Photonic Engineering; CRC Press: Boca Raton, FL, USA, 2003; pp. 2465–2487. [Google Scholar]
- Benner, W.R. Laser Scanners: Technologies and Applications; Pangolin Laser Systems Inc.: Lexington, KY, USA, 2016. [Google Scholar]
- Duma, V.-F.; Tankam, P.; Huang, J.; Won, J.J.; Rolland, J.P. Optimization of galvanometer scanning for Optical Coherence Tomography. Appl. Opt. 2015, 54, 5495–5507. [Google Scholar] [CrossRef]
- Duma, V.-F. Laser scanners with oscillatory elements: Design and optimization of 1D and 2D scanning functions. Appl. Math. Model. 2019, 67, 456–476. [Google Scholar] [CrossRef]
- Grulkowski, I.; Gorczynska, I.; Szkulmowski, M.; Szlag, D.; Szkulmowska, A.; Leitgeb, R.A.; Kowalczyk, A.; Wojtkowski, M. Scanning protocols dedicated to smart velocity ranging in Spectral OCT. Opt. Express 2009, 17, 23736–23754. [Google Scholar] [CrossRef]
- Ju, M.J.; Heisler, M.; Athwal, A.; Sarunic, M.V.; Jian, Y. Effective bidirectional scanning pattern for optical coherence tomography angiography. Biomed. Opt. Express 2018, 9, 2336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; You, X.; Wang, Y.; Gu, K.; Liu, C.; Tan, J. The alpha-beta circular scanning with large range and low noise. J. Microsc. 2017, 266, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Carrasco-Zevallos, O.M.; Viehland, C.; Keller, B.; McNabb, R.P.; Kuo, A.N.; Izatt, J.A. Constant linear velocity spiral scanning for near video rate 4D OCT ophthalmic and surgical imaging with isotropic transverse sampling. Biomed. Opt. Express 2018, 9, 5052. [Google Scholar] [CrossRef] [PubMed]
- Hwang, K.; Seo, Y.-H.; Ahn, J.; Kim, P.; Jeong, K.-H. Frequency selection rule for high definition and high frame rate Lissajous scanning. Sci. Rep. 2017, 7, 14075. [Google Scholar] [CrossRef] [Green Version]
- Tanguy, Q.A.A.; Gaiffe, O.; Passilly, N.; Cote, J.-M.; Cabodevila, G.; Bargiel, S.; Lutz, P.; Xie, H.; Gorecki, C. Real-time Lissajous imaging with a low-voltage 2-axis MEMS scanner based on electrothermal actuation. Opt. Express 2020, 28, 8512. [Google Scholar] [CrossRef] [PubMed]
- Draelos, M.; Viehland, C.; McNabb, R.P.; Kuo, A.N.; Izatt, J.A. Adaptive point-scan imaging beyond the frame rate–resolution limit with scene-reactive scan trajectories. Optica 2022, 9, 1276–1288. [Google Scholar] [CrossRef]
- Li, Y. Beam deflection and scanning by two-mirror and two-axis systems of different architectures: A unified approach. Appl. Opt. 2008, 47, 5976–5985. [Google Scholar] [CrossRef] [PubMed]
- Duma, V.-F. Polygonal mirror laser scanning heads: Characteristic functions. Proc. Rom. Acad. Ser. A 2017, 18, 25–33. [Google Scholar]
- Duma, V.-F.; Duma, M.-A. Optomechanical Analysis and Design of Polygon Mirror-Based Laser Scanners. Appl. Sci. 2022, 12, 5592. [Google Scholar] [CrossRef]
- Available online: https://www.scanlab.de/en/products/scan-systems (accessed on 17 December 2022).
- Gora, M.J.; Suter, M.J.; Tearney, G.J.; Li, X. Endoscopic optical coherence tomography: Technologies and clinical applications. Biomed. Opt. Express 2017, 8, 2405–2444. [Google Scholar] [CrossRef] [Green Version]
- Cogliati, A.; Canavesi, C.; Hayes, A.; Tankam, P.; Duma, V.-F.; Santhanam, A.; Thompson, K.P.; Rolland, J.P. MEMS-based handheld scanning probe with pre-shaped input signals for distortion-free images in Gabor-Domain Optical Coherence Microscopy. Opt. Express 2016, 24, 13365–13374. [Google Scholar] [CrossRef]
- Strathman, M.; Liu, Y.; Keeler, E.G.; Song, M.; Baran, U.; Xi, J.; Sun, M.-T.; Wang, R.; Li, X.; Lin, L.Y. MEMS scanning micromirror for optical coherence tomography. Biomed. Opt. Express 2015, 6, 211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piyawattanametha, W.; Ra, H.; Qiu, Z.; Friedland, S.; Liu, J.T.C.; Loewke, K.; Kino, G.S.; Solgaard, O.; Wang, T.D.; Mandella, M.J.; et al. In vivo near-infrared dual-axis confocal microendoscopy in the human lower gastrointestinal tract. J. Biomed. Opt. 2012, 17, 021102. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, L.; Sun, J.; Zhou, Y.; Zhong, X.; Luan, Z.; Liu, D.; Yan, A.; Xu, N. An Integrated Test-Bed for PAT Testing and Verification of Inter-Satellite Lasercom Terminals. Proc. SPIE 2007, 6709, 670904. [Google Scholar]
- Duma, V.-F.; Schitea, A. Laser scanners with rotational Risley prisms: Exact scan patterns. Proc. Rom. Acad. Ser. A 2018, 19, 53–60. [Google Scholar]
- Duma, V.-F.; Dimb, A.-L. Exact Scan Patterns of Rotational Risley Prisms Obtained with a Graphical Method: Multi-Parameter Analysis and Design. Appl. Sci. 2021, 11, 8451. [Google Scholar] [CrossRef]
- Erb, W. Rhodonea Curves as Sampling Trajectories for Spectral Interpolation on the Unit Disk. Constr. Approx. 2020, 53, 281–318. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Liu, L.; Yun, M.; Wan, L.; Zhang, M. Distortion of beam shape by a rotating double prism wide-angle laser beam scanner. Opt. Eng. 2006, 45, 043004. [Google Scholar] [CrossRef]
- Lavigne, V.; Ricard, B. Fast Risley prisms camera steering system: Calibration and image distortions correction through the use of a three-dimensional refraction model. Opt. Eng. 2007, 46, 43201. [Google Scholar]
- Dimb, A.-L.; Duma, V.-F. Experimental validations of simulated exact scan patterns of rotational Risley prisms scanners. Proc. SPIE 2019, 11354, 113541U. [Google Scholar]
- Dimb, A.-L.; Duma, V.-F. Simulations and experiments of laser scanning with a pair of rotational Risley prisms. Proc. SPIE 2022, 12170, 1217009. [Google Scholar]
- Garcia-Torales, G. Risley prisms applications: An overview. Proc. SPIE 2022, 12170, 121700H. [Google Scholar]
- Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=147 (accessed on 17 December 2022).
- Mnerie, C.; Preitl, S.; Duma, V.-F. Galvanometer-based scanners: Mathematical model and alternative control structures for improved dynamics and immunity to disturbances. Int. J. Struct. Stab. Dyn. 2017, 17, 1740006. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y. Control of a Digital Galvanometer Scanner Using a Discrete-Time Sliding-Mode Variable-Structure Controller Based on a Decoupled Disturbance Compensator. Appl. Sci. 2021, 11, 9788. [Google Scholar] [CrossRef]
- Hayakawa, T.; Watanabe, T.; Senoo, T.; Ishikawa, M. Gain-compensated sinusoidal scanning of a galvanometer mirror in proportional-integral-differential control using the pre-emphasis technique for motion-blur compensation. Appl. Opt. 2016, 55, 5640–5646. [Google Scholar] [CrossRef]





| |M| | Ratio M | Figure | Number of Loops | Number of Axes of Symmetry * A | Structures of Symmetry | Remarks | |
| Number S | [φmin, φmax] | ||||||
| 0 | 0 | 13b | 1 | 1 | - | - | The scan pattern is a circle eccentric to O |
| 1 | 1 | - | 0 | ∞ | ∞ | - | The scan pattern is a circle centered in O |
| −1 | - | 2 | 2 | 1 | [0, π] [−π/2, π/2] | Elliptic scan pattern, with the main axes (of symmetry) on Ox and Oy | |
| 2 | 2 | 4 | 1 | 1 | 1 | [0, π] | Symmetry axis: Ox |
| −2 | 5 | 3 | 3 | 2 | [0, 2π/3] [−π/3, π/3] | Symmetry axis on the axis of each loop | |
| 3 | 3 | 6 | 2 | 2 | 2 | [0, π] [−π/2, π/2] | Symmetry axes: Ox and Oy |
| −3 | 7 | 4 | 4 | 4 | [0, π/2] [−π/4, π/4] [0, π] [−π/2, π/2] | Symmetry axes: Ox, Oy (which are in this case the symmetry axes of the loops), as well as the first and second bisector | |
| 4 | 4 | 8 | 3 | 3 | 3 | [0, 2π/3] [−π/3, π/3] [0, π] | Symmetry axes: the symmetry axes of the loops, from which one is Ox |
| −4 | 9 | 5 | 5 | 3 | [0, 2π/5] [−π/5, π/5] [0, π] [−π/2, π/2] | From the angular intervals of the structures of symmetry defined in this Section 5.1, for each case corresponding to or |M| > 5 (therefore for several loops/axes of symmetry ), there are four possible methods of constructing the full scan pattern without considering all its points: - by rotating the structure of symmetry with angles of 2π/μ for μ times (for the first two structures, of angular intervals [0, 2π/μ] or [−π/μ, π/μ]). - by using a symmetry with regard to Ox or with regard to Oy, for the third and fourth structure, respectively (defined by the angular intervals [0, π] and [−π/2, π/2], respectively, because of the way the structures of symmetry were defined, with the first point on one of the axes Ox or Oy, just like the patterns). | |
| 5 | 5 | 10 | 4 | 4 | 4 | [0, π/2] [−π/4, π/4] [0, π] [−π/2, π/2] | |
| −5 | 11 | 6 | 6 | 4 | [0, π/2] [−π/4, π/4] [0, π] [−π/2, π/2] | ||
| 6 | 6 | 15(b1) 16(a) | 5 | 5 | 4 | [0, 2π/5] [−π/5, π/5] [0, π] [−π/2, π/2] | |
| −6 | 15(b2) 16(b) | 7 | 7 | 4 | [0, 2π/7] [−π/7, π/7] [0, π] [−π/2, π/2] | ||
| ∞ | ∞ | 13a | 1 | 1 | - | - | The scan pattern is a circle eccentric to O |
| Parameters of the Patterns Obtained Graphically from Figure 19 | Value of the Ratio M = ω2/ω1 | |||
|---|---|---|---|---|
| Figure 19a: M = 5 | Figure 19b: M = −5 | |||
| Linear/Radial (mm) | Angular * (°) | Linear/Radial (mm) | Angular * (°) | |
| Polar coordinates of the points that define the FOV/circle circumscribed to the scan pattern (R) | 71.265 | 0/90/180/270 | 71.265 | 0/60/120/180/240/300 |
| Polar coordinates of the points that define the first (i.e., outer) intersection of the lobes (r1) | 61.455 | 45/135/225/315 | 48.459 | 30/90/150/210/270/330 |
| Maximum width of the lobes (w) | 37.121 | 3.591/86.409 93.591/176.409 183.591/266.409 273.591/356.409 | 49.165 | 29.505/30.495 89.505/90.495 149.505/150.495 209.505/210.495 269.505/270.495 229.505/230.495 |
| Polar coordinates of the points that define the second (i.e., middle) intersection (r2) | 34.442 | 0/90/180/270 | 2.205 | 30/90/150/210/270/330 |
| Polar coordinates of the points that define the third (i.e., inner) intersection (r3) | 1.550 | 0/90/180/270 | - | - |
| Polar coordinates of the circle inscribed in the scan pattern (Δ) | 1.069 | 0/90/180/270 | 1.069 | 30/90/150/210/270/330 |
| Ratio of the Rotational Velocities, Equation (2) | M = 2 | M = −2 | M = 6 | M = −6 |
|---|---|---|---|---|
| Mean value of the FOV radius: | 70.846 | 72.692 | 72.125 | 72.544 |
| Standard deviation of the FOV radius: | 0.001 | 0.387 | 0.536 | 0.858 |
| Relative error: | −0.588 | 2.003 | 1.206 | 1.794 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimb, A.-L.; Duma, V.-F. Symmetries of Scan Patterns of Laser Scanners with Rotational Risley Prisms. Symmetry 2023, 15, 336. https://doi.org/10.3390/sym15020336
Dimb A-L, Duma V-F. Symmetries of Scan Patterns of Laser Scanners with Rotational Risley Prisms. Symmetry. 2023; 15(2):336. https://doi.org/10.3390/sym15020336
Chicago/Turabian StyleDimb, Alexandru-Lucian, and Virgil-Florin Duma. 2023. "Symmetries of Scan Patterns of Laser Scanners with Rotational Risley Prisms" Symmetry 15, no. 2: 336. https://doi.org/10.3390/sym15020336







