Novel Properties of q-Sine-Based and q-Cosine-Based q-Fubini Polynomials

Abstract

The main purpose of this paper is to consider q-sine-based and q-cosine-Based q-Fubini polynomials and is to investigate diverse properties of these polynomials. Furthermore, multifarious correlations including q-analogues of the Genocchi, Euler and Bernoulli polynomials, and the q-Stirling numbers of the second kind are derived. Moreover, some approximate zeros of the q-sinebased and q-cosine-Based q-Fubini polynomials in a complex plane are examined, and lastly, these zeros are shown using figures.

1. Introduction

Special polynomials possess an important role in mathematics such as solving numerical problems, determining the composition of certain molecules and compounds, determining combinatorics relations, describing the trajectory of projectiles, solving difference equations, approximation theory, cost analysis in economics, determining pressure in applications of fluid dynamics, and so on, see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Recently, many properties and applications have been studied and investigated by many authors, especially determining approximate zeros in conjunction with showing them in figures. In this paper, we consider q-sine-based and q-cosine-Based q-Fubini polynomials and then investigate diverse properties of these polynomials. Furthermore, we provide several correlations with many earlier q-polynomials. Moreover, we compute the first few q-sine-based and q-cosine-Based q-Fubini polynomials. Finally, we determine some approximate zeros of the q-sine-based and q-cosine-Based q-Fubini polynomials in a complex plane, which are shown in figures and tables.

A brief review of q-calculus taken from (see [4,5,10,11]) is given as follows.

For q, being a complex number with $0<q<1$, the q-number and q-factorial are introduced by

$${\left[z\right]}_q=\frac{1-q^z}{1-q}$$

and

$${\left[0\right]}_q!=1\mathrm{and}{\left[z\right]}_q!=\prod _{u=1}^z{\left[u\right]}_q={\left[1\right]}_q{\left[2\right]}_q\cdots {\left[z\right]}_q\mathrm{for}z\in \mathbb{N},$$

respectively.

The q-extensions of Gauss binomial coefficients are provided by

$${\left(\begin{array}{c}z\hfill \\ u\hfill \end{array}\right)}_q=\frac{{\left[z\right]}_q!}{{\left[u\right]}_q!{[z-u]}_q!}\mathrm{for}u=0,1,\cdots ,z.$$

The q-extensions of the functions ${(x_1+x_2)}^z$ and ${(x_1-x_2)}^z$ are provided by

$${(x_1\oplus x_2)}_q^z=\sum _{u=0}^z{\left(\begin{array}{c}z\hfill \\ u\hfill \end{array}\right)}_q{q}^{u(u-1)/2}{x}_1^{z-u}{x}_2^u\mathrm{for}z\in {\mathbb{N}}_0.$$

(1)

$${(x_1\ominus x_2)}_q^z=\sum _{u=0}^z{\left(\begin{array}{c}z\hfill \\ \gamma \hfill \end{array}\right)}_q{q}^{u(u-1)/2}{x}_1^{z-u}{(-x_2)}^u\mathrm{for}z\in {\mathbb{N}}_0.$$

The q-analogues of the usual exponential function are provided by

$$e_q\left(x_1\right)=\sum _{z=0}^{\infty }\frac{x_1^z}{{\left[z\right]}_q!}0<\mid q\mid <1;\mid x_1\mid <{\mid 1-q\mid }^{-1}$$

(2)

and

$$E_q\left(x_1\right)=\sum _{z=0}^{\infty }\frac{q^{\left(\genfrac{}{}{0pt}{}{z}{2}\right)}}{{\left[z\right]}_q!}{x}_1^{z}0<\mid q\mid <1;x_1\in \mathbb{C},$$

(3)

which satisfies the following relations (see [4,5,10,11])

$$e_q\left(x_1\right)E_q(-x_1)=1,$$

$$e_q\left(x_1\right)E_q\left(x_2\right)=e_q\left({(x_1\oplus x_2)}_q\right)$$

and

$$e_q\left(x_1\right)E_q(-x_2)=e_q\left({(x_1\ominus x_2)}_q\right).$$

The q-derivative operator is provided by

$$D_{q}f\left(x_3\right)=\frac{f\left(q{x}_3\right)-f\left(x_3\right)}{q{x}_3-x_3},0<\mid q\mid <1,$$

and $D_{q}f\left(0\right)=f^{\prime }\left(0\right)$, provided that f is differentiable at $x_3=0$.

This satisfy the following rules

$$D_{q,x_3}\left(\frac{f\left(x_3\right)}{g\left(x_3\right)}\right)=\frac{g\left(q{x}_3\right)D_{q,x_3}f\left(x_3\right)-f\left(q{x}_3\right)D_{q,x_3}g\left(x_3\right)}{g\left(x_3\right)g\left(q{x}_3\right)}$$

(4)

and

$$D_{q,x_3}\left(f\left(x_3\right)g\left(x_3\right)\right)=f\left(x_3\right)D_{q,x_3}g\left(x_3\right)+g\left(q{x}_3\right)D_{q,x_3}f\left(x_3\right).$$

(5)

The q-extensions of the sine and cosine trigonometric functions are provided as follows (see [7,16])

$$si{n}_q\left(x_1\right)=\frac{e_q\left(i{x}_1\right)-e_q(-i{x}_1)}{2i},SI{N}_q\left(x_1\right)=\frac{E_q\left(i{x}_1\right)-E_q(-i{x}_1)}{2i},$$

and

$$co{s}_q\left(x_1\right)=\frac{e_q\left(i{x}_1\right)+e_q(-i{x}_1)}{2},CO{S}_q\left(x_1\right)=\frac{E_q\left(i{x}_1\right)+E_q(-i{x}_1)}{2},$$

which fulfill

$$E_q\left(i{x}_2\right)=CO{S}_q\left(x_2\right)+iSI{N}_q\left(x_2\right)$$

and

$$E_q(-i{x}_2)=CO{S}_q\left(x_2\right)-iSI{N}_q\left(x_2\right),$$

where $i=\sqrt{-1}\in \mathbb{C}$.

The q-Apostol Bernoulli polynomials, q-Apostol Euler polynomials and q-Apostol Genocchi polynomials of order $\alpha$ are introduced by (see [13,14,15]):

$${\left(\frac{\tau }{\lambda e_q\left(\tau \right)-1}\right)}^{\alpha }{e}^{x_1\tau }=\sum _{u=0}^{\infty }{\mathbb{B}}_{u,q}^{\left(\alpha \right)}(x_1;\lambda )\frac{{\tau }^u}{{\left[u\right]}_q!}(\mid \tau +\log \lambda \mid )<2\pi ,$$

(6)

$${\left(\frac{2}{\lambda e_q\left(\tau \right)+1}\right)}^{\alpha }{e}^{x_1\tau }=\sum _{u=0}^{\infty }{\mathbb{E}}_{u,q}^{\left(\alpha \right)}(x_1;\lambda )\frac{{\tau }^u}{{\left[u\right]}_q!}(\mid \tau +\log \lambda \mid )<\pi ,$$

(7)

$${\left(\frac{2\tau }{\lambda e_q\left(\tau \right)+1}\right)}^{\alpha }{e}^{x_1\tau }=\sum _{u=0}^{\infty }{\mathbb{G}}_{u,q}^{\left(\alpha \right)}(x_1;\lambda )\frac{{\tau }^u}{{\left[u\right]}_q!}(\mid \tau +\log \lambda \mid <\pi ),$$

(8)

, respectively.

Furthermore, note that

$${\mathbb{B}}_{u,q}^{\left(\alpha \right)}(0;\lambda ):={\mathbb{B}}_{u,q}^{\left(\alpha \right)}\left(\lambda \right),{\mathbb{E}}_{u,q}^{\left(\alpha \right)}(0;\lambda ):={\mathbb{E}}_{u,q}^{\left(\alpha \right)}\left(\lambda \right)\mathrm{and}{\mathbb{G}}_{u,q}^{\left(\alpha \right)}(0;\lambda ):={\mathbb{G}}_{u,q}^{\left(\alpha \right)}\left(\lambda \right).$$

(9)

In [7], the bivariate q-Bernoulli and q-Euler polynomials are introduced by

$$\sum _{u=0}^{\infty }{\mathbb{B}}_{u,q}^{\left(C\right)}(x_1,x_2)\frac{{\tau }^u}{{\left[u\right]}_q!}=\sum _{u=0}^{\infty }\frac{{\mathbb{B}}_{u,q}\left({(x_1\oplus i{x}_2)}_q\right)+{\mathbb{B}}_u\left({(x_1\ominus i{x}_2)}_q\right)}{2}\frac{{\tau }^u}{{\left[u\right]}_q!}=\frac{\tau e_q\left(x_1\tau \right)CO{S}_q(x_2\tau )}{e_q\left(\tau \right)-1},$$

(10)

$$\sum _{u=0}^{\infty }{\mathbb{B}}_{u,q}^{\left(S\right)}(x_1,x_2)\frac{{\tau }^u}{{\left[u\right]}_q!}=\sum _{u=0}^{\infty }\frac{{\mathbb{B}}_{u,q}\left({(x_1\oplus i{x}_2)}_q\right)-{\mathbb{B}}_{u,q}\left({(x_1\ominus i{x}_2)}_q\right)}{2i}\frac{{\tau }^u}{{\left[u\right]}_q!}=\frac{\tau e_q\left(x_1\tau \right)SI{N}_q\left(x_2\tau \right)}{e_q\left(\tau \right)-1},$$

(11)

and

$$\sum _{u=0}^{\infty }{\mathbb{E}}_{u,q}^{\left(C\right)}(x_1,x_2)\frac{{\tau }^u}{{\left[u\right]}_q!}=\sum _{u=0}^{\infty }\frac{{\mathbb{E}}_{u,q}\left({(x_1\oplus i{x}_2)}_q\right)+{\mathbb{E}}_{u,q}\left({(x_1\ominus i{x}_2)}_q\right)}{2}\frac{{\tau }^u}{{\left[u\right]}_q!}=\frac{2e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{e_q\left(\tau \right)+1},$$

(12)

$$\sum _{u=0}^{\infty }{\mathbb{E}}_{u,q}^{\left(S\right)}(x_1,x_2)\frac{{\tau }^u}{{\left[u\right]}_q!}=\sum _{u=0}^{\infty }\frac{{\mathbb{E}}_u\left({(x_1\oplus i{x}_2)}_q\right)-{\mathbb{E}}_u{\left((x_1\ominus i{x}_2)\right)}_q}{2i}\frac{{\tau }^u}{{\left[u\right]}_q!}=\frac{2e_q\left(x_1\tau \right)SI{N}_q\left(x_2\tau \right)}{e_q\left(\tau \right)+1},$$

(13)

respectively.

The q-cosine polynomials and q-sine polynomials are introduced (see [7,16]) by

$$e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)=\sum _{u=0}^{\infty }{C}_{u,q}(x_1,x_2)\frac{{\tau }^u}{{\left[u\right]}_q!}$$

(14)

and

$$e_q\left(x_1\tau \right)SI{N}_q\left(x_2\tau \right)=\sum _{u=0}^{\infty }{S}_{u,q}(x_1,x_2)\frac{{\tau }^u}{{\left[u\right]}_q!},$$

(15)

which give the following expansions

$$C_{u,q}(x_1,x_2)=\sum _{j=0}^{\left[\frac{u}{2}\right]}{(-1)}^j{\left(\begin{array}{c}u\hfill \\ 2j\hfill \end{array}\right)}_q{(-1)}^j{q}^{2j-1}{x}_1^{u-2j}{x}_2^{2j}$$

(16)

and

$$S_{u,q}(x_1,x_2)=\sum _{j=0}^{\left[\frac{u-1}{2}\right]}{\left(\begin{array}{c}u\hfill \\ 2j+1\hfill \end{array}\right)}_q{(-1)}^j{q}^{(2j+1)j}{x}_1^{u-2j-1}{x}_2^{2j+1}.$$

(17)

The q-Stirling numbers of the second kind are defined by (cf. [9])

$$\sum _{u=0}^{\infty }{S}_2^q(u,m)\frac{{\tau }^u}{u!}=\frac{{(e_q\left(\tau \right)-1)}^m}{m!}\mathrm{for}m\in =\{0,1,2,\cdots ,\}.$$

(18)

Taking $q=1$, Equation (18) reduces to the familiar Stirling numbers of the second kind as follows

$$\sum _{u=m}^{\infty }{S}_2(u,m)\frac{{\tau }^u}{u!}=\frac{{(e_q\left(\tau \right)-1)}^m}{m!}.$$

The q-Stirling polynomials of the second kind are introduced by (see [3])

$$\sum _{u=0}^{\infty }{S}_2^q(u,m:x_1)\frac{{\tau }^u}{u!}=\frac{{(e_q\left(\tau \right)-1)}^m}{m!}{e}_q\left(x_1\tau \right).$$

(19)

The bivariate q-Fubini polynomials are introduced by (see [8])

$$\sum _{u=0}^{\infty }{\mathbb{F}}_{u,q}\left(x_1;x_2\right)\frac{{\tau }^u}{{\left[u\right]}_q!}=\frac{1}{1-x_2(e_q\left(\tau \right)-1)}{e}_q\left(x_1\tau \right).$$

(20)

When $x_1=0$, ${\mathbb{F}}_{u,q}\left(0;x_2\right):={\mathbb{F}}_{u,q}\left(x_2\right)$ are called the q-Fubini polynomials and ${\mathbb{F}}_{u,q}\left(0;1\right):={\mathbb{F}}_{u,q}$ are called the q-Fubini numbers.

2. The $\mathit{q}$-Sine-Based and $\mathit{q}$-Cosine-Based $\mathit{q}$-Fubini Polynomials

Here, we examine some identities of the q-sine and q-cosine Fubini polynomials arising from the following exponential generating function:

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}\left({(x_1\oplus i{x}_2)}_q\right)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{e_q\left(x_1\tau \right)E_q\left(i\tau x_2\right)}{1-x_3(e_q\left(\tau \right)-1)}.$$

(21)

We observe that

$$E_q\left(i\tau x_2\right)e_q\left(x_1\tau \right)=(CO{S}_q\left(x_2\tau \right)+iSI{N}_q\left(x_2\tau \right))e_q\left(x_1\tau \right).$$

(22)

Thus, by (21) and (22), it is derived that

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}\left({(x_1\oplus iy)}_q\right)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{(CO{S}_q\left(x_2{x}_3\right)+iSI{N}_q\left(x_2{x}_3\right))e_q\left(x_1\tau \right)}{1-x_3(e_q\left(\tau \right)-1)},$$

(23)

and

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}\left({(x_1\ominus i{x}_2)}_q\right)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{(CO{S}_q\left(x_2\tau \right)-iSI{N}_q\left(x_2\tau \right))e_q\left(x_1\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}.$$

(24)

From (23) and (24), we obtain

$$\frac{CO{S}_q\left(x_2\tau \right)e_q\left(x_1\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}=\sum _{n=0}^{\infty }\left({\mathbb{F}}_{n,q}\left({(x_1\oplus i{x}_2)}_q\right)+{\mathbb{F}}_{n,q}{(x_1\ominus i{x}_2)}_q\right)\frac{{\tau }^n}{2{\left[n\right]}_q!},$$

(25)

and

$$\frac{SI{N}_q\left(x_2\tau \right)e_q\left(x_1\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}=\sum _{n=0}^{\infty }\left({\mathbb{F}}_{n,q}\left({(x_1\oplus i{x}_2)}_q\right)-{\mathbb{F}}_{n,q}{(x_1\ominus i{x}_2)}_q\right)\frac{{\tau }^n}{2{\left[n\right]}_q!}.$$

(26)

The bivariate q-cosine and q-sine Fubini polynomials are considered by the following generating functions, respectively:

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{CO{S}_q\left(x_2\tau \right)e_q\left(x_1\tau \right)}{1-x_3(e_q\left(\tau \right)-1)},$$

(27)

and

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{SI{N}_q\left(x_2\tau \right)e_q\left(x_1\tau \right)}{1-x_3(e_q\left(\tau \right)-1)},$$

(28)

Note that ${\mathbb{F}}_{n,q}^{\left(C\right)}(0,0;x_3):={\mathbb{F}}_{n,q}\mathrm{and}{\mathbb{F}}_{n,q}^{\left(S\right)}(n,0,0;x_3)=0(n\ge 0)$.

From (25)–(28), we have

$${\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)=\frac{1}{2}({\mathbb{F}}_{n,q}\left({(x_1\oplus i{x}_2)}_q;x_3\right)+{\mathbb{F}}_{n,q}\left({(x_1\ominus i{x}_2)}_q;x_3\right)),$$

(29)

$${\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)=\frac{1}{2i}({\mathbb{F}}_{n,q}\left({(x_1\oplus i{x}_2)}_q;x_3\right)-{\mathbb{F}}_{n,q}\left({(x_1\ominus i{x}_2)}_q;x_3\right)).$$

(30)

Remark 1.

Inserting $x_1=0$ in (27) and (28) gives the q-cosine Fubini polynomials and q-sine Fubini polynomials as follows, respectively:

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{CO{S}_q\left(x_2\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}$$

(31)

and

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(S\right)}(x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{SI{N}_q\left(x_2\tau \right)}{1-x_3(e_q\left(\tau \right)-1)},$$

(32)

We note that

$${\mathbb{F}}_{n,q}^{\left(C\right)}(0;x_3):={\mathbb{F}}_{n,q}\left(x_3\right),\mathrm{and}{\mathbb{F}}_{n,q}^{\left(S\right)}(0;x_3):=0(n\ge 0).$$

Remark 2.

Letting $q\to 1$ gives the usual cosine-Fubini polynomials and sine-Fubini polynomials as follows, respectively:

$$\sum _{n=0}^{\infty }{\mathbb{F}}_n^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{n!}=\frac{e^{x_1\tau }cos\left(x_2\tau \right)}{1-x_3(e^{\tau }-1)},$$

and

$$\sum _{n=0}^{\infty }{\mathbb{F}}_n^{\left(S\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{n!}=\frac{e^{x_1\tau }sin\left(x_2\tau \right)}{1-x_3(e^{\tau }-1)}$$

Here, we analyze some relations and formulas for the bivariate q-cosine and q-sine Fubini polynomials.

Theorem 1.

For $n\ge 0$, we have

$${\mathbb{F}}_{n,q}^{\left(C\right)}(x_2;x_3)=\sum _{v=0}^{\left[\frac{n}{2}\right]}{\left(\begin{array}{c}n+v\hfill \\ 2v\hfill \end{array}\right)}_q{(-1)}^v{q}^{(2v-1)v}{x}_2^{2v}{\mathbb{F}}_{n-2v,q}\left(x_3\right),$$

(33)

and

$${\mathbb{F}}_{n,q}^{\left(S\right)}(x_2;x_3)=\sum _{v=0}^{\left[\frac{n-1}{2}\right]}{\left(\begin{array}{c}n+v\hfill \\ 2v+1\hfill \end{array}\right)}_q{(-1)}^v{q}^{(2v+1)v}{x}_2^{2v+1}{\mathbb{F}}_{n-2v-1,q}\left(x_3\right).$$

(34)

Proof. 

In terms of (31) and (32), it is readily seen that

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{1}{1-x_3(e_q\left(\tau \right)-1)}CO{S}_q\left(x_2\tau \right)$$

$$=\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}\left(x_3\right)\frac{{\tau }^n}{{\left[n\right]}_q!}\sum _{v=0}^{\infty }{(-1)}^v{q}^{(2v-1)v}{\eta }^{2v}\frac{{\tau }^v}{{\left[2v\right]}_q!}.$$

$$=\sum _{n=0}^{\infty }\left(\sum _{v=0}^{\left[\frac{n}{2}\right]}{\left(\begin{array}{c}n+v\hfill \\ 2v\hfill \end{array}\right)}_q{(-1)}^v{q}^{(2v-1)v}{\eta }^{2v}{\mathbb{F}}_{n-2v,q}\left(x_3\right)\right)\frac{{\tau }^n}{{\left[n\right]}_q!},$$

(35)

and

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(S\right)}(x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{1}{1-x_3(e^{\tau }-1)}SI{N}_q\left(x_2\tau \right)$$

$$=\sum _{n=0}^{\infty }\left(\sum _{v=0}^{\left[\frac{n-1}{2}\right]}{\left(\begin{array}{c}n\hfill \\ 2v+1\hfill \end{array}\right)}_q{(-1)}^v{q}^{(2v+1)v}{x}_2^{2v+1}{\mathbb{F}}_{n-2v-1,q}\left(x_3\right)\right)\frac{{\tau }^n}{{\left[n\right]}_q!}.$$

(36)

Therefore, (35) and (36) mean the asserted results (33) and (34). □

Theorem 2.

For $n\ge 0$, we have

$${\mathbb{F}}_{n,q}\left({(x_1\oplus i{x}_2)}_q;x_3\right)=\sum _{k=0}^n{\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_q{(x_1\oplus i{x}_2)}_q^k{\mathbb{F}}_{n-k,q}\left(x_3\right)$$

$$=\sum _{k=0}^n{\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_q{\left(i{x}_2\right)}^k{\mathbb{F}}_{n-k,q}(x_1;x_3),$$

(37)

and

$${\mathbb{F}}_{n,q}\left({(x_1\ominus i{x}_2)}_q;x_3\right)=\sum _{k=0}^n{\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_q{(x_1\ominus i{x}_2)}_q^k{\mathbb{F}}_{n-k,q}\left(x_3\right)$$

$$=\sum _{k=0}^n{\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_q{(-1)}^k{\left(i{x}_2\right)}^k{\mathbb{F}}_{n,q}(x_1;x_3).$$

(38)

Proof. 

In terms of (23) and (24), the claimed result (37) and (38) can be readily derived by utilizing the Cauchy product, so we omit the proof. □

Theorem 3.

For $n\ge 0$, the following relations hold:

$${\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)=\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{k,q}\left(x_3\right){\mathbb{C}}_{n-k,q}(x_1,x_2),$$

(39)

and

$${\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)=\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{k,q}\left(x_3\right){\mathbb{S}}_{n-k,q}(x_1,x_2).$$

(40)

Proof. 

In terms of (27) and (28), we observe that

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}$$

$$=\left(\sum _{k=0}^{\infty }{\mathbb{F}}_{k,q}\left(x_3\right)\frac{{\tau }^k}{{\left[k\right]}_q!}\right)\left(\sum _{n=0}^{\infty }{\mathbb{C}}_{n,q}(x_1,x_2)\frac{{\tau }^n}{{\left[n\right]}_q!}\right)$$

$$=\sum _{n=0}^{\infty }\left(\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{k,q}\left(x_3\right){\mathbb{C}}_{n-k,q}(x_1,x_2)\right)\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which means the claimed result (39). The other proof can be performed similarly. □

Theorem 4.

For $n\ge 0$, we have the following relations:

$${\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+r,x_2;x_3)=\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{k,q}^{\left(C\right)}(x_1,x_2;x_3)r^{n-k},$$

(41)

and

$${\mathbb{F}}_{n,q}^{\left(S\right)}(x_1+r,x_2;x_3)=\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{k,q}^{\left(S\right)}(x_1,x_2;x_3)r^{n-k}.$$

(42)

Proof. 

Replacing $x_1$ by $x_1+r$ in (27), then, we obtain

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+r,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{1}{1-x_3(e_q\left(\tau \right)-1)}{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)e^{r\tau }$$

$$=\left(\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}\right)\left(\sum _{k=0}^{\infty }{r}^k\frac{{\tau }^k}{{\left[k\right]}_q!}\right)$$

$$=\sum _{n=0}^{\infty }\left(\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{k,q}^{\left(C\right)}(x_1,x_2;x_3)r^{n-k}\right)\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which gives the claimed result (41). The other can be performed similarly to that of (41). □

Theorem 5.

For $n\ge 1$, the following relations hold:

$$\frac{\partial }{\partial x_1}{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)={\left[n\right]}_q{\mathbb{F}}_{n-1,q}^{\left(C\right)}(x_1,x_2;x_3),$$

(43)

$$\frac{\partial }{\partial x_2}{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)=-{\left[n\right]}_q{\mathbb{F}}_{n-1,q}^{\left(S\right)}(x_1,q{x}_2;x_3),$$

and

$$\frac{\partial }{\partial x_1}{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)={\left[n\right]}_q{\mathbb{F}}_{n-1,q}^{\left(S\right)}(x_1,x_2;x_3),$$

$$\frac{\partial }{\partial x_2}{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)={\left[n\right]}_q{\mathbb{F}}_{n-1,q}^{\left(C\right)}(x_1,q{x}_2;x_3).$$

Proof. 

In view of (27), it is observed that

$$\sum _{n=1}^{\infty }\frac{\partial }{\partial x_1}{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{1}{1-x_3(e_q\left(\tau \right)-1)}\frac{\partial }{\partial x_1}{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)=\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^{n+1}}{{\left[n\right]}_q!}$$

$$=\sum _{n=1}^{\infty }{\mathbb{F}}_{n-1,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[(n-1)\right]}_q!}=\sum _{n=1}^{\infty }{\left[n\right]}_q{\mathbb{F}}_{n-1,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which means the asserted result (43). The others can be performed similarly to that of (43). □

Theorem 6.

For $n\ge 0$, the following formulas hold

$${\mathbb{C}}_{n,q}(x_1,x_2)={\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)-x_3{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+1,x_2;x_3)+x_3{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3).$$

(44)

$${\mathbb{S}}_{n,q}(x_1,x_2)={\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)-x_3{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1+1,x_2;x_3)+x_3{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3).$$

(45)

Proof. 

In terms of (2.1), it is seen that

$$e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)=\frac{1-x_3(e_q\left(\tau \right)-1)}{1-x_3(e_q\left(\tau \right)-1)}{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)$$

$$=\frac{e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}-\frac{x_3(e_q\left(\tau \right)-1)}{1-x_3(e_q\left(\tau \right)-1)}{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right),$$

which yield the following equality

$$\sum _{n=0}^{\infty }{\mathbb{C}}_{n,q}(x_1,x_2)\frac{{\tau }^n}{{\left[n\right]}_q!}=\sum _{n=0}^{\infty }\left[{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)-x_3{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+1,x_2;x_3)+x_3{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\right]\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which mean the asserted result (44). The proof of (45) can be derived similarly to that of (44). □

Theorem 7.

For $n\ge 0$, the following formulas hold

$$x_3{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+1,x_2;x_3)=(1+x_3){\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)-{\mathbb{C}}_{n,q}(x_1,x_2),$$

(46)

$$x_3{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1+1,x_2;x_3)=(1+x_3){\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)-{\mathbb{S}}_{n,q}(x_1,x_2).$$

Proof. 

By means of Theorem 1, it is observed that

$$\sum _{n=0}^{\infty }\left[{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+1,x_2;x_3)-{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\right]\frac{{\tau }^n}{{\left[n\right]}_q!}$$

$$=\frac{e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}(e_q\left(\tau \right)-1)$$

$$=\frac{1}{x_3}\left[\frac{e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}-e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)\right]$$

$$=\frac{1}{x_3}\sum _{n=0}^{\infty }\left[{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)-{\mathbb{C}}_{n,q}(x_1,x_2)\right]\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which means the asserted result (46). The other proof can be performed similarly. □

Theorem 8.

Let $z_1\ne z_2$ and $n\ge 0$; we have

$$\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{n-k,q}^{\left(C\right)}(x_1,y_1;z_1){\mathbb{F}}_{k,q}^{\left(C\right)}(x_2,y_2;z_2)$$

$$=\frac{z_2{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+x_2,y_1+y_2;z_2)-z_1{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+x_2,y_1+y_2;z_1)}{z_2-z_1},$$

(47)

and

$$\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{n-k,q}^{\left(S\right)}(x_1,y_1;z_1){\mathbb{F}}_{k,q}^{\left(S\right)}(x_2,y_2;z_2)$$

$$=\frac{z_2{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1+x_2,y_1+y_2;z_2)-z_1{\mathbb{F}}_{n,q}^{\left(S\right)}(x_1+x_2,y_1+y_2;z_1)}{z_2-z_1}.$$

(48)

Proof. 

By means of Theorem 1, it is readily seen that

$$\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,y_1;z_1){\mathbb{F}}_{k,q}^{\left(C\right)}(x_2,y_2;z_2)\frac{{\tau }^n}{{\left[n\right]}_q!}\frac{{\tau }^k}{{\left[k\right]}_q!}$$

(49)

$$=\frac{e_q\left(x_1\tau \right)CO{S}_q\left(y_1\tau \right)}{1-z_1(e_q\left(\tau \right)-1)}\frac{e_q\left(x_2\tau \right)CO{S}_q\left(y_2\tau \right)}{1-z_2(e_q\left(\tau \right)-1)}$$

$$\sum _{n=0}^{\infty }\left(\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{n-k,q}^{\left(C\right)}(x_1,y_1;z_1){\mathbb{F}}_{k,q}^{\left(C\right)}(x_2,y_2;z_2)\right)\frac{{\tau }^n}{{\left[n\right]}_q!}$$

$$=\frac{z_2}{z_2-z_1}\frac{e_q\left[(x_1+x_2)\tau \right]CO{S}_q\left[(y_1+y_2)\tau \right]}{1-z_1(e_q\left(\tau \right)-1)}-\frac{z_1}{z_2-z_1}\frac{e_q\left[(x_1+x_2)\tau \right]CO{S}_q\left[(y_1+y_2)\tau \right]}{1-z_2(e_q\left(\tau \right)-1)}$$

$$=\sum _{n=0}^{\infty }\left(\frac{z_2{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+x_2,y_1+y_2;z_2)-z_1{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+x_2,y_1+y_2;z_1)}{z_2-z_1}\right)\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which means the claimed result (47). The proof of (48) can be performed similarly. □

Theorem 9.

For $n\ge 0$, we have

$$x_3\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{n-k,q}^{\left(C\right)}(x_1,x_2;x_3)+{(x_1+x_2)}_q^n=(1+x_3){\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3).$$

(50)

and

$$x_3\sum _{k=0}^n{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{F}}_{n-k,q}^{\left(S\right)}(x_1,x_2;x_3)+{(x_1+x_2)}_q^n=(1+x_3){\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3).$$

(51)

Proof. 

By using the following equality,

$$\frac{1+x_3}{(1-x_3(e_q\left(\tau \right)-1))x_3{e}_q\left(\tau \right)}=\frac{1}{1-x_3(e_q\left(\tau \right)-1)}+\frac{1}{x_3{e}_q\left(\tau \right)},$$

it is observed that

$$\frac{(1+x_3)e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{(1-x_3(e_q\left(\tau \right)-1))x_3{e}_q\left(\tau \right)}=\frac{e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{1-x_3(e_q\left(\tau \right)-1)}+\frac{e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)}{x_3{e}_q\left(\tau \right)}$$

$$(1+x_3)\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}$$

$$=x_3\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}\sum _{k=0}^{\infty }\frac{{\tau }^k}{{\left[k\right]}_q!}-\sum _{n=0}^{\infty }{(x_1+x_2)}_q^n\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which gives the asserted result (50). The proof of (51) can be completed similarly. □

3. Connected Formulas

Here, we investigate many relationships for the bivariate q-sine and q-cosine Fubini polynomials associated with q-Euler polynomials, q-Euler polynomials and q-Bernoulli polynomials and q-Stirling numbers of the second kind.

Theorem 10.

The following relationships hold for $n\ge 0$:

$$\begin{gathered} {\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{C}\right)}({\mathit{x}}_1,{\mathit{x}}_2;{\mathit{x}}_3) \\ =\sum _{s=0}^{n+1}{\left(\begin{array}{c}n+1\hfill \\ s\hfill \end{array}\right)}_q\left[\sum _{k=0}^s{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{B}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}-{\mathbb{B}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right]\frac{{\mathbb{F}}_{\mathit{n}+1-\mathit{s},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)}{{[n+1]}_q}, \end{gathered}$$

(52)

and

$$\begin{gathered} {\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{S}\right)}({\mathit{x}}_1,{\mathit{x}}_2;{\mathit{x}}_3) \\ =\sum _{s=0}^{n+1}{\left(\begin{array}{c}n+1\hfill \\ s\hfill \end{array}\right)}_q\left[\sum _{k=0}^s{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{B}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}-{\mathbb{B}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right]\frac{{\mathbb{F}}_{\mathit{n}+1-\mathit{s},\mathit{q}}^{\left(\mathit{S}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)}{{[n+1]}_q}. \end{gathered}$$

(53)

Proof. 

By using (6) and (27), we have

$$\begin{gathered} \left(\frac{1}{1-x_3(e_q\left(\tau \right)-1)}\right)e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right) \\ =\left(\frac{1}{1-x_3(e_q\left(\tau \right)-1)}\right)\frac{\tau }{e_q\left(\tau \right)-1}\frac{e_q\left(\tau \right)-1}{\tau }{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right) \\ =\frac{1}{\tau }{\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_qß\tau {\mathbb{B}}_{s-k,q}\left(x_1\right)p^{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}\right)\frac{{\tau }^s}{{\left[s\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!} \\ -\frac{1}{\tau }{\displaystyle \sum _{s=0}^{\infty }}{\mathbb{B}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\frac{{\varnothing }^{\mathit{s}}}{{\left[\mathit{s}\right]}_{\mathit{q}}!}{\displaystyle \sum _{\mathit{n}=0}^{\infty }}{\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!} \\ =\frac{1}{\tau }{\displaystyle \sum _{n=0}^{\infty }}\left[{\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n\hfill \\ s\hfill \end{array}\right)}_q{\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{B}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}\right]{\mathbb{F}}_{\mathit{n}-\mathit{s},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!} \\ -\frac{1}{\tau }{\displaystyle \sum _{n=0}^{\infty }}\left[{\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n\hfill \\ s\hfill \end{array}\right)}_q{\mathbb{B}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right]{\mathbb{F}}_{\mathit{n}-\mathit{s},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!}, \end{gathered}$$

which means the asserted result (52). The proof of (53) can be carried out similarly. □

Theorem 11.

The following relationships hold for $n\ge 0$:

$$\begin{gathered} {\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{C}\right)}({\mathit{x}}_1,{\mathit{x}}_2;{\mathit{x}}_3) \\ ={\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n\hfill \\ s\hfill \end{array}\right)}_q\left[{\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{E}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}+{\mathbb{E}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right]\frac{{\mathbb{F}}_{\mathit{n}-\mathit{s},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)}{{\left[2\right]}_q}, \end{gathered}$$

(54)

and

$$\begin{gathered} {\mathbb{F}}_{\mathit{n},\mathit{q}}^{\mathit{S}}({\mathit{x}}_1,{\mathit{x}}_2;{\mathit{x}}_3) \\ ={\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n\hfill \\ s\hfill \end{array}\right)}_q\left[{\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{E}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}+{\mathbb{E}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right]\frac{{\mathbb{F}}_{\mathit{n}-\mathit{s},\mathit{q}}^{\left(\mathit{S}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)}{{\left[2\right]}_q}, \end{gathered}$$

(55)

Proof. 

By using definitions (7) and (27), we obtain

$$\begin{gathered} \left(\frac{1}{1-x_3(e_q\left(\tau \right)-1)}\right)e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right) \\ =\left(\frac{1}{1-x_3(e_q\left(\tau \right)-1)}\right)\frac{{\left[2\right]}_q}{e_q\left(\tau \right)+1}\frac{e_q\left(\tau \right)+1}{{\left[2\right]}_q}{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right) \\ =\frac{1}{{\left[2\right]}_q}\left[{\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{E}}_{\mathit{n}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}\right)\frac{{\tau }^n}{{\left[n\right]}_q!}+{\displaystyle \sum _{n=0}^{\infty }}{\mathbb{E}}_{n,q}\left(x_1\right)\frac{{\tau }^n}{{\left[n\right]}_q!}\right] \\ \times {\displaystyle \sum _{n=0}^{\infty }}{\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!} \\ =\frac{1}{{\left[2\right]}_q}{\displaystyle \sum _{n=0}^{\infty }}\left[{\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n\hfill \\ s\hfill \end{array}\right)}_q{\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{E}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}+{\displaystyle \sum _{\mathit{s}=0}^{\mathit{n}}}{\left(\begin{array}{c}\mathit{n}\hfill \\ \mathit{s}\hfill \end{array}\right)}_{\mathit{q}}{\mathbb{E}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right] \\ \times {\mathbb{F}}_{\mathit{n}-\mathit{s},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!}, \end{gathered}$$

which provides the asserted result (54). The proof of (55) can be performed similarly. □

Theorem 12.

The following relationships hold for $n\ge 0$:

$$\begin{gathered} {\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{C}\right)}({\mathit{x}}_1,{\mathit{x}}_2;{\mathit{x}}_3) \\ ={\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n+1\hfill \\ s\hfill \end{array}\right)}_q\left[{\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{G}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}+{\mathbb{G}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right]\frac{{\mathbb{F}}_{\mathit{n}+1-\mathit{s},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)}{{\left[2\right]}_q{[n+1]}_q}, \end{gathered}$$

(56)

and

$$\begin{gathered} {\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{S}\right)}({\mathit{x}}_1,{\mathit{x}}_2;{\mathit{x}}_3) \\ ={\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n+1\hfill \\ s\hfill \end{array}\right)}_q\left[{\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{G}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}+{\mathbb{G}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right]\frac{{\mathbb{F}}_{\mathit{n}+1-\mathit{s},\mathit{q}}^{\left(\mathit{S}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)}{{\left[2\right]}_q{[n+1]}_q}, \end{gathered}$$

(57)

Proof. 

By utilizing (8) and (27), we obtain

$$\begin{gathered} \left(\frac{1}{1-x_3(e_q\left(\tau \right)-1)}\right)e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right) \\ =\left(\frac{1}{1-x_3(e_q\left(\tau \right)-1)}\right)e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)\frac{{\left[2\right]}_q\tau }{e_q\left(\tau \right)+1}\frac{e_q\left(\tau \right)+1}{{\left[2\right]}_q\tau }{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right) \\ =\frac{1}{{\left[2\right]}_q\tau }\left[{\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left(\begin{array}{c}n\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{G}}_{\mathit{n}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{k}}{2}\right)}\right)\frac{{\tau }^n}{{\left[n\right]}_q!}+{\displaystyle \sum _{n=0}^{\infty }}{\mathbb{G}}_{\mathit{n},\mathit{q}}\left({\mathit{x}}_1\right)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!}\right] \\ \times {\displaystyle \sum _{n=0}^{\infty }}{\mathbb{F}}_{\mathit{n},\mathit{q}}^{\left(\mathit{C}\right)}(0,{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{\left[\mathit{n}\right]}_{\mathit{q}}!} \\ =\frac{1}{{\left[2\right]}_q}{\displaystyle \sum _{n=0}^{\infty }}\left[{\displaystyle \sum _{s=0}^n}{\left(\begin{array}{c}n\hfill \\ s\hfill \end{array}\right)}_q{\displaystyle \sum _{k=0}^s}{\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)}_q{\mathbb{G}}_{\mathit{s}-\mathit{k},\mathit{q}}\left({\mathit{x}}_1\right){\mathit{p}}^{\left(\genfrac{}{}{0pt}{}{\mathit{n}}{2}\right)}+{\displaystyle \sum _{\mathit{s}=0}^{\mathit{n}}}{\left(\begin{array}{c}\mathit{n}\hfill \\ \mathit{s}\hfill \end{array}\right)}_{\mathit{q}}{\mathbb{G}}_{\mathit{s},\mathit{q}}\left({\mathit{x}}_1\right)\right] \\ \times {\mathbb{F}}_{\mathit{n}+1-\mathit{s},\mathit{q}}^{\left(\mathit{C}\right)}(0.{\mathit{x}}_2;{\mathit{x}}_3)\frac{{\mathit{\varnothing }}^{\mathit{n}}}{{[\mathit{n}+1]}_{\mathit{q}}!}. \end{gathered}$$

which proves the claimed result (56). The proof of (57) can be completed similarly. □

Theorem 13.

The following relationships hold for $n\ge 0$:

$${\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)=\sum _{l=0}^n{\left(\begin{array}{c}n\hfill \\ l\hfill \end{array}\right)}_q{\mathbb{C}}_{n-l,q}(x_1,x_2){\displaystyle \sum _{k=0}^l}{x}_3^{k}k!S_2^q(l,k),$$

(58)

and

$${\mathbb{F}}_{n,q}^{\left(S\right)}(x_1,x_2;x_3)={\displaystyle \sum _{l=0}^n}{\left(\begin{array}{c}n\hfill \\ l\hfill \end{array}\right)}_q{\mathbb{S}}_{n-l,q}(x_1,x_2)\sum _{k=0}^l{x}_3^{k}k!S_2^q(l,k).$$

(59)

Proof. 

It is seen from (27) that

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{1}{1-x_3(e_q\left(\tau \right)-1)}{e}_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)$$

$$=e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)\sum _{k=0}^{\infty }{x}_3^k{(e_q\left(\tau \right)-1)}^k$$

$$=e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)\sum _{k=0}^{\infty }{x}_3^k\sum _{l=k}^{\infty }k!S_2^q(l,k)\frac{{\tau }^l}{{\left[l\right]}_q!}$$

$$=\sum _{n=0}^{\infty }{\mathbb{C}}_{n,q}(x_1,x_2)\frac{{\tau }^n}{{\left[n\right]}_q!}\sum _{l=0}^{\infty }{x}_3^k\sum _{k=0}^{l}k!S_2^q(l,k)\frac{{\tau }^l}{{\left[l\right]}_q!}.$$

Changing n by $n-l$, the above equation becomes the following relation

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}$$

$$=\sum _{n=0}^{\infty }\left(\sum _{l=0}^n{\left(\begin{array}{c}n\hfill \\ l\hfill \end{array}\right)}_q{\mathbb{C}}_{n-l,q}(x_1,x_2)\sum _{k=0}^l{x}_3^{k}k!S_2^q(l,k)\right)\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which implies the asserted result (58). The proof of (59) can be completed similarly. □

Theorem 14.

The following relationships hold for $n\ge 0$:

$${\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+r,x_2;x_3)=\sum _{l=0}^n{\left(\begin{array}{c}n\hfill \\ l\hfill \end{array}\right)}_q{\mathbb{C}}_{n-l,q}(x_1,x_2)\sum _{k=0}^l{x}_3^{k}k!S_2^q(l,k:r),$$

(60)

and

$${\mathbb{F}}_{n,q}^{\left(S\right)}(x_1+r,x_2;x_3:q)=\sum _{l=0}^n{\left(\begin{array}{c}n\hfill \\ l\hfill \end{array}\right)}_q{\mathbb{S}}_{n-l,q}(x_1,x_2)\sum _{k=0}^l{x}_3^{k}k!S_2^q(l,k:r).$$

(61)

Proof. 

It is observed from (27) that

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+r,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}=\frac{1}{1-x_3(e_q\left(\tau \right)-1)}{e}_q\left((x_1+r)\tau \right)CO{S}_q\left(x_2\tau \right)$$

$$=e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)e_q\left(r\tau \right)\sum _{k=0}^{\infty }{x}_3^k{(e_q\left(\tau \right)-1)}^k$$

$$=e_q\left(x_1\tau \right)CO{S}_q\left(x_2\tau \right)\sum _{k=0}^{\infty }{x}_3^k\sum _{l=k}^{\infty }k!S_2^q(l,k:r)\frac{{\tau }^l}{{\left[l\right]}_q!}$$

$$=\sum _{n=0}^{\infty }{\mathbb{C}}_{n,q}(x_1,x_2)\frac{{\tau }^n}{{\left[n\right]}_q!}\sum _{l=0}^{\infty }{x}_3^k\sum _{k=0}^{l}k!S_2^q(l,k:r)\frac{{\tau }^l}{{\left[l\right]}_q!},$$

which implies that

$$\sum _{n=0}^{\infty }{\mathbb{F}}_{n,q}^{\left(C\right)}(x_1+r,x_2;x_3)\frac{{\tau }^n}{{\left[n\right]}_q!}$$

$$=\sum _{n=0}^{\infty }\left(\sum _{l=0}^n{\left(\begin{array}{c}n\hfill \\ l\hfill \end{array}\right)}_q{\mathbb{C}}_{n-l,q}(x_1,x_2)\sum _{k=0}^l{x}_3^{k}k!S_2^q(l,k:r)\right)\frac{{\tau }^n}{{\left[n\right]}_q!},$$

which means the claimed result (60). The proof of (61) can be completed similarly. □

4. Some Applications for Bivariate $\mathit{q}$-Cosine Fubini Polynomials

Here, we analyze some properties of the q-cosine Fubini polynomials. We now provide the lists of the first few q-cosine Fubini polynomials as follows:

$$\begin{gathered} {\mathbb{F}}_{0,q}^{\left(C\right)}(x_1,x_2;x_3)=1, \\ {\mathbb{F}}_{1,q}^{\left(C\right)}(x_1,x_2;x_3)=x_1+x_3, \\ {\mathbb{F}}_{2,q}^{\left(C\right)}(x_1,x_2;x_3)=x_1^2-q{x}_2^2+x_3+x_1{x}_3{\left[2\right]}_q!+x_3^2{\left[2\right]}_q!, \\ {\mathbb{F}}_{3,q}^{\left(C\right)}(x_1,x_2;x_3)=x_1^3+x_3+x_1{x}_3^2{\left[3\right]}_q!+x_3^3{\left[3\right]}_q!-{\displaystyle \frac{q{x}_1{x}_2^2{\left[3\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{x_1{x}_3{\left[3\right]}_q!}{{\left[2\right]}_q!}}, \\ +{\displaystyle \frac{x_1^2{x}_3{\left[3\right]}_q!}{{\left[2\right]}_q!}}-{\displaystyle \frac{q{x}_2^2{x}_3{\left[3\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{2x_3^2{\left[3\right]}_q!}{{\left[2\right]}_q!}}, \\ {\mathbb{F}}_{4,q}^{\left(C\right)}(x_1,x_2;x_3)=x_1^4+q^6{x}_2^4+x_3+x_1{x}_3^3{\left[4\right]}_q!+x_3^4{\left[4\right]}_q!-{\displaystyle \frac{q{x}_1^2{x}_2^2{\left[4\right]}_q!}{{({\left[2\right]}_q!)}^2}}+{\displaystyle \frac{x_1^2{x}_3{\left[4\right]}_q!}{{({\left[2\right]}_q!)}^2}}-{\displaystyle \frac{q{x}_2^2{x}_3{\left[4\right]}_q!}{{({\left[2\right]}_q!)}^2}} \\ +{\displaystyle \frac{x_3^2{\left[4\right]}_q!}{{({\left[2\right]}_q!)}^2}}-{\displaystyle \frac{q{x}_1{x}_2^2{x}_3{\left[4\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{2x_1{x}_3^2{\left[4\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{x_1^2{x}_3^2{\left[4\right]}_q!}{{\left[2\right]}_q!}}-{\displaystyle \frac{q{x}_2^2{x}_3^2{\left[4\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{3x_3^3{\left[4\right]}_q!}{{\left[2\right]}_q!}} \\ +{\displaystyle \frac{x_1{x}_3{\left[4\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^3{x}_3{\left[4\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{2x_3^2{\left[4\right]}_q!}{{\left[3\right]}_q!}}, \\ {\mathbb{F}}_{5,q}^{\left(C\right)}(x_1,x_2;x_3)=x_1^5+x_3+x_1{x}_3^4{\left[5\right]}_q!+x_3^5{\left[5\right]}_q!-{\displaystyle \frac{q{x}_1{x}_2^2{x}_3{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}}-{\displaystyle \frac{q{x}_1^2{x}_2^2{x}_3{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}}+{\displaystyle \frac{x_1{x}_3^2{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}} \\ +{\displaystyle \frac{2x_1^2{x}_3^2{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}}-{\displaystyle \frac{2q{x}_2^2{x}_3^2{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}}+{\displaystyle \frac{3x_3^3{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}}-{\displaystyle \frac{q{x}_1{x}_2^2{x}_3^2{\left[5\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{3x_1{x}_3^3{\left[5\right]}_q!}{{\left[2\right]}_q!}} \\ +{\displaystyle \frac{x_1^2{x}_3^3{\left[5\right]}_q!}{{\left[2\right]}_q!}}-{\displaystyle \frac{q{x}_2^2{x}_3^3{\left[5\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{4x_3^4{\left[5\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{2x_1{x}_3^2{\left[5\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^3{x}_3^2{\left[5\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{3x_3^3{\left[5\right]}_q!}{{\left[3\right]}_q!}} \\ -{\displaystyle \frac{q{x}_1^3{x}_2^2{\left[5\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^2{x}_3{\left[5\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^3{x}_3{\left[5\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}-{\displaystyle \frac{q{x}_2^2{x}_3{\left[5\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{2x_3^2{\left[5\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{q^6{x}_1{x}_2^4{\left[5\right]}_q!}{{\left[4\right]}_q!}} \\ +{\displaystyle \frac{x_1{x}_3{\left[5\right]}_q!}{{\left[4\right]}_q!}}+{\displaystyle \frac{x_1^4{x}_3{\left[5\right]}_q!}{{\left[4\right]}_q!}}+{\displaystyle \frac{q^6{x}_2^4{x}_3{\left[5\right]}_q!}{{\left[4\right]}_q!}}+{\displaystyle \frac{2x_3^2{\left[5\right]}_q!}{{\left[4\right]}_q!}}. \end{gathered}$$

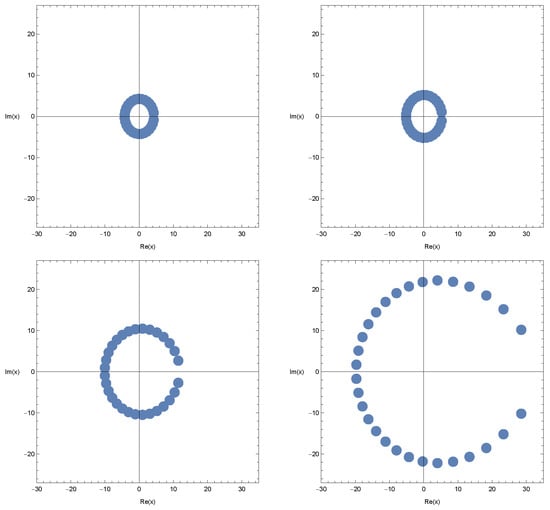
By choosing $n=30$, the zeros of the aforementioned polynomials are represented by the following Figures.

In Figure 1 (top-left), we choose $(x_2,x_3,q)=(2,3,\frac{1}{10})$

In Figure 1 (top-right), we choose $(x_2,x_3,q)=(2,3,\frac{3}{10})$

In Figure 1 (bottom-left), we choose $(x_2,x_3,q)=(2,3,\frac{7}{10})$

In Figure 1 (bottom-right), we choose $(x_2,x_3,q)=(2,3,\frac{9}{10}).$

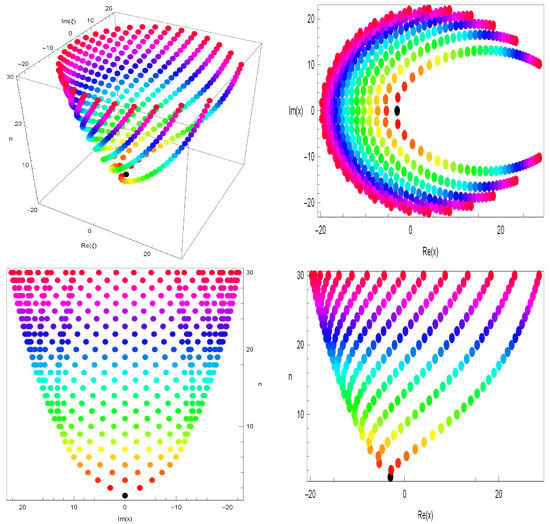
By choosing $n=30$, the stacks of zeros of the aforementioned polynomials are represented by the following Figures, which form a 3D structure (Figure 2):

In Figure 2 (top-left), we plot stacks of zeros of ${\mathbb{F}}_{n,\frac{9}{10}}^{\left(C\right)}(x_1,2;3)=0$.

In Figure 2 (top-right), the zeros are shown by x and y axes but no z axis in 3D.

In Figure 2 (bottom-left), the zeros are shown by y and z axes but no x axis in 3D.

In Figure 2 (bottom-right), the zeros are shown by x and z axes but no y axis in 3D.

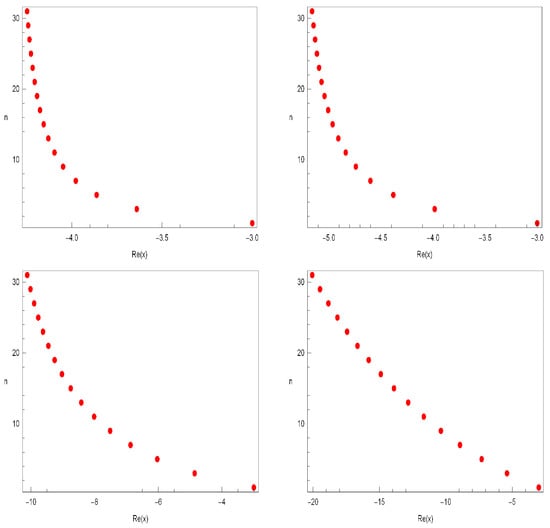
By choosing $n=30$, the zeros of the aforementioned polynomials are represented by the following Figures.

In Figure 3 (top-left), we choose $(x_2,x_3,q)=(2,3,\frac{1}{10})$

In Figure 3 (top-right), we choose $(x_2,x_3,q)=(2,3,\frac{3}{10})$

In Figure 3, (bottom-left), we choose $(x_2,x_3,q)=(2,3,\frac{7}{10})$

In Figure 3, (bottom-right), we choose $(x_2,x_3,q)=(2,3,\frac{9}{10}).$

Approximate solutions that hold the q-cosine Fubini polynomials ${\mathbb{F}}_{n,\frac{9}{10}}^{\left(C\right)}(x_1,2;3)=0$ are provided by

Table 1. Numerical solutions of ${\mathbb{F}}_{n,\frac{9}{10}}^{\left(C\right)}(x_1,2;3)=0$.

Degree n	x1
1	−3.0000
2	−2.8500 −2.8944 i, −2.8500 + 2.8944 i
3	−5.3928, −1.3686 − 5.2991i, −1.3686 + 5.2991 i
4	−5.5540 − 2.4948 i, −5.5540 + 2.4948 i,
	0.3955 − 7.2453 i, 0.3955 + 7.2453 i
5	−7.3029, −4.7486 − 4.9065i, −4.7486 + 4.9065 i,
	2.2574 − 8.7792 i, 2.2574 + 8.7792 i
6	−7.5564 − 2.3290 i, −7.5564 + 2.3290 i, −3.6043 −7.0651 i,
	−3.6043 + 7.0651 i, 4.1323 − 9.9831 i, 4.1323 + 9.9831 i
7	−8.9349, −7.0653 − 4.6682 i, −7.0653 + 4.6682 i, −2.2656 − 8.9090 i,
	−2.2656 + 8.9090 i, 5.9728 − 10.9218 i, 5.9728 + 10.9218 i
8	−9.2292 − 2.2401 i, −9.2292 + 2.2401 i, -6.2532 − 6.8519 i,
	−6.2532 + 6.8519 i, −0.8124 - 10.4654 i, −0.8124 + 10.4654 i,
	7.7519 − 11.6451 i, 7.7519 + 11.6451 i
9	−10.372, −8.9243 − 4.5002 i, −8.9243 + 4.5002 i,
	−5.2321 − 8.7953 i, −5.2321 + 8.7953 i, 0.6992 − 11.7703 i,
	0.6992 + 11.7703 i, 9.454 − 12.192 i, 9.454 + 12.192 i

.

5. Some Applications for Bivariate $\mathit{q}$-Sine Fubini Polynomials

Here, we analyze some properties of the q-sine Fubini polynomials. We now provide the lists of the first few q-sine Fubini polynomials as follows:

$$\begin{gathered} {\mathbb{F}}_{0,q}^{\left(S\right)}(x_1,x_2;x_3)=0, \\ {\mathbb{F}}_{1,q}^{\left(S\right)}(x_1,x_2;x_3)=x_2, \\ {\mathbb{F}}_{2,q}^{\left(S\right)}(x_1,x_2;x_3)=x_1{x}_2{\left[2\right]}_q!+x_2{x}_3{\left[2\right]}_q!, \\ {\mathbb{F}}_{3,q}^{\left(S\right)}(x_1,x_2;x_3)=-q^3{x}_2^3+x_1{x}_2{x}_3{\left[3\right]}_q!+x_2{x}_3^2{\left[3\right]}_q!+{\displaystyle \frac{x_1^2{x}_2{\left[3\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{x_2{x}_3{\left[3\right]}_q!}{{\left[2\right]}_q!}}, \\ {\mathbb{F}}_{4,q}^{\left(S\right)}(x_1,x_2;x_3)=x_1{x}_2{x}_3^2{\left[4\right]}_q!+x_2{x}_3^3{\left[4\right]}_q!+{\displaystyle \frac{x_1{x}_2{x}_3{\left[4\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{x_1^2{x}_2{x}_3{\left[4\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{2x_2{x}_3^2{\left[4\right]}_q!}{{\left[2\right]}_q!}} \\ +{\displaystyle \frac{x_1^3{x}_2{\left[4\right]}_q!}{{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_1{x}_2^3{\left[4\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{x_2{x}_3{\left[4\right]}_q!}{{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_2^3{x}_3{\left[4\right]}_q!}{{\left[3\right]}_q!}}, \\ {\mathbb{F}}_{5,q}^{\left(S\right)}(x_1,x_2;x_3)=q^{10}{x}_2^5+x_1{x}_2{x}_3^3{\left[5\right]}_q!+x_2{x}_3^4{\left[5\right]}_q!+{\displaystyle \frac{x_1^2{x}_2{x}_3{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}}+{\displaystyle \frac{x_2{x}_3^2{\left[5\right]}_q!}{{({\left[2\right]}_q!)}^2}} \\ +\frac{2x_1{x}_2{x}_3^2{\left[5\right]}_q!}{{\left[2\right]}_q!}+{\displaystyle \frac{x_1^2{x}_2{x}_3^2{\left[5\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{3x_2{x}_3^3{\left[5\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{x_1{x}_2{x}_3{\left[5\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^3{x}_2{x}_3{\left[5\right]}_q!}{{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_1{x}_2^3{x}_3{\left[5\right]}_q!}{{\left[3\right]}_q!}} \\ +{\displaystyle \frac{2x_2{x}_3^2{\left[5\right]}_q!}{{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_2^3{x}_3^2{\left[5\right]}_q!}{{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_1^2{x}_2^3{\left[5\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_2^3{x}_3{\left[5\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^4{x}_2{\left[5\right]}_q!}{{\left[4\right]}_q!}}+{\displaystyle \frac{x_2{x}_3{\left[5\right]}_q!}{{\left[4\right]}_q!}}, \\ {\mathbb{F}}_{6,q}^{\left(S\right)}(x_1,x_2;x_3)=x_1{x}_2{x}_3^4{\left[6\right]}_q!+x_2{x}_3^5{\left[6\right]}_q!+{\displaystyle \frac{x_1{x}_2{x}_3^2{\left[6\right]}_q!}{{({\left[2\right]}_q!)}^2}}+{\displaystyle \frac{2x_1^2{x}_2{x}_3^2{\left[6\right]}_q!}{{({\left[2\right]}_q!)}^2}}+{\displaystyle \frac{3x_2{x}_3^3{\left[6\right]}_q!}{{({\left[2\right]}_q!)}^2}} \end{gathered}$$

$$\begin{gathered} +{\displaystyle \frac{3x_1{x}_2{x}_3^3{\left[6\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{x_1^2{x}_2{x}_3^3{\left[6\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{4x_2{x}_3^4{\left[6\right]}_q!}{{\left[2\right]}_q!}}-{\displaystyle \frac{q^3{x}_1^3{x}_2^3{\left[6\right]}_q!}{{({\left[3\right]}_q!)}^2}}-{\displaystyle \frac{q^3{x}_2^3{x}_3{\left[6\right]}_q!}{{({\left[3\right]}_q!)}^2}} \\ +{\displaystyle \frac{2x_1{x}_2{x}_3^2{\left[6\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^3{x}_2{x}_3^2{\left[6\right]}_q!}{{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_1{x}_2^3{x}_3^2{\left[6\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{3x_2{x}_3^3{\left[6\right]}_q!}{{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_2^3{x}_3^3{\left[6\right]}_q!}{{\left[3\right]}_q!}} \\ +{\displaystyle \frac{x_1^2{x}_2{x}_3{\left[6\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{x_1^3{x}_2{x}_3{\left[6\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_1{x}_2^3{x}_3{\left[6\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}-{\displaystyle \frac{q^3{x}_1^2{x}_2^3{x}_3{\left[6\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{2x_2{x}_3^2{\left[6\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}} \\ -{\displaystyle \frac{2q^3{x}_2^3{x}_3^2{\left[6\right]}_q!}{{\left[2\right]}_q!{\left[3\right]}_q!}}+{\displaystyle \frac{x_1{x}_2{x}_3{\left[6\right]}_q!}{{\left[4\right]}_q!}}+{\displaystyle \frac{x_1^4{x}_2{x}_3{\left[6\right]}_q!}{{\left[4\right]}_q!}}+{\displaystyle \frac{2x_2{x}_3^2{\left[6\right]}_q!}{{\left[4\right]}_q!}} \\ +{\displaystyle \frac{x_1^5{x}_2{\left[6\right]}_q!}{{\left[5\right]}_q!}}+{\displaystyle \frac{q^{10}{x}_1{x}_2^5{\left[6\right]}_q!}{{\left[5\right]}_q!}}+{\displaystyle \frac{x_2{x}_3{\left[6\right]}_q!}{{\left[5\right]}_q!}}+{\displaystyle \frac{q^{10}{x}_2^5{x}_3{\left[6\right]}_q!}{{\left[5\right]}_q!}}. \end{gathered}$$

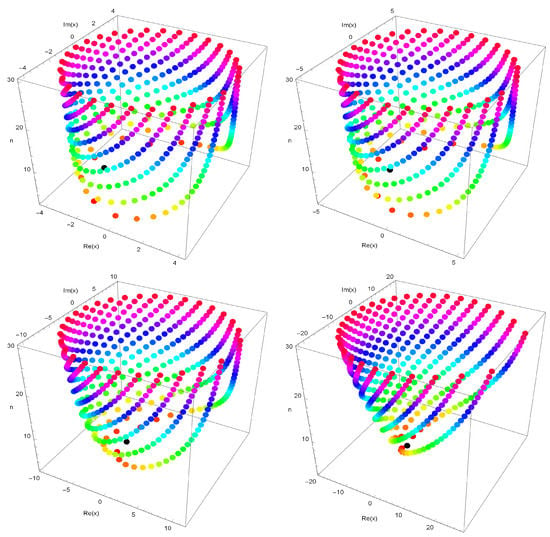
By choosing $n=30$, the zeros of the aforementioned polynomials are represented by the following Figures.

In Figure 4 (top-left), we choose $(x_2,x_3,q)=(2,3,\frac{1}{10})$

In Figure 4 (top-right), we choose $(x_2,x_3,q)=(2,3,\frac{3}{10})$

In Figure 4, (bottom-left), we choose $(x_2,x_3,q)=(2,3,\frac{7}{10})$

In Figure 4, (bottom-right), we choose $(x_2,x_3,q)=(2,3,\frac{9}{10}).$

Approximate solutions that hold the q-sine Fubini polynomials ${\mathbb{F}}_{n,\frac{9}{10}}^{\left(S\right)}(x_1,3;2)=0$ are provided by

Table 2. Numerical solutions of ${\mathbb{F}}_{n,\frac{9}{10}}^{\left(S\right)}(x_1,3;2)=0$.

Degree n	x1
2	−2.0000
3	−1.9 − 1.88917i −1.9 + 1.88917 i
4	−3.85538, −0.782309 − 3.57922 i, −0.782309 + 3.57922 i
5	−3.92997 − 1.60973i, −3.92997 + 1.60973 i,
	0.490973 − 4.96534 i, 0.490973 + 4.96534 i
6	−5.26729, −3.28268 − 3.2959 i, −3.28268 + 3.2959 i,
	1.82123 − 6.06415i, 1.82123 + 6.06415 i
7	−5.40013 − 1.5182 i, −5.40013 + 1.5182 i, −2.43885 − 4.82753 i,
	−2.43885 + 4.82753 i, 3.15339 − 6.93064 i, 3.15339 + 6.93064 i
8	−6.44059, −4.98389 − 3.14942 i, −4.98389 + 3.14942 i,
	−1.46959 − 6.14118 i, −1.46959 + 6.14118 i,
	4.45675 − 7.60899 i, 4.45675 + 7.60899 i
9	−6.60749 − 1.48201i, −6.60749 + 1.48201 i, −4.37523 − 4.69502 i,
	−4.37523 + 4.69502 i, −0.426537 − 7.25441 i, −0.426537 + 7.25441 i,
	5.71393 - 8.13385 i, 5.71393 + 8.13385 i
10	−7.45808, −6.33513 − 3.05623i, −6.33513 + 3.05623 i,
	−3.62958 − 6.07483 i, −3.62958 + 6.07483 i, 0.652655 − 8.19076 i,
	0.652655 + 8.19076 i, 6.9153 − 8.53262 i, 6.9153 + 8.53262 i

.

6. Conclusions

In the present paper, the q-sine-based and q-cosine-Based q-Fubini polynomials have been considered, and several properties for these polynomials have been derived. Furthermore, some correlations covering q-analogues of the Genocchi, Euler and Bernoulli polynomials and the q-Stirling numbers of the second kind have been provided. Moreover, some approximate zeros of the q-sine-based and q-cosine-Based q-Fubini polynomials in a complex plane and a real plane have been analyzed. Finally, these zeros have been shown by figures, and numerical solutions for special cases are given by tables.

It can be added that not only can the idea of the present paper be utilized for similar polynomials, but also the mentioned polynomials possess possible utilizations and applications in scientific fields other than the applications provided at the end of the paper. Moreover, advancing the purpose of this article, we will proceed with this idea in our next research studies in several directions.