Abstract
In this work, computer-assisted writing techniques for linear expressions of the structure of polycyclic molecules, branched molecules and clusters, based on formal languages, are tested. The techniques used only require the ability to process written texts, even just using a text editor, and one of the many available molecular drawing/optimization programs that accept input in the form of a SMILES string. A few specific syntactic operators acting on strings are characterized in terms of their effect on the corresponding structure, and although they are simply examples, they are already capable of producing non-trivial structures. The aim of this work is to encourage experiments that may lead to potentially interesting molecular schemata, in view of their symmetry and stereochemistry, as revealed by optimization, and to develop insight into the connection between formal expressions and structures. Given the simplicity and availability of the required tools, it can also be useful for education.
1. Introduction
The possibility within formal languages of constructing expressions starting from other expressions according to well-defined rules is a well-known tool of logic, generative grammar and computer science [1,2,3]. The strings obtained by repeatedly applying, in a defined order, the established rules to a starting string, the so-called axiom or seed, often have a surprising structure, which can hardly be anticipated even if one fully understands the way in which any single rule affects the structure of its argument. This feature has been exploited to produce models of natural systems, in particular, plants and cellular components for some decades already: the idea in this case is to use the string as a code, or program, which is read and interpreted by an automaton which produces, for example, a drawing [4,5,6,7].
The construction of strings of letters and numbers starting from other strings is an extremely stimulating topic, which originated many ideas in the field of logic, automata theory and recursion, and has also been the inspiration for numerous collections of logic puzzles and games [8].
In recent chemical literature, the string expression of chemical structures has been most often considered a tool in the evaluation of these structures by means of artificial intelligence (AI) techniques, in particular, deep learning nets as an alternative to their expression as graphs [9,10,11,12]. The author has instead proposed [13,14], very recently, to employ this possibility of expression in the context of the classical tradition of logic and generative linguistics, i.e., as tools for the formulation of potentially useful structures by a trained human operator, with the assistance of computers that operate transparently to facilitate the operation of syntactic substitution in a long string. This approach is not addressed in a particular way to the theoretical chemist: the methods described here are not those that are normally at the core of theoretical chemistry. Nor is it particularly aimed at the field of cheminformatics: the experiments are, in fact, designed to be performed primarily by a skilled human. Furthermore, the ideas and principles behind molecular linguistics are discussed here much more than the application to fields, such as automatics retrieval of useful molecules or AI-based design. The spirit of this approach is actually similar to that of the classic book by R. Dawkins on evolution [15]: structures are generated by a partly mechanical process and then evaluated by a human expert. The perspective is that the process of formulating chemical blueprints based on word processing, with some use of logic, might be instrumental in those aspects of chemical research more related to intuition, such as the identification, partially based on serendipity, of a class of molecules that can serve as a problem or as a solution.
Another application arises from the fact that many innovative systems are based on the repetition of complex motifs in an even more complex superstructure, examples are crown ethers and dendrimer molecules. In many cases, linguistic operators, such as those introduced here, may be used to speed up the formulation of input strings for further processing.
A perpective application is to chemical synthesis. Since chemical reactions can be represented by syntactic transformations (see Section 3 later for example), the possibility of the synthesis of a species and the formal derivability of the string expressing its molecule are connected.
The experiments described in this paper have been performed and can be promptly repeated by the sole use of a system for modifying a string of letters (such as for example the search-and-replace and the copy-and-paste functions in a word processor) and a program for the molecular interpretation of strings among the many available, such as [16], which is the one actually used by the author. Only occasionally, small additional programs have been written to speed up a procedure or to the scope of randomizing the string rewriting, as reported later.
The experimentation of string modifications and the observation of the molecular structures that are produced in this way can have a value from a didactic point of view as an exercise in the logic of chemical structure. Chemical language games, such as those described in this paper, have been successfully used to introduce formal grammars to undergraduate students.
Experimenting with strings which can be interpreted as molecular structures and are modified by formal grammars can also be useful for developing the intuition of a biochemist or as a basis to create simple models of molecular evolution.
The systems described in this paper are mostly organic: this limitation is not strictly necessary, simply the formal validity (Lewis-validity) of an organic blueprint can be readily evaluated, perhaps with the additional requirement, which is not formally part of Lewis-validity, that the bonds are not excessively strained. The relation of Lewis-validity with actual chemical stability will be discussed later. The author does not further characterize the systems case by case: this is not an essential aspect, since by playing the language games described in this work, it is possible to produce dozens of such systems in a few minutes. They are to be regarded as formally valid possibilities: in the best case, and this is the aim here, as sources of insight for further studies.
2. Operators Acting on Strings: Polycyclic Alkanes and Amines
SMILES (Simplified Molecular-Input Line-Entry System) [17] will be used as string language throughout. However, the treatment based on the replacement of portions of string with other strings, described in the section relating to branched systems, is actually based on the ideas of the recursive language L developed by the present author [13,14], and consequently the syntax employed in this work, although fully compatible with that of SMILES as input for other applications, it is more restrictive than the standard of the latter in some cases. What we are doing here is in fact defining a type of generative grammar, where expressions that are correctly interpretable as SMILES expressions are formally processed, defining a rule-based syntax. This processing is obviously not part of the SMILES language standard but is built on top of it.
It may be useful to provide a brief introduction to SMILES. The reader unfamiliar with it can practice with any online program that takes it as input and observe the molecular structures represented as a result. The language is very simple. A few hints are, therefore, sufficient.
The language expresses a molecular structure using letters of the English alphabet and a few other symbols, with some conventions mainly derived from the practice of organic chemistry. For example, hydrogen atoms bound to carbon atoms are not written but implied: in the interpretation of the string, they are automatically supplied based on valence electron count. Each atom, if not followed by a special symbol like “=”, is understood to be singly bound to the next atom in the string. Numbers are used to specify bonding between atoms not consecutively written, such that two atoms are bound if followed by the same number. Brackets are used to express branching.
These are a few examples. Note that quotation marks are not used to quote the content of a string: the context should avoid any confusion.
CO is a SMILES expression of methanol molecule, not of carbon monoxide one: since the C-O bond is single and H atoms are assumed to saturate valence, the corresponding formula in traditional chemical language is CH3OH.
C1CCCCC1 represents cyclohexane (the first atom is bound to the last);
COC represents dimethyl ether;
CC(C)C represents isobutane.
As a first example of the application of operators, let us begin with the expression of cyclohexane just mentioned, which we use now as a seed, or starting string, named ω:
ω = C1CCCCC1
Trivially, if this string is used as input in a molecular drawing software it will result in a representation of the cyclohexane molecule.
We now apply a very simple operator acting on words, D (for “doubling”), inspired by the syntactic systems in [1,8]. A cursive font is used here to differentiate operators from SMILES letters.
D(x) = xx
A rule, such as this one, for modifying strings is not expressed in the language of the strings themselves but in a metalanguage that has the power to express these non-chemical concepts by including other symbols. In the metalinguistic expression of D just seen, the letter x corresponds to any string based on the SMILES repertoire of symbols, while the form xx means the string obtained by writing the x string twice consecutively, obtaining a double-length string. This last potentially, but not always, expresses a new molecule.
In our specific case, the result of D(ω) is ωω, which is:
ωω = C1CCCCC1C1CCCCC1
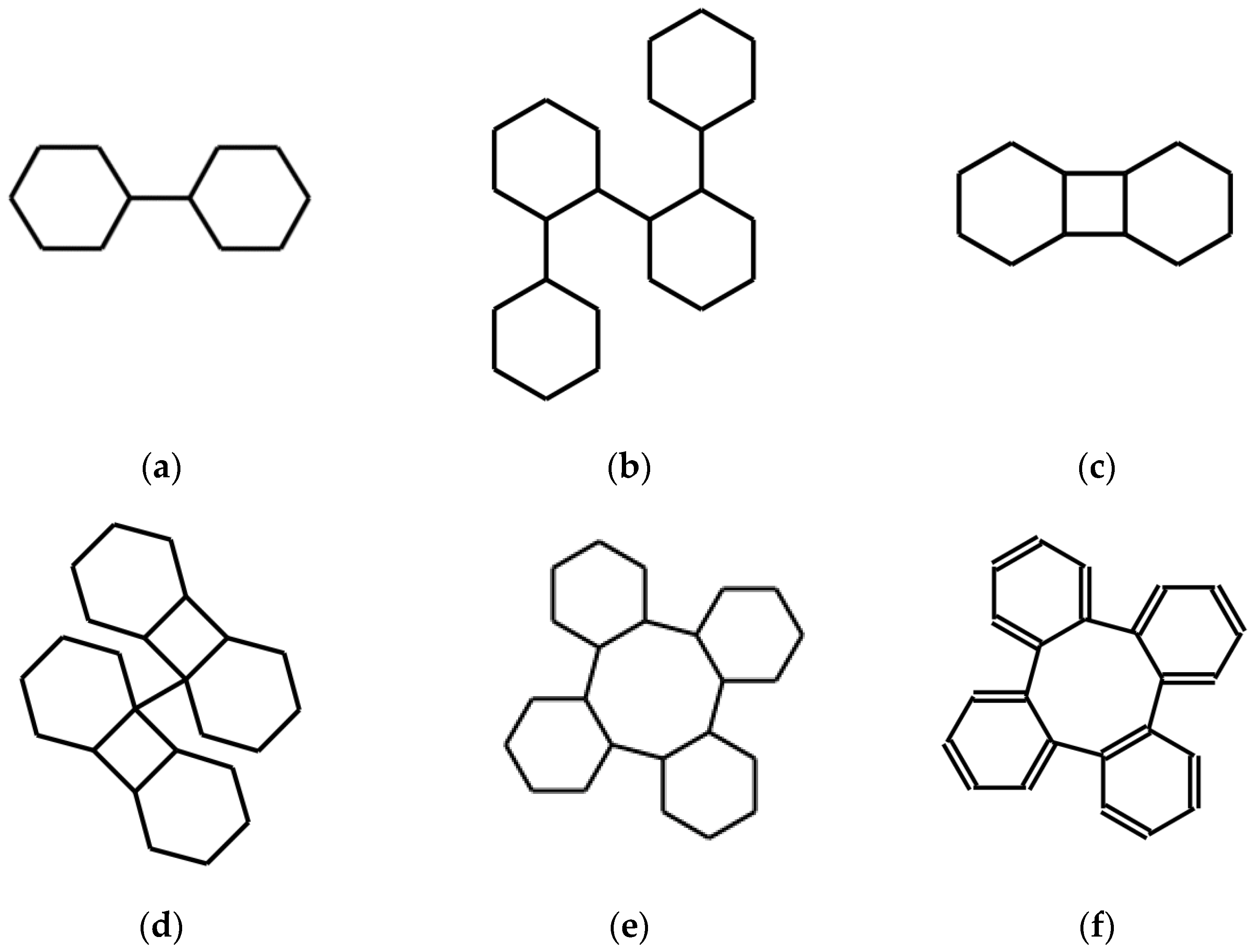
Most SMILES language editors, when fed with an expression of this type, interpret the couple of numbers consecutively: they bind the two atoms corresponding to the number 1 and then the next pair of atoms corresponding to the two following occurrences of the same number 1. They do not bind all the four C atoms marked by the number 1. This is consistent with the standard [17]. Keeping this interpretation, the string ωω expresses the molecule shown in Figure 1a, namely bicyclohexyl’s one. This is indeed the result obtained by feeding ωω into a software, such as [16].
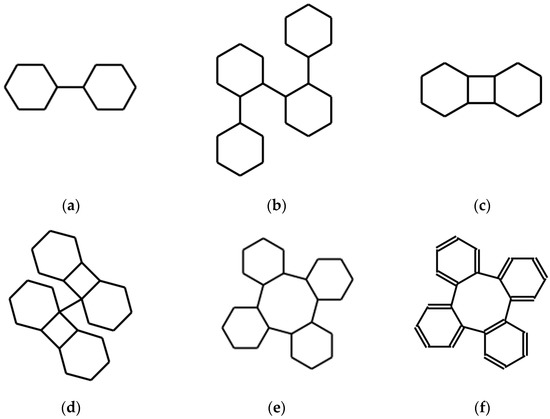
Figure 1.
Molecular structures obtained by the action of syntactic operations, respectively (a) D, (b) DD, (c) AD, (d) DAD, (e) ADD on an initial expression of the cyclohexane molecule. (f) is the effect of ADD on an expression of the benzene molecule. See the text for details.
A double application of D, written DDω, or D(Dω) or D2ω, leads to ωωωω:
corresponding to the structures shown in Figure 1b. Continuing this way, the expression of the structure of a polymer based on cyclohexane is obtained. Note that this fact, which is immediately communicated by the resulting graphic expression, is not so apparent in the textual processing.
DDω = ωωωω = C1CCCCC1C1CCCCC1C1CCCCC1C1CCCCC1
In order to obtain structures of an essentially different type, such as more closed structures, we must introduce at least one additional operator A. This is a very different kind of systematic replacement; still, this is logically formalizable in a rather simple way.
It can be described as follows: A appends to the first and last atomic symbol of the string the lowest number that does not already appear in the string itself.
In the specific case, the number symbol 2 is fed in the two positions prescribed by the definition of A into the string:
A(ωω) = C12CCCCC1C1CCCCC12
The new string A(ωω) is the expression of the structure in Figure 1c, a tricyclo-dodecane.
The doubling operation D may be applied to this expression. If this is performed, the result is:
DAD(ω) = A(ωω)A(ωω) = C12CCCCC1C1CCCCC12C12CCCCC1C1CCCCC12
DAD(ω) expresses the structure in Figure 1d. The system corresponding instead to ADD(ω) is shown in Figure 1e.
Naturally, it is possible to use, as starting strings, expressions of aromatic systems or spiro systems. Alternatively, systems of this kind may result from the action of operators. A simple example of the first case uses a SMILES expression of benzene ω = c1ccccc1 instead of that of cyclohexane as a seed. The result is a string expressing the structure shown in Figure 1f, namely benzannulated cyclooctatetraene or tetraphenylene.
It appears that doubling a string corresponds to doubling the structure and binding the original and the copy by a single bond; this is not always true but depends on the availability of a well-located hydrogen atom implied by the original expression. The resulting two H’s are removed in forming the connecting bond. Instead, the A operator, by introducing two equal new numbers following the first and last atomic symbol in the string produces a new cycle in the structure under the same conditions.
Observing the systems of Figure 1 it can be noted that they may present interest from the point of view of symmetry, obviously after having determined a reasonable three-dimensional structure by means of force-field optimization. All systems but the last, being made up of sp3 C atoms, are actually poor in exact global symmetry. At the same time, some of these structures have at least some approximate global symmetry. For example, ADD produces the description of a system that can be subdivided into four interconnected and equal sub-systems. Longer sequences of these or other, appropriately defined, linguistic operators can certainly produce systems with peculiar stereochemistry and globally highly symmetrical. It must not be forgotten that the very few operators, such as A and D, that are introduced in this work, are just examples. A search for operators that produce systems, both large and with high symmetry when applied to a varied family of seeds, is part of the possible experimentation. The last system in Figure 1f is the most promising for symmetry studies in view of the research in progress concerning its low-energy states and their geometry [18].
To give a different example, let us start from the expression C1CCN as a seed. We observe that, in this case, ω is not a word in SMILES language, since a number cannot appear just once in a SMILES string. However, this number repeats itself in the expressions obtained by applying the D operator.
With this choice of ω, DD(ω), that is ωωωω, is the expression:
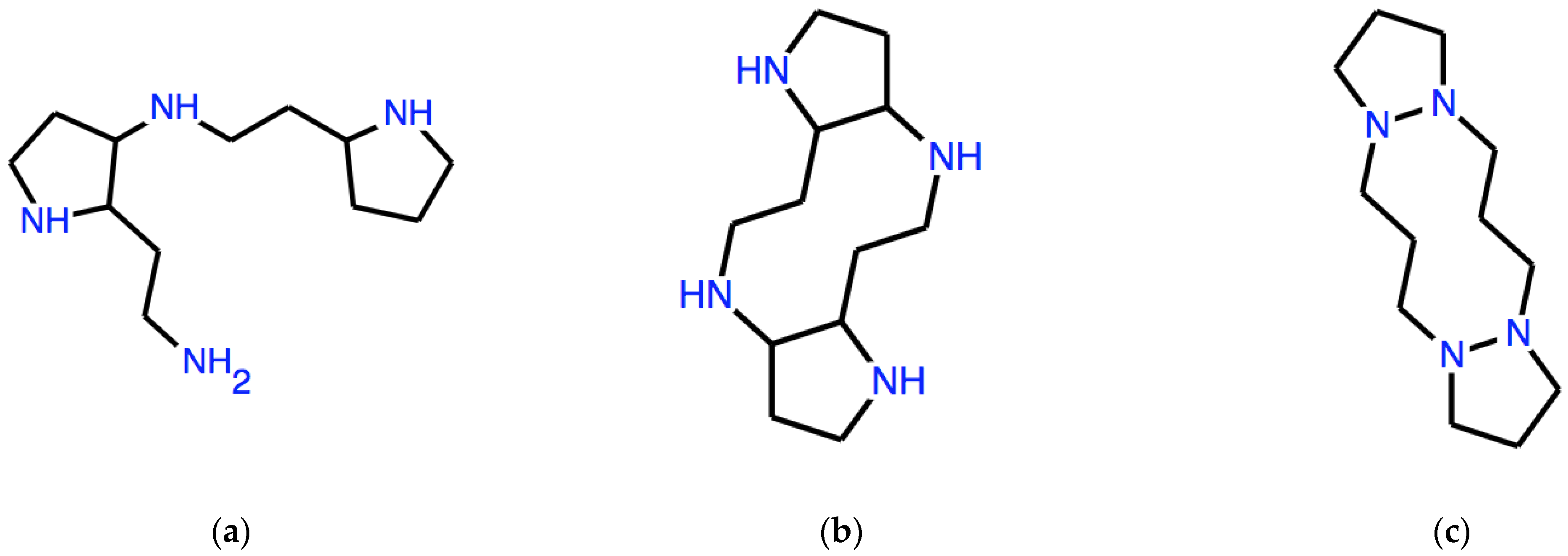
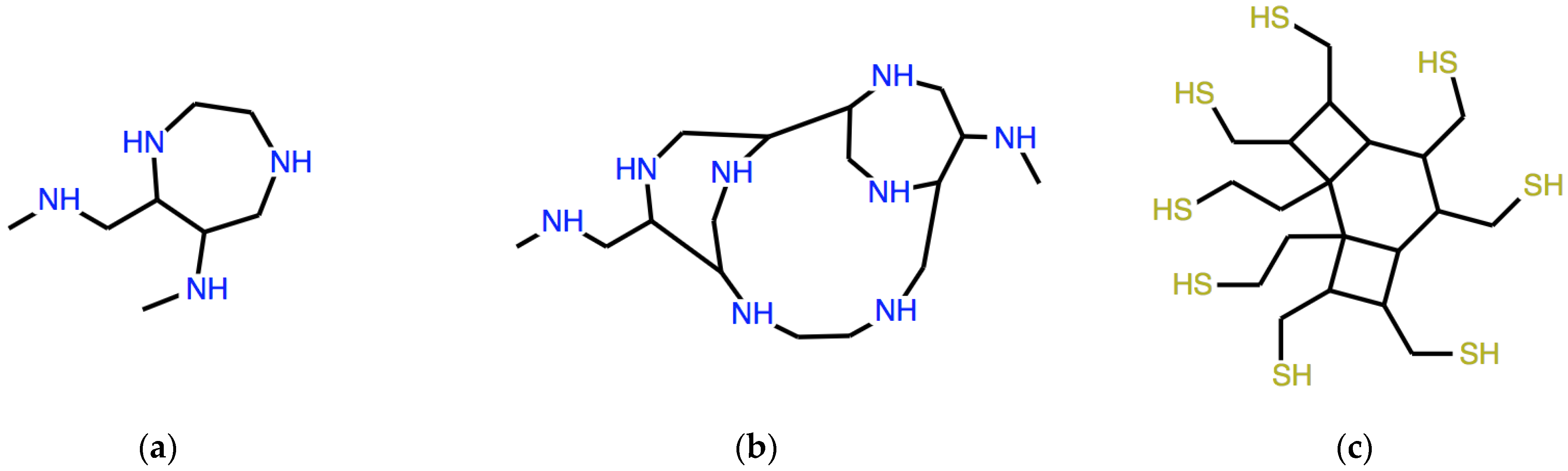
which expresses the structure in Figure 2a.
DD(ω) = C1CCNC1CCNC1CCNC1CCN
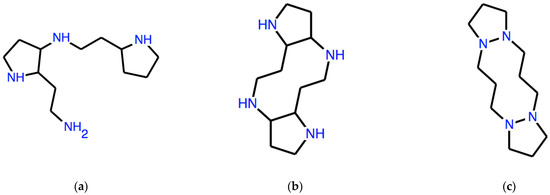
Figure 2.
Structures of polycyclic amines corresponding to the three expressions reported in the text: (a) DD(ω) with ω = C1CCN, (b) ADD(ω), (c) as (b) but different ω = CCCN1.
A subsequent application of the A operator to DD(ω) yields:
corresponding to the structure in Figure 2b. As we see, a non-trivial tricyclic molecular structure is produced as a result of manipulations that are not only completely formal but also very simple and not revealing, at least at first sight, of the resulting structure.
ADD(ω) = C12CCNC1CCNC1CCNC1CCN2
If the seed is only slightly different, such as ω = CCCN1, where the numeral 1 has been moved to follow the last atom in the linear expression, then
which corresponds to the structure in Figure 2c, where the superpositions between rings are single N-N bonds.
ADD(ω) = C2CCN1CCCN1CCCN1CCCN12
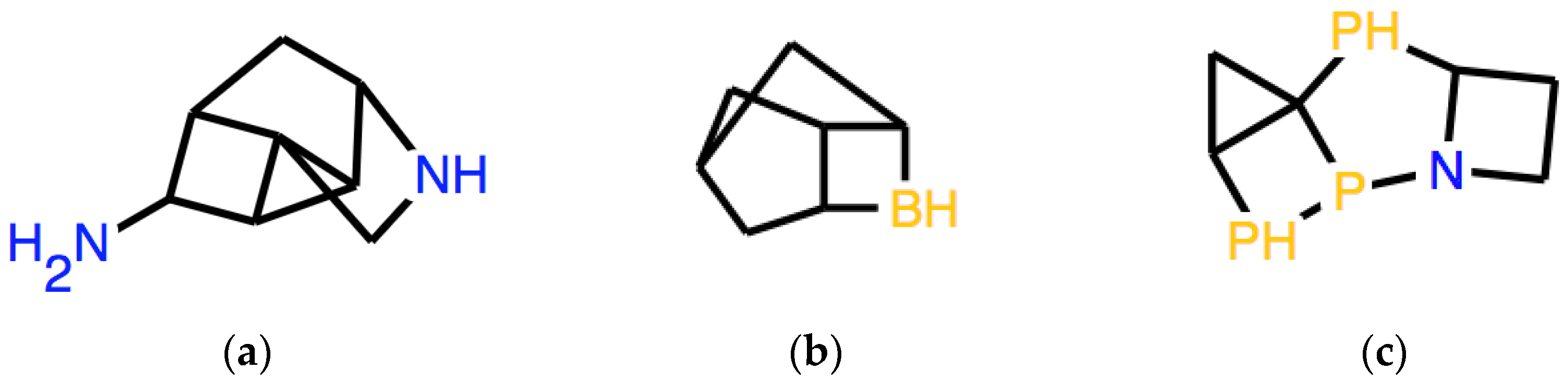
In a Special Issue dedicated to small clusters, it is appropriate to show an application related to this specific class of systems. It is actually possible to employ syntactic transformations to produce instructions that encode structures of this type. An example is to start from a string of limited length of atoms of mostly the same type. A random number generator can propose pairs of positions in the string, which must be followed by equal numbers, for example, from 1-1 to 4-4. It is very simple, both in human-performed processing and in a computer programs, to make sure that the same numbers are not attributed to atoms which are contiguous in the string, where the numbers would not add any information and also to check that any atomic valence is not hyper-saturated. In Figure 3, three structures produced this way are reported, being expressed by the following pseudo-random strings:
for each of which it was possible to successfully conduct a force-field optimization using the same software used for structure drawing [16].
3a: C34C1C23CNC1CC2C4N
3b: C3C2C1CC3CC2B1
3c: C3C2C13PC4CCN4P1P2
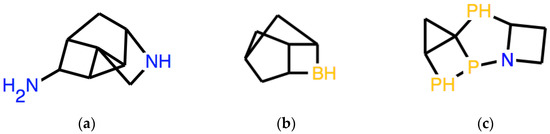
Figure 3.
Three examples of cluster-like structures corresponding to pseudo-random strings reported in the text, respectively: (a) 3a, (b) 3b, (c) 3c. Many such structures are not even locally stable but may be used as initial guesses for subsequent calculations.
A significant limitation of this specific approach, when applied to clusters, is that the indicated procedure also produces clusters that are not Lewis-valid. Lewis-validity is obviously not required by many small inorganic atomic clusters. Furthermore, formally Lewis-valid structures, such as those shown in Figure 3, even those that can be optimized by force-field methods, are probably barely stable or unstable with respect to isomerization, with or without spontaneous dissociation, but they have value as initial guesses for subsequent calculations, with a very well-defined geometry (following force-field optimization). In the examples provided, some contribution to stability could still be provided by the presence of a significant fraction of hydrogen. On the other hand, this specific category of clusters can be interesting from a research point of view, selecting those that are actually locally stable. As a further starting point, it is obviously possible to produce sequences in the SMILES language, which produce clusters with much less restrictive specifications.
An interesting question for future studies is the connection between the string production process and the symmetries of the corresponding optimized structure. The SMILES expression of tetrahedral P4, that is P12P3P1P23, as readily checked, suggests that very symmetrical systems can be obtained by the process just described. In general, however, random number addition on strings of fair length produces systems without global symmetries, as shown in Figure 3, in part, because too much hydrogen is still left. A different procedure might possibly be devised in order to maximize the expected elements of global symmetry in the corresponding system.
Coming back to a more general perspective, we have mentioned that many expressions obtained semi-automatically with the described procedure do not make sense as SMILES expressions, and in the subset that has literal meaning in terms of SMILES, many do not make chemical sense as they are unstable species that isomerize rapidly.
Observing the figures and considering the simplicity of the procedure that has been presented, one can, however, realize that the procedure itself, with a spirit of experimentation and curiosity, may really help intuition. It can do this by proposing blueprints for structures that obviously need to be refined by the capabilities of the researcher.
3. Branching and Cycling: Aliphatic Polyether Polyols and “Necklace” Systems
Another way to obtain more complex but logically organized structures from simpler structures is branching. This aspect of semi-automatic writing of structures has been explored in previous work by the same author [14]. In the context of this study, the branching process can be seen simply as a further proposal for a linguistic operator, which acts on expressions to generate other expressions. In the case of systematic substitution, this procedure falls entirely within the scope of L-systems [4]. To illustrate it, we will use, with a different notation, a system similar to “system 3” in [14]. This linguistic system formally produces the expression of a polyalcohol-polyether [19] of increasing complexity. In the case of the simplified version here, and reformulated in SMILES, the starting point is an expression of glycerol, purposely not the most concise one, but written following the syntax described in the previous work [14]:
ω = C(O)C(O)C(O)
It is then necessary to express the radical, which is obtained by eliminating the hydrogen atom from the central hydroxyl of the glycerol itself, placing the expression of the HO group at the beginning of the string. We select a specific possibility, named r. This is again not the most concise SMILES but is still valid:
r = OC(C(O))CO
The string r is just an alternative expression of the glycerol molecule: it is written in order to describe the molecule starting from the central hydroxyl. The rules of SMILES, in fact, automatically provide the hydrogen atom of the hydroxyl codified by the first symbol “O” in the string. However, in accordance with the rules of language, r becomes an expression of the required radical when it follows another string.
Note the difference between (O) and O in the expression of ω and r. This way one chooses which branches extend and which are terminal. These differences are not significant in SMILES, but they are in this grammar.
Following [14], we can define a systematic substitution operator B (“branch”).
B(x(O)y) = x(r)y
Here, a different notation from that of the cited work has been used and is similar to the one used in the previous examples. In this expression, the symbols x and y once again represent any string. Producing a substitution within a parenthesis, with a string involving further parentheses, leads to a progressive ramification of the structure corresponding to the expression. For example, B(ω) is given by:
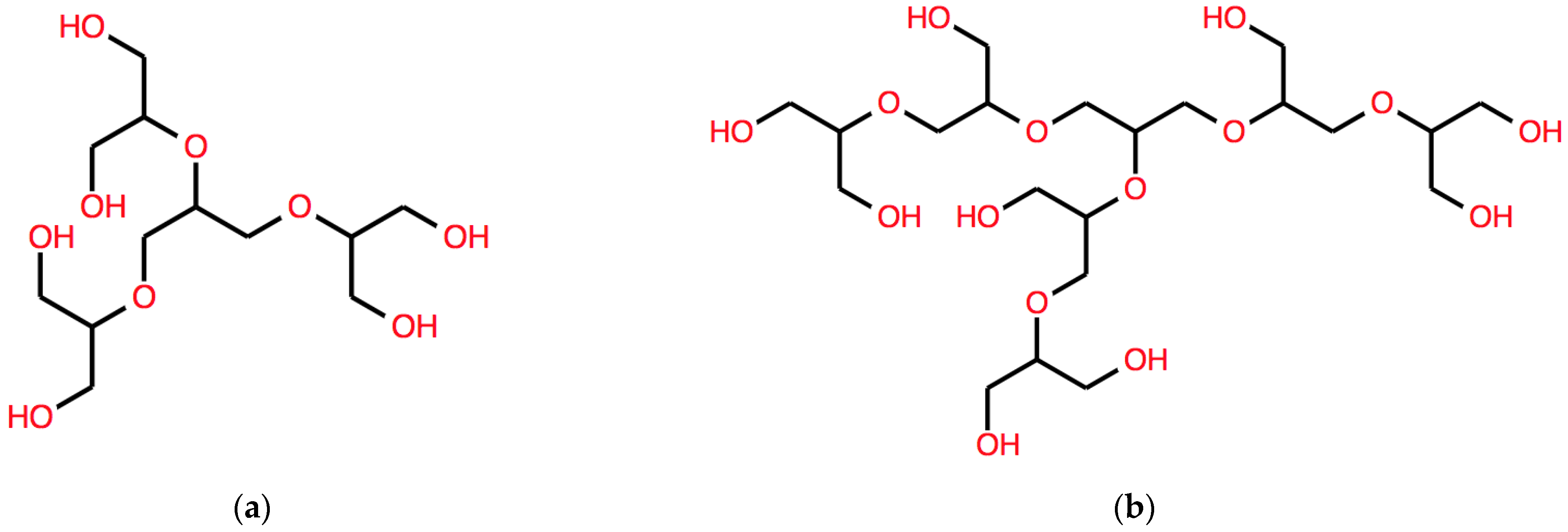
B(ω) = C(OC(C(O))CO)C(OC(C(O))CO)C(OC(C(O))CO)
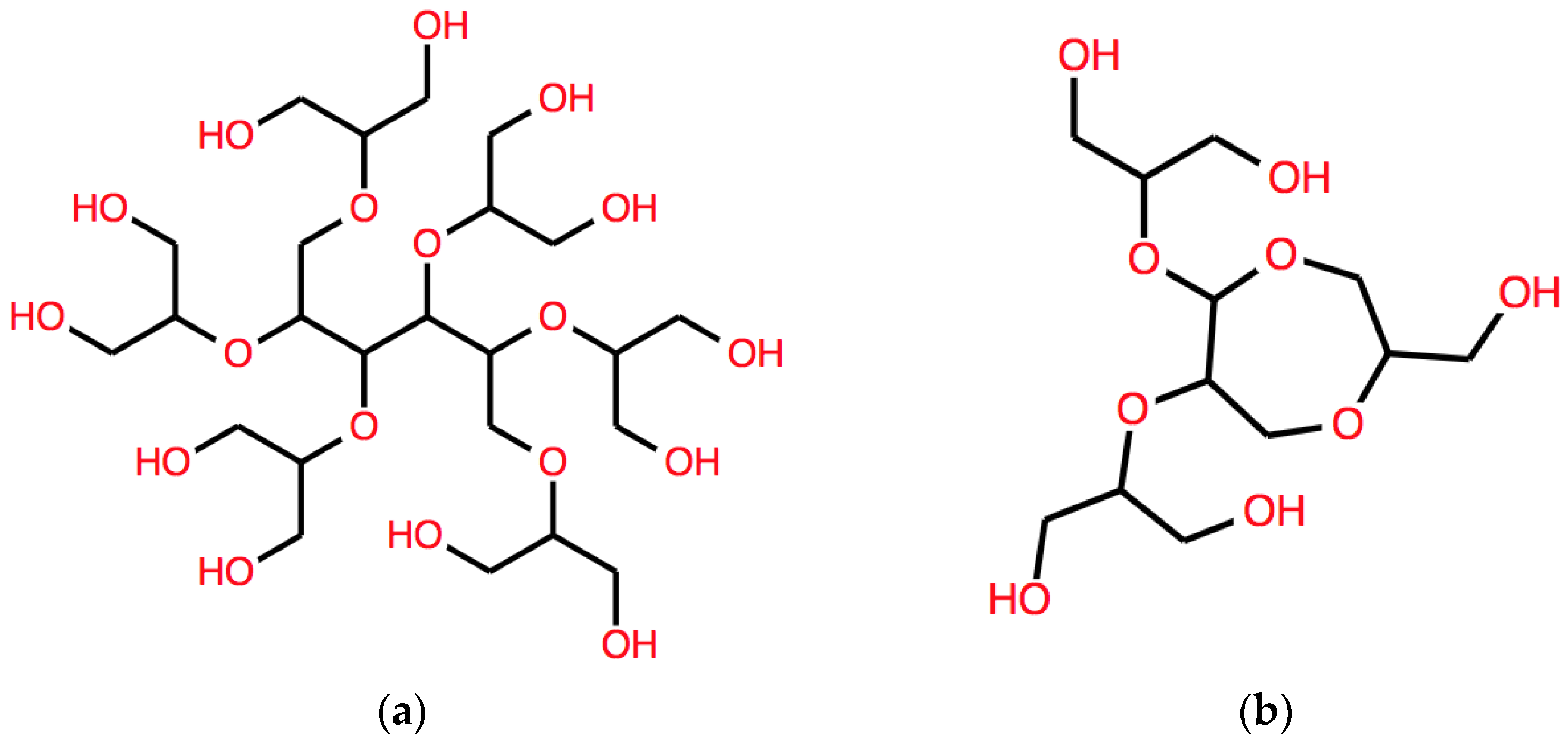
The corresponding structure is shown in Figure 4a.
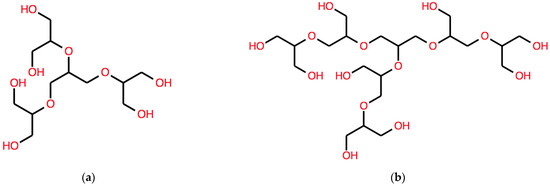
Figure 4.
Examples of structures of polyether polyols corresponding to expressions derived using respectively (a) B and (b) BB. See the text for details.
It is interesting to note that this formal process may be interpreted as the representation of a real process: the formation of an ether from two alcohols molecules with the elimination of water. String transformations can be interpreted as chemical reactions: this is an aspect of formal syntax that deserves further study.
Another application of B leads to the following string:
a much complex branched system, which is represented in Figure 4b.
BB(ω) = C(OC(C(OC(C(O))CO))CO)C(OC(C(OC(C(O))CO))CO)C(OC(C(OC(C(O))CO))CO)
Similar Bn(ω) systems have been characterized in [14]. With the richer language introduced in this work, we may now calculate DB(ω) = B(ω)B(ω) whose result is:
DB(ω) = C(OC(C(O))CO)C(OC(C(O))CO)C(OC(C(O))CO)
C(OC(C(O))CO)C(OC(C(O))CO)C(OC(C(O))CO)
C(OC(C(O))CO)C(OC(C(O))CO)C(OC(C(O))CO)
This string corresponds to another different structure, with a longer aliphatic core, shown in Figure 5a.
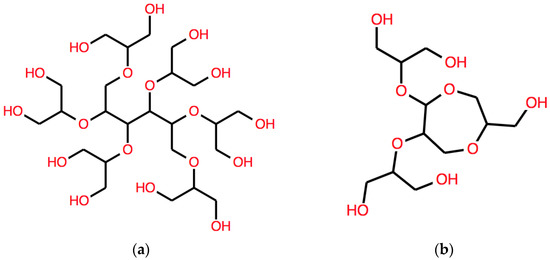
Figure 5.
Other two examples of structures of branched polyether polyols, one with a 6-C aliphatic core (left) and one with a cyclic core (right) obtained by applying different operators, respectively, (a) DB and (b) AB. See the text for details.
We may also use the operator A defined above. This operator needs a more explicit formulation here, to account for the possible presence of closing brackets. In loose terms, actually simply applied, the closing numeral must be placed before a set of closing brackets if present.
With this slightly different definition, A can be applied without limitation, an example being:
AB(ω) = C1(OC(C(O))CO)C(OC(C(O))CO)C(OC(C(O))CO1)
As expected, the action of the A operator leads to a string that describes a structure with cyclic polyether sub-structure, as shown in Figure 5b.
Using the operators D, A and B in different order and starting from different axioms produces a great variety of results.
Only a few element symbols have been used here and we have explored a negligible portion of the accessible structure space. The use of the two operators to increase the number of atoms in two different ways, as well as the use of the “add numerals” operator to produce closed chains, generates a huge set of expressions of structures, including honeycomb-structure polyethers and sugars.
It is not difficult to imagine other syntactic operators that are easily applicable by a text processor.
An example is the following “necklace” operator N, which has been used by the author as an exercise in his teaching.
The “necklace” operator N:
Given a SMILES string:
- Apply the duplication operator D to the string;
- Replace the first and last occurrences of two consecutive carbon atoms CC in the string if at least two of such occurrences are present, with the symbol CnC, where n is the smallest number that does not yet appear in the string.
With the seed ω = CNC (dimethylamine), the result of the second and third iteration is the expression of the molecules in Figure 6a,b, respectively.
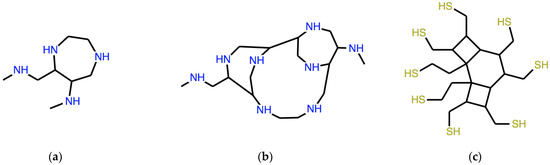
Figure 6.
Two “necklace” systems whose expression is obtained by applying twice (a) and thrice (b) the corresponding syntactic operator to a SMILES expression of dimethylamine. (c) is an exercise system.
A typical exercise asks to find the seed ω, which generates the necklace system in Figure 6c: the answer to this problem is ω = C(CCS)(CCS) and the system shown, whose linear expression is:
is yielded at the second iteration. More advanced students help themselves with the symmetries of the target system.
N2ω = C(C1CS)(C2CS)C(CCS)(C1CS)C(C1CS)(CCS)C(C2CS)(C1CS)
An exercise like this illustrates derivability, a fundamental concept of logic. In this case, derivability is the possibility of obtaining a Lewis-valid structure by manipulating strings in a given formal system. Many structures, which are not derivable as necklace systems from any ω, are found by displacing just a single atom in the derivable ones shown in Figure 3a–c.
For sufficiently expressive languages, the issue of derivability is formally undecidable [1]: this fact may be of conceptual and practical importance, once specific strategies of synthesis are described as derivation systems at a linguistic level.
4. Conclusions
In this work, we have shown how formal expressions for molecular systems, usable as input for molecular drawing or any kind of further elaboration, can be generated by word-processing techniques, which modify the strings of symbols based on defined rules. The molecular structures corresponding to these expressions show a remarkable variety. This shows the possibilities offered by computer-assisted text modifications to produce patterns of interest from a chemical point of view, in the spirit of previous research on biological shape. Although in this work we have considerably extended the expressive capacity of the generative grammars of the previous work by the same author [14], there are still great development prospects. Chirality and cis-trans isomerism, which fall within the expressive capacity of SMILES, have been ignored in this work. We have also generally kept, in order not to increase the degrees of freedom to be explored too much, the strong limitation inherited by L-systems for which substitutions are systematic. We have only considered a negligible part of the possible linguistic operators that can modify molecular expressions. The syntactic operators D, A, B and N used here are just examples. Each researcher will be able to develop own set of linguistic operators, perhaps half a dozen in number, whose iterations and combinations express an almost infinite repertoire of structures sharing a common peculiar style. This molecular kaleidoscope can be created with a text processing program and a program for the graphical rendering of structures from SMILES strings, both easily accessible. The possibility of promptly carrying out an optimization, at least of the force-field type, allows to obtain further insights from a supposed three-dimensional arrangement of the atoms. Experimentation, as it has been shown, is very simple and can be pursued without limitation.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Révész, G.E. Introduction to Formal Languages; Courier Corporation: Chelmsford, MA, USA, 1991. [Google Scholar]
- Bezem, M.; Klop, J.W.; de Vrijer, R. (Eds.) Term Rewriting Systems; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Matiyasevich, Y.; Sénizergues, G. Decision problems for semi-Thue systems with a few rules. Theor. Comput. Sci. 2005, 330, 145–169. [Google Scholar] [CrossRef]
- Lindenmayer, A. Developmental algorithms for multicellular organisms: A survey of L-systems. J. Theor. Biol. 1975, 54, 3–22. [Google Scholar] [CrossRef] [PubMed]
- Djezzar, N.; Djedi, N.; Cussat-Blanc, S.; Luga, H.; Duthen, Y. L-systems and artificial chemistry to develop digital organisms. In Proceedings of the 2011 IEEE Symposium on Artificial Life (ALIFE), Paris, France, 11–15 April 2011; pp. 225–232. [Google Scholar]
- Salcedo-Sanz, S.; Cuadra, L. Hybrid L-systems–Diffusion Limited Aggregation schemes. Phys. A Stat. Mech. Its Appl. 2019, 514, 592–605. [Google Scholar] [CrossRef]
- Barlow, P.; Lück, J. Transformations of cellular pattern: Progress in the analysis of stomatal cellular complexes using L-systems. In Progress in Botany 71; Springer: Berlin/Heidelberg, Germany, 2010; pp. 61–99. [Google Scholar]
- Smullyan, R.M. The Gödelian Puzzle Book: Puzzles, Paradoxes and Proofs; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Galati, S.; Di Stefano, M.; Martinelli, E.; Macchia, M.; Martinelli, A.; Poli, G.; Tuccinardi, T. VenomPred: A Machine Learning Based Platform for Molecular Toxicity Predictions. Int. J. Mol. Sci. 2022, 23, 2105. [Google Scholar] [CrossRef] [PubMed]
- Skinnider, M.A.; Stacey, R.G.; Wishart, D.S.; Foster, L.J. Chemical language models enable navigation in sparsely populated chemical space. Nat. Mach. Intell. 2021, 3, 759–770. [Google Scholar] [CrossRef]
- Ikebata, H.; Hongo, K.; Isomura, T.; Maezono, R.; Yoshida, R. Bayesian molecular design with a chemical language model. J. Comput. Mol. Des. 2017, 31, 379–391. [Google Scholar] [CrossRef] [PubMed]
- Ferruz, N.; Höcker, B. Controllable protein design with language models. Nat. Mach. Intell. 2022, 4, 521–532. [Google Scholar] [CrossRef]
- Longo, S. Hints for a formal language inspired by Lewis structures. Found. Chem. 2022, 24, 315–330. [Google Scholar] [CrossRef]
- Longo, S. Generative grammars for branched molecular structures. Chem. Phys. Lett. 2022, 809, 140151. [Google Scholar] [CrossRef]
- Dawkins, R. The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe without Design; WW Norton & Company: New York, NY, USA, 1996. [Google Scholar]
- Available online: https://biomodel.uah.es/en/DIY/JSME/ (accessed on 10 December 2022).
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Bachrach, S.M. Tetraphenylene Ring Flip Revisited. J. Org. Chem. 2009, 74, 3609–3611. [Google Scholar] [CrossRef] [PubMed]
- Schömer, M.; Schüll, C.; Frey, H. Hyperbranched aliphatic polyether polyols. J. Polym. Sci. Part A Polym. Chem. 2013, 51, 995–1019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).