Abstract
A review of computational–theoretical and experimental works devoted to the study of the flow of bodies by two-phase (dispersed) flows is carried out. The features of particle motion in the vicinity of bodies of various shapes, as well as the effect of the dispersed phase on resistance and heat transfer, are considered. Some consequences of the interaction of particles and droplets with the surface of streamlined bodies (erosive destruction, gas-dynamic spraying, icing, glowing) are analyzed.
1. Introduction
The gas dynamics of heterogeneous flows with dispersed admixtures in the form of solid particles or liquid droplets has been one of the most rapidly developing areas of the mechanics of multiphase (two-phase) media for many decades. This is due to the numerous engineering applications of such flows (steam generators, facilities for the thermal pretreatment of coal, heat exchangers with two-phase working fluid, sand and bead blasting facilities, dust collectors of different types) and their wide distribution in nature (tornados, dust storms, volcanic eruptions, snow, rain). One of the most important classes of two-phase flows is the flow of gas with an admixture of solid particles or droplets near the limiting surfaces and when flowing around bodies and obstacles.
Interest in the problem of the flow of bodies by a gas stream containing dispersed particles or droplets arose in the early 1950s. Initially, it was caused by the problems such as the filtration of impurities, sampling from dusty streams for their dispersion analysis in relation to the study of a wide range of problems of atmospheric aerosol dynamics. A little later, interest in two-phase aerodynamics appeared in aviation in connection with the problems of aircraft icing and the gas-drop erosion of propellers when flying in clouds, fog, and in the presence of rain.
In the following years, the relevance of the study of two-phase flows was supported by the rapid development of aerospace technology. Initially, these were mainly internal tasks related to the flow of two-phase media in the nozzles of rocket engines. Somewhat later, there was interest in the problems of external flow of bodies with two-phase flows. This was due to two circumstances. Firstly, numerous experiments have revealed a sharp (sometimes multiple) increase in heat flow at the critical point of blunted head parts. Secondly, the effect of the erosive destruction of the surfaces of aircraft bodies in a dusty atmosphere was detected. Most recently, this interest has been associated with international programs for a flight to Mars, which has a dusty atmosphere.
The phenomena of thermal erosive destruction are caused by the combined action of a number of reasons: (1) a change in the structure of the flow of a stream running into the body [1,2,3,4,5]; (2) a change in the characteristics of the boundary layer [6,7,8,9] developing on a streamlined body; (3) a change in the parameters of vortex zones and turbulent traces [10,11,12,13,14]; (4) the presence of collisions of particles (droplets) with the surface and with each other; (5) a change in the roughness of the surface and others.
The intensity of the processes accompanying the flow of two-phase flows around bodies depends primarily on the inertia and concentration of particles (droplets). It should be noted that the particle inertia is directly determined by the geometry and flow parameters and can vary for the same particles (droplets) within very wide limits. The presence of various characteristic times (length) of the carrier flow (near the critical point of the streamlined body, along its surface, the actual turbulent scales, etc.) greatly complicates the study of such flows and the generalization of data. As for the concentration of the dispersed phase, its value can be many times higher than the “initial” value in an undisturbed flow due to the sharp deceleration of the flow when approaching the body, the interaction of particles (droplets) with the wall, as well as interparticle (inter-drop) collisions.
The main tasks of studying the flow of bodies by two-phase flows with particles or droplets include (1) investigation of the movement of particles (droplets) and determination of their trajectories; (2) determination of the influence of particles (droplets) on the flow of gas; (3) investigation of the processes of interaction of the dispersed phase with the streamlined surface, including erosive wear, gas-dynamic spraying, icing, etc.
As far as the authors know, despite the significant number of available works devoted to most different aspects of two-phase flows past bodies and the colossal breadth of their possible practical applications, there are no monographs or reviews devoted to this important class of two-phase flows. It is this gap that the present work aims to fill.
This review presents and analyzes the results of computational, theoretical, and experimental works devoted to the study of the flow of bodies by two-phase flows containing particles or droplets.
2. The Flow of Bodies by Streams with Particles (Drops): The Main Characteristics
Some characteristics of the particle inertia and droplets moving in two-phase flows will be described below, as well as the main dimensionless criteria used to summarize the research results.
2.1. Particle Inertia (Droplets): Dynamic Relaxation Time
The behavior of particles and droplets in gas flows is largely determined by their inertia. The particle inertia (droplets) moving in the flow depends primarily on their size (diameter) and physical density .
The most complex characteristic of the particle inertia is the dynamic relaxation time , represented in the following form:
Here, is the dynamic relaxation time of a Stokesian particle (drop); is the dynamic viscosity. Note that the relaxation time of a particle (drop) also depends on the dynamic viscosity of the medium in which its motion occurs. The correction function considers the effect of inertia forces on the relaxation time of a non-Stokesian particle (drop).
2.2. Stokes Numbers
One-phase turbulent flows are characterized by several spatial and corresponding time scales. As a result, it is possible to derive several dimensionless criteria—Stokes numbers—which determine the particle inertia (droplets) relative to certain flow scales, in the following form:
where is the some characteristic time of the carrier phase.
In [1], three main dimensionless criteria are distinguished: , , and —Stokes numbers in time-averaged motion, large-scale fluctuation motion, and small-scale fluctuation motion, respectively. When analyzing these criteria, , , and are chosen as characteristic times—the characteristic time of the carrier phase in averaged motion, large-scale fluctuation motion, and small-scale fluctuation motion, respectively.
Considering the above, when considering the flow of bodies by two-phase flows, the Stokes numbers in averaged motion are defined as
where represents the characteristic velocity of the incoming flow, and R and D are the radius and diameter of the streamlined sphere (cylinder).
To account for the effect of large-scale vortices on the motion of particles (droplets), the Stokes number is used in large-scale fluctuation motion,
where represents the Lagrangian integral scale of turbulence, and is the RMS value of the fluctuating flow velocity.
To account for the effect of small-scale vortices on the motion of particles (droplets), the Stokes number is used in small-scale fluctuation motion,
where represents the Kolmogorov timescale of turbulence, is the kinematic viscosity, and is the turbulence energy dissipation rate.
2.3. Reynolds Number
The Reynolds numbers when considering the flow of bodies by flows are defined as
In two-phase flows, the main criterion determining the flow mode is the particle (droplet) Reynolds number (), calculated from the relative velocity between phases and particle diameter ,
where represents the velocity vector of the carrier gas, and is the velocity vector of particles (droplets).
2.4. The Particle Sedimentation Coefficient
An important characteristic is the particle sedimentation (trapping) coefficient . Its magnitude is the ratio of the number of particles that have collided with the body to the number of particles that could collide with it if their trajectories were straight lines.
In the case of axisymmetric flow (for example, a flow past the sphere), when the particle size is negligible compared to the size of the body, the particles are evenly distributed in the incoming flow, and their trajectories are symmetrical, the sedimentation coefficient can be defined as
where is the dimensionless distance from the axis of symmetry of the flow, at which (in the flow undisturbed by the presence of a body) the particles only meet the body when it flows around. Particles whose coordinates are in the incoming flow do not undergo collisions with the body. For a flat flow (for example, with a transverse flow past an infinite cylinder or plate), the sedimentation coefficient is equal to
3. Features of the Flow of Bodies by Flows with Particles
The features of particle motion in the vicinity of bodies of various shapes, the effect of the dispersed phase on resistance and heat transfer, and the features of high-velocity flows around bodies will be considered below, and some consequences of the interaction of particles with the surfaces of streamlined bodies (erosive destruction, cold gas-dynamic spraying, glowing) will be analyzed.
3.1. Flow around Bodies of Various Shapes
This section contains a description and analysis of the results of computational, theoretical, and experimental studies of the characteristics of two-phase flows in the flow of bodies of various shapes: spheres, cylinders, plates, and airfoil cascades.
The flow past the sphere. One of the early studies of the trajectories of the flow of bodies by a two-phase flow is Ref. [15]. In it, the trajectories of particles with a potential flow past the sphere were calculated. Basic assumptions: (1) the velocities of the gas and particles away from the surface of the body are equal; (2) the resistance of the particles obeys the Stokes law; (3) the particles do not have a reverse effect on the gas; (4) the interaction of the particles with the sphere was not considered, i.e., it was assumed that the particles are absorbed by its surface.
The limiting trajectories of particles corresponding to are calculated. This makes it possible to determine the values of the particle sedimentation coefficients: , , and for Stokes numbers , , and , respectively.
The effect of gravity on particle sedimentation was also studied in [15]. Two cases are considered—the flow past the sphere by descending and ascending two-phase flows. To do this, a term was added to the right side of the Lagrangian equations of motion , where is the acceleration of gravity. It is obvious that the influence of gravity will be significant only in the case when the velocity of the particles and the velocity of the flow are quantities of the same order. It is concluded that considering gravity causes an increase in in the downward flow past the sphere and a decrease in the upward flow.
In [16], the influence of the boundary layer developing on the surface of a streamlined body on the dynamics of particles was studied. In this paper, the viscous flow of a two-phase flow past a sphere for three Reynolds numbers is investigated, i.e., , , and , and the relative diameter of the particles , where . It is believed that the carrier gas is incompressible, and the concentration of particles is negligible, so that they do not affect the flow of a continuous medium.
It is shown in [16] that the boundary layer strongly distorts the trajectories in comparison with the ideal flow. It “repels” particles, preventing their movement to the wall. Viscous gas is inhibited more intensively than ideal, which leads to the more intensive braking of solid particles. Particles moving in the boundary layer near the streamlined surface abruptly lose their speed, “hang”, and then drift along the surface of the body. The particle sedimentation coefficient decreases in this case. In [16], it is concluded that for moderate values of the Stokes number (), the boundary layer has almost no effect on the movement of particles, and at small values (), the impact is very significant. With the growth of the critical value of the Stokes number corresponding to the collisionless flow of particles around the body decreases. This is because the increase in leads to a decrease in the boundary layer thickness, which reduces its repelling effect.
The flow past the cylinder. In [17], the trajectories of particles during transverse flow past the cylinder by a potential flow are calculated. In this study (as well as in [15]), the motion of single particles is considered when collisions between particles and their effect on the gas are not considered. In comparison with [15], the difference between the particle resistance and the Stokes law, as well as the transverse Saffman force, is considered.
The calculation results showed that the flow pattern of the cylinder strongly depends on the particle inertia. In the case of small particles μm (), an almost axial symmetry of their trajectories and is observed. For particles μm (), the influence of gravity becomes noticeable (the symmetry of the trajectories is broken); particles undergo collisions with the body and . In the case of large particles (), they do not follow the gas flow lines well near the body, their trajectories represent almost straight lines, and .
In [18], a detailed study of the flow past the cylinder by a two-phase flow was performed. Special attention was paid to the interaction of particles with the surface of the body, as well as among themselves. The main parameters of two-phase flow: air velocity away from the body m/s, radius of the steel cylinder m, particle diameter μm, particle density (aluminum oxide) kg/m3. Calculations were performed for three values of the volume concentration of particles in the incoming flow: , , and . As a result of calculations, flow patterns and isolines of particle concentration are obtained.
It is easy to show that for conditions [18], . Such inertial particles almost do not change the velocity near the critical point of the body and . Calculations have shown the presence of a “phase” of reflected particles. The presence in the flow of particles reflected from the body moving towards the incoming flow leads to an increase in the concentration of particles near the critical point of the body. It is established that the magnitude of the relative rebound of the particles does not exceed and decreases with an increase in the concentration of particles in the incoming flow. Note that the distance at which the reflected particles penetrate towards the incoming flow is lower than that obtained in experiments [19] with close values of particle inertia. This discrepancy is a consequence of the relatively high gas velocity in [18], when a large drag force acts on the reflected particles, leading to the more intense deceleration of the particles and a decrease in their rebound from the body. Such conclusions are consistent with the calculations of the magnitude of the rebound of particles in [20].
Collisions of incident and reflected particles lead to a significant increase (up to 10 times) in the local concentration of particles at the surface of the body [18]. A decrease in the size of the near-surface area of an increased concentration of particles is seen with an increase in . This is explained as follows. An increase in the concentration of particles in the incoming flow leads to an increase in the frequency of collisions of incident and reflected particles. This leads to a decrease in the magnitude of the bounce of the reflected particles. A decrease in the existence of the “phase” of reflected particles leads to a decrease in the near-surface area of the increased particle concentration.
In [21], the flow past a cylinder by a two-phase flow is investigated, considering the boundary layer, the inverse effect of particles on the gas, as well as the influence of reflected particles. At the same time, the interaction between the particles is not considered. Only the aerodynamic drag force is considered in the equations of particle motion.
When the particles collide with the surface, they lose part of their motion and change the direction of motion. As noted in [21], the rebound parameters are statistical in nature and are determined mainly by the angle of incidence of the particle. During the calculations, empirical relations were used for the coefficients of speed recovery after impact.
In study [21], the trajectories of quartz particles of various sizes moving in the air flow while flowing past the cylinder are obtained ( kg/m3) ( mm) for . It is shown that small particles do not collide with the surface of the body, while large particles collide with the body and bounce to the side. The influence of the boundary layer on the motion of particles is confirmed. Considering the viscosity of the gas leads to an increase in the effective size of the cylinder due to the displacement boundary layer thickness, which reduces the sedimentation coefficient. The disadvantage is the lack of consideration of gravity, which, for the conditions [21], should have a significant impact, changing the trajectories of particles and violating the symmetry of the flow in the considered case of horizontal flow.
The flow of a weakly dusty two-phase flow around a cylinder under non-isothermal conditions is considered in the review [22]. Analysis of the non-isothermal sedimentation process has shown that in the region of low-inertia particles, for which the inertial sedimentation mechanism no longer works (), the sedimentation intensity increases sharply with the increase in non-isothermicity and is largely determined by the phenomenon of thermophoresis. This was confirmed in a later paper [23] devoted to the study of the influence of the temperature factor on the inertial sedimentation of particles in the case of a supersonic flow past a sphere.
In Refs. [19,20], experiments were carried out to study the longitudinal flow of cylinders with ends of various shapes—hemispherical and flat. Experiments were carried out for the downward flow of air in the pipe at m/s. Cylinders with a diameter of 11 mm were installed inside the pipe on its axis. Spherical glass particles were used ( μm). Measurements were carried out for two concentrations of the dispersed phase: low— and high—.
Large-inertia particles practically did not change their velocity in the critical point region, i.e., . The dynamics of incident and reflected particles from the surface were studied. At , two “additional” velocity distributions of incident and reflected particles that collided with each other were revealed. The dimensions of the region of existence of the “phase” of the reflected particles were measured. With the increase in the particle inertia, the magnitude of their rebound from the surface increased. After deceleration, when moving upstream, the “phase” of reflected particles passed into the “phase” of particles repeatedly falling on the body. In the case of a flat end, the penetration of reflected particles reached a much greater distance (compared to the hemispherical end) towards the incoming flow.
The growth of leads to an increase in the probability of collisions between incident and reflected particles, which complicates the “decoding” of particle velocity distributions and the construction of trajectories. Nevertheless, such data are useful for verifying mathematical models of highly concentrated two-phase flows.
In research [24], a three-dimensional numerical study of the dispersion of particles when a two-phase flow flows around a cylinder for Reynolds numbers determined by the diameter of the cylinder and the velocity of the incoming flow was performed. Special emphasis was placed on the study of the motion of particles of different inertia () in the vortex and recirculation zones behind the cylinder. The results of calculations showed that low-inertia particles follow the lines of the carrier gas current and easily penetrate the recirculation zone behind the cylinder. They undergo collisions with the rear surface of the cylinder. More inertial particles () are concentrated at the outer boundary of the vortices due to the action of centrifugal force. Such particles are not able to penetrate the core of the vortex, forming “void” zones (areas free of particles). Even more inertia particles ( and ) collide with the front surface of the cylinder due to the large inertia, but when they enter into the vortex structures behind the cylinder, they do not retain the direction of their initial movement, forming “mushroom-shaped” structures.
Numerical simulation of the transverse flow past a cylinder by a two-phase flow with particles was performed in [25]. The Mach number of the incoming flow was equal to , and the ratio of the phase densities . The influence of the Stokes () and Reynolds numbers () on the collisions of particles with the surface was studied.
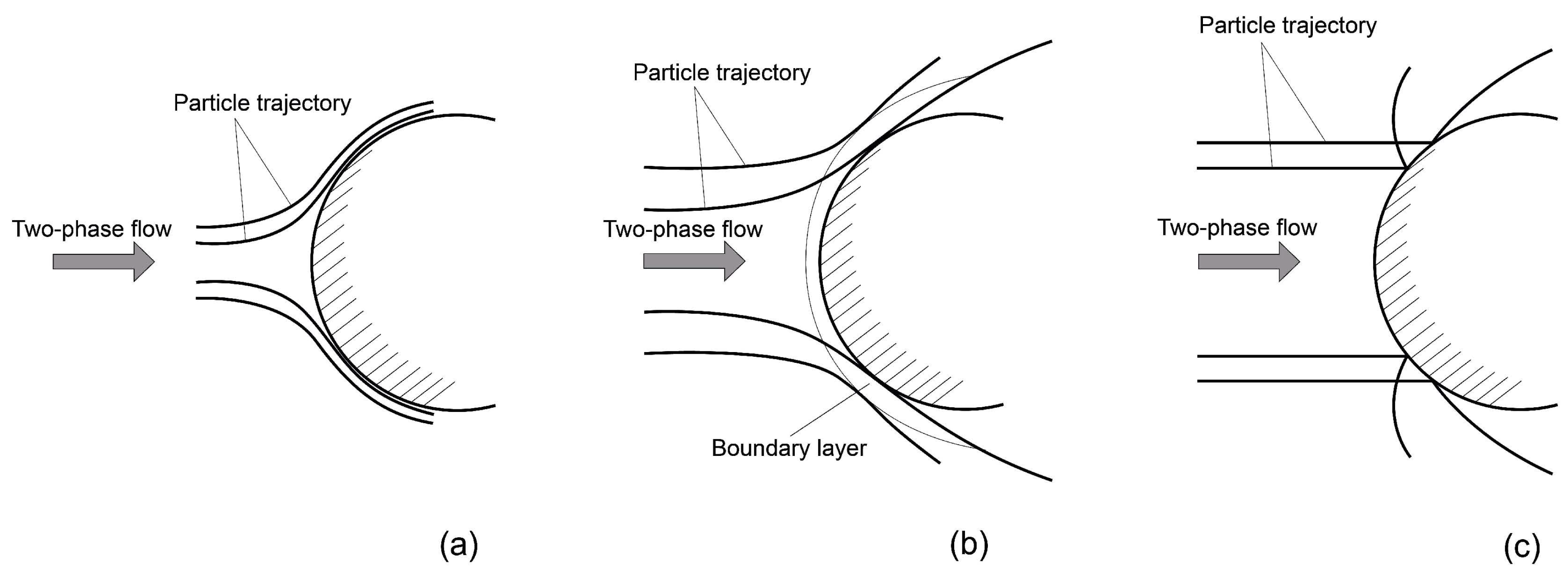
Three modes of particle impact (Figure 1) on the cylinder surface [25] are distinguished: blocking (border crossing mode), boundary layer (particle braking mode in the boundary layer), and inertial (classical collision mode). At extremely low inertia of particles (), they almost perfectly track the gas flow lines, but, nevertheless, they undergo collisions with the cylinder due to their finite radius (blocking mode). Infinitesimal (point) particles will not collide with the cylinder. With an increase in the inertia of the particles (), their sedimentation coefficient increases greatly. A viscous boundary layer (boundary layer mode) developing on the surface of the cylinder begins to play an important role in the sedimentation process of relatively low-inertia particles. In the inertial regime (), the inertia of the particles is already large enough that the boundary layer does not have a significant effect on their sedimentation. It should be noted that changing the Reynolds number leads to a shift in the ranges of the Stokes number, at which the modes described above are implemented. Thus, the border-layer mode for takes place at , and for already at . This is because, at small Reynolds numbers, when the boundary layer thickness increases, its repelling effect increases.
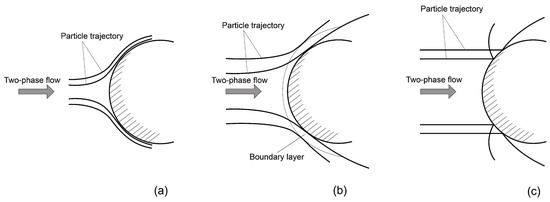
Figure 1.
Three modes of interaction of particles with the surface of a cylinder in a two-phase flow: (a)—blocking mode; (b)—boundary layer mode; (c)—inertial mode.
In article [25], the conditions for the existence of a particle impact on the rear surface of the cylinder were also studied. In particular, it is shown that at small Reynolds numbers ( and ), there are no impacts on the back surface, and at high values of the Reynolds number, they are observed only up to a certain limiting Stokes number .
In [26], the effect of the turbulence of the incoming flow on the transverse flow past the cylinder by a two-phase flow was studied by direct numerical modeling (DNS). The model of high-intensity homogeneous isotropic turbulence (HIT) was used for calculations. The Stokes number in the averaged motion varied in the range . Calculations were performed for two values of the Reynolds number— and . The Stokes number was changed by varying the radius of the particles. For these Stokes and Reynolds numbers, the particle diameter was chosen using the following function [26]:
where is the ratio of phase densities.
Calculations were performed for two values of the Lagrangian integral scale of turbulence of the incoming flow— and .
For conditions [26], the Stokes numbers in large-scale fluctuation motion are equal to for and for . It follows from this that it is impossible to neglect the influence of large-scale vortices on the motion of particles.
Stokes numbers in small-scale fluctuation motion [26] for and for . It is well known that there is a particle clustering effect [27] if the particle dynamic relaxation time lies in the range , i.e., the condition is met. From this, it follows that the clustering effect of particles in the incoming flow will take place—in particular, at and , because at for the specified Reynolds number.
In Ref. [26], an expression is proposed for the resulting particle sedimentation coefficient in the case of accounting for the turbulence of the incoming flow in the following form:
where and are the particle sedimentation coefficient in turbulent and laminar flows, respectively.
Calculations clearly showed that accounting for turbulence significantly increases the sedimentation coefficient () in the range of small Stokes numbers . This is in good agreement with the conclusions of [28], where it is shown that turbulence has an effect if the Stokes number is less than a certain critical value, i.e., . For example, for in [28], was obtained. The indicated value is consistent with the results of [26], where a small effect of turbulence was revealed at at . For particles with , the value of approaches unity as the Stokes number increases.
It is concluded [26] that for the small Reynolds numbers considered in the paper, the effect of turbophoresis can be neglected. This effect consists in the transfer of particles from areas with high turbulence intensity to areas with low turbulence intensity. Turbophoresis is an important physical mechanism [29] that leads to the collision of particles with the cylinder surface if the dynamic relaxation time is of the same order as the characteristic lifetimes of small-scale vortices.
The flow past the plate. The conditions of the inertial sedimentation of Stokesian particles on a plane at the outflow of a laminar two-phase jet from a plane-parallel channel were studied in [30,31,32]. Initial assumptions: the absence of the influence of particles on the gas and the interaction of particles with each other. The modified Stokes number was determined as follows—. It is shown that for the inertia particles (), the decrease in due to changes in the trajectories of particles in the boundary layer, even at small Reynolds numbers, does not exceed 15% [32]. However, the tangent and normal components of the particle velocity at the wall underwent a significant decrease. For low-inertia particles (), a multiple increase in the concentration of particles on the surface was revealed, which raises the question of the applicability of the initial assumptions.
Flow past the airfoil cascades. The modern design of gas turbines involves modeling the flow of the working medium in the flow part. The gaseous medium often contains a dispersed admixture in the form of solid particles or liquid droplets. This is due to the chemical or mechanical underburning of fuel in the combustion chamber, the operation of the turbine in a dusty environment, etc. The presence of particles can lead to additional losses and erosion of the blades. Knowledge of particle dynamics is necessary when predicting areas of the nozzle and working blades that are vulnerable from the point of view of erosive destruction.
In [33], the behavior of electro-corundum particles during transonic flow around a stationary two-dimensional airfoil cascade was studied. It was assumed that the concentration of particles is small, so that their reverse effect on the flow of the carrier gas and the interaction between the particles are insignificant. At the entrance to the airfoil cascades, the flow was considered homogeneous, subsonic with Mach number ( m/s), and the braking temperature K. The airfoil cascade chord ( m), lattice pitch ( m), and the angle of inclination of the velocity vector at the entrance to the lattice () were set.
Considering the complex flow pattern of the airfoil cascades, determined by the complex geometry of the blades and variable angles of attack, the geometric scale for evaluating the modified can be represented as
where is the radius of the input edge of the vane; is half of the chord of the vane; is the the angle between the velocity vector at the entrance to the grid and the chord of the airfoil cascades ( for working conditions [33]). Thus, in two extreme cases, and , we have and , respectively.
The results of calculations showed that particles with a diameter of 3 μm () do not collide with the airfoil cascades. Some particles collide with the concave surface of the airfoil cascades, but this does not change the overall picture of movement ( is small). The growth of particle inertia (10 μm, ) leads to the fact that all particles collide with the airfoil cascades ( is high). For those particles that are reflected from the front edges of the blades, further collisions with the troughs of neighboring blades are characteristic. The effect of the redistribution of particles by the airfoil cascades is maximal. A further increase in the particle inertia (30 μm, ) greatly complicates the flow picture due to an increase in the proportion of particles undergoing collisions with the leading edges of the blades. Some particles reflected from the leading edges experience collisions with the leading edges of adjacent blades. A significant number of the particles experience multiple collisions with the airfoil cascades’ troughs. Particles of extreme inertia (100 μm, ), after rebounding from the front edges of the blades, penetrate towards the incoming flow, thus forming a thick layer of reflected particles. At the same time, the particles reflected from the front edges of the airfoil cascades further interact not with neighboring but with more distant blades. This case is also characterized by multiple reflections from the concave surfaces of the vanes.
The airfoil cascades have a strong influence on the redistribution of particles in space. In the entire considered range of particle inertia, a particle-free region is formed near the convex surface of the blades.
3.2. Features of High-Velocity Flow around Bodies
The analysis of the features of high-velocity (supersonic, hypersonic) flows around bodies by two-phase flows will be carried out below.
The first papers studying the structure of shock waves in flows with particles are studies [34,35,36]. It was shown that the structure of a shock wave in a two-phase flow is well described by a model that includes an infinitely small wave front (on which particles do not change their parameters) and an extended zone behind the jump, in which the velocities of the gas and dispersed phases relax. Dimensionless parameters determining the nature of the relaxation zone are found: the particle Reynolds number, the particle inertia, the ratio of the heat capacities of the phases, and the mass concentration of the particles.
In later studies [37,38], the dependences of the relaxation zone width and jump characteristics on the particle parameters (density, mass concentration, heat capacity) were studied in detail. Important conclusions were made: (1) the intensity of the shock wave increases, and the width of the relaxation zone decreases, with an increase in the mass concentration of particles; (2) the process of leveling the phase parameters slows down with an increase in the particle inertia (the relaxation zone increases); (3) the increase in the heat capacity of the particles leads to an increase in the length of the phase temperature relaxation zone.
We also note the reviews [39,40], which describe and analyze the results of studies of shock wave parameters in two-phase flows in a wide range of properties of the gas and dispersed phases.
Modeling of the external supersonic transverse flow past the plate by a two-phase flow considering the inverse effect of particles on the gas was carried out in [41,42]. The particle motion was calculated based on the Eulerian approach. The trajectories of particles are obtained when a dusty flow transversely flows past a plate of finite thickness. The distributions of the longitudinal velocity of the gas in the presence of particles of various sizes and the particles themselves are calculated without considering their reflection from the surface of the body. It was found [41] that the velocities of the gas and dispersed phases differ greatly. With an increase in the particle inertia, their velocity on the surface of the plate increases. The presence of large particles in the flow has a greater influence on the velocity distribution of the carrier gas in the braking region. Calculations have confirmed that small, low-inertia particles tend to follow the gas flow lines, and their trajectories are significantly curved. Large-inertia particles, on the contrary, have almost rectilinear trajectories near the surface of the plate.
In [42], calculations of the flow past the plate were carried out considering the particles reflected from the frontal surface within the framework of the developed model of a three-speed and three-temperature medium. Thus, along with the gas phase and the “phase” of falling particles near the frontal surface, the “phase” of reflected particles moving towards the incoming flow is also introduced. At certain concentration values, collisions occur between incident and reflected particles, leading to a change in the velocities of both types of particles. There is a need to consider among the acting forces some effective force of interaction between particles, as well as the “phase” transition from incident particles to reflected ones, and vice versa. Since the resulting “phase” transition will be the transition from reflected particles to incident ones [42], only one source term is introduced in the continuity equations of these “phases”.
The analysis of the equations revealed eight dimensionless parameters that determine the physics of supersonic flow around bodies by two-phase flows [42]. Among them are (1) the Mach number of the undisturbed flow; (2) the gas adiabatic index; (3) the coefficient of recovery of the longitudinal component of the velocity; (4) the mass concentration of particles in the undisturbed flow; (5) the degree of the particle inertia; (6) the parameter of the velocity disequilibrium of incident and reflected particles; (7) the parameter characterizing the change in mass concentration due to collisions; (8) the particle Reynolds number.
Among the subsequent works on the calculation of supersonic flow around bodies by two-phase flows, we refer to studies [43,44,45,46].
The calculation of the parameters of a two-phase flow with supersonic flow around a blunted body was performed in [43]. Particular attention is paid to interparticle collisions and considering the inverse effect of particles on the parameters of the carrier gas.
In [44], numerous results of measurements of the recovery coefficients of the normal and tangential components of the velocity of particles colliding with a solid are systematized. Simple interpolations of experimental data are proposed, considering the limiting rate of adhesion (adhesion) and the basic physical and mechanical properties of materials of colliding bodies. Calculations of the flow around a steel ball by an axisymmetric supersonic air jet containing silicon dioxide particles are performed. It is shown that the coefficient of recovery of the normal velocity component varies very widely—from almost zero to one—while, for the tangential component, it does not fall below 0.7. For a flow with polydisperse particles, it is shown that small particles have time to heat up in the compressed layer and cause the heating of the streamlined body, while large particles cooled before the compaction jump, on the contrary, lower the enthalpy of the body after the rebound.
Numerical studies of the features of supersonic flow past a sphere by a dusty stream carrying mono- and polydisperse particles of SiO2 (radius from 1 to 70 μm) were carried out in [45]. It is shown that considering the rotation of monodisperse particles leads to the removal of caustics (the envelope of the trajectory of reflected particles) from the streamlined body. Calculations have shown that an increase in particle size causes the caustics of reflected particles to move away from the body, and large particles after reflection can reach a compaction jump in front of the body and even travel beyond it.
In [46], a further improvement of the model [45] of the flow around a solid by a supersonic jet with the formation of a “chaotic” particle layer at the surface was carried out. This model, in addition to the equations of motion of the carrier gas and equations for calculating the motion of particles falling and reflected from the body, also contains equations for the “gas” of chaotically moving particles formed because of collisions. Several physical effects have been identified: (1) removal of the seal jump from the streamlined body with an increase in the mass concentration of particles; (2) the presence of a screening effect of particles reflected from the body and “chaotic” domain, leading to a decrease in the thermal effect of a two-phase jet; (3) blurring of the “caustics” of reflected particles in a cloud of “chaotic” matter while reducing the thickness of their layer.
In [47], it is concluded that the deceleration of particles in a compressed gas layer can be neglected when the following inequality is met:
where is the gas density before the seal jump.
Thus, only relatively inertial particles retain their rectilinear trajectories; they have the same velocities and angles of encounter with the shock wave and the surface of the body. Particles with low inertia can significantly change their trajectories and heat up when moving in a compressed gas layer.
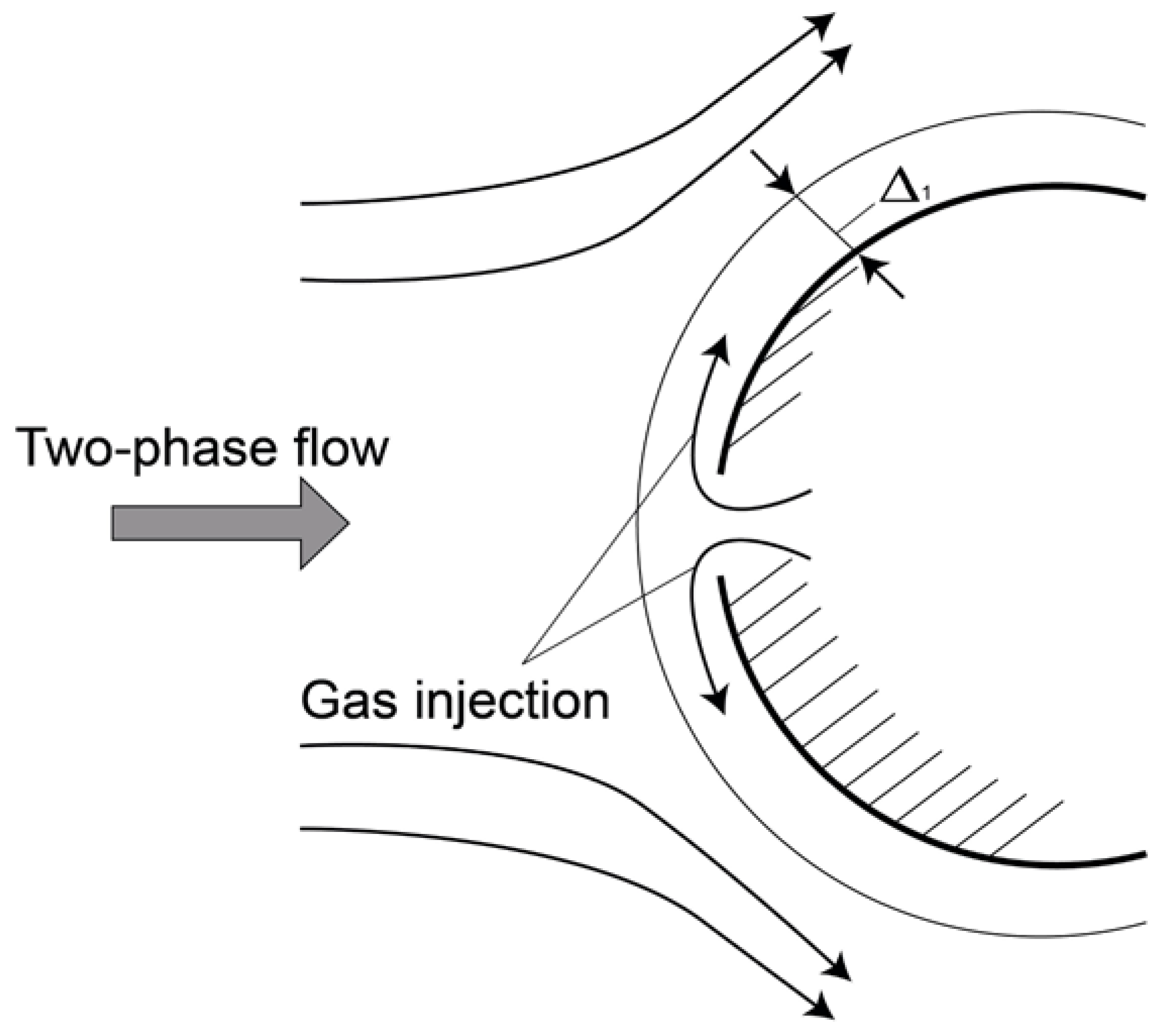
In [47], one of the methods of protection from the negative effects of particles is considered—protection by gas injection through the surface of the body. This method is based on increasing the thickness of the gas layer in which the particles are decelerated. The injected gas leads to the displacement of the main flow to a certain distance from the surface of the body (Figure 2). In [47], a simple analytical expression for the coefficient is obtained (—the boundary layer thickness).
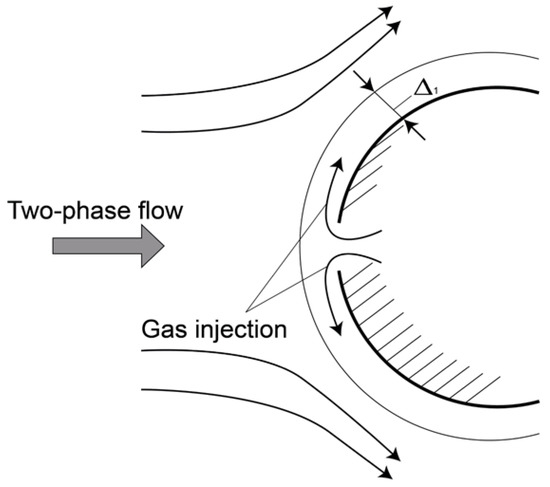
Figure 2.
Protecting the surface of a body in a two-phase flow by means of gas injection.
There are only a few experimental studies on the possibility of protecting the surfaces of bodies flowed by a two-phase flow by means of an injection [48,49].
In [48], it is shown that when a body is flowed by a dusty supersonic high-temperature flow, the intensity of heat transfer to its frontal surface can be significantly reduced by cooling gas injection through a tangential gap located in the vicinity of the critical point of the body.
In [49], a dimensionless criterion is proposed that characterizes the particle inertia in the vicinity of the critical point of a body under conditions of injection from its surface,
where and are the functions of the intensity (velocity) of the injection , taking into account the decrease in the particle inertia due to their braking in the area of the injection flow and an increase in the effective size of the braking area, respectively. The coefficient (in the range of ), in accordance with the data [50] on the development of the jet in the oncoming flow.
The functions and satisfy two limiting cases (infinitely weak injection and infinitely strong injection). When , we have and , which leads to (the injection does not affect the flow around the body). Where , we have and , which leads to (the injection pushes the particles away from the surface).
3.3. Aerodynamic Drag of Bodies in Two-Phase Flow
There are only a few experimental works devoted to the aerodynamic drag of bodies in two-phase flows [51,52,53].
In [53], using strain weights, the drag of flat aluminum wedges with angles at the apex in an air flow ( m/s) with aluminum oxide particles (Al2O3, kg/m3) with average mass dimensions μm was studied. The average cross-section flow concentration of the particles varied in the range . It was assumed that the total force acting on the model in the two-phase flow consisted of two independent components—the force from the gas phase and the force from the particles. It was found that the aerodynamic drag of the body in the two-phase flow only from the impact of particles (at certain sizes of particles and angles of wedge solution) exceeded the drag in “pure” air by eight times.
Dependences of the relative drag coefficient on the particle size for different wedge solution angles were obtained. In all dependences, two areas are highlighted, i.e., the boundary between which falls on the particles of μm. When the wedges are streamlined by a flow with particles whose size , there is a strong dependence of the drag coefficient on the size of the dispersed phase. For the flow with particles , the momentum transfer from the dispersed phase to the model (aerodynamic drag) ceases to depend on the particle size at all angles of wedge solution.
Quite unexpected (as defined in [53]) is the effect of the wedge solution angle on its drag. It is found that the maximum effect of the solid phase is achieved at the angle for any particle size, and the relative drag of blunt bodies in a heterogeneous flow is less than that of sharper bodies.
The growth of the aerodynamic drag of bodies in two-phase flows is caused primarily by the process of the interaction of particles with the surface. This process directly depends on the value of the sedimentation coefficient, which (as shown above) is determined by the inertia of particles (Stokes number). It is not difficult to obtain estimates of Stokes number for these experiments. The characteristic time of carrying gas , where ( is the half-height of the base of the cone).
It is obvious that the Stokes number increases with the increase in the particle size and angle of wedge solution. As the Stokes number increases, the number of particles interacting with the surface of the body increases, which leads to an increase in aerodynamic drag. The effect of this mechanism ends when the sedimentation coefficient stops growing ( at ). Estimations show that for particles with sizes of μm and at solution angles , the sedimentation coefficient . Thus, when the specified values of particle size and solution angle of wedges are reached, the growth of aerodynamic drag due to collisions of the dispersed phase with the surface of the streamlined body should stop.
In addition to the direct impact of particles on a wall on the drag coefficient of a body are such processes as the inverse influence of particles on gas parameters and collisions between particles. The particles falling on the body due to their inertia have a higher velocity than the braking gas. Therefore, they accelerate the gas, which increases the drag of the body. In contrast, the particles reflected from the body move toward the gas, which reduces its velocity and the aerodynamic drag coefficient of the body. Note that the particles reflected from the body have a greater (compared to the falling ones) effect on the gas flow as they move under conditions wherein the dynamic slip between the phases is several times higher. As the size (inertia) of the dispersed phase and the wedge solution angle increase, the number of reflected particles and their effect on the supporting phase increases sharply, which leads to a decrease in aerodynamic drag. Apparently, as observed in experiments, the decrease in the relative drag of blunt bodies in comparison with sharp ones is connected with the above-described mechanism of the inverse influence of particles on gas.
3.4. Heat Transfer in Two-Phase Flow
Studies of heat transfer in two-phase flows in pipes (channels) have been conducted for several decades [54,55] and were initiated by the supposed use of such flows as coolants for nuclear reactors. For two-phase turbulent flows in tubes, many authors have found a drop in the heat transfer intensity in the range of mass flow particle concentrations up to 5. Note that no such anomalies were found for laminar flows, which confirms that the particles suppress turbulent fluctuations of the carrier phase. At high mass concentrations, an increase in heat fluxes from the two-phase flow to the pipe wall was noted in the vast majority of experiments. Nevertheless, the change in heat flux in the tubes due to the addition of particles did not exceed two to three times [54]. The main reason for the weak intensification of heat transfer is the low-velocity slip of particles in the tubes.
In supersonic flowing by two-phase flows of blunted bodies, the intensification of heat transfer at the critical point was found to be more significant [56].
The total heat flux to the flowed body can be represented as
where is the heat flux in one-phase flow, and is the increase in heat flux due to particles (includes a radiation component, which is usually neglected).
The change in the heat flux in the two-phase flow, occurring due to the transfer of part of the kinetic and thermal energy of the particles in interaction with the surface, is usually represented as [57]
where is the energy accommodation coefficient of particles, is the mass flux density of particles on the body surface, is the velocity of particles on the body surface, is the heat capacity of the particle material, is the temperature of particles, and is the temperature of the body surface.
Note that for small values of the sedimentation coefficient () in the region of low-inertia particles, . As the particle size increases, the ratio between these energy flux components changes inversely, and for large (inertial) particles, () has .
In [57], it was found that the change in heat flux caused by large (inertial) particles in the boundary layer is a function of the following set of defining parameters:
where is the velocity of particles on the surface of a body, is the coefficient defining the angular coordinate of a sound point ( is for a hemispherical face, is for a flat face), is the dimensionless factor allowing for compressibility and the temperature factor (), is the distance from the front critical point, is the coefficient of aerodynamic drag of particles, is the gas viscosity after a compaction jump, and is the critical value of sound velocity.
It should be noted that there is a very strong dependence of heat transfer intensification on the value of particle velocity on the wall.
Available experimental data ([55], etc.) suggest that in a supersonic flow with particles (droplets), the heat flux to the surface of the blunted body increases by up to 10 times and more [47]. Such a significant intensification cannot be explained by the direct conversion of the kinetic energy of the particles into heat. The following physical mechanisms of heat transfer growth due to particles are distinguished: (1) intensification of heat transfer due to violation of the laminar structure of the near-wall flow by falling particles; (2) significant acceleration of the laminar–turbulent transition in the boundary layer due to dynamic slippage of the dispersed phase; (3) intensification of heat transfer due to the formation of craters on the exposed surface, leading to an increase in roughness; (4) violation of the gas dynamic structure of the flow (in particular, changing the shape of the head shock wave) by reflected particles and products of erosive destruction of the body surface.
Among the calculation–theoretical studies of the last decade, we should highlight the research [58,59,60]. In [58], the thermal effect of particles of different materials (Al2O3, SiO2, Cu) on an obstacle (ball) in a wide range of mass concentrations (up to ) was studied. Numerical studies were performed taking into account the model of chaotization of particles reflected from the body. They noted a priori the obvious fact of the non-monotone dependence of the heat flux from the particles to the body due to a screening effect of the reflected and chaotized particles, which grows with an increase in .
In [59,60], we continued our investigations of the mass density distributions of mono- and polydisperse particles at pressures up to 2 MPa and stopping temperatures up to 1750 K, as well as their collision rates with the streamlined body. The calculations varied the material, size, and initial mass concentration of particles in the prechamber. The areas of absolutely inelastic (erosive) and elastic (rebound) interaction of particles with the body were studied.
3.5. Erosive Destruction
According to [47], erosive destruction is the process of the mass entrainment of a material (obstacle) under the action of a stream of falling particles, which can be both solid and liquid.
To ensure the durability of elements of various power machines (blades of compressors and turbines, flow parts of steam and gas turbines, helicopter propellers), interacting under operating conditions with dust particles, it is necessary to know the parameters of the dispersed phase on the surface of the streamlined body. As numerous studies [47,61,62,63,64] have shown, the intensity of erosive wear increases sharply with the increasing speed of interaction of falling particles with the destroyed body (surface). Consequently, the relevance of taking into account erosive destruction is maximal where the velocity of falling particles reaches the maximum values, namely when creating structures affected by solid propellant rocket engine jets operating on fuel with metallized additives [65,66], as well as when developing flying vehicles (FVs) capable of traversing areas of the atmosphere containing dispersed impurities in the form of rain, snow, and ice particles.
Multiple impacts on the surface to be destroyed are composed of successive impacts of single particles. However, it should be noted that there are fundamental differences between single and multiple impacts. In [47], among the mentioned differences, the following are distinguished: (1) the presence of an establishment period, when the dimensionless mass entrainment velocity gradually increases to its quasi-stationary value [67]; (2) changes in the impact conditions of subsequent particles with the surface—for example, due to changes in the surface roughness resulting from its interaction with previous particle “echelons” [68]; (3) a shielding effect [69,70], which consists of the formation of a high-concentration layer near the model surface from particles moving at low speeds, as well as particles (splinters) of the destroyed material; (4) surface heating [71] due to multiple particle impacts on the surface, which change its properties and lead, as a rule, to a decrease in the strength of the target material, etc. The abovementioned factors exclude the possibility of transferring the results of single particle impact studies to multiple impacts occurring in the real process.
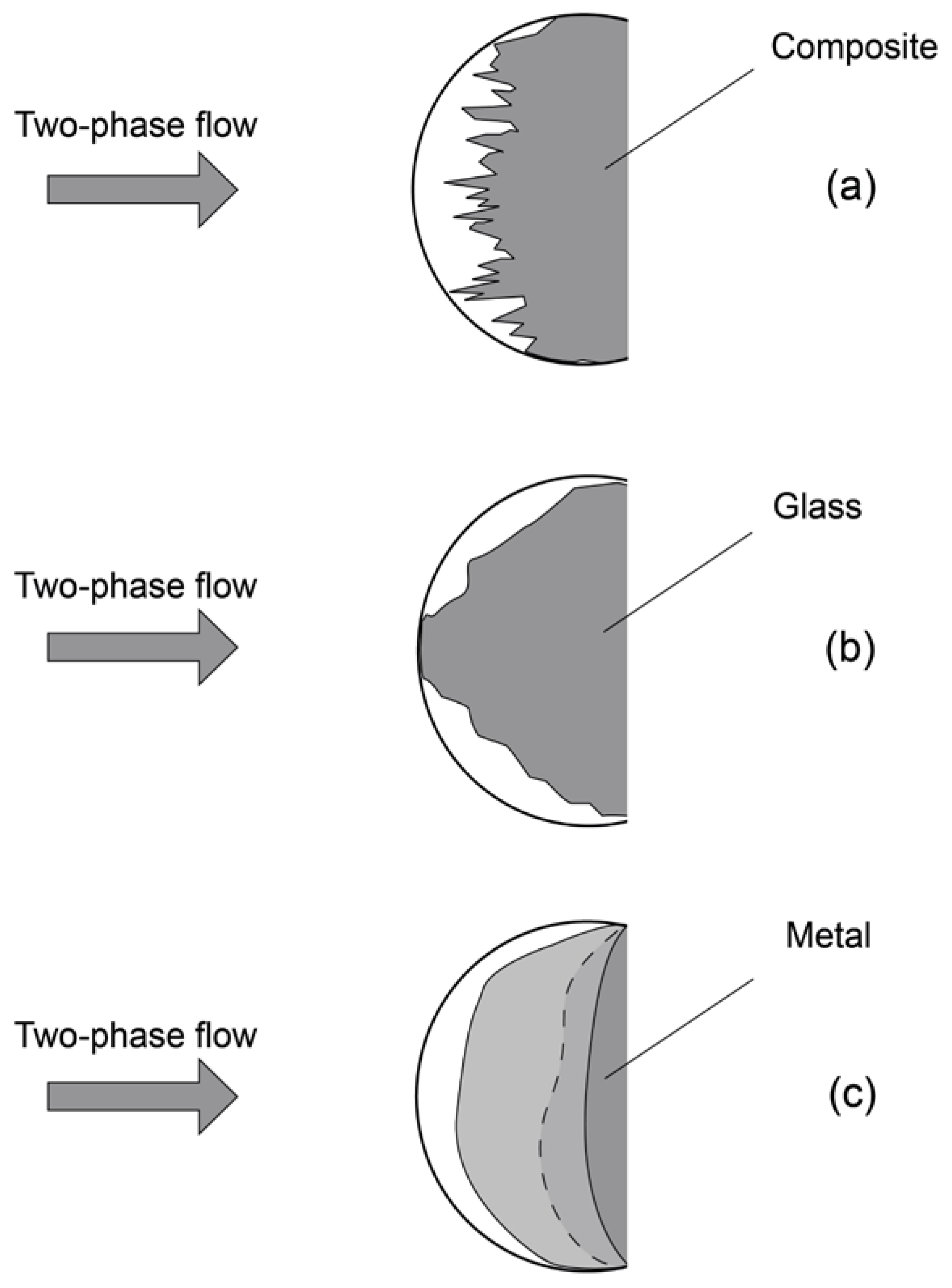
In [72], two types of erosion were found to exist—“brittle” and “viscous” for brittle and ductile materials, respectively.
“Brittle” erosion, which is characteristic of brittle materials (glass, ceramics, etc.), is characterized by the fact that the maximum intensity of fracture occurs at values of the interaction angle close to 90°. The mechanism of such erosion is caused by fatigue phenomena due to the continuous impact of particles on the surface, associated with the normal component of the impact force and leading to the formation of microcracks and pitting of its sections (see Figure 3a). The described mechanism of “brittle” erosion has been confirmed by numerous microstructural analyses [62,73,74] of surfaces subjected to erosive wear.
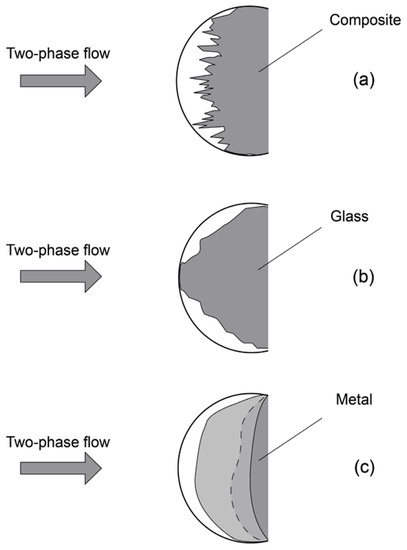
Figure 3.
Scheme of the erosive destruction of bodies from different materials in two-phase flow: (a)—composite; (b)—glass; (c)—metal.
“Viscous” erosion, which is characteristic of ductile materials (most metals belong to them), is characterized by the fact that the maximum intensity of destruction occurs at fairly sharp interaction angles, usually ranging from 20° to 30° (see Figure 3b). The mechanism of this erosion is similar to metal cutting by sharp angles of particles acting as peculiar micro-cutters [75].
There are a number of studies [76,77,78,79,80,81,82] on the effect of the temperature of the barrier material on the intensity of erosive destruction. In the experiments, the models were heated by blowing them with a hot one-phase flow [78,79], or by electric heating [76,77]. In [76], it is shown that up to the temperature of 400–500 °C, the erosion drag of steels changes little; with a further increase in the temperature of the barrier material, there is a sharp increase in the intensity of erosive destruction.
The primary information in the experimental study of erosion is usually presented in the form of a “kinetic curve” , where is the mass loss from a surface unit, which is a measured (unknown) quantity; is the mass flux of particles per surface unit.
Note that even with a constant collision velocity of the particles with the surface (), the mass loss is not a linear function of the mass of the deposited particles . This is a consequence of the fact that in the initial stage of the fracture process, damage accumulation and rebirth of the subsurface layer due to the appearance of cracks and delamination occur. In [67,83], the following interpretation of this phenomenon is given. After a number of successive collisions, some “saturation”, or, more precisely, the establishment of the erosive destruction process (the mass entrainment from different particles is the same), occurs. In the steady-state erosion mode , the dimensionless rate of fracture (or the intensity of erosive destruction) is constant, i.e., .
In [47], numerous experimental studies are systematized, which made it possible to establish some boundaries or “thresholds” of some physical parameters, upon reaching which the erosive wear process changes. These parameters include (1) the critical particle mass flux per unit surface ; (2) the critical collision velocity of particles with the surface ; (3) the critical body surface temperature .
The critical impact velocity is the velocity at which the so-called hydrodynamic mechanism of erosive destruction is established. At a low impact velocity, elastoplastic deformation of the obstacle material occurs without mass entrainment. As the velocity increases, the strength characteristics of the obstacle material have a significant influence on the intensity of fracture. In determining the hydrodynamic mechanism of erosive destruction, the only process parameter is the effective enthalpy of erosive destruction . This concept was first introduced by Yu. V. Polezhaev in 1979, in [67]. As with the melting heat, this characteristic does not depend on the level of energy impact (on the impact velocity ), but is a more complex parameter determined by the structure (for composite materials), as well as by the ratio of the strength properties of the particle and the obstacle. Comparing with the effective enthalpy of thermochemical fracture , in [47], their formal similarity is noted; however, . As a rule, is determined experimentally for different classes of materials.
The threshold value of the barrier temperature for metals is approximately half the melting temperature. The erosion drag of most metals weakly depends on the temperature at low values of the latter (e.g., [76]). Therefore, the dissipation of part of the impact energy in the undamaged part of the material almost does not affect the value of .
In the case of a one-parameter model of erosive destruction that satisfactorily describes the real mechanisms of mass entrainment at and , the intensity of erosion is described by the following relation:
Here it is taken into account that the energy conversion factor of the particle impact is close to unity, because their velocity exceeds the threshold value.
3.6. Cold Gas-Dynamic Spraying
Among the numerous methods of coating deposition and surface modification, powder spraying methods—plasma, gas flame [84], detonation, and their variants—occupy an important position. These methods make it possible to spray various substances, create homogeneous and heterogeneous coatings, and process products of complex geometry. The coating properties for each method are determined by a complex of physical and chemical processes occurring between the two-phase flow (gas + solid particles, gas + droplets) and the streamlined body (barrier), as well as the interaction between the carrier and dispersed phases.
The cold gas-dynamic spraying (CGS) method is based on the phenomenon of coating formation, which was first discovered in ITAM SB RAS in the early 1980s when studying the flow around blunted bodies by a supersonic heterogeneous low-temperature flow [85,86,87,88]. The main difference between the CGS method and the well-known gas-thermal methods is that the main energy source in the coating formation process is the kinetic energy of high-velocity solid particles. The above papers show that the main physical mechanism of CGS is the high-velocity deformation of the sprayed particles during shock interaction, leading to intense shear flows of the material at the contact boundaries and the formation of adhesion–cohesion bonds.
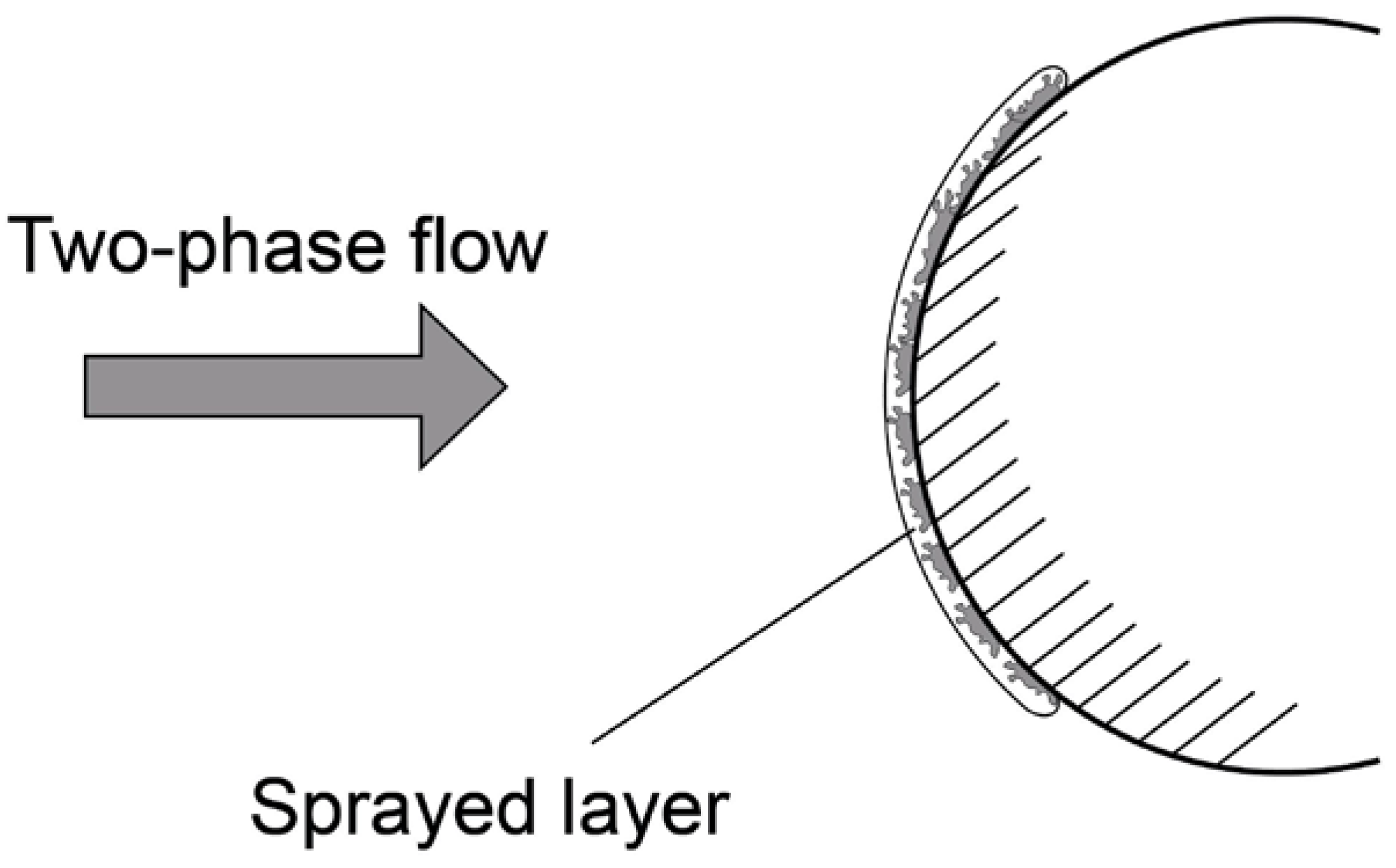
In [86], the peculiarities of the deformation of particles fixed on a polished substrate were studied using electron and optical microscopy. Figure 4 shows a scheme of spraying aluminum particles on the copper surface. It is shown that at the final stage of plastic deformation, corona-shaped metal ejections are formed at the contact periphery. Apparently, they are formed as a result of the formation of a high-velocity radial jet of metal near the wall, which resembles a cumulative jet. Under the conditions of the intense deformation and conversion of mechanical energy into thermal energy, a thin layer of molten metal may form in the vicinity of the wall, the formation of which depends on the balance of heat generation and heat rejection.
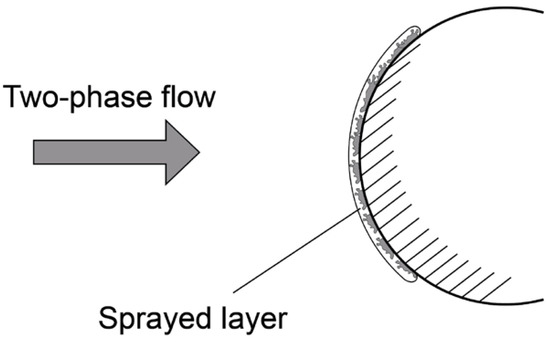
Figure 4.
Scheme of cold gas-dynamic spraying in a two-phase flow.
One of the most important characteristics of the coating formation process is the spraying coefficient, defined as follows:
where is an increase in the substrate mass due to particle sedimentation, and is the total mass of the consumed powder.
The spraying coefficient depends on the particle velocity on the surface , i.e., . The dependencies obtained in [88] clearly illustrate the main concept of CGS—the coating is formed using a high-velocity flow of “cold” particles on a “cold” substrate. Two characteristic regions of the spraying coefficient value separated by the critical velocity were found. The first region () corresponds to the substrate erosion process; the second region () corresponds to the spraying process. If the particle velocity significantly exceeds the critical value , the spraying coefficient increases rapidly up to 50–70%. Typical values for different metals (Al, Cu, Ni) are in the range of 500–700 m/s.
It was shown in [87,88] that various metals and alloys can be sprayed without any heating at all if the particles reach the required velocity. This erosion–adhesion transition, with the increasing velocity of “cold” solid particles falling on the substrate, was the physical basis for the development of the CGS method.
3.7. Glowing
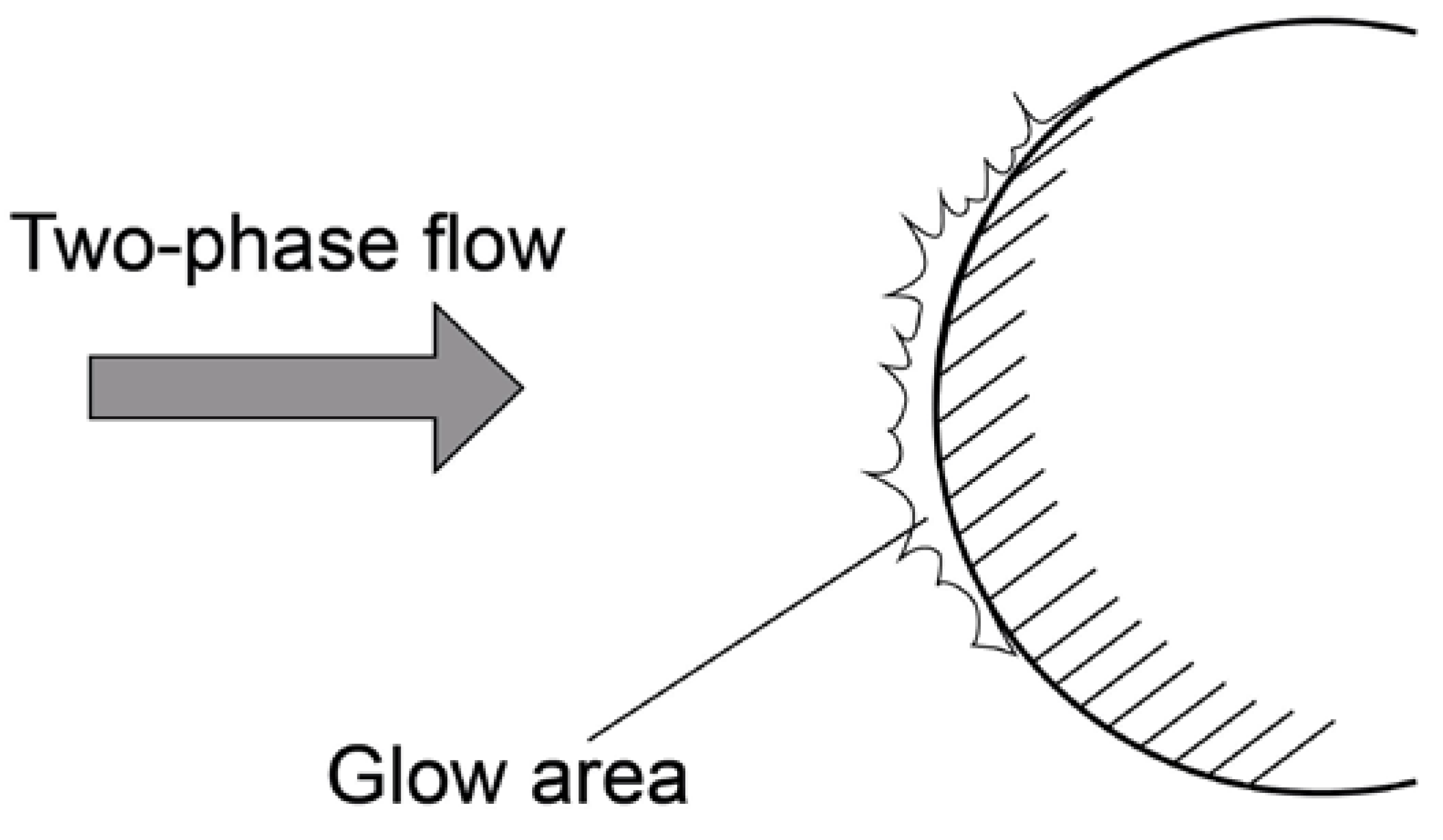
A number of physical phenomena are observed when a high-velocity gas-dispersed flow flows around bodies, among which glowing occupies an important position. Repeated collisions of particles with each other in the vicinity of the critical point of the streamlined body can significantly reduce the average speed of particles hitting the surface. The energy flux perceived by the obstacle is reduced. Thus, the shielding layer acts as an absorber of kinetic energy, which may cause it to glow (Figure 5).
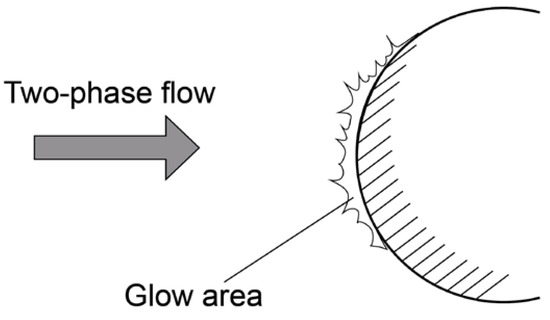
Figure 5.
Scheme of glowing near a body in a two-phase flow.
Experimental study [89] noted electrophysical and optical phenomena in a compressed layer near a metal sphere in a supersonic air flow carrying microparticles of metal oxides.
In [90], the optics of the compressed layer were studied based on the previously developed model of the gas-thermodynamics of a two-phase jet (a nonviscous nonthermal conductive gas and a nonvolatile “gas” of particles accelerated by it) flowing around a blunted body. Numerical calculations of the influence of scattering by particles of monochromatic radiation on the phenomenon of “glowing” in the laser knife plane, observed earlier in the experiments, were performed. The results of studies carried out with a wide range of sizes and optical characteristics of particles clearly showed that, even for the case of an optically transparent cloud of particles in a compressed layer near a streamlined body (in the single scattering approximation), one should take into account the Bouguer attenuation of the probing beam on the entire optical trace. Neglecting this phenomenon leads to the significant distortion of the spatial distribution of the particle concentration obtained from the experiment.
In [91], a model was developed that makes it possible to estimate the density of the reverse current from particles electrically charged by collision with a body streamlined by an axisymmetric gas-dispersed jet, as well as the spatial distribution of the radiation intensity of gas molecules excited by this reverse current. The influence of the particle radius, particle material, and initial mass fraction on the radiation intensity in the compressed layer near the streamlined body is shown.
4. Peculiarities of Streamline Flowing of Bodies with Droplets
In computational theoretical studies of two-phase flows without walls, often, no distinction is made in calculations of flows with solid particles and droplets. This is justified only for small Weber numbers, when there is no difference in the behavior of particles and droplets, and in the case of low concentrations, when there is no hydrodynamic (in trace) or mechanical (collision) interaction between particles (droplets). Real two-phase flows (in technical devices and in experiments) usually contain particles (droplets) of different sizes, i.e., they are polydisperse. In addition, real flows are accompanied by phase and chemical transformations, which change the size of the dispersed phase. The mentioned circumstances greatly complicate the matter, because the difference in size leads to a difference in velocity (and temperature in the case of non-isothermal flow), which leads to enormous growth in the collision cross-section.
Below, the results of research that sheds light on the qualitative differences in the process of interaction of particles and drops with the surface of a streamlined body are presented and analyzed.
There are recently published papers [92,93,94,95,96] in which various aspects of the collision of single drops with curvilinear surfaces and small bodies of various shapes were studied.
In contrast to a colossal number of studies (e.g., [97,98,99]) where the impact of a droplet against a flat surface was studied, in [92], the features of a normal impact of droplets against curved solid surfaces were considered. The physics of droplet impact with curved surfaces was studied for different Weber numbers (), radii of curvature, and surface wettability. Using the original theoretical approach and the axisymmetric lattice Boltzmann method (LBM), it was concluded that all the varying parameters had a great influence on the processes of spreading and bouncing of the droplet. The parametric studies revealed the presence of five interaction modes, from complete deposition to complete rebound. The results of [92] provide important information about the structure of the curved surface to control the behavior of the droplet and the time of its contact with the surface.
In research [93], the characteristics of the axisymmetric impact of a water drop against a thin vertical dry solid cylinder were studied numerically using the volume of fluid (VOF) method. It is obtained that the surface of the droplet undergoes continuous deformation during impact on a thin cylindrical target, which leads to various stages: free fall, impact, cap formation, encapsulation, opening, and detachment. The ratio of cylinder diameter to droplet diameter () was varied from 0.13 to 0.4 in order to observe different droplet deformation patterns. The effect of the boundary angle, ratio , and dimensionless criteria (, , and ) on the maximum strain coefficient was studied. The data obtained showed, in particular, that the maximum strain factor increases with an increasing and decreasing marginal angle.
The process of the maximum spreading of a droplet due to its collision with a dry stationary spherical particle was studied numerically using the level contour reconstruction method (LCRM) in [94]. The Weber number , Ohnesorge number , drop size to particle size ratio , as well as fluid viscosity and surface curvature were varied in the calculations. Calculations showed that the maximum flowout increases at smaller particles for both capillary and viscous modes. The increase in maximum spreading is mainly determined by surface rim deformation for the capillary mode and viscous dissipation for the viscous mode. An empirical correlation is also presented, which can be applied to the impact of a droplet on both a particle and a flat surface.
Experimental and numerical studies of drop impact on a cone were performed in [95]. The Weber number and cone angle were varied. In particular, it was found that in the phase at which the droplet leaves the surface in the form of a ring, its contact time is reduced by 54% compared to a flat surface. The influence of the Weber number and cone angle on the contact time of a droplet with the cone surface was studied.
In Ref. [96], numerical and theoretical studies of the behavior of a water droplet upon impact with small cylindrical superhydrophobic targets were performed. The effect of the Weber number and the ratio of the target diameter to the droplet diameter (less than unity) on the droplet impact behavior, including the droplet profile and the deformation coefficient, was investigated. The results show that a larger Weber number accelerates the spreading and droplet fall and promotes droplet decay. Increasing the diameter ratio delays the spreading and droplet fall from the target side, thereby increasing the deformation and rebound of the droplet. Increasing both the Weber number and the diameter ratio contributes to increasing the maximum strain coefficient.
In [100], using high-velocity video imaging, the effect of the appearance of droplets with near-zero velocities in the flowing of bodies by gas droplet flows was discovered for the first time. The formation of levitating droplets was due to the emergence of falling and reflected by the model droplets. It has been suggested that the main mechanism of the appearance of droplets with near-zero velocities is an exchange of momentum as a result of the collision of droplets having an opposite direction and velocity values that are close in magnitude. The effect of increasing the size of large levitating droplets due to the merging of falling droplets with them as a result of multiple collisions was found.
Geometrical, kinematic, and temporal characteristics of collision processes accompanying gravitational droplet sedimentation on a model with a hemispherical face were studied in [101]. Data on the velocities and sizes of both small (secondary droplets) and large (fragments) droplets in the case of high (close to dynamic Leidenfrost temperature) model temperatures have been obtained. Data were obtained on the effect of droplet size on the velocity recovery coefficient during their interaction with a curved surface. The experiments revealed a decrease in the velocity recovery coefficient with the increasing inertia of the droplets due to a greater loss of momentum, attributed to a longer interaction with the surface. The effect of mismatching the touch and rebound points of the droplets during their interaction with the curvilinear surface of the model was revealed. It was found that with increasing drop size, the effect of gravity increases, which leads to a change in the drop’s rebound to its flow. This effect contributes to an increase in the interaction time of the droplet with the model and the distance between the points of contact and detachment from the surface.
4.1. Filtration
Traditional air filtration systems often use fibrous filters and are based on the interaction of particles with individual fibers. Several filtration mechanisms are usually distinguished: inertial, blocking, diffusion, and electrostatic. For a droplet of the size of the order of a few micrometers, the inertial mechanism is considered to be the dominant filtration mechanism [102]. The collision of a droplet with a single fiber is determined by two criteria—the Stokes number or , which is responsible for the droplet’s ability to follow the carrier air current lines, and the droplet’s Reynolds number in the oncoming flow, on which its aerodynamic drag depends. Numerous studies have shown (e.g., [103]) that the droplet trapping efficiency increases with increasing , since, in this case, the particles cannot move around the cylinder. It is also known that at a fixed Stokes number , the droplet entrapment efficiency decreases with increasing Reynolds number due to an increase in the drag force acting on the droplets. The described classical theory of the single-fiber model is widely used to calculate droplet trapping by fiber filters (e.g., [104,105]). A limitation of the single-fiber model is that it does not account for changes in the flow field by neighboring fibers and the real distribution of droplets behind the fiber downstream.
In [106], the effect of the upstream cylinder on the efficiency of droplet capture by the test cylinder was investigated. It is shown that the efficiency of droplet capture by the test cylinder depends on its relative displacement in the transverse direction (normal to the flow) relative to the front cylinder. At relatively small displacements, there is complete shielding, i.e., the droplets do not collide with the test cylinder. As the displacement increases, the droplet trapping efficiency increases and exceeds the corresponding value for an isolated cylinder at medium displacements and a Stokes number close to unity. At larger displacements and larger Stokes numbers, the effect of the front cylinder on aerosol capture by the test cylinder decreases and eventually disappears. The main achievement of this research is the detection of extremely high trapping ratios (over 100%) and the determination of the ranges of Stokes numbers and displacements at which this effect is observed.
4.2. Icing
One of the most well-known and serious safety problems in modern aviation is aircraft icing in flight [107,108,109,110]. Supercooled water droplets contained in clouds under certain conditions can freeze, hitting the nose part of the fuselage, wings, elements of the fins, and parts of aircraft engines. The formation of the ice crust leads to a number of negative consequences—changes in the streamline regime, reduced wing lift, loss of thrust, reduced controllability, weight increase, etc. Note that ice formation on the surface of the compressor inlet guide apparatus and the nacelle shell of an aircraft engine can occur during adiabatic air expansion, even at positive ambient air temperatures. Subsequently, the ice crust can collapse and enter the engine, causing possible damage to the compressor blades and even engine failure.
There are three basic types of ice—loose ice, transparent (glassy) ice, and mixed ice [108].
Loose ice has a brittle, porous, milky white structure, which is a mixture of tiny ice particles; it is formed by the crystallization of small supercooled droplets on the leading edges, when the amount of water after the beginning of the solidification process is not sufficient to form a continuous water layer. The use of de-icing systems prevents the formation of such ice or easily removes it if it occurs.
Transparent (glassy) ice has a smooth surface; it forms when large (diameter greater than 20 μm) supercooled droplets freeze on the contour of the streamlined profile, when the solidification of an individual droplet on the surface occurs gradually and some of the surface droplets have time to spread on the surface before freezing. When heat is applied, such ice forms new droplets and streams that migrate downstream and form new ice in the form of ridged growths (“barrier ice”).
Mixed ice is a combination of loose and glassy ice; it is formed by the presence of droplets of different sizes in clouds. In its pure form, loose ice is formed when FV moves in high cumulonimbus clouds, and glassy ice is formed in low layers in rain clouds.
Taking into account the existence of different types of ice and using the concept of the frozen ice fraction, three icing modes are distinguished [109]—wet, liquid, and dry.
Wet mode is realized when the surface temperature is equal to the water crystallization temperature. In this case, the fraction of frozen ice varies from zero to one. The supercooled droplets that have fallen to the surface combine to form large droplets. Large droplets partially solidify and are transformed by air flow into streams or films, under which a thin ice layer is formed.
Liquid mode is characterized by the fact that the temperature of the streamlined surface is higher than the solidification temperature of water. In this case, the proportion of frozen ice is zero. Water is present on the surface in the form of drops, streams, or a film. Ice on the surface melts in the water film.
Dry mode is realized when the temperature of the outer ice layer is lower than the crystallization temperature of water. In this case, the fraction of frozen ice is equal to one. The supercooled droplets precipitated on the surface solidify, being transformed into loose ice and not reaching a sufficiently large size to be carried away by the external flow.
In study [110], the results of calculating the icing of the cylinder and the NACA 0012 profile when flowing with a viscous compressible air flow carrying droplets in a two-dimensional formulation are presented. The developed model takes into account the interaction of the carrier phase and droplets, the form of existence of moisture on the profile, the mode of ice build-up, and changes in the geometry of the streamlined body. As a result of the calculations, the characteristic shapes of ice films (growths) for various modes of icing—dry, wet, and mixed—were obtained.
In paper [111], the main physical processes accompanying the flow of bodies in a supercooled cloud are studied. The interaction of water nanodrops consisting of a different number of molecules (54, 159, 349, 647, and 1080) with the surface, which can be considered as the beginning of the icing process, has been studied by the method of molecular dynamics. It is shown that with a decrease in the size of the nanocapsule and an increase in the potential energy of the interaction of droplet molecules with surface wall molecules, the wetting edge angle and the size of the contact area increase. It is concluded that an increase in the wetting angle leads to an increase in the velocity of the droplets and prevents them from freezing.
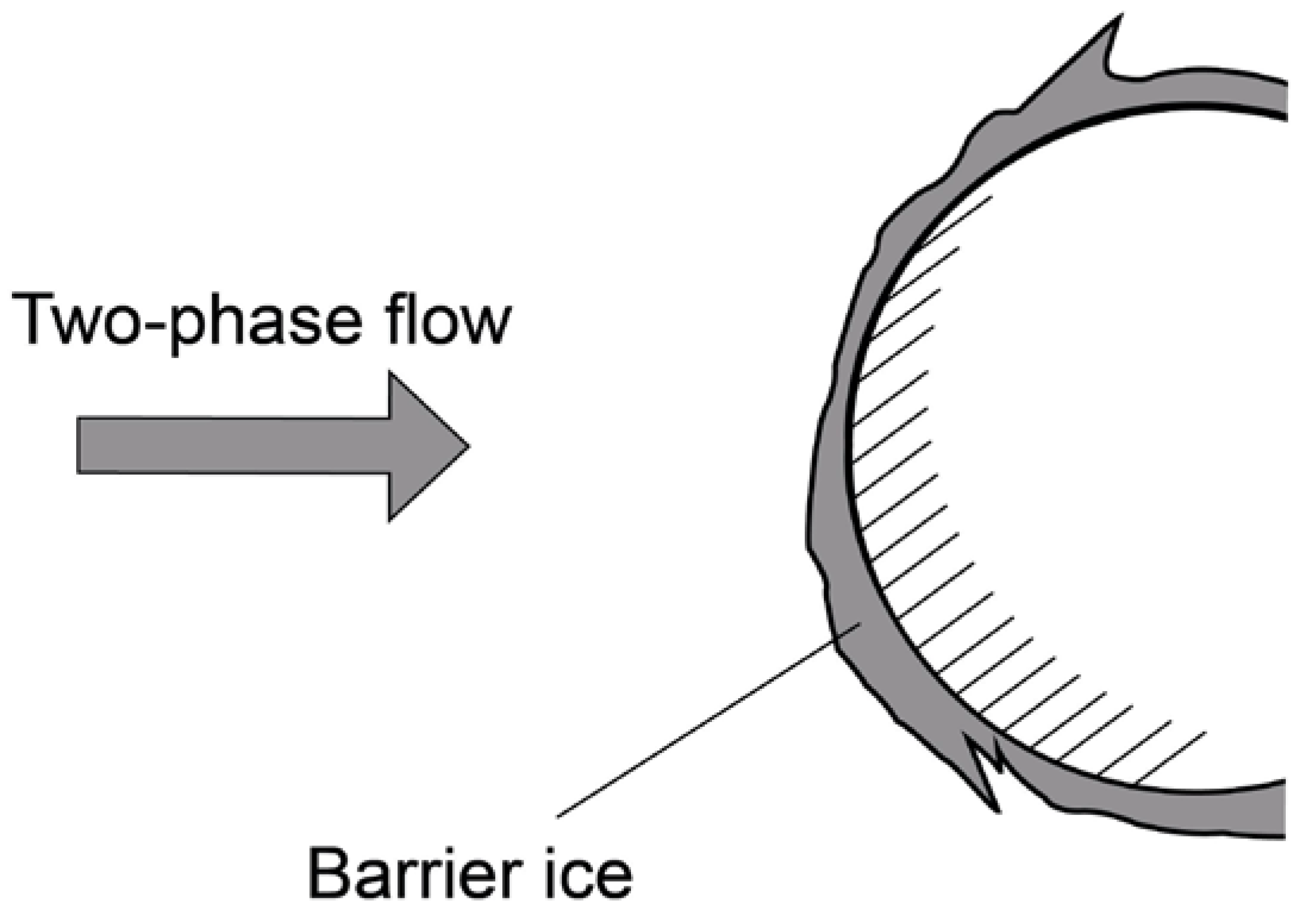
One of the most unpleasant forms of icing is the so-called barrier ice, which is formed, as a rule, as a result of the controlled melting of ice formed on the leading edge of the wing. Efforts to address it are complicated by the fact that the areas of its formation are unknown in advance and poorly predictable compared to the locations of formation of ordinary ice (leading edges of the wing, stabilizer, etc.).
At the very beginning of the study of the problem of icing, concerns were expressed about finding a material to which ice would not stick [112]. There was an attempt to use fluorocarbon materials (for example, Teflon), well known for their water-repellent properties, in this capacity. However, studies have shown that the adhesion of Teflon with respect to drip ice (formed by droplets moving on the surface) does not differ from the adhesion of other materials. A further goal of the researchers was to search for a material with low adhesion to ice formed when a two-phase flow flows around the FV, i.e., under other physical conditions [113,114,115,116,117,118,119].
In [112], the results of an experimental study of the effectiveness of using nanomodified surfaces to combat icing are presented. The conditions of barrier ice formation have been studied experimentally. The flow rate in the experiments was 80 m/s; the temperature was minus 20 °C; the water content (mass water content) was 0.57 g/m3. The model was a wing profile: the nanomodified sample under study was installed on top of the profile, and an ordinary plate of untreated duralumin was placed below for comparison. The leading edge of the wing was heated by an ohmic heater. The characteristic appearance of the barrier ice formed is schematically shown in Figure 6. The effect of the periodic self-cleaning of superhydrophobic surfaces from ice was found under the same conditions in which an ice barrier grows on the surfaces of ordinary materials. The marginal wetting angle of superhydrophobic surfaces was, at the same time, more than 160°. This effect and direct measurements of the adhesion strength confirmed its significant decrease in the case of the nanomodified superhydrophobic material.
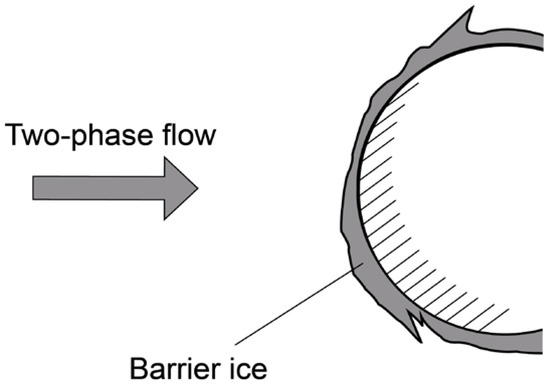
Figure 6.
Scheme of the formation of barrier ice in a two-phase flow.
Among the recent investigations devoted to various aspects of icing problems, we refer to [120,121,122,123].
In Ref. [120], a physical and mathematical model of a cooling and solidifying liquid film entrained by air along the heated surface of a streamlined body with a given distribution of heat flux density on the surface is developed. In [121], the motion of nonspherical particles in a two-phase flow was studied. The coefficients of recovery of the velocity components of ice crystals colliding with the surface of a solid body in a wide range of values of the control parameters of the process have been calculated. In [122], a physical and mathematical model of the spatial and temporal evolution of an ice layer growing during the collision of individual droplets with the surface of a solid body, sliding along the surface and solidifying on it, which leads to two-dimensional roughness (bumpy ice), was developed. In [123], the effect of ice crystals in the air flow on the evolution of barrier ice on the surface of a wing model in an aero-cooling tube was investigated numerically. The results confirm that the change in the mass of ice deposits detected in the experiment when crystals are introduced into the flow is associated with the absorption of a film of water formed on the surface of the solid, part of the crystals’ mass at low flow rates (increase in barrier ice), and the spilling of the film at high speeds (decrease in barrier ice).
5. Conclusions
A review of the studies devoted to the mathematical and physical modeling of the flow around bodies by two-phase (dispersed) flows has been performed. The most important characteristics of the inertia of particles (drops) determining the presence and intensity of interaction of the dispersed phase with the surface of a body (barrier) are presented. The characteristics of two-phase flows when flowing around bodies of different shapes—a sphere, a cylinder, a plate, and airfoil cascades—are considered.
On the basis of the calculated and experimental data analyzed in the review, conclusions can be made about the main factors affecting the value of the sedimentation coefficient: (1) the potential of streamlined flow (the influence of the boundary layer leads to a decrease in the sedimentation coefficient and becomes significant at low Stokes numbers (less than 0.2)); (2) gravity (leads to a significant increase in the sedimentation coefficient at small Stokes numbers (less than 0.3) and in the case of a downward flow, and to a significant decrease in the sedimentation coefficient at moderate Stokes numbers (less than 2) in the case of an upward flow); (3) non-isothermal flow (causes an increase in the sedimentation coefficient at low Stokes numbers (less than 0.1)); (4) axisymmetric flow (curvature of the gas current lines begins at a smaller distance compared to a flat flow, which leads to an increase in the inertia of particles and an increase in the sedimentation coefficient).
The subject in question in this review has a long history, but, despite this, new directions have recently appeared, such as respiratory aerosols, microplastics, sedimentation, drug delivery, Mars’ atmosphere, etc. Particular emphasis is placed on considering the trajectories of particles (droplets) in the vicinity of the critical points of bodies streamlined by a two-phase flow. Some peculiarities of the high-velocity flowing of bodies, and the influence of particles on drag and heat transfer, are described. Some possible consequences of the interaction of two-phase flows carrying particles and droplets with bodies—erosive destruction, gas-dynamic spraying, glowing, and icing—are analyzed.
Author Contributions
Conceptualization, A.Y.V.; formal analysis, S.V.R.; data curation, A.Y.V.; writing—original draft preparation, A.Y.V.; writing—review and editing, S.V.R.; visualization, A.Y.V.; project administration, S.V.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research (VAYu) was funded by the Russian Science Foundation, grant number 20-19-00551.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Varaksin, A.Y.; Ryzhkov, S.V. Turbulence in Two-Phase Flows with Macro-, Micro- and Nanoparticles: A Review. Symmetry 2022, 14, 2433. [Google Scholar] [CrossRef]
- Elghobashi, S. Particle-Laden Turbulent Flows: Direct Simulation and Closure Models. Appl. Sci. Res. 1991, 48, 301–314. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Zaichik, L.I. The Effect of a Fine Divided Impurity on the Turbulence Intensity of a Carrier Flow in a Pipe. High Temp. 1998, 36, 983–986. [Google Scholar]
- Zaichik, L.I.; Varaksin, A.Y. Effect of the Wake behind Large Particles on the Turbulence Intensity of Carrier Flow. High Temp. 1999, 37, 655–658. [Google Scholar]
- Pakhomov, M.A.; Protasov, M.V.; Terekhov, V.I.; Varaksin, A.Y. Experimental and Numerical Investigation of Downward Gas-Dispersed Turbulent Pipe Flow. Int. J. Heat Mass Transf. 2007, 50, 2107–2116. [Google Scholar] [CrossRef]
- Osiptsov, A.N. Structure of the Laminar Boundary Layer of a Disperse Medium on a Flat Plate. Fluid Dyn. 1980, 15, 512–517. [Google Scholar] [CrossRef]
- Osiptsov, A.N. Investigation of Regions of Unbounded Growth of the Particle Concentration in Disperse Flows. Fluid Dyn. 1984, 19, 378–385. [Google Scholar] [CrossRef]
- Osiptsov, A.N. Motion of a Dusty Gas at the Entrance to a Flat Channel and a Circular Pipe. Fluid Dyn. 1988, 23, 867–874. [Google Scholar] [CrossRef]
- Naumov, V.A. Calculation of the Laminar Boundary Layer on a Plate with Allowance for the Lifting Forces Acting on a Dispersed Mixture. Fluid Dyn. 1988, 23, 943–945. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. The Effect of Drop Evaporation on Gas Turbulence and Heat Transfer for Two-Phase Flow Behind Sudden Pipe Expansion. High Temp. 2016, 54, 330–337. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Structure of the Nonisothermal Swirling Gas-Droplet Flow Behind an Abrupt Tube Expansion. Fluid Dyn. 2016, 51, 70–80. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Effect of Flow Swirling on Heat Transfer in Gas-Droplet Flow Downstream of Abrupt Pipe Expansion. High Temp. 2018, 56, 410–417. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Particle Concentration Distribution in a Gas-Droplet Confined Swirling Flow: Euler and Lagrange Approaches. High Temp. 2020, 58, 835–838. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Vortex Flows with Particles and Droplets (A Review). Symmetry 2022, 14, 2016. [Google Scholar] [CrossRef]
- Michael, D.H.; Norey, P.W. Particle Collision Efficiencies for a Sphere. J. Fluid Mech. 1969, 17, 565–575. [Google Scholar] [CrossRef]
- Tsirkunov, Y.M. Influence of the Viscous Boundary Layer on the Deposition of Particles from a Gas Suspension Flowing Past a Sphere. Fluid Dyn. 1982, 17, 48–55. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An Investigation of Particle Trajectories in Two-Phase Flow Systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Tsirkunov, Y.M. Gas–Particle Flows around Bodies—Key Problems, Modeling and Numerical Analysis. In Proceedings of the Proc. Fourth International Conference on Multiphase Flow (ICMF’01), New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Varaksin, A.Y.; Ivanov, T.F. Investigation of the Behavior of Reflected Particles Under Conditions of Heterogeneous Flow Past Blunt Bodies. High Temp. 2003, 41, 62–67. [Google Scholar] [CrossRef]
- Ivanov, T.F.; Varaksin, A.Y. Investigation of the Behavior of Reflected Particles under Conditions of Heterogeneous Flow Past a Blunt Body: Experiment and Calculation. High Temp. 2005, 43, 310–313. [Google Scholar] [CrossRef]
- Vittal, B.V.R.; Tabakoff, W. Two-Phase Flow Around a Two-Dimensional Cylinder. AIAA J. 1987, 25, 648–654. [Google Scholar] [CrossRef]
- Spokoinyi, F.E.; Gorbis, Z.R. Properties of Precipitation of Finely Dispersed Particles from a Cooled Gas-Flow Transverse to a Heat-Exchanging Surface. High Temp. 1981, 19, 142–158. [Google Scholar]
- Tsirkunov, Y.M.; Tarasova, N.V. Influence of the Temperature of an Obstacle on the Precipitation of a Finely-Dispersed Impurity from Supersonic Flow of a Gas Suspension. High Temp. 1992, 30, 955–962. [Google Scholar]
- Luo, K.; Fan, J.; Li, W.; Cen, K. Transient, Three-Dimensional Simulation of Particle Dispersion in Flows Around a Circular Cylinder (Re=140-260). Fuel 2009, 88, 1294–1301. [Google Scholar] [CrossRef]
- Haugen, N.E.L.; Cragset, S. Particle Impaction on a Cylinder in a Crossflow as Function of Stokes and Reynolds Numbers. J. Fluid Mech. 2010, 661, 239–261. [Google Scholar] [CrossRef]
- Aarnes, J.R.; Haugen, N.E.L.; Andersson, H.I. Inertial Particle Impaction on a Cylinder in Turbulent Cross-Flow at Modest Reynolds Numbers. Int. J. Multiph. Flow 2019, 111, 53–61. [Google Scholar] [CrossRef]
- Yoshimoto, H.; Goto, S. Self-Similar Clustering if Inertial Particles in Homogeneous Turbulence. J. Fluid Mech. 2007, 577, 275–286. [Google Scholar] [CrossRef]
- Weber, R.; Schaffel-Mancini, N.; Mancini, M.; Kupka, T. Fly Ash Deposition Modelling: Requirements for Accurate Prediction of Particle Impaction on Tubes Using RANS-Based Computational Fluid Dynamics. Fuel 2013, 108, 586–596. [Google Scholar] [CrossRef]
- Mitra, D.; Haugen, N.E.L.; Rogachevskii, I. Turbophoresis in Forced Inhomogeneous Turbulence. Eur. Phys. J. Plus 2018, 133, 35–42. [Google Scholar] [CrossRef]
- Dombrovskii, L.A.; Yukina, E.P. Critical Conditions of Inertial Particle Deposition from a Gas-Flow Near Retardation Point. High Temp. 1983, 21, 402–408. [Google Scholar]
- Dombrovskii, L.A.; Yukina, E.P. Critical Conditions for the Inertial Precipitation of Particles from Aerocolloidal Flow in the Vicinity of a Stagnation Point—Influence of Blowing. High Temp. 1984, 22, 587–591. [Google Scholar]
- Dombrovskii, L.A. Inertial Deposition of Particles from Gas-Disperse Flow in the Vicinity of a Stagnation Point. High Temp. 1986, 24, 429–434. [Google Scholar]
- Sukhorukov, A.L. Numerical Simulation of a Transonic Two-Phase Gas Flow Past a Lattice of Airfoils. Vestn. Molod. Uch. Ser. Prikl. Mat. Mech. 2002, 1, 98–104. (In Russian) [Google Scholar]
- Carrier, G.F. Shock Waves in a Dusty Gas. J. Fluid Mech. 1958, 4, 376–382. [Google Scholar] [CrossRef]
- Kriebel, A.R. Analysis of Normal Shock Waves in a Particle Laden Gas. J. Basic Eng. Trans. ASME 1964, 86, 655–665. [Google Scholar] [CrossRef]
- Rudinger, G. Some Properties of Shock Relaxation in Gas Flow Carrying Small Particles. Phys. Fluids 1964, 7, 658–663. [Google Scholar] [CrossRef]
- Igra, O.; Ben-Dor, G. Parameters Affecting the Relaxation Zone Behind Normal Shock Waves in Dusty Gases. Isr. J. Technol. 1980, 18, 159–168. [Google Scholar]
- Ben-Dor, G.; Mond, M.; Igra, O.; Martsiano, Y.A. Nondimensional Analysis of Dusty Shock Waves in Steady Flows. KSME J. 1988, 2, 28–34. [Google Scholar] [CrossRef]
- Igra, O.; Ben-Dor, G. Dusty Shock Waves. Appl. Mech. Rev. 1988, 41, 379–437. [Google Scholar] [CrossRef]
- Ben-Dor, G. Dusty Shock Waves—An Update. Appl. Mech. Rev. 1996, 49, 141–146. [Google Scholar] [CrossRef]
- Davydov, Y.M.; Nigmatulin, R.I. Analysis of Outer Heterogeneous Flow of a Gas Containing Droplets or Particles Past Blunt Bodies. Dokl. Akad. Nauk SSSR 1981, 259, 57–60. (In Russian) [Google Scholar]
- Davydov, Y.M.; Enikeev, I.K.; Nigmatulin, R.I. Calculation of the Flow of a Gas with Particles Past Bluff Bodies with Allowance for the Effect of Reflected Particles on the Flow of the Aerosol. J. Appl. Mech. Tech. Phys. 1990, 31, 860–867. [Google Scholar] [CrossRef]
- Volkov, A.N.; Tsirkunov, Y.M.; Oesterle, B. Numerical Simulation of a Supersonic Gas-Solid Flow over a Blunt Body: The Role of Inter-Particle Collisions and Two-Way Coupling Effects. Int. J. Multiph. Flow 2005, 31, 1244–1275. [Google Scholar] [CrossRef]
- Molleson, G.V.; Stasenko, A.L. The Interaction Between Gas-Dynamically Accelerated Particles and a Body Subjected to Flow. High Temp. 2009, 47, 680–691. [Google Scholar] [CrossRef]
- Molleson, G.V.; Stasenko, A.L. Peculiarities of Flow Over a Blunted Body by a Supersonic Polydispersed Jet with a Swirl of Reflected Particles. High Temp. 2011, 49, 72–80. [Google Scholar] [CrossRef]
- Molleson, G.V.; Stasenko, A.L. Interaction of a Two-Phase Jet with Solid Body with Generation of a “Chaos” of Particles. High Temp. 2013, 51, 537–550. [Google Scholar] [CrossRef]
- Mikhatulin, D.S.; Polezhaev, Y.V.; Reviznikov, D.L. Heat Transfer and Destruction of Bodies in Supersonic Heterogeneous Flow; Yanus-K: Moscow, Russia, 2007; 392p. (In Russian) [Google Scholar]
- Vasilevskii, E.B.; Yakovleva, L.V. The Tangential Gas Blowing into a High-Temperature High-Speed Dusted Flow. Vestn. Nizhegorod. Univ. im. N.I. Lobachevskogo 2011, 4, 2053–2054. (In Russian) [Google Scholar]
- Varaksin, A.Y.; Protasov, M.V. The Effect of Gas Injection on the Protection of Body Surfaces Streamlined by a Two-Phase Flow. High Temp. 2017, 55, 945–948. [Google Scholar] [CrossRef]
- Ginevskii, A.S. Theory of Turbulent Jets and Traces; Mashinostroenie: Moscow, Russia, 1969; 400p. (In Russian) [Google Scholar]
- Balanin, B.A.; Zlobin, V.V. Experimental Investigation of the Drag of Simple Bodies in a Two-Phase Flow. Fluid Dyn. 1979, 14, 456–458. [Google Scholar] [CrossRef]
- Balanin, B.A. Influence of Reflected Particles on the Ablation of a Body in Two-Phase Flow. Fluid Dyn. 1984, 19, 841–845. [Google Scholar] [CrossRef]
- Balanin, B.A.; Lashkov, V.A. Drag of a Flat Wedge in a Two-Phase Flow. Fluid Dyn. 1982, 17, 317–321. [Google Scholar] [CrossRef]
- Sukomel, A.S.; Tsvetkov, F.F.; Kerimov, R.V. Heat Transfer and Hydraulic Resistance in the Motion of Gas Suspension in Pipes; Energiya: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Boothroyd, R.G. Flowing Gas-Solids Suspensions; Chapman and Hall: London, UK, 1971. [Google Scholar]
- Dunbar, L.E.; Courtney, J.P.; McMillen, L.D. Heating Augmentation in Erosion Hypersonic Environments. AIAA J. 1975, 13, 908–912. [Google Scholar] [CrossRef]
- Polezhaev, Y.V.; Repin, I.V.; Mikhatulin, D.S. Heat Transfer in a Heterogeneous Supersonic. High Temp. 1992, 30, 949–954. [Google Scholar]
- Molleson, G.V.; Stasenko, A.L. Kinetic-Thermal Effect of Gas-Dispersed Supersound Jet on an Axisymmetric Body. High Temp. 2014, 452, 881–889. [Google Scholar] [CrossRef]
- Molleson, G.V.; Stasenko, A.L. Gas-Dispersed Jet Flow Around a Solid in a Wide Range of Stagnation Parameters. High Temp. 2017, 55, 87–94. [Google Scholar] [CrossRef]
- Molleson, G.V.; Stasenko, A.L. Gasdynamic Acceleration of Microparticles and Their Interaction with a Solid Body. High Temp. 2017, 55, 906–913. [Google Scholar] [CrossRef]
- Perelman, R.G.; Pryakhin, V.V. Erosion of Elements of Steam Turbines; Energoatomizdat: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Preece, C.M. (Ed.) Treatise on Materials Science and Technology; Academic: New York, NY, USA, 1979; Volume 16. [Google Scholar]
- Springer, G.S. Erosion by Liquid Impact; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Mikhatulin, D.S.; Polezhaev, Y.V.; Reviznikov, D.L. Investigation of Failure of Carbon Heat-Shielding Material Under Conditions of Flight in Dusty Atmosphere. High Temp. 2003, 41, 88–94. [Google Scholar] [CrossRef]
- Shumeiko, A.I.; Telekh, V.D.; Ryzhkov, S.V. Probe Diagnostics and Optical Emission Spectroscopy of Wave Plasma Source Exhaust. Symmetry 2022, 14, 1983. [Google Scholar] [CrossRef]
- Rudinskii, A.V.; Yagodnikov, D.A.; Ryzhkov, S.V.; Onufriev, V.V. Features of Intrinsic Electric Field Formation in Low-Temperature Oxygen–Methane Plasma. Tech. Phys. Lett. 2021, 47, 520–523. [Google Scholar] [CrossRef]
- Polezhaev, Y.V. Stabilization of the Erosion Process Affecting the Material of a Barrier Under Repetitive Impact by Particles. J. Eng. Phys. 1979, 37, 1007–1011. [Google Scholar] [CrossRef]
- Hooker, W.Y.; Watson, R.; Morsell, A.L. Measurements with Powdered Solids in Shock Tubes. Phys. Fluids 1969, 12, 1169–1172. [Google Scholar] [CrossRef]
- Trunev, A.P.; Fomin, V.M. Erosion of a Blunt Body in a Dusty Hypersonic Stream. J. Appl. Mech. Tech. Phys. 1984, 25, 591–597. [Google Scholar] [CrossRef]
- Shebeko, V.N. Screening of a Surface by Reflected Particles. J. Eng. Phys. 1986, 51, 1062–1068. [Google Scholar] [CrossRef]
- Pankratov, B.M.; Polezhaev, Y.V.; Rudko, A.K. Interaction of Materials with Gas Flows; Mashinostroenie: Moscow, Russia, 1976; 224p. (In Russian) [Google Scholar]
- Sheldon, G.L. Similarities and Differences in the Erosion Behavior of Materials. Trans. ASME J. Basic Eng. 1970, 92, 619–626. [Google Scholar] [CrossRef]
- Rickerby, D.G.; McMillan, N.H. The Erosion of Aluminum by Solid Particles Impingement at Oblique Incident. Wear 1982, 79, 171–190. [Google Scholar] [CrossRef]
- Rickerby, D.G.; McMillan, N.H. Mechanism of Solid Particles Erosion in Crystalline Materials. Wear 1980, 60, 369–382. [Google Scholar] [CrossRef]
- Kleis, I. On the Wear of Metals in the Abrasive Jet. Tr. Tallin. Politekh. Inst. Ser. A 1959, 163, 3. (In Russian) [Google Scholar]
- Suur, U.K. On the Effect of Temperature on the Wear Mechanism of Metals in an Abrasive Jet. Tr. Tallin. Politekh. Inst. Ser. A 1966, 237, 63–88. (In Russian) [Google Scholar]
- Young, J.P.; Ruff, A.W. Particle Erosion Measurements on Metals. J. Eng. Mater. Technol. 1977, 99, 121–125. [Google Scholar] [CrossRef]
- Ives, L.K. Erosion of 310 Stainless Steel at 975 °C in Combustion Gas Atmosphere. J. Eng. Mater. Technol. 1977, 99, 126–132. [Google Scholar] [CrossRef]
- Wakeman, T.; Tabakoff, W. Erosion Behavior in a Simulated Jet Engine Environments. J. Aircr. 1979, 16, 828–833. [Google Scholar] [CrossRef]
- Gat, N.; Tabakoff, W. Some Effects of Temperature on the Erosion of Metals. Wear 1978, 50, 85–94. [Google Scholar] [CrossRef]
- Tabakoff, W.; Greut, G. An Experimental Investigation of Certain Aerodynamic Effects on Erosion. In Proceedings of the 8th Aerodynamic Testing Conference, Bethesda, MD, USA, 8–10 July 1974. [Google Scholar]
- Swain, C.E. The Effects of Particle/Shock Laden Interaction on Reentry Vehicle Performance. In Proceedings of the 10th Thermophysics Conference, Denver, CO, USA, 27–29 May 1975. [Google Scholar]
- Polezhaev, Y.V.; Panchenko, V.I. Fundamental Relations of Erosion Kinetics. J. Eng. Phys. 1988, 52, 507–512. [Google Scholar] [CrossRef]
- Guo, Y.; Koga, G.Y.; Moreira, J.A.; Savoie, S.; Schulz, R.; Kiminami, C.S.; Bolfarini, C.; Botta, W.J. Microstructural Investigation of Fe-Cr-Nb-B Amorphous/Nanocrystalline Coating Produced by HVOF. Mater. Des. 2016, 111, 608–615. [Google Scholar]
- Alkhimov, A.P.; Kosarev, V.F.; Papyrin, A.N. A Method of Cold Gas-Dynamic Deposition. Sov. Phys.—Dokl. 1990, 35, 1047–1049. [Google Scholar]
- Alkhimov, A.P.; Klinkov, S.V.; Kosarev, V.F. Experimental Study of Deformation and Attachment of Microparticles to an Obstacle Upon High-Rate Impact. J. Appl. Mech. Tech. Phys. 2000, 41, 245–250. [Google Scholar] [CrossRef]
- Alkhimov, A.P.; Kosarev, V.F.; Klinkov, S.V. The Features of Cold Spray Nozzle Design. J. Therm. Spray Technol. 2001, 10, 375–381. [Google Scholar] [CrossRef]
- Alkhimov, A.P.; Klinkov, S.V.; Kosarev, V.F.; Fomin, V.M. Cold Gasdynamic Sputtering: Theory and Practice; Fizmatlit: Moscow, Russia, 2010; 536p. (In Russian) [Google Scholar]
- Vasilevskij, E.B.; Osiptsov, A.N.; Chirikhin, A.V.; Yakovleva, L.V. Heat Exchange on the Front Surface of a Blunt Body in a High-Speed Flow Containing Low-Inertia Particles. J. Eng. Phys. Thermophys. 2001, 74, 1399–1411. [Google Scholar] [CrossRef]
- Molleson, G.V.; Stasenko, A.L. Gas Thermodynamics and Optics of a Monodisperse Supersonic Jet Interacting with an Aerodynamic Body. High Temp. 2012, 50, 755–764. [Google Scholar] [CrossRef]
- Molleson, G.V.; Stasenko, A.L. Electro-Optical Phenomena in a Gas-Dispersed Jet Flow Around a Solid Body. High Temp. 2015, 53, 855–864. [Google Scholar] [CrossRef]
- Dalgamoni, H.N.; Yong, X. Numerical and Theoretical Modeling of Droplet Impact on Spherical Surfaces. Phys. Fluids 2021, 33, 052112. [Google Scholar] [CrossRef]
- Sahoo, P.C.; Senapati, J.R.; Rana, B.K. Numerical Observation and Analytical Formulation of Droplet Impact and Spreading Around the Thin Vertical Cylinder. Phys. Fluids 2022, 34, 042114. [Google Scholar] [CrossRef]
- Yoon, I.; Shin, S. Maximal Spreading of Droplet During Collision on Particle: Effects of Liquid Viscosity and Surface Curvature. Phys. Fluids 2021, 33, 083310. [Google Scholar] [CrossRef]
- Luo, J.; Chu, F.; Ni, Z.; Zhang, J.; Wen, D. Dynamics of Droplet Impacting on a Cone. Phys. Fluids 2021, 33, 112116. [Google Scholar] [CrossRef]
- Ding, S.; Liu, X.; Wu, X.; Zhang, X. Droplet Breakup and Rebound During Impact on Small Cylindrical Superhydrophobic Targets. Phys. Fluids 2020, 32, 102106. [Google Scholar] [CrossRef]
- Yarin, A.L. Droplet Impact Dynamics: Splashing, Spreading, Receding, Bouncing…. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S.T. Drop Impact on a Solid Surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef]
- Dalgamoni, H.N.; Yong, X. Axisymmetric Lattice Boltzmann Simulation of Droplet Impact on Solid Surfaces. Phys. Rev. E 2018, 98, 13102. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Vasil’ev, N.V.; Vavilov, S.N. The Mechanism of Droplet Levitation in Gas-Droplet Flows Past Bodies. Dokl. Phys. 2021, 66, 345–347. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Vasil’ev, N.V.; Vavilov, S.N.; Khodakov, K.A. On Some Features of the Gravitational Deposition of Drops on a Model with a Hemispherical End. High Temp. 2022, 60, S70–S76. [Google Scholar]
- Wessel, R.A.; Righi, J. Generalized Correlations for Inertial Impaction of Particles on a Circular Cylinder. Aerosol Sci. Technol. 1988, 9, 9–60. [Google Scholar] [CrossRef]
- Pulley, R.A.; Walters, J.K. The Effect of Interception on Particle Collection by Spheres and Cylinders. J. Aerosol Sci. 1990, 21, 733–743. [Google Scholar] [CrossRef]
- Hinds, W.C. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles, 2nd ed.; Wiley & Sons: Hoboken, NJ, USA, 1999; 504p. [Google Scholar]
- Regalado, C.M.; Ritter, A. The Design of an Optimal Fog Water Collector: A Theoretical Analysis. Atmos. Res. 2016, 178–179, 45–54. [Google Scholar] [CrossRef]
- Ratnam, J.J.; Cheng, W.; Kurtyigit, I.E.; DeMauro, E.P.; Drazer, G. The Effect of Neighbors on the Effective Inertial Collision Efficiency of Cylindrical Collectors. J. Aerosol Sci. 2022, 16, 105910. [Google Scholar] [CrossRef]
- Advisory Group for Aerospace Research and Development. Ice Accretion Simulation; AGARD-AR-344; Canada Communication Group Inc.: Ottawa, ON, Canada, 1997; 280p. [Google Scholar]
- Aircraft Icing Handbook; Civil Aviation Authority: Wellington, New Zeland, 2000; 97p.
- Fortin, G.; Ilinca, A.; Laforte, J.-L.; Brandi, V. A New Roughness Computation Method and Geometric Accretion Model for Airfoil Acing. J. Aircr. 2004, 41, 119–127. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Prihod’ko, A.A. Numerical Simulation of Cylinder and Profile Icing. Review of Models and Results of Calculations. Uch. Zap. TsAGI 2013, 44, 25–57. (In Russian) [Google Scholar]
- Amelyushkin, I.A.; Grinats, E.S.; Stasenko, A.L. Kinetics of Molecular Clusters and Hydrothermodynamics of Drops in the Problem of Aircraft Icing. Vest. Mosk. Gos. Obl. Univ. Ser. Fiz.-Mat. 2012, 2, 152–161. (In Russian) [Google Scholar]
- Grinats, E.S.; Miller, A.B.; Potapov, Y.F.; Stasenko, A.L. Experimental and Theoretical Studies of Icing Processes of Nanomodified Superhydrophobic and Conventional Surfaces. Vest. Mosk. Gos. Obl. Univ. Ser. Fiz.-Mat. 2013, 3, 84–92. (In Russian) [Google Scholar]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. The Adaptive Composite Block-Structured Grid Calculation of the Gas-Dynamic Characteristics of an Aircraft Moving in a Gas Environment. Mathematics 2022, 10, 2130. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Approximate calculation of convective heat transfer near hypersonic aircraft surface. J. Enhanc. Heat Transf. 2018, 25, 181–193. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Numerical Simulation of Pulsed Jets of a High-Current Pulsed Surface Discharge. Comput. Therm. Sci. 2021, 13, 45–56. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Approximate method for calculating convective heat flux on the surface of bodies of simple geometric shapes. J. Phys. Conf. Ser. 2017, 815, 012024. [Google Scholar] [CrossRef]
- Ryzhkov, S.V.; Kuzenov, V.V. New realization method for calculating convective heat transfer near the hypersonic aircraft surface. Z. Angew. Math. Phys. 2019, 70, 46. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Calculation of heat transfer and drag coefficients for aircraft geometric models. Appl. Sci. 2022, 12, 11011. [Google Scholar] [CrossRef]
- Ryzhkov, S.V.; Kuzenov, V.V. Analysis of the ideal gas flow over body of basic geometrical shape. Int. J. Heat Mass Transf. 2019, 132, 587–592. [Google Scholar] [CrossRef]
- Kashevarov, A.V.; Stasenko, A.L. Evolution of the Water Film and Run-Back Ice on the Surface of a Body on Plane Airflow. Thermophys. Aeromech. 2019, 26, 223–230. [Google Scholar] [CrossRef]
- Amelyushkin, I.A.; Stasenko, A.L. Simulation of the Interaction of Ice Crystals with the Surface of a Flying Vehicle. J. Eng. Phys. Thermophys. 2020, 93, 576–584. [Google Scholar] [CrossRef]
- Kashevarov, A.V.; Stasenko, A.L. Discrete-Drop Mode of Ice Accretion on a Cylinder in Transverse Supercooled Flow. Tech. Phys. 2020, 65, 41–47. [Google Scholar] [CrossRef]
- Kashevarov, A.V.; Miller, A.B.; Potapov, Y.F.; Stasenko, A.L. Effect of the Ice Crystals on Run-Back Ice Evolution on a Wing Model. Thermophys. Aeromech. 2021, 28, 21–28. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).