More Insights into Symmetries in Multisymplectic Field Theories
Abstract
1. Introduction
2. Symmetries on (Pre)multisymplectic Fiber Bundles
2.1. (Pre)Multisymplectic Bundles
2.2. Conserved Quantities and Symmetries
- 1.
- A symmetry of the (pre)multisymplectic system is a diffeomorphism such that .
- 2.
- An infinitesimal symmetry of the (pre)multisymplectic system is a vector field whose local flows are local symmetries or, equivalently, .

2.3. Noether Symmetries
- 1.
- A Noether or Cartan symmetry of the (pre)multisymplectic system is a diffeomorphism such that, . In the particular case where , then Φ is called an exact Noether or exact Cartan symmetry.
- 2.
- An infinitesimal Noether or Cartan symmetry of the (pre)multisymplectic system is a vector field for which . In the particular case where , Y is called an infinitesimal exact Noether or infinitesimal exact Cartan symmetry.
2.4. Gauge Symmetries
- 1.
- .
- 2.
- It is a ϱ-vertical vector field, .
- 3.
- It is tangent to , .
2.5. Multimomentum Map
3. Lifting Transformations from the Base Space of a Jet Bundle
3.1. First-Order Jet Bundles
3.2. Lifting Transformations from M to E
- 1.
- Let be a diffeomorphism. Thecanonical lift of to Eis the diffeomorphism defined as follows: for every where , define , where denotes the canonical transformation of tensors on M induced by . Thus, .
- 2.
- Let be the vector field induced by local one-parameter groups of diffeomorphisms of M, denoted . The canonical lift of Z to E is the vector field induced by local one-parameter groups of diffeomorphisms which are the canonical lifts of to the configuration bundle E.
3.3. Lifting Transformations from E to
4. Symmetries for Lagrangian and Hamiltonian Field Theories
4.1. First-Order Lagrangian Field Theories
4.2. De Donder–Weyl Hamiltonian Formalism
4.3. Symmetries, Conserved Quantities, and Multimomentum Maps
- 1.
- A (Noether) symmetry of a Lagrangian system is said to be natural if Φ is a canonical lift; i.e., for a diffeormorphism .
- 2.
- An infinitesimal (Noether) symmetry of a Lagrangian system is said to be natural if X is a canonical lift; i.e., for some .
- 1.
- A Lagrangian symmetry of a Lagrangian system is a diffeomorphism that leaves invariant: .If for some fiber-preserving diffeomorphism , then the Lagrangian symmetry is said to be natural.
- 2.
- An infinitesimal Lagrangian symmetry of a Lagrangian system is a vector field that leaves invariant.If , for some π-projectable vector field , then the infinitesimal Lagrangian symmetry is said to be natural.
- 1.
- A geometric Lagrangian symmetry of a Lagrangian system is a diffeomorphism such that:
- (a)
- .
- (b)
- The canonical geometric structures of are invariant by Φ.
- 2.
- An infinitesimal geometric Lagrangian symmetry of a Lagrangian system is a vector field such that:
- (a)
- .
- (b)
- The canonical geometric structures of are invariant under the action of X.
4.4. Symmetries in the Presence of Constraints
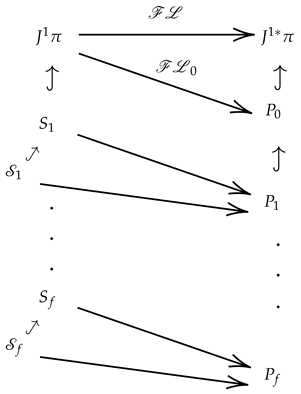
- There exists some such that and is -projectable only from the constraint submanifold . Then, on the corresponding Hamiltonian constraint submanifold , there exists the vector field such that . Furthermore, the vector field may or may not be the local extension of some to for some .
- There exists some such that , and X is -projectable only from . Then, on the corresponding Hamiltonian constraint submanifold , there exists the vector field such that . Furthermore, it is possible to construct a local extension of Y to , denoted as , but may or may not be the local extension of some to for some .
5. Some Examples
5.1. Bosonic String Theories
5.2. Yang–Mills Theory
5.3. Chern–Simons Theory
5.4. Electric Carrollian Scalar Field Theory
5.5. Magnetic Carrollian Scalar Field Theory
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Multivector Fields on Manifolds and Fiber Bundles
References
- Kosmann-Schwarzbach, Y. The Noether Theorems. Invariance and Conservation Laws in the Twentieth Century; Sringer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Aldaya, V.; de Azcarraga, J.A. Variational Principles on rth order jets of fibre bundles in Field Theory. J. Math. Phys. 1978, 19, 1869–1875. [Google Scholar] [CrossRef]
- Echeverría-Enríquez, A.; Muñoz-Lecanda, M.C.; Román-Roy, N. Geometry of Lagrangian first-order classical field theories. Forts Phys. 1996, 44, 235–280. [Google Scholar] [CrossRef]
- García, P.L. The Poincaré-Cartan invariant in the calculus of variations. Symp. Math. 1973, 14, 219–246. [Google Scholar]
- Goldschmidt, H.; Sternberg, S. The Hamilton-Cartan formalism in the calculus of variations. Ann. Inst. Fourier Grenoble 1973, 23, 203–267. Available online: http://eudml.org/doc/74112 (accessed on 27 January 2023). [CrossRef]
- Hélein, F.; Kouneiher, J. Covariant Hamiltonian formalism for the calculus of variations with several variables: Lepage–Dedecker versus De Donder–Weyl. Adv. Theor. Math. Phys. 2004, 8, 565–601. [Google Scholar] [CrossRef]
- Saunders, D.J. The Geometry of Jet Bundles; London Mathematical Society, Lect. Notes Ser. 142; Cambridge University Press: Cambridge, MA, USA; New York, NY, USA, 1989. [Google Scholar] [CrossRef]
- Dedecker, P. On the Generalization of Symplectic Geometry to Multiple Integrals in the Calculus of Variations. In Differential Geometrical Methods in Mathematical Physics (Proc. Sympos., Univ. Bonn, Bonn, 1975); Lecture Notes in Math.; Springer: Berlin, Germany, 1977; Volume 570, pp. 395–456. [Google Scholar] [CrossRef]
- de León, M.; Martín de Diego, D.; Santamaría-Merino, A. Symmetries in classical field theory. Int. J. Geom. Meths. Mod. Phys. 2004, 1, 651–710. [Google Scholar] [CrossRef]
- Forger, M.; Soares, B.L. Local symmetries in gauge theories in a finite-dimensional setting. J. Geom. Phys. 2012, 62, 1925–1938. [Google Scholar] [CrossRef]
- Giachetta, G.; Mangiarotti, L.; Sardanashvily, G. New Lagrangian and Hamiltonian Methods in Field Theory; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 1997. [Google Scholar] [CrossRef]
- Krupka, D. Introduction to Global Variational Geometry; Atlantis Studies in Variational Geometry; Atlantis Press: Paris, France, 2015; Available online: https://link.springer.com/book/10.2991/978-94-6239-073-7 (accessed on 27 January 2023).
- Echeverría-Enríquez, A.; Muñoz-Lecanda, M.C.; Román-Roy, N. Multivector field formulation of Hamiltonian field theories: Equations and symmetries. J. Phys. A Math. Gen. 1999, 32, 8461–8484. [Google Scholar] [CrossRef]
- Gaset, J.; Prieto-Martínez, P.D.; Román-Roy, N. Variational principles and symmetries on fibered multisymplectic manifolds. Comm. Math. 2016, 24, 137–152. [Google Scholar] [CrossRef]
- Gaset, J.; Román-Roy, N. Symmetries and gauge symmetries in multisymplectic first and second-order Lagrangian field theories: Electromagnetic and gravitational fields. Rev. Acad. Cienc. Canar. Math. arXiv. arXiv:2107.08846.
- Gotay, M.J.; Isenberg, J.; Marsden, J.E.; Montgomery, R. Momentum maps and classical relativistic fields. I. Covariant theory. arXiv 2004, arXiv:physics/9801019. [Google Scholar]
- Ryvkin, L.; Wurzbacher, T.; Zambon, M. Conserved quantities on multisymplectic manifolds. J. Austral Math. Soc. 2020, 108, 120–144. [Google Scholar] [CrossRef]
- Blacker, C. Reduction of multisymplectic manifolds. Lett. Math. Phys. 2021, 111, 64. [Google Scholar] [CrossRef]
- Echeverría-Enríquez, A.; Muñoz-Lecanda, M.C.; Román-Roy, N. Remarks on multisymplectic reduction. Rep. Math. Phys. 2018, 81, 415–424. [Google Scholar] [CrossRef]
- Madsen, T.B.; Swann, A. Multimoment maps. Adv. Math. 2012, 229, 2287–2309. [Google Scholar] [CrossRef]
- Sniatycki, J. Multisymplectic reduction for proper actions. Can. J. Math. 2004, 56, 638–654. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Graduate Texts in Mathematics 60; Springer: New York, NY, USA, 1989. [Google Scholar] [CrossRef]
- Mangiarotti, L.; Sardanashvily, G. Gauge Mechanics; World Scientific: Singapore, 1998. [Google Scholar] [CrossRef]
- Sarlet, W.; Cantrijn, F. Higher-order Noether symmetries and constants of the motion. J. Phys. A Math. Gen. 1981, 14, 479–492. [Google Scholar] [CrossRef]
- Bleecker, D. Gauge Theory and Variational Principles; Dover Publications: New York, NY, USA, 1981; ISBN 0486445461. [Google Scholar]
- Henneaux, M.; Salgado-Rebolledo, P. Carroll contractions of Lorentz-invariant theories. J. High Energy Phys. 2021, 2021, 180. [Google Scholar] [CrossRef]
- de León, M.; Marín-Solano, J.M.; Marrero, J.C.; Muñoz-Lecanda, M.C.; Román-Roy, N. Premultisymplectic constraint algorithm for field theories. Int. J. Geom. Meth. Mod. Phys. 2005, 2, 839–871. [Google Scholar] [CrossRef]
- Román-Roy, N. A summary on symmetries and conserved quantities of autonomous Hamiltonian systems. J. Geom. Mech. 2020, 12, 541–551. [Google Scholar] [CrossRef]
- Gaset, J. Geometric Gauge Freedom in Multisymplectic Field Theories. arXiv 2022, arXiv:2209.11212. [Google Scholar]
- Bergvelt, M.J.; de Kerf, E.A. The Hamiltonian structure of Yang-Mills theories and instantons (Part I). Physica 1986, 139A, 101–124. [Google Scholar] [CrossRef]
- Gotay, M.J.; Nester, J.M. Presymplectic Hamilton and Lagrange systems, gauge transformations and the Dirac theory of constraints. In Group Theoretical Methods in Physics; Beigelbock, W., Böhm, A., Takasugi, E., Eds.; Lect. Notes in Phys.; Springer: Berlin, Germany, 1979; Volume 94, pp. 272–279. [Google Scholar] [CrossRef]
- Batlle, C.; Gomis, J.; París, J.; Roca, J. Field-antifield formalism and Hamiltonian BRST approach. Nucl. Phys. B 1990, 329, 139–154. [Google Scholar] [CrossRef]
- Gomis, J.; París, J.; Samuel, S. Antibracket, antifields and gauge-theory quantization. Phys. Rep. 1995, 259, 1–145. [Google Scholar] [CrossRef]
- Gràcia, X.; Pons, J.M. Symmetries and infinitesimal symmetries of singular differential equations. J. Phys. A Math. Gen. 2002, 35, 5059. [Google Scholar] [CrossRef]
- Kolár, I.; Slovák, J.; Michor, P.W. Natural Operations in Differential Geometry; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar] [CrossRef]
- Michor, P.W. Topics in Differential Geometry; Grad. Stud. in Math. 93; American Mathematical Soc.: Wien, Austria, 2008; ISBN 0821820036. [Google Scholar]
- Echeverría-Enríquez, A.; Muñoz-Lecanda, M.C.; Román-Roy, N. Multivector fields and connections: Setting Lagrangian equations in field theories. J. Math. Phys. 1998, 39, 4578–4603. [Google Scholar] [CrossRef]
- Gomis, J.; Guerra, A., IV; Román-Roy, N. Multisymplectic Constraint Analysis of Scalar Field Theories, Chern-Simons Gravity, and Bosonic String Theory. Nucl. Phys. B 2023, 987, 116069. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Crampin, M.; Ibort, L.A. On the multisymplectic formalism for first order field theories. Diff. Geom. Appl. 1991, 1, 345–374. [Google Scholar] [CrossRef]
- de León, M.; Marín-Solano, J.M.; Marrero, J.C. A Geometrical approach to Classical Field Theories: A constraint algorithm for singular theories. In New Developments in Differential Geometry; Tamassi, L., Szenthe, J., Eds.; Kluwer Acad. Press: Amsterdam, The Netherlands, 1996; pp. 291–312. [Google Scholar] [CrossRef]
- Román-Roy, N. Multisymplectic Lagrangian and Hamiltonian formalisms of classical field theories. Symm. Integ. Geom. Meth. Appl. (SIGMA) 2009, 5, 100. [Google Scholar] [CrossRef]
- Castrillón, M.; Muñoz-Masqué, J.; Rosado, E. First-order equivalent to Einstein–Hilbert Lagrangian. J. Math. Phys. 2014, 55, 082501. [Google Scholar] [CrossRef]
- Adame-Carrillo, D.; Gaset, J.; Román-Roy, N. The second-order problem for k-presymplectic Lagrangian field theories: Application to the Einstein–Palatini model. RACSAM 2022, 116, 20. [Google Scholar] [CrossRef]
- Becker, K.; Becker, M.; Schwarz, J.H. String Theory and M-Theory. A Modern Introduction; Cambridge University Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Blacker, C. Reduction of L∞-algebras of observables on multisymplectic manifolds. arXiv 2022, arXiv:92206.03137. [Google Scholar]
- Ciaglia, F.M.; Cosmo, F.D.; Ibort, A.; Marmo, G.; Schiavone, L. Covariant reduction of classical Hamiltonian Field Theories: From D’Alembert to Klein–Gordon and Schrödinger. Mod. Phys. Lett. A 2020, 35, 2050214. [Google Scholar] [CrossRef]
- Cantrijn, F.; Ibort, L.A.; de León, M. Hamiltonian structures on multisymplectic manifolds. Rend. Sem. Mat. Univ. Pol. Torino 1996, 54, 225–236. Available online: https://www.researchgate.net/publication/233917958 (accessed on 27 January 2023).
- Cantrijn, F.; Ibort, L.A.; de León, M. On the geometry of multisymplectic manifolds. J. Aust. Math. Soc. 1999, 66, 303–330. Available online: https://www.researchgate.net/publication/231926129 (accessed on 27 January 2023). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra, A., IV; Román-Roy, N. More Insights into Symmetries in Multisymplectic Field Theories. Symmetry 2023, 15, 390. https://doi.org/10.3390/sym15020390
Guerra A IV, Román-Roy N. More Insights into Symmetries in Multisymplectic Field Theories. Symmetry. 2023; 15(2):390. https://doi.org/10.3390/sym15020390
Chicago/Turabian StyleGuerra, Arnoldo, IV, and Narciso Román-Roy. 2023. "More Insights into Symmetries in Multisymplectic Field Theories" Symmetry 15, no. 2: 390. https://doi.org/10.3390/sym15020390
APA StyleGuerra, A., IV, & Román-Roy, N. (2023). More Insights into Symmetries in Multisymplectic Field Theories. Symmetry, 15(2), 390. https://doi.org/10.3390/sym15020390






