Image Encryption Using Dynamic Image as a Key Based on Multilayers of Chaotic Permutation
Abstract
:1. Introduction
2. Literature Review
3. Proposed Algorithm
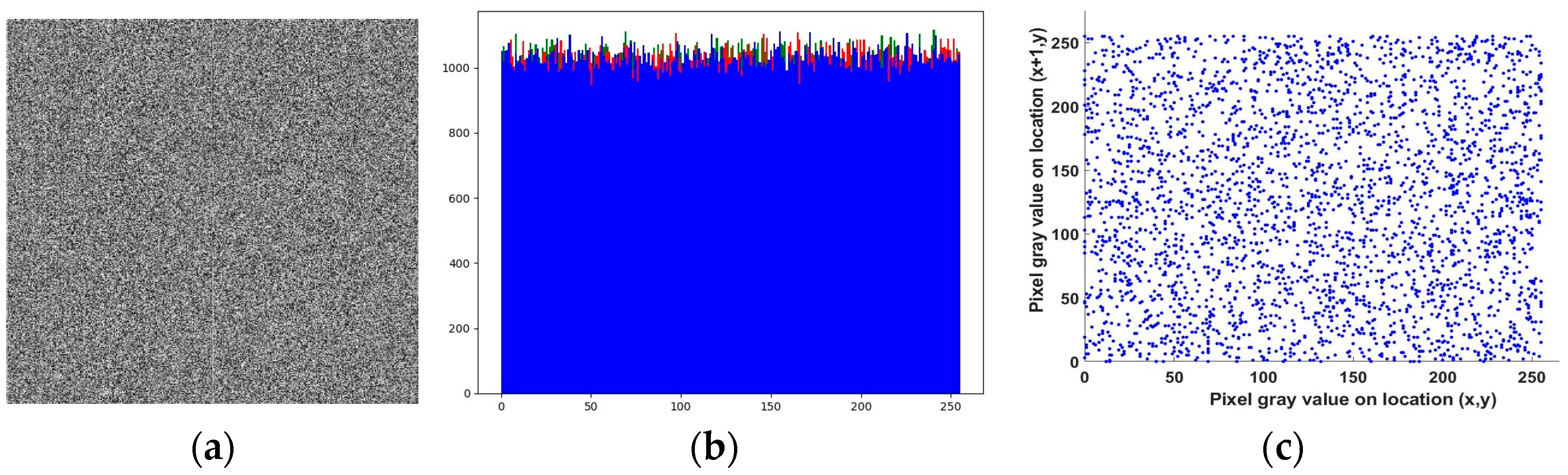
- The content information randomness in the image is very high.
- The histogram is very close to flat pixels for all level values.
- Correlations among adjacent image pixels in the key image are kept to a minimum.
- The dimensions of the image will be determined by the system designer and according to the dimensions of the images to be encrypted.
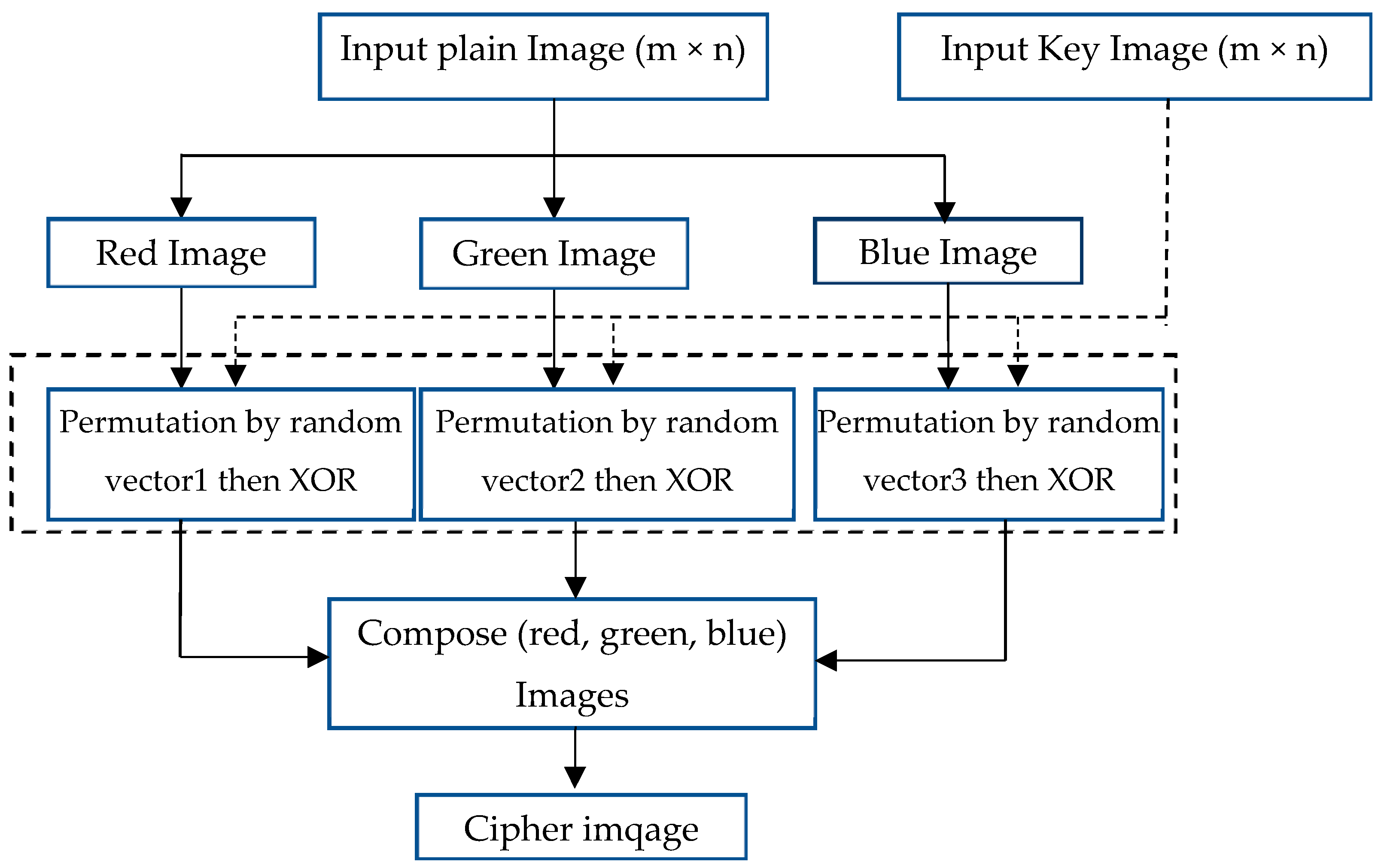
3.1. Encryption Process
3.1.1. Pixel Permutation (Level 1)
| Algorithm 1: Proposed Pixel Permutation |
| Input: Plain image I and key image k of size r × c. |
| Output: The permutation plain image IR and the permutation key image KR. |
|
3.1.2. XOR Logical Operation (Level 2)
| Algorithm 2: XOR Logical Operation |
| Input: Permutation plain image IC and permutation key image KR. |
| Output: Permuted XOR image X |
|
3.1.3. Append Random Numbers to Encrypted Image (Level 3)
| Algorithm 3: Append Random Numbers |
| Input: Permuted XOR image X, key image K, and vectors that were created from Algorithm 1 (VR,VC) |
| Output: Cipher image XC of size (r + 1, c + 1) |
|
- Pixel Bytewise Permutation:Create random values vector for row permutation of size 6, where the range of each location is 1–8: VR [6] = [2,4,7,1,3,0]; create a second vector for column permutation of size 8, where the range of each location is 1–6: VC [8] = [5,1,0,2,5,3,1,4].Depending on the random vector generated VR [6], rotate each row in key image k [6,8]. For the first row r1, rotate in a circular fashion by 2 positions, rotate r2 to the right 4 times, rotate r3 7 times, rotate r4 once to the right, and rotate r5 3 times. At the conclusion of this operation, a matrix called KR [r, c] is generated. Then, repeat the permutation for columns with respect to VC [8]; rotate c1 5 times, rotate c2 once, rotate c4 two times, rotate c5 5 times, rotate c6 3 times, rotate c7 once, and rotate c8 4 times; thus, a matrix KC [r, c] is generated. Row and column permutation is repeated on the plain image I [r, c] to obtain IC [r, c]. Figure 2 denotes the permutation of the plain and key image.
- XOR Operation:In general, in this process, the XOR operation is applied to the two matrices KC [6,8] and IC [6,8], then the two random vectors generated in Section 3.1 are appended as a new row and column for the XOR-manipulated matrix to obtain X [n + 1,m + 1].
- Permutation XOR-manipulated Image:The second round of permutation applies to the XOR-manipulated matrix and depends on first the row and first column of the key image by creating new two vectors VKr [r] and VKc [c]. The first column of the key image is [22,45,231,106,108,22,25], obtained by using modulo operation to return the remainder of 6 division and keep the range 0-5. The new generated vector is called VKr [7] = [4,3,3,4,0,4,1]. The first row of the key image is [22,166,161,115,129,163,57,66,248], obtained by using modulo 8, generating a new vector in the range 0–7 called VKc [9] = [6,6,1,4,1,3,1,2,2].
3.2. Decryption Process
- Level 1. Reading the first row and first column vectors (VKr,VKc) from the key image and using them to permutate the cipher image.
- level 2. Reading the row and column vectors (VR,VC) from the image generated from level 1 and using them in the process of permutate the key image and then applying the XOR process.
- level 3. Permuting the image that was produced from Level 2 by (VR,VC) to obtain the plain image.
4. Experimental Results and Security Analysis
4.1. Statistical Cryptanalysis
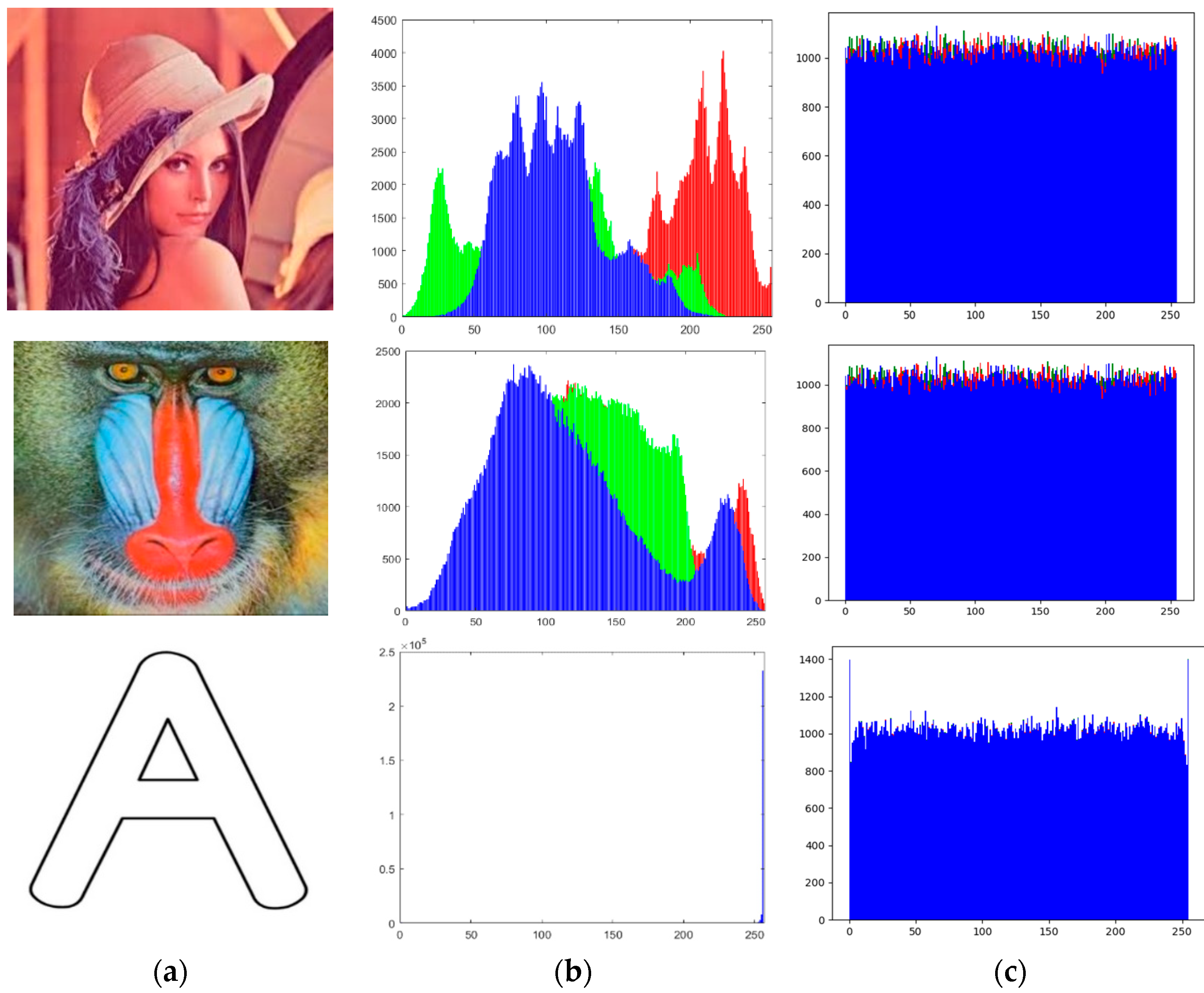
4.1.1. Histogram Analysis
4.1.2. Correlation Analysis
4.1.3. Entropy
4.2. Statistical Cryptanalysis
4.2.1. Robustness for Mitigating Data Losses and Noise
4.2.2. Key Magnitude
4.2.3. Sensitivity Analysis
4.3. Performance Comparison with Other Image Encryption Techniques
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saracevi’c, M.H.; Adamovi’c, S.Z.; Miskovic, V.A.; Elhoseny, M.; Macek, N.D.; Selim, M.M.; Shankar, K. Data encryption for internet of things applications based on catalan objects and two combinatorial structures. IEEE Trans. Reliab. 2020, 70, 819–830. [Google Scholar] [CrossRef]
- Banu, S.A.; Amirtharajan, R. A robust medical image encryption in dual domain: Chaos-DNA -IWT combined approach. Med. Biol. Eng. Comput. 2020, 58, 1445–1458. [Google Scholar] [CrossRef] [PubMed]
- Pourasad, Y.; Ranjbarzadeh, R.; Mardani, A. A New Algorithm for Digital Image Encryption Based on Chaos Theory. Entropy 2021, 23, 341. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-Y.; Li, Z.-M. A color image encryption algorithm based on hopfield chaotic neural network. Opt. Lasers Eng. 2019, 115, 107–118. [Google Scholar] [CrossRef]
- Abd-El-Hafiz, S.K.; AbdElHaleem, S.H.; Radwan, A.G. Novel permutation measures for image encryption algorithms. Opt. Lasers Eng. 2016, 85, 72–83. [Google Scholar] [CrossRef]
- Mahdi, M.S.; Azeez, R.A.; Hassan, N.F. A proposed lightweight image encryption using ChaCha with hyperchaotic maps. Period. Eng. Nat. Sci. 2020, 8, 2138–2145. [Google Scholar]
- Liu, Y.; Jiang, Z.; Xu, X.; Zhang, F.; Xu, J. Optical image encryption algorithm based on hyper-chaos and public-key cryptography. Opt. Laser Technol. 2020, 127, 106171. [Google Scholar] [CrossRef]
- Akkasaligar, P.T.; Biradar, S. Medical image encryption with integrity using DNA and chaotic map. In Proceedings of the International Conference on Recent Trends in Image Processing and Pattern Recognition, Solapur, India, 21–22 December 2018; pp. 143–153. [Google Scholar]
- Ye, G.; Pan, C.; Huang, X.; Mei, Q. An efficient pixel-level chaotic image encryption algorithm. Nonlinear Dyn. 2018, 94, 745–756. [Google Scholar] [CrossRef]
- Cai, Q. A secure image encryption algorithm based on composite chaos theory. Treat. Du Signal 2019, 36, 31–36. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X. An image encryption algorithm based on dynamic row scrambling and zigzag transformation. Chaos Solitons Fractals 2021, 147, 110962. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Cui, G.; Niu, Y. Entropy-based block scrambling image encryption using des structure and chaotic systems. Int. J. Opt. 2021, 2019, 3594534. [Google Scholar] [CrossRef] [Green Version]
- Sarosh, P.; Parah, S.A.; Bhat, G.M. An efficient image encryption scheme for healthcare applications. Multimed. Tools Appl. 2022, 81, 7253–7270. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Wang, G.; Sun, K. Cryptanalysis and improvement on an image encryption algorithm design using a novel chaos based S-box. Symmetry 2018, 10, 399. [Google Scholar] [CrossRef]
- Masood, F.; Ahmad, J.; Shah, S.A.; Jamal, S.S.; Hussain, I. A novel hybrid secure image encryption based on julia set of fractals and 3d Lorenz chaotic map. Entropy 2020, 22, 274. [Google Scholar] [CrossRef]
- Zhang, R.; Yu, L.; Jiang, D.; Ding, W.; Song, J.; He, K.; Ding, Q. A novel plaintext-related color image encryption scheme based on cellular neural network and Chen’s chaotic system. Symmetry 2021, 13, 393. [Google Scholar] [CrossRef]
- Xian, Y.; Wang, X. Fractal sorting matrix and its application on chaotic image encryption. Inf. Sci. 2021, 547, 1154–1169. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, D.; Sun, K.; Rawat, U. Color image encryption using non-dominated sorting genetic algorithm with local chaotic search based 5d chaotic map. Future Gener. Comput. Syst. 2020, 107, 333–350. [Google Scholar] [CrossRef]
- Chen, X.; Qian, S.; Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Deng, Z.; Li, Y.; Du, S. Pseudorandom number generator based on three kinds of four-wing memristive hyperchaotic system and its application in image encryption. Complexity 2020, 2020, 8274685. [Google Scholar] [CrossRef]
- Jiao, K.; Ye, G.; Dong, Y.; Huang, X.; He, J. Image encryption scheme based on a generalized Arnold map and RSA algorithm. Secur. Commun. Netw. 2020, 2020, 9721675. [Google Scholar] [CrossRef]
- Patel, S.; Bharath, K.; Kumar, R. Symmetric keys image encryption and decryption using 3d chaotic maps with DNA encoding technique. Multimed. Tools Appl. 2020, 79, 31739–31757. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. A novel chaos-based color image encryption scheme using bit-level permutation. Symmetry 2020, 12, 1497. [Google Scholar] [CrossRef]
- Himeur, Y.; Boukabou, A. A robust and secure key-frames based video watermarking system using chaotic encryption. Multimed. Tools Appl. 2018, 77, 8603–8627. [Google Scholar] [CrossRef]
- Jabbar, A.K.; Hashim, A.T.; Al-Doori, Q.F. Secured medical image hashing based on frequency domain with chaotic map. Eng. Technol. J. 2021, 39, 711–722. [Google Scholar] [CrossRef]
- Zhang, G.; Ding, W.; Li, L. Image encryption algorithm based on tent delay-sine cascade with logistic map. Symmetry 2020, 12, 355. [Google Scholar] [CrossRef]
- Hamad, A.; Farhan, A.K. Image encryption algorithm based on substitution principle and shuffling scheme. Eng. Technol. J. 2020, 38, 98–103. [Google Scholar] [CrossRef]
- Ravichandran, D.; Banu, S.A.; Murthy, B.; Balasubramanian, V.; Fathima, S.; Amirtharajan, R. An efficient medical image encryption using hybrid DNA computing and chaos in transform domain. Med. Biol. Eng. Comput. 2021, 59, 589–605. [Google Scholar] [CrossRef]
- Tawfic, I.S. Design and development of e-passport scheme using multi encryption biometric information. Iraqi J. Comput. Commun. Control. Syst. Eng. 2019, 19, 27–34. [Google Scholar]
- Song, C.; Qiao, Y. A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos. Entropy 2015, 17, 6954–6968. [Google Scholar] [CrossRef]
- Natiq, H.; Al-Saidi, N.M.; Obaiys, S.J.; Mahdi, M.N.; Farhan, A.K. Image Encryption Based on Local Fractional Derivative Complex Logistic Map. Symmetry 2022, 14, 1874. [Google Scholar] [CrossRef]
- Wen, H.; Ma, L.; Liu, L.; Huang, Y.; Chen, Z.; Li, R.; Liu, Z.; Lin, W.; Wu, J.; Li, Y.; et al. High-quality restoration image encryption using DCT frequency-domain compression coding and chaos. Sci. Rep. 2022, 12, 16523. [Google Scholar] [CrossRef]
- Li, C.; Shen, X.; Liu, S. Cryptanalyzing an Image Encryption Algorithm Underpinned by 2D Lag-Complex Logistic Map. arXiv 2022, arXiv:2208.06774. [Google Scholar]
- Lima, V.S.; Madeiro, F.; Lima, J.B. Encryption of 3D medical images based on a novel multiparameter cosine number transform. Comput. Biol. Med. 2020, 121, 103772. [Google Scholar] [CrossRef] [PubMed]
- Jirjees, S.W.; Yousif, N.A.; Hashim, A.T. Colour image privacy based on cascaded design of symmetric block cipher. J. Eng. Sci. Technol. 2022, 17, 2135–2156. [Google Scholar]
- Wang, X.; Çavuşoğlu, Ü.; Kacar, S.; Akgul, A.; Pham, V.-T.; Jafari, S.; Alsaadi, F.E.; Nguyen, X.Q. S-Box Based Image Encryption Application Using a Chaotic System without Equilibrium. Appl. Sci. 2019, 9, 781. [Google Scholar] [CrossRef] [Green Version]
- Gan, Z.H.; Chai, X.L.; Han, D.J.; Chen, Y.R. A chaotic image encryption algorithm based on 3-D bit-plane permutation. Neural Comput. Appl. 2019, 31, 7111–7130. [Google Scholar] [CrossRef]
- Hua, Z.; Zhu, Z.; Yi, S.; Zhang, Z.; Huang, H. Cross-plane colour image encryption using a two-dimensional logistic tent modular map. Inf. Sci. 2021, 546, 1063–1083. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L. A novel image encryption algorithm based on SPWLCM and DNA coding. Math. Comput. Simul. 2021, 190, 723–744. [Google Scholar] [CrossRef]
- Albahrani, E.A.; Maryoosh, A.A.; Lafta, S.H. Block image encryption based on modified playfair and chaotic system. J. Inf. Secur. Appl. 2020, 51, 102445. [Google Scholar] [CrossRef]
- Shengtao, G.; Tao, W.; Shida, W.; Xuncai, Z.; Ying, N. A novel image encryption algorithm based on chaotic sequences and cross-diffusion of bits. IEEE Photonics J. 2020, 13, 1–15. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, H.; Sun, J.; Zhang, H. An efficient multi-level encryption scheme for stereoscopic medical images based on coupled chaotic system and Otsu threshold segmentation. Comput. Biol. Med. 2022, 146, 105542. [Google Scholar] [CrossRef]
- Zheng, J.; Luo, Z.; Tang, Z. An image encryption algorithm based multichroic system and DNA coding. Discret. Dyn. Nat. Soc. 2020, 2020, 5982743. [Google Scholar] [CrossRef]








| Colour Image Size | Encryption | Decryption | ||
|---|---|---|---|---|
| Grayscale | Colour Image | Grayscale | Colour Image | |
| 256 × 256 | 0.0036 | 0.06 | 0.004 | 0.07 |
| 512 × 512 | 0.01 | 0.1 | 0.02 | 0.17 |
| 1024 × 1024 | 0.04 | 0.3 | 0.06 | 0.29 |
| Image | Colour | Plain Image | Cipher Image | ||||
|---|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal | ||
| Lena | Red | 0.9887 | 0.9947 | 0.9815 | −0.0004 | 0.0036 | −0.0035 |
| Green | 0.9892 | 0.995 | 0.9826 | −0.0026 | 0.0059 | 0.0019 | |
| Blue | 0.9793 | 0.9898 | 0.9668 | −0.0007 | 0.0056 | −0.0004 | |
| Baboon | Red | 0.99 | 0.0083 | 0.9744 | −0.0037 | 0.0071 | −0.0027 |
| Green | 0.9971 | 0.9966 | 0.9909 | −0.0029 | 0.0073 | −0.0028 | |
| Letter A | Red | 0.9493 | 0.9656 | 0.9185 | −0.0013 | 0.0051 | −0.0030 |
| Green | 0.9493 | 0.9656 | 0.9185 | −0.0005 | 0.009 | −0.0008 | |
| Blue | 0.9493 | 0.9656 | 0.9185 | 0.0027 | 0.0086 | −0.0015 | |
| Image | Original | Encrypted | ||||
|---|---|---|---|---|---|---|
| Red | Green | Blue | Red | Green | Blue | |
| Lena | 7.2865 | 7.5592 | 7.0527 | 7.9981 | 7.998 | 7.9978 |
| Baboon | 7.6202 | 7.3139 | 7.6277 | 7.9981 | 7.998 | 7.9981 |
| Letter A | 1.1608 | 1.1608 | 1.1608 | 7.9973 | 7.9973 | 7.9973 |
| Image | NPCR | UACI | ||||
|---|---|---|---|---|---|---|
| Red | Green | Blue | Red | Green | Blue | |
| Lena | 99.21 | 99.3 | 99.11 | 33.38 | 33.41 | 33.49 |
| Baboon | 98.98 | 98.94 | 98.91 | 32.31 | 32.28 | 32.29 |
| Letter A | 99.6 | 99.6 | 99.6 | 33.46 | 33.46 | 33.46 |
| Scheme | Image | Entropy | NPCR | UACI | Correlation | ||
|---|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | |||||
| Ref. [22] | Baboon | 7.9992 | 99.6174 | 33.392 | 0.0049 | −0.0026 | 0.0068 |
| Ref. [39] | Baboon | 7.9986 | 99.167 | 33.326 | 0.0021 | −0.0159 | −0.0017 |
| Ref. [42] | Baboon | 7.9971 | 99.596 | 33.459 | 0.6578 | 0.7301 | 0.6387 |
| Proposed | Baboon | 7.9980 | 99.352 | 33.453 | −0.0037 | 0.0071 | −0.0027 |
| Ref. [30] | Lena | 7.9995 | 99.680 | 33.120 | 0.0045 | 0.0016 | 0.0017 |
| Ref. [38] | Lena | 7.9969 | 99.624 | 33.502 | 0.0040 | −0.0012 | −0.0021 |
| Ref. [40] | Lena | 7.9023 | 99.606 | 33.444 | −0.0020 | −0.0065 | 0.0087 |
| Proposed | Lena | 7.9980 | 99.252 | 33.455 | −0.0004 | 0.0036 | −0.0035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jirjees, S.W.; Alkalid, F.F.; Shareef, W.F. Image Encryption Using Dynamic Image as a Key Based on Multilayers of Chaotic Permutation. Symmetry 2023, 15, 409. https://doi.org/10.3390/sym15020409
Jirjees SW, Alkalid FF, Shareef WF. Image Encryption Using Dynamic Image as a Key Based on Multilayers of Chaotic Permutation. Symmetry. 2023; 15(2):409. https://doi.org/10.3390/sym15020409
Chicago/Turabian StyleJirjees, Seerwan W., Farah F. Alkalid, and Waleed F. Shareef. 2023. "Image Encryption Using Dynamic Image as a Key Based on Multilayers of Chaotic Permutation" Symmetry 15, no. 2: 409. https://doi.org/10.3390/sym15020409
APA StyleJirjees, S. W., Alkalid, F. F., & Shareef, W. F. (2023). Image Encryption Using Dynamic Image as a Key Based on Multilayers of Chaotic Permutation. Symmetry, 15(2), 409. https://doi.org/10.3390/sym15020409







