Vacuum Polarization of a Quantized Scalar Field in the Thermal State on the Short Throat Wormhole Background
Abstract
1. Introduction
2. Non-Renormalized Expression
2.1. Contribution
2.2. Contribution
2.3. General Expression
3. Renormalization and the Result
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Sushkov, S. A selfconsistent semiclassical solution with a throat in the theory of gravity. Phys. Lett. A 1992, 164, 33–37. [Google Scholar] [CrossRef]
- Hochberg, D.; Popov, A.; Sushkov, S.V. Self-Consistent Wormhole Solutions of Semiclassical Gravity. Phys. Rev. Lett. 1997, 78, 2050–2053. [Google Scholar] [CrossRef]
- Popov, A.A. Long throat of a wormhole created from vacuum fluctuations. Class. Quantum Gravity 2005, 22, 5223. [Google Scholar] [CrossRef]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Mamaev, S.G.; Mostepanenko, V.M. Isotropic cosmological models determined by vacuum quantum effects. J. Exp. Theor. Phys. 1980, 51, 20–27. [Google Scholar]
- Kofman, L.; Sakhni, V.; Starobinskii, A.A. Anisotropic cosmological model created by quantum polarization of vacuum. J. Exp. Theor. Phys. 1983, 85, 1876–1886. [Google Scholar]
- Kofman, L.; Sahni, V. A new self-consistent solution of the Einstein equations with one-loop quantum-gravitational corrections. Phys. Lett. B 1983, 127, 197–200. [Google Scholar] [CrossRef]
- Sahni, V.; Kofman, L. Some self-consistent solutions of the Einstein equations with one-loop quantum gravitational corrections: Gik = 8πG〈Tik〉vac. Phys. Lett. A 1986, 117, 275–278. [Google Scholar] [CrossRef]
- Anderson, P.R.; Hiscock, W.A.; Samuel, D.A. Stress-energy tensor of quantized scalar fields in static spherically symmetric spacetimes. Phys. Rev. D 1995, 51, 4337–4358. [Google Scholar] [CrossRef]
- Howard, K.W.; Candelas, P. Quantum Stress Tensor in Schwarzschild Space-Time. Phys. Rev. Lett. 1984, 53, 403–406. [Google Scholar] [CrossRef]
- Candelas, P. Vacuum polarization in Schwarzschild spacetime. Phys. Rev. D 1980, 21, 2185–2202. [Google Scholar] [CrossRef]
- Fawcett, M.S. The energy-momentum tensor near a black hole. Commun. Math. Phys. 1983, 89, 103–115. [Google Scholar] [CrossRef]
- Jensen, B.P.; Ottewill, A. Renormalized electromagnetic stress tensor in Schwarzschild spacetime. Phys. Rev. D 1989, 39, 1130–1138. [Google Scholar] [CrossRef]
- Jensen, B.P.; Mc Laughlin, J.G.; Ottewill, A.C. Anisotropy of the quantum thermal state in schwarzschild space-time. Phys. Rev. D 1992, 45, 3002–3005. [Google Scholar] [CrossRef]
- Anderson, P.R.; Hiscock, W.A.; Loranz, D.J. Semiclassical Stability of the Extreme Reissner-Nordström Black Hole. Phys. Rev. Lett. 1995, 74, 4365–4368. [Google Scholar] [CrossRef] [PubMed]
- Bezerra de Mello, E.R.; Bezerra, V.B.; Khusnutdinov, N.R. Vacuum polarization of a massless spinor field in global monopole spacetime. Phys. Rev. D 1999, 60, 063506. [Google Scholar] [CrossRef]
- Frolov, V.; Zel’nikov, A. Vacuum polarization by a massive scalar field in Schwarzschild spacetime. Phys. Lett. B 1982, 115, 372–374. [Google Scholar] [CrossRef]
- Frolov, V.; Zel’nikov, A. Vacuum polarization of massive fields in Kerr spacetime. Phys. Lett. B 1983, 123, 197–199. [Google Scholar] [CrossRef]
- Frolov, V.P.; Zel’nikov, A.I. Vacuum polarization of massive fields near rotating black holes. Phys. Rev. D 1984, 29, 1057–1066. [Google Scholar] [CrossRef]
- Herman, R. Method for calculating the imaginary part of the Hadamard elementary function G(1) in static, spherically symmetric spacetimes. Phys. Rev. D 1998, 58, 084028. [Google Scholar] [CrossRef]
- Matyjasek, J. Stress-energy tensor of neutral massive fields in Reissner-Nordström spacetime. Phys. Rev. D 2000, 61, 124019. [Google Scholar] [CrossRef]
- Koyama, H.; Nambu, Y.; Tomimatsu, A. Vacuum Polarization of Massive Scalar Fields on the Black Hole Horizon. Mod. Phys. Lett. A 2000, 15, 815–824. [Google Scholar] [CrossRef]
- Matyjasek, J. Vacuum polarization of massive scalar fields in the spacetime of an electrically charged nonlinear black hole. Phys. Rev. D 2001, 63, 084004. [Google Scholar] [CrossRef]
- Nakazawa, N.; Fukuyama, T. On the energy-momentum tensor at finite temperature in curved space-time. Nucl. Phys. B 1985, 252, 621–634. [Google Scholar] [CrossRef]
- Christensen, S.M. Vacuum expectation value of the stress tensor in an arbitrary curved background: The covariant point-separation method. Phys. Rev. D 1976, 14, 2490–2501. [Google Scholar] [CrossRef]
- Christensen, S.M. Regularization, renormalization, and covariant geodesic point separation. Phys. Rev. D 1978, 17, 946–963. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Bezerra de Mello, E.R.; Khusnutdinov, N.R.; Sushkov, S.V. Vacuum stress-energy tensor of a massive scalar field in a wormhole spacetime. Phys. Rev. D 2010, 81, 084034. [Google Scholar] [CrossRef]
- Bateman, H.; Erdélyi, A. Higher Transcendental Functions; California Institute of Technology, Bateman Manuscript Project, McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Frolov, V.P.; Zel’nikov, A.I. Killing approximation for vacuum and thermal stress-energy tensor in static space-times. Phys. Rev. D 1987, 35, 3031–3044. [Google Scholar] [CrossRef]
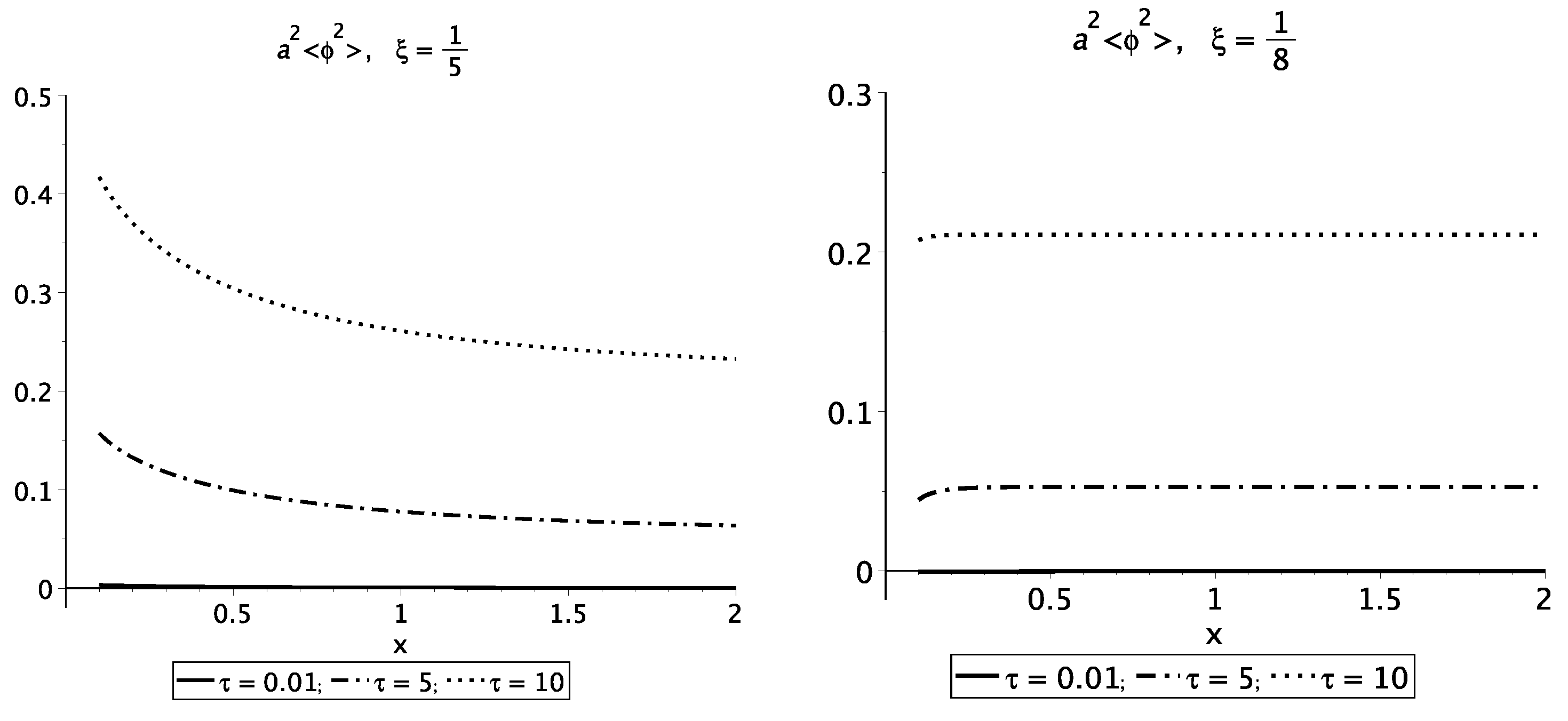
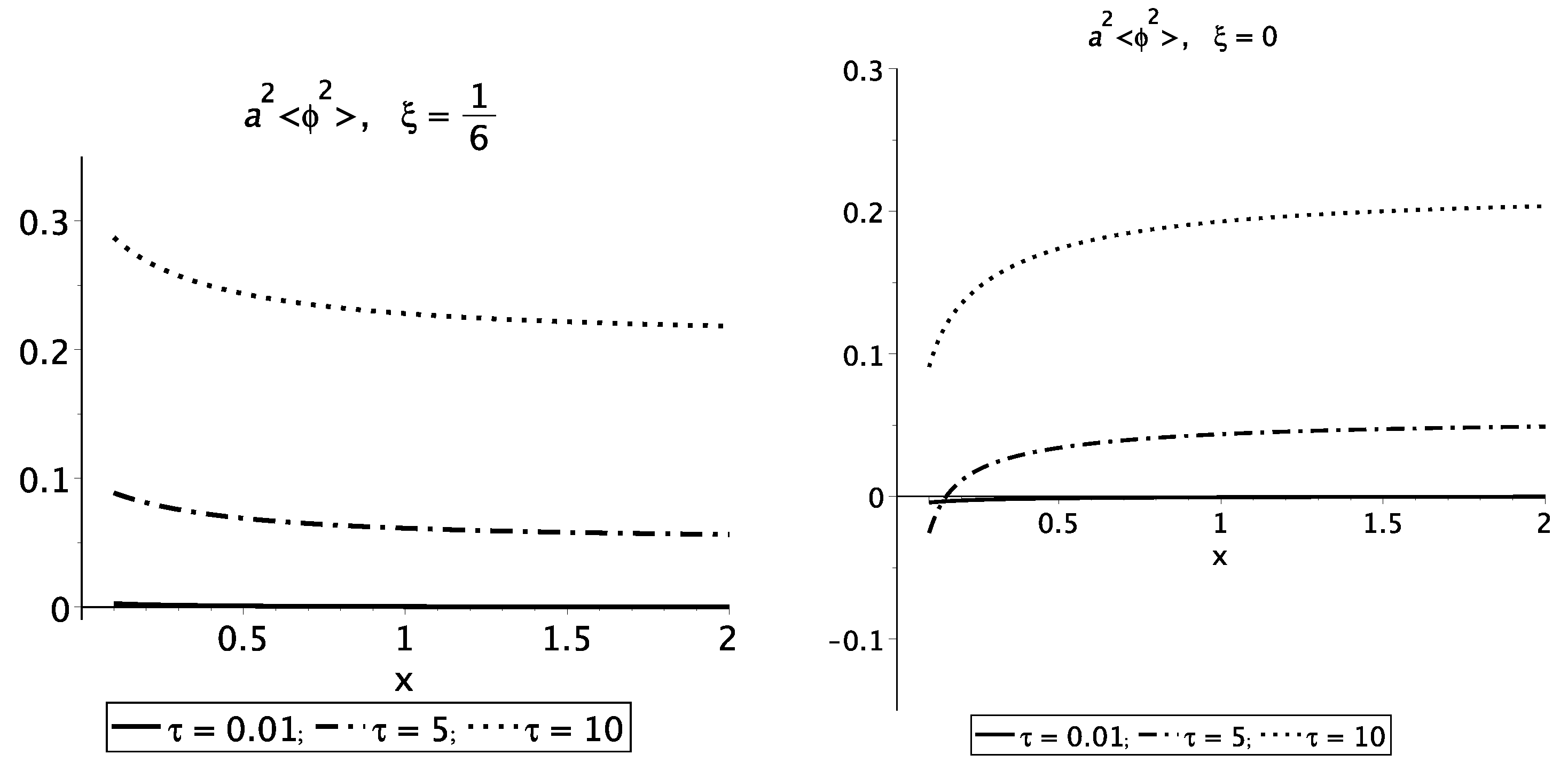
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisenkov, D.; Popov, A. Vacuum Polarization of a Quantized Scalar Field in the Thermal State on the Short Throat Wormhole Background. Symmetry 2023, 15, 426. https://doi.org/10.3390/sym15020426
Lisenkov D, Popov A. Vacuum Polarization of a Quantized Scalar Field in the Thermal State on the Short Throat Wormhole Background. Symmetry. 2023; 15(2):426. https://doi.org/10.3390/sym15020426
Chicago/Turabian StyleLisenkov, Dmitriy, and Arkady Popov. 2023. "Vacuum Polarization of a Quantized Scalar Field in the Thermal State on the Short Throat Wormhole Background" Symmetry 15, no. 2: 426. https://doi.org/10.3390/sym15020426
APA StyleLisenkov, D., & Popov, A. (2023). Vacuum Polarization of a Quantized Scalar Field in the Thermal State on the Short Throat Wormhole Background. Symmetry, 15(2), 426. https://doi.org/10.3390/sym15020426





