Research on Control Strategy of Electro-Hydraulic Lifting System Based on AMESim and MATLAB
Abstract
:1. Introduction
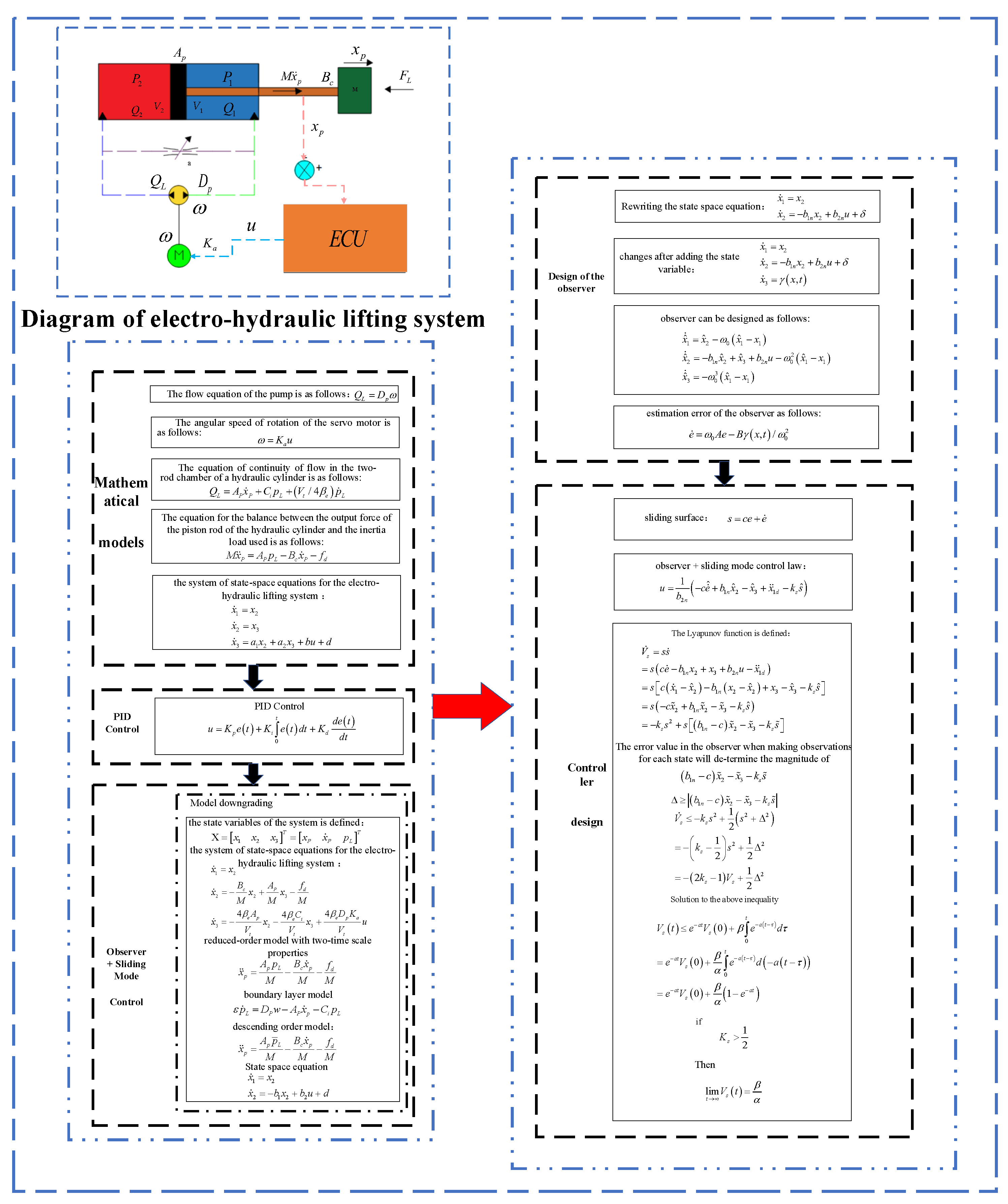
2. Electro-Hydraulic Lifting System Structure and Working Principle
3. Mathematical Models and Control Strategy
3.1. Mathematical Models
3.2. Electro-Hydraulic Lifting System Control Strategy
3.2.1. Conventional PID Control
3.2.2. Observer–Sliding Mode Control
- (1)
- Model downgrading
- (2)
- Controller design
- ①
- Design of the observer [25]:
- ②
- Controller design
4. Simulation and Test Studies
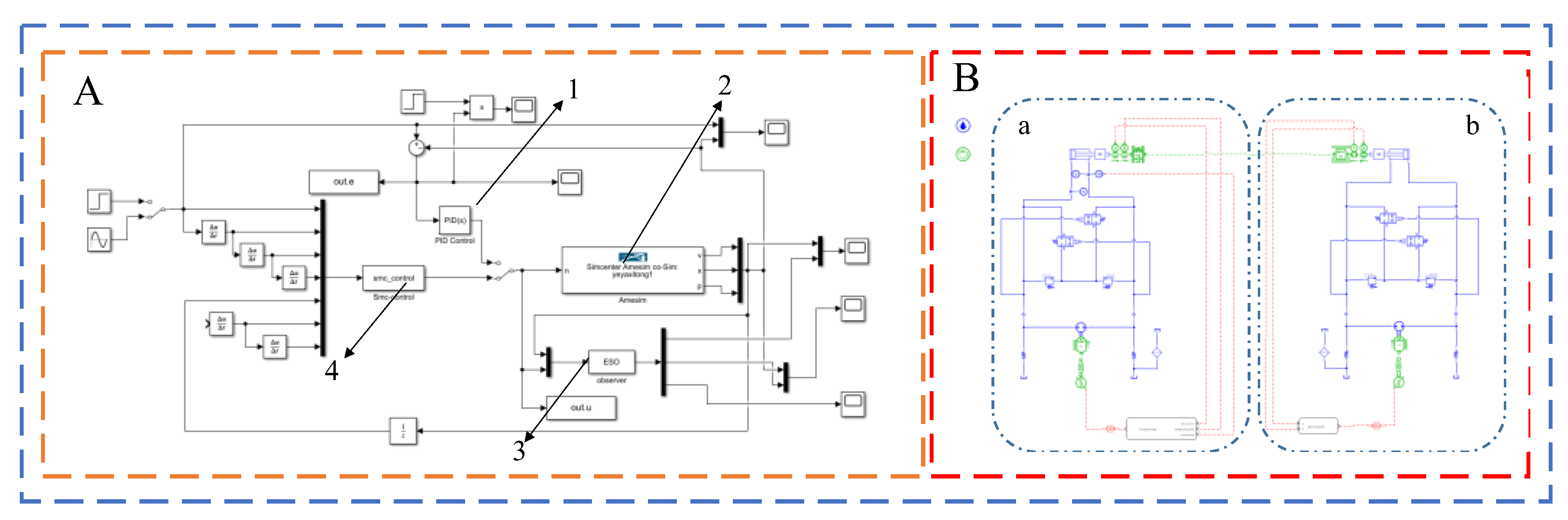
4.1. Simulation and Experimental Principles
4.2. Simulation Studies
4.3. Test Studies
5. Results
5.1. Analysis under Constant Load Conditions
5.1.1. PID Parameter Optimization Analysis under Constant Load Conditions
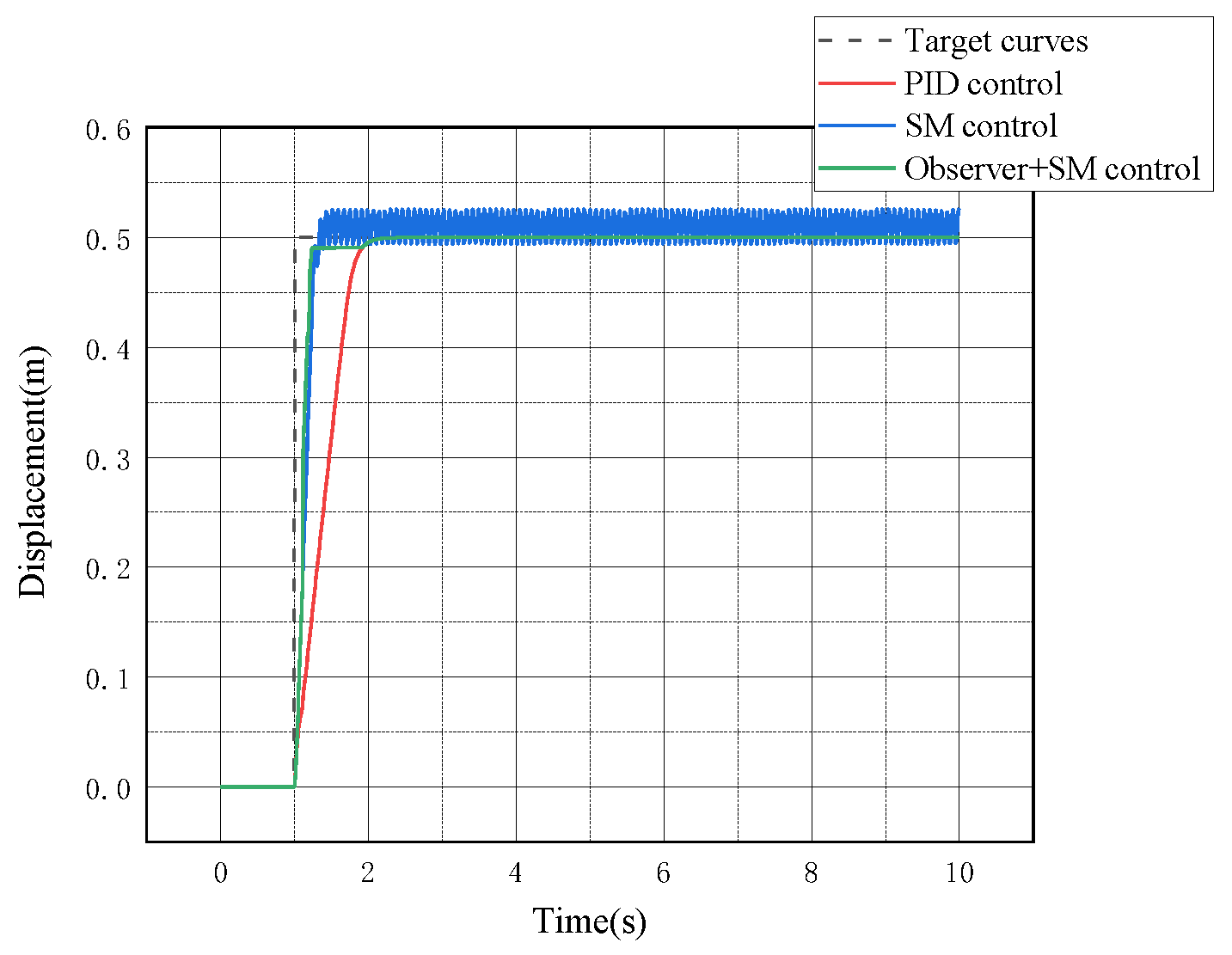
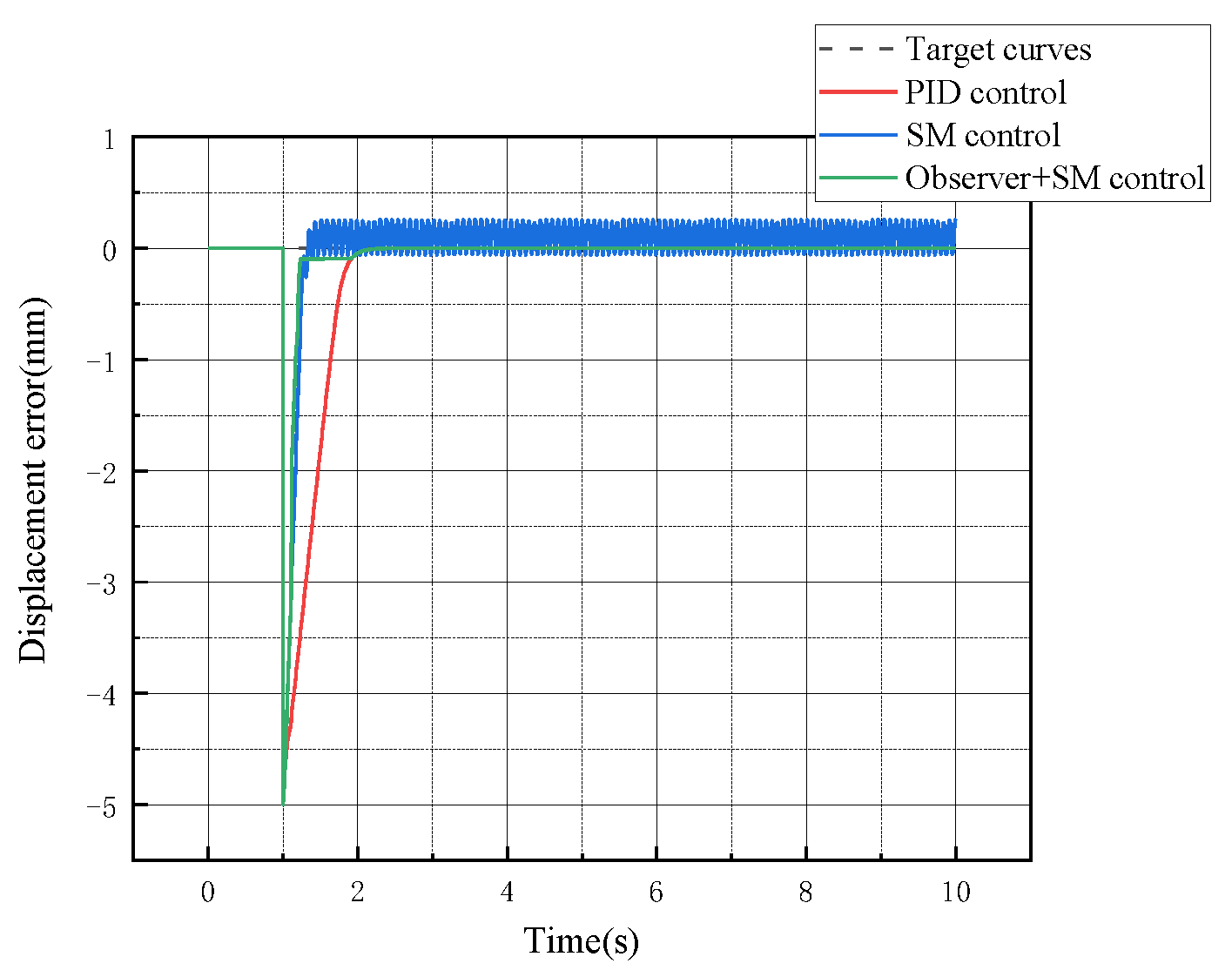
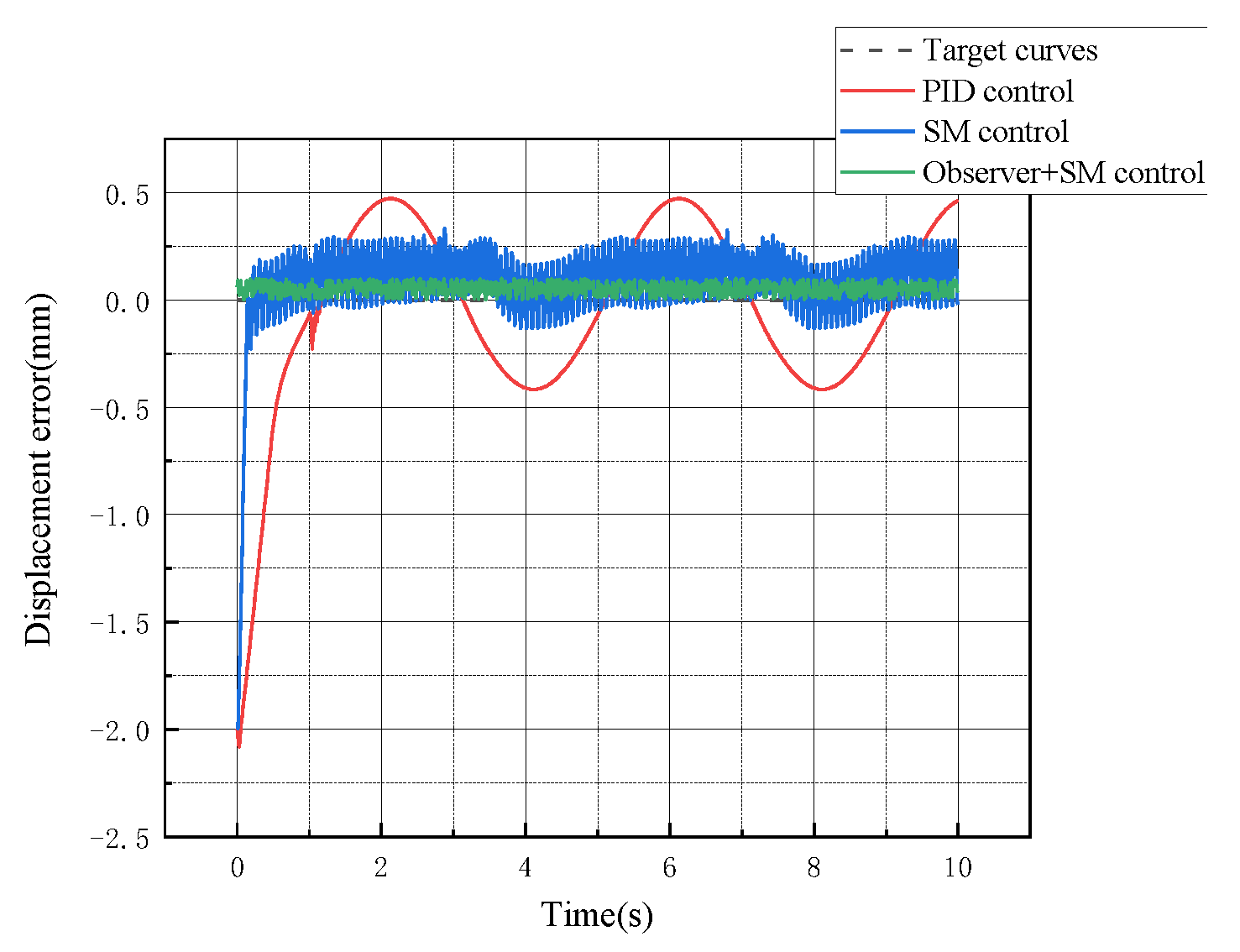
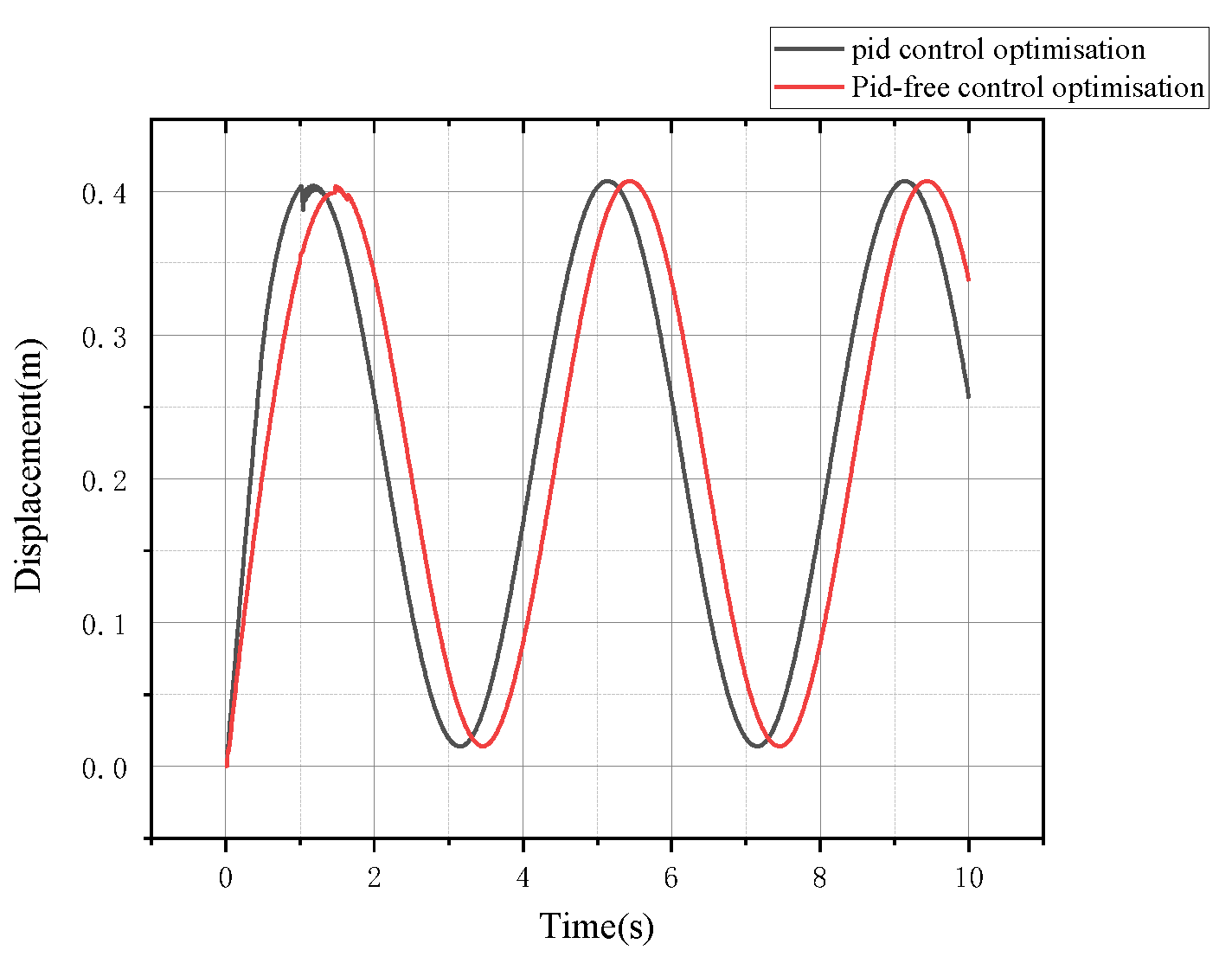
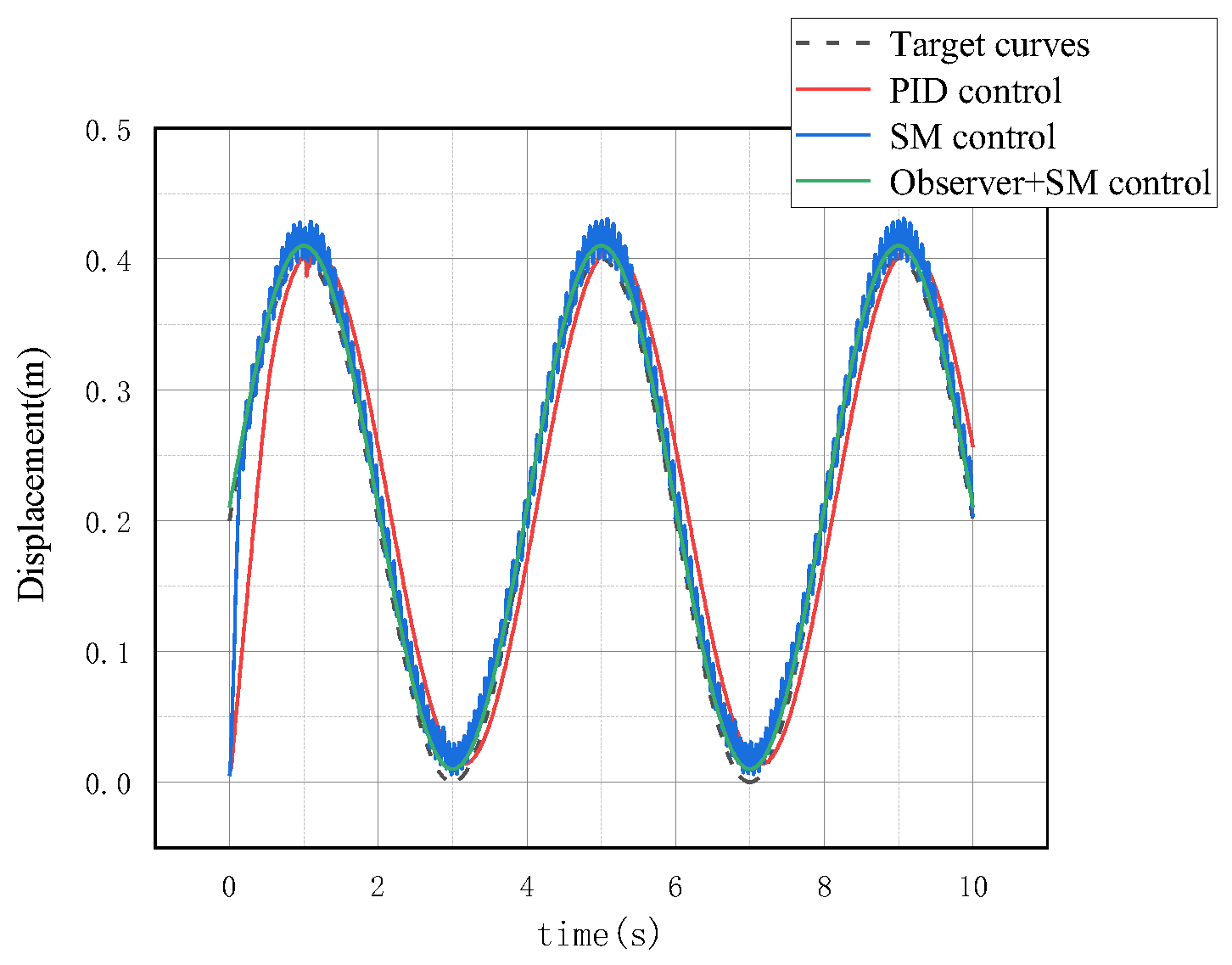
5.1.2. System Displacement Curve Analysis
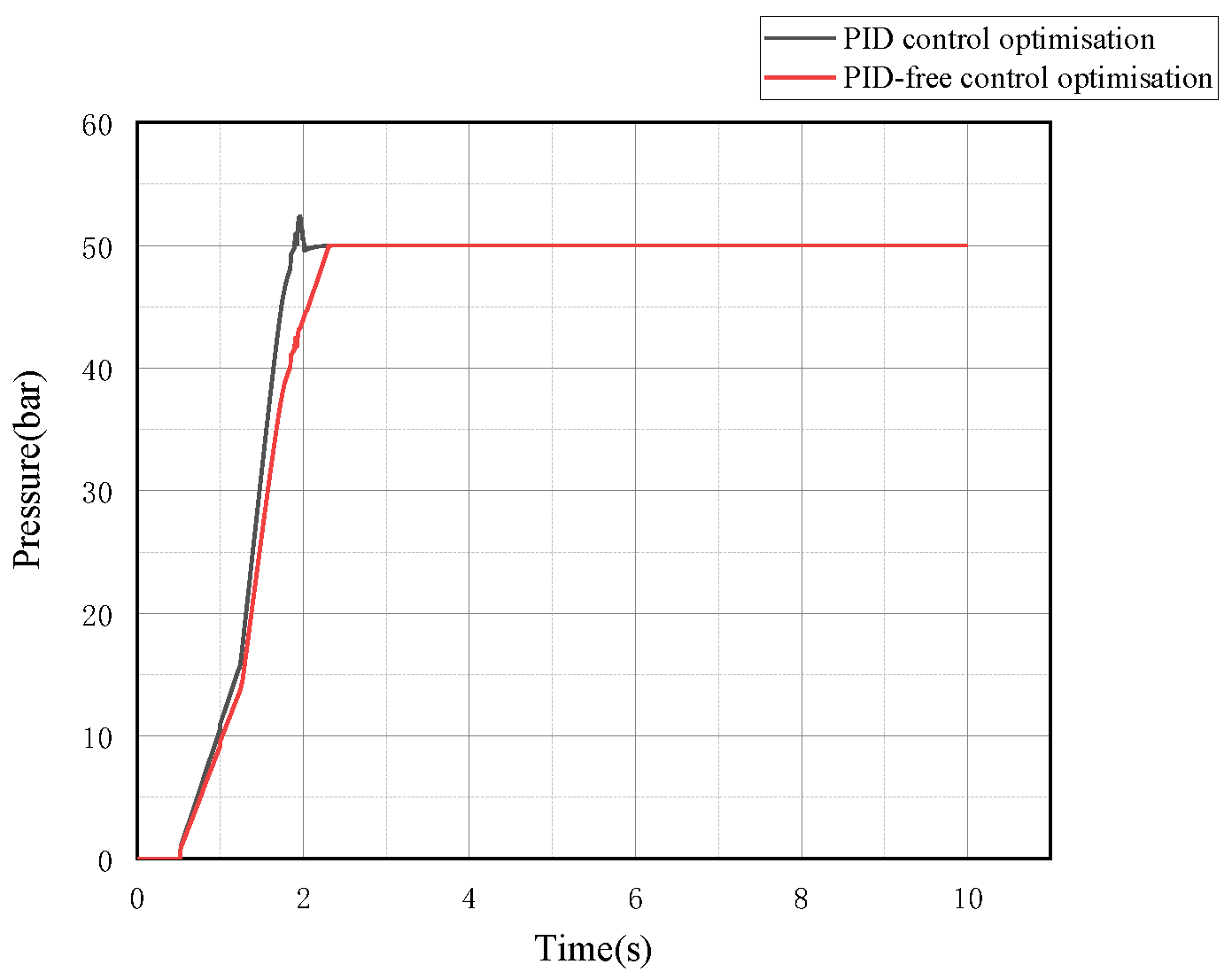
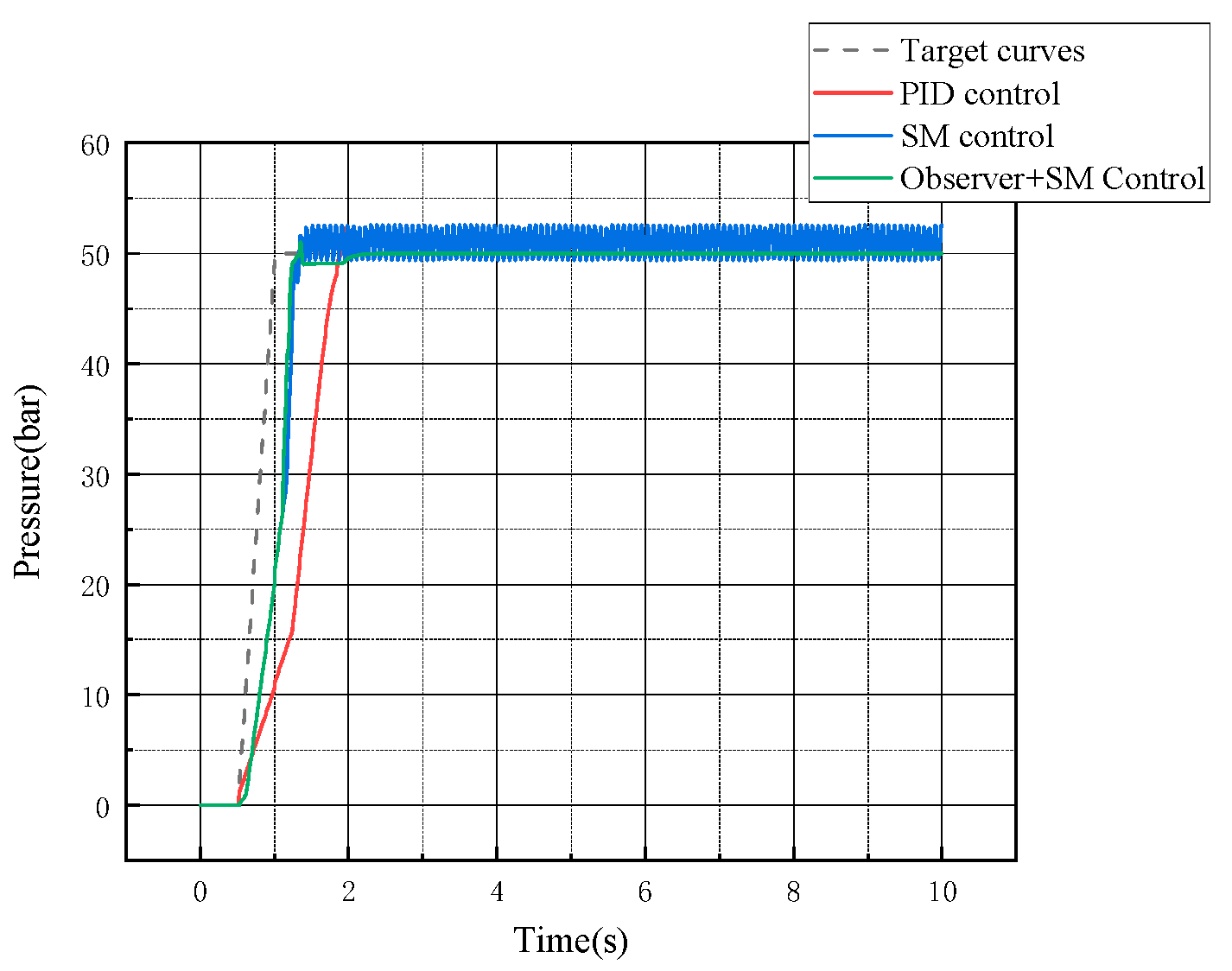
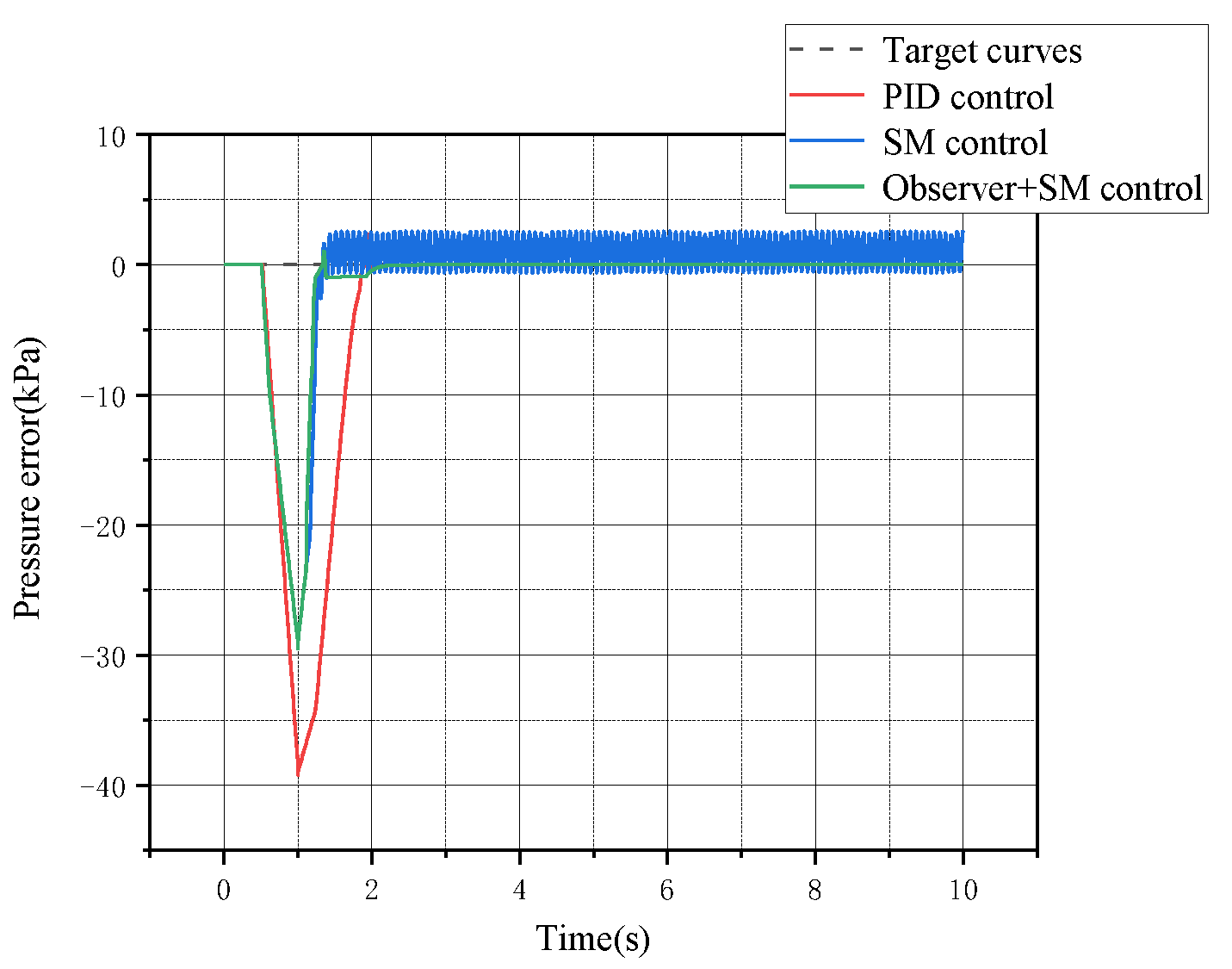
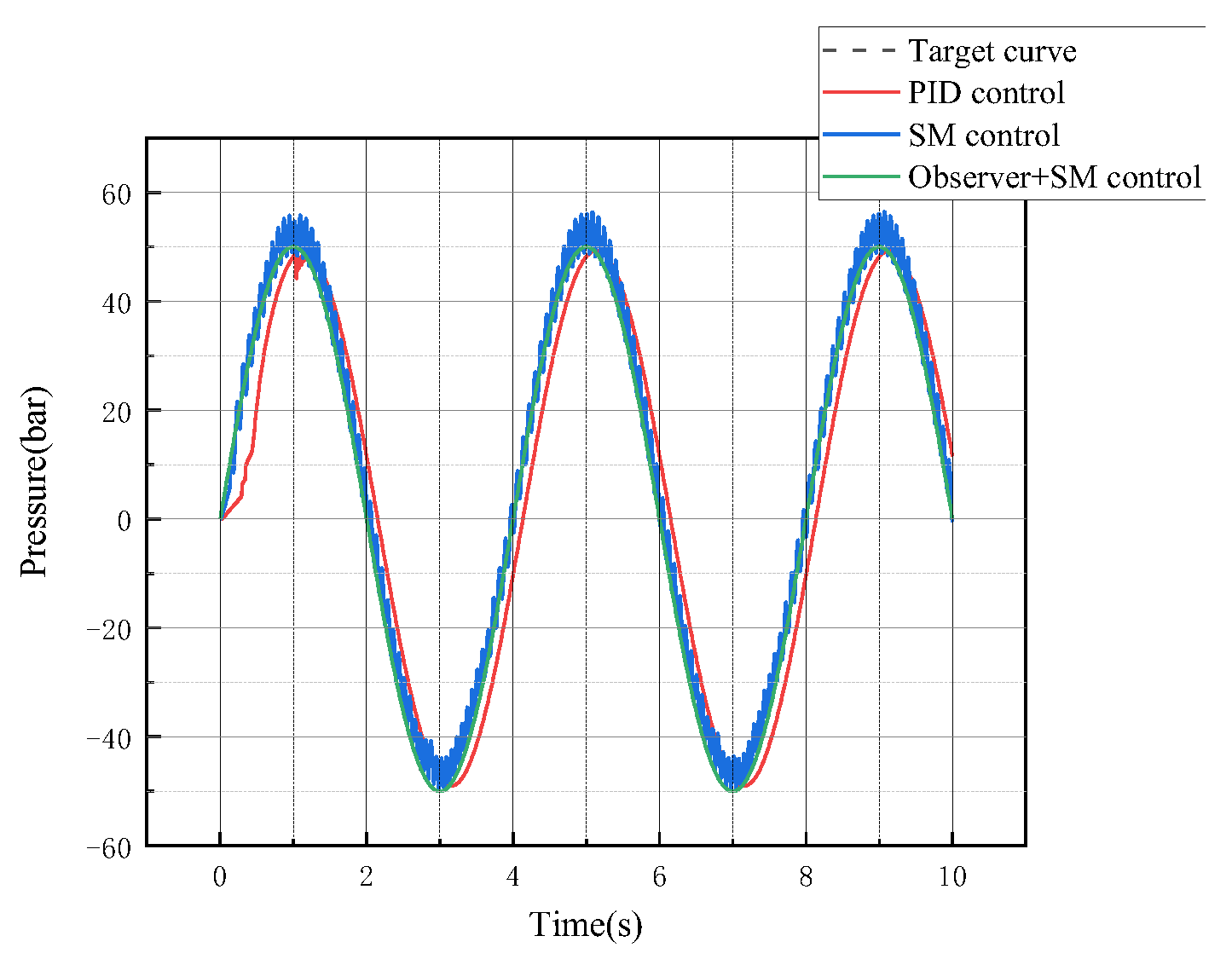
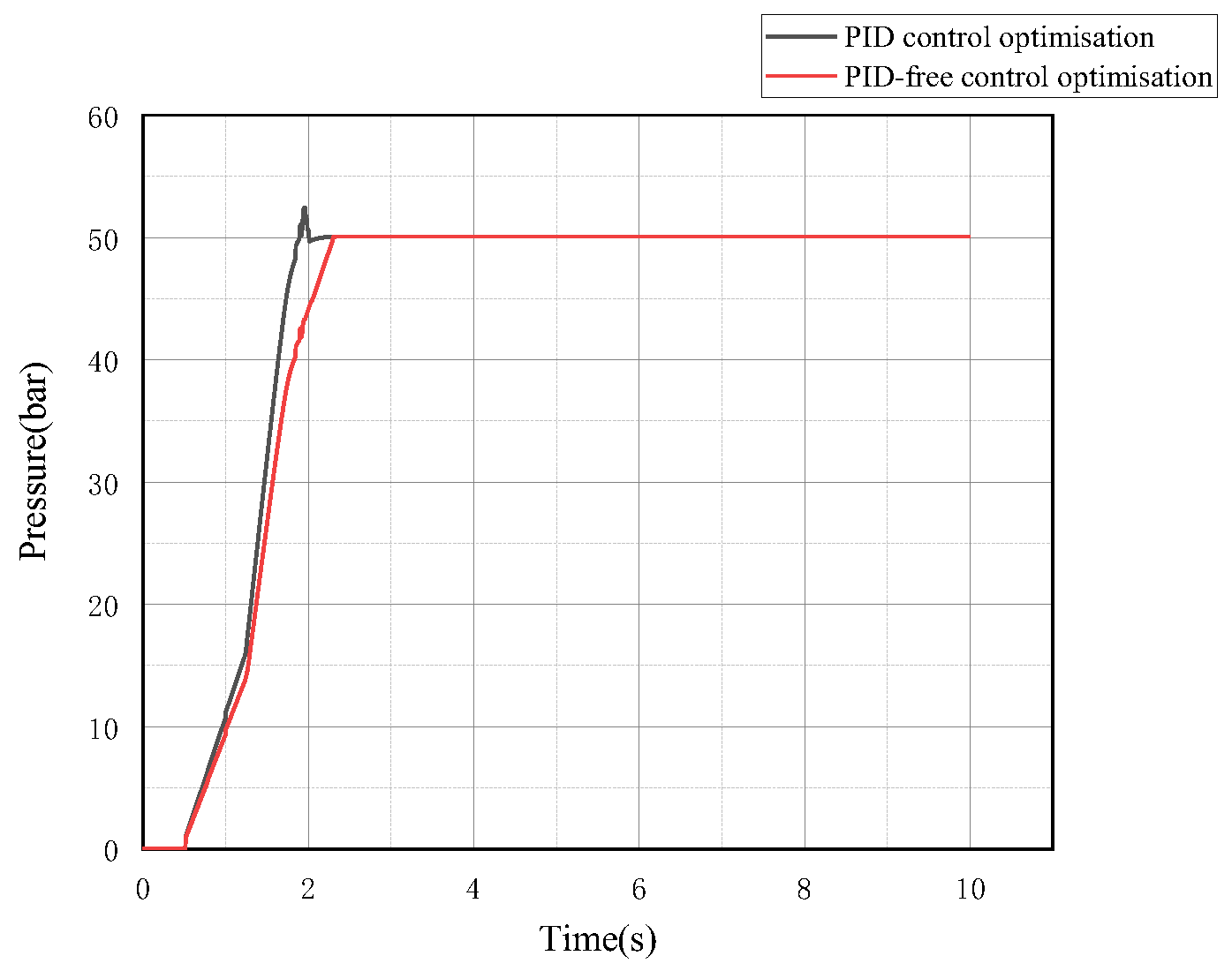
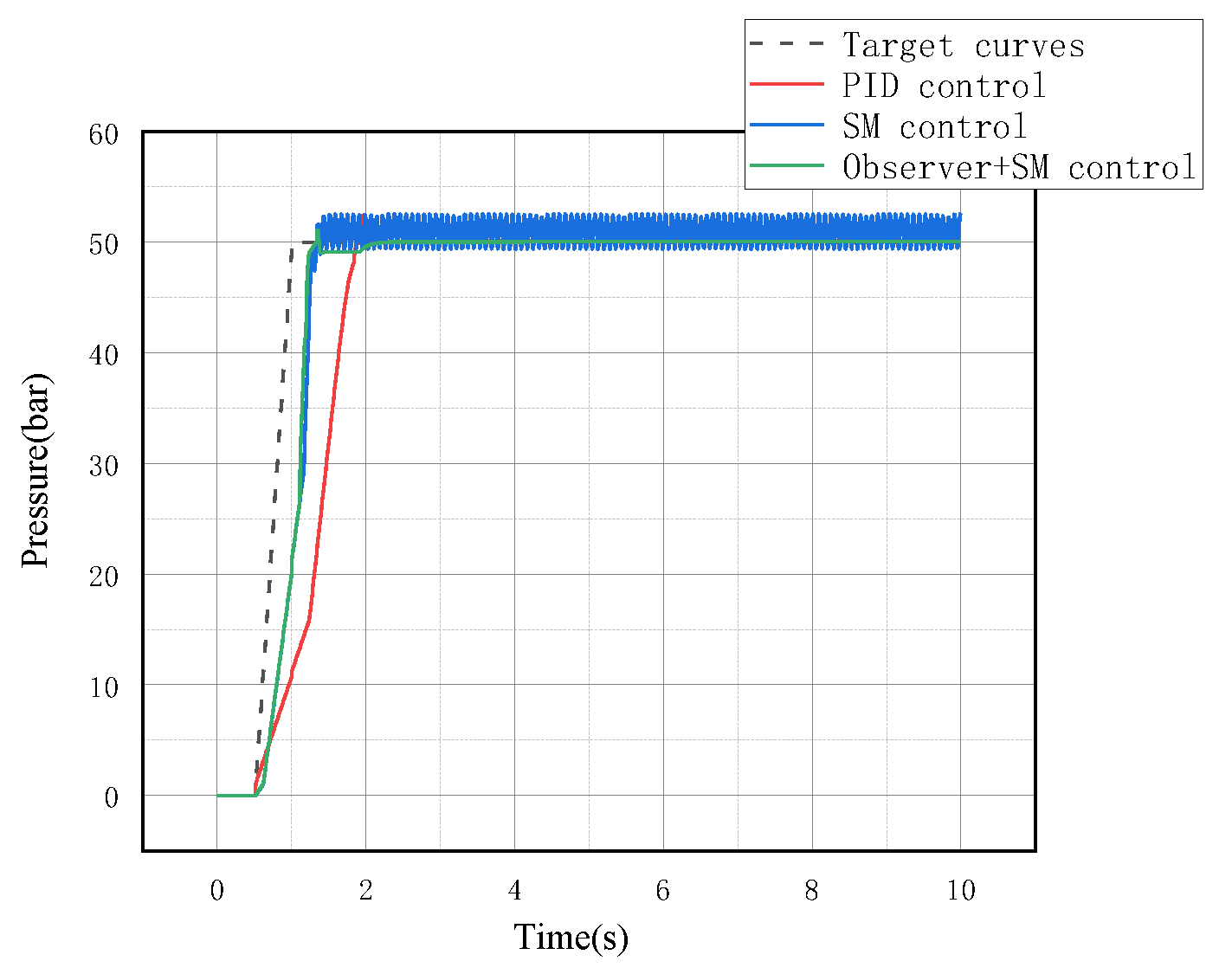
5.1.3. System Pressure Curve Analysis
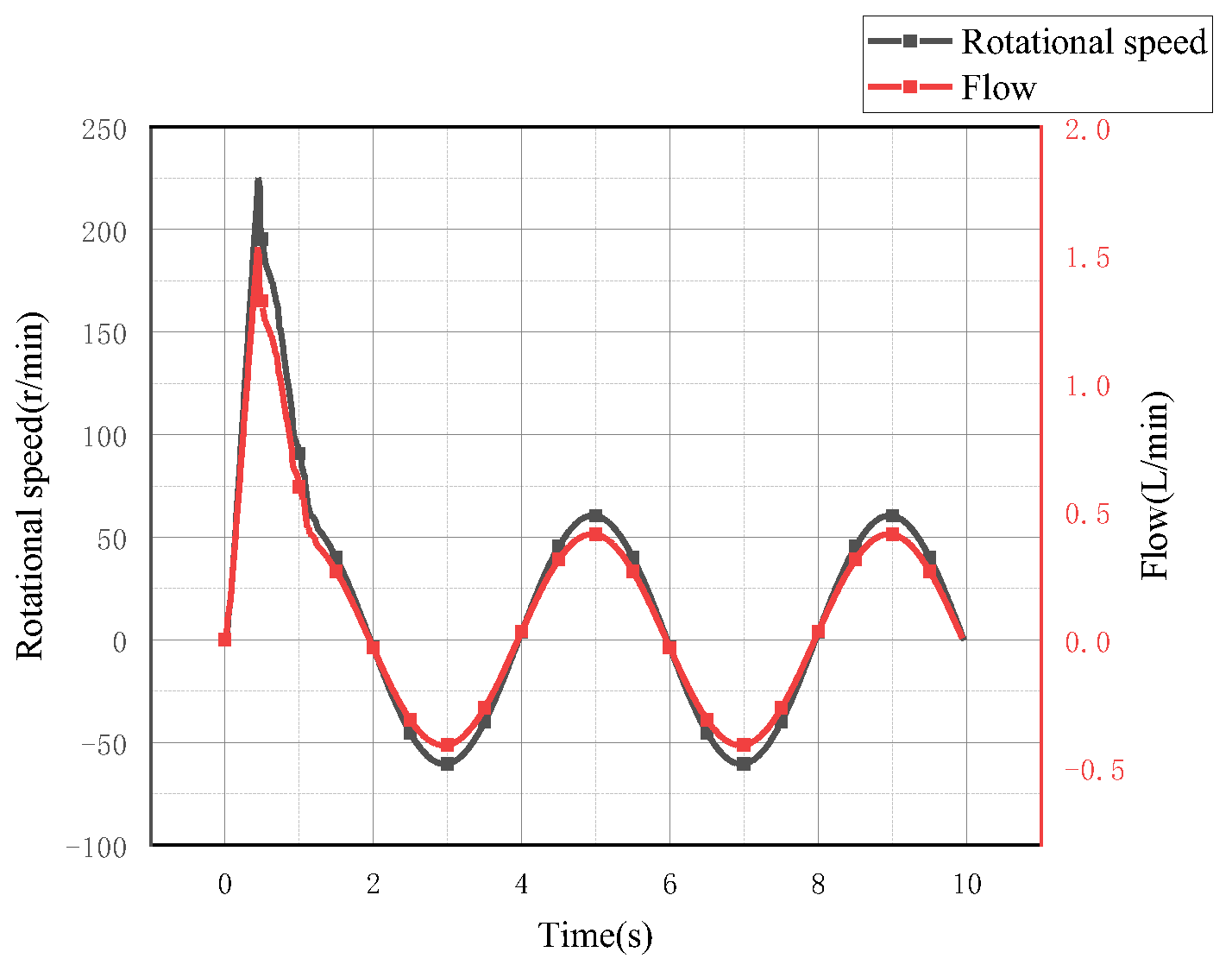
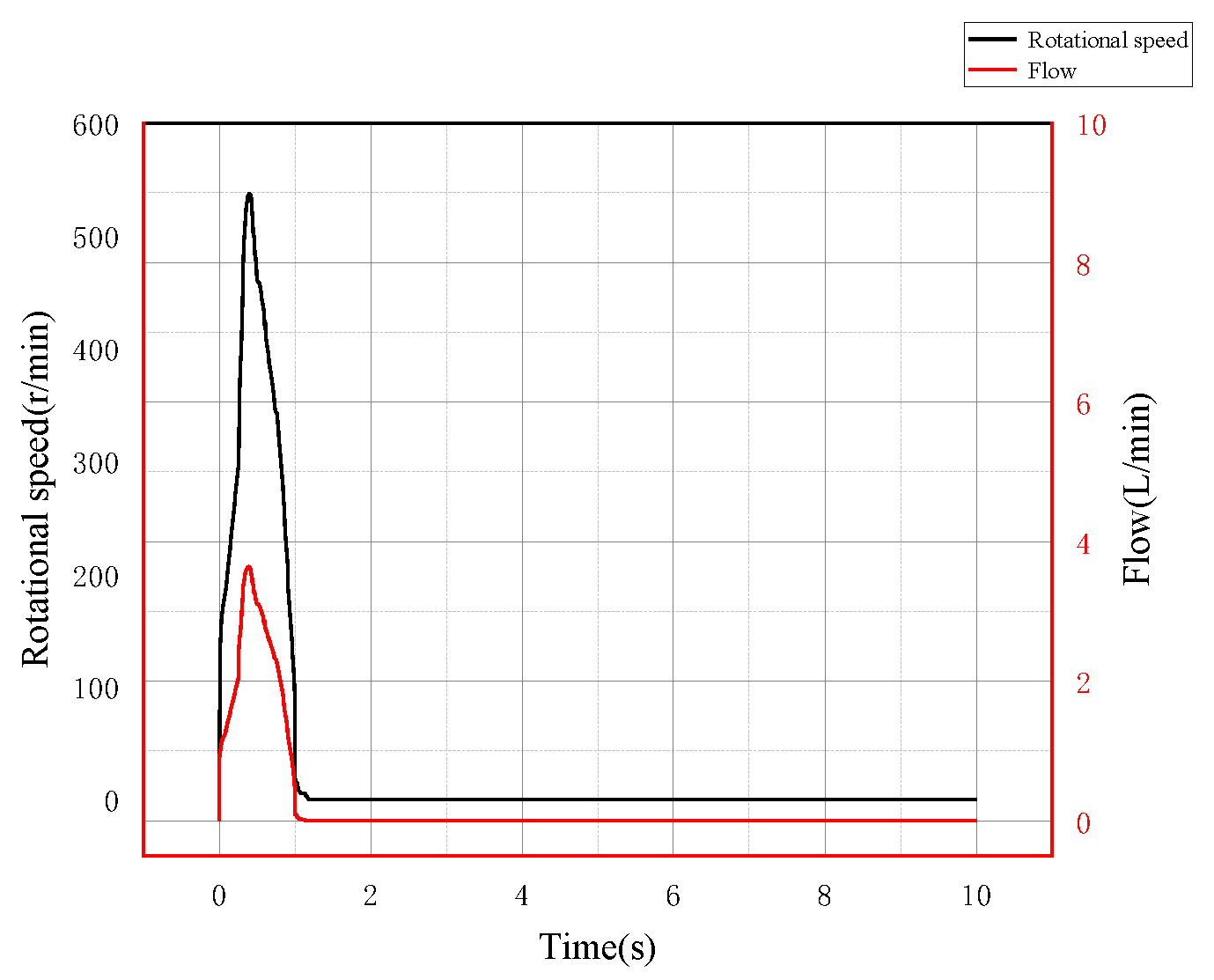
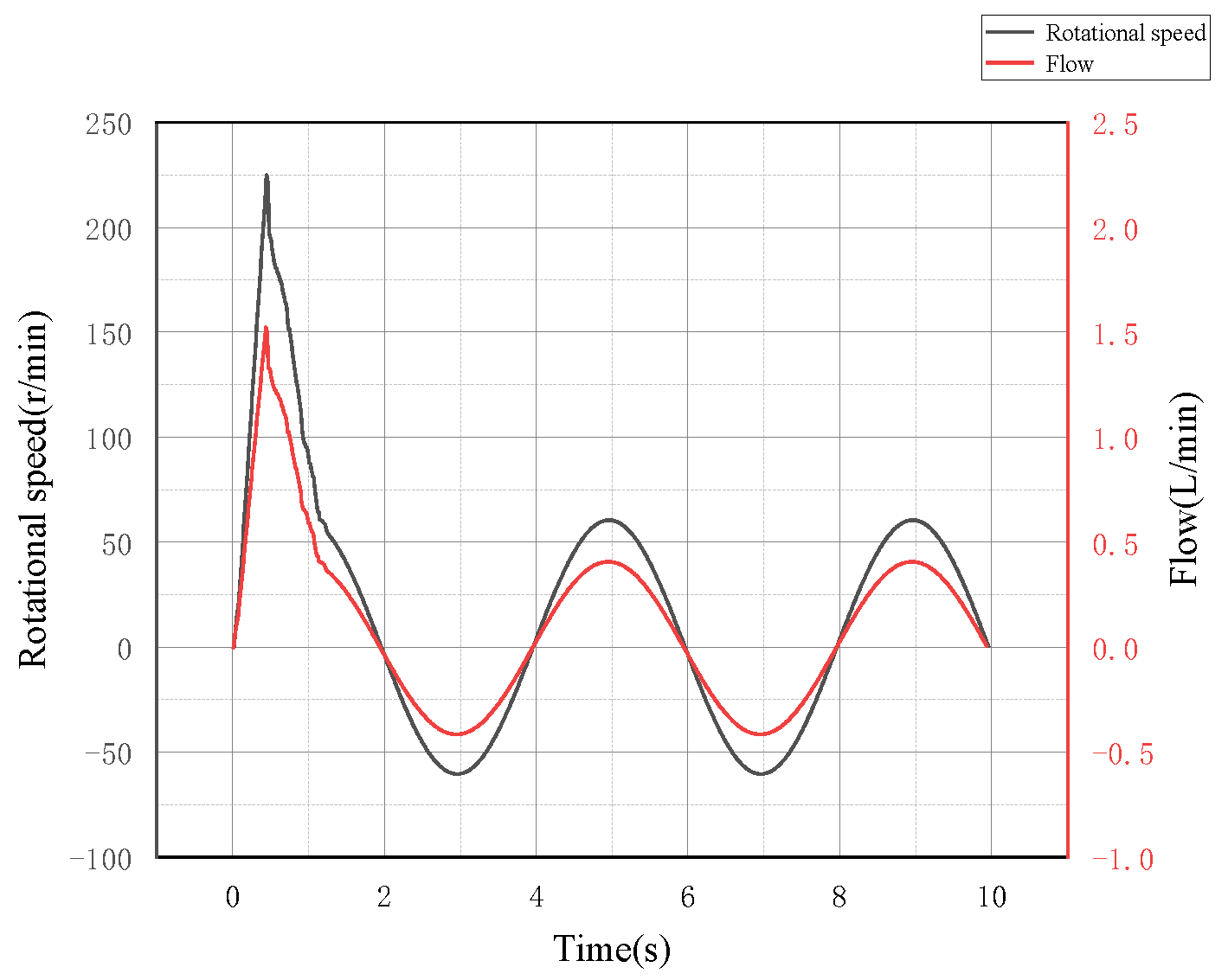
5.1.4. System Speed and Flow Analysis
5.2. Analysis under Variable Load Conditions
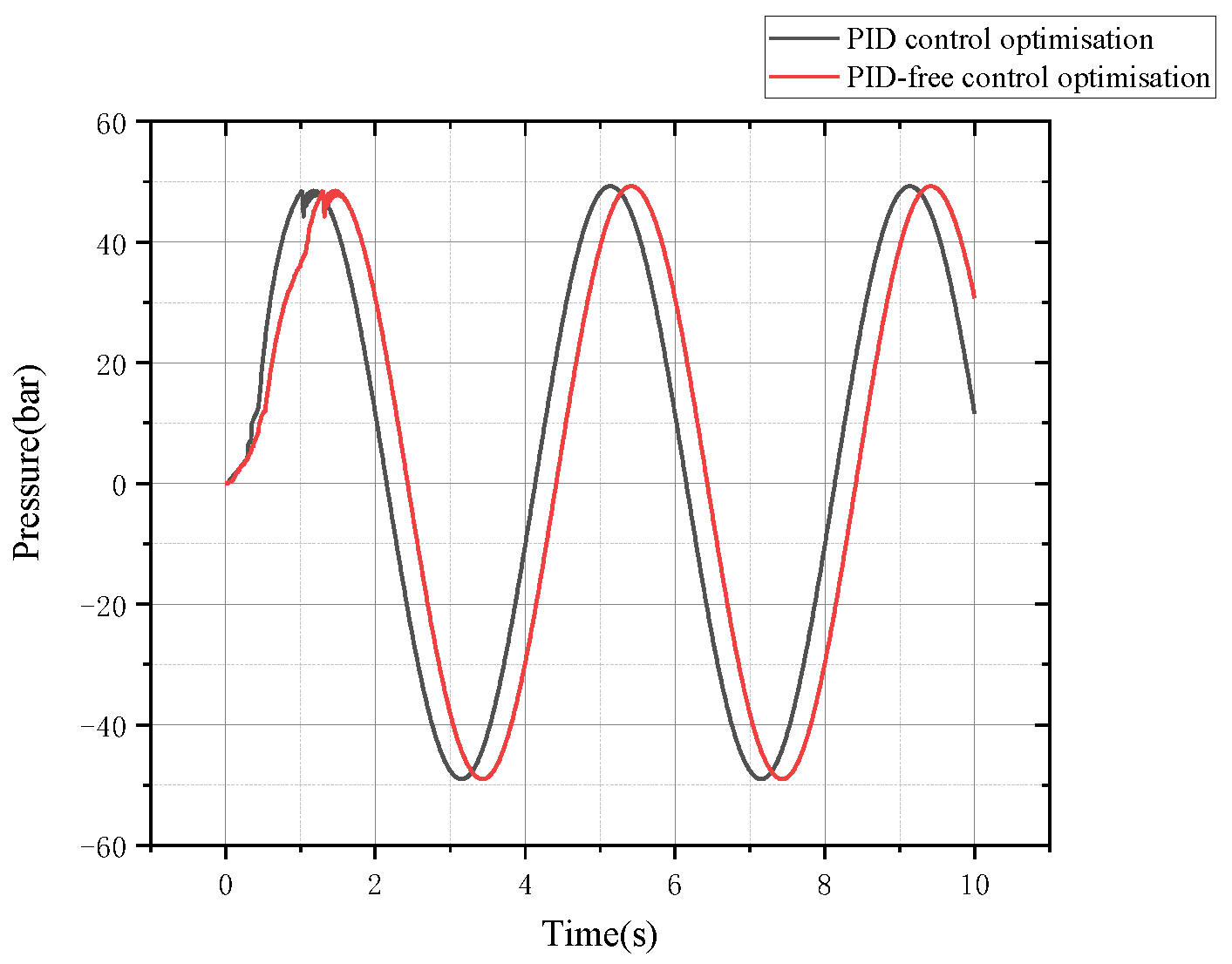
5.2.1. PID Parameter Optimization Analysis in Variable Load Conditions
5.2.2. System Displacement Curve Analysis
5.2.3. System Pressure Curve Analysis
5.2.4. System Speed and Flow Analysis
5.3. Test Validation Results
5.3.1. Test Validation of PID Parameter Optimization in Constant Target Tillage Depth Values
5.3.2. Test Results for Constant Target Tillage Depth Values
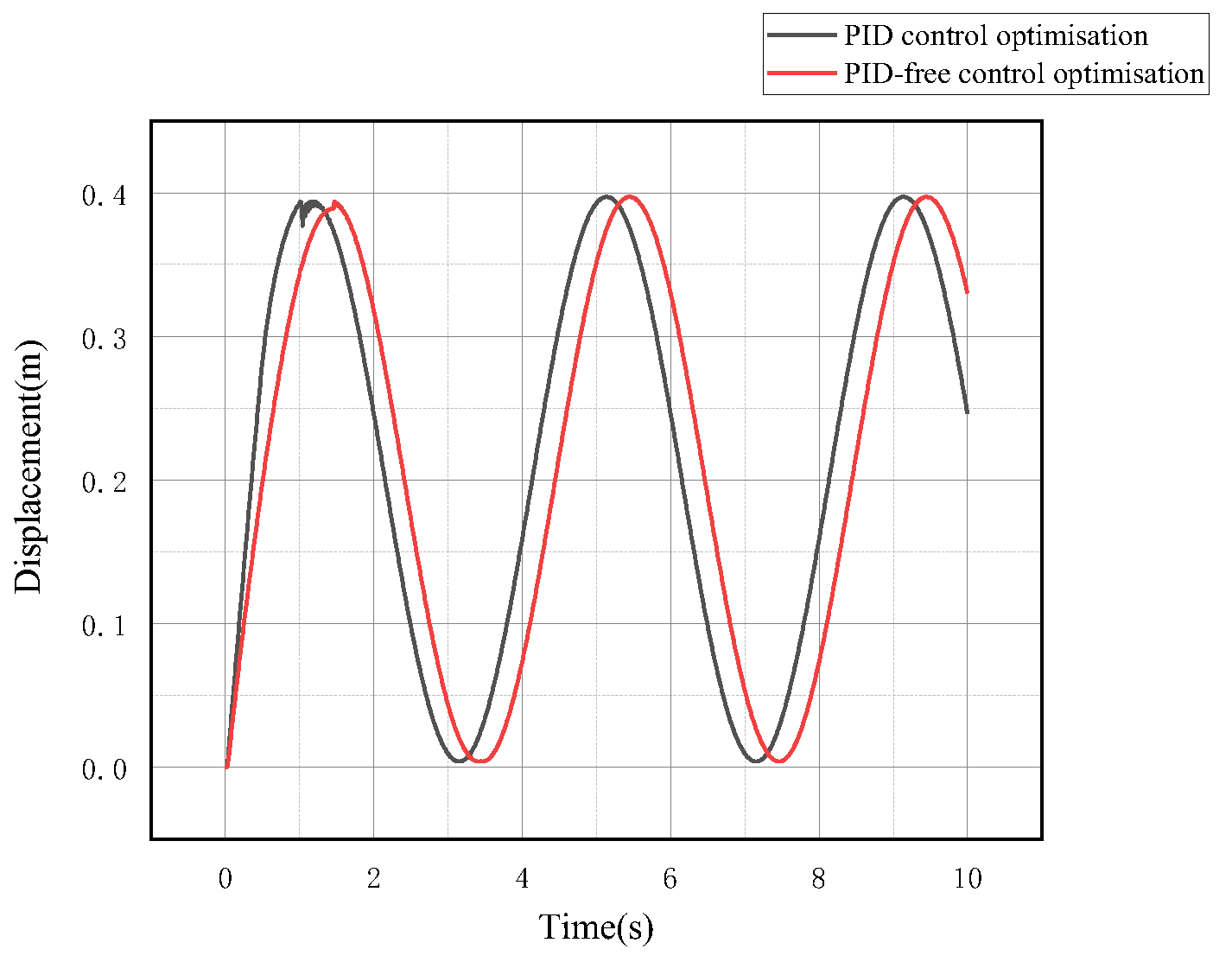
5.3.3. Test Validation of PID Parameter Optimization in Continuously Varying Target Tillage Depth Values
5.3.4. Test Results for Continuously Varying Target Tillage Depth Values
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.S. Discussion on the Development of Advanced Technology of Tractors in China. Agric. Technol. Equip. 2021, 10, 55–57. [Google Scholar]
- Wang, Y.S.; Wei, G.J. Tractor electro-hydraulic suspension technology application status and outlook. Jiangsu Agricultural Mechanization. Jiangsu Agric. Mech. 2022, 01, 36–37. [Google Scholar]
- Kut’kov, G.M. The development of the technical concept of the tractor. Tract. Agric. Mach. 2019, 86, 27–35. [Google Scholar] [CrossRef]
- Volk, R.; Rambhia, M.; Schultmann, F. Urban Resource Assessment, Management, and Planning Tools for Land, Ecosystems, Urban Climate, Water, and Materials—A Review. Sustainability 2022, 14, 7203. [Google Scholar] [CrossRef]
- Ou, Y.; Cui, T.; Lin, L. Development status and countermeasures of intelligent agricultural machinery equipment industry. Sci. Technol. Rev. 2022, 11, 55–66. [Google Scholar]
- Sun, X.X.; Lu, Z.X.; Song, Y.; Cheng, Z.; Jiang, C.; Qian, J.; Lu, Y. Development Status and Research Progress of a Tractor Electro-Hydraulic Hitch System. Agriculture 2022, 12, 1547. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Dai, D.; Wang, X.; Wang, S. Review of electro-hydraulic hitch system control method of automated tractors. Int. J. Agric. Biol. Eng. 2021, 14, 1–11. [Google Scholar] [CrossRef]
- Singha, P.S.; Kumar, A.; Sarkar, S.; Baishya, S.; Kumar, P. Development of Electro-Hydraulic Hitch Control System through Lower Link Draft Sensing of a Tractor. J. Sci. Ind. Res. 2022, 81, 384–392. [Google Scholar]
- Pranav, P.K.; Tewari, V.K.; Pandey, K.P.; Jha, K. Automatic wheel slip control system in field operations for 2WD tractors. Comput. Electron. Agric. 2012, 84, 1–6. [Google Scholar] [CrossRef]
- Anche, G.; Velmurugan, M.; Kumar, A.; Subramanian, S.C.; Sreenivasulu, R.M. Model Based Compensator Design for Pitch Plane Stability of a Farm Tractor with Implement. IFAC-Pap. OnLine 2018, 51, 208–213. [Google Scholar] [CrossRef]
- Fernandez, B.; Herrera, P.J.; Cerrada, J.A. Self-tuning regulator for a tractor with varying speed and hitch forces. Comput. Electron. Agric. 2018, 145, 282–288. [Google Scholar] [CrossRef]
- Yang, J.R.; Li, N.; Li, R.C.; Jing, B.Y.; Li, H.; Mu, C.P. Control method and experimental study of tractor tillage depth based on sliding mode variable structure. Res. Agric. Mech. 2022, 44, 238–243. [Google Scholar]
- Li, M.S.; Ye, J.; Song, H.L.; Chen, J.J. Design and test of semi-physical simulation system for tractor electro-hydraulic suspension. J. Southwest Univ. Nat. Sci. Ed. 2018, 40, 14–21. [Google Scholar]
- Li, S.Z.; Wei, J.H.; Guo, K.; Zhu, W.-L. Nonlinear Robust Prediction Control of Hybrid Active-Passive Heave Compensator with Extended Disturbance Observer. IEEE Trans. Ind. Electron. 2017, 64, 6684–6694. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, M.N.; Xu, L.Y. Design and simulation of hydraulic suspension system of electric tractor. Res. Agric. Mech. 2022, 44, 238–243. [Google Scholar]
- Xu, J.K.; Li, R.C.; Li, Y.C.; Zhang, Y.; Sun, H.; Ding, X.; Ma, Y. Research on Variable-Universe Fuzzy Control Technology of an Electro-Hydraulic Hitch System. Processes 2020, 9, 1920. [Google Scholar] [CrossRef]
- Gao, Q.; Lu, Z.X.; Xue, J.L.; Gao, H.; Sar, D. Fuzzy-PID controller with variable universe for tillage depth control on tractor-implement. J. Comput. Methods Sci. Eng. 2021, 21, 19–29. [Google Scholar] [CrossRef]
- Shafaei, S.M.; Loghavi, M.; Kamgar, S. A practical effort to equip tractor-implement with fuzzy depth and draft control system. Eng. Agric. Environ. Food 2019, 12, 191–203. [Google Scholar] [CrossRef]
- Timene, A.; Ngasop, N.; Djalo, H. Tractor-Implement Tillage Depth Control Using Adaptive Neuro-Fuzzy Inference System (ANFIS). Proc. Eng. Technol. Innov. 2021, 19, 53–61. [Google Scholar] [CrossRef]
- Zhou, M.K.; Xia, J.F.; Zhang, S.; Hu, M.; Liu, Z.; Liu, G.; Luo, C. Development of a Depth Control System Based on Variable-Gain Single-Neuron PID for Rotary Burying of Stubbles. Agriculture 2022, 12, 30. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, Z.H.; Dai, L. Model order reduction method based on Laguerre polynomial expansion of matrix exponential function. Appl. Math. 2020, 33, 1002–1009. [Google Scholar]
- Liu, X.X.; Wang, Z.S. Lyapunov function optimization: Orthogonal matrix construction scheme. Control Theory Appl. 2022, 39, 1–10. [Google Scholar]
- Guo, X.P.; Wang, C.W.; Liu, H.; Zhang, Z.Y.; Ji, X.H.; Zhao, B. Extended-state-observer based sliding mode control for pump-controlled electro-hydraulic servo system. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1159–1168. [Google Scholar]
- Besova, M.; Kachalov, V. Analytical Aspects of the Theory of Tikhonov Systems. Mathematics 2021, 10, 72. [Google Scholar] [CrossRef]
- Zhang, S.Z.; Li, S.; Dai, F.Q. Integral Sliding Mode Backstepping Control of an Asymmetric Electro-Hydrostatic Actuator Based on Extended State Observer. Proceedings 2020, 64, 13. [Google Scholar]
- Hu, S.N.; Liu, J.H.; Qin, Z.T. The Number of Solutions of Certain Equations over Finite Fields. Wuhan Univ. J. Nat. Sci. 2022, 27, 49–52. [Google Scholar] [CrossRef]
- Cheng, C.; Liu, S.Y.; Wu, H.Z. Sliding mode observer-based fractional-order proportional–integral–derivative sliding mode control for electro-hydraulic servo systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 234, 1887–1898. [Google Scholar] [CrossRef]
- Du, H.; Shi, J.J.; Chen, J.D.; Zhang, Z.; Feng, X. High-gain observer-based integral sliding mode tracking control for heavy vehicle electro-hydraulic servo steering systems. Mechatronics 2021, 74, 49–52. [Google Scholar] [CrossRef]











| Component Parameters | Numerical | |
|---|---|---|
| Servo motors | Rated power/kW | 2.3 |
| Rated speed/ (r·min−1) | 2300 | |
| Dosing gear pumps | Displacement/(cc·r−1) | 3 |
| Rated speed/(r·min−1) | 2300 | |
| Dosing gear pumps | Bore/mm | 50 |
| Rod diameter/mm | 28 | |
| Trips/mm | 500 | |
| Coefficient of viscous friction/ (N·(m·s)−1) | 1000 | |
| Hydraulic oil density/(kg·m3) | 880 | |
| Accumulator volume/L | 1 | |
| Relief valve opening pressure/bar | 180 | |
| Component Parameters | Numerical |
|---|---|
| Power supply | 24VDC |
| Displacement range | 800 mm |
| Linearity error | 10 μm |
| Update time | 0.5 ms |
| Responsive | 1 mm/s |
| Working temperature | −40 °C–80 °C |
| Repetition error | 2 μm |
| Output signal | CAN |
| Component Parameters | Numerical |
|---|---|
| Measurement range | 0–10 L/min |
| Precision | 0.01 L/min |
| Responsive | 80 ms |
| Hysteresis | 10 mL/min |
| Working mode | Instantaneous flow |
| Average display time | 0.05 s |
| Component Parameters | Numerical |
|---|---|
| Measurement range | −0.1~+10.0 MP |
| Precision | 0.02 Mpa |
| Responsive | 2 ms |
| Working temperature | −20 °C~+80 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Yuan, Q.; Xu, Y.; Wang, X.; Bai, S.; Zhao, L.; Hua, Y.; Ma, X. Research on Control Strategy of Electro-Hydraulic Lifting System Based on AMESim and MATLAB. Symmetry 2023, 15, 435. https://doi.org/10.3390/sym15020435
Zhang W, Yuan Q, Xu Y, Wang X, Bai S, Zhao L, Hua Y, Ma X. Research on Control Strategy of Electro-Hydraulic Lifting System Based on AMESim and MATLAB. Symmetry. 2023; 15(2):435. https://doi.org/10.3390/sym15020435
Chicago/Turabian StyleZhang, Wei, Qinghao Yuan, Yifan Xu, Xuguang Wang, Shuzhan Bai, Lei Zhao, Yang Hua, and Xiaoxu Ma. 2023. "Research on Control Strategy of Electro-Hydraulic Lifting System Based on AMESim and MATLAB" Symmetry 15, no. 2: 435. https://doi.org/10.3390/sym15020435
APA StyleZhang, W., Yuan, Q., Xu, Y., Wang, X., Bai, S., Zhao, L., Hua, Y., & Ma, X. (2023). Research on Control Strategy of Electro-Hydraulic Lifting System Based on AMESim and MATLAB. Symmetry, 15(2), 435. https://doi.org/10.3390/sym15020435




