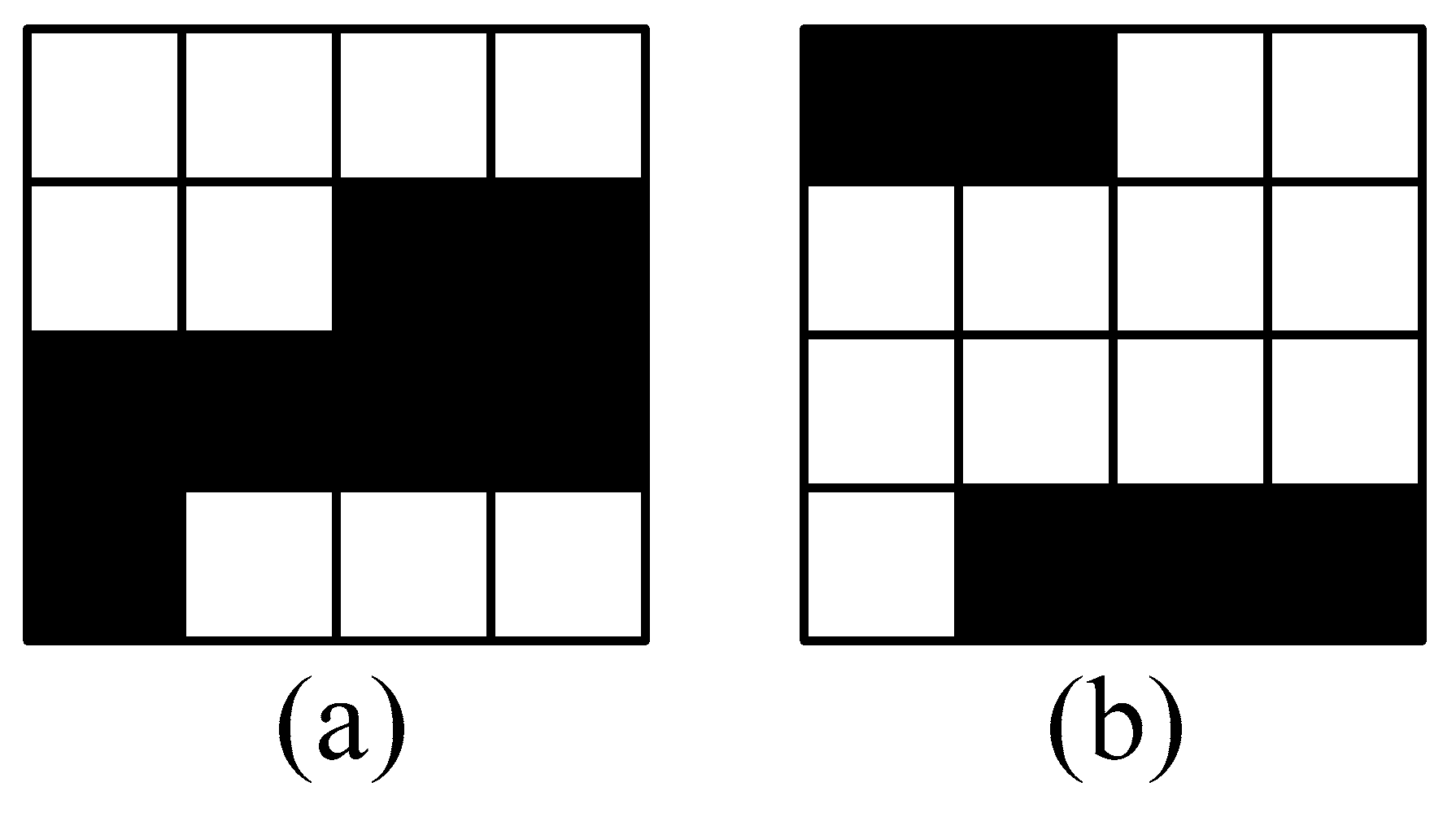
Figure 1.
Two bad blocks which can be marked as good ones with new designed structure information. (a) 4 bits “0110” are used to record the starting location of the consecutive black pixels and 4 bits “0111” to the length; (b) 4 bits “0010” are used to record the starting location of the consecutive white pixels and 4 bits “1011” to the length.
Figure 1.
Two bad blocks which can be marked as good ones with new designed structure information. (a) 4 bits “0110” are used to record the starting location of the consecutive black pixels and 4 bits “0111” to the length; (b) 4 bits “0010” are used to record the starting location of the consecutive white pixels and 4 bits “1011” to the length.
Figure 2.
The arrangement of pixel sequences in a block for different and .
Figure 2.
The arrangement of pixel sequences in a block for different and .
Figure 3.
Binary image (a) constructed with pixels of the 1th bit-plane, (b) constructed with pixels of the 5th bit-plane of the image Lena, respectively. Note: the size of the basic block is 4 × 4 pixels, and the EB-I, EB-II, EB-III, EB-IV, EB-V, EB-VI and NEB block are displayed with the white, black, yellow, blue, orange, green and red colors, respectively.
Figure 3.
Binary image (a) constructed with pixels of the 1th bit-plane, (b) constructed with pixels of the 5th bit-plane of the image Lena, respectively. Note: the size of the basic block is 4 × 4 pixels, and the EB-I, EB-II, EB-III, EB-IV, EB-V, EB-VI and NEB block are displayed with the white, black, yellow, blue, orange, green and red colors, respectively.
Figure 4.
(a) Test binary image, (b) the distribution of basic blocks, and (c) the distribution of all blocks after combination.
Figure 4.
(a) Test binary image, (b) the distribution of basic blocks, and (c) the distribution of all blocks after combination.
Figure 5.
Block-labeling bits and payloads for different block types.
Figure 5.
Block-labeling bits and payloads for different block types.
Figure 6.
The vacation procedure of spare space for different blocks. (a,e–g), the blocks with the type of EB-II1, EB-IV, EB-VI, and NEB1 are taken as examples to explain the vacating processes for different basic blocks. (b–d,h–j), the blocks with the type of EB-II2, EB-II3, EB-II4, NEB2, NEB3 and NEB4 are taken as examples to explain the vacating processes for different combined blocks.
Figure 6.
The vacation procedure of spare space for different blocks. (a,e–g), the blocks with the type of EB-II1, EB-IV, EB-VI, and NEB1 are taken as examples to explain the vacating processes for different basic blocks. (b–d,h–j), the blocks with the type of EB-II2, EB-II3, EB-II4, NEB2, NEB3 and NEB4 are taken as examples to explain the vacating processes for different combined blocks.
Figure 7.
The flowchart of the proposed method.
Figure 7.
The flowchart of the proposed method.
Figure 8.
The flowchart of random sequence generation for encryption.
Figure 8.
The flowchart of random sequence generation for encryption.
Figure 9.
Data hiding and extraction using the proposed method where the embedding rate is 2.0384 bpp. (a) The original image, (b) the marked encrypted image, (c) the approximately decrypted image, and (d) the completely decrypted image.
Figure 9.
Data hiding and extraction using the proposed method where the embedding rate is 2.0384 bpp. (a) The original image, (b) the marked encrypted image, (c) the approximately decrypted image, and (d) the completely decrypted image.
Figure 10.
Test images used in experiments. (a) Boat, (b) Lake, (c) Airplane, (d) Man, (e) Splash, (f) Barbara, (g) Peppers, (h) Road, (i) Temple, (j) Couple.
Figure 10.
Test images used in experiments. (a) Boat, (b) Lake, (c) Airplane, (d) Man, (e) Splash, (f) Barbara, (g) Peppers, (h) Road, (i) Temple, (j) Couple.
Figure 11.
Comparison of maximal embedding rate using different methods, including Yi et al. [
39], Ma et al. [
34], Zhang [
24], Puteaux et al. [
37], Fu et al. [
31], Qin et al. [
30], Chen [
32] and Wang et al. [
33].
Figure 11.
Comparison of maximal embedding rate using different methods, including Yi et al. [
39], Ma et al. [
34], Zhang [
24], Puteaux et al. [
37], Fu et al. [
31], Qin et al. [
30], Chen [
32] and Wang et al. [
33].
Figure 12.
PSNR comparison for the marked decrypted images using different methods for test images (
a)
Lena, (
b)
Lake, (
c)
Airplane, and (
d)
Peppers, respectively [
24,
25,
34,
35,
39].
Figure 12.
PSNR comparison for the marked decrypted images using different methods for test images (
a)
Lena, (
b)
Lake, (
c)
Airplane, and (
d)
Peppers, respectively [
24,
25,
34,
35,
39].
Figure 13.
Histograms of (a) the test image Boat, (b) the encrypted image, and (c) the marked encrypted image.
Figure 13.
Histograms of (a) the test image Boat, (b) the encrypted image, and (c) the marked encrypted image.
Figure 14.
Differential analysis to the original image. (a,b) Two test images, where there is one bit difference between them; (c) the difference between two test images; (d,e) the marked encrypted images embedded with the same secret data; and (f) the difference between two marked encrypted results.
Figure 14.
Differential analysis to the original image. (a,b) Two test images, where there is one bit difference between them; (c) the difference between two test images; (d,e) the marked encrypted images embedded with the same secret data; and (f) the difference between two marked encrypted results.
Figure 15.
Differential analysis to the secret data. (a) Test image; (b,c) the marked encrypted images embedded with two pieces of secret data, where there is one bit difference between them; and (d) the difference between the two marked encrypted results.
Figure 15.
Differential analysis to the secret data. (a) Test image; (b,c) the marked encrypted images embedded with two pieces of secret data, where there is one bit difference between them; and (d) the difference between the two marked encrypted results.
Figure 16.
MSE versus the deviation of the initial key . (a–c) The mean square error curve versus the deviation of the initial value , respectively.
Figure 16.
MSE versus the deviation of the initial key . (a–c) The mean square error curve versus the deviation of the initial value , respectively.
Figure 17.
MSE versus the deviation of the initial key . (a–c) The mean square error curve versus the deviation of the initial value , respectively.
Figure 17.
MSE versus the deviation of the initial key . (a–c) The mean square error curve versus the deviation of the initial value , respectively.
Figure 18.
The performance of secret data extraction under potential attacks for different test images.
Figure 18.
The performance of secret data extraction under potential attacks for different test images.
Table 1.
Block types in Yi and Zhou’s method.
Table 1.
Block types in Yi and Zhou’s method.
| Condition | Block Type | Block Explanation | Labeling Bits |
|---|
| Bad | Cannot embed data | 00 |
| Good-I | All pixels with value of 1 | 11 |
| Good-II | All pixels with value of 0 | 10 |
| Good-III | Most pixels with value of 1 | 011 |
| Good-IV | Most pixels with value of 0 | 010 |
Table 2.
Basic block types in the proposed method.
Table 2.
Basic block types in the proposed method.
| Condition | Block Type | Block Explanation |
|---|
| NEB | Not suitable for embedding data |
| EB-I | All pixels with value of 1 |
| EB-II | All pixels with value of 0 |
| EB-III | Most pixels with value of 1 |
| EB-IV | Most pixels with value of 0 |
| EB-V | Including a sequence of consecutive pixels with the value of 0 |
| EB-VI | Including a sequence of consecutive pixels with the value of 1 |
Table 3.
Classification of basic and combined blocks.
Table 3.
Classification of basic and combined blocks.
| Index | Block Type | Block Size | Codewords | Block Explanation |
|---|
| 1 | EB-I1 | 1 × 1 | 011 | A basic block where all pixels are 1, i.e., a white basic block |
| 2 | EB-I2 | 2 × 2 | 111111 | A square block containing 4 white basic blocks |
| 3 | EB-I3 | 4 × 4 | 111101111 | A square block containing 16 white basic blocks |
| 4 | EB-I4 | 2x × 2y | 111101110 | Containing at least 16 white basic blocks, excluding EB-I3 blocks |
| 5 | EB-II1 | 1 × 1 | 000 | A basic block where all pixels are 0, i.e., a black basic block |
| 6 | EB-II2 | 2 × 2 | 111110 | A square block containing 4 black basic blocks |
| 7 | EB-II3 | 4 × 4 | 111101101 | A square block containing 16 black basic blocks |
| 8 | EB-II4 | 2x × 2y | 111101100 | Containing at least 16 black basic blocks, excluding EB-II3 blocks |
| 9 | NEB1 | 1 × 1 | 01 | A non-embeddable basic block |
| 10 | NEB2 | 2 × 2 | 110 | A square block containing 4 non-embeddable basic blocks |
| 11 | NEB3 | 4 × 4 | 1111010 | A square block containing 16 non-embeddable basic blocks |
| 12 | NEB4 | 2x × 2y | 111100 | Containing at least 16 non-embeddable basic blocks, excluding NEB3 blocks |
| 13 | EB-III | 1 × 1 | 101 | A basic block where most pixels are 1 |
| 14 | EB-IV | 1 × 1 | 100 | A basic block where most pixels are 0 |
| 15 | EB-V | 1 × 1 | 11101 | A basic block including a sequence of consecutive pixels with the value of 0 |
| 16 | EB-VI | 1 × 1 | 11100 | A basic block including a sequence of consecutive pixels with the value of 1 |
Table 4.
Maximal embedding rate comparison with three existing methods on two image databases.
Table 4.
Maximal embedding rate comparison with three existing methods on two image databases.
| Algorithms | BOSSBase | BOWS2 |
|---|
| Best | Worst | Average | Best | Worst | Average |
|---|
| Qin et al.’s [30] | 3.4885 | 0.1039 | 2.2093 | 3.4265 | 0.1348 | 2.0608 |
| Fu et al.’s [31] | 3.4657 | 0.0015 | 2.1733 | 3.4052 | 0.0296 | 2.0454 |
| Yi et al.’s [39] | 3.4878 | 0.0522 | 2.2957 | 3.4271 | 0.2191 | 2.1748 |
| Proposed | 3.9722 | 0.1367 | 2.5657 | 3.8846 | 0.2840 | 2.4346 |
Table 5.
Comparison of the number of embeddable basic blocks obtained by the proposed method and Yi and Zhou’s method.
Table 5.
Comparison of the number of embeddable basic blocks obtained by the proposed method and Yi and Zhou’s method.
| Test Images | The Number of Embeddable Basic Blocks | Increment |
|---|
| Yi and Zhou | Proposed |
|---|
| Boat | 45,429 | 47,861 | 2432 |
| Lake | 39,089 | 40,573 | 1484 |
| Airplane | 52,807 | 55,461 | 2654 |
| Man | 41,884 | 43,203 | 1319 |
| Splash | 56,929 | 59,033 | 2104 |
| Barbara | 34,862 | 36,318 | 1456 |
| Peppers | 44,599 | 45,899 | 1300 |
| Road | 37,662 | 40,937 | 3275 |
| Temple | 68,871 | 71,316 | 2445 |
| Couple | 35,658 | 39,054 | 3396 |
| Average | 45,779 | 47,966 | 2187 |
Table 6.
The number of embeddable bits created in blocks with the type of EB-V and EB-VI for different images using the proposed method.
Table 6.
The number of embeddable bits created in blocks with the type of EB-V and EB-VI for different images using the proposed method.
| Test Images | The Number of Embeddable Bits | Total |
|---|
| EB-V | EB-VI |
|---|
| Boat | 5883 | 6123 | 12,006 |
| Lake | 4460 | 4693 | 9153 |
| Airplane | 7615 | 6858 | 14,473 |
| Man | 3805 | 4629 | 8434 |
| Splash | 6354 | 6001 | 12,355 |
| Barbara | 4094 | 3937 | 8031 |
| Peppers | 3534 | 4191 | 7725 |
| Road | 8903 | 8351 | 17,254 |
| Temple | 8442 | 8376 | 16,818 |
| Couple | 8185 | 8482 | 16,667 |
| Average | 6128 | 6164 | 12,292 |
Table 7.
Comparison of the number of block-labeling bits for monochromatic blocks using the proposed method and Yi and Zhou’s method.
Table 7.
Comparison of the number of block-labeling bits for monochromatic blocks using the proposed method and Yi and Zhou’s method.
| Test Images | The Number of Block-Labeling Bits | Decrement |
|---|
| Yi and Zhou | Proposed |
|---|
| Boat | 71,266 | 42,465 | 28,801 |
| Lake | 57,474 | 37,209 | 20,265 |
| Airplane | 83,588 | 46,218 | 37,370 |
| Man | 62,754 | 40,467 | 22,287 |
| Splash | 92,538 | 46,407 | 46,131 |
| Barbara | 52,552 | 35,772 | 16,780 |
| Peppers | 66,980 | 43,485 | 23,495 |
| Road | 55,778 | 39,822 | 15,956 |
| Temple | 107,228 | 56,268 | 50,960 |
| Couple | 50,872 | 39,744 | 11,128 |
| Average | 70,103 | 42,786 | 27,317 |
Table 8.
The entropy, NPCR, and UACI of different images before and after encryption.
Table 8.
The entropy, NPCR, and UACI of different images before and after encryption.
| Images | Original Image | Encrypted Image | Marked Encrypted Image |
|---|
| Entropy | Entropy | NPCR | UACI | Entropy | NPCR | UACI |
|---|
| Boat | 7.1238 | 7.9994 | 0.9962 | 0.2944 | 7.9993 | 0.9960 | 0.2941 |
| Airplane | 6.6776 | 7.9992 | 0.9961 | 0.3239 | 7.9992 | 0.9963 | 0.3225 |
| Lake | 7.4570 | 7.9992 | 0.9962 | 0.3141 | 7.9993 | 0.9962 | 0.3137 |
| Splash | 7.2533 | 7.9993 | 0.9961 | 0.3003 | 7.9994 | 0.9959 | 0.3007 |
| Temple | 5.8108 | 7.9993 | 0.9960 | 0.2969 | 7.9994 | 0.9960 | 0.2974 |
| Couple | 7.0581 | 7.9993 | 0.9960 | 0.2818 | 7.9992 | 0.9961 | 0.2803 |