QCD Matter and Phase Transitions under Extreme Conditions †
Abstract
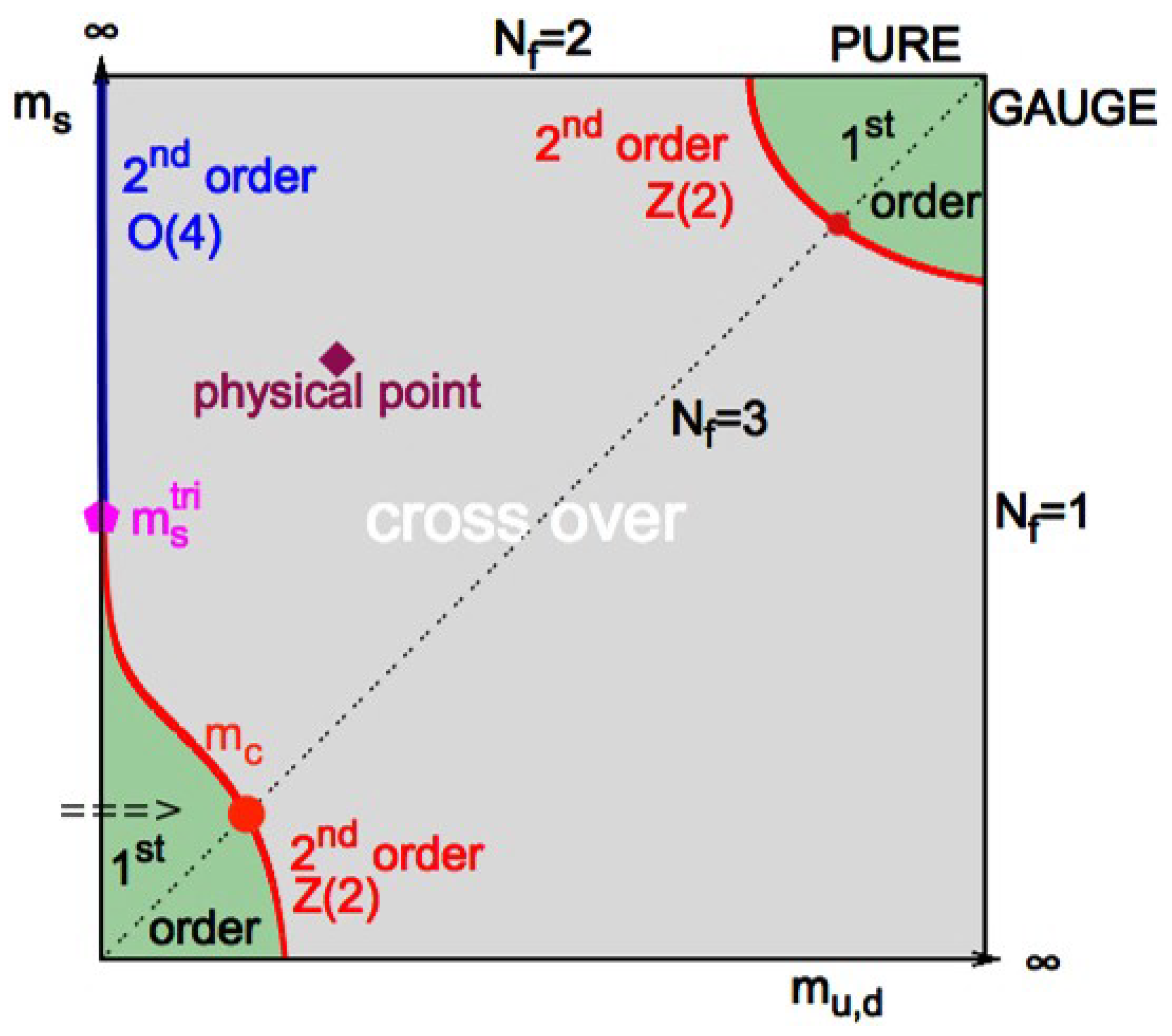
1. Introduction
2. Imprints of QCD Epoch in the Early Universe
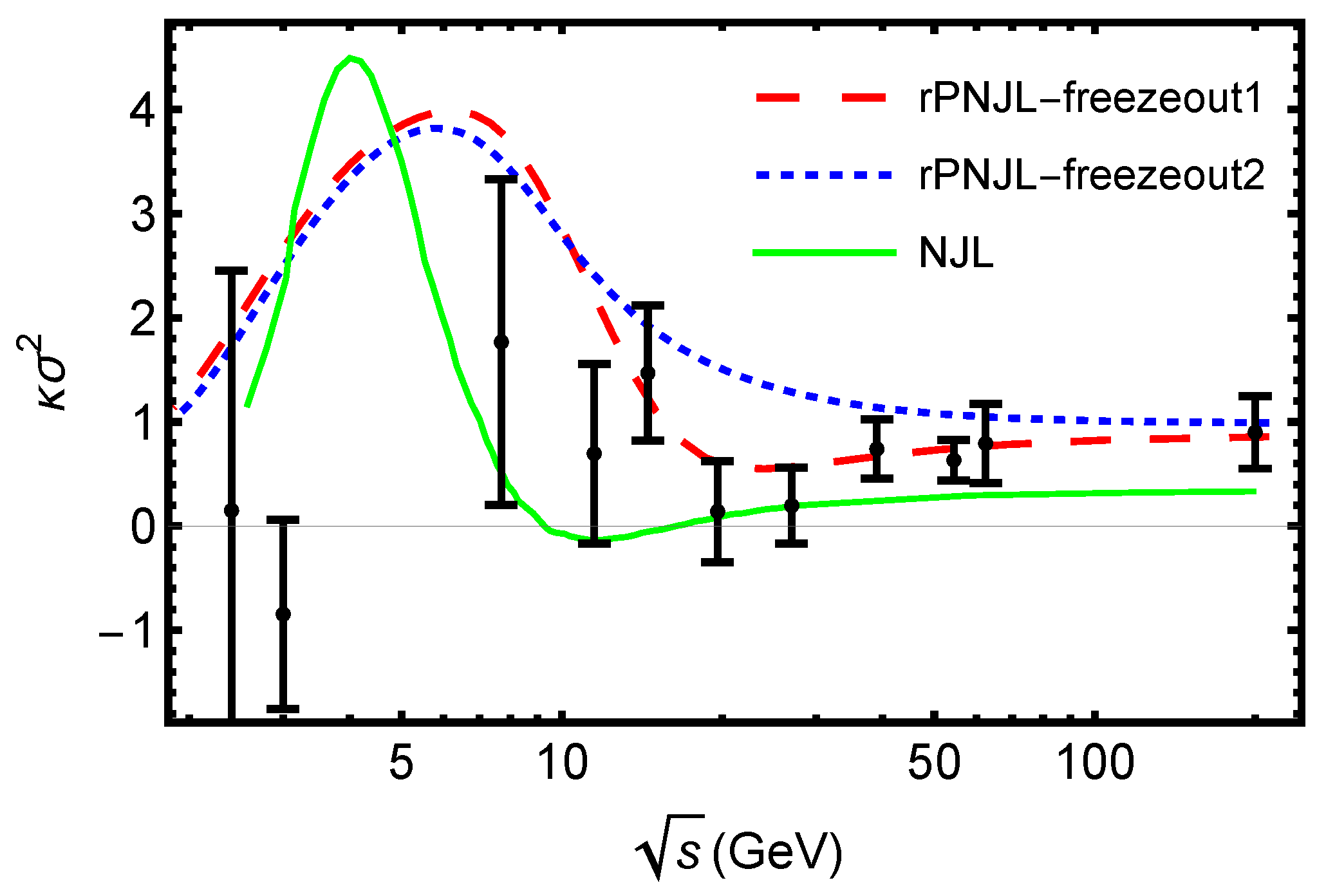
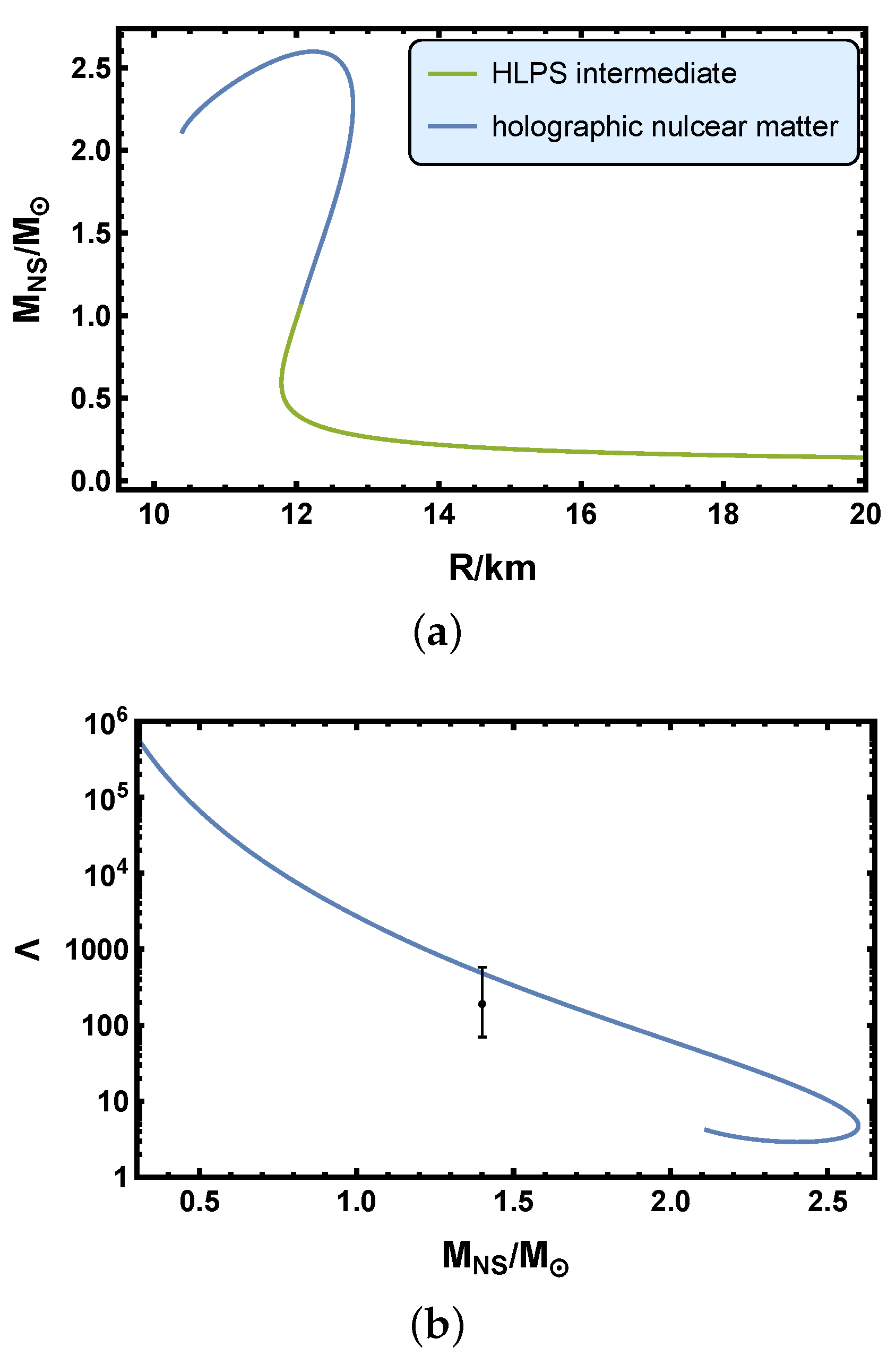
3. Dense QCD Matter
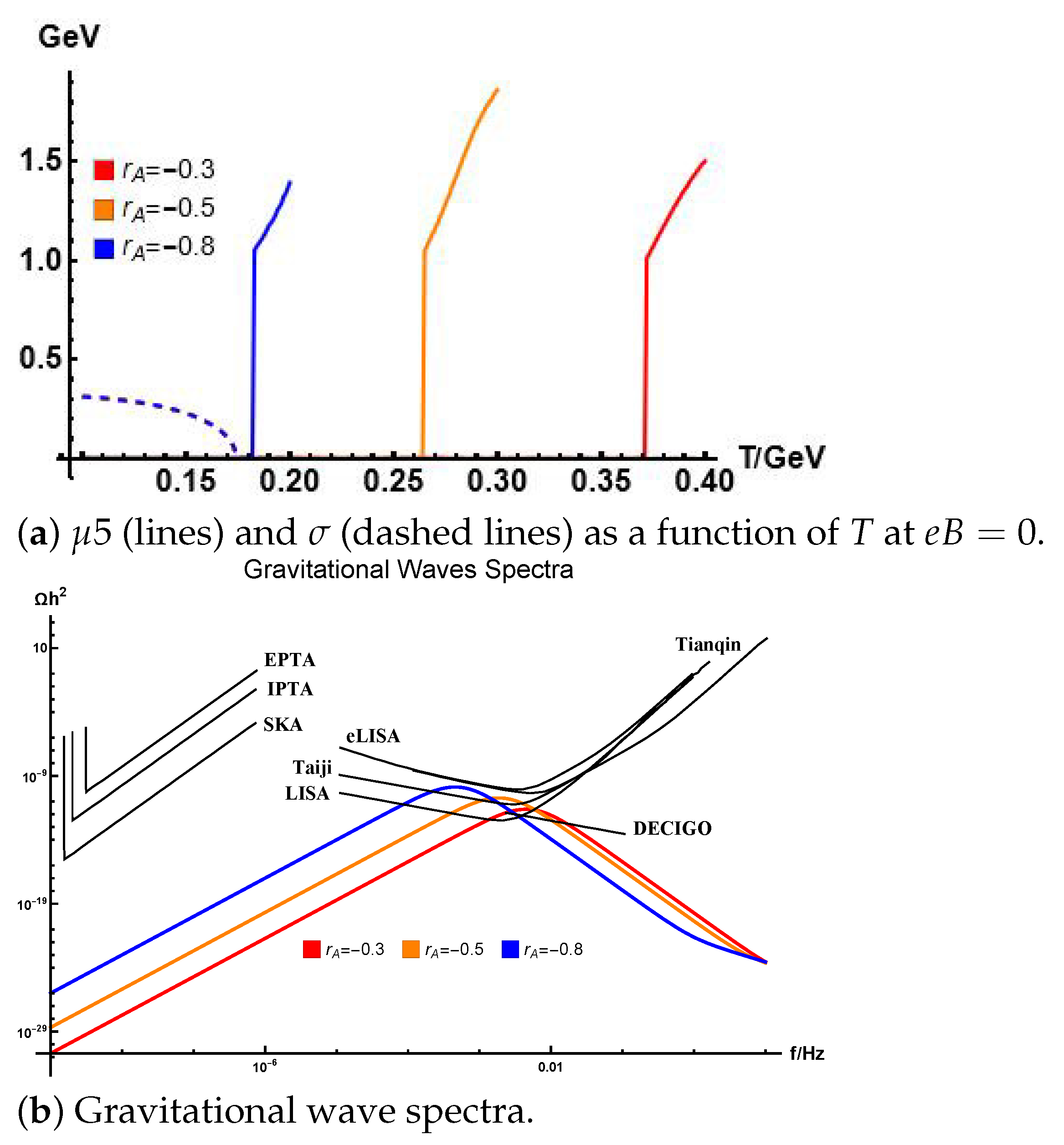
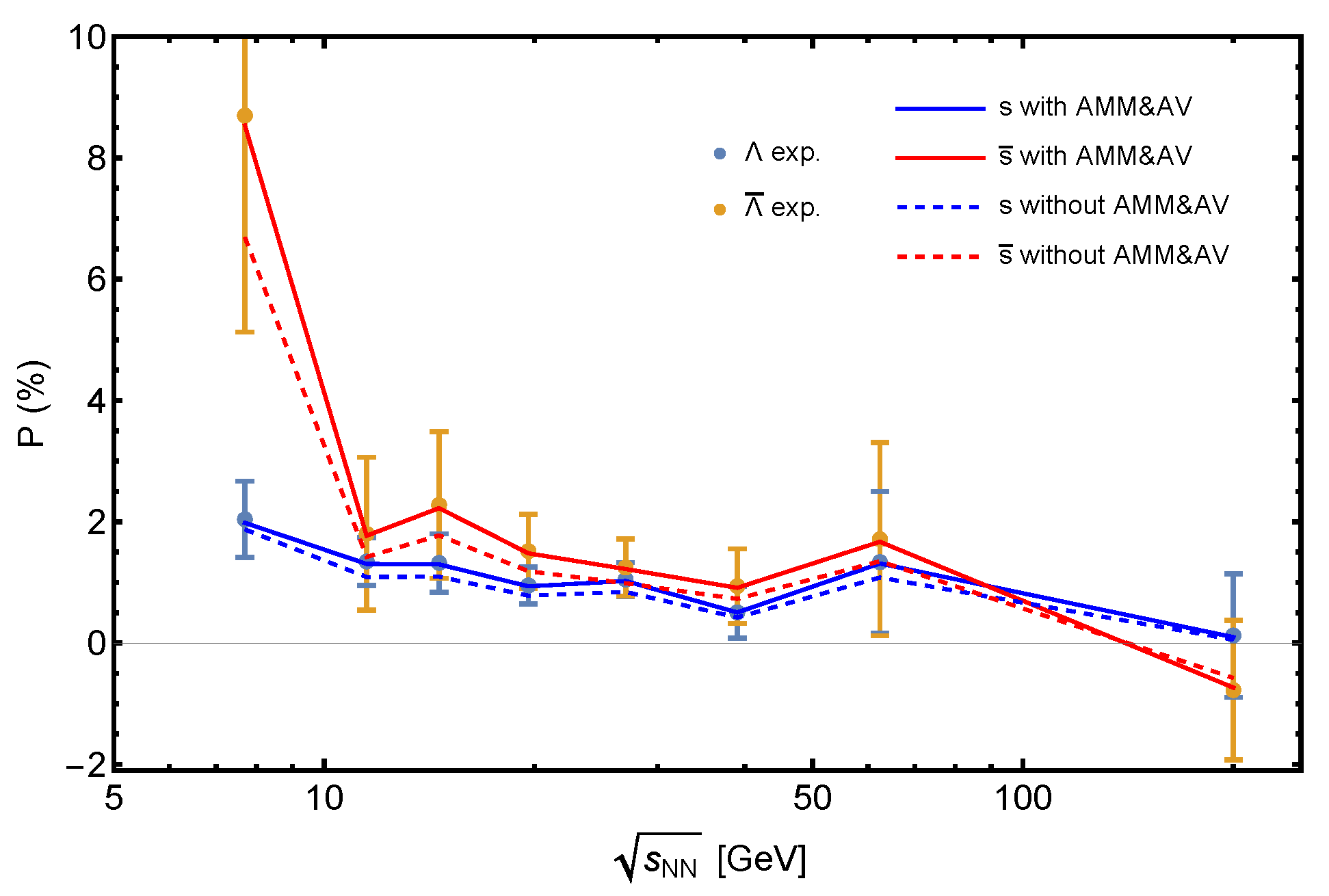
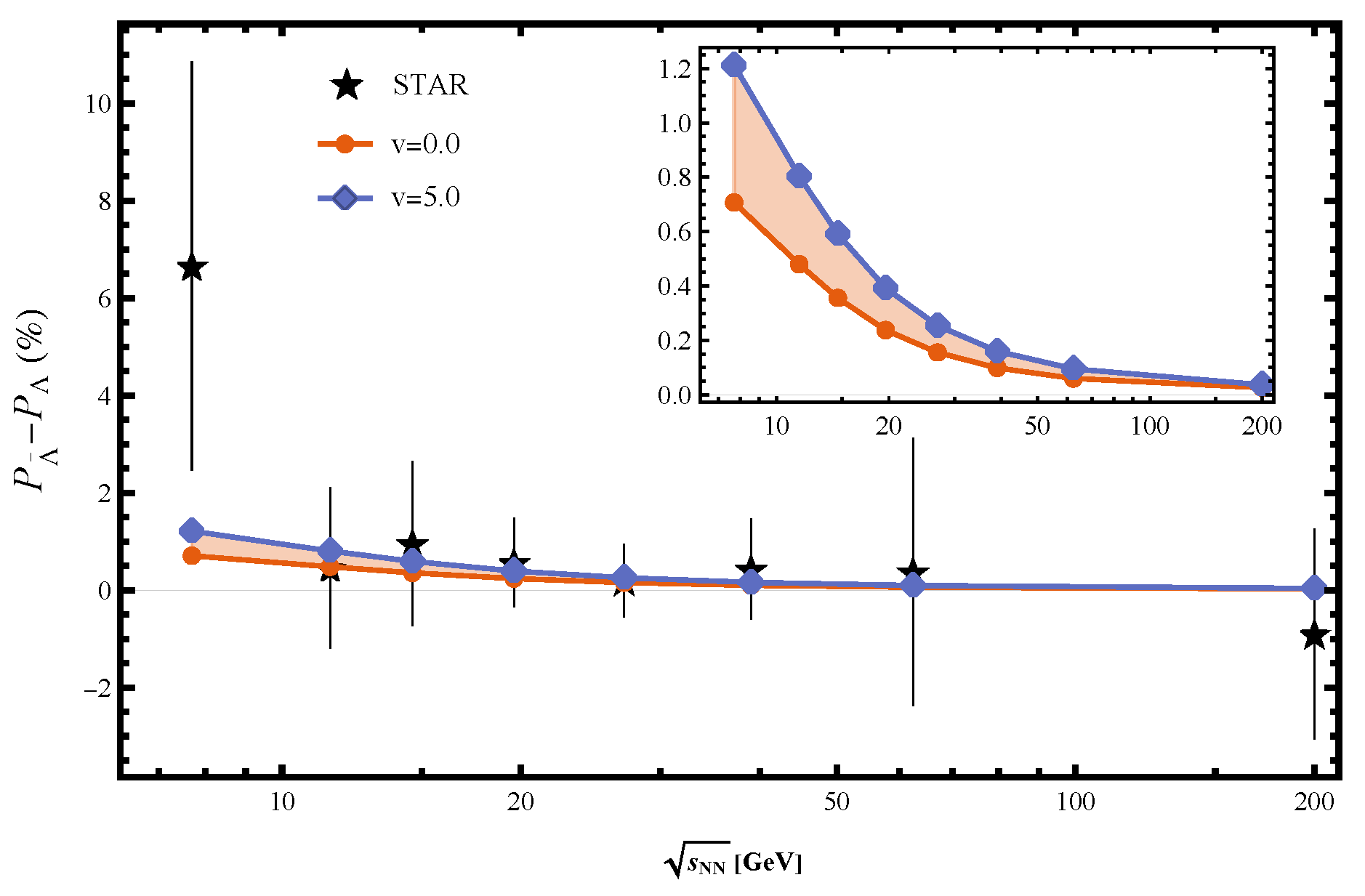
4. QCD Matter under Electromagnetic and Vortical Field
5. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Schwarz, D.J. The first second of the universe. Ann. Phys. 2003, 12, 220–270. [Google Scholar] [CrossRef]
- Baym, G.; Chin, S.A. Can a Neutron Star Be a Giant MIT Bag? Phys. Lett. B 1976, 62, 241–244. [Google Scholar] [CrossRef]
- Collins, J.C.; Perry, M.J. Superdense Matter: Neutrons Or Asymptotically Free Quarks? Phys. Rev. Lett. 1975, 34, 1353. [Google Scholar] [CrossRef]
- Luo, X.; Wang, Q.; Xu, N.; Zhuang, P. (Eds.) Properties of QCD Matter at High Baryon Density; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Karsch, F. Lattice QCD at Non-Zero Temperature and Density. 2022. Available online: http://xxx.lanl.gov/abs/2212.03015 (accessed on 30 December 2022).
- Aarts, G.; Aichelin, J.; Allton, C.; Athenodorou, A.; Bachtis, D.; Bonanno, C.; Brambilla, N.; Bratkovskaya, E.; Bruno, M.; Caselle, M.; et al. Phase Transitions in Particle Physics–Results and Perspectives from Lattice Quantum Chromo-Dynamics. arXiv 2023, arXiv:2301.04382. [Google Scholar]
- de Forcrand, P.; D’Elia, M. Continuum limit and universality of the Columbia plot. PoS 2017, LATTICE2016, 081. [Google Scholar] [CrossRef]
- Karsch, F. Lattice QCD at high temperature and density. Lect. Notes Phys. 2002, 583, 209–249. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The Order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef]
- Allton, C.R.; Ejiri, S.; Hands, S.J.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Schmidt, C.; Scorzato, L. The QCD thermal phase transition in the presence of a small chemical potential. Phys. Rev. D 2002, 66, 074507. [Google Scholar] [CrossRef]
- Allton, C.R.; Doring, M.; Ejiri, S.; Hands, S.J.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Redlich, K. Thermodynamics of two flavor QCD to sixth order in quark chemical potential. Phys. Rev. D 2005, 71, 054508. [Google Scholar] [CrossRef]
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. QCD equation of state at nonzero chemical potential: Continuum results with physical quark masses at order mu2. J. High Energy Phys. 2012, 08, 053. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. The QCD Equation of State to O() from Lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Guenther, J.N.; Kara, R.; Katz, S.D.; Parotto, P.; Pásztor, A.; Ratti, C.; Szabó, K.K. Lattice QCD equation of state at finite chemical potential from an alternative expansion scheme. Phys. Rev. Lett. 2021, 126, 232001. [Google Scholar] [CrossRef] [PubMed]
- Pisarski, R.D.; Wilczek, F. Remarks on the Chiral Phase Transition in Chromodynamics. Phys. Rev. D 1984, 29, 338–341. [Google Scholar] [CrossRef]
- Hatta, Y.; Ikeda, T. Universality, the QCD critical/tricritical point and the quark number susceptibility. Phys. Rev. D 2003, 67, 014028. [Google Scholar] [CrossRef]
- Klevansky, S.P. The Nambu-Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Zhuang, P.; Huang, M.; Yang, Z. Density effect on hadronization of a quark plasma. Phys. Rev. C 2000, 62, 054901. [Google Scholar] [CrossRef]
- Fukushima, K. Phase diagrams in the three-flavor Nambu-Jona-Lasinio model with the Polyakov-loop. Phys. Rev. D 2008, 77, 114028, Erratum in Phys. Rev. D 2008, 78, 039902. [Google Scholar] [CrossRef]
- Ratti, C.; Roessner, S.; Thaler, M.A.; Weise, W. Thermodynamics of the PNJL model. Eur. Phys. J. C 2007, 49, 213–217. [Google Scholar] [CrossRef]
- Shao, G.; Tang, Z.; Gao, X.; He, W. Baryon number fluctuations and the phase structure in the PNJL model. Eur. Phys. J. C 2018, 78, 138. [Google Scholar] [CrossRef]
- Tawfik, A. QCD phase diagram: A Comparison of lattice and hadron resonance gas model calculations. Phys. Rev. D 2005, 71, 054502. [Google Scholar] [CrossRef]
- Redlich, K.; Karsch, F.; Tawfik, A. Heavy ion collisions and lattice QCD at finite baryon density. J. Phys. G 2004, 30, S1271–S1274. [Google Scholar] [CrossRef]
- Tawfik, A. The Influence of strange quarks on QCD phase diagram and chemical freeze-out: Results from the hadron resonance gas model. J. Phys. G 2005, 31, S1105–S1110. [Google Scholar] [CrossRef]
- Xin, X.y.; Qin, S.x.; Liu, Y.x. Quark number fluctuations at finite temperature and finite chemical potential via the Dyson–Schwinger equation approach. Phys. Rev. D 2014, 90, 076006. [Google Scholar] [CrossRef]
- Fu, W.j.; Wu, Y.l. Fluctuations and Correlations of Conserved Charges near the QCD Critical Point. Phys. Rev. D 2010, 82, 074013. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Li, D.; Huang, M. Locating the QCD critical end point through the peaked baryon number susceptibilities along the freeze-out line. Chin. Phys. C 2018, 42, 013103. [Google Scholar] [CrossRef]
- Skokov, V.; Illarionov, A.Y.; Toneev, V. Estimate of the magnetic field strength in heavy-ion collisions. Int. J. Mod. Phys. A 2009, 24, 5925–5932. [Google Scholar] [CrossRef]
- Deng, W.T.; Huang, X.G. Event-by-event generation of electromagnetic fields in heavy-ion collisions. Phys. Rev. C 2012, 85, 044907. [Google Scholar] [CrossRef]
- Chen, H.L.; Huang, X.G.; Liao, J. QCD phase structure under rotation. Lect. Notes Phys. 2021, 987, 349–379. [Google Scholar] [CrossRef]
- Becattini, F.; Piccinini, F.; Rizzo, J. Angular momentum conservation in heavy-ion collisions at very high energy. Phys. Rev. C 2008, 77, 024906. [Google Scholar] [CrossRef]
- Liang, Z.T.; Wang, X.N. Globally polarized quark-gluon plasma in non-central A+A collisions. Phys. Rev. Lett. 2005, 94, 102301, Erratum in Phys. Rev. Lett. 2006, 96, 039901. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; The STAR Collaboration. Global Λ hyperon polarization in nuclear collisions: Evidence for the most vortical fluid. Nature 2017, 548, 62–65. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Einstein, A. Approximative Integration of the Field Equations of Gravitation. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1916, 1916, 688–696. [Google Scholar]
- Einstein, A. Über Gravitationswellen. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1918, 1918, 154–167. [Google Scholar]
- Rummukainen, K. Finite T electroweak phase transition on the lattice. Nucl. Phys. B Proc. Suppl. 1997, 53, 30–42. [Google Scholar] [CrossRef]
- Vaskonen, V. Electroweak baryogenesis and gravitational waves from a real scalar singlet. Phys. Rev. D 2017, 95, 123515. [Google Scholar] [CrossRef]
- Beniwal, A.; Lewicki, M.; Wells, J.D.; White, M.; Williams, A.G. Gravitational wave, collider and dark matter signals from a scalar singlet electroweak baryogenesis. J. High Energy Phys. 2017, 08, 108. [Google Scholar] [CrossRef]
- Beniwal, A.; Lewicki, M.; White, M.; Williams, A.G. Gravitational waves and electroweak baryogenesis in a global study of the extended scalar singlet model. J. High Energy Phys. 2019, 02, 183. [Google Scholar] [CrossRef]
- Alves, A.; Ghosh, T.; Guo, H.K.; Sinha, K.; Vagie, D. Collider and Gravitational Wave Complementarity in Exploring the Singlet Extension of the Standard Model. J. High Energy Phys. 2019, 04, 052. [Google Scholar] [CrossRef]
- Cline, J.M.; Lemieux, P.A. Electroweak phase transition in two Higgs doublet models. Phys. Rev. 1997, D55, 3873–3881. [Google Scholar] [CrossRef]
- Basler, P.; Krause, M.; Muhlleitner, M.; Wittbrodt, J.; Wlotzka, A. Strong First Order Electroweak Phase Transition in the CP-Conserving 2HDM Revisited. J. High Energy Phys. 2017, 02, 121. [Google Scholar] [CrossRef]
- Dorsch, G.C.; Huber, S.J.; Konstandin, T.; No, J.M. A Second Higgs Doublet in the Early Universe: Baryogenesis and Gravitational Waves. J. Cosmol. Astropart. Phys. 2017, 1705, 052. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Greiner, C. Early Universe Thermodynamics and Evolution in Nonviscous and Viscous Strong and Electroweak epochs: Possible Analytical Solutions. Entropy 2021, 23, 295. [Google Scholar] [CrossRef]
- Tawfik, A.; Harko, T. Quark-Hadron Phase Transitions in Viscous Early Universe. Phys. Rev. D 2012, 85, 084032. [Google Scholar] [CrossRef]
- Tawfik, A. Cosmological Consequences of QCD Phase Transition(s) in Early Universe. AIP Conf. Proc. 2009, 1115, 239–247. [Google Scholar] [CrossRef]
- Tawfik, A.; Wahba, M.; Mansour, H.; Harko, T. Viscous Quark-Gluon Plasma in the Early Universe. Annalen Phys. 2011, 523, 194–207. [Google Scholar] [CrossRef]
- Hogan, C.J. Gravitational radiation from cosmological phase transitions. Mon. Not. R. Astron. Soc. 1986, 218, 629–636. [Google Scholar] [CrossRef]
- Kosowsky, A.; Turner, M.S.; Watkins, R. Gravitational waves from first order cosmological phase transitions. Phys. Rev. Lett. 1992, 69, 2026–2029. [Google Scholar] [CrossRef]
- Kosowsky, A.; Turner, M.S. Gravitational radiation from colliding vacuum bubbles: Envelope approximation to many bubble collisions. Phys. Rev. D 1993, 47, 4372–4391. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kosowsky, A.; Turner, M.S. Gravitational radiation from first order phase transitions. Phys. Rev. D 1994, 49, 2837–2851. [Google Scholar] [CrossRef]
- Hawking, S.W.; Moss, I.G.; Stewart, J.M. Bubble Collisions in the Very Early Universe. Phys. Rev. D 1982, 26, 2681. [Google Scholar] [CrossRef]
- Jung, T.H.; Okui, T. Primordial black holes from bubble collisions during a first-order phase transition. arXiv 2021, arXiv:2110.04271. [Google Scholar]
- Khlopov, M.Y.; Konoplich, R.; Rubin, S.; Sakharov, A.S. First order phase transitions as a source of black holes in the early universe. arXiv 1999, arXiv:hep-ph/9912422. [Google Scholar]
- Carr, B.; Clesse, S.; García-Bellido, J. Primordial black holes from the QCD epoch: Linking dark matter, baryogenesis and anthropic selection. Mon. Not. R. Astron. Soc. 2021, 501, 1426–1439. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. J. Cosmol. Astropart. Phys. 2018, 08, 041. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial black hole formation during the QCD epoch. Phys. Rev. D 1997, 55, 5871–5875. [Google Scholar] [CrossRef]
- Profumo, S.; Ramsey-Musolf, M.J.; Shaughnessy, G. Singlet Higgs phenomenology and the electroweak phase transition. J. High Energy Phys. 2007, 8, 010. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, M.; Yan, Q.S. Gravitation waves from QCD and electroweak phase transitions. J. High Energy Phys. 2018, 5, 178. [Google Scholar] [CrossRef]
- He, S.; Li, L.; Li, Z.; Wang, S.J. Gravitational Waves and Primordial Black Hole Productions from Gluodynamics. arXiv 2022, arXiv:2210.14094. [Google Scholar]
- Morgante, E.; Ramberg, N.; Schwaller, P. Echo of the Dark: Gravitational Waves from Dark SU(3) Yang-Mills Theory. arXiv 2022, arXiv:2210.11821. [Google Scholar]
- Asadi, P.; Kramer, E.D.; Kuflik, E.; Slatyer, T.R.; Smirnov, J. Glueballs in a thermal squeezeout model. J. High Energy Phys. 2022, 7, 006. [Google Scholar] [CrossRef]
- Carenza, P.; Pasechnik, R.; Salinas, G.; Wang, Z.W. Glueball Dark Matter revisited. Phys. Rev. Lett. 2022, 129, 26. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Huang, M. Gravitational waves and primordial black holes from chirality imbalanced QCD first-order phase transition with P and CP violation. Phys. Rev. D 2023, 107, 043011. [Google Scholar] [CrossRef]
- ’t Hooft, G. Symmetry Breaking Through Bell-Jackiw Anomalies. Phys. Rev. Lett. 1976, 37, 8–11. [Google Scholar] [CrossRef]
- ’t Hooft, G. How Instantons Solve the U(1) Problem. Phys. Rep. 1986, 142, 357–387. [Google Scholar] [CrossRef]
- Belavin, A.A.; Polyakov, A.M.; Schwartz, A.S.; Tyupkin, Y.S. Pseudoparticle Solutions of the Yang-Mills Equations. Phys. Lett. B 1975, 59, 85–87. [Google Scholar] [CrossRef]
- Witten, E. Current Algebra Theorems for the U(1) Goldstone Boson. Nucl. Phys. B 1979, 156, 269–283. [Google Scholar] [CrossRef]
- Veneziano, G. U(1) Without Instantons. Nucl. Phys. B 1979, 159, 213–224. [Google Scholar] [CrossRef]
- Vicari, E.; Panagopoulos, H. Theta dependence of SU(N) gauge theories in the presence of a topological term. Phys. Rept. 2009, 470, 93–150. [Google Scholar] [CrossRef]
- Schäfer, T.; Shuryak, E.V. Instantons in QCD. Rev. Mod. Phys. 1998, 70, 323–426. [Google Scholar] [CrossRef]
- Kharzeev, D.; Zhitnitsky, A. Charge separation induced by P-odd bubbles in QCD matter. Nucl. Phys. A 2007, 797, 67–79. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The Effects of topological charge change in heavy-ion collisions: ‘Event by event P and CP violation’. Nucl. Phys. A 2008, 803, 227–253. [Google Scholar] [CrossRef]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. The Chiral Magnetic Effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Ilgenfritz, E.M.; Shuryak, E.V. Chiral Symmetry Restoration at Finite Temperature in the Instanton Liquid. Nucl. Phys. B 1989, 319, 511–520. [Google Scholar] [CrossRef]
- Ilgenfritz, E.M.; Shuryak, E.V. Quark induced correlations between instantons drive the chiral phase transition. Phys. Lett. B 1994, 325, 263–266. [Google Scholar] [CrossRef]
- Schäfer, T.; Shuryak, E.V.; Verbaarschot, J.J.M. The Chiral phase transition and instanton—Anti-instanton molecules. Phys. Rev. D 1995, 51, 1267–1281. [Google Scholar] [CrossRef]
- Zhang, Z. Correction to the Chiral Magnetic Effect from axial vector interaction. Phys. Rev. D 2012, 85, 114028. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H.; Huang, M. Spontaneous generation of local CP violation and inverse magnetic catalysis. Phys. Rev. D 2014, 90, 074009. [Google Scholar] [CrossRef]
- Ellis, J.; Lewicki, M.; No, J.M. On the Maximal Strength of a First-Order Electroweak Phase Transition and its Gravitational Wave Signal. J. Cosmol. Astropart. Phys. 2019, 04, 003. [Google Scholar] [CrossRef]
- Leitao, L.; Megevand, A. Gravitational waves from a very strong electroweak phase transition. J. Cosmol. Astropart. Phys. 2016, 05, 037. [Google Scholar] [CrossRef]
- Chala, M.; Krause, C.; Nardini, G. Signals of the electroweak phase transition at colliders and gravitational wave observatories. J. High Energy Phys. 2018, 07, 062. [Google Scholar] [CrossRef]
- DeGrand, T.A.; Kajantie, K. Supercooling, Entropy Production and Bubble Kinetics in the Quark—Hadron Phase Transition in the Early Universe. Phys. Lett. B 1984, 147, 273–278. [Google Scholar] [CrossRef]
- Schettler, S.; Boeckel, T.; Schaffner-Bielich, J. Imprints of the QCD Phase Transition on the Spectrum of Gravitational Waves. Phys. Rev. D 2011, 83, 064030. [Google Scholar] [CrossRef]
- Chen, Y.; Li, D.; Huang, M. The dynamical holographic QCD method for hadron physics and QCD matter. Commun. Theor. Phys. 2022, 74, 097201. [Google Scholar] [CrossRef]
- Gursoy, U.; Kiritsis, E. Exploring improved holographic theories for QCD: Part I. J. High Energy Phys. 2008, 02, 032. [Google Scholar] [CrossRef]
- Gursoy, U.; Kiritsis, E.; Nitti, F. Exploring improved holographic theories for QCD: Part II. J. High Energy Phys. 2008, 02, 019. [Google Scholar] [CrossRef]
- Gubser, S.S.; Nellore, A.; Pufu, S.S.; Rocha, F.D. Thermodynamics and bulk viscosity of approximate black hole duals to finite temperature quantum chromodynamics. Phys. Rev. Lett. 2008, 101, 131601. [Google Scholar] [CrossRef]
- Stephanov, M.A. Non-Gaussian fluctuations near the QCD critical point. Phys. Rev. Lett. 2009, 102, 032301. [Google Scholar] [CrossRef]
- Stephanov, M.A. On the sign of kurtosis near the QCD critical point. Phys. Rev. Lett. 2011, 107, 052301. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Energy Dependence of Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2014, 112, 032302. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Alekseev, I.; Alford, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barnby, L.S.; et al. Higher Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2010, 105, 022302. [Google Scholar] [CrossRef]
- Luo, X.; Xu, N. Search for the QCD Critical Point with Fluctuations of Conserved Quantities in Relativistic Heavy-Ion Collisions at RHIC: An Overview. Nucl. Sci. Tech. 2017, 28, 112. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Maity, S.; Raha, S.; Ray, R.; Saha, K.; Upadhaya, S. Reparametrizing the Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2017, 95, 054005. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mukherjee, T.K.; Mustafa, M.G.; Ray, R. PNJL model with a Van der Monde term. Phys. Rev. D 2008, 77, 094024. [Google Scholar] [CrossRef]
- Xu, K.; Li, Z.; Huang, M. QCD critical end point from a realistic PNJL model. EPJ Web Conf. 2018, 192, 00019. [Google Scholar] [CrossRef]
- Li, Z.; Xu, K.; Wang, X.; Huang, M. The kurtosis of net baryon number fluctuations from a realistic Polyakov–Nambu–Jona-Lasinio model along the experimental freeze-out line. Eur. Phys. J. C 2019, 79, 245. [Google Scholar] [CrossRef]
- Das, S. Identified particle production and freeze-out properties in heavy-ion collisions at RHIC Beam Energy Scan program. EPJ Web Conf. 2015, 90, 08007. [Google Scholar] [CrossRef]
- Begun, V.V.; Vovchenko, V.; Gorenstein, M.I. Updates to the p+p and A+A chemical freeze-out lines from the new experimental data. J. Phys. Conf. Ser. 2017, 779, 012080. [Google Scholar] [CrossRef]
- Abdallah, M.S.; Aboona, B.E.; Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, I.; Aggarwal, M.M.; Ahammed, Z.; et al. Measurements of Proton High Order Cumulants in = 3 GeV Au+Au Collisions and Implications for the QCD Critical Point. Phys. Rev. Lett. 2022, 128, 202303. [Google Scholar] [CrossRef] [PubMed]
- Fan, W.; Luo, X.; Zong, H.S. Mapping the QCD phase diagram with susceptibilities of conserved charges within Nambu–Jona-Lasinio model. Int. J. Mod. Phys. A 2017, 32, 1750061. [Google Scholar] [CrossRef]
- Shapiro, I.I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 789–791. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nature Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- van Kerkwijk, M.H.; Breton, R.; Kulkarni, S.R. Evidence for a Massive Neutron Star from a Radial-Velocity Study of the Companion to the Black Widow Pulsar PSR B1957+20. Astrophys. J. 2011, 728, 95. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, M. Holographic cold dense matter constrained by neutron stars. Phys. Rev. D 2022, 106, 096028. [Google Scholar] [CrossRef]
- Karch, A.; Katz, E.; Son, D.T.; Stephanov, M.A. Linear confinement and AdS/QCD. Phys. Rev. D 2006, 74, 015005. [Google Scholar] [CrossRef]
- McLerran, L.; Reddy, S. Quarkyonic Matter and Neutron Stars. Phys. Rev. Lett. 2019, 122, 122701. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, D.; Hou, D.; Huang, M. Quarkyonic phase from quenched dynamical holographic QCD model. J. High Energy Phys. 2020, 03, 073. [Google Scholar] [CrossRef]
- Deng, W.T.; Huang, X.G. Vorticity in Heavy-Ion Collisions. Phys. Rev. C 2016, 93, 064907. [Google Scholar] [CrossRef]
- Li, H.; Pang, L.G.; Wang, Q.; Xia, X.L. Global Λ polarization in heavy-ion collisions from a transport model. Phys. Rev. C 2017, 96, 054908. [Google Scholar] [CrossRef]
- Wei, D.X.; Deng, W.T.; Huang, X.G. Thermal vorticity and spin polarization in heavy-ion collisions. Phys. Rev. C 2019, 99, 014905. [Google Scholar] [CrossRef]
- Klevansky, S.P.; Lemmer, R.H. Chiral symmetry restoration in the Nambu-Jona-Lasinio model with a constant electromagnetic field. Phys. Rev. D 1989, 39, 3478–3489. [Google Scholar] [CrossRef]
- Klimenko, K.G. Three-dimensional Gross-Neveu model in an external magnetic field. Teor. Mat. Fiz. 1991, 89, 211–221. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Miransky, V.A.; Shovkovy, I.A. Dimensional reduction and catalysis of dynamical symmetry breaking by a magnetic field. Nucl. Phys. B 1996, 462, 249–290. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Krieg, S.; Schafer, A.; Szabo, K.K. The QCD phase diagram for external magnetic fields. J. High Energy Phys. 2012, 02, 044. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Schafer, A. QCD quark condensate in external magnetic fields. Phys. Rev. D 2012, 86, 071502. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrodi, G.; Gruber, F.; Schaefer, A. Magnetic field-induced gluonic (inverse) catalysis and pressure (an)isotropy in QCD. J. High Energy Phys. 2013, 04, 130. [Google Scholar] [CrossRef]
- Ding, H.T.; Li, S.T.; Mukherjee, S.; Tomiya, A.; Wang, X.D. Meson masses in external magnetic fields with HISQ fermions. PoS 2020, LATTICE2019, 250. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Constantinou, M.; Costa, M.; Endrodi, G.; Katz, S.D.; Panagopoulos, H.; Schafer, A. Magnetic susceptibility of QCD at zero and at finite temperature from the lattice. Phys. Rev. D 2012, 86, 094512. [Google Scholar] [CrossRef]
- Bali, G.S.; Endrodi, G.; Piemonte, S. Magnetic susceptibility of QCD matter and its decomposition from the lattice. J. High Energy Phys. 2020, 07, 183. [Google Scholar] [CrossRef]
- Xu, K.; Lin, F.; Huang, A.; Huang, M. Λ/Λ¯ polarization and splitting induced by rotation and magnetic field. Phys. Rev. D 2022, 106, L071502. [Google Scholar] [CrossRef]
- Guo, X.; Liao, J.; Wang, E. Spin Hydrodynamic Generation in the Charged Subatomic Swirl. Sci. Rep. 2020, 10, 2196. [Google Scholar] [CrossRef] [PubMed]
| / | |||
|---|---|---|---|
| 27582 | |||
| 16274 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Zhuang, P. QCD Matter and Phase Transitions under Extreme Conditions. Symmetry 2023, 15, 541. https://doi.org/10.3390/sym15020541
Huang M, Zhuang P. QCD Matter and Phase Transitions under Extreme Conditions. Symmetry. 2023; 15(2):541. https://doi.org/10.3390/sym15020541
Chicago/Turabian StyleHuang, Mei, and Pengfei Zhuang. 2023. "QCD Matter and Phase Transitions under Extreme Conditions" Symmetry 15, no. 2: 541. https://doi.org/10.3390/sym15020541
APA StyleHuang, M., & Zhuang, P. (2023). QCD Matter and Phase Transitions under Extreme Conditions. Symmetry, 15(2), 541. https://doi.org/10.3390/sym15020541





