A Study on the Intersection of Ground Reaction Forces during Overground Walking in Down Syndrome: Effects of the Pathology and Left–Right Asymmetry
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design and Participants
2.2. Procedures and Gait Data Processing
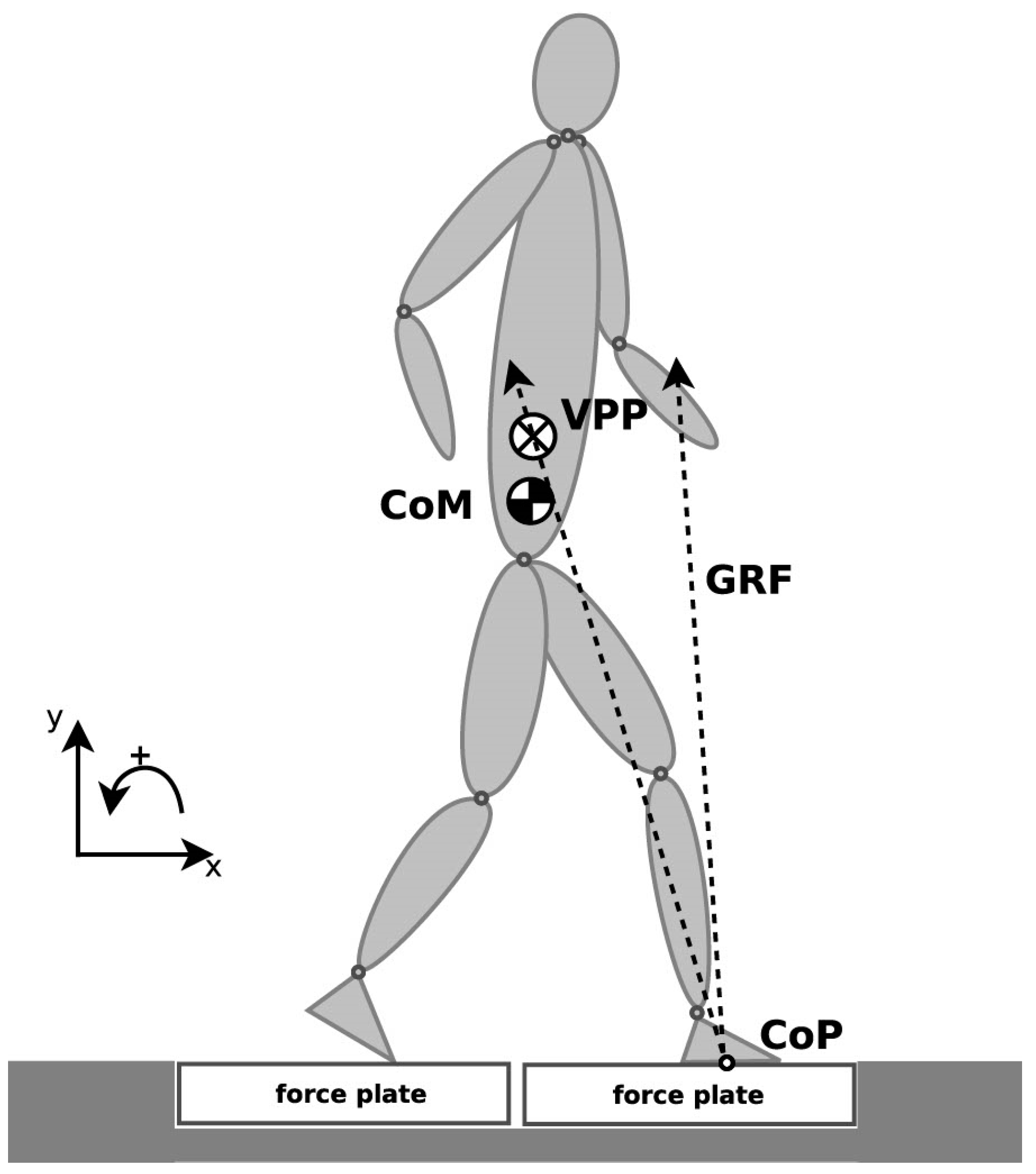
2.3. Virtual Pivot Point Computation
2.4. Symmetry Angle
2.5. Statistical Analysis
3. Results
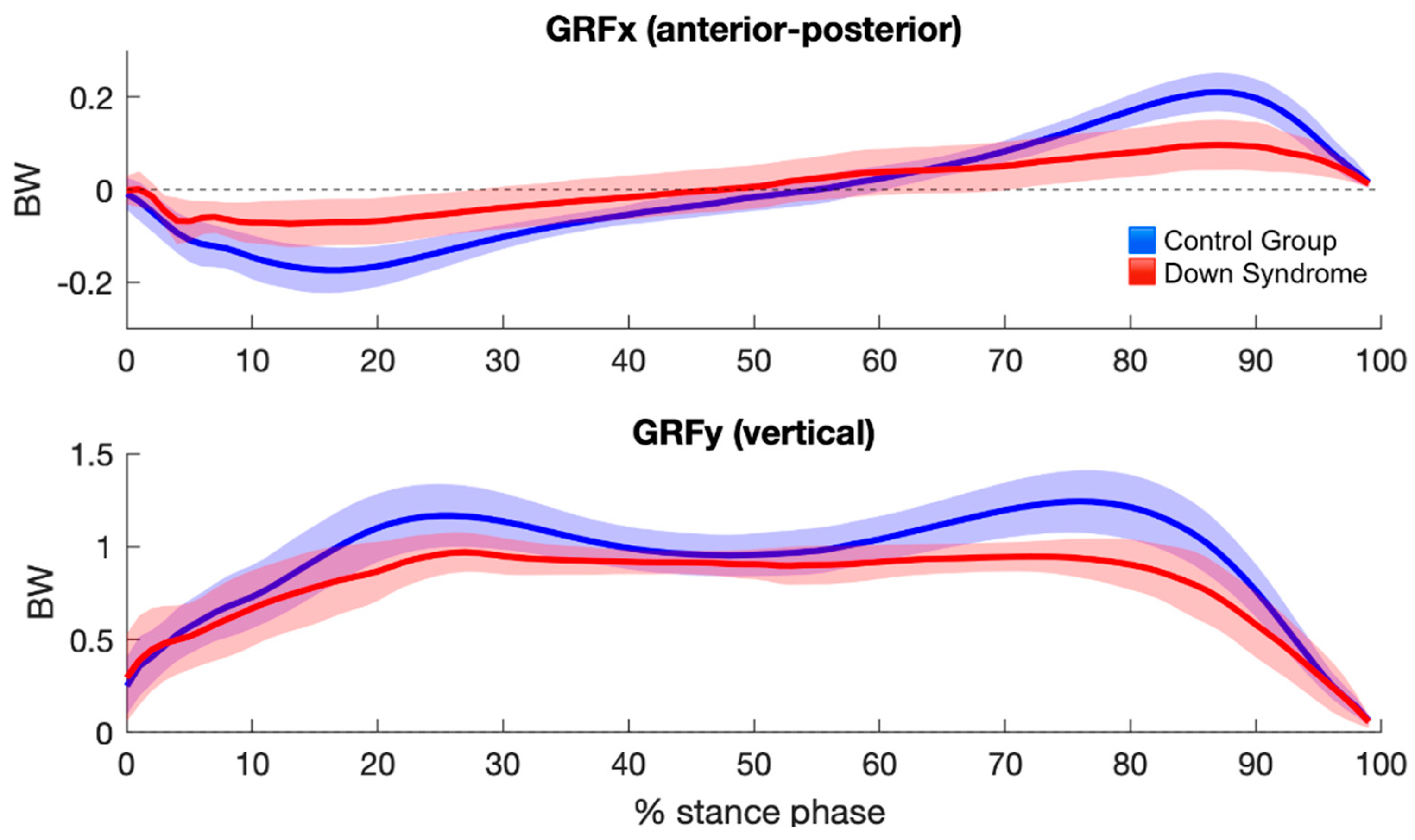
3.1. Ground Reaction Forces
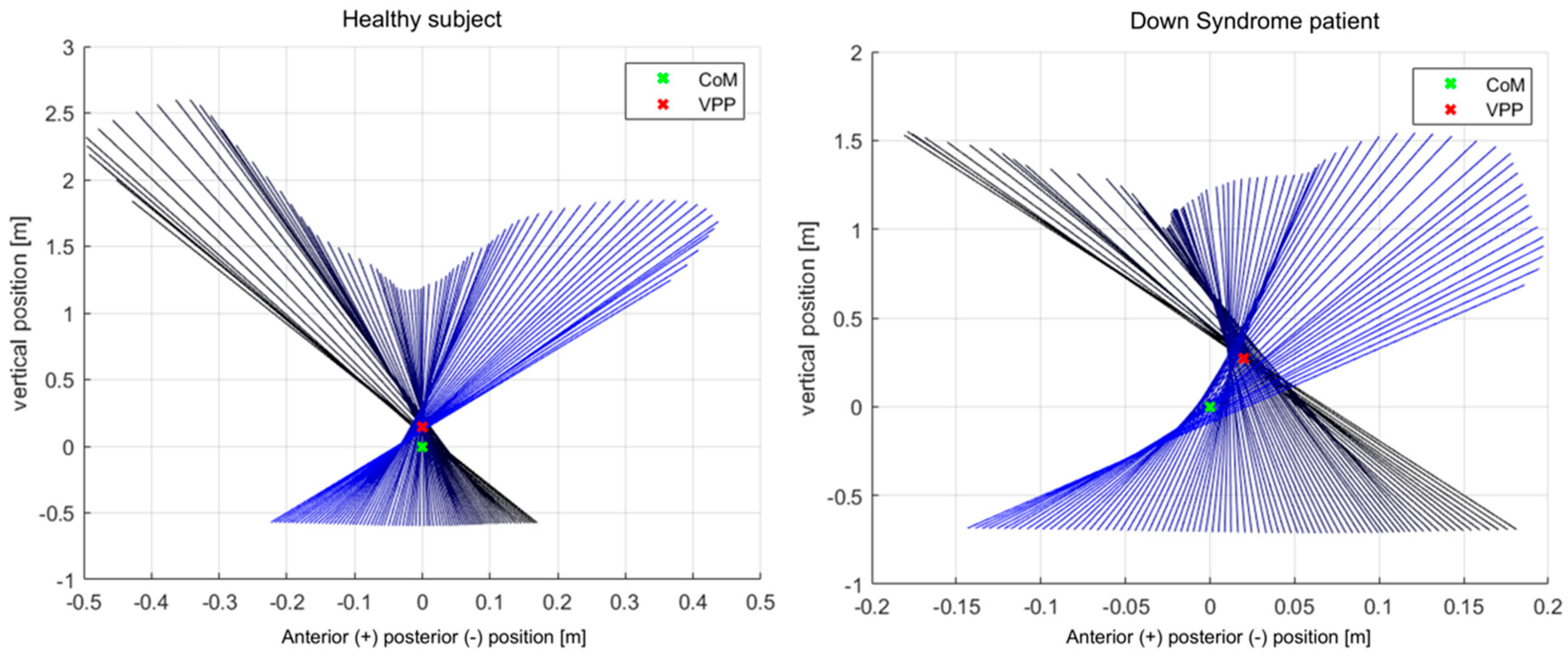
3.2. Virtual Pivot Point Position
3.3. Symmetry
4. Discussion
4.1. Virtual Pivot Point Location during Gait
4.2. Spread around One Point
4.3. Bilateral Asymmetries
4.4. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zago, M.; Duarte, N.A.C.; Grecco, L.A.C.; Condoluci, C.; Oliveira, C.S.; Galli, M. Gait and Postural Control Patterns and Rehabilitation in Down Syndrome: A Systematic Review. J. Phys. Ther. Sci. 2020, 32, 303–314. [Google Scholar] [CrossRef]
- Wiseman, F.K.; Alford, K.A.; Tybulewicz, V.L.J.; Fisher, E.M.C. Down Syndrome–Recent Progress and Future Prospects. Hum. Mol. Genet. 2009, 18, 75–83. [Google Scholar] [CrossRef]
- Anderson-Mooney, A.J.; Schmitt, F.A.; Head, E.; Lott, I.T.; Heilman, K.M. Gait Dyspraxia as a Clinical Marker of Cognitive Decline in Down Syndrome: A Review of Theory and Proposed Mechanisms. Brain Cogn. 2016, 104, 48–57. [Google Scholar] [CrossRef]
- Almuhtaseb, S.; Oppewal, A.; Hilgenkamp, T.I.M. Gait Characteristics in Individuals with Intellectual Disabilities: A Literature Review. Res. Dev. Disabil. 2014, 35, 2858–2883. [Google Scholar] [CrossRef]
- Galli, M.; Rigoldi, C.; Mainardi, L.; Tenore, N.; Onorati, P.; Albertini, G. Postural Control in Patients with Down Syndrome. Disabil. Rehabil. 2008, 30, 1274–1278. [Google Scholar] [CrossRef]
- Rigoldi, C.; Galli, M.; Albertini, G. Gait Development during Lifespan in Subjects with Down Syndrome. Res. Dev. Disabil. 2011, 32, 158–163. [Google Scholar] [CrossRef]
- Cimolin, V.; Galli, M.; Grugni, G.; Vismara, L.; Albertini, G.; Rigoldi, C.; Capodaglio, P. Gait Patterns in Prader-Willi and Down Syndrome Patients. J. Neuroeng. Rehabil. 2010, 21, 7–28. [Google Scholar] [CrossRef]
- Galli, M.; Rigoldi, C.; Brunner, R.; Virji-Babul, N.; Giorgio, A. Joint Stiffness and Gait Pattern Evaluation in Children with Down Syndrome. Gait Posture 2008, 28, 502–506. [Google Scholar] [CrossRef]
- Galli, M.; Cimolin, V.; Rigoldi, C.; Condoluci, C.; Albertini, G. Effects of Obesity on Gait Pattern in Young Individuals with Down Syndrome. Int. J. Rehabil. Res. 2015, 38, 55–60. [Google Scholar] [CrossRef]
- Vali Noghondar, N.; Saberi Kakhki, A.; Sohrabi, M.; Alirezaei Noghondar, F. Variability and Coordination Patterns of Walking with Different Speeds in Active and Non-Active Children with Down Syndrome: A Cross-Sectional Case-Control Study. Int. J. Dev. Disabil. 2022, 68, 723–731. [Google Scholar] [CrossRef]
- Agiovlasitis, S.; McCubbin, J.A.; Yun, J.; Mpitsos, G.; Pavol, M.J. Effects of Down Syndrome on Three-Dimensional Motion during Walking at Different Speeds. Gait Posture 2009, 30, 345–350. [Google Scholar] [CrossRef]
- Salami, F.; Vimercati, S.L.; Rigoldi, C.; Taebi, A.; Albertini, G.; Galli, M. Mechanical Energy Assessment of Adult with Down Syndrome during Walking with Obstacle Avoidance. Res. Dev. Disabil. 2014, 35, 1856–1862. [Google Scholar] [CrossRef]
- Benedetti, M.G.; Beghi, E.; de Tanti, A.; Cappozzo, A.; Basaglia, N.; Cutti, A.G.; Cereatti, A.; Stagni, R.; Verdini, F.; Manca, M.; et al. SIAMOC Position Paper on Gait Analysis in Clinical Practice: General Requirements, Methods and Appropriateness. Results of an Italian Consensus Conference. Gait Posture 2017, 58, 252–260. [Google Scholar] [CrossRef]
- Malloggi, C.; Zago, M.; Galli, M.; Sforza, C.; Scarano, S.; Tesio, L. Kinematic Patterns during Walking in Children: Application of Principal Component Analysis. Hum. Mov. Sci. 2021, 80, 102892. [Google Scholar] [CrossRef]
- Maus, H.M.; Lipfert, S.W.; Gross, M.; Rummel, J.; Seyfarth, A. Upright Human Gait Did Not Provide a Major Mechanical Challenge for Our Ancestors. Nat. Commun. 2010, 1, 70. [Google Scholar] [CrossRef]
- Müller, R.; Rode, C.; Aminiaghdam, S.; Vielemeyer, J.; Blickhan, R. Force Direction Patterns Promote Whole Body Stability Even in Hip-Flexed Walking, but Not Upper Body Stability in Human Upright Walking. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170404. [Google Scholar] [CrossRef]
- Vielemeyer, J.; Grießbach, E.; Müller, R. Ground Reaction Forces Intersect above the Center of Mass Even When Walking down Visible and Camouflaged Curbs. J. Exp. Biol. 2019, 222, jeb.204305. [Google Scholar] [CrossRef]
- Vielemeyer, J.; Müller, R.; Staufenberg, N.S.; Renjewski, D.; Abel, R. Ground Reaction Forces Intersect above the Center of Mass in Single Support, but Not in Double Support of Human Walking. J. Biomech. 2021, 120, 110387. [Google Scholar] [CrossRef]
- Gruben, K.G.; Boehm, W.L. Force Direction Pattern Stabilizes Sagittal Plane Mechanics of Human Walking. Hum. Mov. Sci. 2012, 31, 649–659. [Google Scholar] [CrossRef]
- Sharbafi, M.A.; Barazesh, H.; Iranikhah, M.; Seyfarth, A. Leg Force Control Through Biarticular Muscles for Human Walking Assistance. Front. Neurorobot. 2018, 12, 39. [Google Scholar] [CrossRef]
- Blickhan, R.; Andrada, E.; Müller, R.; Rode, C.; Ogihara, N. Positioning the Hip with Respect to the COM: Consequences for Leg Operation. J. Theor. Biol. 2015, 382, 187–197. [Google Scholar] [CrossRef]
- Andrada, E.; Rode, C.; Sutedja, Y.; Nyakatura, J.A.; Blickhan, R. Trunk Orientation Causes Asymmetries in Leg Function in Small Bird Terrestrial Locomotion. Proc. R. Soc. B Biol. Sci. 2014, 281, 20141405. [Google Scholar] [CrossRef]
- Zago, M.; Federolf, P.A.; Levy, S.R.; Condoluci, C.; Galli, M. Down Syndrome: Gait Pattern Alterations in Posture Space Kinematics. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1589–1596. [Google Scholar] [CrossRef]
- Rigoldi, C.; Galli, M.; Cimolin, V.; Camerota, F.; Celletti, C.; Tenore, N.; Albertini, G. Gait Strategy in Patients with Ehlers-Danlos Syndrome Hypermobility Type and Down Syndrome. Res. Dev. Disabil. 2012, 33, 1437–1442. [Google Scholar] [CrossRef]
- Belluscio, V.; Bergamini, E.; Salatino, G.; Marro, T.; Gentili, P.; Iosa, M.; Morelli, D.; Vannozzi, G. Dynamic Balance Assessment during Gait in Children with Down and Prader-Willi Syndromes Using Inertial Sensors. Hum. Mov. Sci. 2019, 63, 53–61. [Google Scholar] [CrossRef]
- Valero, C.; Mustacchi, Z.; Bezerra, P.M.; Figueiredo, F.W.S.; Martinelli, P.M.; Carvalho, A.A.S.; Feder, D. Foot Rotation Asymmetry in Down Syndrome and the Relationship with Crawling and Walking Onset: A Crosssectional Study. J. Hum. Growth Dev. 2021, 31, 247–256. [Google Scholar] [CrossRef]
- Winter, D.A. Energy Generation and Absorption at the Ankle and Knee during Fast, Natural, and Slow Cadences. Clin. Orthop. Relat. Res. 1983, 175, 147–154. [Google Scholar] [CrossRef]
- Liu, M.Q.; Anderson, F.C.; Schwartz, M.H.; Delp, S.L. Muscle Contributions to Support and Progression over a Range of Walking Speeds. J. Biomech. 2008, 41, 3243–3252. [Google Scholar] [CrossRef]
- Wu, J.; Ajisafe, T. Kinetic Patterns of Treadmill Walking in Preadolescents with and without Down Syndrome. Gait Posture 2014, 39, 241–246. [Google Scholar] [CrossRef]
- Wu, J.; Beerse, M.; Ajisafe, T. Frequency Domain Analysis of Ground Reaction Force in Preadolescents with and without Down Syndrome. Res. Dev. Disabil. 2014, 35, 1244–1251. [Google Scholar] [CrossRef]
- Davis, R.B.; Õunpuu, S.; Tyburski, D.; Gage, J.R. A Gait Analysis Data Collection and Reduction Technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Ganley, K.J.; Powers, C.M. Anthropometric Parameters in Children: A Comparison of Values Obtained from Dual Energy x-Ray Absorptiometry and Cadaver-Based Estimates. Gait Posture 2004, 19, 133–140. [Google Scholar] [CrossRef]
- Muri, J.; Winter, S.L.; Challis, J.H. Changes in Segmental Inertial Properties with Age. J. Biomech. 2008, 41, 1809–1812. [Google Scholar] [CrossRef]
- Avrin, R.; Davis, I.; Higginson, J.; Royer, T. The Symmetry Angle: A Novel, Robust Method of Quantifying Asymmetry. Gait Posture 2008, 27, 622–627. [Google Scholar] [CrossRef]
- Richardson, J.T.E. Eta Squared and Partial Eta Squared as Measures of Effect Size in Educational Research. Educ. Res. Rev. 2011, 6, 135–147. [Google Scholar] [CrossRef]
- Lewis, C.L.; Ferris, D.P. Walking with Increased Ankle Pushoff Decreases Hip Muscle Moments. J. Biomech. 2008, 41, 2082–2089. [Google Scholar] [CrossRef]
- DeVita, P.; Hortobagyi, T. Age Causes a Redistribution of Joint Torques and Powers during Gait. J. Appl. Physiol. 2000, 88, 1804–1811. [Google Scholar] [CrossRef]
- Judge, J.O.; Davis, R.B.; Öunpuu, S. Step Length Reductions in Advanced Age: The Role of Ankle and Hip Kinetics. J. Gerontol.–Ser. A Biol. Sci. Med. Sci. 1996, 51, M303–M312. [Google Scholar] [CrossRef]
- Mueller, M.J.; Minor, S.D.; Sahrmann, S.A.; Schaaf, J.A.; Strube, M.J. Differences in the Gait Characteristics of Patients with Diabetes and Peripheral Neuropathy Compared with Age-Matched Controls. Phys. Ther. 1994, 74, 299–308. [Google Scholar] [CrossRef]
- Drama, Ö.; Vielemeyer, J.; Badri-Spröwitz, A.; Müller, R. Postural Stability in Human Running with Step-down Perturbations: An Experimental and Numerical Study: Postural Stability in Human Running. R. Soc. Open Sci. 2020, 7, 200570. [Google Scholar] [CrossRef]
- Agiovlasitis, S.; McCubbin, J.A.; Yun, J.; Widrick, J.J.; Pavol, M.J. Gait Characteristics of Adults with Down Syndrome Explain Their Greater Metabolic Rate during Walking. Gait Posture 2015, 41, 180–184. [Google Scholar] [CrossRef]
- Masani, K.; Kouzaki, M.; Fukunaga, T. Variability of Ground Reaction Forces during Treadmill Walking. J. Appl. Physiol. 2002, 92, 1885–1890. [Google Scholar] [CrossRef]
- Zago, M.; di Giuli, R.; Beltramini, G.; Bolzoni, A.; Baj, A.; Galli, M.; Giannì, A.B.; Sforza, C. Donor-Site Morbidity after Osteocutaneous Free Fibula Transfer: Longitudinal Analysis of Stair Climbing Asymmetry and Functional Outcome. Symmetry 2022, 14, 1888. [Google Scholar] [CrossRef]

| Group | |||
|---|---|---|---|
| Variable | Unit | Down Syndrome | Control |
| Age | years | 17.7 (6.1) | 15.5 (6.4) |
| Height | m | 1.46 (0.11) | 1.58 (0.15) |
| Weight | kg | 56.9 (14.5) | 55.8 (17.9) |
| Body mass index | kg·m−2 | 25.2 (4.4) | 21.7 (3.5) |
| Gait speed | m·s−1 | 0.94 (0.12) | 1.00 (0.15) |
| Group | Speed | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | Group | Mean | SD | p | F | η2 | p | F | η2 |
| VPPx | CG | 0.1 | 1.4 | 0.006 | 8.30 | 0.142 | 0.579 | 0.31 | 0.006 |
| DS | 1.2 | 1.2 | |||||||
| VPPy | CG | 14.0 | 7.1 | 0.146 | 2.18 | 0.042 | 0.811 | 0.06 | 0.001 |
| DS | 12.7 | 9.7 | |||||||
| R2 | CG | 0.980 | 0.034 | 0.410 | 0.69 | 0.014 | 0.810 | 0.06 | 0.001 |
| DS | 0.971 | 0.054 | |||||||
| SAx | CG | 41.4 | 45.3 | 0.337 | 0.94 | 0.017 | - | - | - |
| DS | 31.3 | 32.0 | |||||||
| SAy | CG | 15.6 | 18.5 | 0.357 | 0.86 | 0.015 | - | - | - |
| DS | 20.4 | 20.6 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vielemeyer, J.; Sole, C.; Galli, M.; Zago, M.; Müller, R.; Condoluci, C. A Study on the Intersection of Ground Reaction Forces during Overground Walking in Down Syndrome: Effects of the Pathology and Left–Right Asymmetry. Symmetry 2023, 15, 544. https://doi.org/10.3390/sym15020544
Vielemeyer J, Sole C, Galli M, Zago M, Müller R, Condoluci C. A Study on the Intersection of Ground Reaction Forces during Overground Walking in Down Syndrome: Effects of the Pathology and Left–Right Asymmetry. Symmetry. 2023; 15(2):544. https://doi.org/10.3390/sym15020544
Chicago/Turabian StyleVielemeyer, Johanna, Cristina Sole, Manuela Galli, Matteo Zago, Roy Müller, and Claudia Condoluci. 2023. "A Study on the Intersection of Ground Reaction Forces during Overground Walking in Down Syndrome: Effects of the Pathology and Left–Right Asymmetry" Symmetry 15, no. 2: 544. https://doi.org/10.3390/sym15020544
APA StyleVielemeyer, J., Sole, C., Galli, M., Zago, M., Müller, R., & Condoluci, C. (2023). A Study on the Intersection of Ground Reaction Forces during Overground Walking in Down Syndrome: Effects of the Pathology and Left–Right Asymmetry. Symmetry, 15(2), 544. https://doi.org/10.3390/sym15020544








