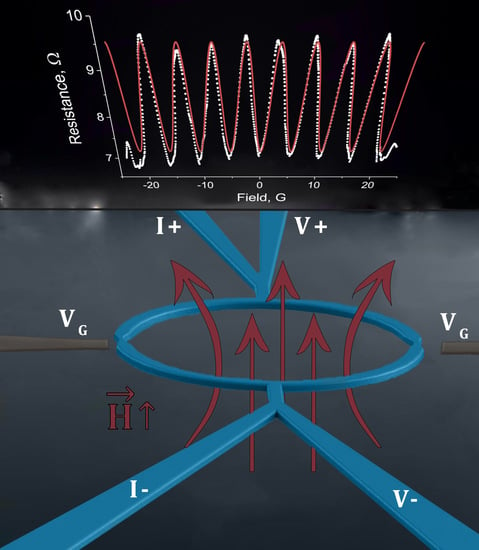
Controlling I-V Hysteresis in Al/Pt Bilayer Symmetric SQUIDs at Millikelvin Temperatures
Abstract
:1. Introduction
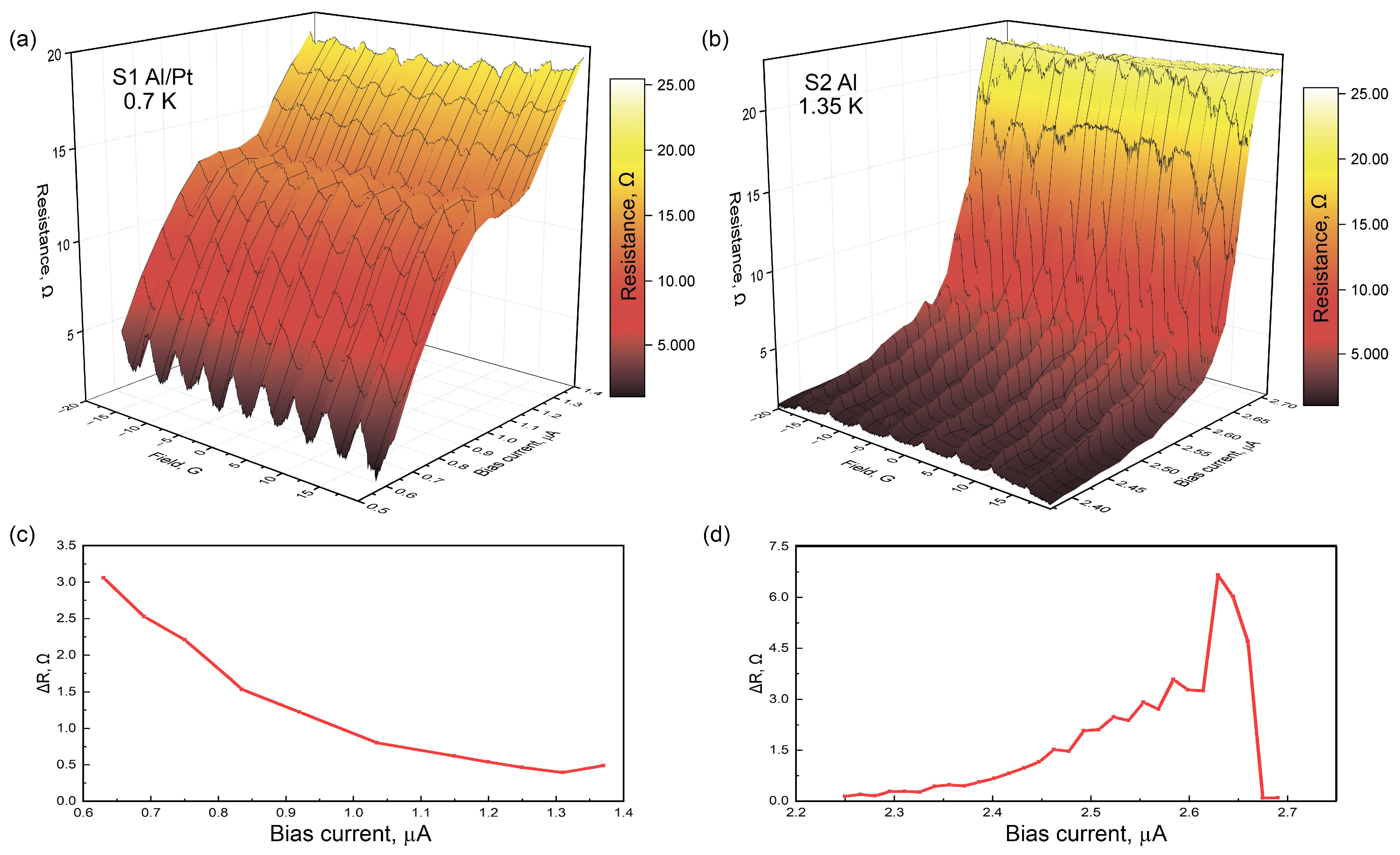
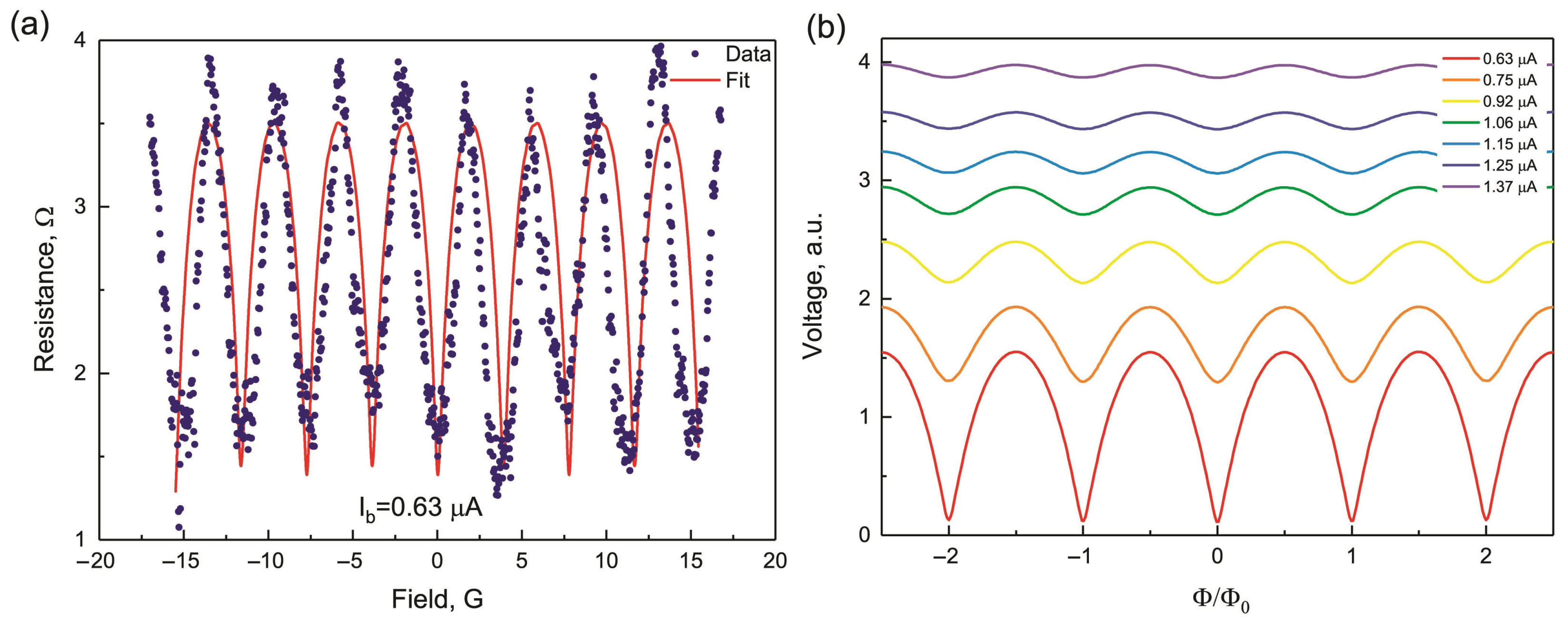
2. Results and Discussion
3. Methods
3.1. E-Beam Lithography and Deposition
3.2. Measurement Details
3.3. Magnetoresistance Oscillation Fitting
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clarke, J. SQUID fundamentals. In SQUID Sensors: Fundamentals, Fabrication and Applications; Springer: Dordrecht, The Netherlands, 1996; pp. 1–62. [Google Scholar]
- Anahory, Y.; Naren, H.; Lachman, E.; Sinai, S.B.; Uri, A.; Embon, L.; Yaakobi, E.; Myasoedov, Y.; Huber, M.; Klajn, R.; et al. SQUID-on-tip with single-electron spin sensitivity for high-field and ultra-low temperature nanomagnetic imaging. Nanoscale 2020, 12, 3174–3182. [Google Scholar] [CrossRef] [PubMed]
- Granata, C.; Vettoliere, A.; Walke, P.; Esposito, E.; Nappi, C.; Silvestrini, P.; Ruggiero, B.; Russo, M. NANO-SQUIDs based on niobium Dayem bridges for nanoscale applications. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2010; Volume 234, p. 042010. [Google Scholar]
- Josephs-Franks, P.; Hao, L.; Tzalenchuk, A.; Davies, J.; Kazakova, O.; Gallop, J.; Brown, L.; Macfarlane, J. Measurement of the spatial sensitivity of miniature SQUIDs using magnetic-tipped STM. Supercond. Sci. Technol. 2003, 16, 1570. [Google Scholar] [CrossRef] [Green Version]
- Huber, M.E.; Koshnick, N.C.; Bluhm, H.; Archuleta, L.J.; Azua, T.; Björnsson, P.G.; Gardner, B.W.; Halloran, S.T.; Lucero, E.A.; Moler, K.A. Gradiometric micro-SQUID susceptometer for scanning measurements of mesoscopic samples. Rev. Sci. Instrum. 2008, 79, 053704. [Google Scholar] [CrossRef] [PubMed]
- Bouchiat, V. Detection of magnetic moments using a nano-SQUID: Limits of resolution and sensitivity in near-field SQUID magnetometry. Supercond. Sci. Technol. 2009, 22, 064002. [Google Scholar] [CrossRef]
- Granata, C.; Vettoliere, A. Nano superconducting quantum interference device: A powerful tool for nanoscale investigations. Phys. Rep. 2016, 614, 1–69. [Google Scholar] [CrossRef] [Green Version]
- Kudriashov, A.; Babich, I.; Hovhannisyan, R.A.; Shishkin, A.G.; Kozlov, S.N.; Fedorov, A.; Vyalikh, D.V.; Khestanova, E.; Kupriyanov, M.Y.; Stolyarov, V.S. Revealing Intrinsic Superconductivity of the Nb/BiSbTe2Se Interface. Adv. Funct. Mater. 2022, 32, 2209853. [Google Scholar] [CrossRef]
- Hazra, D.; Pascal, L.M.; Courtois, H.; Gupta, A.K. Hysteresis in superconducting short weak links and μ-SQUIDs. Phys. Rev. B 2010, 82, 184530. [Google Scholar] [CrossRef] [Green Version]
- Keijers, W.; Baumans, X.D.; Panghotra, R.; Lombardo, J.; Zharinov, V.S.; Kramer, R.B.; Silhanek, A.V.; Van de Vondel, J. Nano-SQUIDs with controllable weak links created via current-induced atom migration. Nanoscale 2018, 10, 21475–21482. [Google Scholar] [CrossRef]
- Ishiguro, R.; Watanabe, E.; Sakuma, D.; Shinozaki, T.; Tsuchiya, S.; Nago, Y.; Osato, H.; Tsuya, D.; Kashiwaya, H.; Kashiwaya, S.; et al. Development of nano and micro SQUIDs based on Al tunnel junctions. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2014; Volume 568, p. 022019. [Google Scholar]
- Gallop, J. SQUIDs: Some limits to measurement. Supercond. Sci. Technol. 2003, 16, 1575. [Google Scholar] [CrossRef]
- Wernsdorfer, W. From micro-to nano-SQUIDs: Applications to nanomagnetism. Supercond. Sci. Technol. 2009, 22, 064013. [Google Scholar] [CrossRef]
- Golikova, T.E.; Wolf, M.J.; Beckmann, D.; Penzyakov, G.A.; Batov, I.E.; Bobkova, I.; Bobkov, A.M.; Ryazanov, V.V. Controllable supercurrent in mesoscopic superconductor-normal metal-ferromagnetcrosslike Josephson structures. Supercond. Sci. Technol. 2021, 34, 095001. [Google Scholar] [CrossRef]
- Frielinghaus, R.; Batov, I.; Weides, M.; Kohlstedt, H.; Calarco, R.; Schäpers, T. Josephson supercurrent in Nb/InN-nanowire/Nb junctions. Appl. Phys. Lett. 2010, 96, 132504. [Google Scholar] [CrossRef] [Green Version]
- Yakovlev, D.S.; Lvov, D.S.; Emelyanova, O.V.; Dzhumaev, P.S.; Shchetinin, I.V.; Skryabina, O.V.; Egorov, S.V.; Ryazanov, V.V.; Golubov, A.A.; Roditchev, D.; et al. Physical Vapor Deposition Features of Ultrathin Nanocrystals of Bi2 (Te x Se1–x) 3. J. Phys. Chem. Lett. 2022, 13, 9221–9231. [Google Scholar] [CrossRef] [PubMed]
- Sotnichuk, S.V.; Skryabina, O.V.; Shishkin, A.G.; Bakurskiy, S.V.; Kupriyanov, M.Y.; Stolyarov, V.S.; Napolskii, K.S. Long Single Au Nanowires in Nb/Au/Nb Josephson Junctions: Implications for Superconducting Microelectronics. ACS Appl. Nano Mater. 2022, 5, 17059–17066. [Google Scholar] [CrossRef]
- Karelina, L.; Hovhannisyan, R.A.; Golovchanskiy, I.; Chichkov, V.; Ben Hamida, A.; Stolyarov, V.; Uspenskaya, L.; Erkenov, S.A.; Bolginov, V.; Ryazanov, V. Scalable memory elements based on rectangular SIsFS junctions. J. Appl. Phys. 2021, 130, 173901. [Google Scholar] [CrossRef]
- Angers, L.; Chiodi, F.; Montambaux, G.; Ferrier, M.; Guéron, S.; Bouchiat, H.; Cuevas, J. Proximity dc squids in the long-junction limit. Phys. Rev. B 2008, 77, 165408. [Google Scholar] [CrossRef] [Green Version]
- Courtois, H.; Meschke, M.; Peltonen, J.; Pekola, J.P. Origin of hysteresis in a proximity Josephson junction. Phys. Rev. Lett. 2008, 101, 067002. [Google Scholar] [CrossRef] [Green Version]
- Kumar, N.; Winkelmann, C.; Biswas, S.; Courtois, H.; Gupta, A.K. Controlling hysteresis in superconducting constrictions with a resistive shunt. Supercond. Sci. Technol. 2015, 28, 072003. [Google Scholar] [CrossRef] [Green Version]
- Foglietti, V.; Gallagher, W.; Ketchen, M.; Kleinsasser, A.; Koch, R.; Sandstrom, R. Performance of dc SQUIDs with resistively shunted inductance. Appl. Phys. Lett. 1989, 55, 1451–1453. [Google Scholar] [CrossRef]
- Nagel, J.; Konovalenko, K.; Kemmler, M.; Turad, M.; Werner, R.; Kleisz, E.; Menzel, S.; Klingeler, R.; Büchner, B.; Kleiner, R.; et al. Resistively shunted YBa2Cu3O7 grain boundary junctions and low-noise SQUIDs patterned by a focused ion beam down to 80 nm linewidth. Supercond. Sci. Technol. 2010, 24, 015015. [Google Scholar] [CrossRef] [Green Version]
- Muck, M.; Heiden, C. Simple DC-SQUID system based on a frequency modulated relaxation oscillator. IEEE Trans. Magn. 1989, 25, 1151–1153. [Google Scholar] [CrossRef]
- Hovhannisyan, R.A.; Kapran, O.M.; Golod, T.; Krasnov, V.M. Accurate Determination of the Josephson Critical Current by Lock-In Measurements. Nanomaterials 2021, 11, 2058. [Google Scholar] [CrossRef] [PubMed]
- Blois, A.; Rozhko, S.; Hao, L.; Gallop, J.; Romans, E. Proximity effect bilayer nano superconducting quantum interference devices for millikelvin magnetometry. J. Appl. Phys. 2013, 114, 233907. [Google Scholar] [CrossRef]
- Vodolazov, D.Y.; Aladyshkin, A.Y.; Pestov, E.; Vdovichev, S.; Ustavshikov, S.; Levichev, M.Y.; Putilov, A.; Yunin, P.; El’kina, A.; Bukharov, N.; et al. Peculiar superconducting properties of a thin film superconductor–normal metal bilayer with large ratio of resistivities. Supercond. Sci. Technol. 2018, 31, 115004. [Google Scholar] [CrossRef]
- Blois, A.; Rozhko, S.; Hao, L.; Gallop, J.; Romans, E. Heat propagation models for superconducting nanobridges at millikelvin temperatures. Supercond. Sci. Technol. 2016, 30, 014003. [Google Scholar] [CrossRef]
- Burnett, J.; Faoro, L.; Wisby, I.; Gurtovoi, V.; Chernykh, A.; Mikhailov, G.; Tulin, V.; Shaikhaidarov, R.; Antonov, V.; Meeson, P.; et al. Evidence for interacting two-level systems from the 1/f noise of a superconducting resonator. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Barone, C.; Rotzinger, H.; Voss, J.N.; Mauro, C.; Schön, Y.; Ustinov, A.V.; Pagano, S. Current-resistance effects inducing nonlinear fluctuation mechanisms in granular aluminum oxide nanowires. Nanomaterials 2020, 10, 524. [Google Scholar] [CrossRef] [Green Version]
- Burin, A.L.; Matityahu, S.; Schechter, M. Low-temperature 1/f noise in microwave dielectric constant of amorphous dielectrics in Josephson qubits. Phys. Rev. B 2015, 92, 174201. [Google Scholar] [CrossRef] [Green Version]
- Sofer, Z.; Shaulov, A.; Yeshurun, Y. Current dependence of the negative magnetoresistance in superconducting NbN nanowires. Sci. Rep. 2022, 12, 22027. [Google Scholar] [CrossRef]
- Jouan, A.; Hurand, S.; Singh, G.; Lesne, E.; Barthélémy, A.; Bibes, M.; Ulysse, C.; Saiz, G.; Feuillet-Palma, C.; Lesueur, J.; et al. Multiband Effects in the Superconducting Phase Diagram of Oxide Interfaces. Adv. Mater. Interfaces 2022, 9, 2201392. [Google Scholar] [CrossRef]
- Müller, C.; Lisenfeld, J.; Shnirman, A.; Poletto, S. Interacting two-level defects as sources of fluctuating high-frequency noise in superconducting circuits. Phys. Rev. B 2015, 92, 035442. [Google Scholar] [CrossRef] [Green Version]
- Bilmes, A.; Zanker, S.; Heimes, A.; Marthaler, M.; Schön, G.; Weiss, G.; Ustinov, A.V.; Lisenfeld, J. Electronic decoherence of two-level systems in a Josephson junction. Phys. Rev. B 2017, 96, 064504. [Google Scholar] [CrossRef] [Green Version]
- Martinis, J.M.; Hilton, G.C.; Irwin, K.D.; Wollman, D.A. Calculation of TC in a normal-superconductor bilayer using the microscopic-based Usadel theory. Nucl. Instrum. Methods Phys. Res. Sect. 2000, 444, 23–27. [Google Scholar] [CrossRef]
- Holzman, I.; Ivry, Y. On-chip integrable planar NbN nanoSQUID with broad temperature and magnetic-field operation range. AIP Adv. 2019, 9, 105028. [Google Scholar] [CrossRef] [Green Version]
- Russo, R.; Esposito, E.; Crescitelli, A.; Di Gennaro, E.; Granata, C.; Vettoliere, A.; Cristiano, R.; Lisitskiy, M. NanoSQUIDs based on niobium nitride films. Supercond. Sci. Technol. 2016, 30, 024009. [Google Scholar] [CrossRef]
- Faley, M.; Fiadziushkin, H.; Frohn, B.; Schüffelgen, P.; Dunin-Borkowski, R. TiN nanobridge Josephson junctions and nanoSQUIDs on SiN-buffered Si. Supercond. Sci. Technol. 2022, 35, 065001. [Google Scholar] [CrossRef]
- Faley, M.I.; Liu, Y.; Dunin-Borkowski, R.E. Titanium nitride as a new prospective material for nanoSQUIDS and superconducting nanobridge electronics. Nanomaterials 2021, 11, 466. [Google Scholar] [CrossRef] [PubMed]
- Shishkin, A.; Skryabina, O.; Gurtovoi, V.; Dizhur, S.; Faley, M.; Golubov, A.; Stolyarov, V. Planar MoRe-based direct current nanoSQUID. Supercond. Sci. Technol. 2020, 33, 065005. [Google Scholar] [CrossRef]
- Rigetti, C.; Gambetta, J.M.; Poletto, S.; Plourde, B.; Chow, J.M.; Córcoles, A.; Smolin, J.A.; Merkel, S.T.; Rozen, J.; Keefe, G.A.; et al. Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Phys. Rev. B 2012, 86, 100506. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, O.; Burnett, J.; Fenton, J.; Constantino, N.; Warburton, P.; Morton, J.; Dupont-Ferrier, E. Tunable Nb superconducting resonator based on a constriction nano-SQUID fabricated with a Ne focused ion beam. Phys. Rev. Appl. 2019, 11, 014006. [Google Scholar] [CrossRef] [Green Version]
- Levenson-Falk, E.; Vijay, R.; Antler, N.; Siddiqi, I. A dispersive nanoSQUID magnetometer for ultra-low noise, high bandwidth flux detection. Supercond. Sci. Technol. 2013, 26, 055015. [Google Scholar] [CrossRef] [Green Version]
- Tesche, C.D.; Clarke, J. DC SQUID: Noise and optimization. J. Low Temp. Phys. 1977, 29, 301–331. [Google Scholar] [CrossRef] [Green Version]
- Soloviev, I.; Klenov, N.; Schegolev, A.; Bakurskiy, S.; Kupriyanov, M.Y. Analytical derivation of DC SQUID response. Supercond. Sci. Technol. 2016, 29, 094005. [Google Scholar] [CrossRef] [Green Version]
- Lam, S.K.; Clem, J.R.; Yang, W. A nanoscale SQUID operating at high magnetic fields. Nanotechnology 2011, 22, 455501. [Google Scholar] [CrossRef] [PubMed]
- Hao, L.; Macfarlane, J.; Gallop, J.; Cox, D.; Beyer, J.; Drung, D.; Schurig, T. Measurement and noise performance of nano-superconducting-quantum-interference devices fabricated by focused ion beam. Appl. Phys. Lett. 2008, 92, 192507. [Google Scholar] [CrossRef] [Green Version]
- Dausy, H.; Nulens, L.; Raes, B.; Van Bael, M.J.; Van de Vondel, J. Impact of Kinetic Inductance on the Critical-Current Oscillations of Nanobridge SQUIDs. Phys. Rev. Appl. 2021, 16, 024013. [Google Scholar] [CrossRef]
- Aref, T.; Levchenko, A.; Vakaryuk, V.; Bezryadin, A. Quantitative analysis of quantum phase slips in superconducting Mo76Ge24 nanowires revealed by switching-current statistics. Phys. Rev. B 2012, 86, 024507. [Google Scholar] [CrossRef] [Green Version]
- Vijay, R.; Levenson-Falk, E.; Slichter, D.; Siddiqi, I. Approaching ideal weak link behavior with three dimensional aluminum nanobridges. Appl. Phys. Lett. 2010, 96, 223112. [Google Scholar] [CrossRef] [Green Version]
- Poli, N.; Morten, J.P.; Urech, M.; Brataas, A.; Haviland, D.B.; Korenivski, V. Spin injection and relaxation in a mesoscopic superconductor. Phys. Rev. Lett. 2008, 100, 136601. [Google Scholar] [CrossRef] [Green Version]
- Jedema, F.; Heersche, H.; Filip, A.; Baselmans, J.; Van Wees, B. Electrical detection of spin precession in a metallic mesoscopic spin valve. Nature 2002, 416, 713–716. [Google Scholar] [CrossRef]
- Scheller, C.P.; Heizmann, S.; Bedner, K.; Giss, D.; Meschke, M.; Zumbühl, D.M.; Zimmerman, J.D.; Gossard, A.C. Silver-epoxy microwave filters and thermalizers for millikelvin experiments. Appl. Phys. Lett. 2014, 104, 211106. [Google Scholar] [CrossRef] [Green Version]
- Stolyarov, V.S.; Roditchev, D.; Gurtovoi, V.L.; Kozlov, S.N.; Yakovlev, D.S.; Skryabina, O.V.; Vinokur, V.M.; Golubov, A.A. Resonant Oscillations of Josephson Current in Nb-Bi2Te2. 3Se0. 7-Nb Junctions. Adv. Quantum Technol. 2022, 5, 2100124. [Google Scholar] [CrossRef]

| Sample | d, nm | L, nm | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Al/Pt | 2.93 | 23 | 55 ± 2 | 30 ± 1 | 50 ± 10 | 5.3 | 3.8 | 0.8 | 40.93 |
| Al | 28.4 | 24 | 52 ± 2 | 25 ± 3 | 50 ± 10 | 4.79 | 4.3 | 1.41 | 35.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakovlev, D.S.; Nazhestkin, I.A.; Ismailov, N.G.; Egorov, S.V.; Antonov, V.N.; Gurtovoi, V.L. Controlling I-V Hysteresis in Al/Pt Bilayer Symmetric SQUIDs at Millikelvin Temperatures. Symmetry 2023, 15, 550. https://doi.org/10.3390/sym15020550
Yakovlev DS, Nazhestkin IA, Ismailov NG, Egorov SV, Antonov VN, Gurtovoi VL. Controlling I-V Hysteresis in Al/Pt Bilayer Symmetric SQUIDs at Millikelvin Temperatures. Symmetry. 2023; 15(2):550. https://doi.org/10.3390/sym15020550
Chicago/Turabian StyleYakovlev, Dmitry S., Ivan A. Nazhestkin, Nidzhat G. Ismailov, Sergei V. Egorov, Vladimir N. Antonov, and Vladimir L. Gurtovoi. 2023. "Controlling I-V Hysteresis in Al/Pt Bilayer Symmetric SQUIDs at Millikelvin Temperatures" Symmetry 15, no. 2: 550. https://doi.org/10.3390/sym15020550
APA StyleYakovlev, D. S., Nazhestkin, I. A., Ismailov, N. G., Egorov, S. V., Antonov, V. N., & Gurtovoi, V. L. (2023). Controlling I-V Hysteresis in Al/Pt Bilayer Symmetric SQUIDs at Millikelvin Temperatures. Symmetry, 15(2), 550. https://doi.org/10.3390/sym15020550