On the Solutions of the Fractional-Order Sawada–Kotera–Ito Equation and Modeling Nonlinear Structures in Fluid Mediums
Abstract
1. Introduction
2. Preliminaries
3. Fundamental Concept of HPTM
4. Fundamental Concept of ZTDM
5. Application
Example
- Implementation of ZTDM
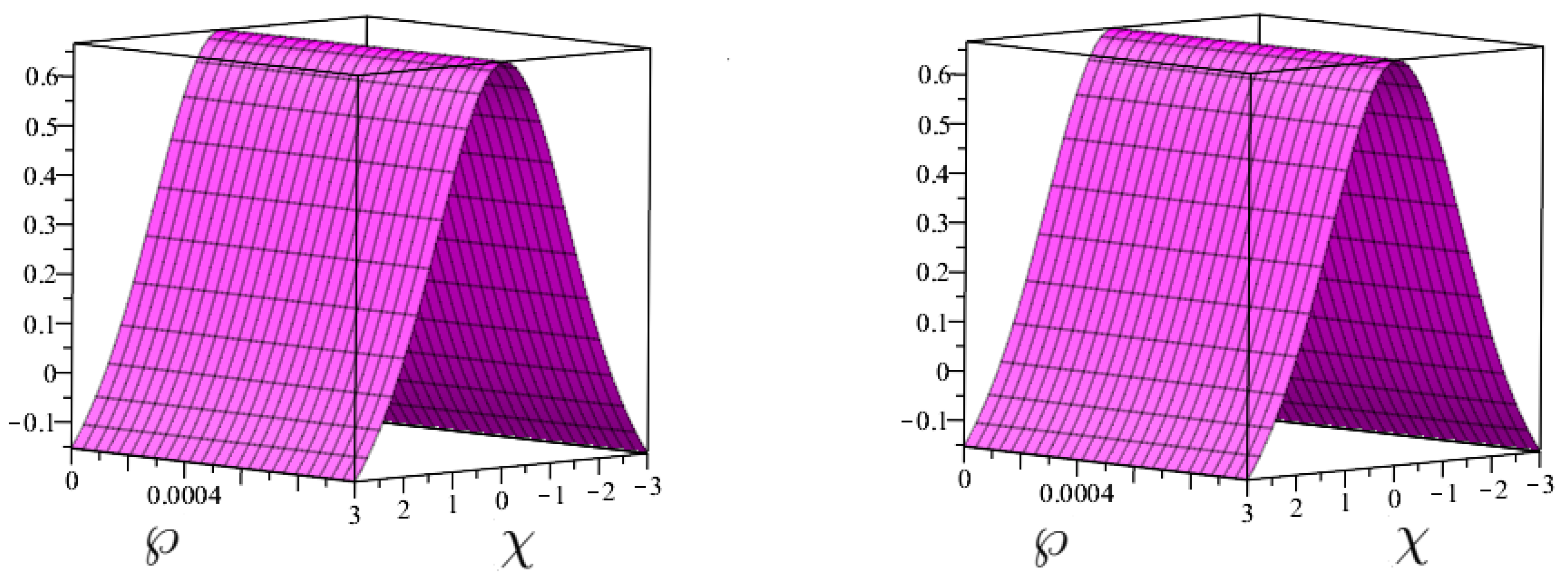
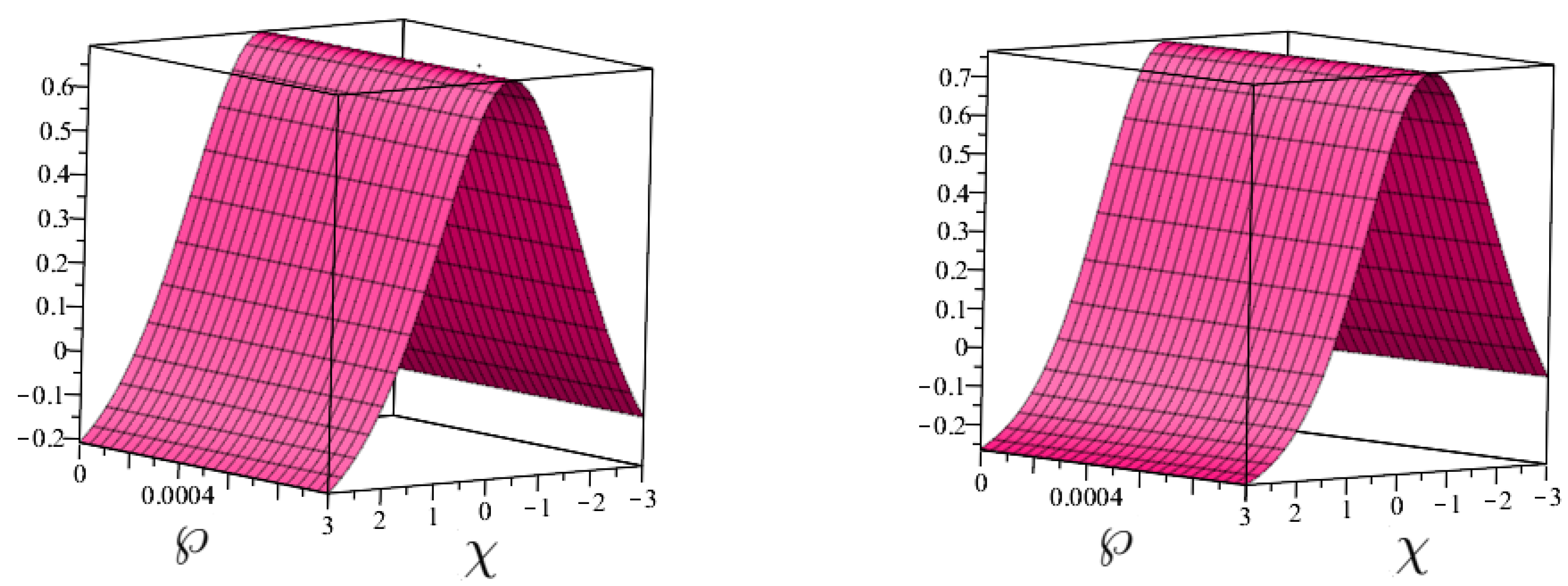
- Numerical Simulation Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dahmani, Z.; Anber, A.; Gouari, Y.; Kaid, M.; Jebril, I. Extension of a Method for Solving Nonlinear Evolution Equations Via Conformable Fractional Approach. In Proceedings of the International Conference on Information Technology, ICIT 2021-Proceedings, Amman, Jordan, 14–15 July 2021; pp. 38–42. [Google Scholar] [CrossRef]
- Hammad, M.A. Conformable Fractional Martingales and Some Convergence Theorems. Mathematics 2021, 10, 6. [Google Scholar] [CrossRef]
- Pitolli, F.; Sorgentone, C.; Pellegrino, E. Approximation of the Riesz-Caputo derivative by cubic splines. Algorithms 2022, 15, 69. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, M.H. A discretization approach for the nonlinear fractional logistic equation. Entropy 2020, 22, 1328. [Google Scholar] [CrossRef] [PubMed]
- Shymanskyi, V.; Sokolovskyy, Y. Variational Formulation of the Stress-Strain Problem in Capillary-Porous Materials with Fractal Structure. In Proceedings of the 2020 IEEE 15th International Conference on Computer Sciences and Information Technologies (CSIT), Zbarazh, Ukraine, 23–26 September 2020; Volume 1, pp. 1–4. [Google Scholar]
- Li, D.; Liu, J. Analysis of a fractional order time-dependent Sawada-Kotera equation. Commun. Nonlinear Sci. Numer. Simul. 2021, 78, 105183. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Liu, J. Exact Solutions and Stability of the seventh order time-fractional Sawada-Kotera equation. J. Differ. Equ. 2020, 288, 509–539. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S.; Zhang, L.; Pan, G.; Yu, J. Multi-UUV Maneuvering Counter-Game for Dynamic Target Scenario Based on Fractional-Order Recurrent Neural Network. IEEE Trans. Cybern. 2022, 1–14. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Liu, Y.; Liu, S.; Yang, B.; Yin, L.; Liu, M.; Zheng, W. User OCEAN Personality Model Construction Method Using a BP Neural Network. Electronics 2022, 11, 3022. [Google Scholar] [CrossRef]
- Chen, H.; Li, S. Multi-Sensor Fusion by CWT-PARAFAC-IPSO-SVM for Intelligent Mechanical Fault Diagnosis. Sensors 2022, 22, 3647. [Google Scholar] [CrossRef]
- Li, X.; Dong, Z.; Wang, L.; Niu, X.; Yamaguchi, H.; Li, D.; Yu, P. A magnetic field coupling fractional step lattice Boltzmann model for the complex interfacial behavior in magnetic multiphase flows. Appl. Math. Model. 2023, 117, 219–250. [Google Scholar] [CrossRef]
- Xie, X.; Wang, T.; Zhang, W. Existence of solutions for the (p,q)-Laplacian equation with nonlocal Choquard reaction. Appl. Math. Lett. 2023, 135, 108418. [Google Scholar] [CrossRef]
- Lu, S.; Liu, S.; Hou, P.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. Soft Tissue Feature Tracking Based on Deep Matching Network. Comput. Model. Eng. Sci. 2023, 136, 363–379. [Google Scholar] [CrossRef]
- Song, X.; Liu, J. Numerical analysis of the seventh order time-fractional Sawada-Kotera equation. Appl. Math. Comput. 2021, 393, 125155. [Google Scholar] [CrossRef]
- Jang, J.S.; Kim, H.K. The Seventh Order Time-Fractional Sawada-Kotera Equation and its Applications in Financial Engineering. Int. J. Eng. Technol. 2020, 12, 210–217. [Google Scholar] [CrossRef]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive control of time delay teleoperation system with uncertain dynamics. Front. Neurorobot. 2022, 16, 928863. [Google Scholar] [CrossRef]
- Sun, L.; Hou, J.; Xing, C.; Fang, Z. A Robust Hammerstein-Wiener Model Identification Method for Highly Nonlinear Systems. Processes 2022, 10, 2664. [Google Scholar] [CrossRef]
- Ismaeel, S.M.E.; Wazwaz, A.-M.; Tag-Eldin, E.; El-Tantawy, S.A. Simulation Studies on the Dissipative Modified Kawahara Solitons in a Complex Plasma. Symmetry 2023, 15, 57. [Google Scholar] [CrossRef]
- Alharbey, R.A.; Alrefae, W.R.; Malaikah, H.; Tag-Eldin, E.; El-Tantawy, S.A. Novel Approximate Analytical Solutions to the Nonplanar Modified Kawahara Equation and Modeling Nonlinear Structures in Electronegative Plasmas. Symmetry 2023, 15, 97. [Google Scholar] [CrossRef]
- Shohaib, M.; Masood, W.; Jahangir, R.; Siddiq, M.; Alkhateeb, S.A.; El-Tantawy, S.A. On the dynamics of nonlinear propagation and interaction of the modified KP solitons in multicomponent complex plasmas. J. Ocean. Eng. Sci. 2022, 7, 555–564. [Google Scholar] [CrossRef]
- Albalawi, W.; El-Tantawy, S.A.; Alkhateeb, S.A. The phase shift analysis of the colliding dissipative KdV solitons. J. Ocean. Eng. Sci. 2022, 7, 521–527. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; El-Sherif, L.S.; Bakry, A.M.; Alhejaili, W.; Wazwaz, A.-M. On the analytical approximations to the nonplanar damped Kawahara equation: Cnoidal and solitary waves and their energy. Phys. Fluids 2022, 34, 113103. [Google Scholar] [CrossRef]
- Alharthi, M.R.; Alharbey, R.A.; El-Tantawy, S.A. Novel analytical approximations to the nonplanar Kawahara equation and its plasma applications. Eur. Phys. J. Plus 2022, 137, 1172. [Google Scholar] [CrossRef]
- Chen, H.; Xiong, Y.; Li, S.; Song, Z.; Hu, Z.; Liu, F. Multi-Sensor Data Driven with PARAFAC-IPSO-PNN for Identification of Mechanical Nonstationary Multi-Fault Mode. Machines 2022, 10, 155. [Google Scholar] [CrossRef]
- Pomeau, Y.; Ramani, A.; Grammaticos, B. Structural stability of the Korteweg-de Vries solitons under a singular perturbation. Physica D 1988, 31, 127–134. [Google Scholar] [CrossRef]
- Arora, R.; Sharma, H. Application of HAM to seventh order KdV equations. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 131–138. [Google Scholar] [CrossRef]
- El-Sayed, S.M.; Kaya, D. An application of the ADM to seven-order Sawada-Kotara equations. Appl Math Comput. 2004, 157, 93–101. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Jena, S.K.; Sedighi, H.M. On the wave solutions of time-fractional Sawada-Kotera-Ito equation arising in shallow water. Math Methods Appl. Sci. 2021, 44, 583–592. [Google Scholar] [CrossRef]
- Akinyemi, L. q-Homotopy analysis method for solving the seventh-order time-fractional Lax’s Korteweg-de Vries and Sawada-Kotera equations. Comput Appl Math. 2019, 38, 191. [Google Scholar] [CrossRef]
- Yaşar, E.; Yildirim, Y.; Khalique, C.M. Lie symmetry analysis, conservation laws and exact solutions of the seventh-order time fractional Sawada-Kotera-Ito equation. Results Phys. 2016, 6, 322–328. [Google Scholar] [CrossRef]
- Al-Shawba, A.A.; Gepreel, K.A.; Abdullah, F.A.; Azmi, A. Abundant closed form solutions of the conformable time fractional Sawada-Kotera-Ito equation using (G’/G)-expansion method. Results Phys. 2018, 9, 337–343. [Google Scholar] [CrossRef]
- Guner, O. New exact solutions for the seventh-order time fractional Sawada-Kotera-Ito equation via various methods. Waves Random Complex Media 2020, 30, 441–457. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: New York, NY, USA, 1994. [Google Scholar]
- Adomian, G. Nonlinear Stochastic Operator Equations; Springer: New York, NY, USA, 1995. [Google Scholar]
- Wazwaz, A.-M. The Adomian Decomposition Method for Nonlinear Differential Equations. In Handbook of Analytical Solutions for Nonlinear Differential Equations; Springer: New York, NY, USA, 2011; pp. 1–24. [Google Scholar]
- Thompson, J. The Adomian Decomposition Method for Solving Nonlinear Differential Equations. J. Math. Anal. Appl. 2002, 270, 527–541. [Google Scholar]
- El-Metwally, M.A.; Ismail, M.A. The Adomian Decomposition Method for Solving Nonlinear Partial Differential Equations. J. Math. Anal. Appl. 2007, 330, 1232–1244. [Google Scholar]
- Aljahdaly, N.H.; El-Tantawy, S.A. Simulation study on nonlinear structures in nonlinear dispersive media. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 053117. [Google Scholar] [CrossRef] [PubMed]
- Aljahdaly, N.H.; El-Tantawy, S.A.; Wazwaz, A.-M.; Ashi, H.A. Adomian decomposition method for modelling the dissipative higher-order rogue waves in a superthermal collisional plasma. J. Taibah Univ. Sci. 2021, 15, 971–983. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Shan, S.A.; Mustafa, N.; Alshehri, M.H.; Duraihem, F.Z.; Turki, N.B. Homotopy perturbation and Adomian decomposition methods for modeling the nonplanar structures in a bi-ion ionospheric superthermal plasma. Eur. Phys. J. Plus 2021, 136, 561. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1993, 139, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Some new perturbation techniques of nonlinear problems. Int. J.-Non-Linear Mech. 1999, 34, 699–707. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method-a kind of non-linear analytical technique: Some examples. Int. J.-Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Kashkari, B.S.; El-Tantawy, S.A.; Salas, A.H.; El-Sherif, L.S. Homotopy perturbation method for studying dissipative nonplanar solitons in an electronegative complex plasma. Chaos Solitons Fractals 2020, 130, 109457. [Google Scholar] [CrossRef]
- Kashkari, B.S.; El-Tantawy, S.A. Homotopy perturbation method for modeling electrostatic structures in collisional plasmas. Eur. Phys. J. Plus 2021, 136, 121. [Google Scholar] [CrossRef]
- Almutlak, S.A.; El-Tantawy, S.A. On the approximate solutions of a damped nonplanar modified Korteweg–de Vries equation for studying dissipative cylindrical and spherical solitons in plasmas. Results Phys. 2021, 23, 104034. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alharthi, M.R. On the analytical and numerical solutions of the damped nonplanar Shamel Korteweg–de Vries Burgers equation for modeling nonlinear structures in strongly coupled dusty plasmas: Multistage homotopy perturbation method. Phys. Fluids 2021, 33, 043106. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method. Appl. Math. Comput. 2002, 135, 73–79. [Google Scholar]
- He, J.H. The homotopy perturbation method for nonlinear oscillators with weak damping. Nonlinear Dyn. 2005, 41, 245–252. [Google Scholar]
- He, J.H. Introduction to Homotopy Perturbation Method; World Scientific Publishing Company: Singapore, 2010. [Google Scholar]
- Zhang, Y.; He, J.H. A comparison of homotopy perturbation method, Adomian decomposition method, and variational iteration method. J. Appl. Math. 2010, 2010, 308628. [Google Scholar]
- Aboodh, K.S. Application of new transform “Aboodh Transform” to partial differential equations. Glob. J. Pure Appl. Math. 2014, 10, 249–254. [Google Scholar]
- Aboodh, K.S. Solving fourth order parabolic PDE with variable coefficients using Aboodh transform homotopy perturbation method. Pure Appl. Math. J. 2015, 4, 219–224. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Baleanu, D.; Alqurashi, M.M. New aspects of ZZ transform to fractional operators with Mittag-Leffler kernel. Front. Phys. 2020, 8, 352. [Google Scholar] [CrossRef]
- Riabi, L.; Belghaba, K.; Cherif, M.H.; Ziane, D. Homotopy perturbation method combined with ZZ transform to solve some nonlinear fractional differential equations. Int. J. Anal. Appl. 2019, 17, 406–419. [Google Scholar]
- Zafar, Z.U.A. Application of ZZ transform method on some fractional differential equations. Int. J. Adv. Eng. Global Technol. 2016, 4, 1355–1363. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasmin, H.; Abu Hammad, M.; Shah, R.; Alotaibi, B.M.; Ismaeel, S.M.E.; El-Tantawy, S.A. On the Solutions of the Fractional-Order Sawada–Kotera–Ito Equation and Modeling Nonlinear Structures in Fluid Mediums. Symmetry 2023, 15, 605. https://doi.org/10.3390/sym15030605
Yasmin H, Abu Hammad M, Shah R, Alotaibi BM, Ismaeel SME, El-Tantawy SA. On the Solutions of the Fractional-Order Sawada–Kotera–Ito Equation and Modeling Nonlinear Structures in Fluid Mediums. Symmetry. 2023; 15(3):605. https://doi.org/10.3390/sym15030605
Chicago/Turabian StyleYasmin, Humaira, Ma’mon Abu Hammad, Rasool Shah, Badriah M. Alotaibi, Sherif. M. E. Ismaeel, and Samir A. El-Tantawy. 2023. "On the Solutions of the Fractional-Order Sawada–Kotera–Ito Equation and Modeling Nonlinear Structures in Fluid Mediums" Symmetry 15, no. 3: 605. https://doi.org/10.3390/sym15030605
APA StyleYasmin, H., Abu Hammad, M., Shah, R., Alotaibi, B. M., Ismaeel, S. M. E., & El-Tantawy, S. A. (2023). On the Solutions of the Fractional-Order Sawada–Kotera–Ito Equation and Modeling Nonlinear Structures in Fluid Mediums. Symmetry, 15(3), 605. https://doi.org/10.3390/sym15030605






